Structures of dolomite at ultrahigh pressure and their influence on the deep carbon cycle

Abstract

Carbon-bearing solids, fluids, and melts in the Earth's deep interior may play an important role in the long-term carbon cycle. Here we apply synchrotron X-ray single crystal micro-diffraction techniques to identify and characterize the high-pressure polymorphs of dolomite. Dolomite-II, observed above 17 GPa, is triclinic, and its structure is topologically related to CaCO₃-II. It transforms above 35 GPa to dolomite-III, also triclinic, which features carbon in [3 + 1] coordination at the highest pressures investigated (60 GPa). The structure is therefore representative of an intermediate between the low-pressure carbonates and the predicted ultra-high pressure carbonates, with carbon in tetrahedral coordination. Dolomite-III does not decompose up to the melting point (2,600 K at 43 GPa) and its thermodynamic stability demonstrates that this complex phase can transport carbon to depths of at least up to 1,700 km. Dolomite-III, therefore, is a likely occurring phase in areas containing recycled crustal slabs, which are more oxidized and Ca-enriched than the primitive lower mantle. Indeed, these phases may play an important role as carbon carriers in the whole mantle carbon cycling. As such, they are expected to participate in the fundamental petrological processes which, through carbon-bearing fluids and carbonate melts, will return carbon back to the Earth’s surface.

Carbonates are key phases in the chemistry and dynamics of our planet (1–3). Mass balance considerations and direct observation of inclusions in diamonds (4–6) strongly support the idea that carbonates are stable phases within the Earth’s interior, especially in oxidized environments, such as deep subduction zones. While recent investigations on diamonds support the idea that the global carbon cycle extends to the deep Earth (7), the fate of Ca-rich carbonate with complex chemistry is still poorly known (8). Indeed, the knowledge of the transformation of carbonates in the mantle transition zone and lower mantle would constitute the missing link to complete our knowledge of the C-cycle.

It has long been known that carbonates are transferred from ocean reservoirs through subduction processes (9) and, depending on pressure, temperature, and composition, they undergo chemical variation and decomposition processes. In particular, at shallow depths, and depending on Ca content, carbonated eclogites contains coexisting assemblages of dolomite + magnesite or dolomite + calcite, or, at relatively high pressure, aragonite + magnesite (10). At higher pressures, experimental studies have shown that the double carbonate dolomite, CaMg(CO₃)₂, decomposes into the denser aragonite (CaCO₃) + magnesite (MgCO₃) phase assemblage at Earth’s mantle pressures and temperatures (11, 12). For this reason, much of the recent research effort has been dedicated into the investigation of the phase behavior of the pure Ca and Mg end-member components (13, 14). The presence of Fe, through the sideritic (FeCO₃) component, has been recognized to modify the phase relationships of carbonates at high pressures and temperatures significantly (15), and it stabilizes, at least at moderate pressures (16), ternary Ca-Mg-Fe carbonates. In more complex systems, representative of a carbonated subduction slab composition, the occurrence of the so-called Mg- or Mg-Fe-calcites is also observed systematically (17, 18). These phases quite clearly deviate from pure aragonite composition, and their compositional field extends from the calcite to the dolomite-ankerite join. These phases still have not received an appropriate structural interpretation, especially under the key conditions that are relevant to deep Earth processes.

It has been pointed out (19) that double carbonates, and in particular dolomite, could transform to a significantly denser phase at high pressure with a volume comparable, and therefore thermodynamically competitive, to the assemblage of aragonite + magnesite. In such a case, thermodynamic considerations would imply that the high-pressure form of dolomite is the stable phase. Furthermore, entropic contributions could prove to be significant and favor a single phase with dolomite composition, especially at high temperature when cation disorder processes are likely to be activated, whereby decreasing the free energy of the system. Yet all this possible speculation must be based on very robust structural data. It is obvious that in the absence of precise structure refinements, or even structure determinations, the estimation of density at high pressure could be erroneous and then lead to significant misinterpretation.

We report the crystal structures of two high-pressure polymorphs of dolomite observed above 17 GPa and 35 GPa. The occurrence of two polymorphs of dolomite in a similar pressure range has also been reported recently for a dolomite with a composition of Ca(Mg_0.92Fe_0.08)(CO₃)₂ (20). We investigated a more Fe-enriched sample, by means of single crystal synchrotron X-ray micro-diffraction, applying a newly developed setup, well-suited for structural determination at extreme pressures and after multiple phase transitions (21–23). Single crystals from natural Fe-rich dolomite, CaMg_0.6Fe_0.4(CO₃)₂, were compressed in diamond-anvil cells (DACs) up to 60 GPa in a quasi-hydrostatic Ne environment. The same material was also laser heated in DACs in several separate experiments at pressures up to 70 GPa and temperatures over 2500 K. The samples were analyzed in situ and after decompression by means of X-ray diffraction and Raman spectroscopy in order to determine the thermodynamic stability of representative structures at high pressures and temperatures (Table S1).

Results

Dolomite-II.

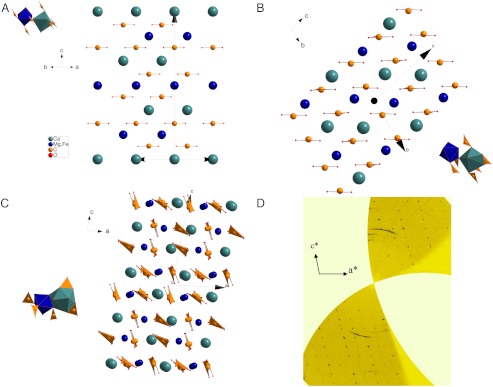
On compression at ambient temperature, the rhombohedral dolomite structure (Fig. 1A) was observed up to 17 GPa, in line with other very recent results (20). Above this pressure, the transition to a high pressure polymorph, CaMg_0.6Fe_0.4(CO₃)₂-II, is observed. All the diffraction peaks can be indexed with a triclinic unit cell, and no higher symmetry cell is detected from experimental unwarped precession-like images. We have solved the structure by a combination of the charge flipping algorithm and difference-Fourier analysis (24, 25) in order to locate all the atoms in the 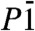space group. Dolomite-II contains 4 formula units in the primitive cell, with two independent divalent cation sites (Tables 1 and 2 and Table S2). From refined bond distances and cation occupancies, it is apparent that the original cation ordering between Ca and (Mg + Fe) of dolomite is maintained. The crystal structure remains characterized by co-planar CO₃ groups (Fig. 1B). Barring the different chemistries, the structures of dolomite-II and monoclinic calcite-II (26) are topologically identical (Fig. S1). The ordered substitution of (Mg_0.6Fe_0.4) over one half of the Ca²⁺ sites in calcite-II is sufficient on its own to reduce the overall symmetry of the unit cell to 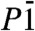and results in a dolomite-II-like lattice and site distribution. The main difference from the room pressure structure, and from the calcite-II structure, comes from a change in coordination polyhedra occupied by Ca, from coordination number (C.N.) 6 to 8, while the other coordination polyhedra remains in C.N. 6. No volume variation, within experimental accuracy, is observed upon transformation (Fig. 2A), an indication of the displacive nature of the transition.

Fig. 1.

(A) The crystal structure of dolomite and (B) dolomite-II. The main difference is in the coordination site of Ca (C.N 6 in dolomite and C.N 7/8 in dolomite-II. (C) The crystal structure of dolomite-III. In this structure, there are 8 nonequivalent cation sites, one half of which are occupied by Ca and the other by (Mg,Fe). The coordination environment is variable (C.N. 7–9), always with larger sites occupied by Ca and smaller by (Mg,Fe). (D) Unwarped reciprocal plane 0kl from experimental data collected at 56 GPa [Blue balls: Ca, green: (Mg,Fe), yellow: carbon].

Table 1.

Refined atomic coordinates of dolomite-II [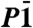, a = 4.7407(10) Å b = 5.3885(10) Å c = 6.7430(10) Å α = 101.42(1)° β = 89.27(1)° γ = 95.72(1)° V = 168.01(5) Å³; R% 5.8] and selected, and 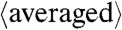, interatomic distances, from data collected at 34.4 GPa

Dolomite-II
Atoms	x	y	z	Uiso
Mg,Fe	−0.2000(10)	0.7473(7)	−0.2016(10)	0.0167(9)
Ca	−0.2418(10)	0.7926(6)	0.3039(8)	0.0167(8)
C1	0.300(4)	0.730(3)	−0.486(3)	0.013(2)
C2	0.262(4)	0.740(3)	−0.014(4)	0.018(2)
O1	0.143(3)	0.586(2)	−0.147(3)	0.0143(17)
O2	−0.129(3)	0.1226(19)	−0.123(2)	0.0206(19)
O3	0.546(3)	0.742(2)	0.026(3)	0.0201(18)
O4	0.493(3)	0.863(2)	−0.372(3)	0.0139(17)
O5	0.349(2)	0.5819(18)	−0.638(2)	0.0190(19)
O6	0.041(3)	0.791(2)	−0.447(3)	0.0169(18)

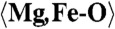	1.998 (x6)
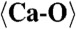	2.249 (x8)
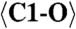	1.263 (x3)
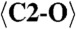	1.280 (x3)

Table 2.

Refined atomic coordinates of dolomite-III [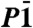, a = 6.2346(9) Å b = 9.3025(11) Å c = 10.9893(12) Å α = 75.89(1)° β = 81.05(1)° γ = 89.48(1)° V = 610.32(14) Å3; R% 6.8] and selected, and averaged interatomic distances, from data collected at 56.0 GPa

Dolomite-III
Atoms	x	y	z	Uiso
Ca1	0.1922(16)	0.6205(9)	0.1122(5)	0.0217(9)
Ca2	0.2305(15)	1.0713(8)	0.1045(5)	0.0191(9)
Ca3	−0.1562(16)	0.6793(9)	0.3897(5)	0.0185(9)
Ca4	−0.1442(16)	0.1796(9)	0.3877(5)	0.0116(8)
Mg,Fe1	0.7000(17)	0.5627(10)	0.1274(5)	0.0124(9)
Mg,Fe2	−0.2669(17)	1.1131(9)	0.1354(5)	0.0176(9)
Mg,Fe3	−0.6401(16)	0.6585(9)	0.3968(5)	0.0193(10)
Mg,Fe4	−0.3616(15)	0.8440(9)	0.6112(5)	0.0201(10)
O1	0.125(5)	0.800(3)	0.4001(17)	0.029(3)
O2	−0.028(5)	0.207(3)	0.1877(15)	0.021(3)
O3	−0.113(5)	0.712(3)	0.1803(16)	0.024(3)
O4	0.447(5)	0.882(3)	0.4780(15)	0.022(3)
O5	−0.142(5)	−0.073(3)	0.4513(17)	0.029(3)
O6	−0.433(5)	0.606(3)	0.5237(14)	0.017(2)
O7	0.110(5)	0.374(3)	0.0292(17)	0.023(3)
O8	−0.059(4)	1.133(3)	−0.0210(15)	0.022(3)
O9	−0.418(5)	1.052(3)	0.3132(15)	0.016(2)
O10	−0.593(4)	0.684(2)	0.6887(14)	0.008(2)
O11	−0.054(5)	0.929(3)	0.2045(16)	0.021(3)
O12	−0.316(7)	1.314(4)	0.084(2)	0.042(4)
O13	0.606(6)	0.805(3)	0.3179(18)	0.024(3)
O14	0.415(6)	0.464(3)	0.124(2)	0.039(4)
O15	−0.856(4)	0.564(3)	0.3216(14)	0.013(2)
O16	0.296(5)	0.821(3)	0.1833(16)	0.026(3)
O17	0.140(5)	0.042(3)	0.3267(15)	0.023(3)
O18	0.562(4)	0.751(3)	0.0583(15)	0.019(2)
O19	0.940(5)	0.442(3)	0.1930(14)	0.012(2)
O20	−0.440(5)	0.973(3)	0.0898(16)	0.027(3)
O21	−0.163(7)	0.695(4)	0.611(2)	0.039(4)
O22	−0.874(4)	0.570(2)	0.5598(13)	0.011(2)
O23	−0.575(5)	0.444(3)	0.7002(15)	0.018(2)
O24	−0.625(6)	1.221(3)	0.1847(18)	0.037(3)
C1	−0.015(6)	0.353(3)	0.128(2)	0.009(3)
C2	−0.520(7)	0.573(4)	0.639(2)	0.017(4)
C3	0.544(7)	0.918(4)	0.366(2)	0.020(4)
C4	0.049(7)	−0.075(4)	0.389(2)	0.017(4)
C5	0.475(7)	0.849(4)	0.111(2)	0.022(4)
C6	−0.064(10)	0.569(6)	0.616(3)	0.043(7)
C7	−0.536(6)	1.340(4)	0.129(2)	0.011(4)
C8	−0.044(7)	0.835(4)	0.139(2)	0.022(4)

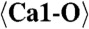	2.215 (x7)		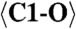1.262 (x3)		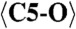1.251 (x3)
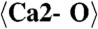	2.301 (x9)	C1-O12	2.067	C5-O20	2.451
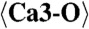	2.276 (x9)		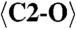1.279 (x3)		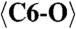1.293 (x3)
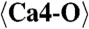	2.308 (x9)	C2-O21	2.449	C6-O19	2.322
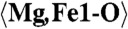	2.048 (x7)		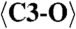1.273 (x3)		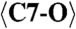1.177 (x3)
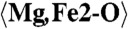	2.049 (x7)	C3-O5	2.312	C7-O10	2.234
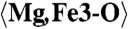	2.010 (x6)		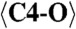2.010 (x6)		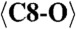1.251 (x3)
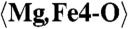	1.999 (x7)	C4-O11	2.216	C8-O16	2.24

Fig. 2.

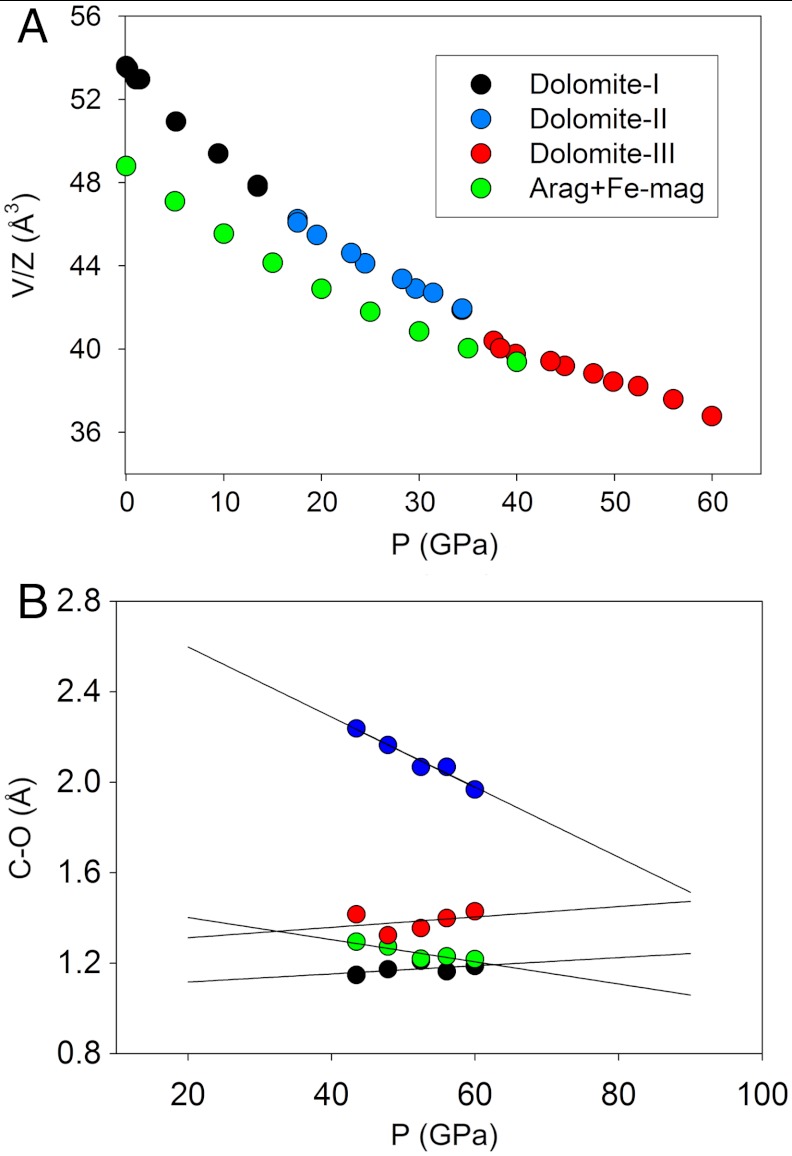
(A) Pressure dependence of volume per formula unit of CaMg_0.6Fe_0.4(CO₃)₂ dolomite (black), dolomite-II (blue) and dolomite-III (red) as investigated by single crystal X-ray diffraction studies at ambient temperature. For comparison, the volume of a isochemical mixture of aragonite and the (Mg,Fe)CO₃ phase in the magnesite-siderite solid-solution is also reported (green). Data are taken (23,35,36) (B) Evolution of C─O distances (for selected carbon atom) in dolomite-III structure as function of pressure, and linear extrapolation over an extended pressure range.

Dolomite-III.

CaMg_0.6Fe_0.4(CO₃)₂-II is observed to pressures of up to 35 GPa, whereupon a phase transition is observed. The diffraction peaks of the CaMg_0.6Fe_0.4(CO₃)₂-III phase were necessarily indexed with a larger triclinic cell, and no higher symmetry lattice can be used to index all the single crystal diffraction spots. The observed volume variation on transition is about 3%, an indication of a probable first order transition. The structure has also been solved by the charge flipping method and Fourier analysis. CaMg_0.6Fe_0.4(CO₃)₂-III, 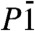(Fig. 1C), has 8 dolomite formula units and 80 atoms in the unit cell. The crystal structures of the two high-pressure polymorphs are different, and CaMg_0.6Fe_0.4(CO₃)₂-III could not be considered a simple distortion of dolomite-II. Significantly, the CO₃ groups are no longer co-planar, and some of them edge-share with the large Ca and Fe cation coordination polyhedra (C.N. 7–9). It can be further noticed that a few of the C atoms in the structure are actually displaced from the plane defined by the three nearest oxygens. Some of the C atoms are also present at a next-nearest O distance of C…O = 2.0–2.2 Å (at 55 GPa), and then they must be considered as contributing to the bonding environment of these displaced C sites. This feature is more evident if we consider the evolution and the extrapolation of the C coordination at higher pressures (Fig. 2B). In the structure there are 8 nonequivalent C sites, each of them presenting a slightly different 4th C─O distance (Table 1 and Table S3). We can, therefore, speculate about the possible coexistence in the structure, within a large pressure range, of both triangular and tetrahedral coordination for C atoms. It is worth noting that such features are not unusual and are present in stable, high-pressure polymorphs of borates, in the REE(BO₃) phases in particular (27, 28). The presence of Fe in the structure can reduce the cation-size misfit between Ca and Mg, as in pure dolomite, and may play an important role in stabilizing high-pressure polymorphs over a wider P and T range.

The presence of nonplanar CO₃ groups and the [3 + 1] quasi-tetrahedral coordination of carbon atoms, show that CaMg_0.6Fe_0.4(CO₃)₂-III is developing features expected for ultrahigh-pressure carbonates, predicted by computational methods (14, 29–31). These results can, therefore, confirm the crystallochemical trend towards an increased C coordination number in carbonates at high pressure. Moreover, the extrapolated variation of the determined C─O bond lengths as function of pressure indicates that, above 80–90 GPa, regular tetrahedral coordination will form, in line with the predicted pressure for this observation of this structural feature (14, 29, 30).

Discussion

Relationship with Previous Studies.

In order to properly describe the high-pressure evolution of dolomite structure, and to appropriately compare our structure determination with previous reported works (19, 20) (Table S4), it is useful to also refer to the high-pressure polymorphism observed in CaCO₃ (23, 26, 32). The crystal structures of the high-pressure polymorphs CaCO₃, CaCO₃-II and CaCO₃-III are all based on the presence of triangular CO₃ groups. While in CaCO₃ and CaCO₃-II the CO₃ groups are co-planar in the structure, CaCO₃-III presents a significant modification of the structure, with the CO₃ groups no longer parallel. The transition CaCO₃ to CaCO₃-II is displacive, and both structures are closely related by a minimal distortion. The transition CaCO₃-II-CaCO₃-III, on the contrary, presents a volume discontinuity, CO₃ group tilting and strong Ca coordination polyhedra distortion (23), that indicate a first order character of the transition. The newly determined structures of Ca(Mg_0.6Fe_0.4)(CO₃)₂-II and Ca(Mg_0.6Fe_0.4)(CO₃)₂-III present features that are comparable, respectively, to the CaCO₃-II and CaCO₃-III structures: Ca(Mg_0.6Fe_0.4)(CO₃)₂-II (dolomite-II) is a distortion of the dolomite structure, but it still possesses parallel CO₃ triangular groups; Ca(Mg_0.6Fe_0.4)(CO₃)₂-III (dolomite-III) has, on the contrary, tilted CO₃ molecules and nonequivalent cation coordination polyhedra. The clear difference between CaCO₃-III and Ca(Mg_0.6Fe_0.4)(CO₃)₂-III, is the presence of higher coordination (3 + 1) of some carbon atoms in dolomite-III. This feature is related to the higher pressure of occurrence of Ca(Mg_0.6Fe_0.4)(CO₃)₂-III compared to CaCO₃-III.

The diffraction data reported in ref. (20) for the Ca(Mg_0.92Fe_0.08)(CO₃)₂-II phase are related to dolomite-II. The reported high increase of density (15%) upon transition from Ca(Mg_0.92Fe_0.08)(CO₃)₂-I to Ca(Mg_0.92Fe_0.08)(CO₃)₂-II is based on the assumption that the orthorhombic unit cell contains 3 formula units (Z = 3). However, it is possible to derive a different formula unit content, based on our structure determination. There is, in fact, a common subcell between orthorhombic lattice reported in ref. (20) and the currently reported triclinic lattice. Matrix reduction of the orthorhombic lattice in ref. (20) to the common sublattice allows us to specify exactly the actual number of formula units, Z = 8/3, in a cell with the dimensions proposed in ref. (20). The number of formula units per volume is then used to obtain a corrected density or Z-normalized volume (SI Text). Furthermore, the powder pattern reported in ref. (20) can also be indexed directly with a CaCO₃-II like lattice. These considerations indicate that Ca(Mg_0.92Fe_0.08)(CO₃)₂-II, of ref. (20), presents a very small, if any, volume discontinuity with Ca(Mg_0.92Fe_0.08)(CO₃)₂-I, consistent with a second order displacive transition.

The dolomite-III structure has been probably observed in pure dolomite (19). Spectroscopic and diffraction signatures, together with large hysteresis observed, are in fact consistent with a first order transition and to the features observed for CaCO₃-III polymorph. Also the magnitude of volume discontinuity is consistent with the volume change reported in this current work between extrapolated dolomite volume and dolomite-III. The different pressure of occurrence may be related to different composition and experimental procedures. The dolomite-II phase, coming from a second order group-subgroup relation, may have been not readily observable in ref. (19).

The diffraction data for the Ca(Mg_0.92Fe_0.08)(CO₃)₂-III phase reported in ref. (20) do not appear consistent with the dolomite-III structure presented here. Without a structural model, the density estimation for Ca(Mg_0.92Fe_0.08)(CO₃)₂-III may be open to reconsideration. With the same Z-correction identified for Ca(Mg_0.92Fe_0.08)(CO₃)₂-II, the density of Ca(Mg_0.92Fe_0.08)(CO₃)₂-III is consistent with our results, as well as those data from (19), which, we suspect, is dolomite-III. However, the Ca(Mg_0.92Fe_0.08)(CO₃)₂-III phase reported in ref. (20) could also constitute a different polymorph, since the composition is different. Structural investigations of the high-pressure polymorphs of CaCO₃ (23), for example, suggest that CaCO₃-III can form closely related, but crystallographically different, structures. The extent to which this occurs in dolomite as a function of composition remains to be determined.

Stability of Fe-Bearing Ca, Mg-Carbonate at Earth’s Lower Mantle Conditions.

The results reported in the current work identify an unexpected complexity in carbonate polymorphism, which suggest that the thermodynamic phase stability of Fe-bearing Ca,Mg- carbonates must be also reinvestigated.

Dolomite is known to undergo a decomposition into aragonite + magnesite above 2 GPa at moderate temperature, and the field of coexistence opens towards high temperature with increasing pressure. The assemblage aragonite + magnesite is considerably denser than dolomite. As there is no significant change of density upon transition from dolomite to dolomite-II (Fig. 2A), it can therefore be expected that, even at high temperature, a mixture of the pure end-members will remain thermodynamically favored. This scenario, however, changes drastically when the dolomite-III structure is stabilized. In fact the density of this phase is demonstrably comparable to the density of the mixture aragonite + magnesite (also taking into account the FeCO₃ component), and that the entropy of dolomite-III must be expected to play a major role, especially at high temperature, where competing stabilities of the two-phase mixture and dolomite-III will be influenced by the larger number of atoms, the low symmetry, and the number of independent cation sites. The configurational and vibrational entropy will be therefore increased and, with comparable densities under these conditions, dolomite-III is stabilized over the aragonite-magnesite mixture.

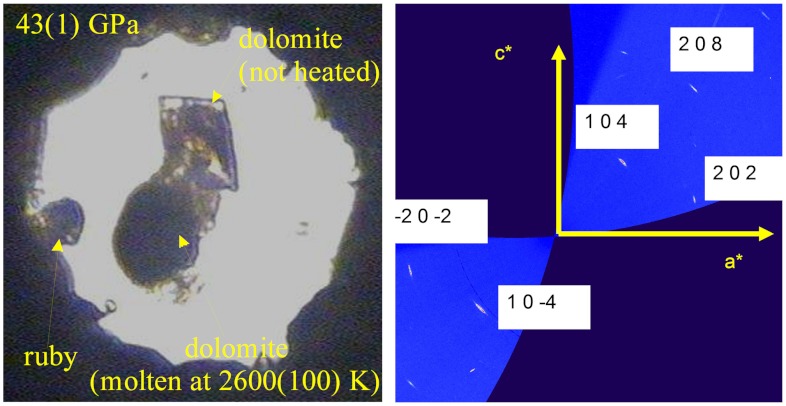
To illustrate the stability of dolomite-III at Earth’s lower mantle conditions, we performed two different experiments. In the first one, we compressed a single crystal of dolomite to 43(1) GPa, in order to transform the starting material into dolomite-III, and then heated the sample to 2600(100) K (see Materials and Methods). The sample reached the melting point, as evidenced by the formation of a particle with spherical shape (Fig. 3A) and the absence of diffraction spots during in situ data collection. After temperature quench, we observed the crystallization of a single crystal domain, which transformed, after pressure quench, to an indexable single crystal of dolomite with no indication of decomposition evident (Fig. 3B). The second experiment has been conducted using Raman spectroscopy to detect phase stability, or decomposition, of dolomite along a lower mantle geotherm (Fig. S2). In separate loadings, we compressed single crystals of dolomite to several pressures, then laser-heated to 2,000–2,400 K (Fig. S3). On quenching, we observed decomposition of all the samples laser-heated at pressures below approximately 35 GPa. On the contrary, all the samples heated at higher pressures, back-transformed into the original dolomite structure, revealing that the unquenchable dolomite-III structure is indeed a stable high-pressure, high-temperature polymorph. Thus, we have this important primary evidence that single-phase complex carbonates with intermediate composition in the dolomite-ankerite binary join do not decompose at lower mantle conditions and may constitute fundamental accessory phases in lower mantle. Our results are also in agreement with experimental results obtained in a Fe-poor dolomite system (20).

Fig. 3.

(A) An in diamond anvil cell micrograph of the Fe-dolomite samples used for high-pressure and high-temperature experiments, showing a rhomb-shaped crystal (not heated and used only for laser alignment) and, below it, the sample used for X-ray data collection after heating up to the melting point (2600 K at 43 GPa). (B) Unwarped reciprocal space h0l after pressure release, revealing the nature of the back-transformation of the high pressure polymorph to single crystal dolomite. Despite that the mosaicity increases significantly, the peaks are still indexed with the rhombohedral cell.

Clearly, the occurrence of carbonates depends not only on the thermodynamic stability of a discrete and isolated phase, but also on the bulk composition of the petrologic system. In carbonated-primitive lower mantle, polymorph(s) of (Mg,Fe)CO₃ are likely the only possible occurring carbonate phase(s) and their actual presence will depend, mostly, on red-ox conditions (3, 33). On the other hand, in subduction processes, so important for the transfer of C into the upper mantle, slabs are Ca-enriched and the environment is more oxidized than the surrounding mantle. In these petrologic systems, Ca-bearing carbonates can be stabilized.

Yet, the coexistence of CaCO₃ + MgCO₃ phase assemblages requires that CaCO₃ must be thermodynamically stable in the basaltic/eclogitic system. In fact, any reaction between carbonates and silicate phases (CaCO₃ + SiO₂ = CaSiO₃(pv) + CO₂) would lead to a pristine decarbonation. The stability of dolomite-III, on the contrary, is expected to promote the incorporation of Ca in a carbonate phase, with the fundamental consequence of increasing the possibility of carbon storage and transport in the subducting plate. The fate of carbonate is still poorly understood (8, 34), yet our study demonstrates that, at lower mantle conditions, a single phase with intermediate composition in the ternary carbonate system is actually favored with respect to the end-member decomposition mixture. This, taken together with the results on relatively Fe-poor (20) compositions, shows evidence of the possible wide chemical variation in Fe-dolomites at lower mantle pressures and temperatures. The recent solution of the CaCO₃-III structure (23), which possess a structure similar to that of dolomite-III, suggests the possibility that a continuous solid solution from CaCO₃ end member to the dolomite-ankerite compositional join can, and is likely, to establish in the Earth’s mantle. Such a complex composition would adopt the dolomite-III structure and would constitute the primary C-carrier in subduction processes, through the mantle transition zone and into the lower mantle.

Stagnant slabs below the transition zone are expected to participate in different fundamental petrological and geochemical processes, such as carbonatitic melt formation and red-ox reactions (7, 33). In this scenario the dolomite-III polymorph and related structures are of fundamental importance for understanding all the chemical reactions occurring in lower mantle that determine carbon residence time and affect transfer process between the different geochemical reservoirs involved in the deep global carbon geochemical cycle, which has been also shown to extend to the whole mantle (7).

Materials and Methods

Natural samples of Fe-dolomite have been collected near the hamlet Chachatier, Vaulnaveys, an ancient mining area close to Vizille (France). Elemental analysis, lattice parameters, and refined site occupancies are coincident on a mineral composition of CaMg_0.6Fe_0.4(CO₃)₂. High-pressure diffraction experiments have been performed at ID09A synchrotron beamline (ESRF) using parallel monochromatic X-Ray beam (E = 30 keV, λ = 0.413 Å) focused to 15 × 10 μm² on the sample. We used a membrane-driven high-pressure cell equipped with Boehler-Almax seats and diamond anvil design, allowing an opening cone of 60°. Single-crystal data have been collected by a vertical-acting ω-axis rotation, with an integrated step scan of 0.5° and a counting time of 1 s per frame. Diffraction intensities have been recorded with a Mar555 flat-panel detector. Diffraction data have been processed and analyzed with CrysalisRed-171.32.29, Superflip, and Jana2006 software. Experimental data have not been corrected for absorption, because of the high energy of the X-ray beam. Frames have been rescaled using Friedel diffraction pairs, in order to correct for variable diffracting volume as function of ω position. Structure solutions have been performed with a combination of charge flipping algorithm (to derive the position of the heavier atoms) and Fourier difference analysis, in order to locate all the remaining atoms in the structure. To solve crystal structure of dolomite-III, we merged two different datasets, collected on two crystals (with different crystallographic orientation) in the same DAC at the same pressure, in order to increase reciprocal space coverage. We succeeded in having about 50% of coverage up to 0.8 Å resolution. Crystal structure refinements have been performed without any crystallographic constraint. High-pressure and high-temperature experiments have been performed with the portable laser heating system that has been designed and developed specifically for single-crystal diffraction studies (21). Raman spectroscopy measurements were conducted at BGI using Dilor XY system (Ar-laser with an excitation wavelength of 514 nm, x50 objective and 2 cm^-1 resolution).