Electron spin resonance of nitrogen-vacancy centers in optically trapped nanodiamonds

Abstract

Using an optical tweezers apparatus, we demonstrate three-dimensional control of nanodiamonds in solution with simultaneous readout of ground-state electron-spin resonance (ESR) transitions in an ensemble of diamond nitrogen-vacancy color centers. Despite the motion and random orientation of nitrogen-vacancy centers suspended in the optical trap, we observe distinct peaks in the measured ESR spectra qualitatively similar to the same measurement in bulk. Accounting for the random dynamics, we model the ESR spectra observed in an externally applied magnetic field to enable dc magnetometry in solution. We estimate the dc magnetic field sensitivity based on variations in ESR line shapes to be approximately 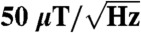. This technique may provide a pathway for spin-based magnetic, electric, and thermal sensing in fluidic environments and biophysical systems inaccessible to existing scanning probe techniques.

The room temperature quantum coherence and optical addressability of negatively charged nitrogen-vacancy (NV) color center spins in diamond (1) make NV centers particularly effective for a variety of sensing applications. The spin-dependent fluorescent readout of ground-state electron-spin resonance (ESR) transitions in NV centers has been used for single-spin magnetic (2–11), electric (12), and thermal (13) metrology at the nanoscale. The photostability and biocompatibility of fluorescent NV centers within nanodiamonds (14–18) have also permitted quantum control of NV centers within living cells (19), pointing to potential applications of sensing, tracking, and tagging in submicron biophysical systems. While techniques utilizing scanning probe tips have been the focus of intensive efforts for precise spatial control of nanodiamonds (2–4, 9–11, 20–22), this approach is less suitable within complex environments such as microfluidic channels or the interiors of biological cells.

Laser-based optical trapping is another method of precise nanopositioning, but it occurs without physical contact. Optical tweezers utilize tightly focused light to noninvasively trap and move small dielectric particles in three dimensions (23, 24). This powerful and biocompatible technique has allowed investigation of molecular motors (25), cell-sorting of a population of Eschericha coli based on single-cell viability (26), and even the observation of single-base-pair stepping (3.7 Å) of RNA polymerase along DNA (27). With ultrastable, dual-beam optical tweezers achieving repeatable displacements at the nanometer scale and below (27, 28), the prospect of combining optical tweezers with quantum-based sensors is particularly attractive for biosensing.

We demonstrate a biocompatible approach to scanning nanodiamond magnetometry in solution using a single-beam optical tweezers apparatus. The optical trap uses the radiation pressure of a focused infrared laser beam to attract and hold an ensemble of diamond nanoparticles at the focus, while a second confocal green laser optically excites the embedded NV centers. The spin-dependence of the NV center’s luminescence, together with a nearby microwave antenna, allow us to perform optically detected ESR measurements with simultaneous three-dimensional control in solution. We develop a model of the observed ESR spectra based on the ground-state Hamiltonian that accounts for the random motion of NV centers in the trap and incorporates the orientation-dependent absorption and luminescence collection efficiency. Using this model, we are able to infer the magnetic field experienced by the ensemble of NV centers and show an estimated magnetic sensitivity of approximately .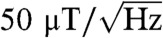

Results and Discussion

Optically Trapping Nanodiamonds.

We study nanodiamond ensembles in a home-built confocal microscope that combines optical trapping, NV-center optical excitation, and fluorescence detection. The optical trapping is performed with a 1,064 nm continuous wave laser while a separate 532 nm continuous wave laser is used for optical excitation of the NV centers. Both beams are tightly focused using an oil-immersion objective (NA = 1.3). A dichroic mirror and optical filter are used to collect the red-shifted fluorescence from the phonon side band of the NV center, while a separate notch filter is used to remove the laser scatter from the trapping laser. The filtered light is focused into a single-photon counting avalanche photodiode, whose counts are read out with a data acquisition card (see SI Text for details). All measurements are performed at room temperature.

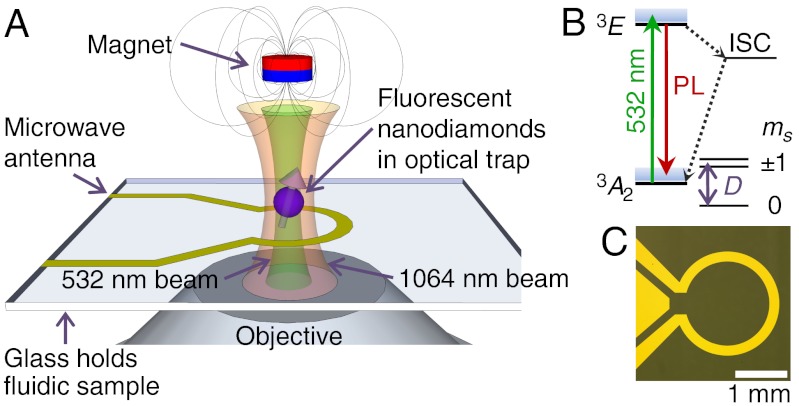
The measurement geometry at the objective is shown in Fig. 1A. A drop of aqueous nanodiamond solution (see Materials and Methods for details) is placed on a glass coverslip and brought to the focus of the objective. The relative position of the sample with respect to the beam is adjusted with an XYZ piezoelectric stage. The sequence of micrographs in Fig. 2 shows an ensemble of nanodiamonds held by the optical trap near the edge of a microwave antenna patterned lithographically on the coverslip. These images demonstrate lateral and axial control of the particles in suspension.

Fig. 1.

(A) Schematic of nanodiamond optical trapping, photoexcitation, and luminescence detection at the focus of the objective. The magnetic field is applied externally, along the axis of the objective. The microwave antenna and glass coverslip are also shown. (B) Energy level diagram of the diamond NV center. The 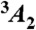ground state is expanded to show the spin sublevels split by the zero-field splitting, D. The spin system is optically excited by 532 nm laser into the excited state (³E), where it has a spin-dependent probability of either returning to the ground state with a red-shifted photoluminescence (PL) or decaying nonradiatively through the intersystem crossing (ISC). (C) Micrograph of the 50-Ω-impedance-matched antenna that drives coherent transitions between spin states.

Fig. 2.

Spatial control of optically trapped nanodiamonds near the (black) microwave antenna (individual frames from Movie S1). (A–B) The antenna is brought into focus, moving axially by 4.2 μm with respect to the trapped nanodiamonds from A to B. An arrow indicates the position of the optical trap, with nanodiamonds visible in both frames. (C) The antenna is moved laterally by 8.75 μm while the nanodiamonds remain trapped. (D) The trapping laser is blocked, releasing the nanodiamonds and allowing Brownian motion to scatter them away from the focus.

ESR Experiments with Trapped Nanodiamonds.

The optical spin polarization and spin-dependent photoluminescence intensity, I_PL, of NV centers enable optically detected ESR measurements. When combined with electromagnetically and thermally sensitive spin states, optically detected ESR permits the measurement of the local electric, magnetic, or thermal environment. The NV center defect in diamond consists of a substitutional nitrogen atom adjacent to a vacancy in the diamond lattice. The negatively charged NV center’s unperturbed electronic energy level structure, shown in Fig. 1B, consists of a ground-state spin triplet with lowest-energy spin sublevel m_s = 0 along with two m_s =  ± 1 spin sublevels (29, 30), which are nominally degenerate at zero magnetic field and energetically higher than m_s = 0 by the crystal field splitting, D = 2.87 GHz. The energy of the NV center spin system is magnetically sensitive, much like that of its classical analogue, the magnetic dipole. Specifically, a magnetic field B will shift the energy of the NV center’s spin states according to the ground-state Hamiltonian,

[1]

where g = 2 is the electronic g-factor, μ_B is the Bohr magneton, and 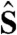is the electronic spin-1 operator. The measurement of spin energy eigenvalues in the presence of a magnetic field is the experimental basis for magnetic sensing using NV centers. The optical readout of the spin state is possible because the m_s =  ± 1 states have a higher probability of a nonradiative transition via an intersystem crossing (ISC) through a series of singlets (13, 31, 32), so I_PL is lower in these states than in the brighter m_s = 0 state. Control of the spin state is achieved with a combination of optical and microwave pumping: Optical excitation initializes the system into the m_s = 0 state through the same ISC, while a microwave field resonant with the energy splitting between the m_s = 0 and the m_s = +1 or -1 states will coherently rotate the spin into a superposition of the spin sublevels, which we detect as a darker I_PL. In order to apply microwave fields, we designed a microwave antenna that is lithographically patterned on the glass coverslip and impedance matched near 2.87 GHz to optimize power transmission and reduce heating, shown in Fig. 1C. In continuous wave ESR measurements, the photoluminescence intensity (I_PL) is read out under the continuous application of both the 532 nm laser and microwave fields, leading to resonances in the observed intensity as the applied microwave field is swept in frequency across the spin sublevel transitions. The photoluminescence contrast measured between spin states can exceed 20% in fixed nanodiamonds (see SI Text).

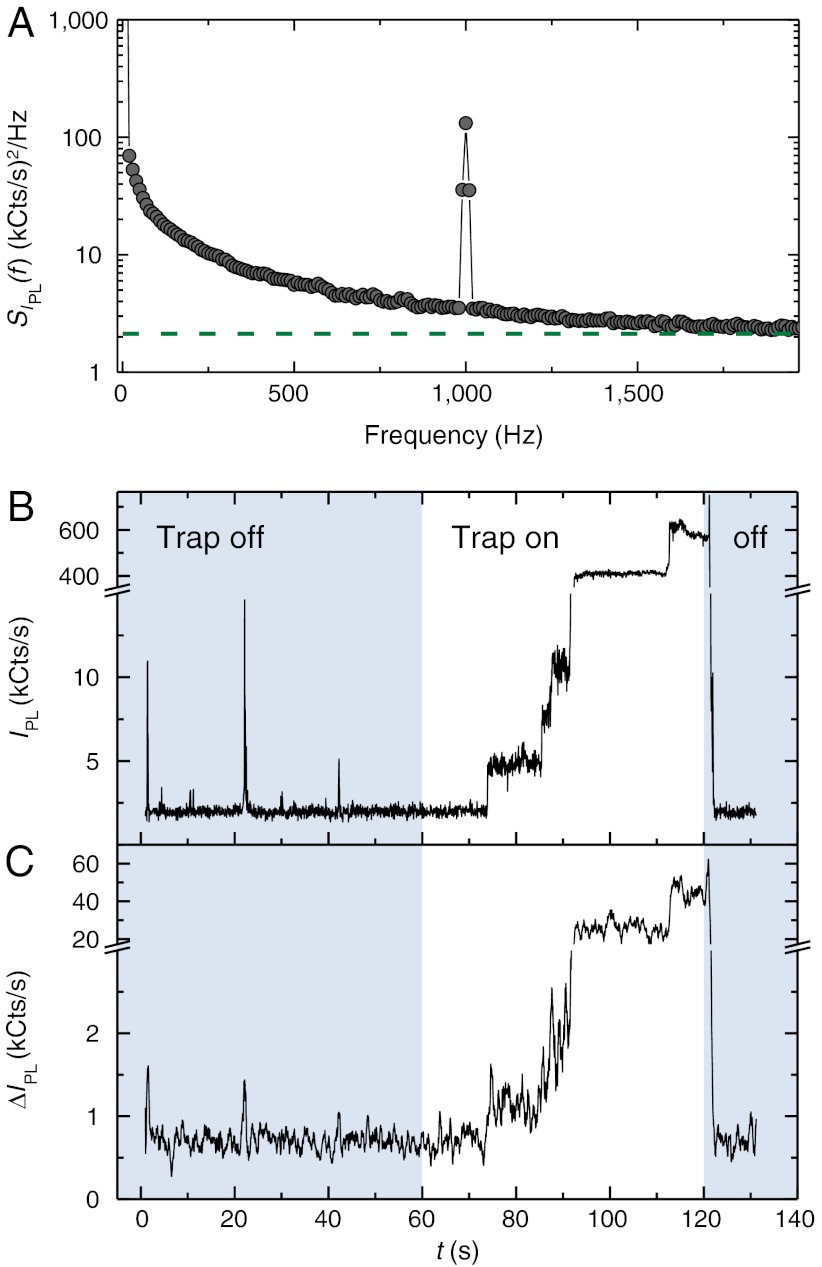
Random fluctuations in the photoluminescence of optically trapped fluorescent nanodiamonds present experimental challenges in measuring the ESR contrast. The Brownian motion in solution, collisions between nanoparticles, and the entry and exit of nanodiamonds from the optical trap contribute to a large, low-frequency noise component in the observed I_PL. “Blinking,” attributed to charge instabilities related to surface effects (33) may augment the observed fluorescence fluctuations. To a lesser extent, spin bath effects (34) also contribute to noise. To increase the signal-to-noise ratio during ESR measurements, we use commercial nanodiamonds that have been He⁺ irradiated to create vacancies and subsequently annealed to form approximately 500 NV centers per ∼100 nm diameter nanodiamond. Additionally, by performing amplitude modulation of the applied microwaves with a software-based photon-counting lock-in technique (35, 36), we improve the signal-to-noise ratio of the experiment by more than a factor of ten (see SI Text for further details). In this way, ESR dips in I_PL are converted to peaks in the differential luminescence ΔI_PL. Fig. 3A shows the power spectral density of I_PL for trapped nanodiamonds, displaying both the low-frequency noise and the NV ESR contrast response from resonant microwaves that are amplitude modulated at 1 kHz. Fig. 3 B and C shows the measured I_PL and contrast ΔI_PL before and after turning on the trapping beam. As the trapping beam remains on, fluorescent nanodiamonds stochastically enter the trap and cause I_PL to increase in discrete steps, with coincident rises in ΔI_PL indicating the presence of NV centers. When the trapping beam is turned off, the nanodiamonds scatter out of the trap from Brownian motion, causing the luminescence to cease. We typically observe the contrast ΔI_PL/I_PL at zero field to be near 10% at most; this is smaller than the contrast observed in bulk, which may be a consequence, in part, of non-NV background fluorescence in the nanoparticles. Ongoing research in the production of high purity nanodiamonds has the potential to significantly reduce these complications.

Fig. 3.

(A) Bimodal power spectral density S_IPL(f) of the luminescence with on-resonant microwaves at frequency f_MW = 2.87 GHz and amplitude-modulation frequency f_AM = 1 kHz. The peak at 1 kHz corresponds to the NV response to the amplitude-modulated carrier signal. The green dashed line shows the expected shot noise floor for the bimodal power spectral density, S_IPL(f) = I_PL = 2.1 MHz. The noise at f_AM = 1 kHz is higher than the expected floor, indicating that the measurement is not shot-noise limited. The power spectral density was calculated from I_PL data taken for 100 ms, our typical lock-in time; the average of 1,000 sets of data is shown. (B) Time trace of I_PL showing discrete steps of increasing photoluminescence as clusters of NV centers enter the optical trap with the green excitation laser on. The trapping laser is initially blocked (blue shaded times). The trapping laser is unblocked at time t = 60 s, and I_PL remains low, indicating an empty trap, until the first discrete step at t ∼ 75 s. At time t ∼ 120 s, the trapping laser is blocked to release the particles from the trap, with I_PL dropping commensurately. (C) The coincident ESR response of resonant microwaves, applied at f_MW = 2.87 GHz, indicates that the fluorescent particles in the trap are indeed nanodiamonds that contain NV centers. Data in (C) are smoothed.

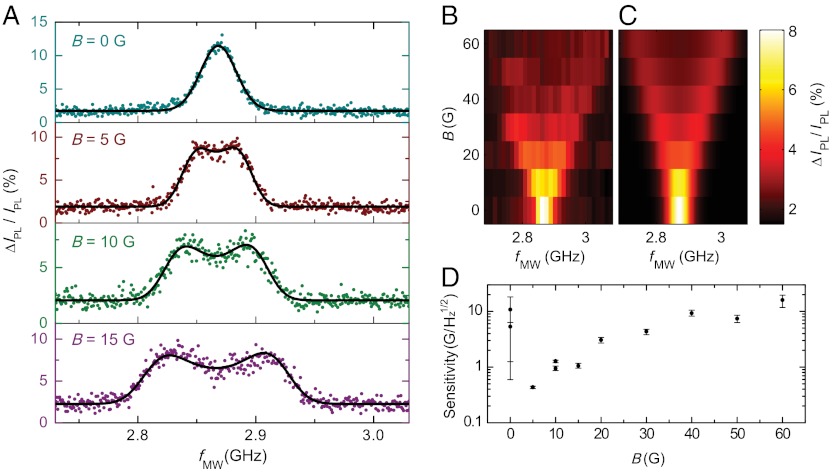
Although the measured ESR signal is effectively an average over ensembles of randomly oriented, mobile NV centers, ESR spectra (Fig. 4A) at low magnetic fields retain qualitative similarities to measurements of aligned NV centers in bulk diamond: The spectra exhibit two distinct peaks that shift approximately linearly (about 2.5 MHz/G) as a magnetic field is applied. However, unlike aligned NVs, the spectral peaks broaden with increased magnetic field. To understand the lineshape and magnetic field dependence of the observed spectra, we develop a model consisting of a statistical average over all possible NV center orientations with respect to a fixed magnetic field, incorporating the directional dependence of the transition frequencies from Eq. 1 and the anisotropic excitation and collection efficiencies of our confocal microscope. In this model, the orientation of the NV center’s symmetry axis, relative to the magnetic field and optical axis, determines its ESR resonance frequency and contribution to the overall spectrum: A perpendicular orientation yields a minimal contrast contribution and frequency shift, while a parallel NV center gives a maximal contribution and shift (2.80 MHz/G). Summing over an isotropic distribution of NV center orientations, we expect the overall ESR spectrum to have two broadened peaks, in accord with our experimental observations. To infer the model parameters and their associated uncertainties for each measured spectrum, we apply a Bayesian Markov Chain Monte Carlo approach (37) and plot the best-fit curves over the plotted data. Measured ESR spectra up to 60 G are shown in Fig. 4B. In Fig. 4C, we fix the model parameters found at 0 G, adjust only the parameter for the applied magnetic field, and obtain excellent qualitative agreement with the data.

Fig. 4.

(A) Optically detected ESR spectra of trapped nanodiamond ensembles at calibrated low field strengths. The best-fit curve from the model with five fitting parameters is shown (black lines). The measurements occurred at calibrated applied magnetic fields of 0, 5, 10, and 15 G. By fitting to the model, we obtain estimated magnetic fields of 1.5, 9.4, 14.5, and 20.8 G, respectively. This discrepancy is discussed further in the SI Text. Each ESR spectrum has a total acquisition time of about 200 s. I_PL ≈ 510 kCts/s and f_AM = 1 kHz. (B) Measured ESR spectra of trapped nanodiamonds up to 60 G. (C) Predicted ESR spectra from the model are computed by fixing all parameters except B to their best-fit values at zero field and adjusting B to the calibrated field values. (D) Estimated sensitivity of the diamond-based magnetometer using the optimal measuring scheme. The estimates are computed using values inferred from experiment, and the error bars reflect the 68.2% highest probability intervals from the propagated uncertainties.

From the model, we can gain an intuition for the optimal conditions for dc magnetometry in our system. Because the splitting of the peaks is approximately linear with increasing field and the contrast diminishes, we would expect that the magnetic sensitivity generally worsens at higher fields. Similarly, when the two resonances become unresolved near zero magnetic field, the line shape becomes weakly dependent on B and the sensitivity is poor. For this reason, an optimum condition exists at low fields near 5 G when the resonances are split but the contrast is still large. We estimate from the statistical analysis the optimal magnetic sensitivities in Fig. 4D, which depend on the noise and lineshape inferred from experiment (see the Materials and Methods for details). The most sensitive estimate of approximately 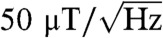, measured with I_PL ≈ 510 kCts/s, occurs at low fields (approximately 5 G) when the peaks are at least partially split. Further improvements to the collection efficiency and operating at a higher modulation frequency could improve the sensitivity of this technique by a factor of approximately 20, making it competitive with existing NV scanning-probe dc magnetometry protocols (7, 10, 11). Stable trapping of single nanodiamonds would ameliorate noise from collisions within the trap and improve the spatial resolution of the technique. The use of shaped diamond particles trapped with a controlled orientation (38) and aligned along the appropriate crystallographic axis would remove the degrees of freedom that complicate the ESR lineshape from the situation in bulk, opening the possibility of improved contrast and even vector magnetometry (6).

Conclusions

The combination of optical trapping and NV-center-based sensing developed in this work enables the three-dimensional mapping of magnetic fields in solution and addresses the need to probe complex environments, such as the interiors of microfluidic channels. Together, these two powerful techniques could pave the way for exploiting the unique electromagnetic and thermal sensing properties of NV centers at the nanoscale. Using optically trapped nanodiamonds for intracellular sensing (19), the mapping of electrical fields and thermal gradients around cells (39, 40), or the mapping of neurons (8, 41) are particularly exciting applications of this technique. The three-dimensional position control and on-demand release of optically trapped nanodiamonds achieved herein enables applications requiring nanoscale precision placement of NV centers within existing systems, such as the controlled tagging of a single biological cell. Additionally, this technique may serve as a tool for monitoring physical and chemical processes at liquid/solid interfaces, which could help improve the understanding of electrochemical cells, surface catalysis, or lipid membranes in biomedicine.

Materials and Methods

Microwave Antenna Microfabrication.

For antenna fabrication, 10 nm of titanium and 1,000 nm of gold were evaporated onto the freshly piranha-etched 150 μm thick glass coverslips 35 mm × 50 mm in dimension. Standard photolithography was used to define a resist etch mask, then gold and titanium etchants were used to transfer the desired antenna pattern to the substrate. Antennas were wire bonded to a coplanar waveguide on a printed circuit board, as shown in the SI Text. The circuit board was then fastened down to the XYZ piezoelectric stage and connected to a microwave signal generator and amplifier for measurements.

Nanodiamonds.

We used commercially available synthetic high-pressure high-temperature type Ib nanodiamonds from Adámas Nanotechnologies. The nanodiamonds have been He⁺ irradiated, annealed, and purified with acids by the manufacturer. The particles, typically 100 nm across, are specified to contain 500 or more NV centers per particle on average. All measurements were taken in filtered, deionized water. See the SI Text for electron microscopy images of the nanodiamonds.

Estimating Trap Population of NV Centers.

The number of NV centers in the trap and in the measurement volume during our experiments can be estimated from the NV density of the particles. The density is specified to be approximiately 500 NV centers per 100 nm diameter diamond, corresponding to a nearest neighbor separation of 13 nm. We estimate the trapping and measurement volume from the beam waist (w₀ ≈ nλ/πNA) and Rayleigh range (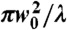) of a focused Gaussian beam. Ignoring dependence on beam power, the volume is given by the expression 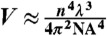, where n is the index of refraction (n = 1.515), NA is the numerical aperture of the objective (NA = 1.3), and λ is the laser wavelength. Using this approximation, the trapping beam volume is V_trap ∼ 0.06 μm³ and the measurement volume is V_msr ∼ 0.007 μm³. The trap width is w₀ ∼ 0.4 μm, in good agreement with the width observed in optical images (see Fig. 2). Assuming a unity packing fraction, the maximum number of 100 nm diameter particles, each of approximate volume 0.001 μm³, that can occupy the trap and measurement volumes is 60 and 7, respectively. In terms of NV centers, the upper bound in the measurement volume is approximately 3,500 centers. The highest stable I_PL we observed in our experiments was 3,000 kCts/s. Assuming this value corresponds to a full trap with approximately 3,500 NV centers, we would expect each NV to contribute approximately 0.9 kCts/s. This value agrees with the experimentally measured value of 1 kCts/s, obtained by measuring the minimum step height of I_PL as 35 nm diameter nanodiamonds (also from Adámas Nanotechnologies), each specified to contain approximately 1 to 4 NV centers, enter the optical trap.

Modeling ESR Spectra.

We model the magnetic field dependence of the ESR signal by assuming the measurement volume contains a large ensemble of isotropically oriented NV centers. The large ensemble assumption is justified by an estimate for the NV population in the trap’s measurement volume (see above) that yields approximately 3,500 NV centers. The orientation of an NV center with respect to the magnetic field vector determines the level splitting according to the Hamiltonian in Eq. 1, while the orientation with respect to the objective affects the strength of the optical absorption and the collection efficiency of the total emitted photoluminescence. From geometrical considerations of the two NV center transition dipoles (42), we approximate the angular dependence of the absorption of each NV center to be 1 + cos²θ, where θ is the angle between the NV symmetry axis and the optical axis. We integrate the far-field emission of each transition dipole over the collection cone of a 1.3 numerical aperture oil-immersion objective to account for the angular dependence of the collected luminescence signal. To obtain the final spectral shape, the individual splittings for each orientation are convolved with a Gaussian function to account for the natural linewidth with power broadening and finally integrated over an isotropic orientation density.

Because the typical ESR contrast in experiment is around 7% and the measurements are not shot-noise limited (by a factor of approximately two), the error at each point is assumed to be identical (homoscedastic) and normal, and is treated as a free parameter in the model. Further technical details regarding the analysis are found in the SI Text.

Magnetic Sensitivity Calculations.

The theoretical magnetic sensitivity is related to the noise and the lineshape of the associated ESR spectrum. At a given microwave frequency, f_MW, small changes in the measured contrast signal C ≡ ΔI_PL/I_PL occur with a change in magnetic field according to 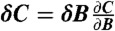and thus the most efficient magnetometry measurement would take place with f_MW fixed at the frequency for which the derivative 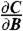is largest in magnitude. In the low-field limit, this maximum in 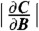occurs for f_MW centered between the two peaks, approximately f_MW = 2.87 GHz; however, once the two peaks split by about twice the FWHM, the most sensitive f_MW for measurement occurs on the downward slope of the highest frequency peak. If the minimum detectable change in magnetic field is δB_min, then the estimated optimal magnetic sensitivity is (3, 43)

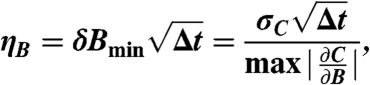[2]

where σ_C is the estimated standard deviation of C for measurement time Δt from the analysis.

We calculate the maximum-magnitude derivative of the model with respect to the parameter B and corresponding error parameter over samples from the Markov Chain Monte Carlo output to obtain a probability density for the optimal sensitivity given the lineshape inferred from experiment. The mean estimated and 68.2% highest probability density intervals from this distribution are plotted in Fig. 4D (44). In addition, the standard deviation of the marginal density for B, scaled by the square root of the total acquisition time, serves as an empirical measure of the actual sensitivity obtained in the experiment, and is plotted in the SI Text for comparison to the optimal estimates.