Abstract
Key to efficient harvesting of sunlight in photosynthesis is the first energy conversion process in which electronic excitation establishes a trans-membrane charge gradient. This conversion is accomplished by the photosynthetic reaction center (RC) that is, in case of the purple photosynthetic bacterium Rhodobacter sphaeroides studied here, surrounded by light harvesting complex 1 (LH1). The RC employs six pigment molecules to initiate the conversion: four bacteriochlorophylls and two bacteriopheophytins. The excited states of these pigments interact very strongly and are simultaneously influenced by the surrounding thermal protein environment. Likewise, LH1 employs 32 bacteriochlorophylls influenced in their excited state dynamics by strong interaction between the pigments and by interaction with the protein environment. Modeling the excited state dynamics in the RC as well as in LH1 requires theoretical methods, which account for both pigment-pigment interaction and pigment-environment interaction. In the present study we describe the excitation dynamics within a RC and excitation transfer between light harvesting complex 1 (LH1) and RC, employing the hierarchical equation of motion method. For this purpose a set of model parameters that reproduce RC as well as LH1 spectra and observed oscillatory excitation dynamics in the RC is suggested. We find that the environment has a significant effect on LH1-RC excitation transfer and that excitation transfers incoherently between LH1 and RC.
INTRODUCTION
Photosynthesis is the process by which life on earth is sustained through the utilization of solar energy. Solar energy absorbed by pigment molecules, such as bacteriochlorophyll (BChl), in pigment-protein complexes is passed between pigments until it arrives at a photosynthetic reaction center (RC), where it is converted into a charge gradient. The RC, common to all photosynthetic species, achieves the first critical energy conversion needed for long term storage of solar energy in living cells.1
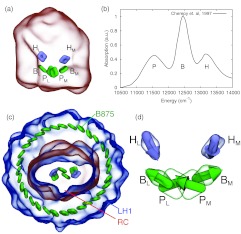
The structure of the reaction center from the purple bacterium Rhodobacter (Rb.) sphaeroides was solved in 1987,2 revealing the atomic positions and conformation of the pigment molecules (Fig. 1a). Noteworthy in the structure was how two of the six primary pigment molecules, the special pair BChls, were placed very close together (separated by only 7.5 Å).3 Additionally, two further BChls and two bacteriopheophytin (BPheo) molecules were also identified and placed. Altogether the six pigments can be classified into three groups, special pair BChls (P), accessory BChls (B), and BPheos (H), each of which has been assigned to one of the the three peaks seen in the RC’s equilibrium absorption spectrum4, 5 (Fig. 1b).
Figure 1.
(a) Position of bacteriochlorophylls (PM, PL, BM, BL) and bacteriopheophytins (HM, HL) in the reaction center (RC) from Rhodobacter sphaeroides. (b) RC equilibrium infrared absorption spectrum from Ref. 5. (c) Light harvesting complex 1 surrounding the RC; shown is also the B875 ring of pigments. (d) Orientation of bacteriochlorophyll and bacteriopheophytin transition dipole moments in the RC.
The reaction center in purple bacteria is surrounded by an antenna complex known as light harvesting complex 1 (LH1),6 thus forming the LH1-RC core complex. In Rb. sphaeroides the presence of an additional protein, known as PufX, results in the dimerization of LH1-RC.7 The precise position of PufX is, however, still debated. In PufX- mutants of Rb. sphaeroides the core complex is found only in its monomeric form, which is shown in Fig. 1c. To avoid the confusion relating to PufX placement, the monomeric form of LH1-RC, also found in Rhodospirillum photometricum, is considered henceforth. It is expected that the results and conclusions extend also to the dimeric form of the core complex.
LH1 contains 32 additional BChls that result in a strong absorption peak at 875 nm and, hence, are called the B875 BChls. By surrounding the RC with additional pigment molecules the amount of sunlight that the cell can absorb is greatly increased,8, 9 thus allowing the cell to exploit, through rapid turn-over, electron transfer in the RC.10, 11, 12, 13, 14, 15, 16, 17, 18 An additional antenna complex, light harvesting complex 2 (LH2), is also present in purple bacteria. It has recently been shown that LH2 and LH1 are sufficiently separated for excitation transfer between them to be incoherent,19 thus allowing the calculation of excitation dynamics of LH1-RC without including LH2.
A slight asymmetry in the structure of the RC leads to a similar asymmetry in the energy levels of the pigments. This results in a highly dominant path for charge separation, labelled the “L” side, whereas the non-dominant side is labelled “M”.20, 21, 22, 23, 24, 25 Accordingly, there are altogether six pigment excitation energies to model with site energies , , . The close proximity of the special pair BChls suggests strong interaction between their excited states, leading to strong, i.e., thermally robust, coherent sharing of excitation between the two BChls.26 Recent experiments27 have also revealed coherence effects between the B and H pigments. The three-peaked RC absorption spectrum, therefore, is not simply the sum of the spectra of three separate pigment groups, but results from their coherent mixing.
To account for the RC excited state dynamics, the vertical excitation energies and pigment-pigment interaction energies need to be characterized. There have been many efforts towards this goal,26, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 but only parts of the system were modeled at a time. In the present work we furnish an overall description of RC excitation dynamics employing a method that has become widely accepted,40, 41, 42, 43, 44, 45 namely the hierarchy equations of motion (HEOM) method. To apply the method we suggest an effective Hamiltonian and coupling to the environment. We demonstrate that the suggested model reproduces well the observed RC absorption spectrum. We examine then the excited state dynamics of the RC pigments.
Similar to the RC, light harvesting complex 1 (LH1) represents a fundamental, much studied photosynthetic system that is also governed by strong pigment-pigment interaction and strong coupling to a finite temperature environment. LH1 and RC interact closely with each other and so they are investigated jointly in the present study by the HEOM approach. For LH1 we resort to a previously chosen effective Hamiltonian.46, 47 The close proximity of LH1 and RC brings into question whether excitation transfer occurs incoherently between them, as has been previously assumed, but to be expected only for transfer between distant groups of pigments.48, 49, 50 By using the HEOM the assumption's validity can be tested.
For the application of the HEOM method we employ the program PHI developed by the authors.19 The program, made available to other researchers51 integrates the HEOM efficiently on single processor and multi-processor shared memory computers.
In Sec. 2 we briefly introduce the effective Hamiltonian and model of the coupling to the thermal environment. Stating then two possible choices of the associated model parameters, we present the resulting excitation dynamics of the RC and the LH1-RC excitation transfer.
METHODS
To determine how excitation transfers between LH1 and RC a description of the quantum system comprising the excited LH1 and RC pigments and their interaction with the surrounding protein environment is needed. Due to the complexity of systems like those seen in light-harvesting an effective Hamiltonian description is often used to characterize such systems.42, 43, 48, 52, 53, 54 The effective Hamiltonian involves only the most relevant subset of states. In case of excitation dynamics of light harvesting systems, the low-light photon level in the habitat of the biological organisms permits one to confine the effective Hamiltonian to the manifold of single pigment excitations, yielding an effective Hamiltonian given by
| (1) |
where describes the state in which the nth pigment is excited and all the others are in the ground state. En are the vertical excitation energies, Vn are the interaction matrix elements between the excited states of pigments n and m. There exist many parameterizations of the system Hamiltonian, some of which are listed in Table S1 in the accompanying supplementary material.55
Interaction energies between the excited states of pigments are typically determined using the point-dipole approximation and are then
| (2) |
where rnm is the vector connecting the center of pigment n to the center of pigment m, dn and dm are the transition dipole moments of pigments n and m (see Fig. 1d); the constant C = 146 798 cm−1 is chosen to reproduce BChl Qy excited state interactions in a protein environment.48 The point dipole approximation has been shown to account well for interaction energies of well separated pigments (>1.5 nm Mg-Mg distance), but in case of neighboring pigments in the RC and LH1 (<1 nm) the interaction energies need to be determined case by case following, for example, the procedure suggested in Ref. 26.
The pigments are embedded in protein-complexes, which in turn are surrounded by lipids, other proteins, water, and ions, all comprising the environment. In living bacteria, the environment is at a temperature of 300 K and it is expected that thermal noise plays an important role. The thermal environment is modeled as an infinite bath of harmonic oscillators, such that the bath Hamiltonian HB is given by
| (3) |
The thermal bath is coupled to each pigment independently through the system-bath interaction term
| (4) |
where cnξ is the coupling strength of vibrational mode ξ to pigment n. This coupling introduces a shift in the minimum energy positions of the bath coordinates, which is balanced by the renormalization term
| (5) |
where λn is the so-called reorganization energy. The total Hamiltonian is thus given by HT = HS + HB + HSB, where HS = H0 + HREN is the renormalized system Hamiltonian.
The bath degrees of freedom are not of interest in the final result and are traced out of the dynamics yielding the bath-averaged density matrix, formally written
| (6) |
where β = 1/T. There have been many attempts to find methods to calculate the bath-averaged time evolution of the density matrix, few of which turned out computationally feasible for all but model two-state systems.56, 57, 58, 59, 60, 61 Typically, approximations are made regarding the quantum nature of the dynamics or regarding the relative interaction strengths in the Hamiltonian. By restricting oneself to simple spectral densities and higher temperatures, one can employ the hierarchy equations of motion (HEOM) to avoid the previously mentioned approximations,60 though at a computational cost.43 By developing an efficient parallel implementation of the HEOM it becomes possible to describe large systems such that ρ(t) can be calculated for the reaction center.43, 62 As stated in the introduction our study employs for the integration of the HEOM the program PHI.19
After performing the bath average, the influence of the bath on excited state is wholly determined by the spectral density
| (7) |
A drawback of the HEOM is that, in practice, it is limited to only the Drude spectral density, given by
| (8) |
where λn is the reorganization energy, and 1/γn is the bath response time. The reorganization energy parameter λn determines the coupling of thermal fluctuations to the excited state . Higher values of λn lead to stronger damping of excited state dynamics compared to lower values, thus λn is also referred to as the damping strength. The Drude spectral density describes the influence of an over-damped harmonic oscillator with damping time τ = ℏ/λ, ℏ being the reduced Planck's constant. This spectral density has been shown to reproduce experimental absorption spectra and excitation dynamics in the context of the HEOM.42, 43, 54, 62
The HEOM exploit the structure of the correlation function associated with the spectral density, Eq. 7, by introducing auxiliary density matrices (ADMs) that take into account the non-Markovian dynamics induced by the environment.58 The number of ADMs, in principle, are infinite, but can be truncated to a finite level L, depending on the highest oscillation frequency in the system.60 Furthermore, the finite temperature of 300 K introduces an additional set of ADMs that can also be truncated to a level K. In the present study we apply Markovian truncation (see Refs. 42, 59 for detail) to both sets of ADMs with L = 8 and K = 1 for the RC absorption spectra and excited state dynamics calculations, and L = 5 and K = 0 for the LH1-RC transfer calculations. In case of LH1 spectra and excitation dynamics the system size (32 pigments), presently, precludes computations with static disorder, even with the effective program PHI.19
In addition to the fluctuations introduced by the thermal environment, one needs to account for long-time, structural disorder that is not accounted for in the harmonic bath model. In case of the RC calculations disorder is phenomenologically included in the form of Gaussian disorder, often termed static disorder, of the diagonal elements of the system Hamiltonian with widths σP, σB, and σH for the P, B, and H pigments. We have assumed that static disorder is uncorrelated between pigments, as suggested by Olbrich and Kleinekathöfer,63 though recent evidence indicates that for the Fenna-Matthews-Olson complex static disorder may indeed be correlated.64 An ensemble average over 1000 realizations of static disorder was done for the calculation of the RC absorption spectra. Previously reported bath parameters for the RC pigments in our calculations are given in Table S2 of the supplementary material.55
Equilibrium absorption spectra can be calculated using the HEOM employing the dipole autocorrelation coefficient. In the site-basis the equation for the equilibrium absorption spectrum resulting from δ-shaped laser pulses reads65
| (9) |
where is the transition dipole operator, is defined through Eq. 6 and the initial state is given by . Calculating the absorption spectrum thus amounts to calculating, according to Eq. 6, three independent density matrix evolutions with the initial states given by the x, y, and z components of the state transition dipole moments dn.
RESULTS
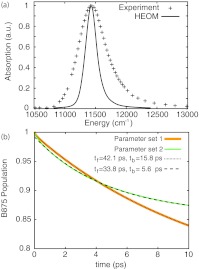
To reproduce the equilibrium absorption spectrum of the reaction center using non-Markovian excitation dynamics as calculated by the HEOM, two sets of parameters, largely based on previous choices, are suggested here. The two sets are able to yield the observed RC absorption spectrum, parameter set 1 assuming strong damping (high dynamic disorder) and parameter set 2 assuming weak damping (low dynamic disorder). The RC absorption spectra resulting from parameter sets 1 and 2 are shown in Fig. 2. The parameters for the system Hamiltonian, listed in Table 1, are very similar for sets 1 and 2 and also show little deviation from what has been reported in the literature.26, 29, 30, 31, 33 The calculated linear absorption spectra exhibit greater sensitivity to the effective Hamiltonian parameters than to the bath parameters. The low sensitivity to the bath parameters is apparent from the good fits to the experimental absorption spectrum obtained for both parameter sets.
Figure 2.
Comparison of 300 K linear equilibrium absorption spectra calculated by the HEOM and observed experimentally as reported in Ref. 5.
Table 1.
Parameters for the RC Hamiltonian, HS, and spectral densities Jn, obtained from fits to experimental spectra (all in cm−1).
| Parameter | Parameter | Parameter | Parameter | ||
|---|---|---|---|---|---|
| set 1 | set 2 | set 1 | set 2 | ||
| 1 | 12 190 | 12 180 | λP | 280 | 80 |
| 1 | 12 090 | 12 080 | λB | 110 | 40 |
| 1 | 12 510 | 12 500 | λH | 160 | 50 |
| 1 | 12 540 | 12 530 | ℏγP | 52.9 | 52.9 |
| 1 | 13 280 | 13 200 | ℏγB | 52.9 | 52.9 |
| 1 | 13 140 | 13 170 | ℏγH | 52.9 | 52.9 |
| VPP | 500 | 500 | σP | 240 | 380 |
| –60 | –50 | σB | 90 | 190 | |
| –60 | –50 | σH | 120 | 240 | |
| –70 | –60 | ||||
| –70 | –60 | ||||
| 140 | 130 | ||||
| 140 | 130 |
Parameters include the renormalization term HREN.
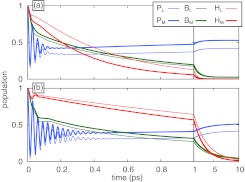
The excited state populations calculated using parameter sets 1 and 2 are shown in Fig. 3. The populations shown are not averaged over static disorder to provide a view for a single RC, as opposed to a view for an ensemble average that may hide detail.45 The damping times associated with parameter set 1 are τP = 19 fs, τB = 48 fs, and τH = 33 fs; for parameter set 2 they are τP = 66 fs, τB = 130 fs, and τH = 100 fs. Figure 3 clearly shows that coherent oscillations of the B and H pigments, similar to those seen in Ref. 27 at 180 K, are rapidly damped out for parameter set 1, but last longer for parameter set 2.
Figure 3.
Excitation dynamics of the reaction center calculated with system and bath parameters taken from Table 1, where parameter set 1 (a) assumes high dynamic disorder and parameter set 2 (b) assumes low dynamic disorder. Populations are shown for the pigments initially excited in each calculation.
As the diagonal entries in the effective Hamiltonians of parameter set 1 and 2 differ little, the steady-state populations of the pigments are very similar between the parameter sets, as expected. The relaxation times, however, are very different: in case of parameter set 1, the assumed high damping results in the populations reaching their steady-state values in about 2 ps, compared to 10 ps in the case of parameter set 2 that assumes weak damping.
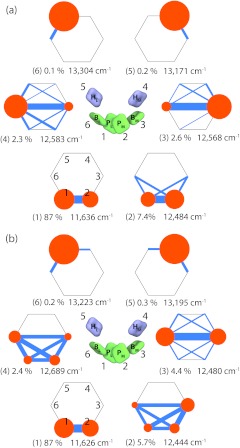
To obtain insight into which pigments comprise the absorption peaks, the exciton states were also computed. The exciton states were obtained by diagonalizing the steady state density matrix ρe, i.e., by solving for and diagonalizing the resulting ρe. A graphical representation of the exciton states is given in Fig. 4, which shows how much a pigment participates in an exciton state and illustrates the quantum coherence between the pigments associated with each exciton state.
Figure 4.
Reaction center exciton states. The exciton states, , are defined as eigenstates of the stationary state density matrix, namely, ; parameters were taken from Table 1, where parameter set 1 (a) assumes high dynamic disorder and parameter set 2 (b) assumes low dynamic disorder. Orange circles (radius scales with diagonal elements of ) indicate the participation of each pigment in an exciton state, and blue lines (thickness scales with absolute value of off-diagonal elements of ) indicate inter-pigment coherence. Listed are also the steady-state population Pν and energy εν of each exciton state. The numbering of the states is in energetically ascending order.
There is little difference between the two parameter sets of the most populated (lowest energy) exciton states. Indeed, the primary difference is only that the exciton states in parameter set 2 exhibit a bit stronger coherence, which is expected due to the localizing effect of the stronger damping for parameter set 1. The special pair BChls are seen to carry the majority of the steady-state population, the accessory BChls carrying only about 10% of the steady state population and the BPheos almost none. The correspondence between pigments and peaks in the absorption spectra can also be discerned from Fig. 4. For both parameter sets the lowest energy peak, around 11 500 cm−1, is produced by only a single exciton state. The middle peak, around 12 500 cm−1 is produced by a combination of three exciton states that are energetically nearly degenerate. These states are coherently delocalized over the P and B pigments due to the pigments' strong interactions and energetic proximity. The highest energy peak, around 13 300 cm−1, is made up of two exciton states that correspond almost exactly to each H pigment.
The spectrum of LH1 and excitation transfer between LH1 and RC were also examined using the HEOM. For these calculations the parameters for the effective Hamiltonian describing the B875 pigments were adopted from Ref. 67 and reorganization energy λ and frequency γ were set to 180 cm−1 and 10 ps−1, respectively, matching experimental values.47 The LH1 absorption spectrum calculated with these parameters is shown in Fig. 5a. Static disorder has been excluded from these calculations due to a prohibitive computational expense incurred otherwise. As a result the width of the calculated spectrum is significantly smaller, i.e., only 40%, of the width of the measured spectrum. The difference is particularly large as LH1 apparently is rather flexible; indeed a comparison of spectral width of the B875 ring of LH1 (FWHM = 530 cm−1) and of the B850 ring of LH2 (FHWM = 400 cm−1) suggests that LH1 is significantly more flexible than LH2.66, 68
Figure 5.
(a) LH1 absorption spectrum. Shown is a comparison of spectra from Ref. 66 and calculated here using the HEOM approach, but excluding static disorder. (b) Excitation transfer from LH1 to RC. Excitation transfer was determined both for parameter sets 1 and 2. Shown are close comparisons between the HEOM results and descriptions in terms of the kinetic model in Eq. 10 where tf is the LH1→RC transfer time and tb is the RC→LH1 transfer time.
The transfer of excitation from the B875 ring to RC pigments is shown in Fig. 5b. Although strong damping results in fast equilibration within a complex (see Fig. 3), it hinders inter-complex excitation transfer. To obtain inter-complex transfer rates the dynamics were fitted to a simple kinetic model, namely
| (10) |
where P is the LH1 excited state population, kf is the LH1→RC transfer rate and kb is the RC→LH1 transfer rate. The transfer rates obtained for parameter set 1 are kf = 1/(42.1 ps), kb = 1/(15.8 ps), and for parameter set 2 are kf = 1/(33.8 ps), kb = 1/(5.6 ps). The transfer rates obtained with parameter set 2 are closest to previously reported values of kf = 1/(25 ps) and kb = 1/(8 ps).11, 12, 28, 67, 69, 70 Including static disorder in the excitation transfer calculation should increase the transfer times by 10%–20%.62
CONCLUSION
To investigate excitation transfer between the pigments in the reaction center (RC) and light harvesting complex 1 (LH1), i.e., the complexes comprising the core particle in purple photosynthetic bacteria, a consistent set of parameters for the RC pigments is needed. We have determined an effective Hamiltonian and coupling to a heat bath for the RC pigments from Rhodobacter sphaeroides that reproduce, in the framework of non-Markovian dynamics as described by the HEOM,43, 60, 62, 71 the 300 K linear absorption spectrum and experimental results stemming from particularly sensitive probes of RC excitation dynamics.27
Prior studies investigating excitation transfer in LH1-RC postulated an incoherent hopping process even though the pigments complexes of RC and LH1 are in relatively close proximity. By employing the HEOM, excitation transfer between LH1 and RC could be investigated without making such an assumption. It was shown that population relaxation due to LH1-RC excitation transfer indeed follows a single exponential function, concluding that it is incoherent and is, as shown in Fig. 5b, well described by a simple kinetic model. As LH1-RC excitation transfer is incoherent for the extreme cases of weak and strong damping, we conclude that it is likely incoherent for all parameter sets that reproduce the absorption spectrum. This result justifies the use of generalized Förster theory67 in describing LH1-RC excitation transfer.
Our results reveal that the rate of LH1-RC excitation transfer is strongly affected by the environmental coupling of the RC pigments. We find that weak damping leads to slow intra-complex relaxation, but results in fast inter-complex excitation transfer. Although at first glance counter-intuitive, RC→LH1 transfer is faster than LH1→RC transfer. The fast back-transfer is still slower than photo-induced P→HL electron transfer and allows captured photon energy, which would otherwise be lost, to be funneled to a different RC in case it reaches one that has recently undergone charge separation;49 back-transfer also spreads superfluous excitation energy across all pigments, avoiding radiation damage to the RC. Our results show that the back-transfer rate RC→LH1 is significantly faster with weak damping compared to strong damping. Weak coupling between RC pigments and environment, thus, promotes protection from radiation damage and results in overall improvement of light harvesting efficiency.
ACKNOWLEDGMENTS
The authors are grateful for insightful discussions with Melih Sener. Funding for J.S. and K.S. was provided by NSF grant PHY0822613 and NIH grants MCB-0744057 and P41-RR05969.
References
- Blankenship R. E., Molecular Mechanisms of Photosynthesis (Blackwell Science, Malden, MA, 2002). [Google Scholar]
- Allen J. P., Yeates T. O., Komiya H., and Rees D. C., “Structure of the reaction center from Rhodobacter sphaeroides R-26: the protein subunits,” Proc. Natl. Acad. Sci. U.S.A. 84, 6162–6166 (1987). 10.1073/pnas.84.17.6162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen J. P., Yeates T. O., Komiya H., and Rees D. C., “Structure of the reaction center from Rhodobacter sphaeroides R-26: the cofactors,” Proc. Natl. Acad. Sci. U.S.A. 84, 5730–5734 (1987). 10.1073/pnas.84.16.5730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonas D. M., Lang M. J., Nagasawa Y., Joo T., and Fleming G. R., “Pump-probe polarization anisotropy study of femtosecond energy transfer within the photosynthetic reaction center of rhodobacter sphaeroides r26,” J. Phys. Chem. 100, 12660–12673 (1996). 10.1021/jp960708t [DOI] [Google Scholar]
- Cherepy N. J., Shreve A. P., Moore L. J., Boxer S. G., and Mathies R. A., “Temperature dependence of the qy resonance raman spectra of bacteriochlorophylls, the primary electron donor, and bacteriopheophytins in the bacterial photosynthetic reaction center,” Biochemistry 36(28), 8559–8566 (1997). 10.1021/bi970024r [DOI] [PubMed] [Google Scholar]
- Hu X., Damjanović A., Ritz T., and Schulten K., “Architecture and function of the light harvesting apparatus of purple bacteria,” Proc. Natl. Acad. Sci. U.S.A. 95, 5935–5941 (1998). 10.1073/pnas.95.11.5935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsin J., LaPointe L., Kazy A., Chipot C., Senes A., and Schulten K., “Oligomerization state of photosynthetic core complexes is correlated with the dimerization affinity of a transmembrane helix,” J. Am. Chem. Soc. 133, 14071–14081 (2011). 10.1021/ja204869h [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sener M., Strümpfer J., Hsin J., Chandler D., Scheuring S., Neil Hunter C., and Schulten K., “Förster energy transfer theory as reflected in the structures of photosynthetic light harvesting systems,” ChemPhysChem 12, 518–531 (2011). 10.1002/cphc.201000944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strumpfer J., Sener M., and Schulten K., “How quantum coherence assists photosynthetic light harvesting,” J. Phys. Chem. Lett. 3, 536–542 (2012). 10.1021/jz201459c [DOI] [PMC free article] [PubMed] [Google Scholar]
- Won Y. and Friesner R. A., “Simulation of optical spectra from reaction center of rhodopseudomonas viridis,” J. Phys. Chem. 92, 2208–2214 (1988). 10.1021/j100319a025 [DOI] [Google Scholar]
- Timpmann K., Zhang F. G., Freiberg A., and Sundström V., “Detrapping of excitation energy from the reaction centre in the photosynthetic purple bacterium rhodospirillum rubrum,” Biochim. Biophys. Acta 1183(1), 185–193 (1993). 10.1016/0005-2728(93)90017-A [DOI] [Google Scholar]
- Timpmann K., Freiberg A., and Sundström V., “Energy trapping and detrapping in the photosynthetic bacterium rhodopseudomonas viridis: Transfer-to-trap-limited dynamics,” Chem. Phys. 194, 275–283 (1995). 10.1016/0301-0104(95)00072-V [DOI] [Google Scholar]
- Pawlowicz N. P., Van Grondelle R., Van Stokkum I. H. M., Breton J., Jones M. R., and Groot M. L., “Identification of the first steps in charge separation in bacterial photosynthetic reaction centers of rhodobacter sphaeroides by ultrafast mid-infrared spectroscopy: electron transfer and protein dynamics,” Biophys. J. 95(3), 1268–1284 (2008). 10.1529/biophysj.108.130880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y. C. and Fleming G. R., “Dynamics of light harvesting in photosynthesis,” Annu. Rev. Phys. Chem. 60, 241–262 (2009). 10.1146/annurev.physchem.040808.090259 [DOI] [PubMed] [Google Scholar]
- Lin S., Jaschke P. R., Wang H., Paddock M., Tufts A., Allen J. P., Rosell F. I., Mauk A. G., Woodbury N. W., and Beatty J. T., “Electron transfer in the rhodobacter sphaeroides reaction center assembled with zinc bacteriochlorophyll,” Proc. Natl. Acad. Sci. U.S.A. 106(21), 8537 (2009). 10.1073/pnas.0812719106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawlowicz N. P., van Stokkum Ivo H. M., Breton J., van Grondelle R., and Jones M. R., “Identification of the intermediate charge-separated state in a leucine m214 to histidine mutant of the rhodobacter sphaeroides reaction center using femtosecond midinfrared spectroscopy,” Biophys. J. 96(12), 4956–4965 (2009). 10.1016/j.bpj.2009.03.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins A. M., Kirmaier C., Holten D., and Blankenship R. E., “Kinetics and energetics of electron transfer in reaction centers of the photosynthetic bacterium roseiflexus castenholzii,” Biochim. Biophys. Acta 1807(3), 262–269 (2011). 10.1016/j.bbabio.2010.11.011 [DOI] [PubMed] [Google Scholar]
- Guo Z., Lin S., Xin Y., Wang H. Y., Blankenship R. E., and Woodbury N., “Comparing the temperature dependence of photosynthetic electron transfer in chloroflexus aurantiacus and rhodobactor sphaeroides reaction centers,” J. Phys. Chem. B 115(38), 11230–11238 (2011). 10.1021/jp204239v [DOI] [PubMed] [Google Scholar]
- Strümpfer J. and Schulten K., “Open quantum dynamics calculations with the hierarchy equations of motion on parallel computers,” J. Chem. Theor. Comp. (in press). [DOI] [PMC free article] [PubMed]
- Kirmaier C., Holten D., and Parson W. W., “Temperature and detection-wavelength dependence of the picosecond electron-transfer kinetics measured in rhodopseudomonas sphaeroides reaction centers. resolution of new spectral and kinetic components in the primary charge-separation process,” Biochim. Biophys. Acta 810(1), 33–48 (1985). 10.1016/0005-2728(85)90204-X [DOI] [Google Scholar]
- Steffen M. A., Lao K., and Boxer S. G., “Dielectric asymmetry in the photosynthetic reaction center,” Science 264(5160), 810–816 (1994). 10.1126/science.264.5160.810 [DOI] [PubMed] [Google Scholar]
- van Brederode M. E. and van Grondelle R., “New and unexpected routes for ultrafast electron transfer in photosynthetic reaction centers,” FEBS Lett. 455, 1–7 (1999). 10.1016/S0014-5793(99)00810-8 [DOI] [PubMed] [Google Scholar]
- van Brederode M. E., van Mourik F., van Stokkum I. H. M., Jones M. R., and van Grondelle R., “Multiple pathways for ultrafast transduction of light energy in the photosynthetic reaction center of rhodobacter sphaeroides,” Proc. Natl. Acad. Sci. U.S.A. 96, 2054–2059 (1999). 10.1073/pnas.96.5.2054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuang J. I., Boxer S. G., Holten D., and Kirmaier C., “Temperature dependence of electron transfer to the M-side bacteriopheophytin in rhodobacter capsulatus reaction centers,” J. Phys. Chem. B 112(17), 5487–5499 (2008). 10.1021/jp800082m [DOI] [PubMed] [Google Scholar]
- Wang H., Hao Y., Jiang Y., Lin S., and Woodbury N. W., “Role of protein dynamics in guiding electron-transfer pathways in reaction centers from rhodobacter sphaeroides,” J. Phys. Chem. B 116(1), 711–717 (2012). 10.1021/jp211702b [DOI] [PubMed] [Google Scholar]
- Hu X., Ritz T., Damjanović A., and Schulten K., “Pigment organization and transfer of electronic excitation in the purple bacteria,” J. Phys. Chem. B 101, 3854–3871 (1997). 10.1021/jp963777g [DOI] [Google Scholar]
- Lee H., Cheng Y.-C., and Fleming G. R., “Coherence dynamics in photosynthesis: Protein protection of excitonic coherence,” Science 316(5830), 1462–1465 (2007). 10.1126/science.1142188 [DOI] [PubMed] [Google Scholar]
- Pullerits T., Visscher K. J., Hess S., Sundstr V.öm, Freiberg A., and Timpmann K., “Energy transfer in the inhomogeneously broadened core antenna of purple bacteria: A simultaneous fit of low-intensity picosecond absorption and fluorescence kinetics,” Biophys. J. 66, 236–248 (1994). 10.1016/S0006-3495(94)80770-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordanides X. J., Scholes G. D., and Fleming G. R., “The mechanism of energy transfer in the bacterial photosynthetic reaction center,” J. Phys. Chem. B 105(8), 1652–1669 (2001). 10.1021/jp003572e [DOI] [Google Scholar]
- Chang C. H., Hayashi M., Liang K. K., Chang R., and Lin S. H., “A theoretical analysis of absorption spectra of photosynthetic reaction centers: Mechanism of temperature dependent peak shift,” J. Phys. Chem. B 105(6), 1216–1224 (2001). 10.1021/jp0020438 [DOI] [Google Scholar]
- Jordanides X. J., Scholes G. D., Shapley W. A., Reimers J. R., and Fleming G. R., “Electronic couplings and energy transfer dynamics in the oxidized primary electron donor of the bacterial reaction center,” J. Phys. Chem. B 108(5), 1753–1765 (2004). 10.1021/jp036516x [DOI] [Google Scholar]
- Linnanto J. and Korppi-Tommola J., “Quantum chemical simulation of excited states of chlorophylls, bacteriochlorophylls and their complexes,” Phys. Chem. Chem. Phys. 8, 663–687 (2006). 10.1039/b513086g [DOI] [PubMed] [Google Scholar]
- Linnanto J. M. and Korppi-Tommola J. E. I., “Modelling excitonic energy transfer in the photosynthetic unit of purple bacteria,” Chem. Phys. 357(1-3), 171–180 (2009). 10.1016/j.chemphys.2009.01.001 [DOI] [Google Scholar]
- Jing Y., Zheng R., Li H., and Shi Q., “Theoretical study of the electronic-vibrational coupling in the q_y states of the photosynthetic reaction center in purple bacteria,” J. Phys. Chem. B 116(3), 1164–1171 (2012). 10.1021/jp209575q [DOI] [PubMed] [Google Scholar]
- Dilworth Y., Lee H., and Fleming G. R., “Measuring electronic coupling in the reaction center of purple photosynthetic bacteria by two-color, three-pulse photon echo peak shift spectroscopy,” J. Phys. Chem. B 111(25), 7449–7456 (2007). 10.1021/jp070029q [DOI] [PubMed] [Google Scholar]
- Cheng Y. C., Lee H., and Fleming G. R., “Efficient simulation of three-pulse photon-echo signals with application to the determination of electronic coupling in a bacterial photosynthetic reaction center,” J. Phys. Chem. A 111(38), 9499–9508 (2007). 10.1021/jp0735177 [DOI] [PubMed] [Google Scholar]
- Frolov D., Marsh M., Crouch L. I., Fyfe P. K., Robert B., van Grondelle R., Hadfield A., and Jones M. R., “Structural and spectroscopic consequences of hexacoordination of a bacteriochlorophyll cofactor in the rhodobacter sphaeroides reaction center,” Biochemistry 49(9), 1882–1892 (2010). 10.1021/bi901922t [DOI] [PubMed] [Google Scholar]
- Vassiliev S., Mahboob A., and Bruce D., “Calculation of chromophore excited state energy shifts in response to molecular dynamics of pigment–protein complexes,” Photosynth. Res. 110(1), 1–14 (2011). 10.1007/s11120-011-9689-2 [DOI] [PubMed] [Google Scholar]
- Linnanto J., Freiberg A., and Korppi-Tommola J., “Quantum chemical simulations of excited-state absorption spectra of photosynthetic bacterial reaction center and antenna complexes,” J. Phys. Chem. B 115(18), 5536–5544 (2011). 10.1021/jp111340w [DOI] [PubMed] [Google Scholar]
- Schröder M., Schreiber M., and Kleinekathöfer U., “Reduced dynamics of coupled harmonic and anharmonic oscillators using higher-order perturbation theory,” J. Chem. Phys. 126, 114102 (2007). 10.1063/1.2538754 [DOI] [PubMed] [Google Scholar]
- Ishizaki A. and Fleming G. R., “On the adequacy of the Redfield equation and related approaches to the study of quantum dynamics in electronic energy transfer,” J. Chem. Phys. 130(23), 234110 (2009). 10.1063/1.3155214 [DOI] [PubMed] [Google Scholar]
- Chen L., Zheng R., Shi Q., and Yan Y., “Optical line shapes of molecular aggregates: Hierarchical equations of motion method,” J. Chem. Phys. 131(9), 094502 (2009). 10.1063/1.3213013 [DOI] [PubMed] [Google Scholar]
- Strümpfer J. and Schulten K., “Light harvesting complex II B850 excitation dynamics,” J. Chem. Phys. 131, 225101 (2009). 10.1063/1.3271348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly A. and Rhee Y. M., “Mixed quantum-classical description of excitation energy transfer in a model Fenna-Matthews-Olsen complex,” J. Phys. Chem. Lett. 2, 808–812 (2011). 10.1021/jz200059t [DOI] [Google Scholar]
- Ishizaki A. and Fleming G. R., “On the interpretation of quantum coherent beats observed in two-dimensional electronic spectra of photosynthetic light harvesting complexes,” J. Phys. Chem. B 115(19), 6227–6233 (2011). 10.1021/jp112406h [DOI] [PubMed] [Google Scholar]
- Sener M. K., Hsin J., Trabuco L. G., Villa E., Qian P., Hunter C. N., and Schulten K., “Structural model and excitonic properties of the dimeric RC-LH1-PufX complex from Rhodobacter sphaeroides,” Chem. Phys. 357, 188–197 (2009). 10.1016/j.chemphys.2009.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freiberg A., Ratsep M., Timpmann K., and Trinkunas G., “Excitonic polarons in quasi-one-dimensional LH1 and LH2 bacteriochlorophyll a antenna aggregates from photosynthetic bacteria: A wavelength-dependent selective spectroscopy study,” Chem. Phys. 357(1-3), 102–112 (2009). 10.1016/j.chemphys.2008.10.043 [DOI] [Google Scholar]
- Sener M. K., Olsen J. D., Hunter C. N., and Schulten K., “Atomic level structural and functional model of a bacterial photosynthetic membrane vesicle,” Proc. Natl. Acad. Sci. U.S.A. 104, 15723–15728 (2007). 10.1073/pnas.0706861104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Şener M. K. and Schulten K., “From atomic-level structure to supramolecular organization in the photosynthetic unit of purple bacteria,” in The Purple Phototrophic Bacteria, Volume 28 of Advances in Photosynthesis and Respiration, edited by Hunter C. N., Daldal F., Thurnauer M. C., and Beatty J. T. (Springer, 2008), pp. 275–294. [Google Scholar]
- Sener M., Strumpfer J., Timney J. A., Freiberg A., Hunter C. N., and Schulten K., “Photosynthetic vesicle architecture and constraints on efficient energy harvesting,” Biophys. J. 99, 67–75 (2010). 10.1016/j.bpj.2010.04.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- PHI is available at http://www.ks.uiuc.edu/Research/phi.
- Hu X., Ritz T., Damjanović A., Autenrieth F., and Schulten K., “Photosynthetic apparatus of purple bacteria,” Q. Rev. Biophys. 35, 1–62 (2002). 10.1017/S0033583501003754 [DOI] [PubMed] [Google Scholar]
- Şener M. and Schulten K., “Physical principles of efficient excitation transfer in light harvesting,” in Energy Harvesting Materials, edited by Andrews D. L. (World Scientific, Singapore, 2005), pp. 1–26. [Google Scholar]
- Ishizaki A. and Fleming G. R., “Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature,” Proc. Natl. Acad. Sci. U.S.A. 106(41), 17255 (2009). 10.1073/pnas.0908989106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.4738953 for a summary of effective Hamiltonian and system–environment coupling parameters determined in past studies to describe the Rhodobacter sphearoides reaction center bacteriochlorophylls and bacteriopheophytins.
- Prior J., Chin A. W., Huelga S. F., and Plenio M. B., “Efficient simulation of strong system-environment interactions,” Phys. Rev. Lett. 105(5), 50404 (2010). 10.1103/PhysRevLett.105.050404 [DOI] [PubMed] [Google Scholar]
- Chin A. W., Rivas Á., Huelga S. F., and Plenio M. B., “Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials,” J. Math. Phys. 51, 092109 (2010). 10.1063/1.3490188 [DOI] [Google Scholar]
- Tanimura Y. and Kubo R., “Two-time correlation functions of a system coupled to a heat bath with a Gaussian-Markoffian interaction,” J. Phys. Soc. Jpn. 58(4), 1199–1206 (1989). 10.1143/JPSJ.58.1199 [DOI] [Google Scholar]
- Ishizaki A. and Tanimura Y., “Quantum dynamics of system strongly coupled to low-temperature colored noise bath: Reduced hierarchy equations approach,” J. Phys. Soc. Jpn. 74, 3131–3134 (2005). 10.1143/JPSJ.74.3131 [DOI] [Google Scholar]
- Ishizaki A. and Fleming G. R., “Unified treatment of quantum coherent and incoherent hopping dynamics in electronic energy transfer: Reduced hierarchy equation approach,” J. Chem. Phys. 130(23), 234111 (2009). 10.1063/1.3155372 [DOI] [PubMed] [Google Scholar]
- Topaler M. and Makri N., “System-specific discrete variable representations for path integral calculations with quasi-adiabatic propagators,” Chem. Phys. Lett. 210(4), 448–457 (1993). 10.1016/0009-2614(93)87052-5 [DOI] [Google Scholar]
- Strümpfer J. and Schulten K., “The effect of correlated bath fluctuations on exciton transfer,” J. Chem. Phys. 134, 095102 (2011). 10.1063/1.3557042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olbrich C. and Kleinekathfer U., “Time-dependent atomistic view on the electronic relaxation in light-harvesting system II,” J. Phys. Chem. B 114(38), 12427–12437 (2010). 10.1021/jp106542v [DOI] [PubMed] [Google Scholar]
- Hayes D., Panitchayangkoon G., Fransted K. A., Caram J. R., Wen J., Freed K. F., and Engel G. S., “Dynamics of electronic dephasing in the Fenna-Matthews-Olsen complex,” New J. Phys. 12, 065042 (2010). 10.1088/1367-2630/12/6/065042 [DOI] [Google Scholar]
- Zhu K. B., Xu R. X., Zhang H. Y., Hu J., and Yan Y. J., “Hierarchical dynamics of correlated system-environment coherence and optical spectroscopy,” J. Phys. Chem. B 115(18), 5678–5684 (2011). 10.1021/jp2002244 [DOI] [PubMed] [Google Scholar]
- Jimenez R., van Mourik F., Yu J. Y., and Fleming G. R., “Three-pulse photon echo measurements on LH1 and LH2 complexes of Rhodobacter sphaeroides: A nonlinear spectroscopic probe of energy transfer,” J. Phys. Chem. B 101, 7350–7359 (1997). 10.1021/jp970299g [DOI] [Google Scholar]
- Damjanović A., Ritz T., and Schulten K., “Excitation energy trapping by the reaction center of Rhodobacter sphaeroides,” Int. J. Quantum Chem. 77, 139–151 (2000). [DOI] [Google Scholar]
- Ma Y. Z., Cogdell R. J., and Gillbro T., “Energy transfer and exciton annihilation in the B800-850 antenna complex of the photosynthetic purple bacterium Rhodopseudomonas acidophila (strain 10050). A femtosecond transient absorption study,” J. Phys. Chem. B 101, 1087–1095 (1997). 10.1021/jp962470e [DOI] [Google Scholar]
- van Grondelle R., Dekker J. P., Gillbro T., and Sundström V., “Energy transfer and trapping in photosynthesis,” Biochim. Biophys. Acta 1187, 1–65 (1994). 10.1016/0005-2728(94)90166-X [DOI] [Google Scholar]
- Freiberg A., “Coupling of antennas to reaction centers,” Anoxygenic Photosynthetic Bacteria (Springer, Netherlands, 2004), pp. 385–398. [Google Scholar]
- Shi Q., Chen L., Nan G., Xu R.-X., and Yan Y., “Efficient hierarchical Liouville space propagator to quantum dissipative dynamics,” J. Chem. Phys. 130(8), 084105 (2009). 10.1063/1.3077918 [DOI] [PubMed] [Google Scholar]