Characterization of the transport topology in patient-specific abdominal aortic aneurysm models

Abstract

Abdominal aortic aneurysm (AAA) is characterized by disturbed blood flow patterns that are hypothesized to contribute to disease progression. The transport topology in six patient-specific abdominal aortic aneurysms was studied. Velocity data were obtained by image-based computational fluid dynamics modeling, with magnetic resonance imaging providing the necessary simulation parameters. Finite-time Lyapunov exponent (FTLE) fields were computed from the velocity data, and used to identify Lagrangian coherent structures (LCS). The combination of FTLE fields and LCS was used to characterize topological flow features such as separation zones, vortex transport, mixing regions, and flow impingement. These measures offer a novel perspective into AAA flow. It was observed that all aneurysms exhibited coherent vortex formation at the proximal segment of the aneurysm. The evolution of the systolic vortex strongly influences the flow topology in the aneurysm. It was difficult to predict the vortex dynamics from the aneurysm morphology, motivating the application of image-based flow modeling.

INTRODUCTION

Abdominal aortic aneurysm (AAA) is a permanent localized widening of the abdominal aorta. It is characterized by disturbed flow patterns, including low and oscillatory wall shear stress with high gradients,¹ increased particle residence time,² mild turbulence,³ and a decrease in wall strength.⁴ Moreover, most AAAs are accompanied by mural thrombus,⁵ due in part to flow recirculation in the aneurysm.⁶ Aneurysm rupture kills thousands annually, and a reliable predictor for aneurysm progression remains unknown, though maximum AAA diameter, AAA expansion rate, and peak AAA wall stress have been used with varying success.⁴

Studies into AAA hemodynamics have helped reveal possible biomechanical mechanisms underlying AAA pathogenesis and progression, and these mechanisms have been reviewed in Refs. ^{4, 7, 8}. Early studies started from idealized models, e.g., to track the formation and propagation of vortices, and to determine regions of high shear stresses at the proximal and distal ends of an aneurysm.⁹ Finol et al.¹⁰ and Deplanoa et al.¹¹ studied common asymmetry in AAA, reporting the appearance of asymmetric vortices, and a relative higher shearing of the posterior wall of the aneurysm, which is the most prevalent location of rupture.⁷ Peattie et al.¹² and Salsac et al.¹³ demonstrated changes to the flow patterns based on bulge diameter, and Egelhoff et al.¹⁴ considered the effects of exercise.

In vivo flow conditions can be far more complex than flow in simplified aneurysm models. Patient-specific computational models have been used to predict possible in vivo flow patterns and wall shear stress in AAA.¹⁵ Patient-specific AAA models have also been used in studies of fluid structure interaction,¹⁶ particle image velocimetry,¹⁷ intraluminal thrombus formation,^{18, 19} and validation of image-based flow modeling.²⁰ Vessel morphology has a wide variability in AAA and the geometry of the aneurysm and surrounding vasculature is critical in determining the hemodynamics. Les et al.³ compared different Eulerian-based flow measures in multiple patient-specific computational models, and Suh et al.^{2, 21} investigated AAA flow using a Lagrangian-based particle residence time (PRT) measure.

The purpose of the study herein is to provide a more detailed description of blood flow inside AAA. Specifically, this is the first study to compare the transport topology inside different patient-specific AAA models. Previous studies investigating AAA hemodynamics have reported on Eulerian measures, or generic transport characteristics (e.g., PRT), that are unable to convey the complete flow topology. Instantaneous Eulerian measures place inherent limits on interpretation due to flow unsteadiness. While it may be reasonable to infer the bulk fluid motion from velocity data, inferences into transport mechanisms can easily result in misinterpretations. This is noteworthy because transport processes, and disruption of such processes, have significant physiologic relevance. Furthermore, the transport mechanics can be tightly and synergistically coupled to the fluid forces that may influence cellular function.²² Our objective is to provide more precise characterization of the unsteady transport topology observed over different patient-specific abdominal aortic aneurysms under physiological conditions. We utilize the computation of Lagrangian coherent structure (LCS) from finite-time Lyapunov exponent (FTLE) fields. This method has been applied previously to cardiovascular applications,²³ including flow near clots,²⁴ in the carotid arteries,^{23, 25} and flow through the aortic valve.^{26, 27} The present study is organized as follows: In Sec. 2A, the procedures for image-based flow modeling are discussed. Section 2B describes the computation of FTLE and LCS. Relevant features of the flow topology of the six patients considered are presented in Sec. 3, and discussed in Sec. 4.

METHODS

Six patients with small AAA (maximal diameter <5 cm) were considered for this study. These aneurysms demonstrated wide variability, which enabled comparison of flow topologies resulting from a range of morphology. Magnetic resonance imaging (MRI) was used to obtain anatomical and volumetric flow data for image-based computational fluid dynamics (CFD) simulation, and the resulting velocity data were used for subsequent FTLE/LCS computations.

Image based computational fluid dynamics

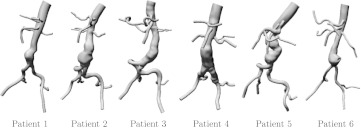
Details on the image-based CFD modeling are provided in Ref. 3, and a brief review of the process is presented here. Image-based geometric models were constructed using the software package SimVascular.²⁸ Contrast-enhanced magnetic resonance angiography (MRA) was used to obtain image stacks of the abdominopelivic cavity, creating a bright-blood image of the aorta and surrounding vessels. Paths were created along each vessel of interest, and segments of the vessels were obtained along each path. The segments were subsequently lofted and blended into a unified geometric model, as described in Ref. 29. Each model nominally included the aorta starting from the level of the diaphragm, and the celiac trunk (with hepatic and splenic arteries), superior mesenteric artery, the renal arteries, and continued through the internal and external iliac arteries. The model geometry represents the fluid domain; i.e., in some regions, the model boundary could be due to mural thrombus rather than the native vessel wall. The computational models are displayed in Fig. 1.

Figure 1.

AAA computer models derived from MRI.

Each geometric model was discretized into a computational mesh that was used for CFD simulation of the blood flow. Blood was modeled as an incompressible, Newtonian fluid by the Navier-Stokes equations

$$\rho \frac{\partial \mathbf{v}}{\partial t}+\rho \mathbf{v}·\nabla \mathbf{v}=-\nabla p+\mu \nabla ·\nabla \mathbf{v},$$ (1)

$$\mathrm{where}\nabla ·\mathbf{v}=\mathbf{0},$$

and the velocity v and pressure p are functions of space and time (x, t) and the density ρ and viscosity μ were assumed constant with values of 1.06 g/cm³ and 0.04 P, respectively. To solve Eq. 1, initial and boundary conditions were specified. The velocity was specified at the inflow face v(x, t) = g(x, t) using phase contrast magnetic resonance imaging (PCMRI) data, as described below. Zero velocity (no slip) was specified along the walls. At the outlets, a Neumann-type boundary condition was imposed by coupling lower order models as described below using the coupled-multidomain formulation.³⁰ An initial value for velocity v(x, t) = v⁰(x) was assumed known, which was obtained from a steady simulation. The Navier-Stokes equations were discretized using a streamline-upwind Petrov-Galerkin finite element formulation³¹ with same order interpolation for velocity and pressure. The discretization was semidiscrete, i.e., the spatial domain was discretized by finite elements (tetrahedra), leaving a system of ordinary differential equations to be integrated in time using an implicit, second-order accurate generalized-α method. The finite-element formulation and integration method were described in more detail in Ref. 32. The solver has been extensively used and validated for image-based blood flow modeling, including validation in aortic flow studies.^{20, 33}

Direct numerical simulation was used since the flow conditions were observed to be predominantly laminar or transitional, and turbulence was transient due to the pulsatile nature of the flow. Vessel wall motion was assumed negligible since the abdominal aorta becomes stiffer with AAA progression due to an increase in collagen and decrease in elastin,³⁴ and often an increase of mural thrombus. Nonetheless, the incorporation of realistic variable wall properties and external tissue support remains an outstanding challenge, though progress is being made.³⁵

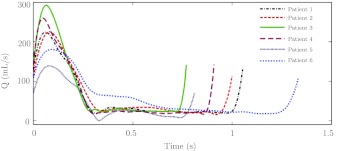
Planar phase contrast magnetic resonance imaging was used to obtain through-plane blood flow velocities under resting condition at a cross-section of the supraceliac aorta over time. The expected error in the PCMRI measurement (≈5%) is less than typical variation of cardiac output for a given patient over a day. The inlet of each model was chosen to correspond to the PCMRI measurement plane. The PCMRI velocity was integrated over the cross-section to provide a time-dependent supraceliac volumetric flow, shown in Fig. 2 for each patient. The resulting waveform was used to prescribe a time-dependent Womersley velocity profile at the model inlet.²⁹ Three-element Windkessel models were used to impose outflow boundary conditions at each outlet of the model. These lower order models of the downstream vascular beds were coupled to the computational domain using methods described in Ref. 30. The solver was run until the blood pressure, measured as the maximum in space at each time instant, became periodic in time. The simulation was continued for an additional five cardiac cycles to produce converged velocity data that were used for post processing as described in Sec. 2B. Mesh independence tests were performed for one patient (Patient 1) by comparing results from ≈2 million, ≈8 million, and ≈32 million element meshes as described in Ref. 3. The 8 M and 32 M element meshes showed relative agreement in the flow field and the nominal tetrahedral edge size (500 μm) for the 8 M element mesh was used for all patients.

Figure 2.

Volumetric flow rates prescribed at the inlet of the models.

The peak Reynolds number and the Womersley number based on the infrarenal artery were computed as

$$R{e}_{\text{max}}=\frac{4\rho Q_{\text{max}}}{\pi D\mu },$$ (2)

$$\alpha =\frac{D}{2}\sqrt{{\displaystyle \frac{\omega \rho }{\mu }}},$$ (3)

where D is the mean diameter at the infrarenal section, Q_max is the peak systolic flow rate at the infrarenal section, μ is the dynamic viscosity, ρ is the density, and ω is the heartbeat frequency. Table 1 compares these nondimensional parameters, the maximum diameter of the aneurysm, the ratio of the maximum diameter to the infrarenal diameter, and the fraction of the supraceliac flow to the infrarenal level, between the patient models.

Table 1.

Fluid dynamic and geometric parameters of computer models.

Patient no.	Remax	α	Dmax (cm)	Dmax /Dinfra	Qinfra/Qsupra
Patient 1	2002	4.92	3.36	1.71	0.48
Patient 2	2241	5.20	3.72	1.84	0.66
Patient 3	2256	6.22	3.16	1.49	0.59
Patient 4	1667	5.86	3.24	1.49	0.47
Patient 5	1791	4.86	3.00	1.76	0.69
Patient 6	1419	3.63	3.89	2.39	0.31

LCS computations

A recent tool to study advective transport is the computation of Lagrangian coherent structures. LCS are material surfaces in the flow that have distinguished attracting or repelling properties.³⁶ While the computation of LCS originated to understand chaotic transport, LCS have been shown to organize both laminar and turbulent fluid motion. This method is compelling for unsteady flow conditions where fluid transport can be difficult to impossible to understand using traditional Eulerian techniques. Numerous applications have demonstrated the utility of LCS for understanding unsteady flow, including the ability to delineate boundaries of unsteady and interacting vortices, flow attachment or separation profiles, and the mechanisms underlying mixing, see Ref. 37 for a review. Computationally, LCS can be identified as hypersurfaces that locally maximize a finite time Lyapunov exponent measure.^{38, 39} This method is relatively straightforward and robust, and hence has become widely used.

The computation of the FTLE field requires the advection of a dense grid of fluid tracers over the domain of interest. Velocity data, v(x, t), obtained by image-based CFD, were used to solve the advection equation

$$\begin{array}{ccc}\dot{\mathbf{x}}\left(t\right)\hfill & =\hfill & \mathbf{v}(\mathbf{x},t),\hfill \\ \mathbf{x}\left(t_0\right)\hfill & =\hfill & {\mathbf{x}}_0,\hfill \end{array}$$ (4)

over a grid of initial conditions x₀ to provide final locations x(t₀ + T) after an integration time T. The FTLE was computed at each initial location x₀ as

$$\Lambda ({\mathbf{x}}_0,t_0;T)=\frac{1}{\left|T\right|}\ln {‖{\nabla }_{{\mathbf{x}}_0}\mathbf{x}(t_0+T)‖}_2.$$ (5)

Advection of the particle grid forward in time (T > 0) revealed repelling LCS in the FTLE field, whereas advection backward in time (T < 0) revealed attracting LCS in the FTLE field. As the notation in Eq. 5 indicates, the FTLE field corresponds to time t₀ and likewise the values are plotted at the initial locations x₀, and the integration time T is considered a parameter. Thus, while computed from a Lagrangian frame, the FTLE values are mapped back to the initial locations, and plotted as an Eulerian measure. Locally, high values of FTLE appear along hypersufaces that are generally identified with LCS. This procedure is repeated for a range of initial times t₀ to obtain the time evolution of the LCS.

The identification of LCS is relatively robust to changes in the integration length |T| used to compute FTLE. Nonetheless, the signature of any particular LCS in the FTLE field is dependent on the Lagrangian time scales of the dynamics. In general, since we seek to understand inherently transient phenomena, the integration time should be chosen long enough for dominant features to be revealed, but short enough for the FTLE to be representative of the transient dynamics. Herein, the integration time for each patient was set to the respective cardiac cycle length, which is suitable for cardiovascular applications.²³ Specifically, the dominant structures become well-defined in less than one cycle and the field does not change much by further increase in integration time length since most of the tracers used to compute the FTLE become flushed from the domain. The FTLE field was sampled every t₀ = 1/25th of the cardiac cycle. In our computations, we dropped the 1/T multiplication factor in the definition of FTLE (Eq. 5). This helps prevent tracers that leave the computational domain in a short time from erroneously increasing the FTLE value.³⁷

Effect of aperiodicity on LCS

The presence of transitional flow or mild turbulence observed in the aneurysms leads to cycle to cycle variation of the flow field, and the relevance of LCS derived from a single cardiac cycle may not be clear. Therefore, three additional methods for evaluating FTLE/LCS were explored. We defined an ensemble FTLE from a cycle-based temporal average of the FTLE field, i.e.,

$${⟨\Lambda ⟩}_{\mathrm{ens}}(\mathbf{x},t;T)=\frac{1}{n}\sum _{k=0}^{n-1}\Lambda (\mathbf{x},t+kT;T),$$ (6)

where t ∈ [0, T), and n is the number of cardiac cycles considered. Second, we defined a max-ensemble FTLE as the maximum FTLE among the corresponding ensembles of the FTLE data, i.e.,

$${\Lambda }_{\max -\mathrm{ens}}(\mathbf{x},t,T)=\underset{0\le k\le n-1}{\max }\left\{\Lambda (\mathbf{x},t+kT,T)\right\}.$$ (7)

Finally, we defined a velocity-ensemble FTLE, Λ_vel-ens, as the FTLE obtained from the ensembled average velocity field

$${⟨\mathbf{v}⟩}_{\mathrm{ens}}(\mathbf{x},t)=\frac{1}{n}\sum _{k=0}^{n-1}\mathbf{v}(\mathbf{x},t+kT).$$ (8)

We used five cardiac cycles of FTLE data for ensemble FTLE and max-ensemble FTLE, and five cardiac cycles of velocity data for velocity-ensemble FTLE computations.

RESULTS

Sections of the 3D FTLE field are shown in the results below. Curves of high FTLE correspond to cross-sectional slices of embedded LCS hypersurfaces. Nominally, two planes are shown for each patient. A sagittal plane approximately bisects the left and right hemispheres of the aneurysm, and a transverse plane was chosen slightly distal to the location of maximal bulge, see Fig. 3. For Patient 4, a cross-sectional view of the flow in an iliac aneurysm was added, and for Patient 5, additional sections of the AAA were chosen due to the complexity of the aneurysm shape. Sections of the backward and forward FTLE fields are presented in Figs. 4567891011 for the six patients. The Eulerian velocity field is also included for comparison. The colorbars are scaled based on the specific maximum range of each case.

Figure 3.

Cross-sections used for displaying results.

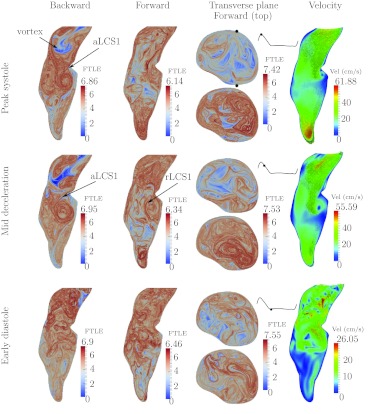
Figure 4.

Sagittal and transverse sections of the forward and backward FTLE fields, and sagittal section of velocity field for Patient 1 at different times of the cardiac cycle. The two points in the top transverse plane show where the sagittal plane intersects.

Figure 5.

Sagittal and transverse sections of the forward and backward FTLE fields, and sagittal section of velocity field for Patient 2 at different times of the cardiac cycle. The two points in the top transverse plane show where the sagittal plane intersects.

Figure 6.

Sagittal and transverse sections of the forward and backward FTLE fields, and sagittal section of velocity field for Patient 3 at different times of the cardiac cycle. The two points in the top transverse plane show where the sagittal plane intersects.

Figure 7.

Sagittal and transverse sections of the forward and backward FTLE fields, and sagittal section of velocity field for Patient 4 at different times of the cardiac cycle. The two points in the top transverse plane show where the sagittal plane intersects.

Figure 8.

Section of the forward and backward FTLE fields in Patient 4's iliac aneurysm at different times of the cardiac cycle.

Figure 9.

Coronal (left) and sagittal (right) sections of the forward and backward FTLE fields, and velocity field for Patient 5 at different times of the cardiac cycle.

Figure 10.

Transverse sections of FTLE in the proximal and distal lobes for Patient 5. The points show where the sagittal plane intersects.

Figure 11.

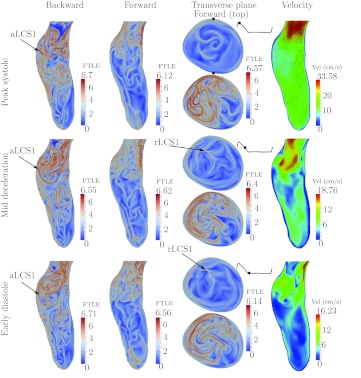
Sagittal and transverse sections of the forward and backward FTLE fields, and sagittal section of velocity field for Patient 6 at different times of the cardiac cycle. The two points in the top transverse plane show where the sagittal plane intersects.

Patient 1

Figure 4 shows the FTLE and velocity fields for Patient 1. During peak systole (top row), there is a region of low backward FTLE in the proximal segment. This region indicates a penetrating inflow jet into the aneurysm. The low backward FTLE values indicate low sensitivity to initial conditions when particles in this region are integrated backward in time. This implies that the inflow jet is coherent. The indicated aLCS1 marks the boundary of the jet. The jet penetrates deep into the aneurysm and as it enters the expansion region, it rolls up into a large vortex ring. The cores of this vortex ring on the sagittal cross-section are clear in the backward FTLE during mid-deceleration. The jet impinges on the anterior wall just distal to the region of maximal bulge as indicated by the arrow in the forward FTLE field during mid-deceleration. Specifically, in the forward FTLE field, there is an accumulation of repelling LCS orthogonal to the anterior wall, indicating the flow is directly impinging and rolling up on either side of this location.

As the jet penetrates into the abdominal aorta, it separates from the anterior aortic wall, as indicated by the separation profile marked aLCS2. This separation induces vortical motion along the proximal anterior aspect of the bulge and, along with the vortical motion induced from the roll up of the inflow jet, contributes to a persistent region of recirculation in the proximal anterior bulge. The aLCS3 and aLCS4 are separation surfaces from the posterior wall that are formed by the jet and roll-up. The distal separation from the posterior wall persists during much of the cardiac cycle. In both anterior and posterior regions of separation, there are dense sets of LCS, indicating well mixed separation regions, as opposed to stagnant. During the diastolic phase, both the forward and backward FTLE indicate several coherent vortices spanning the entire aneurysm, which indicates strong stirring/mixing during diastole from mechanisms described in Ref. 40.

Patient 2

The results for Patient 2 are shown in Fig. 5. For this patient, the inflow jet does not penetrate into the main aneurysm bulge. While a vortex ring can be seen in the proximal abdominal aorta in the backward FTLE field during systole (top left), the vortex breaks up, and results in mixing and dissipation in the proximal segment, and relatively low flow in the main bulge. This appears to be a self-sustaining process; the break up of the vortex and subsequent dissipation during diastole leads to dense LCS in the proximal region that causes the early break-up of the subsequent systolic inflow jet/vortex. This leads to stronger mixing proximal to the aneurysm than in the aneurysm. Large flow separation is observed from the posterior wall (aLCS1). The indicated attracting and repelling LCS (aLCS1 and rLCS1) together form a boundary to a large vortex formed in the separation region, cf. Ref. 41 for a discussion on the relationship of LCS to vortex rings. However, this separated region is well-mixed, as indicated by high FTLE inside the vortex. It is the shedding of this posterior wall vortex during diastole that leads to the majority of the mixing observed in the main bulge, i.e., the mixing appears less due to the break up of the inflow jet, and more due to the distal vortex formation and dissipation.

Patient 3

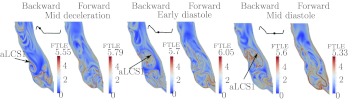
Figure 6 shows the results for Patient 3. There is a lack of coherent structures in the forward FTLE field during most of systole, whereas there are several LCS indicated in the backward FTLE. This indicates relatively low mixing in the aneurysm itself but high mixing proximal to the aneurysm. Indeed, at the end of systole, there is significant retrograde flow in the abdominal aorta for this patient and a vortex forms at the proximal segment and propagates upstream resulting in vortex pinch off⁴² as indicated. This vortex pinch off event and subsequent dissipation into several vortices during the diastolic phase contributes to the subsequent high backward FTLE values and prevalent coherent structures observed during systole in the backward FTLE plots. Specifically, the vortices formed in the proximal segment due to the retrograde flow get pushed into the aneurysm during systole. There are few and sparse LCS in the forward FTLE field, which indicates that the vortices originating from the proximal segment rapidly dissipate as they are advected into the main bulge. Therefore, relatively low mixing occurs in the distal segment. For example, the indicated rLCS1, which partitions fluid flushed from the aneurysm, showed very slow rate of change in its structure or movement.

Patient 4

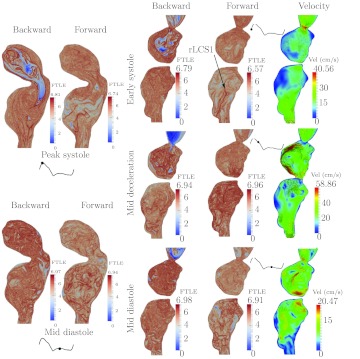
Figure 7 shows the results for Patient 4. The aLCS1 is the boundary of a proximal inflow jet to the aneurysm, which forms a well-defined vortex ring. The vortex ring impinges on the proximal anterior wall of the aneurysm at the end of systole. The vortex subsequently breaks up and dissipates during diastole, but maintains a relatively coherent large scale vortical structure over much of the cardiac cycle. As with Patient 3, because of the strong dissipation in the proximal segment, and relatively smooth aneurysm geometry, there is a lack of coherent structures in the forward time FTLE field in the majority of the distal segment, leading to low mixing. This patient demonstrated very little change in the FTLE field with time in both planes (cf. rLCS1); in fact, the forward FTLE in the transverse plane changed very little over the cycle even though there was more evident change to the velocity field.

Patient 4 had a mild aneurysm in the right iliac artery. Figure 8 shows the FTLE fields in the right iliac. The aLCS1 captures flow separation that occurs at the proximal aspect of the aneurysm. Similar to the posterior wall separation described for Patient 2, the separation surface moves proximal and expands during diastole, extending the recirculating region, however, flow here is more laminar and less mixing occurs in the separated region.

Patient 5

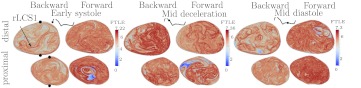
The results for Patient 5 are provided in Figs. 910. This patient had a significantly bi-lobed aneurysm. There is transitional/mild turbulence in both lobes during most of the cardiac cycle. This is indicated by high FTLE throughout both lobes. More specifically, the flow topology contains fine scale LCS throughout the aneurysm, which when viewed as shown, appear as regions of high FTLE, but when viewed closer are tightly spaced individual structures. This indicates small scale vortices dominating the flow topology throughout. These small scale LCS are apparent in the other patients, but to lesser extent. Due to the randomness this imparts to the flow field, the incoming jet during systole quickly destabilizes. During the acceleration phase of systole, an inflow jet can be distinguished in the backward FTLE field forming a vortex ring. This jet can be distinguished in both sagittal and coronal views in Fig. 9. Following peak systole it is difficult to identify any large scale Lagrangian structure from this vortex (even though it appears well-defined in the Eulerian field). The rLCS1 in the forward FTLE plot of Fig. 9 divides the flow in the second bulge into two regions at the beginning of systole. This LCS marks the boundary of particles that are flushed from the distal bulge on the posterior side from a region on the anterior side that recirculates. Figure 10 shows the FTLE field for two transverse planes, one section for each lobe. The regions of low backward FTLE show the inflow into the first bulge.

Patient 6

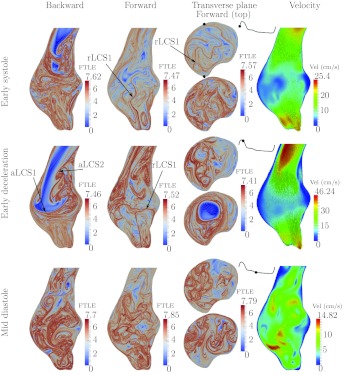
Figure 11 shows the results for Patient 6. The flow topology is similar to that observed in Patient 1. There is a large jet that penetrates far into the aneurysm during systole, with boundary marked by aLCS1. Since the backward FTLE in the jet is low, the inflow jet is highly coherent. Flow separates (aLCS2) from the posterior wall before the aneurysm bulge, which forces the inflow jet to the anterior side, shearing the anterior wall. The jet rolls up into a large vortex ring that spans nearly the entire aneurysm and impinges on the distal anterior wall. The dissipation of the vortex leads to relatively large scale mixing by vortical structures throughout the aneurysm during diastole as observed in both the forward and backward FTLE fields. The rLCS1 partitions the particles that are advected out of the aneurysm from the posterior side.

Aperiodicity

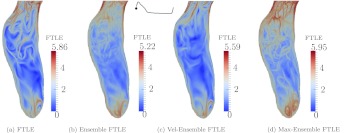
Figure 12 shows the different representations of FTLE discussed in Sec. 2B1. Results are only shown for Patient 4, but similar observations were made from data of the other patients. The max-ensemble FTLE presents more structures due to cycle to cycle variations of the flow and a combining of the maximum FTLE from each cycle. This was even more pronounced in other patients. The ensemble FTLE dissipates the flow structures and only the most persistent structures remain. The velocity-ensemble FTLE represents the structures based on the average behavior of the flow, which most closely resembled the FTLE based on a single realization of the flow. For all patients, the dominant LCS and flow features discussed above persist in all representations, which motivated the use of one realization for presentation of the results.

Figure 12.

Comparison of different representations of FTLE for Patient 4. The figure is based on forward FTLE.

DISCUSSION

The results demonstrate dramatic difference in the AAA flow patterns between patients. One persistent trait of all aneurysms studied was the formation of a proximal vortex during systole. High flow enters the expansion region during systole, and an adverse pressure gradient causes separation and subsequent roll-up. The implication of this vortex formation must be considered on a patient-to-patient basis. Whether this vortex penetrated into the main bulge seemed to depend on the initial orientation of the inflow jet, or perhaps more importantly the complexity of the flow in the proximal aneurysm during diastole. The dynamics of the flow topology during diastole, which is roughly 2/3 of the cardiac cycle, and the systolic vortex propagation appeared tightly coupled. Specifically, the dynamics of the vortex depended strongly on the diastolic flow topology, and the diastolic flow topology depended strongly on the inflow vortex. Another general trait was that even though flow separation was prevalent in several of the aneurysms, flow in the separated regions was well-mixed. This is likely due to the unsteadiness and transitional nature of the flow. Indeed, even small levels of unsteadiness are known to induce significant entrainment and detrainment⁴¹ in cases where the steady background flow would result in a closed vortex or recirculation bubble.

In some situations, the Eulerian velocity field could also be used to identify the flow features revealed by the LCS. For example, the velocity field during mid-deceleration in Fig. 5 shows a recirculation region near the posterior wall. This is the same vortex described by aLCS1 and rLCS1. The attracting LCS gives, however, clearer indication to the exact location of separation. The attracting and repelling LCS together give a more precise boundary to the vortex. In most other cases, the LCS provided delineation of vortex boundaries or other flow features that were much more difficult, or impossible, to distinguish from snapshots of the velocity data.

Flow impingement, an important parameter in the rupture of intracranial aneurysms,⁴³ was observed in some of the AAA models, e.g., Patients 1, 4, and 6. Impingement may cause degradation of the vessel wall, thereby affecting AAA progression and subsequently rupture potential. This may be especially relevant for patients with a coherent inflow jet, since greater momentum transfer to the wall may occur. In other patients, complexity of the flow in the proximal segment may have prevented such impingement on the aneurysm wall, however this led to relatively lower mixing in the aneurysm. The results in Figs. 67 show less repelling LCS and mixing in the distal segments of the aneurysms of Patients 3 and 4. These aneurysms had relatively long lengths and our results are similar to previous findings that demonstrated increased length of the aneurysm diminishes the strength of the vortices and disturbances to the flows.¹ In most patients, separation occurred on the posterior wall, which shielded the posterior side of the aneurysm from the inflow jet. This result was contrary to previous reports of aneurysm asymmetry resulting in higher shearing of posterior wall compared to the anterior wall of the aneurysm. LCS results were primarily presented beginning at peak systole since most structures observed were formed in the acceleration phase and further developed until peak systole.

The non-Newtonian nature of blood may change the vortex structures in a AAA, e.g., by increasing dissipation.^{44, 45} Similarly, the flow topology could also change by fluid structure interaction between the blood flow and vessel motion. These effects were neglected in the present study. However, the flow topology changes from cycle to cycle and it is unclear that non-Newtonian rheology or vessel motion would dominate these changes to the flow. Furthermore, other physiologic considerations that manifest in changes to the inflow or outlet boundary conditions may have greater influence.

Regions of transitional or mildly turbulent flow resulted in small scale LCS that appeared as regions of high FTLE when viewed from the scale of the aneurysm. It was verified that in these regions, it is possible to extract well-defined coherent structures on smaller scales by locally refining the FTLE mesh. This brings up an important point that Lagrangian flow features can be revealed at scales smaller than the Eulerian flow data/features. This is because trajectory data incorporate spatiotemporally interpolated data, not solely instantaneous data. Therefore, it is typically prudent to make the FTLE mesh more resolved than the velocity mesh for LCS identification.

Previous AAA studies have used instantaneous Eulerian fields to identify disturbed flow patterns. Most of these studies focused on tracking vortices,¹² with the consequences of vortex interaction or mixing remaining unclear. For example, the λ₂-method has been used for detecting the vortical structures in AAA,⁴⁴ however, these Eulerian measures break down for unsteady flow, or vortex interaction, and do not provide any indication of the mechanisms of transport.

It has been hypothesized that vortices may trap platelets in a region that is separated from the rest of the flow inside AAA (Ref. ⁴⁴) leading to the progression of mural thrombus. However, our results indicated that the vortices typical to AAA show strong entrainment, detrainment, and interaction, leading to well mixed flow even in separated regions. The results herein begin to address the complexity of transport in AAA but more in-depth studies are needed to clarify the extent and effects of mixing on thrombus formation in aneurysms.

Maximal AAA diameter has been the standard parameter for AAA intervention. Indeed, there are correlations between AAA size and rupture. However, there are numerous cases of small to medium aneurysms unexpectedly rupturing, and numerous cases of aneurysms growing to copious size without rupturing. While acute rupture is due to mechanical wall failure, the progression of the AAA over time is likely influenced strongly by fluid mechanical processes. The flow topology is difficult to predict from AAA morphology alone, much less from maximal diameter. Therefore, a closer look into the flow topology of AAA along with relevant hemodynamic parameters may enable better understanding, and perhaps predictions, of aneurysm progression. This will ultimately require close comparisons of AAA flow topologies to actual progression data. These comparisons are in progress and will appear in a subsequent publication.

CONCLUSION

The transport topology in six patient-specific AAAs was studied. This was achieved by obtaining flow field information by image-based CFD and using the resulting velocity field data to compute Lagrangian coherent structures to identify and characterize transport. These methods enabled separation regions, vortex boundaries, vortex interaction, mixing, flow impingement, and particle advection patterns in aneurysms to be more clearly revealed than previous Eulerian metrics used to study flow in AAA. The AAAs demonstrated different forms of chaotic flow topologies. Results demonstrated that a major factor determining the AAA flow topology was the propagation of a systolic vortex that formed at the aneurysm entrance in all patients. The dynamics of this vortex could have important biomechanic implications. In some cases, this vortex dissipated in the proximal segment, whereas in other cases, the vortex penetrated through the aneurysm. The systolic vortex dynamics did not appear obvious from aneurysm shape or size. This implied that similar aneurysm shapes may have significantly different flow topologies.