Abstract
Green [J. Acoust. Soc. Am. 87, 2662–2674 (1990)] suggested an efficient, maximum-likelihood-based approach for adaptively estimating thresholds. Such procedures determine the signal strength on each trial by first identifying the most likely psychometric functions among the pre-proposed alternatives based on responses from previous trials, and then finding the signal strength at the “sweet point” on that most likely function. The sweet point is the point on the psychometric function that is associated with the minimum expected variance. Here, that procedure is extended to reduce poor estimates that result from lapses in attention. The sweet points for the threshold, slope, and lapse parameters of a transformed logistic psychometric function are derived. In addition, alternative stimulus placement algorithms are considered. The result is a relatively fast and robust estimation of a three-parameter psychometric function.
INTRODUCTION
In psychoacoustics, listeners’ performance on a task is often quantified by the psychometric function, the proportion of correct responses as a function of signal strength. For example, for a pure-tone detection task evaluated using an n-interval, m-alternative forced choice procedure, as the sound pressure level of the signal tone increases, listeners’ percent correct will increase monotonically from chance to 100% correct. The threshold is defined at some point along the psychometric function (e.g., the 75%-correct point). The method of constant stimuli (e.g., Engen, 1971) is often used to estimate the psychometric function, where stimuli with preset signal strengths are presented repeatedly in random orders. Percent correct values can then be calculated at these signal strengths and used to fit models of the psychometric function to the data (Wichmann and Hill, 2001a,b).
A common model of the psychometric function is a transformed logistic function
| (1) |
where x is the signal strength and φ is the parameter vector {α, β, γ, λ}. For this psychometric function, α describes the horizontal position of the function, β describes the slope of the function, γ defines the lower bound of the function and the proportion correct at chance (e.g., 0.5 for a 2-alternative forced choice task and 0.33 for a 3-alternative forced choice task), and λ is the distance between the upper asymptote of the function and 100% correct. A non-zero lapse parameter, λ, indicates that the listener failed to attend to the task on some proportion of trials, and so the highest performance levels achieved are (100 – λ)% correct.
Although frequently used, the method of constant stimuli might not be the most efficient procedure for estimating psychometric functions in all situations (e.g., Leek, 2001). There are several disadvantages of having inefficient estimation procedures. For example, time consuming experimental procedures can undermine the usefulness of an auditory task to be implemented as a diagnostic tool in the hearing clinic. Also, for subject populations such as laboratory animals or young children, the behavioral psychometric functions can be very shallow (e.g., Nelson and Kiester, 1978; Allen and Wightman, 1994; Buss et al., 2009). This could mean a very large number of trials would have to be collected to accurately estimate the psychometric function, despite the fact that these subjects often have only limited time available for the experiment. To provide a third example, for research focused on developmental aspects of the auditory system and the effects of learning, the time required to obtain an estimate of the psychometric function must be minimized to ensure the temporal resolution of the assessment (e.g., Rosen et al., 2010; Sarro et al., 2011).
In an effort to provide fast and accurate estimation of the thresholds, Green and colleagues (Green, 1990, 1993, 1995; Gu and Green, 1994) described a maximum-likelihood procedure that optimized the placement of the signal strength adaptively based on responses collected from previous trials. Briefly, using the signal strengths previously tested, and the listeners’ responses, the most likely among candidate psychometric functions is chosen. Then, based on that function, the signal strength for the next trial is chosen so as to minimize the expected variance in the threshold estimate (the sweet point).1 This procedure, coupled with yes/no psychophysical methods, has been adopted for the study of auditory perception in hearing-impaired listeners (e.g., He et al., 1998; Florentine et al., 2000; Dubno and Ahlstrom, 2001) as well as young children (e.g., Wright et al., 1997). Grassi and Soranzo (2009) provide an implementation of this procedure using MATLAB (The MathWorks, Inc., Natick, MA).
While the maximum-likelihood procedure is theoretically sound, from a pragmatic perspective, concerns arise regarding the resulting patterns of signal placement (Leek et al., 2000) and the reliability of the estimated thresholds. One concern is that the signal strength varies dramatically from trial to trial at the outset of each track (the sequence of trials at signal strengths provided by the procedure). Under these circumstances, it may be difficult for some listeners to comprehend the task and maintain consistent decision criteria. Second, if the candidate psychometric functions are quite different from the true psychometric functions, or if the candidate functions are not discernible from one another on the basis of just the threshold signal levels, errors in the threshold estimate can occur. This is particularly true if the psychometric function reflects a process with frequent lapses of attention (λ > 0; Green, 1995).
Subsequent to this initial work, solutions for the maximum-likelihood procedure in which the slope of the psychometric function is also estimated have been developed (King-Smith and Rose, 1997; Brand and Kohlmeier, 2002). King-Smith and Rose examined the choice of signal strengths for efficient estimation of the slope of the psychometric function while Brand and Kohlmeier recommended a “compromise” sampling strategy at two points of the psychometric function to provide a balance between the estimation of both the slope and the threshold parameters. In the present study, the maximum-likelihood procedure was further extended to estimate the midpoint (threshold, α), the slope (β), and the lapse rate (λ) for a psychometric function of the form shown in Eq. 1; i.e., for each of these three parameters, the sweet points are estimated assuming that γ is known exactly. In Sec. 2, we first provide a brief review of the maximum-likelihood procedure and the reasons the sweet point is important for efficient parameter estimation. Second, the solution for the sweet points associated with the parameters α, β, and λ are derived, and their properties are explored in Sec. 3. Third, in Sec. 4, potential strategies for stimulus placement among the sweet points are considered in order to best estimate all parameters (i.e., the psychometric function) rather than a single parameter (e.g., α). Finally, this extended procedure is compared with the original single-parameter procedure through simulations in Sec. 5.
MAXIMUM-LIKELIHOOD PROCEDURE
Assuming a logistic model [Eq. 1], the single-parameter maximum-likelihood procedure involves the following steps: First, an array of psychometric functions is proposed spanning a range of α values. The other parameters of the logistic function are preset by the experimenter and are fixed. The experiment begins with a signal strength at some initial value. Then, the signal strength is updated after obtaining each response from the listener. After the nth trial, the likelihood that each of the candidate psychometric functions (different values of the parameter α) is the true function is evaluated based on all previously collected responses (r1, r2,…, rn). Let r = 1 indicate a correct response, and r = 0 an incorrect response. Then the likelihood function L(α) is proportional to
| (2) |
where p is the probability of a correct response.
Among the candidates values of α, the α that yields the largest L(α) corresponds to the current maximum-likelihood estimate of the psychometric function. The signal strength on the (n + 1)th trial is determined as the signal strength at a certain fixed proportion-correct point on the current psychometric function estimate. After a number of trials, the α estimate begins to converge, and the track terminates either when a fixed number of trials has been completed, or when the estimate of α or x is known to within a predefined tolerance.
As demonstrated by Green (1990), there is an optimal proportion-correct point on the psychometric function, the sweet point, which should be used with the maximum-likelihood procedure. The sweet point is calculated as the point on the psychometric function that is associated with the minimum expected variance. This point is the optimal sampling point on the function if the primary interest is to accurately estimate thresholds. Presenting the stimulus at the sweet point of the estimated psychometric function on each trial minimizes the variability in the threshold estimate. If it is assumed that the psychometric function can be treated as locally linear for each x, the ratio between the expected variances of x and p(x, φ), , and , can be approximated as (e.g., Green, 1990)
| (3) |
Because the observed response on each trial is a binomial variable, the expected variance of p(x, φ)() for a given x is proportional to p(x, φ)[1 − p(x, φ)]. Therefore, the signal strength x on the next trial is selected to minimize the variability in x
| (4) |
Green (1993) provided an analytical solution of the sweet point px, the percent correct point on the psychometric function where is minimal with λ = 0
| (5) |
For the cases where lapses of attention (λ) are non-zero, numerical solutions of the sweet point can be obtained from Eq. 4.
Using the procedure described above, the signal strength at the sweet point can be reliably estimated, but the estimate of the psychometric function itself may not be accurate if the slopes of the candidate psychometric functions, associated with the parameter β, deviate from the true value. One might expand the pool of proposed psychometric functions to include not only a range of α’s but also a range of β’s. However, this is not helpful because the sweet point does not depend on the slope parameter β [see Eq. 5]. The presence of lapses of attention (λ > 0) poses a more significant challenge; when the true psychometric function has a non-zero λ, the threshold estimate can be quite biased, and estimates of the lapse parameter can be very poor (Green, 1995).
SWEET POINTS FOR THE THRESHOLD, SLOPE, AND LAPSE RATE OF THE PSYCHOMETRIC FUNCTION
To provide reliable estimates of the shape of a 3-parameter psychometric function [e.g., Eq. 1], one approach is to adjust the placement of the signal strength to minimize the variability in the estimates of the α, β, and λ parameters. The procedure is similar to that described above, except that the variability in α, β, and λ are estimated rather than (i.e., x is treated as a parameter rather than α in the development above). The resulting expected variances of the α, β, and λ estimates from a single trial, , , and , respectively, are
| (6) |
| (7) |
| (8) |
Note that the results for have been considered elsewhere for the case λ = 0 (King-Smith and Rose, 1997; Brand and Kohlmeier, 2002). The analytical expressions for , , and are provided in the Appendix.
These three expected variances [Eqs. 6, 7, 8] are functions of the signal strength x. The expected variance of λ, , is a monotonically decreasing function of x. Therefore, no true minimum can be found; to maximize the accuracy in the λ estimates, a large signal strength consistent with the experimental design should be used (an empirical recommendation suggested by Green, 1995, when considering yes/no procedures and listeners with lapses of attention). The proportion correct that corresponds to this large signal strength will be referred to as the λ-sweet point. For a sufficiently large maximum signal strength, the λ-sweet point will approximate the proportion correct value of 1−λ. For the and functions, there do exist values of x that minimize these expected variances, although for two minima emerge near the upper and lower asymptote of the function.2 The percent correct scores associated with the minima of and are the α-sweet point and β-sweet points. Together, four sweet points indicate the values of percent correct that yield the smallest expected variances of α, β, and λ, and the associated signal strengths should be tested when the goal is to quickly and accurately estimate the parameters α, β, and λ. Although not considered here, the γ-sweet point may also be derived.3
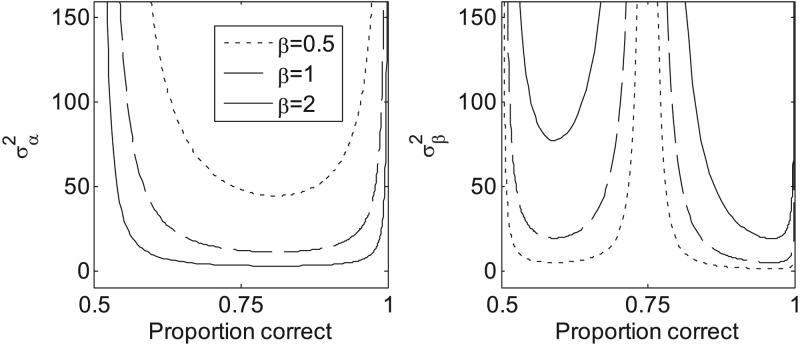
Figure 1 plots the expected variances of the α (left) and β (right) estimates as a function of proportion correct for psychometric functions with β values of 0.5 (dotted curves), 1 (dashed curves), and 2 (solid curves). The α and λ are both fixed at 0, and γ is fixed at 0.5. The expected variance of α exhibits a minimum near a proportion correct of 0.8 on the psychometric function. This means that repeatedly presenting the signal strength at that proportion correct on the psychometric function would result in an estimate of α with minimal variability, i.e., α-sweet point. Although the α-sweet point does not change with changes in the slope of the psychometric function, the expected variance of α grows with decreases in the slope of the psychometric function (for a fixed number of trials; from solid to dotted lines).
Figure 1.
The expected variances of the α (left) and β (right) estimates as a function of the proportion correct for psychometric functions with β values of 0.5 (dotted curves), 1 (dashed curves), and 2 (solid curves). The α, γ, and λ parameters are 0, 0.5, and 0, respectively.
In contrast to the results for α, the expected variance of β has two minima, and so two β-sweet points (see also King-Smith and Rose, 1997; Brand and Kohlmeier, 2002). At the midpoint of the psychometric function the expected variance of β approaches infinity, indicating that placing the signal strength at the midpoint of the psychometric function provides no information regarding the value of β. The β-sweet points do not depend on the slope of the psychometric function, but at the β-sweet points increase as the function becomes steeper in slope.
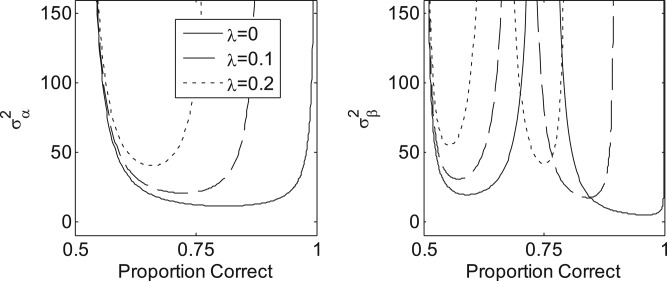
Figure 2 plots the expected variances of the α (left) and β (right) estimates as a function of proportion correct for psychometric functions with λ values of 0.2 (dotted curves), 0.1 (dashed curves), and 0 (solid curves). The values of α, β, and γ are set to 0, 1, and 0.5, respectively. The expected variability in the α and β estimates increase with increases in λ, and the α- and β-sweet points shift to lower percent corrects as the value of λ increases.
Figure 2.
The expected variances of the values of α (left) and β (right) estimates as a function of proportion correct for psychometric functions with λ values of 0.2 (dotted curves), 0.1 (dashed curves), and 0 (solid curves). The α, β, and γ parameters are 0, 1, and 0.5, respectively.
MODIFICATIONS TO THE MAXIMUM-LIKELIHOOD PROCEDURE
Introducing prior distributions for the psychometric-function parameters
Here a Bayesian approach is adopted in which a prior distribution for each of the free parameters (α, β, and λ; γ is assumed to be known) is set by the experimenter (see also King-Smith and Rose, 1997). The posterior distribution for each parameter is updated after every trial as new likelihoods are generated. This procedure differs from other Bayesian approaches, which choose the signal strength so as to minimize the entropy in parameter estimates (e.g., Kontsevich and Tyler, 1999), in that the sweet points are used as target values. The current approach is adopted because it allows the experimenter to choose a sampling strategy depending on, for example, whether the listener can withstand large changes in signal strength or whether one parameter is of particular importance and should be oversampled.
Bayes’ rule states that for data D, and alternative hypothesis φi (parameters)
| (9) |
where P(φi|D) is the posterior probability for hypothesis φi and P(φi) is the prior probability for the hypothesis given values of the parameters φi. The remaining ratio, , is the likelihood. Because the goal is the estimate the maximum likelihood among the population of potential parameters, the denominator is not necessary. That is, whether a normalized or unnormalized posterior is used, the location in the parameter space with the maximum likelihood remains the same. In practice the likelihood is computed as in Eq. 2, except that the probabilities depend on the parameter vector φ, not just α.
The process is as follows. The prior distributions, which are described in three dimensions (α, β, λ), are initially set by the experimenter. Then, on trial n, the likelihood ratio is described in three dimensions based on candidate three-tuples formed by potential values of α, β, and λ. The posterior is formed by multiplying the posterior from trial n − 1 and the likelihoods from trial n. The product is the posterior for trial n and its maximum is used to choose the most likely set of parameters, and so the new set of sweet points.
After the track terminates, the best fitted parameters as well as their confidence limits can be estimated from the final posterior distributions.
The introduction of the prior distributions of the parameters α, β, and λ has the potential of reducing the number of trials needed for the procedure to converge, it also reduces the number of large changes in signal strength that might otherwise occur for the first several trials. The choice of the priors is considered in more detail below (in Sec. 5B).
Following data collection, the resulting signal strengths, and listeners responses may be analyzed using a variety of algorithms (for example, the psignifit routine by Wichmann and Hill, 2001a,b, and the Bayesian Markov-chain Monte Carlo procedure by Kuss et al., 2005) to achieve an improved parameter fit and estimation of confidence limits for each parameter. However, for simplicity, in the following discussion, we consider the means of the posterior parameter distributions at the output of the updated maximum-likelihood procedure as the “final” fit.
Sweet-point/stimulus placement selection strategy
From the above analysis, we see that there are four sweet points on the psychometric function considered here, the lower β-sweet point, the α-sweet point, the upper β-sweet point, and the λ-sweet point, in order from low to high proportion correct. Recall that the λ-sweet point has no minimum, and is assumed to take on a value corresponding to a large signal strength. When estimating the psychometric function using the proposed updated maximum-likelihood procedure, one might place the signal strength on the next trial at any of these sweet points. The question of interest is how to best sample these signal strengths among the sweet points. Next, two algorithms for the selection among sweet points are considered. These two algorithms are not exhaustive; alternative algorithms may be appropriate depending on constraints that the experimental question and/or subject population exerts on data collection.
Random sweet-point selection
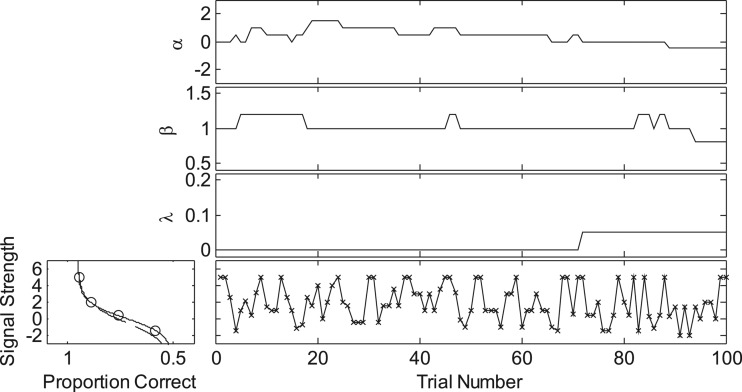
One simple rule for selecting the sweet point is to draw from the four possible sweet points at random, with equal probability, on each trial. A sample adaptive track using this random sweet-point selection rule is shown in Fig. 3 for a virtual listener with α = 0, β = 1, γ = 0.5, and λ = 0.05. For this example, the initial signal strength was 5, which was also the level used in association with the λ-sweet point. There were 21 possible values of α (ranging from −5 to 5), 10 possible values of β (ranging from 0.2 to 2), and 5 possible values of λ (ranging from 0 to 0.2). The potential parameters in this three-dimensional parameter space were equally spaced on a linear scale. The prior distribution for each of the three parameters had a Gaussian shape. For α the mean was 0 and the standard deviation was 2.5; for β the mean was 1 and the standard deviation was 0.75; and for λ the mean was 0 and the standard deviation was 0.1 (with a domain that ranged from 0.2 to 0, yielding minimal and maximal percent correct values allowed). A total of 100 trials were tested. It should be noted that the virtual listener did not “guess” on some number of trials; inattention is folded into the form of the psychometric function as the true λ.
Figure 3.
A sample track using a random sweet-point selection rule. Left: the sweet points (circles) on the psychometric function of a virtual observer with α = 0, β = 1, γ = 0.5, and λ = 0.05 (solid curve), and the estimated psychometric function (dashed curve). Right: the maximum-likelihood estimates of α, β, and λ, as well as the signal strength (from top to bottom), in a simulated track that consists of 100 trials.
The top three panels of Fig. 3 show the values of α, β, and λ estimated after each trial. The bottom panel on the right shows the signal strengths tested (see ordinate labels to the left). The panel on the left plots the true underlying psychometric function (solid curve, plotted with signal strength on the ordinate and percent correct on the abscissa), the four sweet points (circles), and the estimated psychometric function (dashed curve). The psychometric function is fitted quite well using only 100 trials.
Up-down procedure for sweet-point selection
A second sweet-point selection rule is based on an up-down adaptive algorithm (Levitt, 1971). For example, in a 3-down, 1-up track, after three consecutive correct responses the signal strength would be switched to that associated with the adjacent lower sweet point for the subsequent presentation (e.g., from the upper β-sweet point to the α-sweet point, from the α-sweet point to the lower β-sweet point, etc.), and after an incorrect response the signal strength would be switched to the signal strength associated with the adjacent higher sweet point (e.g., from the lower β-sweet point to the α-sweet point, etc.). Note that three of the four sweet points (the signal strength associated with the λ-sweet point is fixed at a large value) are updated on a trial by trial basis, therefore even if the choice of sweet point were consistent across two trials the actual signal strengths might vary. One of the advantages of this hybrid procedure combining the maximum-likelihood and the up-down methods is that the change in signal strength is constrained across sequential trials. For the logistic psychometric with γ = 0.5, the step size is maintained at about one-quarter to one-third of the total dynamic range of the psychometric function. Second, this method also maintains a fairly consistent percent correct performance level across different conditions, which might lead to more consistent performance by the observers across conditions. Third, by this hybrid approach, the experimenter has the option to emphasize some sweet points over others. For example, if a 3-down, 1-up method is used, a relatively large number of trials would be drawn from the α-sweet point. This means the estimate of α-would converge quickly; on the other hand, when a 4-down, 1-up method would emphasize the upper β- and λ-sweet points.
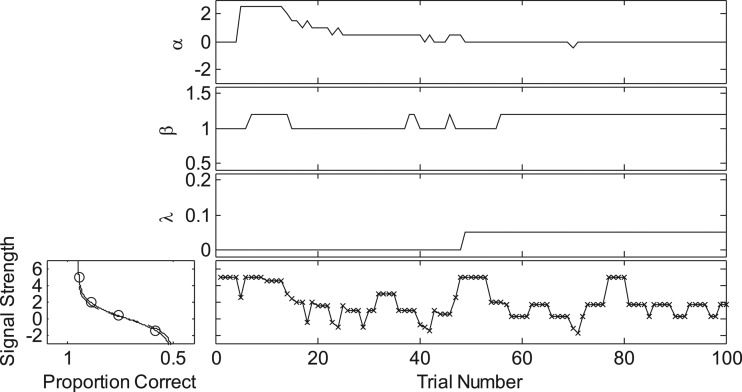
An example of a track using the hybrid procedure is shown in Fig. 4 for the same virtual listener (α = 0, β = 1, γ = 0.5, and λ = 0.05), priors, and parameter spaces described for the simulation outlined above. A 4-down, 1-up tracking rule was implemented for this example. As the number of trials increased, the track stabilized in that relatively fewer signal strengths were tested, indicating the stability of the parameter estimates.
Figure 4.
Same as Fig. 3, except this example is based on a hybrid, 4-down, 1-up sweet-point selection rule.
SIMULATIONS
A series of Monte Carlo simulations were conducted to test the updated maximum-likelihood methods and compare the procedure with the original one-parameter maximum-likelihood procedure (e.g., Green, 1990). Virtual listeners were implemented, each of whom generated responses according to a psychometric function described by a parameter vector φ0 = {α0, β0, γ0, λ0}. Four different procedures were used to estimate the psychometric function parameters, they were (i) the original maximum-likelihood procedure with proposed psychometric functions in a two-dimensional (α, λ) space (Green, 1990, 1995), (ii) the original maximum-likelihood procedure in three-dimensional [using Eqs. 6, 7, 8] (α, β, λ) space, (iii) the updated maximum-likelihood procedure with 4-down, 1-up sweet-point selection rule, and (iv) the updated maximum-likelihood procedure with a random sweet-point selection rule. For the original maximum-likelihood procedure [(i) and (ii), above), the signal strength was set at the level corresponding to the α-sweet point, and the α-sweet point was updated using equations with just α and λ, or equations with α, β, and λ. For the updated maximum-likelihood procedure [(iii) and (iv), above] four sweet points were used, and the sweet point selection rule differed. For both the original and updated procedures a Bayesian approach was adopted, i.e., sweet points were chosen on the basis of the maximal posterior. This approach was not emphasized in the original work by Green and colleagues, but provides stimulus placement that will typically converge more quickly than the original.
Two virtual listeners were tested with a total of 100 Monte Carlo adaptive tracks, each based on 200 trials, for each of the four procedures indicated above. All algorithms and simulations were developed in MATLAB (The MathWorks, Inc., Natick, MA). For these simulations the values of α ranged from −5 to 5 with a spacing of 0.5 (21 values); the proposed values of β ranged from 0.2 to 2 with a spacing of 0.2 (10 values), except for the first procedure where β was fixed at 1; the proposed λ ranged from 0 to 0.2 with a spacing of 0.05 (5 values). The γ parameter was fixed at γ0 = 0.5, assuming a task design with a chance performance level of 50% correct. The prior distribution for α was a normal distribution with a mean of 0 and standard deviation of 2.5; the prior distribution for β [except in procedure (i)] was a normal distribution with a mean of 1 and a standard deviation of 0.75; the prior distribution for λ was a normal distribution with a mean of 0 and a standard deviation of 0.1 and constrained to remain between 0.2 and 0. The maximum signal strength, 12, was also the signal level associated with the λ-sweet point. This ensured that for all φ0 included in the simulations, the λ-sweet point was always higher than the upper β-sweet point.
Comparison of different maximum-likelihood-based approaches
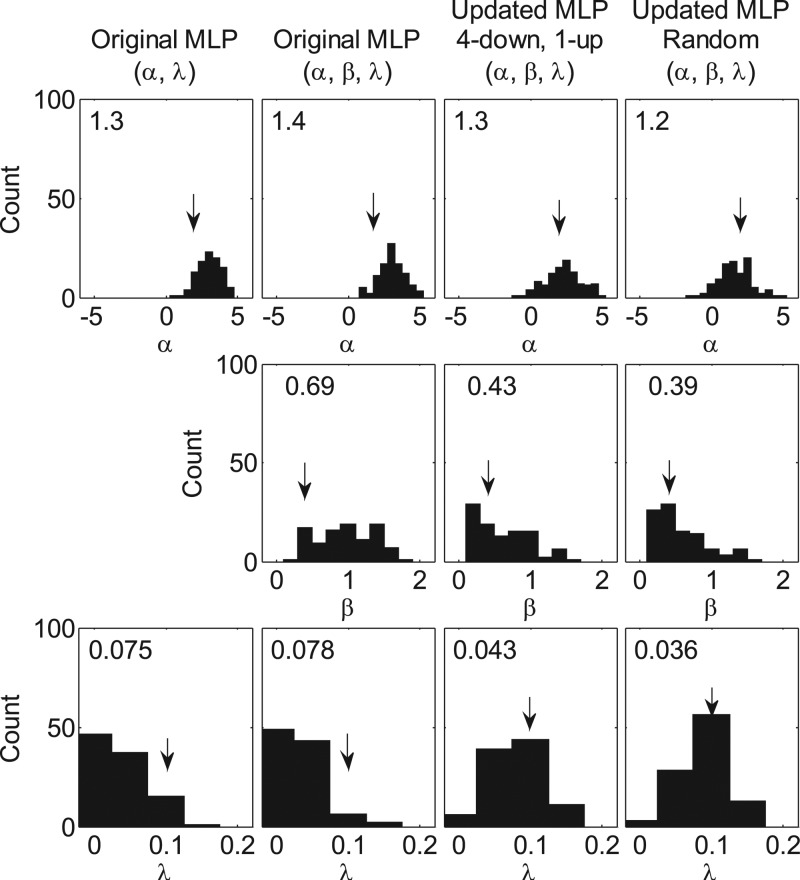
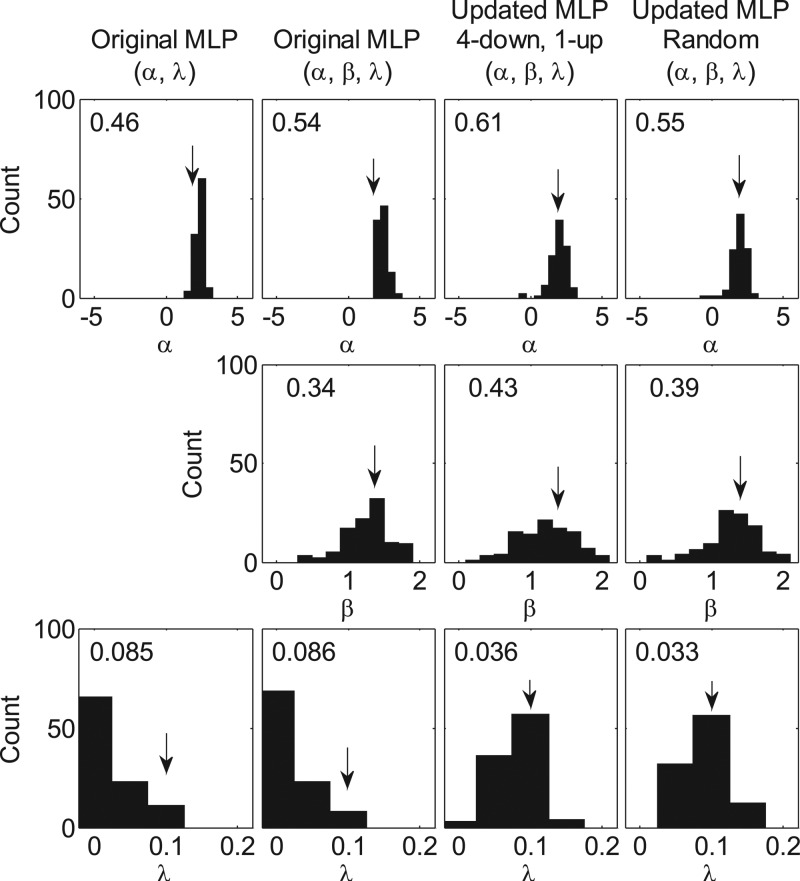
Figures 56 plot histograms of the parameter estimates (α, β, and λ, arranged in three rows from top to bottom) for the four procedures (in columns). The results for two virtual listeners with φ0 = {2, 0.4, 0.5, 0.1} and {2, 1.4, 0.5, 0.1} for {α, β, γ, λ} are shown in Figs. 56, respectively. The numerical value in each panel indicates the root-mean-square (rms) deviation between the estimated parameter and the true parameter. Smaller rms deviation values suggest a more accurate estimation of the parameter.
Figure 5.
Histograms of the α (top), β (middle), and λ (bottom) estimates from 100 Monte Carlo simulated procedures using the original maximum-likelihood procedure in which signal strengths are chosen based on just the α-sweet point (first two columns) or based on the updated method that samples four sweet points (last two columns). For the former, the candidate psychometric functions either did (2nd column) or did not (1st column) include the parameter β. For the updated procedures, the four sweet points were either sampled using a 4-down, 1-up algorithm or at random. The number inside each panel indicates the rms error of the estimates relative to the true value. The true psychometric function had parameters α = 2, β = 0.4, γ = 0.5, and λ = 0.1.
Figure 6.
As Fig. 5 but the true psychometric function had values of α = 2, β = 1.4, γ = 0.5, and λ = 0.1.
For all four procedures and for both listeners, estimates of α were very good (top row) with rms deviations ranging from 1.2 to 1.4 for the virtual listener with the shallower psychometric function (β0 = 0.4; Fig. 5) and from 0.46 to 0.61 for the steeper-sloped listener (β0 = 0.4; Fig. 5). These deviations were less than one-tenth of the dynamic ranges of the psychometric functions. A detailed inspection suggested that the original maximum-likelihood procedures gave slightly higher α estimates than the true value. This could be due to the misestimation of the λ parameter as suggested by Green (1995), and this bias was more evident when the true slope of the psychometric function was shallow (Fig. 5).
Next consider the estimated values of λ (bottom row). Results from the first and second procedures (first and second columns of Figs. 56) failed to estimate λ. The estimated values of λ show little information beyond the properties of the original prior distribution. Had the prior distribution not constrained the choice of λ, it seems likely that the estimates of λ would have been essentially random, potentially interfering with estimates of α. For the two updated procedures, there was little advantage of one over the other with regard to the quality of fit to λ. Presumably this reflects the fact that both procedures visited the λ-sweet point fairly frequently.
Finally, consider the estimation of β (middle row). For the original maximum-likelihood procedure (second column), the estimate of β was poor when the slope was shallow (Fig. 5) and quite accurate when the slope was steep (Fig. 6). For the former the estimate appeared to rely only on the prior distribution. With regard to the relatively good fit of β when the function was steep, this result may reflect the fact that changes in the α-sweet point covered a larger proportion of the dynamic range of the psychometric function when the slope was steep than when the slope was shallow; and so there was more opportunity to estimate the true value of the slope. For the updated procedures, the estimates of β were also quite good, and possibly superior when the sweet points were sampled at random than when they were sampled using a 4-down, 1-up procedure. This might reflect the relatively few samples at the lower β-sweet point when the 4-down, 1-up procedure was tested. Nonetheless, both of the updated procedures provided reasonably good estimates of the slope parameter β relatively independent of the value of β.
Choice of prior distributions
The same priors were used for the simulation results shown in Figs. 56. This was done to allow “fair” comparisons across various procedures. Previous studies have suggested that the choice of priors can affect the estimation of posteriors (e.g., Kuss et al., 2005), especially when small numbers of trials are tested. Therefore, it is of interest to investigate the effect of the prior distributions on the psychometric function estimates.
Prior distributions describe an experimenter’s belief regarding the likelihood across all the candidate psychometric functions in the parameter space. When the experimenter does not wish to make assumptions regarding the distributions of the parameters, uninformative priors could be used. Two common choices of uninformative priors include the Jeffrey’s prior and the conjugate prior (Gelman et al., 2004). However, it is often the case that the experimenter does have some knowledge on the most likely range of parameters (e.g., based on the published data and previous experiences with similar experiments). In such situations, informative priors, typically narrower than uninformative priors, might be used, which would accelerate the convergence of the posterior distributions. A proper choice of priors would also prevent the maximum-likelihood-based algorithms from scanning through the extremes of the parameter space and varying the signal strength widely during the first few trials. That is, informative priors lead to relative stable psychometric function estimates during the first few trials, independent of whether subjects make early errors. This, however, does not mean that the narrower priors are always better; using priors that are too narrow (or have too-small standard deviations) increases the risk of misestimating the parameters when relatively few trials are tested.
In order to evaluate the effects of priors on the estimation of the psychometric function, a virtual listener with φ0 = {2, 0.4, 0.5, 0.1} was used and the accuracy in parameter estimation was estimated across systematic variations in the standard deviation of the prior distribution for each parameter. The same virtual listener was used for the simulations shown in Fig. 5. As in the previous simulations, the means of the prior distributions for α, β, and λ were 0, 1, and 0, which are misaligned relative to the true values. One hundred Monte Carlo adaptive tracks, each based on 200 trials, were tested.
Table TABLE I. lists the rms of the deviations between the estimated and the true parameters across variations in the standard deviations of the α, β, and λ priors. In general, decreasing the standard deviation of the α prior had similar effects on the accuracy of the α estimates across the three procedures tested [the original maximum-likelihood procedure with α, β, and λ (MLP 3D), the updated procedure with an up-down sweet-point switching rule, and the updated procedure with a random switching rule]: the rms deviation first decreased then increased, forming a minimum for a moderate value of standard deviation. The decreasing portion reflects the improvement associated with a more informative prior, while the increasing portion reflects a bias in the estimates caused by the mismatch between the means of the prior and the true parameter values. It is interesting that increasing the standard deviations of the β and λ priors had similar effect on the α estimates, suggesting that using informative priors on β and λ could improve the estimation of α, but not when too narrow priors were used.
TABLE I.
The rms deviations from the estimated to the true parameters listed as functions of the standard deviations for the α (top), β (middle), and λ (bottom) prior distributions. In each of the three simulations, the prior distributions for the non-varying α, β, and λ parameters had fixed standard deviations of 2.5, 0.75, and 0.1, respectively. The true psychometric function was defined by φ0 = {2, 0.4, 0.5, 0.1}. Results are shown for three procedures: the original maximum-likelihood procedure (left), the updated procedure with an up-down sweet-point switching rule (center), and the updated procedure with a random sweet-point switching rule.
| Original MLP 3D | Updated MLP up-down | Updated MLP random | |||||||
|---|---|---|---|---|---|---|---|---|---|
| α | β | λ | α | β | λ | α | β | λ | |
| Standard deviation of α prior | |||||||||
| 15 | 2.1 | 0.75 | 0.091 | 1.5 | 0.49 | 0.046 | 1.6 | 0.37 | 0.049 |
| 6.25 | 1.9 | 0.67 | 0.091 | 1.7 | 0.47 | 0.045 | 1.4 | 0.44 | 0.04 |
| 2.5 | 0.54 | 0.34 | 0.086 | 0.61 | 0.43 | 0.036 | 0.55 | 0.39 | 0.033 |
| 1 | 1.1 | 0.56 | 0.048 | 1.5 | 0.28 | 0.036 | 1.4 | 0.27 | 0.04 |
| 0.4 | 1.7 | 0.5 | 0.068 | 2 | 0.22 | 0.035 | 1.9 | 0.21 | 0.042 |
| Standard deviation of β prior | |||||||||
| 3 | 1.3 | 0.95 | 0.069 | 1.3 | 0.6 | 0.049 | 1.1 | 0.53 | 0.038 |
| 1.5 | 1.4 | 0.79 | 0.077 | 1.1 | 0.53 | 0.04 | 1.3 | 0.44 | 0.042 |
| 0.75 | 0.54 | 0.34 | 0.086 | 0.61 | 0.43 | 0.036 | 0.55 | 0.39 | 0.033 |
| 0.375 | 1.5 | 0.58 | 0.076 | 1.4 | 0.46 | 0.034 | 1 | 0.42 | 0.036 |
| 0.2 | 1.4 | 0.6 | 0.075 | 1.4 | 0.56 | 0.031 | 0.96 | 0.54 | 0.039 |
| Standard deviation of λ prior | |||||||||
| 0.4 | 1 | 0.75 | 0.082 | 1.4 | 0.46 | 0.039 | 1.2 | 0.45 | 0.046 |
| 0.2 | 1.2 | 0.69 | 0.067 | 1.3 | 0.5 | 0.037 | 1.3 | 0.43 | 0.042 |
| 0.1 | 0.54 | 0.34 | 0.085 | 0.61 | 0.43 | 0.036 | 0.55 | 0.39 | 0.033 |
| 0.05 | 1.7 | 0.64 | 0.095 | 1.3 | 0.33 | 0.049 | 1.2 | 0.31 | 0.052 |
| 0.025 | 1.7 | 0.63 | 0.1 | 1.4 | 0.31 | 0.074 | 1.3 | 0.28 | 0.078 |
The changes in the accuracy of the β and λ estimates were less systematic than for α. For the original maximum-likelihood procedure, the rms deviation of the β estimates increased as the standard deviation of all three prior became too large or small, while the λ estimates were fairly poor independent of the changes in the prior distributions. For the two updated maximum-likelihood procedures, the β and λ estimates were not strongly influenced by the changes in priors. The rms deviations for these two procedures were generally smaller than the corresponding conditions for the original procedure.
Summarizing these observations, a rule of thumb is that the priors with standard deviations that are between one-half and one-quarter of the range of the parameter space produce the most satisfactory results. Moreover, the estimation of the β and λ parameters is more resistant to the alterations in the prior distributions for the updated maximum-likelihood procedures. Therefore, if the experimenter’s goal is to estimate the complete psychometric function, including the slope and lapse parameters, the updated procedures provide superior results. On the other hand, the estimates of α are not greatly affected by the misestimation of the β and λ parameters. Thus, if the experimenter’s research interest is in the threshold estimates, the original maximum-likelihood procedure might be used with appropriate priors, since it sometimes provides slightly better estimates of α.
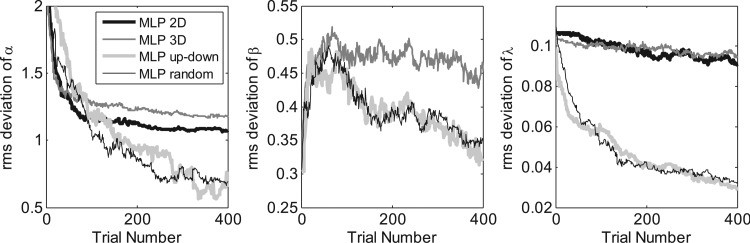
Rates of convergence
Figure 7 plots the rms deviation of the parameter estimates from the true parameter values as a function of trial number. To provide a robust generalization, the values of the parameters used by the virtual listener’s true psychometric function, φ0, were chosen at random for each Monte Carlo simulated procedure. The values of α0 were drawn from a uniform distribution with a range of −4 to 4, β0 was drawn from a uniform distribution with a range of 0.4 to 1.4, and λ0 was drawn from a uniform distribution with a range of 0 to 0.2. Using the same four procedures described in Sec. 5A, each “track” included 400 sequential trials, and the rms error was based on the deviations across K = 100 replicates. In other respects the simulation methods were as described earlier. Let φ0,k denote the parameters drawn for the kth replicate and let φk,n denote the parameter estimate obtained from the kth replicate after the nth trial. The average rms deviation was given by
| (10) |
Figure 7.
The rms deviations between the parameter estimates and the true parameters of the underlying psychometric function as a function of the number of trials. Changes in the functions indicate the rate at which the parameters converge for three parameters: α, β, and λ (left to right panels). Four procedures were tested: (i) MLP 2D: the original MLP procedure with two parameters, (α, λ); (ii) MLP 3D: the original MLP procedure with two parameters, (α, β, λ); (iii) MLP up-down: the updated MPL procedure a 4-down, 1-up sweet-point selection rules; (iv) MLP random: the updated MLP procedure with random sweet-point selection rule. These are as described for Fig. 5.
First consider the results for the estimates of α (left panel of Fig. 7). All four procedures initially fell quickly, and as the number of trials exceeded 100 or so, the rms values for the original maximum-likelihood procedures tended to asymptote while those from the updated maximum-likelihood procedures continued to fall. By 400 trials all four of the functions appeared to have reached an asymptote. Presumably, estimates of α continued to improve with more trials for the updated procedures because the values of β and λ were also being better estimated. It should be noted that at 100 trials, the updated maximum-likelihood procedure with the random sweet point selection rule outperformed the other three procedures, a result not apparent in Figs. 56. This indicates that the convergence rates for α depends on the properties of the true psychometric function.
The middle panel of Fig. 7 plots the rms deviations for β (recall, β is not estimated for the curve indicated as “MLP 2D”). For all procedures, the rms value increased sharply across the first 50 trials, indicating the dispersion of the prior distributions for β. Beyond 50 trials, the deviation for the original maximum-likelihood procedure continued to grow slowly whereas the updated procedures converged toward a solution. It may be somewhat surprising that the two updated procedures had approximately equal convergence rates; the 4-down, 1-up procedure under-represents the lower β-sweet point. Potentially this procedure was somewhat more efficient than one might expect because there was less expected variance associated with the upper β-sweet point than the lower β-sweet point (at least for the example shown in Fig. 2).
The right panel of Fig. 7 plots the rms deviations for λ. This function converged more rapidly for the updated than the original maximum-likelihood procedures. For the updated procedures, the estimates converged within 200 trials.
Considering only the sweet-point selection rules for the updated maximum-likelihood procedures, the random selection rule seemed to provide better threshold (α) estimates and the 4-down, 1-up procedure provided slightly better estimates of λ. This result was not surprising because the 4-down, 1-up procedure maintains a relatively high overall proportion correct, emphasizing visits to high signal strengths at the cost of presenting relatively few mid- and low-level signal strengths. What was surprising was that the estimates of β appear to be approximately the same for the two updated procedures, even though the lower β-sweet point would be expected to be visited less often by the 4-down, 1-up procedure stimulus selection method than for the random selection procedure. Potentially this result reflected differences in the asymptotic amount of expected variance associated with the upper vs lower β-sweet points, but that explanation was not further explored.
SUMMARY AND CONCLUSIONS/RECOMMENDATIONS
The sweet-points for logistic psychometric functions with four parameters: mean (α), slope (β), lower asymptote (γ), and lapse (λ) were derived. For the current work, the value of γ was assumed to be known (e.g., n-alternative procedures assumed). This yielded a total of four sweet points, the percent correct values on the points on the psychometric function which, when sampled, minimize the expected variance in the parameter estimation. For α the sweet point is near the mean. For β (and the logistic as psychometric function model), there are two sweet points, one above and one below the α-sweet point. For λ a minimal expected variance cannot strictly be achieved; it is reasonable to use a high signal strength as a proxy to the signal strength at the sweet point.
Several simulations indicated that the proposed updated maximum-likelihood procedure using four sweet points can be as efficient in estimating the mean as the single-parameter (α) estimation method proposed studied by Green (e.g., 1990; referred to as the “original” maximum likelihood-procedure in the current description), and additionally provided information regarding the slope and lapse of the true psychometric function. In addition to the introduction of additional sweet points, the proposed updated maximum-likelihood procedure differs from the original in that it minimizes the estimated posterior probability, rather than the likelihood through the use of a prior distribution on each of the parameters. This approach can be adopted for the original single-parameter maximum-likelihood procedure, and has the potential virtues of both increasing the convergence rate and reducing the large variations in signal strength that occur across the first few trials of a track (e.g., Leek et al., 2000).
An important motivation for deriving the four sweet points described above was to provide the experimenter with the freedom to introduce a stimulus sampling procedure appropriate to their research interest. Once the sweet points are known, the experimenter has the opportunity to fashion a sampling strategy appropriate for the population under study, expectations regarding the lapse rate, etc. Two example strategies were considered, one which randomly chose among the four sweet points, and one that sampled the sweet points using an adaptive procedure. The latter was introduced as a method that would maintain a relatively constant percent correct performance level and also avoid large changes in signal strength. Both sampling strategies performed well in simulations, although the random sampling procedure converged more rapidly in the estimation of α. If there is no interest in controlling the stimulus sampling strategy, alternative Bayesian procedures that minimize entropy (e.g., Kontsevich and Tyler, 1999) appear to be a good choice of procedures because such procedures are easily extended to include several free parameters.
Finally, it should be appreciated that when one uses a maximum-likelihood procedure, what constitutes a “most efficient” stimulus placement is not clear cut; it depends on the experimental goals. If one or another parameter is of utmost importance, one might increase the number of trials at that parameter’s sweet point(s). If the goal is to estimate the three parameters (mean, slope, and lapse) with equal certainty, the sweet points might be sampled with a number of visits inversely related to the expected standard deviation at the sweet point (e.g., see Fig. 2). The crucial advantage of knowing the values of the sweet points is that sampling strategies can be fashioned to fit with the requirements of the experiment.
ACKNOWLEDGMENTS
This work was supported by NIH NIDCD Grant Nos. R01 DC02012 and R21 DC010058. We thank Theodore S. Lin and Suhayem H. Chowdhury for assistance in preparing this manuscript. The authors would also like to thank Robert A. Lutfi and an anonymous reviewer for helpful suggestions that substantially improved the manuscript.
APPENDIX: EXPECTED VARIANCES FOR THE PARAMETERS OF THE PSYCHOMETRIC FUNCTION
For a psychometric function that takes the form of a logistic function, as given in Eq. 1, the expected variances for its parameters α, β, and λ (, , and ) can be written as
| (A1) |
| (A2) |
and
| (A3) |
From these expressions, the signal strength x that minimizes each of these expected variances can be determined. The resulting signal strengths are the sweep points for the logistic psychometric function.
Although all the simulations in the current study were based on the logistic psychometric function, for some experiments the signal strength is known to be a positive number. In such situations, the Weibull function is commonly used for the psychometric function. A form of the Weibull function convenient for the derivation of sweet points is
| (A4) |
where the parameter vector φ consists of four parameters k, β, γ, and λ. The γ and λ parameters are defined as in the logistic formulation. The k parameter is related to the percent correct at x = 1, because p(1, φ) = γ + (1−γ−λ)(1−k). The β parameter describes the slope of the function. For the Weibull psychometric function, the expected variances of the k, β, and λ parameters are
| (A5) |
| (A6) |
| (A7) |
Plotting these expected variances as functions of the signal strength x, a single minimum, hence a sweet point, for , and occurs for the Weibull psychometric function; does not have a minimum, and so a large signal strength then can be taken as a proxy for the λ-sweet point. Therefore, there are a total of three sweet points. They correspond to the k, β, and λ parameters, in the order of low to high signal strengths. These sweet points can then be used in the updated maximum-likelihood procedure, in which the signal strength is chosen among the three sweet points associated with the 3-tuple with the minimum.
Footnotes
It should be noted that this approach can be contrasted with alternative Bayesian sampling strategies in which the goal is to find, on each trial, the level that will minimize the total entropy. Kontsevich and Tyler (1999) provide an excellent overview of such procedures for the estimation of psychometric functions.
Note that the number of β sweet points depends on the formulation of the psychometric function. In the Appendix, it is shown that for a Weibull psychometric function there exists only a single β sweet point.
The γ-sweet point parallels the λ-sweet point except that the expected variance is minimal for the percent correct associated with the weakest signal strength rather than the strongest. This possibility was considered by Gu and Green (1994), who added “catch trials” to their yes-no procedure. For the present development, the value of γ is assumed to be fixed because (a) n-interval, m-alternative forced choice procedures are prevalent, and (b) fixing γ substantially reduces the time needed to search the candidate parameter space.
References
- Allen, P., and Wightman, F. (1994). “ Psychometric functions for children’s detection of tones in noise,” J. Speech Hear. Res. 37, 205–215. [DOI] [PubMed] [Google Scholar]
- Brand, T., and Kollmeier, B. (2002). “ Efficient adaptive procedures for threshold and concurrent slope estimates for psychophysics and speck intelligibility tests,” J. Acoust. Soc. Am. 111, 2801–2810. 10.1121/1.1479152 [DOI] [PubMed] [Google Scholar]
- Buss, E., Hall, J. W., and Grose, J. H. (2009). “ Psychometric functions for pure tone intensity discrimination: Slope differences in school-aged children and adults,” J. Acoust. Soc. Am. 125, 1050–1058. 10.1121/1.3050273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubno, J. R., and Ahlstrom, J. B. (2001). “ Forward- and simultaneous-masked thresholds in bandlimited maskers in subjects with normal hearing and cochlear hearing loss,” J. Acoust. Soc. Am. 110, 1049–1057. 10.1121/1.1381023 [DOI] [PubMed] [Google Scholar]
- Engen, T. (1971). “ Psychophysics. I. Discrimination and detection,” in Experimental Psychology, 3rd ed., edited by Kling J. W. and Riggs L. A. (Holt, Rinehard, and Winston, New York), Chap. 2, pp. 23–32. [Google Scholar]
- Florentine, M., Buus, S., and Geng, W. (2000). “ Toward a clinical procedure for narrowband gap detection I: A psychophysical procedure,” Audiology 39, 161–167. 10.3109/00206090009073069 [DOI] [PubMed] [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, J. S., and Rubin, D. B. (2004). Statistical Data Analysis, 2nd ed. (Chapman and Hall/CRC, Boca Raton, FL: ), pp. 1–698. [Google Scholar]
- Grassi, M., and Soranzo, A. (2009). “ MLP: A MATLAB toolbox for rapid and reliable auditory threshold estimation,” Behav. Res. Methods 41, 20–28. 10.3758/BRM.41.1.20 [DOI] [PubMed] [Google Scholar]
- Green, D. M. (1990). “ Stimulus selection in adaptive psychophysical procedures,” J. Acoust. Soc. Am. 87, 2662–2674. 10.1121/1.399058 [DOI] [PubMed] [Google Scholar]
- Green, D. M. (1993). “ A maximum-likelihood method for estimating thresholds in a yes-no task,” J. Acoust. Soc. Am. 93, 2096–2105. 10.1121/1.406696 [DOI] [PubMed] [Google Scholar]
- Green, D. M. (1995). “ Maximum-likelihood procedures and the inattentive observer,” J. Acoust. Soc. Am. 97, 3749–3760. 10.1121/1.412390 [DOI] [PubMed] [Google Scholar]
- Gu, X., and Green, D. M. (1994). “ Further studies of a maximum-likelihood yes-no procedure,” J. Acoust. Soc. Am. 96, 93–101. 10.1121/1.410378 [DOI] [PubMed] [Google Scholar]
- He, N. J., Dubno, J. R., and Mills J. H. (1998). “ Frequency and intensity discrimination measured in a maximum-likelihood procedure from young and aged normal-hearing subjects,” J. Acoust. Soc. Am. 103, 114–126. 10.1121/1.421127 [DOI] [PubMed] [Google Scholar]
- King-Smith, P. E., and Rose, D. (1997). “ Principles of an adaptive method for measuring the slope of the psychometric function,” Vision Res. 37, 1595–1604. 10.1016/S0042-6989(96)00310-0 [DOI] [PubMed] [Google Scholar]
- Kontsevich, L. L., and Tyler, C. W. (1999). “ Bayesian adaptive estimation of psychometric slope and threshold,” Vision Res. 39, 2729–2737. 10.1016/S0042-6989(98)00285-5 [DOI] [PubMed] [Google Scholar]
- Kuss, M., Jäkel, F., and Wichmann, F. A. (2005). “ Bayesian inference for psychometric functions,” J. Vision 5, 478–492. 10.1167/5.5.8 [DOI] [PubMed] [Google Scholar]
- Leek, M. R. (2001). “ Adaptive procedures in psychophysical research,” Percept. Psychophys. 63, 1279–1292. 10.3758/BF03194543 [DOI] [PubMed] [Google Scholar]
- Leek, M. R., Dubno, J. R., He, N., Ahlstrom, J. B. (2000). “ Experience with a yes-no single-interval maximum-likelihood procedure,” J. Acoust. Soc. Am. 107, 2674–2684. 10.1121/1.428653 [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “ Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 49 467–477. 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- Nelson, D. A., and Kiester, T. E. (1978). “ Frequency discrimination in the chinchilla,” J. Acoust. Soc. Am. 64, 114–126. 10.1121/1.381977 [DOI] [PubMed] [Google Scholar]
- Rosen, S., Cohen, M., and Vanniasegaram, I. (2010). “ Auditory and cognitive abilities of children suspected of auditory processing disorder (APD),” Int. J. Pediatr. Otorhinolaryngol. 74, 594–600. 10.1016/j.ijporl.2010.02.021 [DOI] [PubMed] [Google Scholar]
- Sarro, E. C., Rosen, M. J., and Sanes D. H. (2011). “ Taking advantage of behavioral changes during development and training to assess sensory coding mechanisms,” Ann. N.Y. Acad. Sci. 1225, 142–154. 10.1111/j.1749-6632.2011.06023.x [DOI] [PubMed] [Google Scholar]
- Wichmann, F. A., and Hill, N. J. (2001a). “ The psychometric function: I. Fitting, sampling, and goodness of fit,” Percept. Psychophys. 63, 1293–1313. 10.3758/BF03194544 [DOI] [PubMed] [Google Scholar]
- Wichmann, F. A., and Hill, N. J. (2001b). “ The psychometric function: II. Bootstrap-based confidence intervals and sampling,” Percept. Psychophys. 63, 1314–1329. 10.3758/BF03194545 [DOI] [PubMed] [Google Scholar]
- Wright, B., Lombardino, L. J., King, W. M., Puranikm, C. S., Leonard, C. M., and Merzenich, M. M. (1997). Deficits in auditory temporal spectral resolution in language-impaired children,” Nature 387, 176–178. 10.1038/387176a0 [DOI] [PubMed] [Google Scholar]