Use of a compound approach to derive auditory-filter-wide frequency-importance functions for vowels and consonants

Abstract

Speech recognition in noise presumably relies on the number and spectral location of available auditory-filter outputs containing a relatively undistorted view of local target signal properties. The purpose of the present study was to estimate the relative weight of each of the 30 auditory-filter wide bands between 80 and 7563 Hz. Because previous approaches were not compatible with this goal, a technique was developed. Similar to the “hole” approach, the weight of a given band was assessed by comparing intelligibility in two conditions differing in only one aspect—the presence or absence of the band of interest. In contrast to the hole approach, however, random gaps were also created in the spectrum. These gaps were introduced to render the auditory system more sensitive to the removal of a single band and their location was randomized to provide a general view of the weight of each band, i.e., irrespective of the location of information elsewhere in the spectrum. Frequency-weighting functions derived using this technique confirmed the main contribution of the 400–2500 Hz frequency region. However, they revealed a complex microstructure, contrasting with the “bell curve” shape typically reported.

INTRODUCTION

Evidence has accumulated to suggest that the normal auditory system takes advantage of momentary improvements in local signal-to-noise ratio (SNR) to extract speech from noise (Brungart et al., 2006; Li and Loizou, 2007; Apoux and Healy, 2009). More specifically, it is believed that the auditory system processes primarily the output of the auditory filters that contain a relatively undistorted view of local target signal properties (i.e., a favorable SNR) to create an interpretable representation of the signal of interest. Inversely, the auditory-filter outputs considered as noise are essentially ignored (e.g., Apoux and Healy, 2010). The strategy involving a representation of the target signal created from a limited number of auditory-filter outputs with a relatively favorable SNR has been referred to as the glimpsing strategy (Miller and Licklider, 1950; Cooke, 2006).

According to the glimpsing view, two factors should play a central role in the speech recognition performance of normal-hearing (NH) listeners in the presence of background noise. A first factor is the overall number of available auditory-filter outputs containing a relatively undistorted view of local target signal properties. This quantity was recently assessed in a study by Apoux and Healy (2009). To provide an estimate of the number of auditory-filter outputs necessary to understand speech, the authors developed a technique in which the stimuli are divided into 30 contiguous equivalent rectangular bandwidths (ERB_N; Glasberg and Moore, 1990) spanning 80–7563 Hz. The listeners are then presented with limited numbers of bands having frequency locations determined randomly from trial to trial. Apoux and Healy (2009) showed that phoneme intelligibility increases with increasing number of 1-ERB_N wide bands and that NH listeners require 20 bands to accurately identify vowels and 16 to identify consonants.

A second factor that may potentially affect the speech recognition performance of NH listeners in the presence of background noise is the spectral location of the auditory-filter outputs containing a relatively undistorted view of local target signal properties. Indeed, it is well established that speech information is not distributed uniformly across frequency and that the contribution of a speech band is determined by its spectral location (French and Steinberg, 1947; Fletcher and Galt, 1950; ANSI, 1969; ANSI, 1997). As a consequence, the intelligibility that can be achieved with a fixed number of auditory-filter outputs may vary with the center frequency of these auditory filters. While they acknowledged the likely influence of band location, Apoux and Healy (2009) did not investigate this factor. Instead, the authors randomized the spectral location of the bands to provide a general view, i.e., irrespective of specific band location, of the number of 1-ERB_N-wide speech bands needed to identify vowels and consonants.

The primary purpose of the present study was to assess the importance or weight of each auditory-filter output as operationally defined in Apoux and Healy (2009). However, it was not possible to use their technique because it does not appear well suited for such assessment. Indeed, use of the technique developed by Apoux and Healy (2009) would require measurement of all the possible combinations of bands. To put this into perspective, it should be noted that Apoux and Healy (2009) sampled 9216 data points in their ten-band condition when there are $C_{30}^{10}$  = 30 045 015 possible combinations of ten bands. Accordingly, a preliminary objective of the present study was to find a suitable approach to estimate the relative importance of discrete frequency regions.

Various techniques have been used to derive the so-called band-importance functions (BIFs). Perhaps one of the earliest attempts to evaluate systematically the frequency-specific information content of a speech signal may be attributed to the development of the Articulation Index [(AI); ANSI, 1969], and its successor, the Speech Intelligibility Index [(SII); ANSI, 1997]. The AI is based on the premise that speech intelligibility can be modeled as the sum of the individual contributions of independent frequency bands. The index has many strengths and has considerably shaped current views of speech perception. However, the BIFs used for the calculation of the AI are typically derived from speech recognition experiments involving low- and high-pass filtering (e.g., French and Steinberg, 1947; Fletcher and Galt, 1950; Studebaker and Sherbecoe, 1991). One consequence of using low- and high-pass filtering is that the resulting BIFs do not reflect the considerable synergetic and redundant interactions that exist across frequency (Breeuwer and Plomp, 1984, 1985, 1986; Warren et al., 1995; Lippmann, 1996; Müsch and Buus, 2001; Healy and Warren, 2003; Healy and Bacon, 2007). Consistent with this, several studies have demonstrated that the AI does not accurately predict intelligibility when the audible speech spectrum is partitioned into two or more spectrally disjoint frequency bands (Kryter, 1962; Grant and Braida, 1991). It is apparent that with such a limitation, the AI approach could not be used in the present study.

A few techniques for circumventing this limitation of the AI have been proposed over the past two decades. One technique (the “hole” technique) consists of creating a single hole or gap in the speech spectrum (Shannon et al., 2001; Kasturi et al., 2002; Apoux and Bacon, 2004). The weight of a given frequency region is then assessed from the increase in performance observed when this particular frequency band is re-introduced. One may reasonably expect, however, that a single 1-ERB_N hole in the speech spectrum would not produce a significant drop, if any, in performance, especially in the absence of background noise. Therefore, the traditional hole approach may not be suited for estimating the weight of auditory-filter outputs. A second technique is based on the use of a correlational procedure (Doherty and Turner, 1996; Turner et al., 1998; Apoux and Bacon, 2004; Calandruccio and Doherty, 2007). To determine the weights applied to various frequency regions of speech, the information in each speech band is independently and randomly degraded by a given amount on each trial by the addition of noise. The weight the listener places upon each band is obtained by calculating the correlation between the amount of degradation in each band (specified as the SNR in the band) and the accuracy of the responses. While this technique could perhaps be used with relatively narrow bands of speech, it is well established that the presence of noise may significantly affect the frequency that divides the speech spectrum into two equally intelligible halves (Pollack, 1948; Webster and Klumpp, 1963) and more importantly, the general shape of the BIFs. For instance, Apoux and Bacon (2004) estimated BIFs for consonants using both the hole and the correlational techniques. The hole technique was used with and without a background noise. Noise was always present when using the correlational technique. Comparison of the three BIFs obtained in this study showed no influence of the technique used to derive the functions, as the shape of the BIFs obtained with the hole (in noise) and the correlational techniques was almost identical. In contrast, the shape of the BIFs obtained in quiet and in noise with the hole technique differed substantially. The BIF obtained in quiet was essentially flat, while the BIF obtained in noise indicated a larger contribution of the highest frequency band. Apoux and Bacon attributed this effect to the differential effect of noise on various acoustic speech cues. Accordingly, BIFs derived from noisy stimuli should not be used to estimate the amount of information potentially available in each of a series of frequency bands.

In the present study, a new technique, similar in spirit to the hole approach, is proposed for deriving BIFs of 1-ERB_N-wide speech bands while accounting for much of the synergetic and redundant interactions that exists across frequency. This technique will be referred to as the “compound” technique or approach. Similar to the original hole technique, the importance of a given frequency band is estimated by comparing percent-correct scores obtained in two conditions that differ only by the presence or absence of that particular band. In the compound approach, however, not all other bands are presented to the listener on a given trial. Moreover, the number of other bands, n, may vary from trial to trial (experiments 1 and 2) or remain fixed (experiment 3). In both cases, the spectral locations of the bands are randomized across trials. The exclusion of several other bands was implemented to force listeners to rely more heavily on the bands that are available, rendering the auditory system more sensitive to the removal of a single narrow band of speech. As a consequence of this increased sensitivity, the individual bands can be made quite narrow and so higher spectral resolution can be achieved. Further, the spectral locations of the limited number of bands are randomized from trial to trial so that the data do not reflect a particular combination of speech bands. In other words, the compound technique provides an average estimate of each band’s weight. Finally, it should be noted that this randomization is also a way to account for much of the considerable synergetic and redundant interaction that exists across frequency. Indeed, unlike the AI/SII approach, the weight of a given band reflects many band interactions.

An apparent trade-off is that the target signal is no longer broadband and one could argue that it may somehow limit the implications of the present approach. However, it should be noted that the BIFs used in the ANSI standard are also obtained with filtered stimuli. More importantly, the present approach is based on the assumption that the auditory system reconstructs a representation of the speech signal by combining frequency regions (i.e., auditory-filter outputs) in which the signal is relatively preserved from the background noise as advocated by the glimpsing model. Accordingly, the frequency-importance functions obtained using the present approach should provide a reasonable estimate of the potential contribution of each auditory-filter output when listening to speech.

EXPERIMENTS 1 AND 2: RANDOM NUMBER OF BANDS

Method

Listeners

Sixty-four NH listeners participated in the first two experiments (61 females). Their ages ranged from 18 to 52 years (average = 22 years). All listeners had pure-tone air-conduction thresholds of 20 dB HL or better at octave frequencies from 250 to 8000 Hz (ANSI, 2004). They were paid an hourly wage for their participation. This study was approved by the Institutional Review Board of The Ohio State University.

Speech material and processing

The target stimuli consisted of 9 vowels (/æ, ɔ, ɛ, i, I, a, u, ℧, ∧/) in /h/-vowel-/d/ environment recorded by six speakers (three for each gender) for a total of 54 consonant-vowel-consonant utterances (CVCs), and 16 consonants (/p, t, k, b, d, g, θ, f, s, ∫, ð, v, z, ʒ, m, n/) in /a/-consonant-/a/ environment recorded by four speakers (two for each gender) for a total of 64 vowel-consonant-vowel utterances (VCVs).

The stimuli were filtered into 30 contiguous frequency bands ranging from 80 to 7563 Hz using two cascaded 12th-order digital Butterworth filters (see Table TABLE I.). Stimuli were filtered in both the forward and reverse directions (i.e., zero-phase digital filtering) so that the filtering process would produce zero phase distortion. Each band was one ERB_N wide so that the filtering simulated to some extent the frequency selectivity of the normal auditory system (Apoux and Healy, 2009).

TABLE I.

Center frequencies of the 30 1-ERB_N analysis bands (in Hz).

Band number	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Center frequency	97	134	175	221	272	329	393	463	542	630	727	836	957	1091	1241
Band number	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Center frequency	1408	1594	1801	2032	2289	2575	2893	3248	3642	4082	4572	5117	5725	6401	7154

In an attempt to limit off-frequency listening, a background noise was presented simultaneously with the speech bands. This background noise was a simplified speech spectrum-shaped noise (constant spectrum level below 800 Hz and 6 dB/octave roll-off above 800 Hz) with a duration equal to speech duration. The background noise was also filtered into 30 1-ERB_N-wide bands and only the complementary noise bands were presented with the speech bands so that speech and noise did not overlap substantially. As a result, each one of the 30 possible bands was filled with either speech or noise.

The overall A-weighted level of the 30 summed speech bands was normalized and calibrated to produce 65 dB. The overall level of the 30 summed noise bands was adjusted to achieve +6 dB SNR when compared to the 30 summed target speech bands. As demonstrated by Apoux and Healy (2009), the presence of interleaved bands of noise at +6 dB SNR has essentially no effect on speech intelligibility. Speech and noise bands were combined after level adjustment.

Procedure

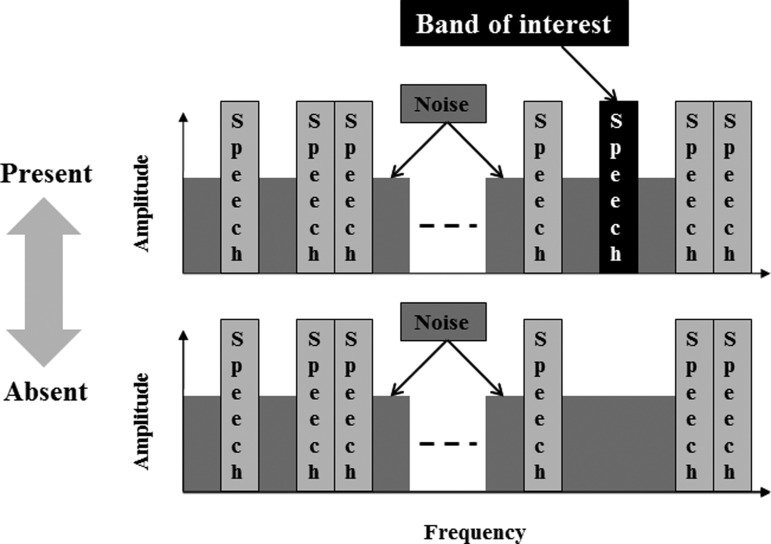
As mentioned in Sec. 1, the technique used to estimate the importance or weight of each band consisted of comparing speech recognition performance in the presence and in the absence of the band of interest. For instance, to evaluate the importance of band 21, listeners completed two blocks with each block corresponding to recognition of all 54 CVCs or 64 VCVs. In one block, the band of interest (i.e., band 21) was always present (“PRS” condition). In the other block, the band of interest was systematically absent (“ABS” condition). In both conditions, n additional speech bands were always present. The spectral location of these n speech bands was chosen randomly from trial to trial and across listeners. However, the spectral location of the n speech bands was kept constant across the two PRS/ABS conditions for each phoneme/talker and listener (see Fig. 1). For instance, listener 1 may have been presented with bands 2, 5, 11, 21, 22, and 30 in the PRS condition and bands 2, 5, 11, 22, and 30 in the ABS condition when recognizing /apa/ produced by talker 4, while listener 2 was presented with bands 6, 11, 17, 21, 24, and 28 in the PRS condition and bands 6, 11, 17, 24, and 28 in the ABS condition when recognizing the same phoneme produced by the same talker. The purpose of this manipulation was twofold. First, it allowed for the presence of the band of interest to be the only difference between a trial in the PRS condition and the corresponding trial in the ABS condition (i.e., same phoneme/talker). Second, this manipulation allowed the derivation of the importance of each band by simply calculating the difference between performance in the PRS condition and that in the ABS condition.1

Figure 1.

Schematic of two trials designed to assess the weight of a given speech band.

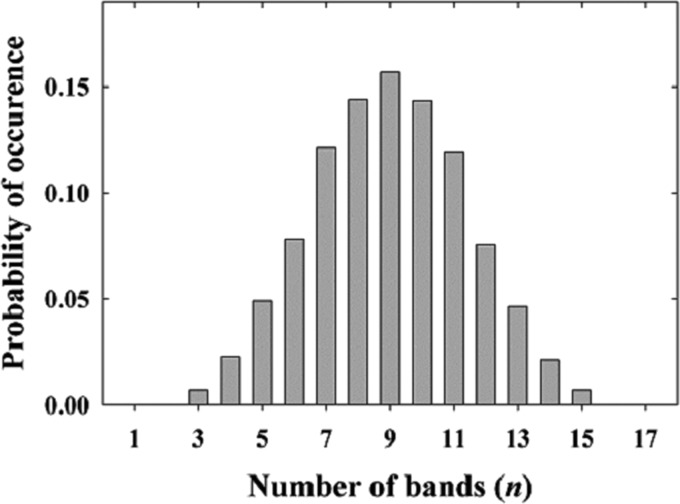
The overall number of bands used in the present study was set to 10 ± 6 for both vowels and consonants. In other words, n varied from 3 to 15 according to the Gaussian function shown in Fig. 2.2 The mean value (n = 9) was chosen according to the results of Apoux and Healy (2009) so that average performance would be in the steep portion of the psychometric function relating number of bands to intelligibility. The motivation for using a Gaussian distribution was twofold. First, the number of bands had to reflect, at least to some extent, the various situations that may be encountered in the real world, from challenging (i.e., limited number of bands) to relatively easy (i.e., large number of bands). In other words, the range (±6 bands) was selected to produce scores that cover the range of possible recognition scores from floor to ceiling [also according to Apoux and Healy (2009)]. Second, the use of a Gaussian distribution instead of, for instance, a rectangular distribution offered the advantage to limit the number of trials near floor or ceiling. Because the number of random band placements in each condition is so large, it is reasonable to assume that the amount of speech information conveyed by the n speech bands will be—on average—similar across conditions.

Figure 2.

Probability that a given number of bands (n) will appear in a given trial, during the first two experiments.

Listeners were tested individually in a double-walled, sound-attenuated booth. Stimuli were played to the listeners binaurally through Sennheiser HD 250 Linear II circumaural headphones. The experiments were controlled using custom Matlab routines running on personal computers equipped with high-quality digital-to-analog converters (Echo Gina24). Percent-correct identification was measured using a single-interval, 9 - or 16-alternative forced-choice procedure for the vowel and consonant tests, respectively. Listeners were instructed to report the perceived vowel or consonant and responded using the computer mouse to select 1 of 9 or 16 buttons on the computer screen.

The BIF for vowels (V10r; vowels, ten bands, random) and consonants (C10r; consonants, ten bands, random) was estimated in experiments 1 and 2, respectively (see Table TABLE II.). Each experiment consisted of 30 blocks in the PRS condition and the 30 corresponding blocks in the ABS condition (i.e., one pair of blocks per band), resulting in a total of 60 blocks per experiment. Again, one block corresponded to recognition of all 54 CVCs or 64 VCVs. Each experiment was divided into two sub-experiments. One sub-experiment measured the weight of the odd-numbered bands (every other band from 1 to 29), while the other sub-experiment evaluated the weight of the even-numbered bands (every other band from 2 to 30), for a total of four sub-experiments. Each sub-experiment was conducted independently. Listeners were randomly assigned to one of the four sub-experiments and a total of 20 listeners participated in each sub-experiment so that the relative weight of a given band in experiments 1 and 2 corresponds to the data averaged across 20 listeners. Because a number of listeners completed two sub-experiments, only 64 listeners were needed instead of the 80 otherwise necessary. Those who completed two sub-experiments did so in random order. A series of t-tests on PRS-ABS difference scores indicated that performance was equivalent on conditions run first versus second for all individuals hearing both odd- and even-numbered bands. Prior to data collection, listeners completed recognition of all 54 CVCs or 64 VCVs in quiet with all 30 speech bands present. Then, listeners completed recognition of all 54 CVCs or 64 VCVs three more times but with only n + 1 speech bands plus 30 -(n + 1) complementary noise bands. Visual on-screen feedback was provided after each trial during the practice session but not during the experimental sessions.

TABLE II.

Conditions tested in the current study.

Experiment number	Condition	Speech material	Number of other bands	Approach	Bands	N
1	V10r	Vowels	9	Random	Even	20
	V10r	Vowels	9	Random	Odd	20
2	C10r	Consonants	9	Random	Even	20
	C10r	Consonants	9	Random	Odd	20
3	C10f	Consonants	9	Fixed	Even	10
	C10f	Consonants	9	Fixed	Odd	10
	C6f	Consonants	5	Fixed	Even	10

Results and discussion

Percent-correct scores

As expected, performance was generally better in the PRS condition when compared to the ABS condition. Percent correct scores for vowels ranged across bands from 41.0 to 50.1 (mean = 46.5) and from 44.1 to 56.1 (mean = 50.3) in the ABS and PRS conditions, respectively. Percent-correct scores for consonants ranged from 55.2 to 61.9 (mean = 58.1) and from 57.1 to 68.0 (mean = 62.5) in the ABS and PRS conditions, respectively. The average standard deviation was about 8 percentage points for vowels and about 7 for consonants with no noticeable difference between ABS and PRS for any speech material. Paired t-tests indicated a significant effect of adding the band of interest in each experiment (pooled PRS conditions > pooled ABS conditions, p < 0.001 for consonants and for vowels).

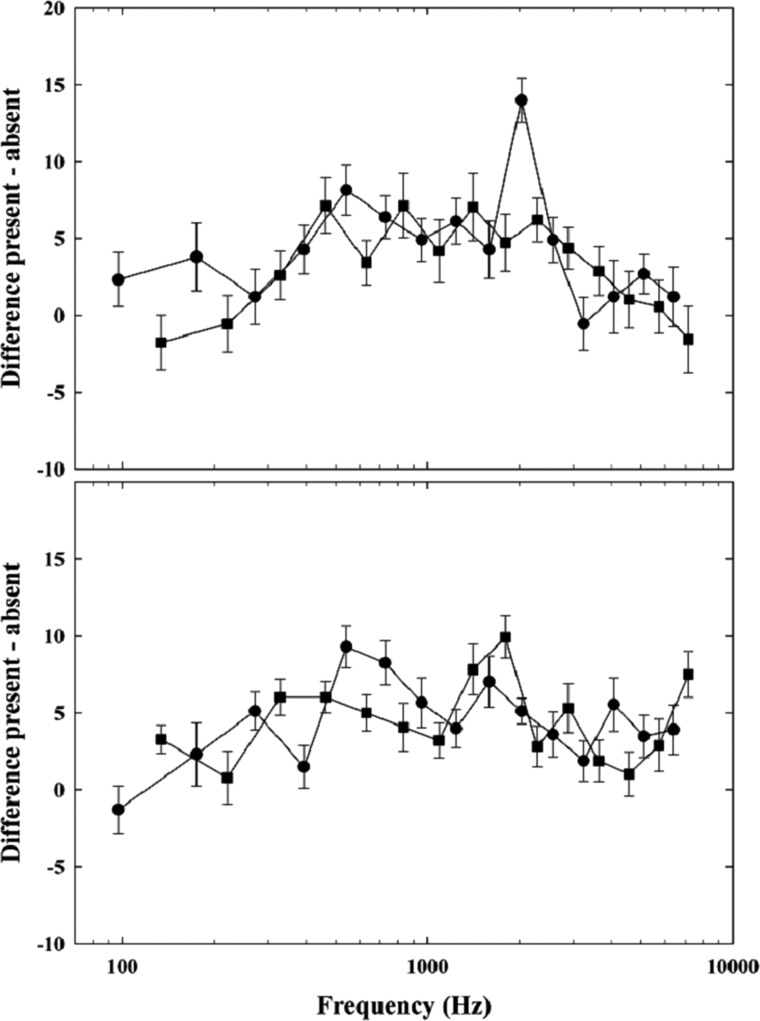
Figure 3 shows the average difference between PRS and ABS as a function of the center frequency of the band for V10r (top panel) and C10r (bottom panel). In each panel, data for the odd bands are represented by circles, while data for the even bands are represented by squares, which correspond to different listener groups. It should be noted that, while mean performance was about 10 percentage points lower in V10r compared to C10r, the average difference was similar (3.7 and 4.4 points, respectively).

Figure 3.

Averaged differences between percent-correct scores in the present (PRS) and absent (ABS) conditions as a function of band center frequency. Error bars represent the standard error of the mean. The separate groups hearing the odd-numbered bands are represented by circles and those hearing even-numbered bands are represented by squares. Data for vowels (condition V10r) are plotted in the top panel, while data for consonants (condition C10r) are plotted in the bottom panel.

Band-importance functions

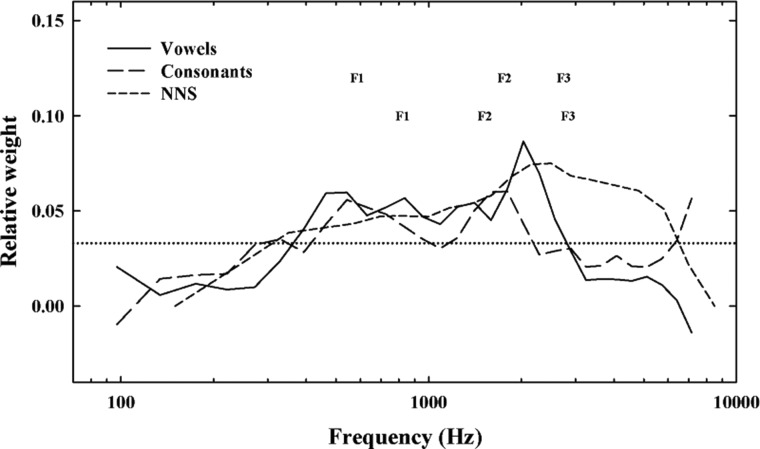
The raw differences for each listener were transformed to relative weights by summing their values and expressing each band’s weight as the raw difference divided by this sum. Therefore, the sum of the relative weights of the 30 bands was set to 1.0. Figure 4 shows the relative weights obtained in this way as a function of the center frequency of the band. Similar to previous work (e.g., Studebaker and Sherbecoe, 1991), smoothing, although milder, was applied to the data.3 For reference, a dotted line indicates the average band weight (i.e., 1/30). This reference may be used to determine which bands are more important and which bands are less important for speech intelligibility. The average frequency of the first three formants is also indicated in Fig. 4. Values were determined in PRAAT using linear predictive coding and a maximum formant frequency limit of 5000 Hz for the male talkers and 5500 Hz for the female talkers (Boersma and Weenick, 2011). The upper and lower rows correspond to the values for vowels and consonants, respectively. Also plotted is the critical-band-importance function for various nonsense syllable tests (ANSI, R2007, Table B.1). This function, later referred to as the NNS function, is considered appropriate for CVC tests when a group of talkers is used.

Figure 4.

Relative weight as a function of the center frequency of the 1-ERB_N band for vowels (solid line) and consonants (long dashes). Data have been normalized so that the sum of all the weights equals 1. Also plotted is the function representing various nonsense syllable tests (NNS) from the Speech Intelligibility Index (short dashes). The horizontal dotted line indicates the average band weight (i.e., 1/30). Note that for the NNS data, the average band weight is 1/21.

For vowels, the individual bands contributing relatively more to recognition (i.e., >0.033) were all located between about 400 and 2500 Hz. In this region, the relative weight of all the bands was roughly similar except for one band centered at 2032 Hz whose weight was almost twice as large as the other bands. For consonants, the individual bands contributing more to recognition were primarily located between 500 and 2000 Hz. In contrast to vowels, the relative weight of the bands was not similar within this range and two regions of importance clearly emerged. The first region, centered at 600 Hz, included bands 8–12. The second region, centered at 1700 Hz, included bands 16–19. Another remarkable difference between the two BIFs is the weight of the highest band. This band, centered at 7154 Hz, did not contribute at all to vowel recognition, but contributed substantially to consonant recognition. According to a simple estimate of the average formant frequencies for both speech materials, the 400–2500 Hz frequency region generally encompassed the first and second formants (Fig. 4).

Information transmission analysis

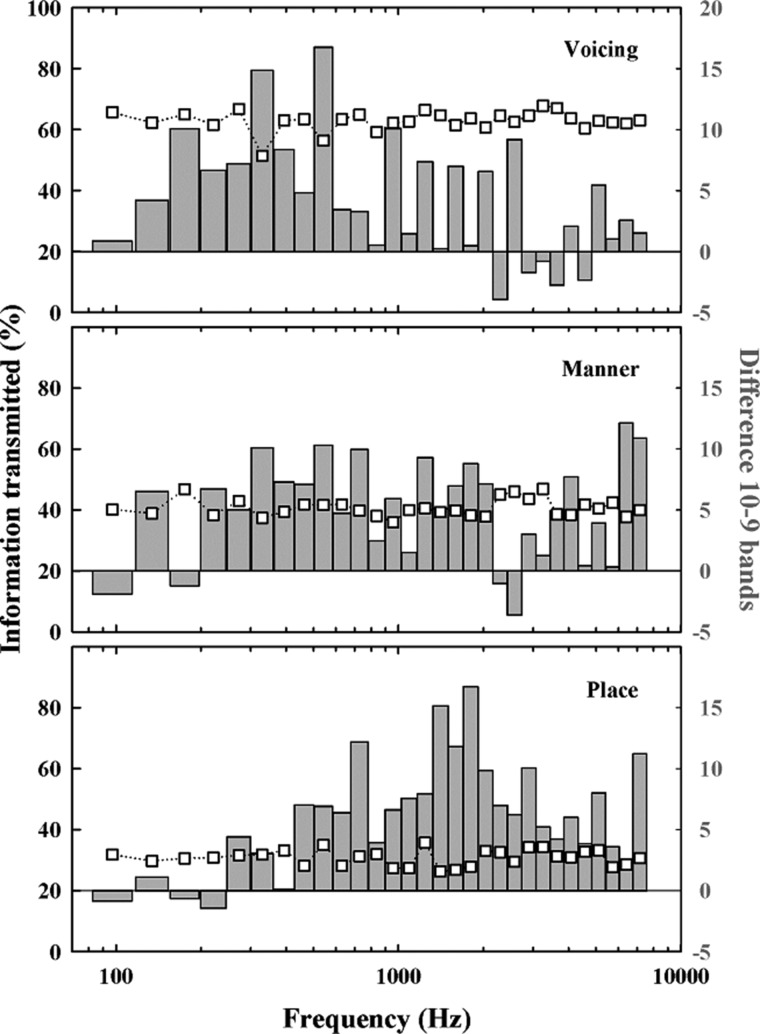
The average consonant confusion matrices from experiment 2 (C10r) were analyzed in terms of information transmission (Miller and Nicely, 1955). An analysis of information transmission was not performed for vowels because reasonable ways to group the stimuli in order to summarize the pattern of confusions could not be determined. In particular, duration and formant frequency, the acoustic features commonly considered for vowels, were not consistent across talkers (see Table V in Hillenbrand et al., 1995). The reception of voicing, manner, and place of articulation was evaluated for each band. The results of this evaluation are shown in Fig. 5. In each panel, the open squares correspond to the percentage of information transmitted in the ABS (i.e., 9 band; left axis) condition and the bars correspond to the difference in percent information transmitted PRS-ABS (right axis).

Figure 5.

The top, middle, and bottom panels display data for the features voicing, manner, and place of articulation, respectively. In each panel, the open squares show the mean percentage of information transmitted as a function of the center frequency of the 1-ERB_N band in the ABS condition (left axis). The bars shows the difference between percentage of information transmitted in the PRS and ABS conditions, also as a function of the center frequency of the 1-ERB_N band (right axis).

The top panel shows that transmission of voicing was relatively good with only nine 1-ERB_N-wide bands, as percent of information ranged from 51 to 67. Adding the tenth band was especially beneficial to the transmission of voicing when the band was centered from 175 to 542 Hz. This region is largely consistent with the fundamental frequency and its lower harmonics. There were also a number of bands between about 1000 and 2500 Hz that were important for distinguishing voiced and unvoiced consonants. Transmission of manner was poorer overall than transmission of voicing, with the percent of information ranging from 36 to 47 (middle panel). The addition of the tenth band was generally beneficial to the transmission of manner. Although manner cues seemed more evenly distributed across frequency, three specific frequency regions of importance may be identified. These three regions include bands centered from 221 to 727 Hz, from 1241 to 2032 Hz, and from 6401 to 7154 Hz. Interestingly, they seem to mirror the three regions of the BIF discussed previously. Finally, transmission of place (bottom panel) was most affected by the presence of multiple gaps in the spectrum, averaging less than 31% of information correctly transmitted in the ABS condition. Not surprisingly, the addition of the tenth band increased place information by more than 16% (6 points of raw percentage) on average. While the addition of an extra band was generally beneficial, irrespective of the center frequency of the band, the region centered around 1600 Hz (corresponding to the location of F2) seemed especially important for the place distinction.

Overall, the present approach did not produce a BIF exactly like those derived in previous studies. In particular, two differences are apparent. One difference is the frequency range of the functions. The NNS function replotted from ANSI S3.5 (1997) in Fig. 4 (short dashes) indicates a principal contribution of frequencies between about 1000 and 6000 Hz (the average band weight is 1/21 or 0.048), while the present data suggest a larger contribution of frequencies between 400 and 2500 Hz. The other difference is that the functions do not have the same shape. Indeed, the skewed distribution of the NNS function contrasts with the somewhat biphasic and certainly irregular shape observed with the compound approach. More generally, AI/SII studies typically reported BIFs with a “bell curve” shape. While it is difficult to determine precisely which factors contributed most to these slight discrepancies, it is reasonable to assume that the original design of the compound technique played a significant role. First, the compound technique was specifically designed to reflect much of the synergetic and redundant interactions that exist across frequency. As suggested by Turner et al. (1998), these interactions may significantly affect the shape of the BIFs. For instance, the authors showed that when four broad speech bands having the same intelligibility when presented in isolation are presented together, their relative weight is not equal. Second, it should be noted that a specific advantage of the compound technique is to allow the assessment of the weight of relatively narrow speech bands and to reveal fine differences between adjacent bands. Accordingly, only a mild smoothing was applied to the data so that these fine differences could be preserved. It is not surprising then to observe a more irregular shape.

EXPERIMENT 3: FIXED NUMBER OF BANDS

Rationale

In the previous experiments, the number of additional bands, n, varied from trial to trial. This choice was primarily motivated by the idea that in real-world situations the number of auditory-filter outputs that contains a relatively undistorted view of local target signal properties may also vary depending on the noise type and SNR. Therefore, BIFs should reflect this variation. A possible limitation of varying the number of bands from trial to trial, however, is that it may introduce additional variability to the data, therefore necessitating a larger number of trials and/or listeners. Because our initial goal was to develop the most accurate technique possible, we were not overly concerned with this aspect. Others, however, may need to limit the number of trials and/or listeners even at the cost of reduced accuracy. Assuming that varying the number of additional bands from trial to trial is a source of variability, a logical way to limit this variability is to use a fixed number of bands. Moreover, one may reasonably assume that the fundamental shape of a BIF does not change as a function of the number of bands, because the bands that convey the most (and least) information should not change. However, one may expect the weight of the most-important bands to decrease with increasing number of bands as these bands will become less critical. Concomitantly, the weight of the least-important bands should artificially increase because all weights are relative, together resulting in a flatter BIF. This assumption is consistent with the data reported in ANSI S3.5 (1997) (see Tables B.1, B.2, and B.3).

Method

Thirty NH listeners participated in the third experiment (all females). Their ages ranged from 20 to 27 years (average = 21.5 years). All listeners had pure-tone air-conduction thresholds of 20 dB HL or better at octave frequencies from 250 to 8000 Hz. They were paid an hourly wage for their participation. This study was approved by the Institutional Review Board of The Ohio State University. The target stimuli consisted of the 64 consonants only. In contrast to the previous experiments, the overall number of bands was fixed. However, two conditions were tested. One condition (C10f) estimated the BIF with ten bands (n = 9) and the other condition (C6f) estimated the BIF with six bands (n = 5). The six-band condition was introduced to assess directly the effect of the overall number of bands on the shape of the function. Consistent with the ANSI standard, we hypothesized that the BIF obtained with ten bands may be smoother (more flat) than that obtained with six bands. In the C10f condition, the weight of all 30 bands was measured. Similar to the previous experiments, this condition was divided into two sub-experiments. One sub-experiment measured the weight of the odd-numbered bands, while the other sub-experiment evaluated the weight of the even-numbered bands. In the C6f condition, only the weight of the even bands was measured. Listeners were randomly assigned to one of the three sub-experiments. Data from 20 listeners were collected in the C10f condition (10 in each sub-experiment), while data from 10 listeners were obtained in the C6f condition. All other methodological and procedural details were identical to those used in the previous experiments.

Results and discussion

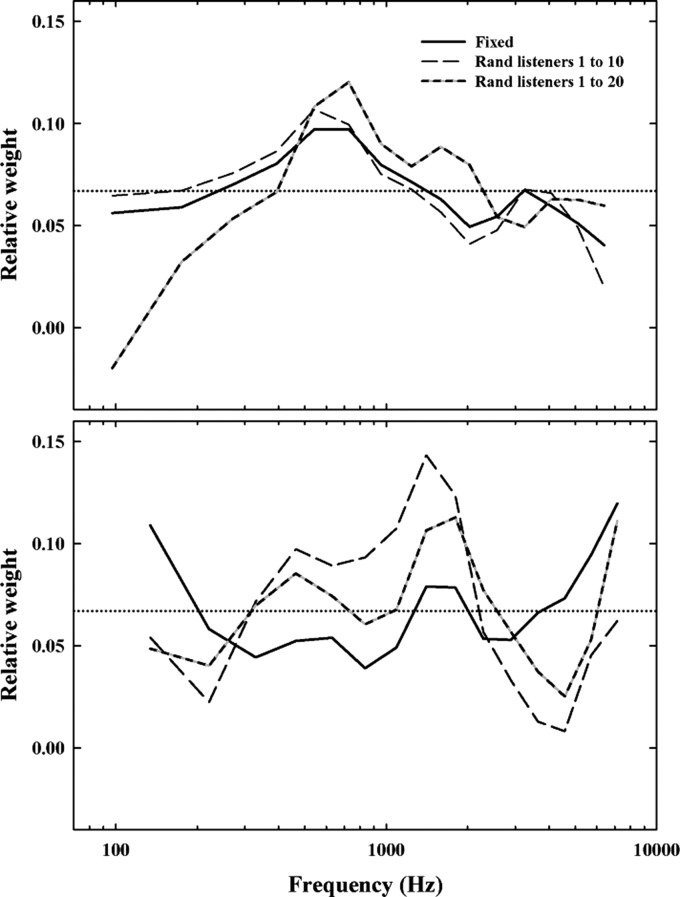
The top and bottom panels of Fig. 6 show the BIFs based on the odd-numbered and even-numbered bands, respectively. Each panel shows the BIF derived using a fixed number of additional bands (solid lines) as well as two BIFs estimated in the previous experiments using a random number of bands. One function (black and grey dashes) shows the results of all 20 listeners who participated in the previous corresponding sub-experiment. The other function (black and white dashes) shows the same data but for the first 10 listeners only (in chronological order). For reference, a dotted line indicates the average band weight (i.e., 1/15). It should be noted that the sole purpose of Fig. 6 is to compare the BIFs obtained with the random and the fixed approach while taking into account the different numbers of listeners. Because we applied a separate smoothing to each function, the shapes of these functions differ substantially from that in Fig. 4. This difference is further increased as we followed the common convention of not smoothing the end points of each function. Accordingly, prospective users should not refer to these functions for band importance.

Figure 6.

The top and bottom panels display functions based on the odd-numbered and even-numbered bands, respectively. Each panel shows the relative weight as a function of the center frequency of the 1-ERB_N band for a fixed number of bands (solid line) or a random number of bands (dashed lines). The black and white line shows data from the first 10 listeners, while the black and grey line shows data from all 20 listeners. Data have been normalized so that the sum of all the weights equals 1. The dotted line indicates the average band weight (i.e., 1/15). Because a separate smoothing was applied to each function, the shapes of these functions differ substantially from that in Fig. 4. Accordingly, prospective users should not refer to these functions for band importance.

Overall, BIFs obtained using both approaches were consistent in that the same regions of relatively high and low importance were systematically observed. Comparison of the BIFs within each panel of Fig. 6 suggests that at least some of the discrepancies between the random and the fixed approaches may be attributed to difference in the number of listeners. Indeed, the difference between random and fixed conditions is comparable to the difference between the data from the first 10 listeners in the random condition and that of the entire group. A two-way mixed analysis of variance (ANOVA) was performed on the mean weight for each listener and condition. All 20 and 10 listeners were included for the random and fixed approach, respectively. The results of this analysis indicated a significant effect of the location of the band of interest [F(29,522) = 1.68, p < 0.05] but no effect of approach (random versus fixed; p = 0.06). More importantly, the interaction between approach and location of the band of interest was not significant (p = 0.09), confirming that the overall shape of the function was not influenced by the approach. This last result also provides an indirect indication of the number of listeners required to achieve a stable BIF with these two approaches (and this specific speech material). Indeed, the absence of an interaction suggests that both functions were approaching a point where they could be considered stable. In other words, it may be possible to achieve a stable function with as few as 20 or 10 listeners when using the random and the fixed approaches, respectively. The fact that a larger number of listeners seems necessary when using the random approach may potentially be attributed to the greater variability introduced by the varying number of other bands (i.e., 3–15 other bands).

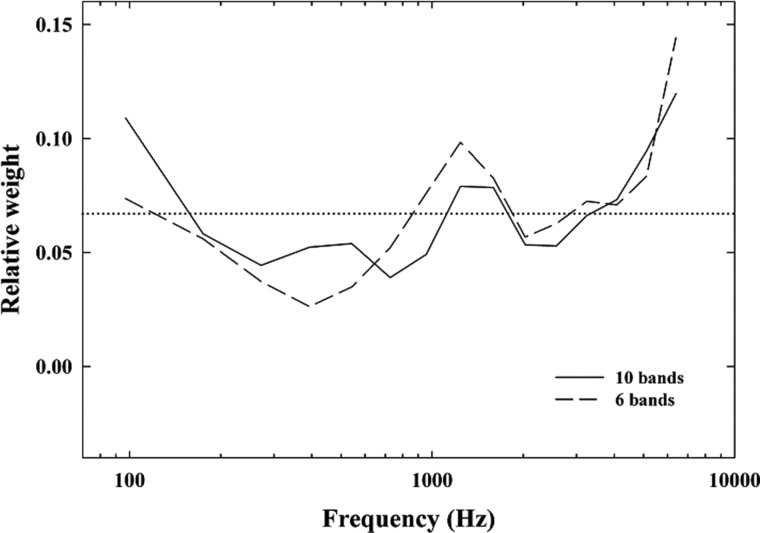
As hypothesized previously, the overall number of bands may have an effect on the shape of the function, and this effect may have contributed to the slight discrepancies between the random and the fixed approaches. Figure 7 shows two BIFs derived using a fixed but different number of additional bands. In Fig. 7, the solid and the dashed lines correspond to the ten- and six-band conditions, respectively. Consistent with our earlier hypothesis, the general shape of the BIF did not change drastically with the number of bands and the BIF obtained with six bands was slightly less smooth, although only in the mid-frequency region. Indeed, the shape of the two functions was almost identical in the low- and high-frequency regions. More importantly, the same three regions of relatively high weight were observed in both conditions. A two-way mixed ANOVA with factors of number of additional bands and location of the band of interest revealed a significant effect of only the latter factor [F(14,252) = 2.42, p < 0.01]. More importantly, the interaction between number of bands and location of the band of interest was not significant (p = 0.82), confirming that the overall shape of the function was not influenced by the number of additional bands. In other words, the above results indicate that the BIFs derived using the compound technique are not qualitatively affected by the number of bands present in the stimulus.

Figure 7.

Relative weight as a function of the center frequency of the odd-numbered 1-ERB_N bands for ten (solid line) or six fixed bands (dashed line). Data have been normalized so that the sum of all the weights equals 1. The dotted line indicates the average band weight (i.e., 1/15).

GENERAL DISCUSSION

Consistent with previous work showing a greater contribution of the mid-frequency region (French and Steinberg, 1947; Studebaker and Sherbecoe, 1991; Bell et al., 1992; DePaolis et al., 1996), BIFs estimated in the present study indicated a main contribution of the 400–2500 Hz frequency region (i.e., 400–2500 Hz for vowels and 500–2000 Hz for consonants). Because the compound technique allowed for a higher resolution than previous approaches, it was possible to observe a detailed microstructure for both vowels and consonants. As mentioned previously, this microstructure was especially pronounced for consonants as two frequency regions of relative importance emerged within that 400–2500 Hz range. In contrast, all the bands contributed more or less equally to overall recognition of vowels within that same range.

The present study can be viewed as an extension of Apoux and Healy (2009) and therefore, further our understanding of the mechanisms underlying speech recognition in noise in the context of the glimpsing model. In their study, Apoux and Healy (2009) demonstrated that NH listeners can achieve nearly perfect vowel and consonant recognition, provided that at least half of the spectrum (in perceptual units) is preserved. One limitation of this study, however, is that it did not provide any indication about the influence of speech band location. This influence was apparent in the present study as the BIFs derived with the compound approach were not flat. It is still unclear, however, how much performance might be affected by the spectral location of the bands.

To provide a sense of the effect of band location, five NH listeners were informally tested in two supplementary conditions. In one condition, the listeners were presented with the ten bands whose importance before smoothing was the largest (see Fig. 3). In the other condition, the listeners were presented with the ten bands whose raw importance was the smallest. These two conditions were implemented for both vowels and consonants for a total of four conditions with each condition corresponding to recognition of all 54 CVCs or 64 VCVs two times. The results of this informal evaluation showed that when listeners were presented with the ten most-important bands, intelligibility was 74.6% for vowels and 72.0% for consonants. When presented with the ten least-important bands, vowel and consonant recognition dropped to 20.4% and 44.7%, respectively. These data show that vowel and consonant recognition may vary by as much as 54 and 27 percentage points, respectively, depending on the spectral location of the ten bands. Such a wide range of performance suggests that, while speech recognition performance in noise depends highly upon the available number of auditory-filter outputs with a relatively undistorted view of local target signal properties, it depends also to a great extent upon the spectral location of these filters. It should be noted that the larger range of performance observed with vowels is consistent with the assumption that vowel recognition relies more heavily on spectral cues than consonants. Finally, the results of this informal evaluation can be considered as an indirect validation of the detailed microstructure observed in the present study. Indeed, it is very unlikely that such a large difference in performance would have been observed if this microstructure was principally due to large variability.

CONCLUSIONS

The purpose of the present study was to estimate the importance of auditory-filter wide frequency bands while taking into account potential synergistic and redundant interactions. Because previous approaches were not compatible with these goals, a new approach was developed. In this approach, the weight of a given band is assessed by comparing percent-correct scores in two conditions that differ in only one aspect—the presence or absence of the band of interest. In contrast to the traditional hole technique, however, random auditory-filter wide gaps are created in the spectrum. These gaps serve two purposes. First, they force listeners to rely more heavily on each available band and, therefore, they render the auditory system more sensitive to the removal of a single narrow band of speech. Second, the random location of the gaps allows the derivation of more accurate BIFs because the weight of each band reflects the contribution of that band, irrespective of the location of information elsewhere in the spectrum. The following conclusions may be drawn.

• (1)The compound approach may be implemented using a random or a fixed number of target speech bands. According to the current evaluation, BIFs derived using the compound approach are not highly sensitive to the presence of a fixed or random number of bands.
• (2)When using a fixed number of bands, it appears that the overall number of bands has a limited influence on the shape of the BIFs, as suggested by ANSI S3.5 (1997). However, prospective users may want to select a number of bands in accordance with the conditions being simulated to achieve the best predictions possible.
• (3)The BIFs derived using the compound approach should account for much of the synergistic and redundant interactions that take place across frequencies.
• (4)The compound approach allows derivation of the importance of single ERB_N-wide speech bands. To our knowledge, this is the highest frequency resolution ever reported for BIFs.
• (5)Taken together, the present experiments suggest that deriving BIFs for CVCs and VCVs requires a large number of subjects and/or trials. Unfortunately, the need for a large number of subjects and/or trials is a limitation common to most approaches used to derive BIFs. However, because the BIFs obtained with the random and the fixed approaches seemed to converge with as few as 20 and 10 listeners, respectively, it may be assumed that only a few more listeners should be required to achieve a stable BIF for this specific speech material. This assumption is supported, at least for the fixed approach, by the recognition scores obtained with the ten least-and most-important bands. Concomitantly, these findings suggest that a stable BIF is achieved more rapidly when using the fixed approach.