Abstract
To test the hypothesis that disturbed flow can impede the transport of nitric oxide (NO) in the artery and hence induce atherogenesis, we used a lumen–wall model of an idealized arterial stenosis with NO produced at the blood vessel–wall interface to study the transport of NO in the stenosis. Blood flows in the lumen and through the arterial wall were simulated by Navier–Stokes equations and Darcy's Law, respectively. Meanwhile, the transport of NO in the lumen and the transport of NO within the arterial wall were modelled by advection–diffusion reaction equations. Coupling of fluid dynamics at the endothelium was achieved by the Kedem–Katchalsky equations. The results showed that both the hydraulic conductivity of the endothelium and the non-Newtonian viscous behaviour of blood had little effect on the distribution of NO. However, the blood flow rate, stenosis severity, red blood cells (RBCs), RBC-free layer and NO production rate at the blood vessel–wall interface could significantly affect the transport of NO. The theoretical study revealed that the transport of NO was significantly hindered in the disturbed flow region distal to the stenosis. The reduced NO concentration in the disturbed flow region might play an important role in the localized genesis and development of atherosclerosis.
Keywords: nitric oxide, atherogenesis, disturbed flow, mathematical model
1. Introduction
Clinical and post-mortem studies revealed that atherosclerotic lesions in the arterial wall develop at certain sites in the human arterial system such as along the inner walls of curved segments and the outer walls of arterial bifurcations, where blood flow may be disturbed and flow separation and re-circulation readily occur [1,2]. This suggests that haemodynamic factors may be involved in the localized genesis and development of atherosclerosis. Flow-induced shear stress has been recognized as one of the most important haemodynamic factors in the localization of atherogenesis [3,4]. Nevertheless, the underlying mechanism is still not very clear.
Nitric oxide (NO) is a pivotal endothelium-derived substance. The hallmark of endothelial dysfunction is impaired shear stress-dependent vasodilation, which is mediated by NO [5]. In addition to causing smooth muscle relaxation, endothelial NO possesses many anti-atherosclerotic properties. It can prevent leucocyte adhesion to the vascular endothelium and migration into the vascular wall [6,7]. NO can also reduce endothelial permeability and thus suppress the influx of lipoproteins into the vascular wall [8]. In addition, NO can inhibit the oxidation of low-density lipoproteins (LDL) [9]. Furthermore, NO can protect the arteries from developing atherosclerosis by inhibiting the proliferation and migration of vascular smooth muscle cells [10,11]. NO can also inhibit platelet aggregation and adhesion to the vascular wall, hence preventing thrombosis [12].
It has been well documented that NO production is wall shear stress (WSS)-dependent [13–15]. Thus, flow disturbance with low WSS in the arterial system may affect endothelial NO synthase (eNOS) and hence NO production. Once it is produced, the concentration of NO is affected by the local flow field through convection. Therefore, local flow patterns in the arterial system can affect the transport process of NO in the arterial lumen and within its wall. Accordingly, abnormal transport of NO due to blood flow disturbance may play an important role in the localized atherogenesis in the arterial system.
Previously, most of the NO transport modelling studies were focused on arterioles to investigate the effective diffusion distance of NO into the arterial wall [16–18]. In these studies, the convection term of NO transport was usually ignored and the NO production rate that should be shear stress-dependent was always assumed to be constant. Using a model with diffusion and convection terms, Smith et al. [19] found that convective transport of NO had an important impact on NO distribution. Unfortunately, they did not take the shear stress-dependent NO production into consideration in their model, and still used the constant NO production rate assumption like others. In contrast, Chen et al. [20] and Sriram et al. [21] included the shear stress-dependent NO production in their modelling studies, but ignored the convection term of the NO transport. Recently, Fadel et al. [22] and Plata et al. [23] theoretically investigated the endothelial NO production and transport in parallel plate flow chambers and re-emphasized the importance of the convective transport in NO concentration distribution. Nevertheless, their modelling studies were carried out in relatively simple flow fields with either parabolic or plug velocity profiles and could therefore offer little information to understand the transport of NO in those arteries with disturbed flows that affected both NO production and transport and hence the distribution of NO in the arteries.
To test the hypothesis that a locally disturbed flow due to sudden changes in geometry can impede the transport of NO in the artery and hence induce atherogenesis in the disturbed flow region, in the present study, we numerically simulated the blood flow and the transport of NO in an axisymmetric arterial stenosis. In this study, a lumen–wall model of the stenosis with NO produced at the blood vessel–wall interface was employed. The NO production rate was assumed to be shear-dependent. In addition, we also investigated the effects of shear-dependent hydraulic conductivity of the endothelium, the non-Newtonian viscous behaviour of blood, the flow rate, the severity of the stenosis, NO production rate, red blood cells (RBCs) and RBC-free layer on NO concentration distribution in the artery.
2. Methods
2.1. Geometry of the model
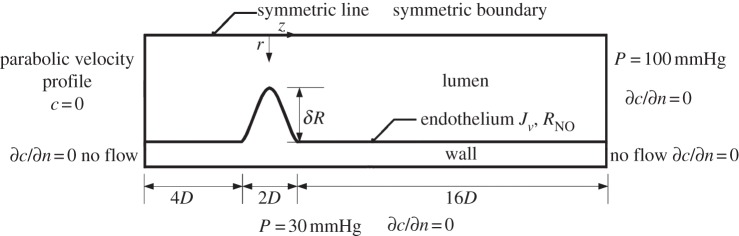
The computational geometry is an axisymmetric stenosis with 75 per cent reduction in the cross-sectional area of the lumen, as shown in figure 1 and table 1. The inner radius of the non-stenosed region and the wall thickness of the artery are chosen to be R = 1.85 mm and t = 0.34 mm, respectively, in accordance with the dimensions of the human left anterior descending (LAD) coronary artery [24,25]. The form of the stenosis is modelled by the equation [26]
| 2.1 |
where r(z) is the inner radius of the artery at location z in the stenosis for −D ≤ z ≤ D with z = 0 at the throat of the stenosis, D the inner diameter of the non-stenosed region of the artery and δ the dimensionless radius reduction at the throat of the stenosis. In the present study, δ was chosen to be 0.5 that led to a 75 per cent reduction in the cross-sectional area of the lumen. The artery was extended 4D upstream and 16D downstream of the stenosis, respectively [27].
Figure 1.
Schematic of the computational geometry with boundary conditions.
Table 1.
Values for parameters used in the model.
| symbol | value, units | description |
|---|---|---|
| R | 1.85 mm | inner radius of non-stenosed region of artery |
| D | 3.70 mm | inner diameter of non-stenosed region of artery |
| t | 0.34 mm | wall thickness of artery |
| ρ | 1050 kg m−3 | density of blood |
| η∞ | 3.45 × 10−3 kg m−1 s−1 | infinite shear viscosity |
| η0 | 5.6 × 10−2 kg m−1 s−1 | zero shear viscosity |
| n | 0.3568 | flow index |
| λ | 3.313 s | characteristic relaxation time |
| Kw | 2.0 × 10−18 m2 | hydraulic permeability of arterial wall |
| μw | 0.72 × 10−3 kg m−1 s−1 | viscosity of plasma in arterial wall |
| Dl | 3.3 × 10−9 m2 s−1 | NO diffusion coefficient in blood |
| Dw | 8.48 × 10−10 m2 s−1 | NO diffusion coefficient in arterial wall |
| koxygen | 7.56 × 10−6 nM−1 s−1 | auto-oxidative NO reaction rate |
| kw | 0.01 s−1 | NO consumption rate in arterial wall |
| kRBC | 2.3 s−1–230 s−1 | NO consumption rate by RBCs |
| Rbasal | 2.13 nM s−1 | basal NO production rate of the hyperbolic model |
| Rmax | 457.5 nM s−1 | maximum NO production rate of the hyperbolic model |
| A | 3.5 Pa | reference WSS of the hyperbolic model |
| Rref | 150 μM s−1 | reference NO production rate of the linear model |
| τref | 2.4 Pa | reference WSS of the linear model |
2.2. Numerical approaches
2.2.1. Governing equations
Fluid dynamics
Lumen. The flow simulation is based on the steady-state incompressible Navier–Stokes equations
| 2.2 |
and
| 2.3 |
where ul and pl represent, respectively, the fluid velocity vector and the pressure, ρ the density of blood (ρ = 1050 kg m−3) and τ the stress tensor [28]
| 2.4 |
where S and 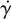 are the rate of deformation tensor and the shear rate, respectively.
are the rate of deformation tensor and the shear rate, respectively. 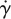 is related to the second invariant of S. η represents the viscosity of blood, which is a function of
is related to the second invariant of S. η represents the viscosity of blood, which is a function of 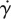 . For the non-Newtonian blood flow simulation, the Carreau model is used to calculate the blood viscosity
. For the non-Newtonian blood flow simulation, the Carreau model is used to calculate the blood viscosity
| 2.5 |
where η∞ = 3.45 × 10−3 kg m−1 s−1, η0 = 5.6 × 10−2 kg m−1 s−1, n = 0.3568 and λ = 3.313 s [28]. For the Newtonian blood flow simulation, η is kept constant as η∞.
Endothelium. To couple the flow dynamics in the arterial lumen with that in the arterial wall, the transmural velocity across the endothelium (Jv) is modelled by the Kedem–Katchalsky equation [29]
| 2.6 |
where Δp is the pressure difference across the endothelium, σ the osmotic reflection coefficient and Δπ the oncotic pressure drop across the endothelium. In the present pilot study, Δπ is neglected to decouple the fluid dynamics from the solute dynamics. Lp is the hydraulic conductivity of the endothelium, which is assumed to be a function of WSS (|τw|) according to Sun et al. [29].
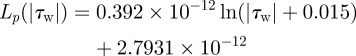 |
2.7 |
Arterial wall. The transmural flow across the arterial wall is described by Darcy's Law
| 2.8 |
and
| 2.9 |
where uw and pw represent, respectively, the velocity vector and pressure, Kw the hydraulic permeability of the wall and μw the viscosity of plasma (Kw = 2.0 × 10−18 m2, μw = 0.72 × 10−3 kg m−1 s−1) [29].
Solute dynamics
Lumen. The mass transport of NO in the flowing blood can be described by the following steady advection–diffusion reaction equation:
| 2.10 |
where cl is the concentration of NO, Dl the diffusion coefficient of NO in blood and taken as 3.3 × 10−9 m2 s−1 and 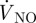 denotes the rate at which NO is consumed by reaction [17]. In the present study, NO is assumed to be auto-oxidized to yield nitrite, which can be described by the following pseudo-second-order reaction [23]:
denotes the rate at which NO is consumed by reaction [17]. In the present study, NO is assumed to be auto-oxidized to yield nitrite, which can be described by the following pseudo-second-order reaction [23]:
| 2.11 |
where koxygen is the pseudo-second-order reaction rate (7.56 × 10−6 nM−1 s−1) [23].
Endothelium. The NO production rate at the endothelium is a critical parameter in the computational simulation of NO transport. In the present study, the NO production rate is given by the following hyperbolic model that is based on real-time experimental measurements made by Andrews et al. [30]:
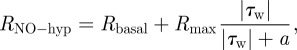 |
2.12 |
where Rbasal = 2.13 nM s−1, Rmax = 457.5 nM s−1 and a = 3.5 Pa.
Arterial wall. The transport of NO in the arterial wall is modelled by the following equation:
| 2.13 |
where cw is the concentration of NO in the arterial wall, Dw the diffusivity of NO in the arterial wall (8.48 × 10−10 m2 s−1) and 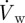 the reaction rate of NO [31]. The reaction rate is treated as a first-order rate expression, which is given by [32]
the reaction rate of NO [31]. The reaction rate is treated as a first-order rate expression, which is given by [32]
| 2.14 |
where kw is the consumption rate constant (0.01 s−1).
2.2.2. Boundary conditions
As shown in figure 1, flow transport equations (2.2)–(2.3) and (2.8)–(2.9) are subject to the following boundary conditions:
BC-A: At the inlet of the lumen of the arterial segment, the flow is set as a fully developed (parabolic) velocity profile. The mean velocity is chosen to be 0.24 m s−1 as the average of the mean diastolic and systolic velocities in the LAD, so that the resulting mean Reynolds number (Re) based on the diameter of the artery is approximately 270 [33].
BC-B: The pressure at the outlet boundary of the artery lumen is set at 100 mmHg.
BC-C: At the lumen side of the endothelial boundary, a transmural outlet velocity in the out normal direction of the lumen domain is prescribed by
| 2.15 |
where Jv is the transmural velocity across the endothelium in (2.6) and nl is the out normal vector of the endothelium.
BC-D: At the wall side of the endothelial boundary, a transmural inlet velocity in the normal direction is prescribed by
| 2.16 |
BC-E: At the media–adventitia interface, a constant pressure boundary condition of 30 mmHg is employed [29].
BC-F: No flow is set on both the axial ends of the arterial wall, i.e. n · uw = 0.
BC-E: Symmetric condition is set at the symmetrical axis.
The boundary conditions for the mass transport equations (2.10) and (2.13) are as follows:
BC-1: The inflow concentration of NO (c0) at the inlet is assumed to be 0 nM.
BC-2: The continuity of NO concentration is maintained and the mass flux across the endothelium is assumed to be the product of the endothelium NO production rate and the thickness of the endothelium. That is,
| 2.17 |
| 2.18 |
and
| 2.19 |
where Nl · nl is the flux of NO from the endothelium into the arterial wall, −Nw · nl the flux of NO from the endothelium into the lumen, T the thickness of endothelium, which is assumed to be 2 µm, and RNO is the NO production rate in (2.12).
BC-3: For other boundaries, the concentration gradient in the boundary normal direction is assumed to be zero.
2.3. Computation procedures
The numerical simulations were carried out by a validated finite element algorithm Comsol Multiphysics. First, flow simulations were performed to obtain the pressure and the velocity fields, which were used later on for the simulations of NO transport. The numerical results were considered to be mesh-independent when the difference in NO concentration between two consecutive simulations was less than 0.1 per cent. For all cases, the final computational mesh consisted of 50 × 1600 cubic elements (50 elements along the radial direction and 1600 elements along the axial direction) in the lumen and 20 × 1600 cubic elements in the arterial wall. The mesh was especially refined at the stenosis and near the endothelium.
3. Results
3.1. Fluid dynamics
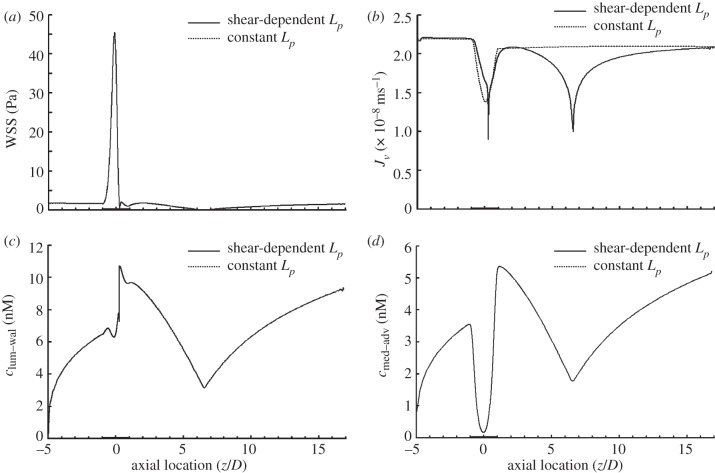
Figure 2a shows the distribution of WSS along the stenosis model. WSS increases sharply reaching a peak value of approximately 45.5 Pa near the stenosis throat. Immediately after the throat WSS decreases drastically and reverses the direction. The two local minima with a WSS value of zero correspond to the separation point (z = 0.2583D) and reattachment point (z = 6.5187D).
Figure 2.
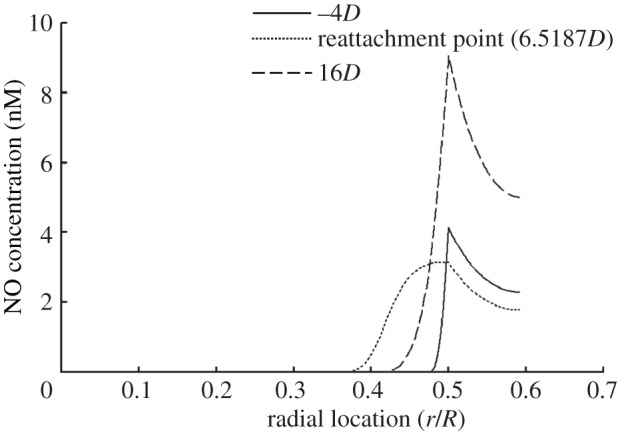
Comparison between the model with shear-dependent hydraulic conductivity (solid line) and the model with a corresponding constant hydraulic conductivity (dashed line) in terms of (a) WSS distribution, (b) transmural velocity distribution across the endothelium (Jv), (c) NO distribution at the lumen–wall interface (clum–wal) and (d) NO distribution at the media/adventitia interface (cmed–adv). The shear-dependent hydraulic conductivity has no effect on both the WSS distribution and the transport of NO. In this set of simulations, Re = 270 and blood is assumed to be a Newtonian fluid.
Figure 2b displays the distributions of the transmural fluid velocity across the endothelium (Jv) for both the model with shear-dependent hydraulic conductivity (solid line) and the model with a corresponding constant hydraulic conductivity of 3 × 10−12 m s−1 Pa−1 (dashed line). For the model with shear-dependent hydraulic conductivity, Jv is approximately 2.19 × 10−8 m s−1 in the upstream region of the stenosis. Owing to the higher resistance provided by the thickened arterial wall, the transmural velocity is relatively low at the stenosis region. After the stenosis throat, two local minima Jv occur at the separation point and reattachment point, which are 9.0 × 10−9 and 1.0 × 10−8 m s−1, respectively.
3.2. Nitric oxide transport
As shown in figure 2c, the concentration distribution of NO at the lumen–wall interface (clum–wal) varies dramatically along the stenosis. The production of NO on the endothelium first leads to a gradual increase in clum–wal. Then clum–wal decreases slightly at the axial coordinate of −0.6D and reaches a local minimum of 6.3 nM near the throat (z = −0.1458D). Immediately from the throat, clum–wal increases sharply reaching a peak value of approximately 10.7 nM near the flow separation point. The lowest clum–wal occurs at the flow reattachment point.
Figure 2d shows the concentration distribution of NO at the interface between the media and the adventitia. NO concentration decreases sharply at the stenosis region and the flow-separated region.
NO concentration profiles within the wall at different axial locations are illustrated in figure 3. Thin concentration boundary layers are predicted in the upstream section (−4D) and the downstream section (16D) of the stenosis, where blood flows are not disturbed. In the separated flow zone the boundary layer grows much thicker, which is because of the absence of the convective transport in this region.
Figure 3.
Profiles of NO concentration (c) within the wall at three different axial locations. −4D (solid line) and 16D (dashed line) are located, respectively, in the upstream and the downstream sections from the stenosis. In this set of simulations, Re = 270, NO production rate = RNO–hyp and blood is assumed to be a Newtonian fluid. The dotted line indicates the reattachment point (6.518D).
3.3. Effect of endothelial hydraulic conductivity
From figure 2, it can be seen that although shear-dependent hydraulic conductivity can significantly affect the transmural fluid velocity across the endothelium, it has no effect on both the WSS distribution and the transport of NO.
3.4. Effect of non-Newtonian blood flow
In the previous sections, calculations were performed assuming blood as a Newtonian fluid. However, blood is a non-Newtonian fluid, particularly at low shear rates. We therefore compared a non-Newtonian model with the Newtonian one. As shown in figure 4a, the WSS profiles for both the Newtonian and the non-Newtonian simulations are similar. Generally speaking, WSS for the non-Newtonian simulation is slightly higher than that for the Newtonian simulation. When compared with the Newtonian blood flow simulation, the reattachment point for the non-Newtonian simulation moves slightly upstream towards the throat.
Figure 4.
Comparison between Newtonian (solid line) and non-Newtonian (dashed line) models in terms of (a) WSS distribution, (b) NO distribution at the lumen–wall interface with a constant NO production rate and (c) NO distribution at the lumen–wall interface with a shear-dependent NO production rate. In this set of simulations, NO production rate = (RNO–hyp). Re = 270.
The non-Newtonian property of blood can affect the transport of NO by both the convection through the flow field and the NO production rate through the WSS (2.12). To clarify the effect of the non-Newtonian behaviour of blood on NO transport, in this set of simulations we analyse two different cases for the transport of NO.
Case 1: To investigate the effect of convection, NO production rate at the endothelium in (2.18) is assumed to be constant and to be the same as that at the inlet section of the stenosis.
Case 2: NO production rate at the endothelium is shear-dependent and modelled by (2.12).
As shown in figure 4b, for case 1, after the stenosis throat, clum–wal for the Newtonian model is much higher than that of the non-Newtonian model. However, for case 2, as illustrated in figure 4c, clum–wal for the Newtonian model is generally lower than that of the non-Newtonian model, following the same trend as WSS. These results demonstrated that non-Newtonian behaviour of blood induces two opposite effects on NO transport and its effect on shear-dependent NO production rate dominates NO transport.
3.5. Effect of the Reynolds number
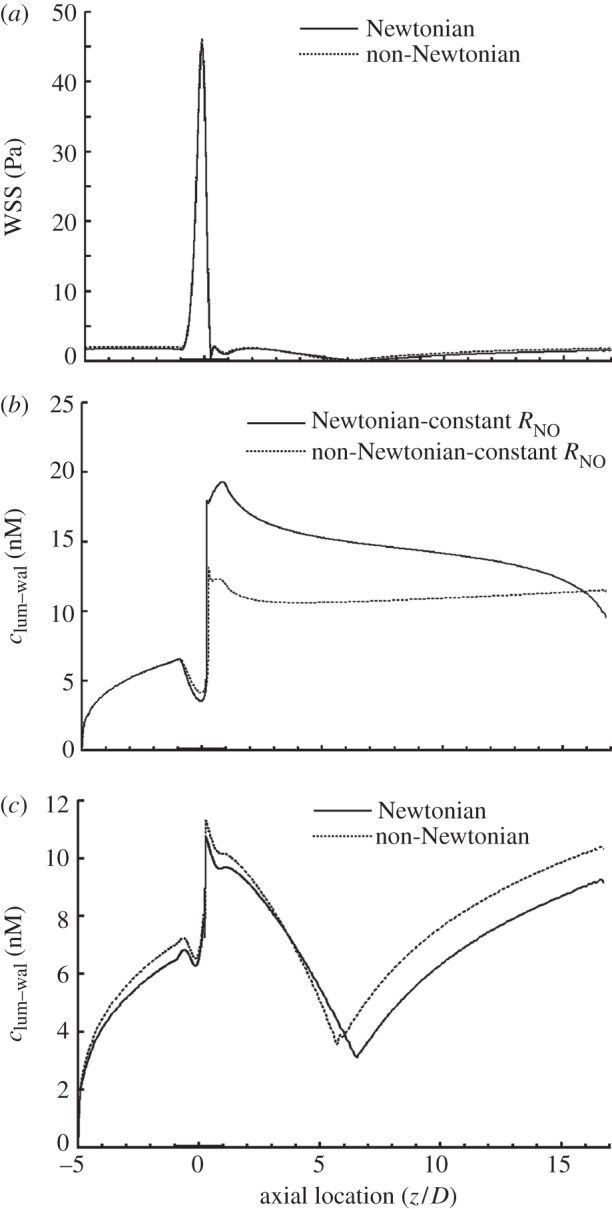
Until now, the numerical simulations have been carried out only for an Re of 270, which represents the average of the mean diastolic and systolic velocities in the LAD. However, the blood flow rate (hence, Re) in the LAD varies dramatically from a resting state to a state of a strenuous exercise. Therefore, to verify the effect of the Reynolds number, we also carried out simulations at Re = 50, 270, 500 and 700.
As shown in figure 5, generally speaking, the increase in Re causes an increase in clum–wal. However, as is evident from the figure, the concentration of NO at the endothelium is strongly affected by the Reynolds number. At Re = 50, clum–wal is higher in the stenosis region than other areas without the stenosis. In contrast to this, at Re = 270, 500 and 700, clum–wal drops to a local minimum near the throat of the stenosis and at the flow reattachment point.
Figure 5.
Effect of Re on the NO distribution at the lumen–wall interface (cmed–adv), showing that the distribution of clum–wal at the endothelium is strongly affected by the Re, and clum–wal increases with increasing Re. In this set of simulations, the NO production rate is RNO–hyp and blood is assumed to be a Newtonian fluid. Re = 50 (dotted line), 270 (solid line), 500 (dashed line) and 700 (dashed-dotted line).
3.6. Effect of nitric oxide production rate
A number of experimental studies measured the oxidation products of NO and estimated the NO production rate at the endothelium [18,34]. However, owing to the differences in experimental protocols, the reported data varied in a very wide range (from 0.035 to 68 μM s−1) [18,34]. To investigate the effect of NO production rate on the transport of NO, two models were compared. The first one was based on (2.12). The second was assumed to have an RNO that was linearly dependent on WSS as described by [20]
| 3.1 |
where Rref = 150 μM s−1 and τref = 2.4 Pa.
Figure 6 shows the distribution of NO concentration at the lumen–wall interface and at the media–adventitia interface. When compared with simulations based on RNO–hyp in (2.12), owing to the much higher NO production rate, the NO concentration obtained for RNO–linear is much higher. For the two models, as illustrated in figure 2d and figure 6, the distribution of NO concentration profiles at the media–adventitia interface is similar. However, there is great difference in clum–wal at the stenosis region of the two models. These results indicate that the magnitude and the form of the NO production model have a significant influence on the concentration distribution of NO in the stenosis.
Figure 6.
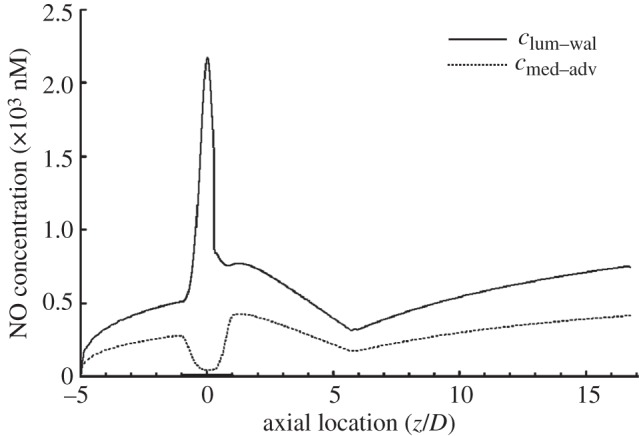
NO distribution when RNO–linear is calculated from (3.1). The solid line is NO distribution at the lumen–wall interface (clum–wal). The dashed line is NO distribution at the media/adventitia interface (cmed–adv). In this set of simulations, Re = 270 and blood is assumed to be a Newtonian fluid.
3.7. Effect of stenosis severity
In the previous sections, the area reduction of the stenosis was set at 75 per cent. In order to clarify the effect of stenosis severity, we carried out three additional simulations with different stenosis area reductions, namely 0, 25 and 50 per cent. Figure 7a shows that the increase in stenosis area reductions causes a sharp increase in WSS at the throat of the stenosis. From figure 7a, it can be seen that the distance between the flow separation point and the reattachement point becomes bigger with increasing stenosis severity, indicating that the size of the vortex distal to the stenosis increases with increasing stenosis severity.
Figure 7.
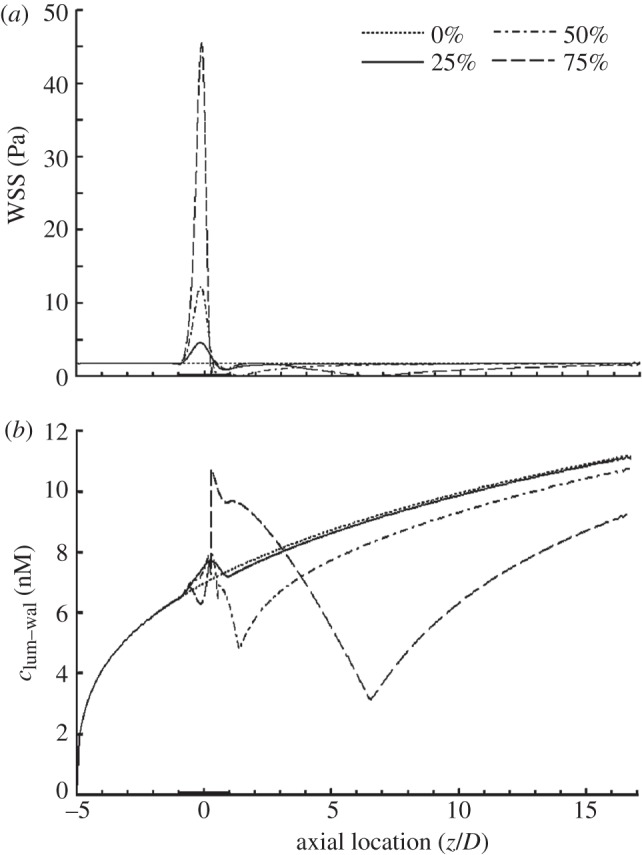
Comparison between stenoses with different area reductions. (a) WSS distribution and (b) NO distribution at the lumen–wall interface (clum–wal). In this set of simulations, Re = 270 and blood is assumed to be a Newtonian fluid. The dashed line indicates 75%; dashed-dotted line, 50%; solid line, 25%; dotted line, 0%.
As illustrated in figure 7b, the luminal surface concentration of NO (clum–wal) at the stenosis in the model with 25 per cent area reduction is slightly higher than that in the model with no stenosis. However, when the stenosis area reduction increases to 50 and 75 per cent, clum–wal is significantly lower than that of the model with no stenosis.
3.8. Effect of red blood cells
NO can be auto-oxidized by oxygen in the lumen and be scavenged by haemoglobin in the RBCs. In order to clarify the effect of RBCs, an additional reaction term was included in the NO transport equation in lumen (2.10), which is described by
| 3.2 |
where kRBC is the first-order reaction rate for NO consumption by RBCs in the lumen. kRBC is taken to be 2.3–230 s−1, which is calculated from the effective second-order rate constant between NO and the RBC-encapsulated haemoglobin (from 103 to 105 M−1 s−1) [35,36], with the assumption that the haemoglobin concentration in blood is 2.3 mM [37].
As shown in figure 8a, when compared with the simulation without RBCs, the presence of RBCs would significantly reduce the luminal surface concentration of NO (clum–wal) in the whole model and as kRBC increases, clum–wal is sharply reduced, indicating that RBC is an effective NO scavenger in the blood. However, with or without RBCs, the transport of NO is significantly hindered in the disturbed flow region distal to the stenosis.
Figure 8.
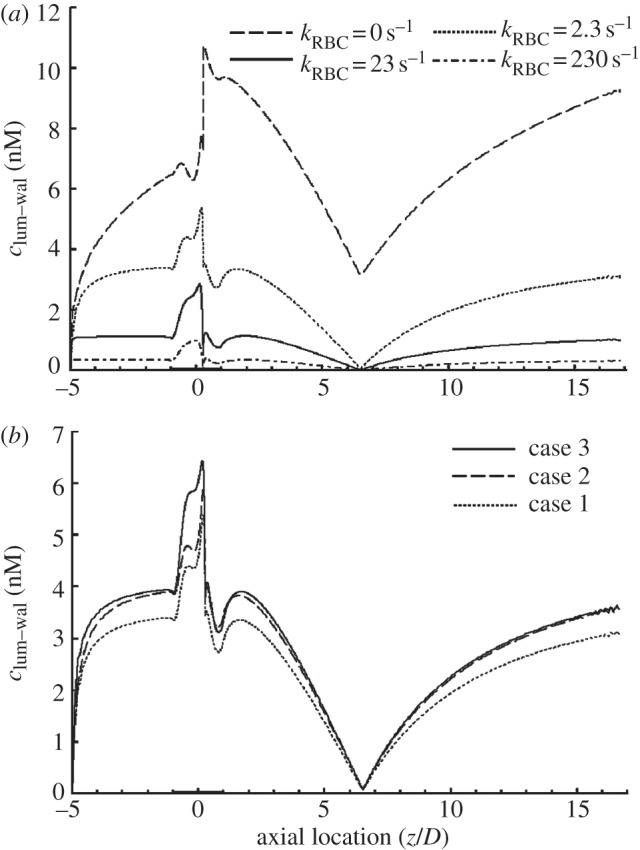
Effect of RBCs and the RBC-free layer on NO distribution at the lumen–wall interface (clum–wal). (a) Effect of RBCs on clum–wal for different NO reaction rates (kRBC=0 s−1 indicates the dashed line; kRBC = 2.3 s−1, dotted line; kRBC = 23 s−1, solid line; kRBC = 230 s−1, dash-dotted line); (b) distributions of clum–wal for the three case simulations. The comparison between case 1 (dotted line) and case 2 (dashed line) shows that the RBC-free layer with a much lower NO reaction rate could enhance clum–wal, and the comparison between case 2 and case 3 (solid line) illustrates that endothelial glycocalyx could further increase clum–wal in the high-WSS region of the stenosis. In this set of simulations, Re = 270, the NO production rate is RNO–hyp and blood is assumed to be a Newtonian fluid.
3.9. Effect of red blood cell-free layer
The reaction rate for auto-oxidation of NO in the RBC-free layer (2 μm plasma layer plus 4 μm glycocalyx layer) is much lower than that for NO consumption by RBCs in the lumen. In addition, owing to the low fluid permeability of the glycocalyx layer, the flow velocity through the glycocalyx was very small [38], which may increase the resistance for NO transport towards the lumen. Therefore, to clarify the effect of the RBC-free layer on NO transport, in this set of simulations we analysed three different cases for the transport of NO.
Case 1: The flow simulation in the RBC-free layer is based on the steady-state incompressible Navier–Stokes equations, the reaction of NO in the RBC-free layer includes the auto-oxidation by oxygen and the consumption by RBCs ((3.2), kRBC = 2.3 s−1).
Case 2: The flow simulation in the RBC-free layer is the same as that in case 1. However, the reaction of NO in the RBC-free layer only includes the auto-oxidation by oxygen ((2.11), kRBC = 0 s−1).
Case 3: The transmural flow across the RBC-free layer is modelled with a porous medium to simulate the glycocalyx, which is described by the Brinkman equation with a hydraulic permeability and a porosity of 6.0383 × 10−18 and 0.6735 [39], respectively. The reaction of NO is the same as that in case 2 (kRBC = 0 s−1).
As shown in figure 8b, when compared with case 1, the luminal surface concentration of NO (clum–wal) for case 2 increases more than 10 per cent in most regions of the model except in the vicinity of the flow separation region, where clum–wal is almost the same for both cases. For case 3, in most parts of the model, clum–wal closely resembles that for case 2. However, in the upstream region of the stenosis where WSS is relatively high, clum–wal in case 3 is significantly higher than that in case 2. These results demonstrate that the RBC-free layer can reduce the scavenging of NO and increase the NO concentration on the endothelial cells. Figure 8b also indicates that the transport of NO is evidently hindered in the disturbed flow region for all the three cases.
4. Discussion
It is well documented that NO may have numerous anti-atherosclerosis properties [6,12,40,41]. In the present study, we hypothesized that locally disturbed flow could impede NO transport in the artery and hence induce the localization of atherogenesis. To substantiate this hypothesis, we numerically studied the transport of NO using an axisymmetric stenosis model that could create a well-defined flow disturbance. Our results demonstrated that the concentration distribution of NO in the disturbed flow region was indeed significantly reduced. In addition, we further investigated the various factors that might influence the transport of NO. The study showed that the Reynolds number (inlet velocity), stenosis severity, NO production rate by the endothelium, RBCs and RBC-free layer could significantly affect the concentration distribution of NO in the artery. The non-Newtonian viscous behaviour of blood had little influence on the transport of NO. The hydraulic conductivity of the endothelium had no impact on the transport of NO.
The present study revealed that the concentration of NO on the endothelium was significantly reduced in the vicinity of the flow separation point, which might enhance leucocyte adhesion to the endothelium, leading to atherogenesis there. This prediction is consistent with the experimental findings by others [42,43]. Cicha et al. [42] found that the disturbed flow at the outer wall of an arterial bifurcation could downregulate the expression of eNOS and hence reduce the release of NO, leading to enhanced monocyte recruitment. Rouleau et al. [43] observed in their experimental study that neutrophil adhesion was significantly enhanced in the recirculation flow zone distal to a stenosis.
The present numerical study predicted a transmural velocity (Jv) of 2.19 × 10−8 m s−1 in the upstream region of the stenosis, which was in the range of data measured by Meyer et al. [44] (1.78 × 10−8 m s−1) and Tedgui & Lever [45] (2.80 × 10−8 m s−1) at the same transmural pressure. In addition, the distribution of transmural velocity across the endothelium with a shear-dependent hydraulic conductivity closely resembles the distribution obtained by Sun et al. [29].
Our simulation demonstrated that when compared with constant hydraulic conductivity, the shear-dependent hydraulic conductivity of the endothelium had almost no effect on the transport of NO. The reason is that the transmural fluid velocity due to the hydraulic conductivity of the endothelium is very low so that the Peclet number (Pe = RJv/Dw) is low. The Peclet number represents the ratio of NO convective transport to NO diffusive transport. Therefore, at such a low transmural fluid velocity, the transport of NO across the arterial wall is dominated by diffusive flux of NO.
The present study indicated that when compared with the Newtonian assumption, the shear thinning behaviour of blood could lead to enhanced WSS in most regions of the stenosis. This was consistent with the flow simulation study in the human aorta by Liu et al. [46]. When compared with the Newtonian model, the flow reattachment point for the non-Newtonian model moved upstream towards the stenosis throat, which was in agreement with the predictions by others [47].
The result of the present study showed that if the production rate of NO by the endothelium was constant, the concentration of NO in the disturbed flow region would be much higher for the Newtonian model than that for the non-Newtonian model. However, if the production rate of NO was shear-dependent, this difference in NO concentration between the Newtonian model and the non-Newtonian one would be significantly attenuated. Because experimental observations [13,15] proved the production rate of NO by the endothelium was shear-dependent, the result indicated that for the simulation of NO transport in the arterial system, treating blood as a Newtonian fluid was reasonable.
The result showed that the increase in Re (inlet velocity) caused an increase in NO concentration on the endothelium (clum–wal). This result was consistent with the experimental results of others [48] who found that increased flow in blood vessels elicited vasodilation responses mediated by increased availability of NO. Nevertheless, the present study also revealed two opposite effects of enhanced Re on endothelial NO concentration distribution. On the one hand, an increase in Re (hence in WSS) could enhance NO production by the endothelial cells. On the other hand, the increase in Re could lead to an increased convection that could wash the NO away from the luminal surface into the bulk flow. This was consistent with predictions by others [22,23] who found that the concentration of NO in a parallel plate flow chamber depended non-monotonically on the Re.
Arterial remodelling is the mechanism by which the size of arterial lumen is preserved despite the development of atherosclerosis [49]. This phenomenon was first reported by Glagov et al. [50]. They studied histological sections of 136 left main coronary arteries obtained at autopsy and found that a nearly normal lumen cross-sectional area was preserved until the atherosclerotic lesion occupies 40 per cent of the area circumscribed by the internal elastic lamina [50]. NO has been proven to play an important role in the arterial remodelling [49,51]. Our simulations demonstrated that the concentration of NO at the endothelium in the model with a 25 per cent stenosis was higher than that in the model without a stenosis. The increased NO due to the mild stenosis might stimulate the remodelling of the artery. However, when the stenosis increased to beyond 50 per cent, the concentration of NO at the endothelium became much lower than that in the model without a stenosis, which might lead to rapid decreases in the lumen cross-sectional area. This phenomenon has been observed by Glagov et al. [50].
NO diffused into the adjacent smooth muscle cells activates soluble guanylate cyclase (sGC), which catalyses the formation of cyclic guanosine monophosphate (cGMP), leading to smooth muscle relaxation and vasodilation. It has been reported that the value of NO concentration required for the activation of sGC varies in a wide range (1–250 nM) for half-maximum activity of sGC [18]. The present study indicated that if the value of RNO was calculated with (2.12), the relatively low NO concentration (cmed–adv) at the media–adventitia interface of the stenotic region (figures 2d and 6) because of the long diffusion distance from the endothelium out to the interface and the relatively low clum–wal at the downstream stenosis in the flow separation zone (figure 2c) might be insufficient to activate the sGC. However, if RNO was calculated using (2.18), the NO concentration in these areas was more than enough to activate the sGC. Therefore, the utilization of different models for NO production rate (RNO) could significantly affect the numerical results on the concentration distribution of NO. Nevertheless, it could not change the conclusion that locally disturbed flow could impede NO transport in the artery.
Owing to the high NO reaction rate by RBCs, the presence of RBCs in the lumen significantly reduced the NO concentration on the endothelium, which has also been demonstrated in the capillaries and arterioles [16,21,37]. However, the effect of RBCs on NO transport in the artery was diminished by the existence of the RBC-free plasma layer at the blood–endothelium interface because of the much lower NO reaction rate in the layer, which was consistent with Liao et al.'s experiments [36]. Moreover, the present study revealed that the endothelial glycocalyx with relatively low fluid permeability coating the endothelium would further increase the NO concentration on the endothelium in the high-WSS region of the stenosis by reducing NO convection from the endothelium to the lumen.
In the present study, we used a steady flow condition in the simulation. The pulsation of blood flow can affect the movement of the arterial wall, which in turn affects the flow of blood. It was reported that when the arterial wall was assumed to be an isotropic material, the compliance of the arterial wall had little effect on the haemodynamics of an arterial stenosis [51]. However, the non-uniform distribution of NO in the stenosis may lead to a non-uniform relaxation of the arterial wall, which in turn may render the arterial wall anisotropic. Therefore, the coupling of NO concentration with blood flow and the arterial wall compliance should be further investigated. In addition, the production rate of NO used in the study is constant, which is different from the reality that has been shown to be transient and burst-like, and facilitates NO delivery to the smooth muscle cells and reduces the scavenging of NO by blood [52]. Therefore the effect of transient NO production should also be studied.
To better understand the transport of NO in the artery, factors such as the compliance of the arterial wall, the transient effects of blood flow and the transient NO production rate should be considered in further studies.
5. Conclusions
A lumen–wall model with NO production at the lumen–wall interface was employed to study the transport of NO in an idealized stenosis. The simulation study revealed that the transport of NO was significantly hindered in the flow disturbed region distal to the stenosis, which may contribute to the development of atherosclerosis.
Acknowledgements
This work was supported by grants-in-aid from the National Natural Science Research Foundation of China (no. 11072023, 31170904, 61190123) and the Innovation Foundation of BUAA for PhD graduates.
References
- 1.Chiu J. J., Chien S. 2011. Effects of disturbed flow on vascular endothelium: pathophysiological basis and clinical perspectives. Physiol. Rev. 91, 327–387 10.1152/physrev.00047.2009 (doi:10.1152/physrev.00047.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.DeBakey M. E., Lawrie G. M., Glaeser D. H. 1985. Patterns of atherosclerosis and their surgical significance. Ann. Surg. 201, 115–131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Caro C. G., Fitz-Gerald J. M., Schroter R. C. 1971. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. Lond. B 177, 109–159 10.1098/rspb.1971.0019 (doi:10.1098/rspb.1971.0019) [DOI] [PubMed] [Google Scholar]
- 4.Malek A. M., Alper S. L., Izumo S. 1999. Hemodynamic shear stress and its role in atherosclerosis. JAMA 282, 2035–2042 10.1001/jama.282.21.2035 (doi:10.1001/jama.282.21.2035) [DOI] [PubMed] [Google Scholar]
- 5.Davignon J., Ganz P. 2004. Role of endothelial dysfunction in atherosclerosis. Circulation 109, III27–III32 10.1161/01.CIR.0000131515.03336.f8 (doi:10.1161/01.CIR.0000131515.03336.f8) [DOI] [PubMed] [Google Scholar]
- 6.De Caterina R., Libby P., Peng H. B., Thannickal V. J., Rajavashisth T. B., Gimbrone M. A., Jr, Shin W. S., Liao J. K. 1995. Nitric oxide decreases cytokine-induced endothelial activation. Nitric oxide selectively reduces endothelial expression of adhesion molecules and proinflammatory cytokines. J. Clin. Invest. 96, 60–68 10.1172/JCI118074 (doi:10.1172/JCI118074) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kubes P., Suzuki M., Granger D. N. 1991. Nitric oxide: an endogenous modulator of leukocyte adhesion. Proc. Natl. Acad. Sci. USA 88, 4651–4655 10.1073/pnas.88.11.4651 (doi:10.1073/pnas.88.11.4651) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Draijer R., Atsma D. E., van der Laarse A., van Hinsbergh V. W. 1995. cGMP and nitric oxide modulate thrombin-induced endothelial permeability. Regulation via different pathways in human aortic and umbilical vein endothelial cells. Circ. Res. 76, 199–208 10.1161/01.RES.76.2.199 (doi:10.1161/01.RES.76.2.199) [DOI] [PubMed] [Google Scholar]
- 9.Goss S. P., Hogg N., Kalyanaraman B. 1997. The effect of nitric oxide release rates on the oxidation of human low density lipoprotein. J. Biol. Chem. 272, 21 647–21 653 10.1074/jbc.272.34.21647 (doi:10.1074/jbc.272.34.21647) [DOI] [PubMed] [Google Scholar]
- 10.Mooradian D. L., Hutsell T. C., Keefer L. K. 1995. Nitric oxide (NO) donor molecules: effect of NO release rate on vascular smooth muscle cell proliferation in vitro. J. Cardiovasc. Pharmacol. 25, 674–678 [PubMed] [Google Scholar]
- 11.Sarkar R., Meinberg E. G., Stanley J. C., Gordon D., Webb R. C. 1996. Nitric oxide reversibly inhibits the migration of cultured vascular smooth muscle cells. Circ. Res. 78, 225–230 10.1161/01.RES.78.2.225 (doi:10.1161/01.RES.78.2.225) [DOI] [PubMed] [Google Scholar]
- 12.Radomski M. W., Palmer R. M., Moncada S. 1987. The anti-aggregating properties of vascular endothelium: interactions between prostacyclin and nitric oxide. Br. J. Pharmacol. 92, 639–646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kanai A. J., Strauss H. C., Truskey G. A., Crews A. L., Grunfeld S., Malinski T. 1995. Shear stress induces ATP-independent transient nitric oxide release from vascular endothelial cells, measured directly with a porphyrinic microsensor. Circ. Res. 77, 284–293 10.1161/01.RES.77.2.284 (doi:10.1161/01.RES.77.2.284) [DOI] [PubMed] [Google Scholar]
- 14.Noris M., Morigi M., Donadelli R., Aiello S., Foppolo M., Todeschini M., Orisio S., Remuzzi G., Remuzzi A. 1995. Nitric oxide synthesis by cultured endothelial cells is modulated by flow conditions. Circ. Res. 76, 536–543 10.1161/01.RES.76.4.536 (doi:10.1161/01.RES.76.4.536) [DOI] [PubMed] [Google Scholar]
- 15.Ranjan V., Xiao Z., Diamond S. L. 1995. Constitutive NOS expression in cultured endothelial cells is elevated by fluid shear stress. Am. J. Physiol. 269, H550–H555 [DOI] [PubMed] [Google Scholar]
- 16.Chen X., Jaron D., Barbee K. A., Buerk D. G. 2006. The influence of radial RBC distribution, blood velocity profiles, and glycocalyx on coupled NO/O2 transport. J. Appl. Physiol. 100, 482–492 10.1152/japplphysiol.00633.2005 (doi:10.1152/japplphysiol.00633.2005) [DOI] [PubMed] [Google Scholar]
- 17.Lancaster J. R., Jr 1994. Simulation of the diffusion and reaction of endogenously produced nitric oxide. Proc. Natl. Acad. Sci. USA 91, 8137–8141 10.1073/pnas.91.17.8137 (doi:10.1073/pnas.91.17.8137) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tsoukias N. M. 2008. Nitric oxide bioavailability in the microcirculation: insights from mathematical models. Microcirculation 15, 813–834 10.1080/10739680802010070 (doi:10.1080/10739680802010070) [DOI] [PubMed] [Google Scholar]
- 19.Smith K. M., Moore L. C., Layton H. E. 2003. Advective transport of nitric oxide in a mathematical model of the afferent arteriole. Am. J. Physiol. Renal. Physiol. 284, F1080–F1096 10.1152/ajprenal.00141.2002 (doi:10.1152/ajprenal.00141.2002) [DOI] [PubMed] [Google Scholar]
- 20.Chen X., Buerk D. G., Barbee K. A., Kirby P., Jaron D. 2011. 3D network model of NO transport in tissue. Med. Biol. Eng. Comput. 49, 633–647 10.1007/s11517-011-0758-7 (doi:10.1007/s11517-011-0758-7) [DOI] [PubMed] [Google Scholar]
- 21.Sriram K., Vazquez B. Y., Yalcin O., Johnson P. C., Intaglietta M., Tartakovsky D. M. 2011. The effect of small changes in hematocrit on nitric oxide transport in arterioles. Antioxid. Redox Signal 14, 175–185 10.1089/ars.2010.3266 (doi:10.1089/ars.2010.3266) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fadel A. A., Barbee K. A., Jaron D. 2009. A computational model of nitric oxide production and transport in a parallel plate flow chamber. Ann. Biomed. Eng. 37, 943–954 10.1007/s10439-009-9658-5 (doi:10.1007/s10439-009-9658-5) [DOI] [PubMed] [Google Scholar]
- 23.Plata A. M., Sherwin S. J., Krams R. 2010. Endothelial nitric oxide production and transport in flow chambers: the importance of convection. Ann. Biomed. Eng. 38, 2805–2816 10.1007/s10439-010-0039-x (doi:10.1007/s10439-010-0039-x) [DOI] [PubMed] [Google Scholar]
- 24.Dodge J. T., Jr, Brown B. G., Bolson E. L., Dodge H. T. 1992. Lumen diameter of normal human coronary arteries. Influence of age, sex, anatomic variation, and left ventricular hypertrophy or dilation. Circulation 86, 232–246 10.1161/01.CIR.86.1.232 (doi:10.1161/01.CIR.86.1.232) [DOI] [PubMed] [Google Scholar]
- 25.Gradus-Pizlo I., Bigelow B., Mahomed Y., Sawada S. G., Rieger K., Feigenbaum H. 2003. Left anterior descending coronary artery wall thickness measured by high-frequency transthoracic and epicardial echocardiography includes adventitia. Am. J. Cardiol. 91, 27–32 10.1016/S0002-9149(02)02993-4 (doi:10.1016/S0002-9149(02)02993-4) [DOI] [PubMed] [Google Scholar]
- 26.Ghalichi F., Deng X., De Champlain A., Douville Y., King M., Guidoin R. 1998. Low Reynolds number turbulence modeling of blood flow in arterial stenoses. Biorheology 35, 281–294 10.1016/S0006-355X(99)80011-0 (doi:10.1016/S0006-355X(99)80011-0) [DOI] [PubMed] [Google Scholar]
- 27.Ryval J., Straatman A. G., Steinman D. A. 2004. Two-equation turbulence modeling of pulsatile flow in a stenosed tube. J. Biomech. Eng. 126, 625–635 10.1115/1.1798055 (doi:10.1115/1.1798055) [DOI] [PubMed] [Google Scholar]
- 28.Cho Y. I., Kensey K. R. 1991. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: steady flows . Biorheology 28, 241–262 [DOI] [PubMed] [Google Scholar]
- 29.Sun N., Wood N. B., Hughes A. D., Thom S. A., Xu X. Y. 2006. Fluid-wall modelling of mass transfer in an axisymmetric stenosis: effects of shear-dependent transport properties. Ann. Biomed. Eng. 34, 1119–1128 10.1007/s10439-006-9144-2 (doi:10.1007/s10439-006-9144-2) [DOI] [PubMed] [Google Scholar]
- 30.Andrews A. M., Jaron D., Buerk D. G., Kirby P. L., Barbee K. A. 2010. Direct, real-time measurement of shear stress-induced nitric oxide produced from endothelial cells in vitro. Nitric Oxide 23, 335–342 10.1016/j.niox.2010.08.003 (doi:10.1016/j.niox.2010.08.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu X., Srinivasan P., Collard E., Grajdeanu P., Zweier J. L., Friedman A. 2008. Nitric oxide diffusion rate is reduced in the aortic wall. Biophys. J. 94, 1880–1889 10.1529/biophysj.107.120626 (doi:10.1529/biophysj.107.120626) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vaughn M. W., Kuo L., Liao J. C. 1998. Estimation of nitric oxide production and reaction rates in tissue by use of a mathematical model. Am. J. Physiol. 274, H2163–H2176 [DOI] [PubMed] [Google Scholar]
- 33.Iliceto S., Marangelli V., Memmola C., Rizzon P. 1991. Transesophageal Doppler echocardiography evaluation of coronary blood flow velocity in baseline conditions and during dipyridamole-induced coronary vasodilation. Circulation 83, 61–69 10.1161/01.CIR.83.1.61 (doi:10.1161/01.CIR.83.1.61) [DOI] [PubMed] [Google Scholar]
- 34.Chen K., Popel A. S. 2006. Theoretical analysis of biochemical pathways of nitric oxide release from vascular endothelial cells. Free Radic. Biol. Med. 41, 668–680 10.1016/j.freeradbiomed.2006.05.009 (doi:10.1016/j.freeradbiomed.2006.05.009) [DOI] [PubMed] [Google Scholar]
- 35.Azarov I., Huang K. T., Basu S., Gladwin M. T., Hogg N., Kim-Shapiro D. B. 2005. Nitric oxide scavenging by red blood cells as a function of hematocrit and oxygenation. J. Biol. Chem. 280, 39 024–39 032 10.1074/jbc.M509045200 (doi:10.1074/jbc.M509045200) [DOI] [PubMed] [Google Scholar]
- 36.Liao J. C., Hein T. W., Vaughn M. W., Huang K. T., Kuo L. 1999. Intravascular flow decreases erythrocyte consumption of nitric oxide. Proc. Natl. Acad. Sci. USA 96, 8757–8761 10.1073/pnas.96.15.8757 (doi:10.1073/pnas.96.15.8757) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vaughn M. W., Kuo L., Liao J. C. 1998. Effective diffusion distance of nitric oxide in the microcirculation. Am. J. Physiol. 274, H1705–H1714 [DOI] [PubMed] [Google Scholar]
- 38.Liu X., Fan Y., Deng X. 2011. Mechanotransduction of flow-induced shear stress by endothelial glycocalyx fibers is torque determined. ASAIO J. 57, 487–494 10.1097/MAT.0b013e318233b5ed (doi:10.1097/MAT.0b013e318233b5ed) [DOI] [PubMed] [Google Scholar]
- 39.Liu X., Fan Y., Deng X. 2011. Effect of the endothelial glycocalyx layer on arterial LDL transport under normal and high pressure. J. Theor. Biol. 283, 71–81 10.1016/j.jtbi.2011.05.030 (doi:10.1016/j.jtbi.2011.05.030) [DOI] [PubMed] [Google Scholar]
- 40.Li H., Forstermann U. 2000. Nitric oxide in the pathogenesis of vascular disease. J. Pathol. 190, 244–254 (doi:10.1002/(SICI)1096-9896(200002)190:3<244::AID-PATH575>3.0.CO;2-8) [DOI] [PubMed] [Google Scholar]
- 41.Lloyd-Jones D. M., Bloch K. D. 1996. The vascular biology of nitric oxide and its role in atherogenesis. Annu. Rev. Med. 47, 365–375 10.1146/annurev.med.47.1.365 (doi:10.1146/annurev.med.47.1.365) [DOI] [PubMed] [Google Scholar]
- 42.Cicha I., Goppelt-Struebe M., Yilmaz A., Daniel W. G., Garlichs C. D. 2008. Endothelial dysfunction and monocyte recruitment in cells exposed to non-uniform shear stress. Clin. Hemorheol. Microcirc. 39, 113–119 10.3233/CH-2008-1074 (doi:10.3233/CH-2008-1074) [DOI] [PubMed] [Google Scholar]
- 43.Rouleau L., Copland I. B., Tardif J. C., Mongrain R., Leask R. L. 2010. Neutrophil adhesion on endothelial cells in a novel asymmetric stenosis model: effect of wall shear stress gradients. Ann. Biomed. Eng. 38, 2791–2804 10.1007/s10439-010-0032-4 (doi:10.1007/s10439-010-0032-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Meyer G., Merval R., Tedgui A. 1996. Effects of pressure-induced stretch and convection on low-density lipoprotein and albumin uptake in the rabbit aortic wall. Circ. Res. 79, 532–540 10.1161/01.RES.79.3.532 (doi:10.1161/01.RES.79.3.532) [DOI] [PubMed] [Google Scholar]
- 45.Tedgui A., Lever M. J. 1984. Filtration through damaged and undamaged rabbit thoracic aorta. Am. J. Physiol. 247, H784–H791 [DOI] [PubMed] [Google Scholar]
- 46.Liu X., Fan Y., Deng X., Zhan F. 2011. Effect of non-Newtonian and pulsatile blood flow on mass transport in the human aorta. J. Biomech. 44, 1123–1131 10.1016/j.jbiomech.2011.01.024 (doi:10.1016/j.jbiomech.2011.01.024) [DOI] [PubMed] [Google Scholar]
- 47.Tu C., Deville M. 1996. Pulsatile flow of non-Newtonian fluids through arterial stenoses. J. Biomech. 29, 899–908 10.1016/0021-9290(95)00151-4 (doi:10.1016/0021-9290(95)00151-4) [DOI] [PubMed] [Google Scholar]
- 48.Palmer R. M., Ferrige A. G., Moncada S. 1987. Nitric oxide release accounts for the biological activity of endothelium-derived relaxing factor. Nature 327, 524–526 10.1038/327524a0 (doi:10.1038/327524a0) [DOI] [PubMed] [Google Scholar]
- 49.Ward M. R., Pasterkamp G., Yeung A. C., Borst C. 2000. Arterial remodeling. Mechanisms and clinical implications. Circulation 102, 1186–1191 10.1161/01.CIR.102.10.1186 (doi:10.1161/01.CIR.102.10.1186) [DOI] [PubMed] [Google Scholar]
- 50.Glagov S., Weisenberg E., Zarins C. K., Stankunavicius R., Kolettis G. J. 1987. Compensatory enlargement of human atherosclerotic coronary arteries. N. Engl. J. Med. 316, 1371–1375 10.1056/NEJM198705283162204 (doi:10.1056/NEJM198705283162204) [DOI] [PubMed] [Google Scholar]
- 51.Lee K. W., Xu X. Y. 2002. Modelling of flow and wall behaviour in a mildly stenosed tube. Med. Eng. Phys. 24, 575–586 10.1016/S1350-4533(02)00048-6 (doi:10.1016/S1350-4533(02)00048-6) [DOI] [PubMed] [Google Scholar]
- 52.Tsoukias N. M., Kavdia M., Popel A. S. 2004. A theoretical model of nitric oxide transport in arterioles: frequency- vs. amplitude-dependent control of cGMP formation. Am. J. Physiol. Heart Circ. Physiol. 286, H1043–H1056 10.1152/ajpheart.00525.2003 (doi:10.1152/ajpheart.00525.2003) [DOI] [PubMed] [Google Scholar]