Abstract
We study the temporal evolution of the structure of the world's largest subway networks in an exploratory manner. We show that, remarkably, all these networks converge to a shape that shares similar generic features despite their geographical and economic differences. This limiting shape is made of a core with branches radiating from it. For most of these networks, the average degree of a node (station) within the core has a value of order 2.5 and the proportion of k = 2 nodes in the core is larger than 60 per cent. The number of branches scales roughly as the square root of the number of stations, the current proportion of branches represents about half of the total number of stations, and the average diameter of branches is about twice the average radial extension of the core. Spatial measures such as the number of stations at a given distance to the barycentre display a first regime which grows as r2 followed by another regime with different exponents, and eventually saturates. These results—difficult to interpret in the framework of fractal geometry—confirm and yield a natural explanation in the geometric picture of this core and their branches: the first regime corresponds to a uniform core, while the second regime is controlled by the interstation spacing on branches. The apparent convergence towards a unique network shape in the temporal limit suggests the existence of dominant, universal mechanisms governing the evolution of these structures.
Keywords: evolution of networks, urban transportation, spatial networks, core and branch geometry
1. Introduction
Transportation systems, especially mass transit, are an important component in cities and their expansion. In a world where more than 50 per cent of the population lives in urban areas [1], and where individual transportation increases in cost as cities grow larger, mass transit and, in particular, subway networks are central to the evolution of cities, their spatial organization [2–4] and dynamical processes occurring in them [5,6]. The percentage s(P) of cities with a subway system versus their population size P is shown in figure 1 (the data were obtained for cities with a population larger than 105 (http://unstats.un.org/)), which confirms that the larger a city, the more likely it is to have some form of mass transit system (see also [7]). Approximately 25 per cent of the cities having more than one million individuals, 50 per cent of those having more than two million and all those having above 10 million have a subway system (as an indication, an exponential fit of the plot in figure 1 gives 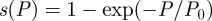 where the typical population P0 is in the order of three million).
where the typical population P0 is in the order of three million).
Figure 1.
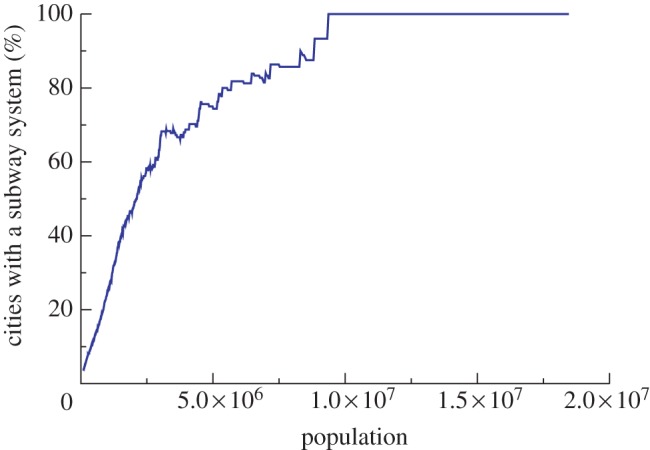
Percentage of cities with a subway system versus the population (data from the UN (http://unstats.un.org/)). (Online version in colour.)
For some cities, subway systems have existed for more than a century. Fascination with the apparent diversity of their structure has led to many studies and to particular abstractions of their representation in the design of idealized transit maps [8], and although these might appear to be planned in some centralized manner, it is our contention here that subway systems like many other features of city systems evolve and self-organize themselves as the product of a stream of rational but usually uncoordinated decisions taking place through time.
Generally speaking, subway systems have been developed to improve movement in urban areas and to reduce congestion. The early history of subways is sometimes connected to large-scale planning, for instance with the need to bring people from a growing periphery to the centre of the city where traditionally production and exchange usually take place. More broadly, it might seem that subway systems are engineered systems and intentionally structured in a core/periphery shape with their self-organization thus playing only a very minor role. This actually would be true if these subway systems were planned from their beginning to their current shape, but this is not the case for most networks. Their shape results from multiple actions, from planning within a time-limited horizon, set within the wider context of the evolution of the spatial distribution of population and related economic activities. We thus conjecture that subway networks actually result from a superimposition of many actions, both at a central level with planning and at a smaller scale with the reorganization and regeneration of economic activity and the growth of residential populations. In this perspective, subway systems are self-organizing systems, driven by the same mechanisms and responding to various geographical constraints and historical paths. This self-organized view leads to the idea that—beside local peculiarities due to the history and topography of the particular system—the topology of world subway networks display general, universal features within the limits of the physical geometry and cultural context in which their growth takes place.
The detection and characterization of these features require us to understand the evolution of these spatial structures. Indeed, subway networks are spatial [9–11] in the sense that they form a graph where stations are the nodes and links represent rail connections. We now understand quite well how to characterize a spatial network but we still lack tools for studying their temporal evolution. The present article tackles this problem, proposing various measures for these time-dependent, spatial networks.
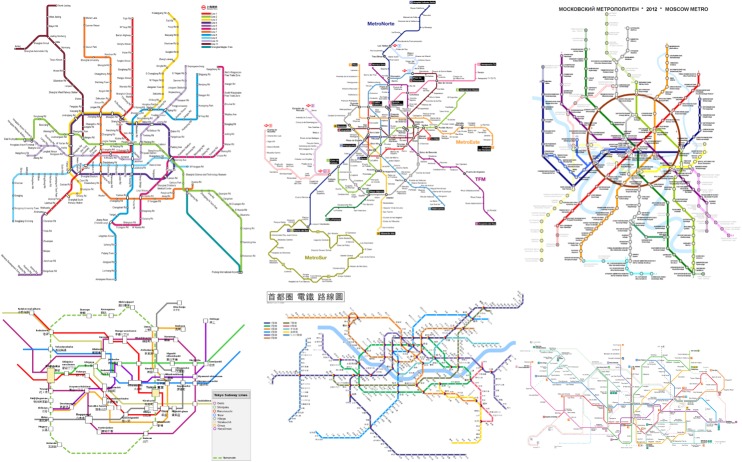
Here we focus on the largest networks in major world cities and thus ignore currently developing, smaller networks in many medium-sized cities. We thus consider most of the largest metro networks (with at least one hundred stations) which exist in major world cities. These are: Barcelona, Beijing, Berlin, Chicago, London, Madrid, Mexico, Moscow, New York City (NYC), Osaka, Paris, Seoul, Shanghai and Tokyo, for which we show a sample in figure 2. Additionally, we focus on urban subway systems and do not consider longer-distance heavy and light-rail commuting systems in urban areas, such as Réseau Express Régional (RER) in Paris or overground NetworkRail in London.
Figure 2.
A sample of large subway networks in large urban areas, all displaying a core and branches structure. From left to right and top to bottom: Shanghai, Madrid, Moscow, Tokyo, Seoul, Barcelona (figures from Wikimedia Commons (http://commons.wikimedia.org)). (Online version in colour.)
Static properties of transportation networks have been studied for many years [12] and, in particular, simple connectivity properties were studied in [13], while fractal aspects were considered in [14]. With the recent availability of new data, studies of transportation systems have accelerated [11] and this is particularly so for subway systems [15–23]. These studies have revealed some significant similarities between different networks, despite differences in their historical development and in the cultures and economies in which they have been developed. In particular, their average shortest path seems to scale with the square root of the number of stations and the average clustering coefficient is large, consistent with general results associated with two-dimensional spatial networks [11]. In the study of Sienkiewicz & Holyst [17], a strong correlation between the number of stations (for bus and tramway systems) and population size has been observed for 22 Polish cities, but such correlations are not observed at the world level (for all public transportation modes [21]).
Our empirical analysis of the evolution of these transportation networks is in line with approaches developed in the 1970s (see [24] and references therein) but we take advantage here of recent progress made in the understanding of spatial networks in general and new historical data sources that provide us with detailed chronologies of how these networks have developed.
1.1. Data
The network topologies at various points in time were built using two main data sources. First, current network maps as for 2009 were used to define lines for each network, and then to define line-based topologies, i.e. which station(s) follow(s) which other station(s) on each line. This information was then combined with opening dates for lines and stations. This second type of data has been gathered from Wikipedia (http://www.wikipedia.org): for most networks, there is one page per station with various information, including the first date of operation, the precise location and address, number of passengers, etc. The network building process for a given year t is then as follows. The list of open lines at year t is first established. For each open line, open stations at year t are listed and connections are created between contiguous stations according to the network topology. A station that is not open at year t on the given line, even if it is already open on a different line, is evidently discarded for the construction of the line. Eventually, those independent line topologies are gathered into the subway graph corresponding to year t. Note that we used 2009 topologies as it was relatively difficult to find and process network maps for all these networks for each year of their existence. As a result, topologies for any given year before 2009 may overlook topology features pertaining to station or line closures: for instance, a station that existed between 1900 and 1940 and that remained closed until now will not appear in any of our network datasets (such is the case for the British Museum Tube station). We suggest, however, that the effect of this bias is limited: on the one hand, generally few stations undergo closure in the course of the network evolution; on the other hand, these stations are rarely hubs, most often intermediary stations (of degree 2, i.e. connected to two stations), thus their non-inclusion bears little topological impact.
2. Exploring static properties
The main characteristics of the networks we have chosen are shown in table 1 where we first observe that the number of different lines appears to increase incrementally with the number of stations and that on average, for these world networks, there are approximately 18 stations per line. Also, the mean interstation distance is on average 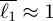 km with Beijing and Moscow showing the longest ones (1.79 and 1.67 km, respectively), and Paris displaying the shortest one (570 m), a diversity which finds its origin in the different historical paths of these networks. Other quantities such as the catchment area (the average number of individuals served by one station) could be computed but should be used with care: residential and economic activity density vary strongly across space and back-of-the-envelope arguments should only serve as a guide. Generally speaking, many parameters such as the population density, land use activity distribution and traffic are important drivers in the evolution of those networks, but we will focus in this first study on the characterization of these networks in terms of space and topology, independently of other socio-economical considerations. A later extension of this research could examine these physical and topological properties with respect to various definitions of density which might include different activity types and various combinations related to the traffic that they generate.
km with Beijing and Moscow showing the longest ones (1.79 and 1.67 km, respectively), and Paris displaying the shortest one (570 m), a diversity which finds its origin in the different historical paths of these networks. Other quantities such as the catchment area (the average number of individuals served by one station) could be computed but should be used with care: residential and economic activity density vary strongly across space and back-of-the-envelope arguments should only serve as a guide. Generally speaking, many parameters such as the population density, land use activity distribution and traffic are important drivers in the evolution of those networks, but we will focus in this first study on the characterization of these networks in terms of space and topology, independently of other socio-economical considerations. A later extension of this research could examine these physical and topological properties with respect to various definitions of density which might include different activity types and various combinations related to the traffic that they generate.
Table 1.
List of various indicators (for the year 2009) for the major subway networks considered in this study (and sorted according to their metro population). P is the metropolitan area population (for 2009). NL is the number of lines, N the number of physical stations, 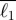 is the average interstation distance, ℓT total route length,
is the average interstation distance, ℓT total route length, 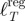 the total route length for a regular graph with the same average degree, area and number of stations and β the final ratio between branch and core stations.
the total route length for a regular graph with the same average degree, area and number of stations and β the final ratio between branch and core stations.
| city | P (millions) | NL | N |
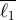 (km) (km) |
ℓT (km) | 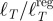 |
β (%) |
|---|---|---|---|---|---|---|---|
| Beijing | 19.6 | 9 | 104 | 1.79 | 204 | 0.14 | 39 |
| Tokyo | 12.6 | 13 | 217 | 1.06 | 279 | 0.13 | 43 |
| Seoul | 10.5 | 9 | 392 | 1.39 | 609 | 0.39 | 38 |
| Paris | 9.6 | 16 | 299 | 0.57 | 205 | 0.18 | 38 |
| Mexico City | 8.8 | 11 | 147 | 1.04 | 170 | 0.15 | 39 |
| NYC | 8.4 | 24 | 433 | 0.78 | 373 | 0.12 | 36 |
| Chicago | 8.3 | 11 | 141 | 1.18 | 176 | 0.08 | 71 |
| London | 8.2 | 11 | 266 | 1.29 | 397 | 0.20 | 47 |
| Shanghai | 6.9 | 11 | 148 | 1.47 | 233 | 0.21 | 61 |
| Moscow | 5.5 | 12 | 134 | 1.67 | 260 | 0.16 | 71 |
| Berlin | 3.4 | 10 | 170 | 0.77 | 141 | 0.30 | 60 |
| Madrid | 3.2 | 13 | 209 | 0.90 | 215 | 0.42 | 46 |
| Osaka | 2.6 | 9 | 108 | 1.12 | 137 | 0.88 | 43 |
| Barcelona | 1.6 | 11 | 128 | 0.72 | 103 | 0.32 | 38 |
To get some initial insight into the topology of these networks, one can first compare the total length ℓT of these networks to the corresponding quantity computed for an almost regular graph 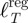 with the same number of stations, area and average degree (the ‘degree’ of a node is the number of its neighbours in a graph). For a random planar graph with small degree fluctuations (k ≈ 〈k〉) and small fluctuations of the spatial distribution of nodes, we can consider that the internode spacing is roughly constant and given by
with the same number of stations, area and average degree (the ‘degree’ of a node is the number of its neighbours in a graph). For a random planar graph with small degree fluctuations (k ≈ 〈k〉) and small fluctuations of the spatial distribution of nodes, we can consider that the internode spacing is roughly constant and given by 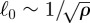 where ρ = N/A is the density of nodes defined as the number of nodes over the total area comprising all the nodes. The total length is then the number of edges E = N〈k〉/2 times ℓ0 which leads to [11]
where ρ = N/A is the density of nodes defined as the number of nodes over the total area comprising all the nodes. The total length is then the number of edges E = N〈k〉/2 times ℓ0 which leads to [11]
| 2.1 |
In real applications, the determination of the quantity A is a difficult problem, but here we choose to use the metropolitan area as given by the various data sources. As shown in the table 1, the ratio 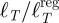 varies from 0.08 to 0.88, has an average of order 0.29 and displays essentially three outliers. First, Osaka (and also Madrid and Seoul) has a very large value indicating a highly reticulated structure. In contrast, Chicago and NYC have a much smaller value (≈0.1) signalling a more heterogeneous structure, which in both these cases is probably due to their strong geographical constraints.
varies from 0.08 to 0.88, has an average of order 0.29 and displays essentially three outliers. First, Osaka (and also Madrid and Seoul) has a very large value indicating a highly reticulated structure. In contrast, Chicago and NYC have a much smaller value (≈0.1) signalling a more heterogeneous structure, which in both these cases is probably due to their strong geographical constraints.
The total length and the comparison with a regular structure gives a first hint about the structure of these networks but other indicators are needed to get a more focused view. There exist many different indicators and variables that describe these networks and their evolution. An important difficulty thus lies in the choice of the many possible indicators and how to extract useful information from them. In addition, the largest networks have a relatively small number of stations (always smaller than 500), which implies that we cannot expect to extract useful information from the probability distributions of various quantities as the results are too noisy. We thus have to compute more globally structured indicators which are, however, sensitive to the usually small temporal variations associated with these networks. In the following, we will focus on a certain number of these indicators, which we consider to be the most informative at this point.
Finally, we will focus in this study on purely spatial and topological properties: we will consider the evolution in space of these subway networks and we will not consider any other parameters that might be used to characterize urban growth. Our study is exploratory and thus a first step towards the integration of the most important factors into this research and despite its simplicity, in that we focus almost entirely on geometrical attributes, we consider that the evolution of the topology encodes many different factors and that its study can point to some important general mechanisms governing the evolution of these networks.
3. Network dynamics
To get an initial impression of the dynamics of these networks, we first estimate the simplest indicator v = dN/dt, which represents the number of new stations built per year. From the instantaneous velocity, we can compute the average velocity over all years. This average can, however, be misleading as there are many years where no stations are built and thus we describe this by the fraction of ‘inactivity’ time f. We provide results for the networks considered in table 2 from which some interesting facts are revealed. Note that it is clear that Shanghai and Seoul are the most recent subway networks experiencing a rapid expansion that has elevated them to among the largest networks in the world.
Table 2.
t0 is the initial year considered here for the different subways networks, 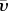 is the average velocity (number of stations built per year),
is the average velocity (number of stations built per year), 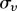 is the standard deviation of v and f is the fraction of years of inactivity (no stations built).
is the standard deviation of v and f is the fraction of years of inactivity (no stations built).
| city | t0 | 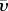 |
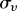 |
f (%) |
|---|---|---|---|---|
| Beijing | 1971 | 3.3 | 7.74 | 79 |
| Tokyo | 1927 | 2.8 | 5.47 | 51 |
| Seoul | 1974 | 11.2 | 14.9 | 20 |
| Paris | 1900 | 2.6 | 5.1 | 60 |
| Mexico City | 1969 | 3.7 | 5.9 | 55 |
| NYC | 1878 | 3.3 | 8.3 | 68 |
| Chicago | 1901 | 1.9 | 6.24 | 71 |
| London | 1863 | 2.3 | 3.8 | 48 |
| Shanghai | 1995 | 14.9 | 20.2 | 31 |
| Moscow | 1936 | 1.7 | 1.9 | 43 |
| Berlin | 1901 | 1.6 | 3.3 | 65 |
| Madrid | 1919 | 2.3 | 4.6 | 59 |
| Osaka | 1934 | 1.4 | 4.1 | 79 |
| Barcelona | 1914 | 1.4 | 4.8 | 78 |
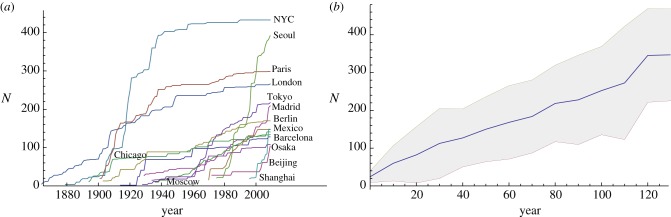
For most of these networks, the average velocity is in a small range (typically 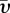 ∈ [1.4, 3.7]) except for Seoul and Shanghai which are more recently developed networks. This is, however, an average velocity and we observe that (i) for all networks, larger velocities occur at earlier stages of the network and (ii) large fluctuations occur from one year to another. Interestingly, the fraction of the inactivity time (i.e. the time when no stations are built) is similar for all these networks with an average of about 58 per cent. We also show in figure 3a, the time evolution for each city of the number of stations, using an absolute timescale. In particular, the sizes of the oldest networks seem to progressively reach a plateau.
∈ [1.4, 3.7]) except for Seoul and Shanghai which are more recently developed networks. This is, however, an average velocity and we observe that (i) for all networks, larger velocities occur at earlier stages of the network and (ii) large fluctuations occur from one year to another. Interestingly, the fraction of the inactivity time (i.e. the time when no stations are built) is similar for all these networks with an average of about 58 per cent. We also show in figure 3a, the time evolution for each city of the number of stations, using an absolute timescale. In particular, the sizes of the oldest networks seem to progressively reach a plateau.
Figure 3.
(a) Evolution of the number of stations for various large world subway networks. (b) Evolution of the number of stations y years after creation, averaged over all networks (tubes mark the standard deviation across all networks). The linear shape indicates that the growth in terms of new stations from a decade to another goes to zero for all these networks, signalling the possible appearance of a stationary limit. (Online version in colour.)
To make growth comparable across all networks, we introduce a second graph on figure 3b featuring the average, over all networks, of the number of stations after a certain number of years since the creation of the network. This average quantity exhibits a linear increase which indicates convincingly that, overall, as these networks become large, for a few decades thereafter, new stations represent an increasingly small percentage of the existing ones. In other words, the time evolution of all these networks is characterized by small additions and not by sudden, abrupt changes with a large number of stations added in a small time duration. This first result anticipates the fact that these large networks may reach some kind of limiting shape that we will characterize in §3.1. This incremental growth of subways might reflect socio-economical concerns and pressure on the transportation networks such as diminishing return on investments as noted by various authors (see, [25] for US highways).
Finally, when we study the evolution of various indicators versus the number N of stations, an important point for our statistical analysis will be the number of subways with a given number N at a given time t. We show this quantity in figure 4 and we can see that, for N ∈ [25, 100] approximately, this number is the largest (almost 15—note that this figure is nonetheless too small to allow a discussion of the normality of the various quantities considered below). Unfortunately, for larger values of N the number of cities is naturally smaller, and at this stage we cannot give definitive answers but suggest some limits for large N.
Figure 4.
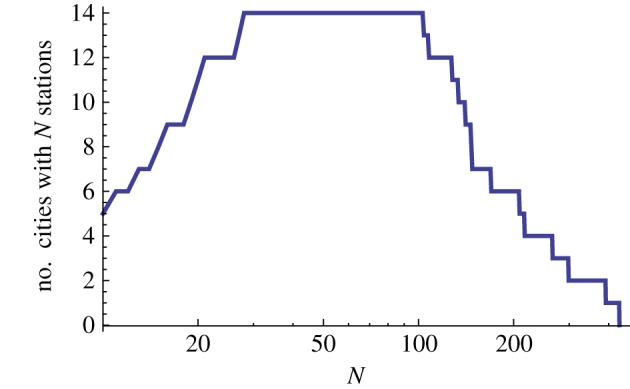
Number of cities with a given number of stations at a given time.
3.1. Characterization of the core and branches structure
The large subway networks considered here thus converge to a long-time limit where there is always an increasingly smaller percentage of new stations added through time. The remarkable point that we will show below is that all these networks, despite their geographical and economical differences, converge to a shape that exhibits several typical topological and spatial features. Indeed, by inspection, we observe that in most large urban areas, the network consists of a set of stations delimited by a ‘ring’ that constitute the ‘core’. From this core, quasi-one-dimensional branches grow and reach out to areas of the city further and further from the core. In figure 2, we show a sample of these networks as they currently exist. We note here that the ring, which is defined topologically as the set of core stations that are either at the junction of branches or on the shortest geodesic path connecting these junction stations, exists or not as a subway line. For instance, for Tokyo, there is a such a circular line (called the Yamanote line), while for Paris the topological ring does not correspond to a single line. It is also worth noting that in those systems where the core is harder to define such as NYC where physical constraints are strongly manifest (the east and west rivers which bound Manhattan), a pseudo core is evident where a series of lines coalesce to enable travellers to move around the core circumferentially.
More formally, branches are defined as the set of stations that are iteratively built from a ‘tail’ station, or a station of degree 1. New neighbours are added to a given branch as long as their degree is 2—continuing the line, or 3—defining a fork. In this latter case, the aggregative process continues if and only if at least one of the two possible new paths stemming from the fork is made up of stations of degree 2 or less. Note that the core of a network with no such fork is thus a k-core with k = 2 [26].
The general structure can schematically be represented as in figure 5.
Figure 5.
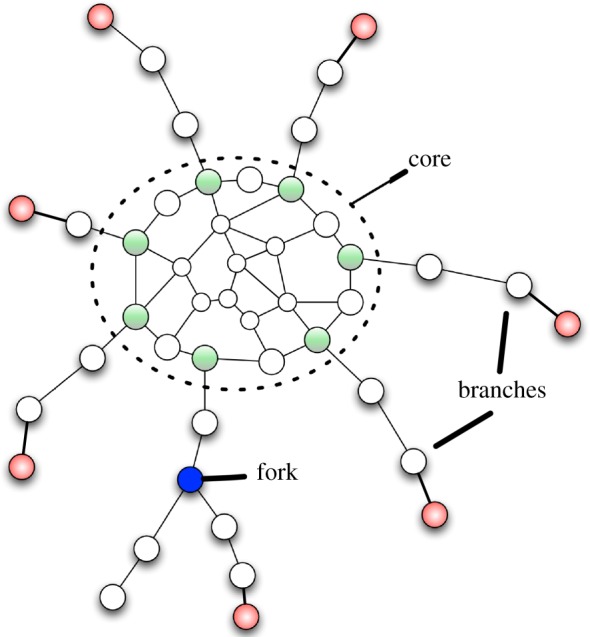
Schematic of subway networks. A large ‘ring’ encircles a core of stations. Branches radiate from the core and reach further areas of the urban system. The branches are essentially characterized by their size (parameter β(t), equation (3.1)), and their spatial extension (parameter η(t) in equation (3.2)). The core is characterized by its average degree (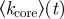 defined in equation (3.3)) and fraction of nodes of degree 2 (f2), its number of stations NC(t) and its size rC(t). Green circles denote junction; red, terminus. (Online version in colour.)
defined in equation (3.3)) and fraction of nodes of degree 2 (f2), its number of stations NC(t) and its size rC(t). Green circles denote junction; red, terminus. (Online version in colour.)
We first characterize this branch and core structure with the parameter β(t) defined as
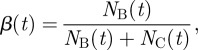 |
3.1 |
where NB(t) and NC(t), respectively, represent the number of stations on branches and the number of stations in the core at time t.
We can also further characterize the structure of branches. Their topological properties are trivial and their complexity resides in their spatial structure. We can then determine the average distance (in kilometres) from the geographical barycentre of the city to all core and branch stations, respectively: 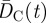 and
and 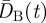 (the barycentre is computed as the centre of mass of all stations, or in other words, the average location of all the stations). This last distance provides information about the spatial extension of the branches when we can form the ratio η(t):
(the barycentre is computed as the centre of mass of all stations, or in other words, the average location of all the stations). This last distance provides information about the spatial extension of the branches when we can form the ratio η(t):
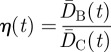 |
3.2 |
which gives a spatial measure of the amount of extension of the branches.
We also need information on the structure of the core. The core is a planar (which is correct at a good accuracy for most networks) spatial network and can be characterized by many parameters [11]. It is important to choose those that are not simply related but ideally represent different aspects of the network (such as those proposed in the form of various indicators; see, for example, [11,12,27]). At each time step t, we will characterize the core structure by the following two parameters. The first parameter is simply the average degree of the core which characterizes its ‘density’:
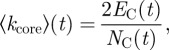 |
3.3 |
where NC(t) is the number of core nodes and EC(t) the number of its edges. The average degree is connected to the standard index 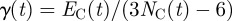 where the denominator is the maximum number of links admissible for a planar network [12].
where the denominator is the maximum number of links admissible for a planar network [12].
The average degree of the core contains useful information about it, and there are many other quantities (such as standard indices such as α, etc.; see, [12]) which can give additional information. We will use another simple quantity which describes in more detail the level of interconnections in the core and which is given by the fraction f2 of nodes in the core with k = 2. In the case of the well-interconnected system, this fraction will tend to be small, while sparse cores with a few interconnections will have a larger fraction of k = 2 nodes.
Once we know this fraction f2 of k = 2 nodes in the core, which characterizes the level of interconnection and the parameter η(t), which characterizes the relative spatial extension of branches, we have key information on the intertwinement of both topological and geographical features in such ‘core/branch’ networks.
3.2. Time evolution of β, 〈kcore〉, f2 and η
The historical development of these networks is very different from one city to another and representing the evolution of a specific quantity versus time would probably not be particularly meaningful. Similarly, city networks often experience significant development in some particular years, while they experience little or no evolution for the rest of the time. To be able to compare the networks across time periods and cities, we propose to study their evolution in terms of the number of stations N that are constructed.
We first plot in figure 6a the parameter β as a function of N for the networks studied here. It is difficult to draw strong conclusions from this plot, but we can bin these data and represent the average value of β per bin and its dispersion as well (figure 6b). In this figure, we may see that the average value of β seems to stabilize slowly to some value in [0.35, 0.55].
Figure 6.
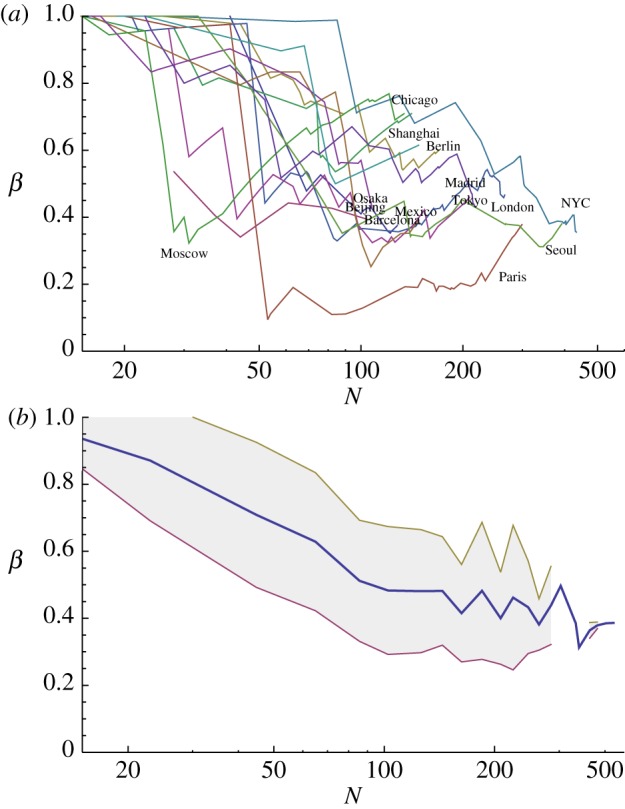
(a) Parameter β as a function of the number of stations N for the different world subways. (b) Same as (a) but averaged over 20 bins and showing the standard deviation. (Online version in colour.)
It is also important to characterize the spatial importance of the branches. The parameter η gives a precious indication about their extension and we show in figure 7 the evolution of this parameter with N (the data are binned). This figure shows that in the interval where we have the largest number of subways, the average value of η is around 2 with relatively large fluctuations which seem to decrease with N.
Figure 7.
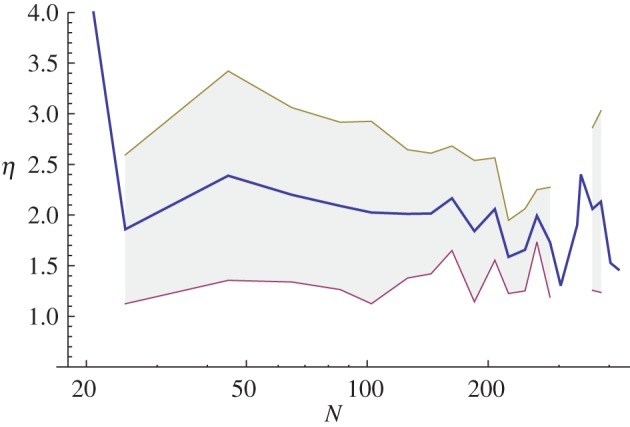
Evolution of the ratio η, which characterizes the spatial extension of branches relative to the core. (Online version in colour.)
The parameters β and η give an indication of the importance of the core but do not say anything about its structure. A first structural indication may be given by its average degree 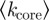 and by the percentage of nodes in the core having a degree k equal to 2. In particular, these two quantities shed light on how interconnections are created in the core. We display in figure 8a the average degree of the core
and by the percentage of nodes in the core having a degree k equal to 2. In particular, these two quantities shed light on how interconnections are created in the core. We display in figure 8a the average degree of the core 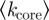 which, even if there is a slow increase with N, displays moderate variations around 2.4 approximately.
which, even if there is a slow increase with N, displays moderate variations around 2.4 approximately.
Figure 8.
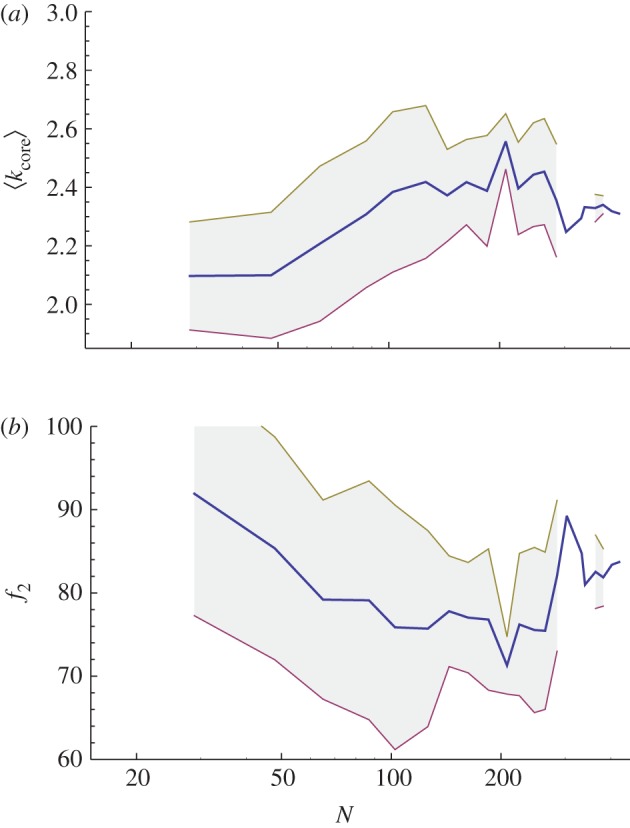
(a) Average degree of the core 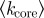 (equation (3.3)) and its dispersion versus number of stations (averaged over 20 bins). (b) Evolution of the percentage f2 of k = 2 core nodes (averaged over 20 bins). (Online version in colour.)
(equation (3.3)) and its dispersion versus number of stations (averaged over 20 bins). (b) Evolution of the percentage f2 of k = 2 core nodes (averaged over 20 bins). (Online version in colour.)
This value is relatively small and indicates that the fraction of connecting stations (i.e. with k > 2) is also small and means that most core stations belong to one single line with few that actually allow connections. More precisely, we observe in figure 8b that, on average, for subways with N < 100 the fraction of interconnecting stations is increasing with N—which probably corresponds to some organization of the subway—but that for larger subways (N > 100), the percentage f2 is increasing again, which probably corresponds to a densification process without the creation of new interconnections. This densification can indeed be confirmed as the diameter of the core (figure 9) seems to reach a plateau for most cities.
Figure 9.
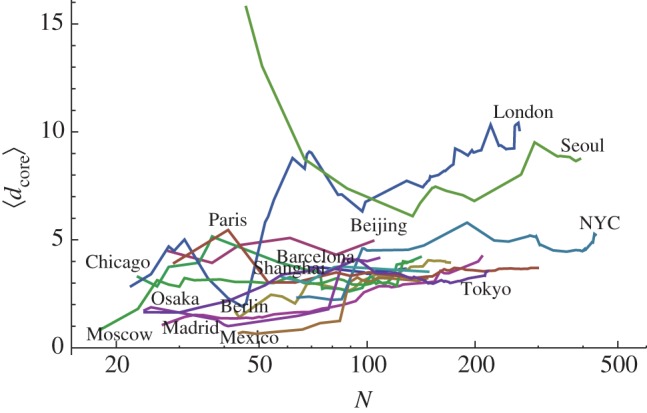
Evolution of the mean distance to the barycentre (in kilometres) of core stations with the number of stations N. (Online version in colour.)
As noted above, the number of subways with large N is smaller and the statistics therefore less reliable. At this point and with this statistical error in mind, we observe that the average value β and its dispersion are decreasing with N and suggests that β could converge to some ‘limiting’ value 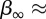 45 per cent. The same remarks also apply to η and suggest a limiting value of order 2. Concerning the core, the dispersion of
45 per cent. The same remarks also apply to η and suggest a limiting value of order 2. Concerning the core, the dispersion of 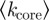 is always moderate and approximately constant, showing that the fluctuations among different networks are also moderate. We observe a slow increase of
is always moderate and approximately constant, showing that the fluctuations among different networks are also moderate. We observe a slow increase of 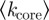 pointing to a mild yet continuing densification of the core, even after a long period of time. The fraction of connecting stations has more complex dynamics and seems to decrease with N for large networks. In these networks, there is an obvious cost associated with the large value of k > 2 and such a decreasing fraction could be due to the fact that a small fraction is enough to enable easy navigation in the network.
pointing to a mild yet continuing densification of the core, even after a long period of time. The fraction of connecting stations has more complex dynamics and seems to decrease with N for large networks. In these networks, there is an obvious cost associated with the large value of k > 2 and such a decreasing fraction could be due to the fact that a small fraction is enough to enable easy navigation in the network.
In summary, our results display non-negligible fluctuations but suggest that large subway networks may converge to a long-time limiting network largely independent of their historical and geographical differences. So far, we can characterize the ‘shape’ of this long-time limiting network with values of 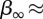 45 per cent,
45 per cent, 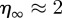 , and a core made of approximately 80 per cent of non-connecting stations. It will be interesting to observe the future evolution of these networks in order to confirm (or not) our current results.
, and a core made of approximately 80 per cent of non-connecting stations. It will be interesting to observe the future evolution of these networks in order to confirm (or not) our current results.
3.3. Number of branches
We now consider the number 𝒩B of different branches. A naive argument would be that the number of branches is actually proportional to the perimeter of the core structure. This implicitly assumes that the distance between different branches is constant. In turn, the perimeter should roughly scale as 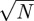 as the core is a relatively dense planar graph and contains a number of nodes proportional to N. These assumptions thus lead to
as the core is a relatively dense planar graph and contains a number of nodes proportional to N. These assumptions thus lead to
| 3.4 |
We display the number of branches versus the number of stations N for the various networks considered here. A power law fit of the data presented in figure 10 gives 𝒩B ∼ Nb with b ≈ 0.6 (r2 = 0.85) consistent with our argument.
Figure 10.
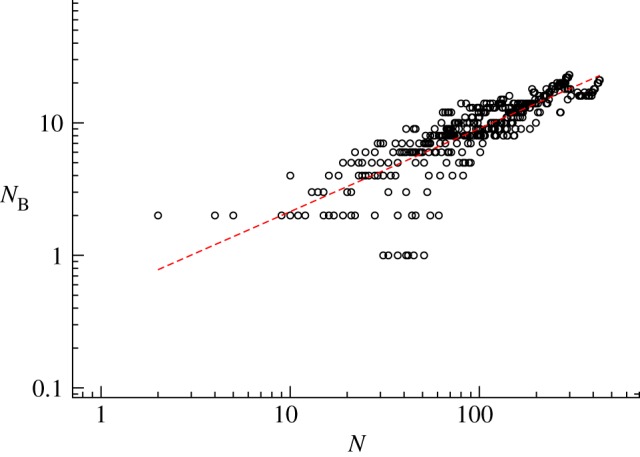
The log–log plot of the number of different branches versus the number of stations for the different subway networks considered here. The dashed line is a power law fit with exponent ≈0.6. (Online version in colour.)
3.4. Balance between the core density and the branch structure
Even if it seems that the values of various indicators converge with the size of the networks, we still have appreciable variations. For example, η varies from ≈1 to ≈3 and exhibits a relatively constant and not negligible relative dispersion. It is thus important to understand the remaining differences between these networks. To achieve this, we focus on the relation between η which characterizes the spatial extension of the branches relative to the core, and the percentage f2 of k = 2 nodes in the core which indicates how well connected the core is. We focus on the ‘final’ values of these parameters obtained for 2009 for the various networks and we obtain the plot shown in figure 11. From this figure, we first see that (η, f2) ranges from (≈1.4, ≈85%) for NYC up to (≈3.3, ≈45%) for Moscow, which is indeed a highly ramified network with a very dense core.
Figure 11.
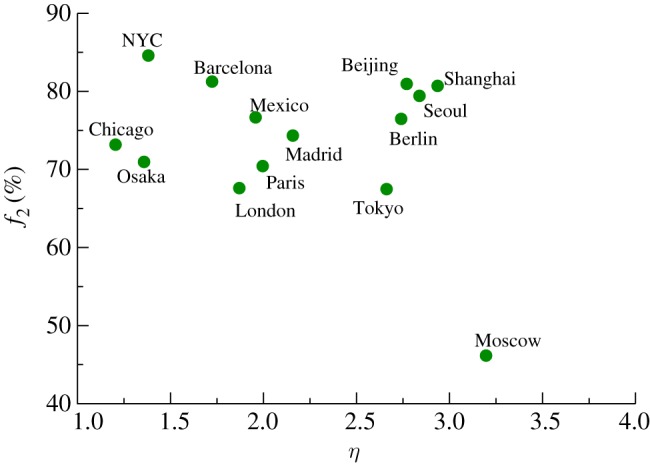
Relation between the spatial extension of branches and the degree of interconnection in the core. The 2009 values for the percentage f2 of k = 2 core nodes and η are plotted for 12 city subways. (Online version in colour.)
Very roughly speaking, we first observe that, for this set of the largest subway systems in the world, the percentage f2 is large and above 60 per cent and relatively independent from η. At a finer level, we observe from this figure that clusters of networks with similar properties also emerge. The first cluster comprises Beijing, Berlin, Shanghai and Seoul which are remarkably close to each other: f2 is of order 80 ± 5% and η(t) ≈ 2.84 ± 0.1. This cluster corresponds thus to subway networks with a large degree of ramification and a lower interconnection level in their core. Not surprisingly, this cluster comprises rapidly evolving networks such as Beijing and Shanghai, for example. Another cluster comprises London, Paris and Madrid with a smaller value of f2 ≈ 70 ± 5%, which might result from their denser city centre structure and a smaller value of η ≈ 2. This other cluster corresponds to denser networks, less ramified but with more interconnections in the core. Finally, we can identify another cluster made of Chicago and Osaka with a small value of η and a relatively dense core (with f2 ≈ 70%).
4. Spatial organization of the core and branches
Following earlier studies on the fractal aspects of subway networks [14], we can inspect the spatial subway organization by considering the number of stations N(r) at a distance less than or equal to r, where the origin of distances is the barycentre of all stations considered as points. Interestingly, the barycentre of all stations is almost motionless, except in the case of NYC where the barycentre moves from Manhattan to Queens, and thus we will exclude NYC from further study. Chicago is a similar case: the spatial structure of the core is peculiar, mainly due to the presence of the lake which constrains the network from expanding in the other directions. We will also exclude this network in this section. It should, however, be noted here that both Chicago and NYC do follow the image of core and branches but that the main difference with the other networks is that the core of these networks has no clear spatial meaning due to the geographical constraints (such as the presence of a lake for Chicago and a particular shape of the land area for NYC).
For the year 2009, the limiting shape made of a core and branches implies that there is an average distance rC which determines the core. In practice, we can measure on the network the size NC of the core and we then define rC such that N(r = rC) = NC (which assumes implicitly an isotropic core shape, which is the case for most networks except for the excluded cases of Chicago and NYC). For the various cities, we can easily compute the function N = N(r) from which we can extract rC and we report the results in table 3.
Table 3.
For each city, we compute the number of stations in the core (for the year 2009) and from the numerical calculation of N(r) we can estimate rC the size of the core (in kilometres) from N(r = rC) = NC.
| City | NC | rC (km) |
|---|---|---|
| Beijing | 63 | 4.4 |
| Tokyo | 123 | 5.0 |
| Seoul | 243 | 11.6 |
| Mexico | 90 | 4.7 |
| Shanghai | 57 | 3.7 |
| Moscow | 39 | 5.9 |
| London | 142 | 7.3 |
| Paris | 186 | 4.2 |
| Madrid | 113 | 4.4 |
| Berlin | 68 | 5.5 |
| Barcelona | 57 | 3.5 |
| Osaka | 46 | 3.6 |
Next, we can rescale r by rC and N(r) by NC and we then obtain the results shown in figure 12.
Figure 12.
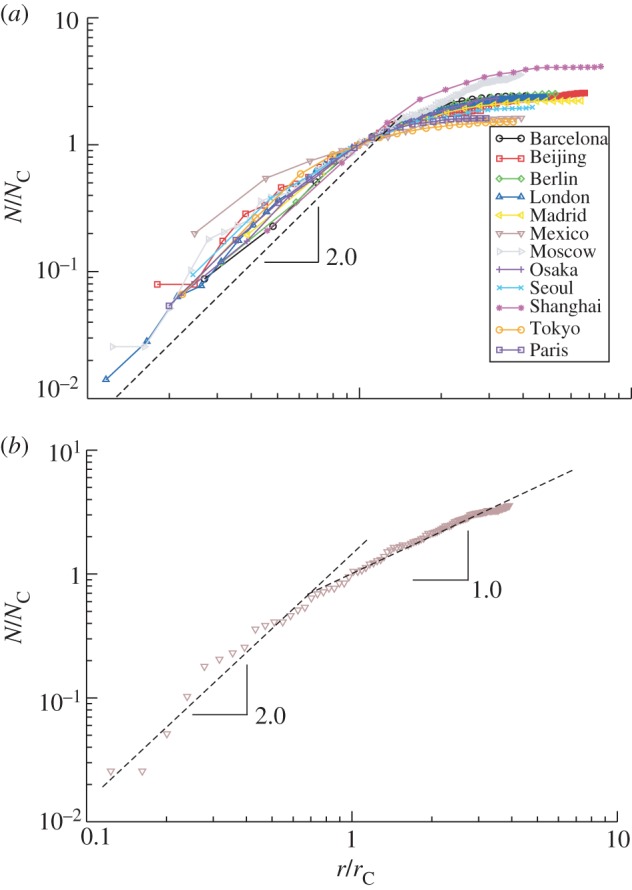
(a) Rescaled number of stations at distance r from the barycentre as a function of the rescaled variable r/rC where rC is the size of the core defined as N(r = rC) = NC (shown here in log–log). The dotted line represents a power law ∼r2 and serves as a guide to the eye. (b) The case of Moscow where the two regimes (r < rC and r > rC) with their different exponents are visible (the dotted lines serve here as a guide to the eye). (Online version in colour.)
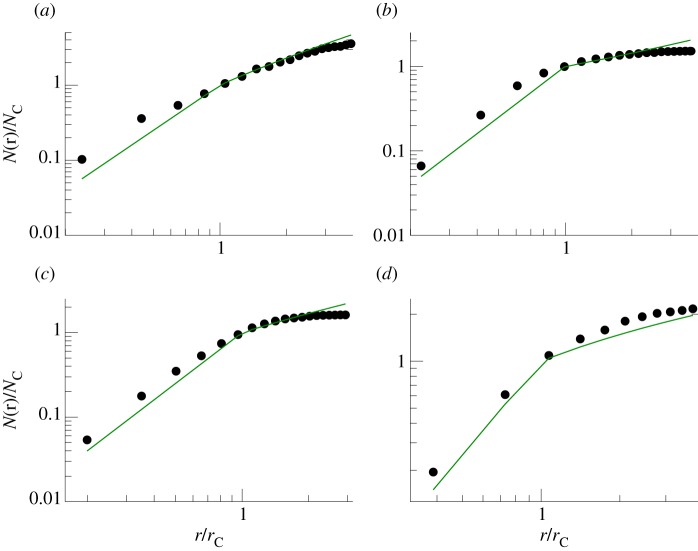
This figure displays several interesting features. First, the short distance regime r < rC is well described by a behaviour of the form N(r) ∼ ρCπr2 consistent with a uniform density ρC of core stations. For very large distances, for most networks we observe a saturation of N(r). The interesting regime is then for intermediate distances when r is larger than the core size but smaller than the maximum branch size rmax. This intermediate regime is characterized by different behaviours with r. A similar result was obtained earlier [14], where the authors observed for Paris that N(r > rc) ∼ r0.5, a result that was at that time difficult to understand in the framework of fractal geometry.
Here we show that these regimes can be understood in terms of the core and branches model, with the additional factor that the spacing between consecutive stations is increasing with r. Within this picture (and assuming isotropy), N(r) is given by
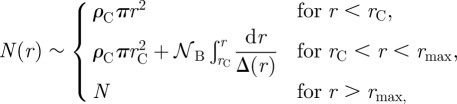 |
4.1 |
where N is the total number of stations, 𝒩B is the number of branches and Δ(r) is the average spacing between stations on branches at distance r from the barycentre.
To test this shape, we can determine the various parameters of equation (4.1)—namely 𝒩B, NC, rC and Δ(r)—and plot the resulting shape of equation (4.1) against the empirical data. It is easy to determine empirically the numbers 𝒩B, NC and rC, but the quantity Δ(r) is extremely noisy due to the small number of points (all these numbers are determined for the year 2009), especially for large values of r closest to rmax, at a distance where, often, there is no more than a handful of stations.
The less noisy situation is obtained in the case of Moscow, which has long branches and for which we obtain a roughly constant interstation spacing. In this case, we obtain, for r > rC, a behaviour of the form N(r) ∼ 𝒩Br (figure 12b).
More generally, the large distance behaviour rC < r < rmax will be of the form
| 4.2 |
where τ denotes the exponent governing the interspacing decay Δ(r) ∼ rτ. For most networks, the regime rC < r < rmax is small and as already mentioned Δ(r) is very noisy. Rough fits in different cases give a behaviour for equation (4.1) consistent with the data (figure 13).
Figure 13.
N(r)/NC versus r/rC for (a) Moscow, (b) Tokyo, (c) Paris and (d) Madrid (from top to bottom and left to right). The circles represent the data and the green solid line the fit using equation (4.1) with parameters estimated from the empirical data. (Online version in colour.)
In particular, for Moscow which has long branches, we observe a behaviour consistent with Δ(r) ≃ constant, while for the other networks we observe an increasing trend, but an accurate estimate of τ is difficult to obtain, given the small variation range of r — with no more than one decade of available data. For example, a fit over this decade of data gives τ ≈ 0.5 for Paris (with r2 = 0.74) in agreement with the result obtained in [14]. Despite the difficulty of obtaining accurate quantitative results, more data are needed to have a definite answer and so far we can only claim that the data are not inconsistent with the behaviour equation (4.1), which supports our picture of a long-time limit network shape made of a core and radial branches.
5. Discussion
In summary, we have observed a number of similarities between different subway systems for the world's largest cities, despite their geographical and historical differences.
First, we have shown that the largest subway networks exhibit a similar temporal decrease of most fluctuations around their long-term stable values and thus converge to a similar structure. We identified and characterized the shape of this long-time limiting graph as a structure made of a core and branches which appears to be relatively independent of the peculiar historical idiosyncracies associated with the evolution of these particular cities.
For large networks, we generally observe a fraction of branches of about 45 per cent for most networks, and a ratio for the spatial extensions of branches to the core of about 2. The number of branches scales roughly as the square root of the number of stations. The core of these different city networks has approximately the same average degree which is increasing with the network size, from ≈2 to ≈2.4 when N ≈ 100, after which it approximately remains within the interval [2.3, 2.5] (with moderate fluctuations). The fraction of k = 2 nodes in the core is generally larger than 60 per cent.
In addition, this picture of a core with branches and an increasing spacing between consecutive stations on these branches is confirmed by spatial measurements such as the number of stations at a given distance r and provides a natural interpretation to these measures.
The evolution of networks in general and urban networks in particular represents an exciting unexplored problem that mixes spatial and topological properties in unusual and often counterintuitive ways. They require a specific set of indicators that describe these phenomena. Other data such as population density, land use activity distribution and traffic flows are likely to bring relevant information to this problem and would undoubtedly enrich our study. We believe, however, that the present approach represents an important exploratory step in our understanding and is crucial for the modelling of the evolution of urban networks. In particular, the existence of unique long-time limit topological and spatial features is a universal signature that fundamental mechanisms, independent of historical and geographical differences, contribute to the evolution of these transportation networks.
Acknowledgements
We thank the anonymous referees for very useful and interesting comments.
References
- 1.Department of Economic and Social Affairs. 2011 UN Population division. http://www.unpopulation.org .
- 2.Hanson S., Giuliano G. (eds) 2004. The geography of urban transportation. New York, NY: Guilford Publications [Google Scholar]
- 3.Batty M. 2005. Cities and complexity. Cambridge, MA: The MIT Press [Google Scholar]
- 4.Niedzielski M. A., Malecki E. J. In press. Making tracks: rail networks in world cities. Ann. Assoc. Am. Geogr. 10.1080/00045608.2011.601212 (doi:10.1080/00045608.2011.601212) [DOI] [Google Scholar]
- 5.Bettencourt L. M. A., Lobo J., Helbing D., Kuehnert C., West G. B. 2007. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl Acad. Sci. USA 104, 7301–7306 10.1073/pnas.0610172104 (doi:10.1073/pnas.0610172104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Balcan D., Colizza V., Goncalves B., Hu H., Ramasco J., Vespignani A. 2009. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl Acad. Sci. USA 106, 21 484–21 489 10.1073/pnas.0906910106 (doi:10.1073/pnas.0906910106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Daganzo C. F. 2009. Structure of competitive transit networks. Transport. Res. B: Meth. 44, 434–446 [Google Scholar]
- 8.Ovenden M. 2007. Transit maps of the world, 2nd edn and revised edition London, UK: Penguin Books [Google Scholar]
- 9.Reggiani A., Nijkamp P. (eds) 2006. Spatial dynamics, networks and modelling. Cheltenham, UK: E. Elgar Publishing [Google Scholar]
- 10.Reggiani A., Nijkamp P. (eds) 2009. Complexity and spatial networks: in search of simplicity. Berlin: Springer [Google Scholar]
- 11.Barthelemy M. 2011. Spatial networks. Phys. Rep. 499, 1–101 10.1016/j.physrep.2010.11.002 (doi:10.1016/j.physrep.2010.11.002) [DOI] [Google Scholar]
- 12.Haggett P., Chorley R. J. 1969. Network analysis in geography. London, UK: Edward Arnold [Google Scholar]
- 13.Bon R. 1979. Allometry in topologic structure of transportation networks, Qual. Quan. 13, 307–326 10.1007/BF00188018 (doi:10.1007/BF00188018) [DOI] [Google Scholar]
- 14.Benguigui L., Daoud M. 1991. Is the suburban railway system a fractal? Geogr. Anal. 23, 362–369 10.1111/j.1538-4632.1991.tb00245.x (doi:10.1111/j.1538-4632.1991.tb00245.x) [DOI] [Google Scholar]
- 15.Latora V., Marchiori M. 2001. Is the Boston subway a small-world network? Physica A 314, 109–113 10.1016/S0378-4371(02)01089-0 (doi:10.1016/S0378-4371(02)01089-0) [DOI] [Google Scholar]
- 16.Seaton K. A., Hackett L. M. 2004. Stations, trains and small-world networks. Physica A 339, 635–644 10.1016/j.physa.2004.03.019 (doi:10.1016/j.physa.2004.03.019) [DOI] [Google Scholar]
- 17.Sienkiewicz J., Holyst J. A. 2005. Statistical analysis of 22 public transport networks in Poland. Phys. Rev. E 72, 046127 10.1103/PhysRevE.72.046127 (doi:10.1103/PhysRevE.72.046127) [DOI] [PubMed] [Google Scholar]
- 18.Gattuso D., Miriello E. 2005. Compared analysis of Metro networks supported by graph theory. Netw. Spat. Econ. 5, 395–414 10.1007/s11067-005-6210-5 (doi:10.1007/s11067-005-6210-5) [DOI] [Google Scholar]
- 19.Angeloudis P., Fisk D. 2006. Large subway systems as complex networks. Physica A 367, 553–558 10.1016/j.physa.2005.11.007 (doi:10.1016/j.physa.2005.11.007) [DOI] [Google Scholar]
- 20.Lee K., Jung W.-S., Park J. S., Choi M. Y. 2008. Statistical analysis of the Metropolitan Seoul Subway System: network structure and passenger flows. Physica A 387, 6231–6234 10.1016/j.physa.2008.06.035 (doi:10.1016/j.physa.2008.06.035) [DOI] [Google Scholar]
- 21.von Ferber C., Holovatch T., Holovach Y., Palchykov V. 2009. Public transport networks: empirical analysis and modeling. Eur. Phys. J. B 68, 261–275 10.1140/epjb/e2009-00090-x (doi:10.1140/epjb/e2009-00090-x) [DOI] [Google Scholar]
- 22.Derrible S., Kennedy C. 2010. The complexity and robustness of metro networks. Physica A 389, 3678–3691 10.1016/j.physa.2010.04.008 (doi:10.1016/j.physa.2010.04.008) [DOI] [Google Scholar]
- 23.Derrible S., Kennedy C. 2010. Characterizing metro networks: state, form, and structure. Transportation 37, 275–297 10.1007/s11116-009-9227-7 (doi:10.1007/s11116-009-9227-7) [DOI] [Google Scholar]
- 24.Xie F., Levinson D. 2009. Topological evolution of surface transportation networks. Comp. Environ. Urban Syst. 33, 211–223 10.1016/j.compenvurbsys.2008.09.009 (doi:10.1016/j.compenvurbsys.2008.09.009) [DOI] [Google Scholar]
- 25.Naridi I., Manumeas T. P. Contribution of highway capital to industrial and national productivity growth. Technical report. 1996 Work Order Number BAT-94-008. Federal Highway Administration (Office of Policy Development). See http://www.fhwa.dot.gov/policy/gro98cvr.htm . [Google Scholar]
- 26.Seidman S. B. 1983. Network structure and minimum degree. Social Netw. 5, 269–287 10.1016/0378-8733(83)90028-X (doi:10.1016/0378-8733(83)90028-X) [DOI] [Google Scholar]
- 27.Xie F., Levinson D. 2007. Measuring the structure of road networks. Geogr. Anal. 39, 336–356 10.1111/j.1538-4632.2007.00707.x (doi:10.1111/j.1538-4632.2007.00707.x) [DOI] [Google Scholar]