Flying in the rain: hovering performance of Anna's hummingbirds under varied precipitation

Abstract

Flight in rain represents a greater challenge for smaller animals because the relative effects of water loading and drop impact are greater at reduced scales given the increased ratios of surface area to mass. Nevertheless, it is well known that small volant taxa such as hummingbirds can continue foraging even in extreme precipitation. Here, we evaluated the effect of four rain intensities (i.e. zero, light, moderate and heavy) on the hovering performance of Anna's hummingbirds (Calypte anna) under laboratory conditions. Light-to-moderate rain had only a marginal effect on flight kinematics; wingbeat frequency of individuals in moderate rain was reduced by 7 per cent relative to control conditions. By contrast, birds hovering in heavy rain adopted more horizontal body and tail positions, and also increased wingbeat frequency substantially, while reducing stroke amplitude when compared with control conditions. The ratio between peak forces produced by single drops on a wing and on a solid surface suggests that feathers can absorb associated impact forces by up to approximately 50 per cent. Remarkably, hummingbirds hovered well even under heavy precipitation (i.e. 270 mm h⁻¹) with no apparent loss of control, although mechanical power output assuming perfect and zero storage of elastic energy was estimated to be about 9 and 57 per cent higher, respectively, compared with normal hovering.

1. Introduction

Rainfall is a conspicuous environmental phenomenon that can potentially influence animal flight performance. Adhered water increases the effective mass of the wings and body and alters the wing's moment of inertia, whereas drop impact imparts downward momentum to the body and elevates the power required to stay airborne [1,2]. Raindrops impacting wings  can also produce superficial roughness and, depending on hydrophilic surface characteristics, can increase aerodynamic drag [3]. Moreover, non-uniform distribution of drops across the body and wings may adversely influence control and manoeuverability. Potential damage to wing microstructures caused by high impact pressures of falling drops, as observed for airfoils [4], might also be expected. Surprisingly, some birds [5], bats [6] and insects [7] have been observed flying even during heavy rain, although the various aforementioned mechanical penalties while doing so have not yet been characterized.

Theoretical and experimental research on airfoils indicates dramatic reduction in the aerodynamic efficiency (i.e. in the lift : drag ratio) as precipitation rate increases above middle-range values [1–3]. For medium-size bats, moderate rain has only a marginal effect on flight performance, although associated fur wetting increases their flight metabolism by a factor of 2 [6]. In contrast to mammalian fur, the microstructural configuration of feathers confers both water repellency as well as resistance to water penetration [8,9]. Thus, we hypothesize that birds face primarily aerodynamic rather than thermoregulatory challenges owing to wetting when they fly in the rain.

Hummingbirds are of special interest in this regard because they approach lower size limits of volant vertebrates [10], possess distinctive hovering abilities similar to those of insects [11,12] and remain active even during heavy rain ([5], V.M.O. & R.D. 2011, personal observation). The more than 325 trochilid species are also most abundant in mid-montane cloud forest regions of the Neotropics as well as in lowland rainforest where heavy rains are common. Persistent inclement weather is particularly characteristic of eastern Andean slopes, a well-known hotspot of hummingbird diversity. We accordingly evaluated the effects of light, moderate and heavy precipitation, as simulated in the laboratory, on the hovering flight of Anna's hummingbirds (Calypte anna). Furthermore, we explored the consequences of raindrop impact forces and total mass of water adhered to the body and wings for estimates of mechanical power produced during flight.

2. Material and methods

Hover-feeding of five male Anna's hummingbirds was studied under three precipitation rates (light: 6.4 ± 0.01 mm h⁻¹; moderate: 14.9 ± 0.56 mm h⁻¹; and heavy: 22.4 ± 0.26 mm h⁻¹) and under control conditions of no rain. Birds were placed individually in a Plexiglas cube (0.6 × 0.6 × 0.6 m) that contained a perch and a feeder. Two nozzles were connected via metal tubing to the cold water tap of the laboratory sink; a water gauge (with accuracy of 7 kPa) was used to control water pressure. One nozzle (Viper flexible mist stand) was placed in the centre of the cube's ceiling 35 cm above the feeder, and was used to produce light and moderate rain (at water pressures of 70 and 210 kPa, respectively). The other nozzle (obtained from a garden water-gun) was oriented upwards on the bottom of one of the cube walls such that emitted water drops followed a ballistic path and fell almost vertically near the feeder. A plastic square mesh (with openings of 15 × 15 mm) was placed vertically in front of this latter nozzle to reduce volume flow and to increase size variability of drops. This nozzle was used to produce heavy rain at a water pressure of 112 kPa.

To estimate flow rates for different rain conditions, a calibrated glass cylinder (external diameter d_cyl of 1.82 cm) was used to measure the height of accumulated water (H_w) as measured over 5 min. Mean values for drop diameter (d_drop) and drop speed (U_drop) were obtained from high-speed video recordings at 1000 Hz; only those drops in focus in the approximate centre of the rain field (corresponding to the typical position of a feeding hummingbird) were analysed (see electronic supplementary material, video SA1). Drop mass (m_d) was calculated as ρ_wπ(d_drop)³/6, where ρ_w is the water density (assumed to be 1 × 10³ kg m⁻³). Physical parameters for each of the three precipitation conditions are provided in table 1.

Table 1.

Physical characteristics for three different conditions of experimentally generated precipitation. Data are shown as mean ± s.e. (sample size n).

variable	light rain	moderate rain	heavy rain
intensity, Hw (mm 5 min−1)	6.4 ± 0.01 (5)	14.9 ± 0.56 (5)	22.4 ± 0.26 (5)
drop diameter, ddrop (mm)	0.59 ± 0.03 (30)	0.55 ± 0.03 (30)	1.52 ± 0.01 (30)
drop speed, Udrop (m s−1)	1.82 ± 0.57 (30)	1.88 ± 0.72 (30)	2.1 ± 0.59 (30)
drops per second, ndropsa	51	150	11
Fsd (mN)b	1.2	1.1	10.6
energy flux, Ek (J m−2 h−1)c	125	318	599
Weber number, Wed	27	27	93

^aCalculated as (3/2)(H_wd_cyl²/d_drop³)/300.

^bSee text for calculation.

^cCalculated as 1200n_drops ρ_w(d_drop)³U_drop²/d_cyl².

^dCalculated as ρ_wU²_dropd_drop/σ, where σ is the surface tension.

Lateral video recordings were also obtained (at 1000 frames per second) of water drops (n = 5) falling from a 35 cm height and impacting on an isolated hummingbird wing (obtained from a salvage specimen of a male Anna's hummingbird) that was positioned horizontally with its planform area nominally perpendicular to gravity. The contact times (t_i) were measured from the videos (see electronic supplementary material, video S3DLH). Two different nominal drop sizes, corresponding to drops under light-to-moderate rain conditions (mean ± s.e.: 0.95 ± 0.10 mm) and heavy conditions (2.2 ± 0.3 mm), were generated using a syringe and attached needle. For light-to-moderate rain, we placed a plastic mesh 5 cm below the needle tip to reduce the size of the impacting drops. The force produced by a single drop on a solid surface (F_sd) was calculated assuming perfect elastic bouncing of a theoretically solid water drop impacting on a surface (=2m_dU²_drop/d_drop; note that such an impact force is proportional to twice the drop momentum).

The total bird area exposed to drop impact was estimated by summing estimates of the exposed wing area and the body area. The former was estimated by filming a hovering hummingbird from above with a high-speed video camera (AOS Technologies, operated at 1000 frames per second), and by measuring with NIH ImageJ the projected wing area of individual frames through the entire wingbeat cycle. The horizontally projected wing area in hovering flight averaged 66 per cent of total planform area (S). The number of drops impacting the bird per second (n_dbird) for each rain condition was estimated as ρ_wH_w[A_btcos(χ_body) + 2(0.66) S]/300m_d, where A_bt is the horizontally projected area of the body excluding the wings (as measured from a digital photograph; 12.89 cm²), χ_body is the body angle and S is the plan area of one wing (see §3). The factor of 300 is included to incorporate the number of seconds in 5 min.

The average total force (F_solid) of drops impacting the bird over time t (assuming the body to be presenting a solid surface to the rain) is then given as n_dbird F_sd t_i. However, as feathers are flexible and form superimposed layers within plumage, they must absorb some of the drop impact. We estimated the drop impact force on the plumage (F_feather) by multiplying F_solid by a correction factor C_sf, which represents an empirically determined ratio of the drop impact force on plumage to that on a solid surface. The aforementioned correction factor was calculated using a force transducer (Nano17, ATI Industrial Automation, Apex, NC, USA). We measured the peak impact force produced by single drops hitting both a hummingbird wing and a flat, rectangular piece of aluminium comparable in size to a hummingbird wing (0.8 × 5.4 cm). Two kinds of drops, corresponding to light-to-moderate and to heavy rain, were generated as in the aforementioned experiment. Force data were recorded at a sampling frequency of 625 Hz using a National Instruments 6251 data acquisition card.

To approximate the mass of water adhered to the plumage for hummingbirds in rain, we also measured mass increments through time of a freshly thawed salvage specimen of a male Anna's hummingbird exposed to each of the aforementioned rain conditions. We fitted the measured data to a cumulative exponential curve (see electronic supplementary material, figure SA). The specimen was fixed in a realistic orientation on an instrumented perch with the wings fully extended (wing span of 12 cm). A similar experiment was made using a single wing that was rapidly oscillated by hand by 5 s at the wing base following 30 s of equivalent rain exposure. We estimated total adhered water mass (m_water) as the sum of that adhered to the body alone (using results from the fixed specimen, and subtracting that of the two wings assuming linear contributions from the horizontally projected wing and body areas) and that adhered to the two flapping wings, estimated as twice the water mass remaining on a single wing after manual shaking. The average duration of a complete stroke cycle during manual shaking (T_ms) was 59 ± 3 ms (n = 4). If we assume that only the hand-wrist contributes to rotational movement of the hummingbird wing, the radius of rotation R_ms is 15.5 cm (incorporating the wing length). Assuming a stroke amplitude of π radians, centripetal acceleration in the manual shaking experiment (calculated as (2πR_ms/T_ms)²/R_ms) is 1468 m s⁻², i.e. about 80 per cent of the centripetal acceleration experienced by a hummingbird wing during hovering motions (1744 m s⁻², calculated assuming simple harmonic motion).

Bouts of hover-feeding under different rain conditions were filmed from above and also laterally using two synchronized high-speed video cameras (500 frames per second; AOS Technologies). Filming was initiated approximately 2 s following the start of hover-feeding to avoid potential transient effects. Camera calibration and digitization were carried using a custom Matlab code [13]. The positions of the eye, the shoulder, the back, the tail tip and the wing tip were digitized in each video sequence frame. We calculated average values for the following kinematic variables using data from five wingbeat cycles per hovering bout: body angle χ_body, tail angle α_tail, stroke amplitude ф, stroke plane angle β and the flapping frequency f_w (figure 1).

Figure 1.

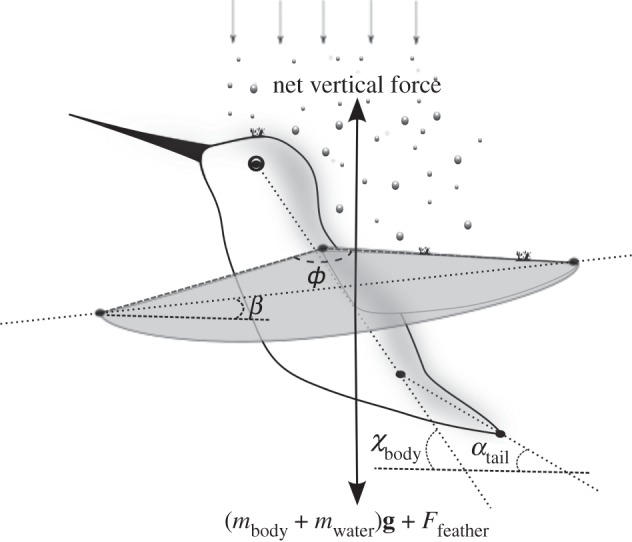
Lateral view of a hummingbird hovering in rain. Digitized points are shown in black (dots), along with the derived kinematic parameters of body angle χ_body, tail angle α_tail, stroke amplitude ф and stroke plane angle β. The net vertical force produced by the wings offsets the gravitational force acting on the body mass (m_body) and adhered water mass (m_water) as well as the average impact force (F_feather) associated with raindrops.

Mechanical power production during flight was calculated for each filmed hovering bout following equations of [14]. The induced power P_ind, corresponding to the energy rate required to generate vertical force, was calculated using an estimated total system mass of (m_b + m_water + [F_feather/g]), where m_b is the body mass and g is the acceleration owing to gravity (figure 1). Profile power P_pro, corresponding to the energy rate required to overcome form and skin drag of the wings, was calculated assuming simple harmonic motion and a drag coefficient of 0.139 [15]. The profile drag coefficient was assumed to be constant for both dry and wet conditions. Inertial power to accelerate the wings and their virtual masses in the first half of a half-stroke, P_acc, was calculated based on mass and chord measurements for each of 10 spanwise wing strips (see electronic supplementary material, table SA). The amount of water attached to the wing (m_ww) was assumed to be uniformly distributed among these strips._. Total mass-specific mechanical power was estimated assuming both perfect (P_per = P_pro + P_ind) and zero (P_zero = 0.5[P_pro + P_ind + P_acc]) elastic energy storage (see derivation details in [14]).

Repeated-measures ANOVA was used for each kinematic variable (i.e. χ_body, α_tail, ф, β and f_w) and for total body mass-specific power calculations (P_per and P_zero), followed by a Tukey post hoc test to evaluate response differences among conditions of light, moderate and heavy rain, and the control condition of no rain. All statistical analyses were performed using R v. 2.10.1 [16]. Results are presented as averages ± s.e.

3. Results

For conditions of light-to-moderate and of heavy rain, drop contact times (t_i) of 1.4 ± 0.2 ms (n = 5) and 2.2 ± 0.2 ms (n = 5) were obtained. Peak impact force for drops for light-to-moderate and for heavy rain conditions were 7.1 ± 0.3 and 16.4 ± 0.7 mN on the hummingbird wing, and 13.1 ± 0.5 and 31.1 ± 0.1 mN on the aluminium section, respectively (n = 30 in all cases; see the electronic supplementary material, figure SB). The force ratio C_sf was 0.54 and 0.53 for light-to-moderate and for heavy rain conditions, respectively.

The amounts of water remaining on a single wing after shaking (m_ww) were 0.012 ± 0.002, 0.018 ± 0.002 and 0.022 ± 0.002 g for light, moderate and heavy rain, respectively (n = 5 in each case). The average difference in adhered mass between static and flapped wings for light, medium and heavy rain conditions was 126, 168 and 182 mg, respectively. Total adhered water mass (i.e. that accumulated on the body and wings of a hummingbird) for light, moderate and heavy rain during 2 s of exposure corresponded to 1.69 ± 0.02%, 2.92 ± 0.04% and 3.94 ± 0.06% of body mass, respectively. The total impact force (F_feather) produced by all the drops during the same exposure period was 0.8 ± 0.01%, 2.0 ± 0.03% and 2.4 ± 0.04% of body weight, respectively.

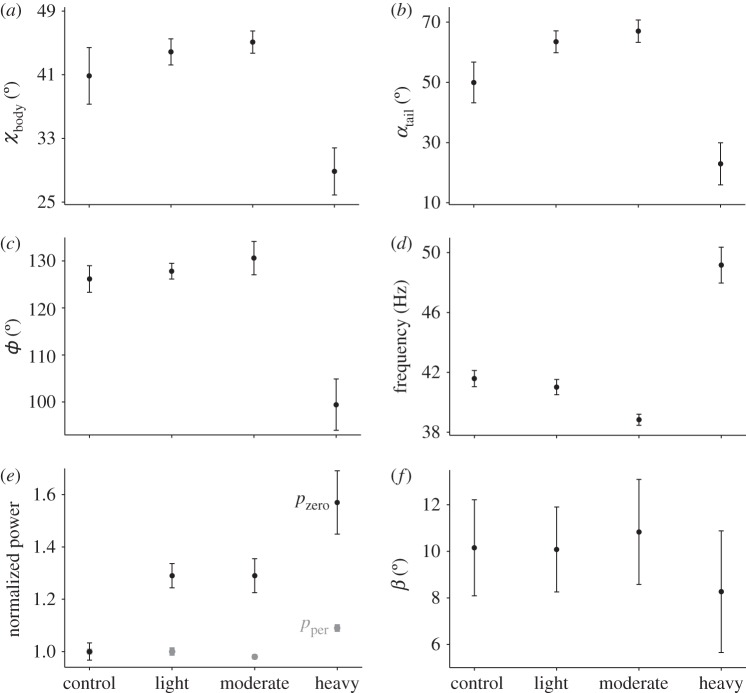
For the five study birds, body mass m_b, wing length R and wing area S averaged 4.45 ± 0.07 g, 5.22 ± 0.05 cm and 7.32 ± 0.07 cm², respectively. Flight in different rain conditions was characterized by significant differences in body angle χ_body (F = 20.06, d.f. = 3,12, p = 5.7 × 10⁻⁵; figure 2a), tail angle α_tail (F = 11.19, d.f. = 3,12, p = 8.6 × 10⁻⁴; figure 2b), stroke amplitude ф (F = 20.7, d.f. = 3,12, p = 4.9 × 10⁻⁵; see figure 2c), wingbeat frequency f_w (F = 43.86, d.f. = 3,12, p = 9.6 × 10⁻⁷; figure 2d) and both mass-specific total powers: P_per (F = 39.7, d.f. = 3,12, p = 1.65 × 10⁻⁶) and P_zero (F = 19.2, d.f. = 3,12, p = 7.2 × 10⁻⁵; figure 2e and table 2). There were no significant differences among rain conditions in values of the stroke plane angle β (F = 0.63, d.f. = 3,12, p = 0.61; figure 2f). Hummingbirds hovering in heavy precipitation showed significantly lower values for χ_body, α_tail and ф, and higher values of f_w, P_per and P_zero relative to controls (Tukey's post hoc test, p < 0.01 for all variables). Birds flying in moderate rain had a significantly lower f_w (Tukey's post hoc test, p = 0.02), a higher P_zero (Tukey's post hoc test, p < 0.001) and a marginally higher χ_body than control birds (Tukey's post hoc test, p = 0.04). Finally, birds flying in light rain presented a higher P_zero relative to controls (Tukey's post hoc test, p < 0.001).

Figure 2.

Flight kinematic parameters and total mechanical power output for hummingbirds hovering in control conditions of no rain, and under light, moderate and heavy precipitation: (a) Body angle χ_body, (b) tail angle α_tail, (c) stroke amplitude ф, (d) wingbeat frequency f_w, (e) normalized mechanical power assuming perfect (P_per: grey) and zero (P_zero: black) elastic energy storage and (f) stroke plane angle β. Values of P_per and P_zero are normalized relative to the average value of control conditions with no rain. Error bars indicate one standard error.

Table 2.

Mean values of kinematic variables and mechanical power estimates for five Anna's hummingbirds hovering in three precipitation conditions, and in the control condition of no rain. Results of a sensitivity analysis for mechanical power estimates are also provided, assuming perfect elastic energy storage (P_per,Cd) and zero elastic storage (P_zero,Cd), and using profile drag coefficients of 0.153, 0.160 and 0.174 for light, moderate and heavy conditions, respectively (see [1] for representative values of drag increase in rain).

variable	control	light rain	moderate rain	heavy rain
χbody (°)	40.86 ± 3.97	43.87 ± 1.84	47.66 ± 1.58	28.86 ± 3.31
αtail (°)	49.95 ± 7.54	63.47 ± 4.08	66.99 ± 4.17	22.97 ± 7.84
frequency (Hz)	41.59 ± 0.61	41.01 ± 0.57	38.84 ± 0.42	49.16 ± 1.34
ф (°)	126.16 ± 3.16	127.82 ± 1.88	130.6 ± 3.98	99.43 ± 6.1
β (°)	10.15 ± 2.06	10.08 ± 1.83	10.84 ± 2.26	8.27 ± 2.62
Ppro (W kg−1)	6.59 ± 0.36	6.34 ± 0.33	5.55 ± 0.43	5.10 ± 0.71
Pind (W kg−1)	18.60 ± 0.37	18.84 ± 0.20	19.19 ± 0.48	22.47 ± 0.91
Pacc (W kg−1)	48.95 ± 2.36	70.32 ± 3.24	70.69 ± 4.80	88.61 ± 9.03
Pper (W kg−1)	25.22 ± 0.18	25.20 ± 0.29	24.76 ± 0.16	27.59 ± 0.28
Pzero (W kg−1)	37.11 ± 1.22	47.80 ± 1.72	47.76 ± 2.40	58.14 ± 4.48
Pper,Cd (W kg−1)	25.22 ± 0.18	25.84 ± 0.32	25.60 ± 0.16	28.87 ± 0.21
Pzero,Cd (W kg−1)	37.11 ± 1.22	48.12 ± 1.74	48.18 ± 2.43	58.79 ± 4.56

4. Discussion

Although it is anecdotally well known that small animal fliers are able to fly even in high-intensity rain [5–7], the present study offers experimental evidence for only marginal effects of light-to-moderate precipitation on hovering flight performance, but also a dramatic effect of heavy precipitation on both kinematics and mechanical power expenditure in Anna's hummingbirds. For birds, thermoregulatory effects owing to plumage wetting during light-to-moderate rain are expected to be minimal, because feathers are highly hydrophobic, are resistant to water penetration and offer effective thermal insulation [8,9,17]. Moreover, hummingbirds have the ability to perform rapid body shakes even in flight to remove almost completely any water adhered to the body [18]. Aerodynamic studies indicate a reduction of lift and an increase in airfoil drag as precipitation increases [1–3]. Such effects may characterize wetted hummingbird wings as well, but presumably are of less significance given aforementioned properties of water shedding from feathers. The main effects of rain during hovering by hummingbirds were seen here only under conditions of heavy rain, and associated metabolic increases would probably derive from elevated induced and total mechanical power expenditure via increased effective mass derived from wetting and drop impacts.

Wing roughness and associated drag for aircraft flying in the rain increase primarily owing to drop cratering and the waviness of a thin but attached water layer. In severe rain (e.g. 2000 mm h⁻¹), airplanes can experience drag increments of up to 50 per cent [1]. For hummingbirds, we conducted sensitivity analyses to determine effects of an increase in the profile drag coefficient by 10 per cent (light rain), 15 per cent (moderate rain) and 25 per cent (heavy rain), as characterizes airplanes under similar rain intensities [1]. For all three conditions, effects on the estimates of mechanical power expenditure were minimal (table 2), suggesting that wettability and drop impact are the most relevant factors degrading hummingbird flight performance in rain (figure 2).

Water attached to the body, in conjunction with the time-averaged drop impact forces on hummingbirds, yielded relatively higher increments for effective wing loading in heavy rain (6.3%) compared with those reached by birds in light-to-moderate rain (up to 4.9%; table 1). Voigt et al. [6], by contrast, found no differences in the effective body mass between wet- and dry-flying bats. Data obtained with the force sensor suggest that the impact force is 50 per cent lower when applied to feathers (see electronic supplementary material, figure SB). Feathers are thus dissipating part of the drop impulse (see below).

The peak force (normalized by gravitational acceleration) produced by a single drop on a wing corresponded to 38 and 16 per cent of body mass for heavy- and light-to-moderate rain conditions, respectively. Peak forces of droplets, nevertheless, will have a relatively short duration [19], and our estimates of adhered water suggest instead that drop impact forces contribute the most to the increased body mass during flight. It is important to note that peak impact forces of drops on solid surfaces are higher than those predicted by classical mechanics owing to compressional waves generated during the impact [20]. Water drops of approximately 4 mm diameter and speeds of 2 m s⁻¹ produced peak forces up to 200 mN [19]. In contrast, peak forces recorded for our light-to-moderate and heavy rain drops impacting a flat piece of aluminium were 13 and 31 mN, respectively. These lower values would be expected because the diameters of the drops in our study were substantially lower. Nonetheless, wing feathers can absorb almost 50 per cent of drop impact forces, probably via elastic energy transferred into reversible bending (see electronic supplementary material, video S3DLH; see also [21]).

Microstructural details of bird feathers also enhance their hydrophobicity [9]. Drop impact dynamics on such hydrophobic surfaces are governed principally by the Weber number We (i.e. by the relative contributions of inertial forces and surface tension; [22]) and by surface roughness. Drops at We between 20 and 260, a range corresponding to our three experimental rain conditions (table 1), exhibit partial rebound after impact [22]. We observed that light-to-moderate raindrops behaved similarly, whereas heavy drops splashed and produced several satellite droplets (see electronic supplementary material, video S3DLH).

Peak impact forces of water drops hitting a flapping wing must also be higher than those impacting either the body or the tail, because the resultant speed will reflect the combined speed of the incoming drop and the flapping speed of the wing. Accordingly, higher drop impact pressures would be expected at the wing tip relative to the base. Birds in heavy precipitation presented an average wingtip speed of 9.0 m s⁻¹ (=2фf_wR, where ф is given in radians), when compared with average drop speeds of 2.0 m s⁻¹. Theoretically, a drop impacting a wing at 9.0 m s⁻¹ would produce a stagnation pressure of 60 kPa (calculated as 0.5ρ_wU_drop²), a value that is 10-fold higher than the maximal resistance to water penetration as measured in avian contour feathers [23]. Data presented here suggest a substantial absorption of the peak impact force for drops impacting a hummingbird wing, which might nonetheless yield some water penetration through wing feathers. Our manual shaking experiments on a wet wing suggest that up to 10 per cent of contacted water remains in the spaces between the barbs and barbules.

Both rain intensity and drop size are factors that vary substantially under natural conditions. Typical light-to-moderate natural rain is characterized by an intensity, drop diameter and terminal velocity of 1–4 mm h⁻¹, 0.5–1 mm, and 2–4 m s⁻¹, respectively; for heavy rain, these values are 15–40 mm h⁻¹, 1.5–2.1 mm and 5–6 m s⁻¹ [24], respectively. The concept of precipitation energy flux is, however, very useful as an indicator of the overall physical effect of raindrops impacting surfaces [25]. The precipitation energy flux for our experimental conditions of light, moderate and heavy rain (table 1) correspond to natural intensities of 6, 14 and 24 mm h⁻¹, respectively, with this last value corresponding to rates during short-term rain events within the natural geographical range for Anna's hummingbird [25,26]. Hummingbirds in heavy rain oriented their bodies and tails much more horizontally relative to controls, paradoxically increasing their dorsally presented surface area, and thus presumably increasing total water loading and the extent of drop impact. The low stroke amplitudes and higher wingbeat frequencies exhibited by birds during heavy rain may also act to reduce the wing disc area and the overall rate of drop impact on wings.

We also observed qualitatively that two birds spread their tails during heavy rain. The role of changes in tail conformation to counteract external perturbation during stable hovering deserves more attention [27]. Although the stroke plane angle was nearly horizontal in all treatments, we also qualitatively observed that elevational angles of the wingtip above the stroke plane were higher in heavy rain, possibly suggesting a role in pitch control given the high downwards momentum associated even with even single drop impacts.

In contrast to these responses in heavy rain, both the body and tail during light-to-moderate rain conditions were oriented more vertically relative to controls (see electronic supplementary material, video S2HvsR). This response will reduce the horizontally projected surface area of these structures, but will also act to reduce both the imparted downwards momentum from the drops as well as the amount of adhered water attached (table 2). For single feathers oriented more vertically, we qualitatively observed downwards rolling of drops following impact. Reduced wingbeat frequencies observed in moderate precipitation may be a response to the high number of raindrops per second for this condition (table 1), although the reduction was only on the order of 7 per cent. Drop impacts on the ventral side of the wings during flapping may also influence the overall force balance given their high rotational velocities. Because hovering wing strokes are close to horizontal, and angles of incidence are fairly low, we consider the majority of drop impacts to derive from vertically descending particles impinging on the dorsal wing surface as it sweeps through the wingbeat. This assumption underpins use of the horizontally projected wing area for calculations of the force balance. Drop impacts on the ventral side of the wing may also influence overall forces given the high flapping velocities. Because raindrop momentum is almost always directed initially downwards, however, it is unlikely that any substantial vertical forces can ensue from this process, particularly as the highest instantaneous angles of attack of the wings relative to horizontal are attained at the ends of half-strokes when flapping velocities are least. Instead, our actuator disk approach was useful to approximate minimal power requirements of hovering during rain. The effects of rain on the wing's boundary layer, leading edge vortices and unsteady lift mechanisms are appropriate and interesting physical topics for future aerodynamic work.

Estimates of mechanical power output assuming either perfect or zero storage of elastic energy showed little change in light-to-moderate rain (figure 2). During heavy precipitation, P_per was 9 per cent and P_zero was 57 per cent higher than controls. Inertial power was almost thrice greater than aerodynamic power estimated under all three conditions of precipitation, suggesting that accelerating and decelerating a wet wing may contribute to mechanical costs even in a light drizzle. However, the assumption of zero elastic energy storage appears to be unrealistic for hummingbirds [14], and the actual increase of power in heavy rain is more likely to be close to the 9 per cent assuming perfect storage. This increase may nonetheless be substantial given the high absolute costs of hovering, particularly under conditions of energetic stress during prolonged rainy periods.

On a biogeographical scale, the New World hummingbirds are most common and taxonomically diverse in wet tropical forests, both in the lowlands and particularly at higher elevations [11]. Hummingbirds are energetically constrained to feed at high rates, and cannot survive without feeding for more than a day or so. Flight in rain is therefore a common, if not necessary, occurrence in this group, and is thus of both biomechanical and ecological relevance. Many tropical hummingbirds also reproduce during the rainy season, in spite of the high energetic costs of such activities as nest building and chick rearing [28]. Many hummingbird-visited flowers also face downwards, which has been proposed as an adaptation to reduce nectar dilution by rain, and thus to retain attractiveness to their pollinators [5].

Flight in rain is not confined to volant vertebrates, as many insects exhibit comparable behaviour. Indeed, nuptial flights of many social Hymenoptera are triggered by heavy rain; flight under such demanding physical conditions is particularly impressive in termite reproductives, which are otherwise known for their weak flight and a remarkable tendency for dealation. Flying insects are typically much smaller than birds, with wingbeat frequencies often 10 times higher than those exhibited by hummingbirds [10]. Moreover, insect cuticles often exhibit higher hydrophobicity than feathers [29]. Given the small size of insects, however, peak impact pressures on their bodies and wings must be relatively higher than those described here for hummingbirds. The implications of such high transient impact forces for insect flight performance are unexplored, and will also be relevant for microair vehicles flying under these conditions. Rain is a ubiquitous feature of most terrestrial environments, and volant taxa potentially use a diversity of kinematic and mechanical responses to this natural perturbation. For hummingbirds hovering in naturally realistic rain conditions, we have demonstrated substantial changes in flight kinematics and mechanical power expenditure associated with increased mass loading and with the impact forces of raindrops. It would now be of particular interest to examine potential scale dependence of these effects, particularly given the diverse insect and bird taxa of wet tropical environments that frequently fly in rain.