Kinetic mechanism of conformational switch between bistable RNA hairpins

Abstract

Transitions between the different conformational states play a critical role in many RNA catalytic and regulatory functions. In this study, we use Kinetic Monte Carlo method to investigate the kinetic mechanism for the conformational switches between bistable RNA hairpins. We find three types of conformational switch pathways for RNA hairpins: refolding after complete unfolding, folding through basepair-exchange pathways and through pseudoknot-assisted pathways, respectively. The result of the competition between the three types of pathways depends mainly on the location of the rate-limiting base stacks (such as the GC base stacks) in the structures. Depending on the structural relationships between the two bistable hairpins, the conformational switch can follow a single or multiple dominant pathways. The predicted folding pathways are supported by the activation energy results derived from the Arrhenius plot as well as the NMR spectroscopy data.

Introduction

Due to the formation of various stable base pairs and base stacks, RNA folding often involves misfolded states and alternative conformations.^1-3 These alternative structures can have similar stabilities but different roles in function. Many RNA functions involve transitions between the different conformations.⁴ An important example is RNA riboswitches, whose structural rearrangement due to ligand binding turns on/off gene expression.^5,6 Other examples include RNA thermometers which alter their structures in response to temperature change and behave as an effective translational regulator⁷ and conformational switch between alternate conformations of the leader of the HIV-1 RNA genome^8-10 that encodes replicative signals.

A full characterization of RNA folding and function requires not only the native structure, but also the folding kinetics including the pathway information.^11,12 Time-resolved RNA folding and conformational switch from a non-equilibrium state has been extensively investigated in experimental studies.^12-26 However, the detailed kinetic mechanism including the transition pathways remains unclear. This in part is due to the rugged energy landscape for RNA.^27-37 The presence of multiple distinct structural transitions makes it difficult to decipher the pathways of the conformational switch.

Unlike refolding from an unfolded polynucleotide chain, RNA conformational switch requires disruption of the interactions in the initial structure and formation of the interactions that stabilize the final state.^38,39 These two processes could occur sequentially⁴⁰ or in parallel.⁴¹ The transition state between the disruption and the formation of the respective interactions is sequence dependent. In general, for the conformational switch between two hairpin structures A → B, there may exist several types of pathways such as the following pathways:^40,41

1. Unfolding-refolding pathway. Structure B is folded from the unfolded state following the complete unfolding of structure A.

2. Pseudoknot-assisted pathway. Structure B is formed through a pseudoknot structure that contains A and B helices. The process often requires disruption of the loop-closing base pairs in A for alternative base pairing.

3. Basepair-exchange pathway. The disruption of a base pair in A is followed by the concurrent formation of a new base pair in B. Such an exchange process usually has low free energy barrier (a “tunnel” through the energy barrier).

Because both the pseudoknot-assisted and the basepair-exchange pathways involve exchange between base pairs in A and in B, they usually have lower kinetic barriers than the unfolding-refolding one. In this study, we use the Kinetics Monte Carlo (KMC) method to investigate the conformational switch between bistable RNA hairpins. By analyzing the ensembles of KMC trajectories, the theory provides information about whether the conformational switch involves a single dominant pathway or multiple pathways and what the partitioning fraction of each pathway is. Such a study would be valuable for facilitating our understanding of the kinetic mechanism of RNA function and for the rational design of RNA folding pathways and transition states.

Theory and Method

Conformational ensemble

RNA secondary structures are stabilized mainly by base-stacking between adjacent base pairs and hydrogen bonding (base pairing).⁴² For a given RNA sequence, we enumerate all the possible structures according to base stacks. Conformations with the same set of base stacks are classified as a conformational state in our calculation. The number of the conformations grows exponentially with the chain length. For example, the number of hairpin conformations increases from 531 for a 16-nt chain to 151963 for a 34-nt chain. In our model, the conformational ensemble for a given RNA sequence includes secondary structures and H-type pseudoknots. The energy parameters for the base stacks and loops are evaluated by the Turner rules^43-45 and pseudoknot folding models.^46-48 We allow the RNA to form H-pseudoknots with and without an interhelix loop (junction). Compared with the pseudoknot-free studies, the main new feature of our model is the complete account of the three types of pathway, especially the pseudoknot-assisted pathways, and the systematic investigation of the occurrence of the different scenarios.

Kinetic move set and rate constant

Since a single (unstacked) base pair is not stable⁴⁹ and can quickly unfold, we define an elementary kinetic move to be the formation/disruption of a base stack or a stacked base pair. Therefore, two conformations are kinetically connected if they can be interconverted through addition or deletion of a base stack and are kinetically disconnected otherwise. This kinetic move model has been tested and validated in the previous theoretical studies for RNA folding kinetics.^50-53

To compute the folding kinetics, we need a model to calculate the rate for each kinetic move. Different choices of the rate constant model may result in the different details in the kinetics. Here, we use the conventional Metropolis rule⁵⁴ to calculate the rate constant for each kinetic move: the rate for the transition from conformation i to j is

$$k_{ij}=\text{min}(k_0,k_0{e}^{-\frac{\Delta G_{ij}}{k_{B}T}})$$ (1)

where ΔG_ij = G_j - G_i is the free energy difference between the two conformations, k₀ is the attempt frequency, k_B is the Boltzmann constant and T is the temperature. The overall kinetics is determined by the collective and correlated events consisting of all the possible kinetic transitions (moves) in the folding/refolding process.

Kinetic Monte Carlo method

Basically, the master equation describes how the population of the conformations evolves with time; i.e., the kinetics for the fractional population (or the probability) p_i(t) for the ith conformation (i = 0,…, Ω–1, where Ω is the total number of chain conformations) is determined by the following rate equation:

$$d{p}_i\left(t\right)∕dt=\sum _j[k_{ji}{p}_j\left(t\right)-k_{ij}{p}_i\left(t\right)],$$ (2)

where k_ij and k_ji are the rates for the transitions from conformation i to conformation j and from j to i, respectively. The master equation has the advantage of providing long-time kinetics for the relaxation of the system. However, the solution to the master equation can only give ensemble-averaged populational kinetics and cannot give detailed information about the microscopic pathways. Moreover, because the size of the rate matrix grows quickly with the chain length, the practical application of the master equation method is limited to short RNA chains.⁵⁵

In the Kinetic Monte Carlo (KMC) method, an ensemble of the transition trajectories is generated and the populational kinetics p_i(t) for the different conformations is calculated from the ensemble average over the trajectories. The KMC not only offers a numerical solution to the master equation⁵⁶ but also provides an effective way to predict the pathways. As illustrated in Fig. 1, the kinetic study using the KMC simulation follows the following steps:

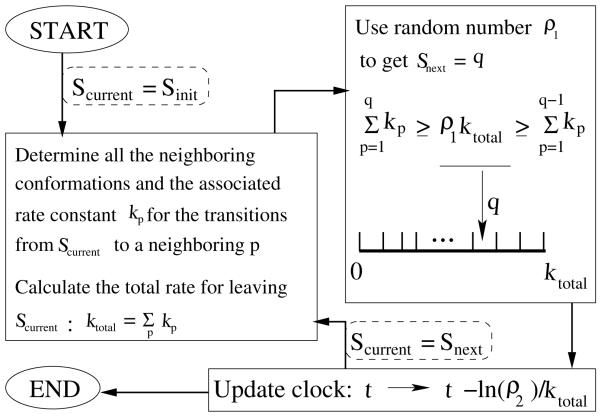
Figure 1.

Flow chart illustrating the steps in the Kinetic Monte Carlo algorithm. Two random numbers ρ₁ and ρ₂ between 0 and 1 are used in each elementary move during the KMC simulation. ρ₁ is used to determine the next conformation S_next from the current conformation S_current. ρ₂ is used to update the system clock. The simulation is terminated if a sufficiently long time span is reached.

1. From an initial conformation S_current, we identify its neighboring conformations each of which is directly connected to S_current through a single kinetic move i.e., only one base stack difference between S _current and its neighboring conformations. We then compute the rate constant k_p for the transition from S_current to the p-th neighbor. Here p = 1, 2, …, P and P is the total number of the neighbors connected to S_current. The total escape rate from the state S_current is the sum of all the transitions from $S_{\text{current}}:{\sum }_{p=1}^p{k}_p$.

2. We then generate a random number ρ₁ ∈ [0-1]. We select the next conformation S_next according to the algorithm shown in Fig. 1. The basic assumption here is that the probability for a transition is proportional to the rate constant. This can be realized in the Monte Carlo simulation by partitioning the total rate k_total into P segments: k₁, k₂, …, k_p, …k_P , and select S_next from the segment where the random number ρ₁k_total falls. For example, if the value of ρ₁k_total is between ${\sum }_{i=1}^{p-1}{k}_i\text{and}{\sum }_{i=1}^p{k}_i$, then we choose the p-th neighbor of S_current as the next conformation S_next.

3. After the S_current → S_next transition, the system clock is updated from t to t – ln(ρ₂)=k_total and S_next is now treated as S_current for the next step on the folding trajectory. Here the second random number ρ₂ ∈ [0-1] is used to generate an exponential distribution of the residence time centered around the average time 1/k_total.

4. The process is terminated after a sufficiently large number of steps is reached. The final equilibrium population of the conformations should obey the Boltzmann distribution.

Transition pathway

A trajectory for the conformational switch consists of a sequence of discrete transitions from the initial conformation A to the final conformation B. A folding trajectory can involve conformations that are visited more than once. Therefore, we use the first passage time FPT ^S_A, the time for the first hit of conformation S from the initial conformation A, to characterize the folding time. The first passage time is a random variable. The order of the first passage time for each conformation gives the information about the kinetic pathway. If the first passage time along a KMC trajectory have the order: FPT ^A_A < FPT ^X1_A < FPT ^X2_A < … < FPT ^B_A, then the transition from A to B goes through the pathway (A, X1, X2, …, B). Since each run of the KMC simulation provides one trajectory, statistically, the ensemble of a sufficient large number of trajectories from the same initial condition can give us the information about the pathways from A to B.

Results and Discussion

Refolding pathways

For the conformational switch from hairpin A to hairpin B, we find that the behavior of individual trajectories falls into the aforementioned three types of pathways. In the following, we give a detailed account for each type of the kinetic pathways.

For the “unfolding-refolding pathway”, the initial structure A is fully unfolded and then the chain refolds into structure B. To calculate the total population that goes through the unfolding-refolding pathway, we sum up the KMC trajectories with FPT ^A_A < FPT ^U_A < FPT ^B_A, where U is the fully unfolded structure.

It is worth commenting that hairpins with only one base stack may be less stable than an unfolded structure due to the large entropic cost to close the loop (except for the YNMG and GNRA tetraloops, which are stabilized by excess intraloop interactions). As a result, the formation of the first base stack from a fully unfolded chain may be an uphill process in the free energy landscape (see Fig. 2-a1). Once the first (loop-closing) stack is formed, the subsequent folding of the helix can be fast. We note that after the first (rate-limiting) stack is formed, there usually exist multiple paths to form the subsequent base stacks (see Fig. 2-a2). Each pathway can further branch out as folding proceeds.

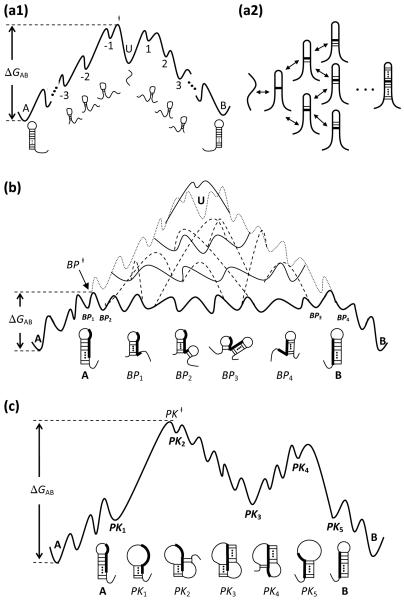
Figure 2.

(a1) A schematic free energy landscape for the unfolding-refolding pathway of the conformational switch between two bistable hairpins A and B. The transition from A to B requires the complete melting of the base pairs in A followed by the formation of the base pairs in B. U is the unfolded structure. (a2) Multiple pathways for the formation and disruption of a hairpin structure. (b) A schematic free energy landscape of the basepair-exchange pathways. Hairpins A and B contain base pairs that are incompatible with each other. BP_i is the structure where A is partially melted from the helix terminus and helix of B is partially formed. The dotted line is the schematic free energy profile for the unfolding-refolding pathway (in a1); the solid lines represent different basepair-exchange pathways, which have much lower energy barriers; the dashed lines show the kinetic connectivity between the different basepair-exchange pathways. The thick solid line denote the basepair-exchange pathway with the lowest energy barrier. (c) A schematic free energy landscape of the pseudoknot-assisted pathway. Hairpins A and B contain base pairs that are incompatible with each other. PK_i is the structure where A is partially melted at the loop side of A so the loop is opened up to allow the formation of helix B. The intermediates between PK₂ and PK₄ are pseudoknots. In all the figures here, the transition states of the corresponding pathways with the lowest energy barrier are denoted as ‡.

For the “basepair-exchange pathway”, a base pair in structure B is formed after a base pair is disrupted in structure A. As shown in Fig. 2b, the process involves three stages: (a) Partial unfolding of the initial structure A followed by the nucleation of the loop-closing base stack in B (A → BP₁ → BP₂). (b) Further formation of a base pair in helix B following the disruption of a base pair in helix A. The process continues until helix A is fully unzipped (BP₂ → BP₃ → BP₄). In the basepair-exchange pathway, the free energy increase for breaking a base pair in A is compensated by the free energy decrease for the formation of a base pair in B. (c) Formation of the remaining base pairs in B (BP₄ → B). The basepair-exchange pathway, which resembles a tunnel across the free energy barrier,⁴¹ has a lower energy barrier than the unfolding-refolding pathway.

We note that the different partially unfolded structures (such as BP₁ in Fig. 2b) can lead to the different basepair-exchange pathways (see the solid lines in Fig. 2b). Furthermore, the different basepair-exchange pathways can be inter-connected by one or several kinetic moves (see the dashed lines connecting the solid lines in the Fig. 2b). It is difficult to determine the population for the transitions through the basepair-exchange pathways (the solid lines in Fig. 2b) because unlike the unfolding-refolding pathways, there is no such a unique conformation that is required for all the basepair-exchange pathways to pass through. However, because the different basepair-exchange pathways are connected (see the dashed lines in Fig. 2b), it may be a valid approximation to estimate the total population of the basepair-exchange transitions by adding up the KMC trajectories with FPT ^A_A < FPT ^BP‡_A < FPT ^B_A. Here conformation BP ^‡ is the transition state of the basepair-exchange pathway with the lowest free energy barrier (shown as the thick solid line shown in Fig. 2b).

For the “pseudoknot-assisted pathway”, as shown in Fig. 2c, several base pairs close to the loop of A are opened up (see PK₁ in Fig. 2c) so that the nucleotides in the loop can base pair with the complementary nucleotides in the dangling ends (see pseudoknot PK₂ in the figure). These new base pairs constitute the helix in structure B. After the base pairs in helix A are completely disrupted (P K₃ → PK₄ → PK₅), the remaining base pairs of B can quickly zip up. Compared to the basepair-exchange pathway, the pseudoknot-assisted pathway is initiated by breaking the base pairs close to the loop (of A) instead of the helix terminal (of A). Throughout the paper, we call the two ends of a helix in a hairpin structure as the loop side and the terminal side, respectively. Second, the pathway may involve two free energy barriers. The first barrier is due to the entropic cost for the nucleation of the pseudoknot loop and the second barrier arises from the disruption of the A helix. Similar to the basepair-exchange pathway, the different PK₂ structures can lead the different pseudoknot-assisted pathways, and the different pathways are connected to each other through one or several kinetic moves.

Moreover, in contrast to the basepair-exchange pathway, the connections between different pseudoknot-assisted pathways can involve higher free energy barrier due to the nucleation of the pseudoknot loop. As a crude approximation, we use the criteria FPT ^A_A < FPT ^PK‡_A < FPT ^B_A to count pseudoknot-assisted pathways. Here PK^‡ is the transition state of the pseudoknot-assisted pathway with the lowest free energy barrier shown in Fig.2c.

To systematically explore the kinetic mechanism for the conformational switch between bistable RNA hairpins, we have designed a series of RNA sequences, each having two bistable hairpins, and applied the KMC method to investigate the kinetic pathways and the rates of the switches. For each sequence, 1000 independent KMC trajectories with the same initial condition are generated. To further distinguish the basepair-exchange and pseudoknot-assisted pathways, which require the disruption of the base pairs from the different ends of the helix in A, we placed a GC stack (two neighboring G-C pairs) at the different locations in the helices. Here the GC stack, which is more stable than other base stacks, serves as a clamp in the helix and can effectively control the direction of the helix unfolding.

(1) GC stack close to the hairpin loop

As shown in Fig. 3a, six RNA sequences are designed with the different distances between the two GC stacks of the two (bistable) hairpins A and B. The purpose of using these designed hairpins is to investigate how the different locations of the GC stacks affect the folding pathway. The KMC simulation (see Fig. 3b) shows no significant population of pseudoknot-assisted pathway for the A → B refolding processes for all the six RNAs. This is because the loop-closing GC clamp in structure A hampers opening up of the hairpin loop (in A) for pseudoknot formation (see PK₁ and PK₂ in Fig. 2c). As a result, the conformational switch can only go through the unfolding-refolding pathway (Fig. 2a) and/or the basepair-exchange pathway (Fig. 2b).

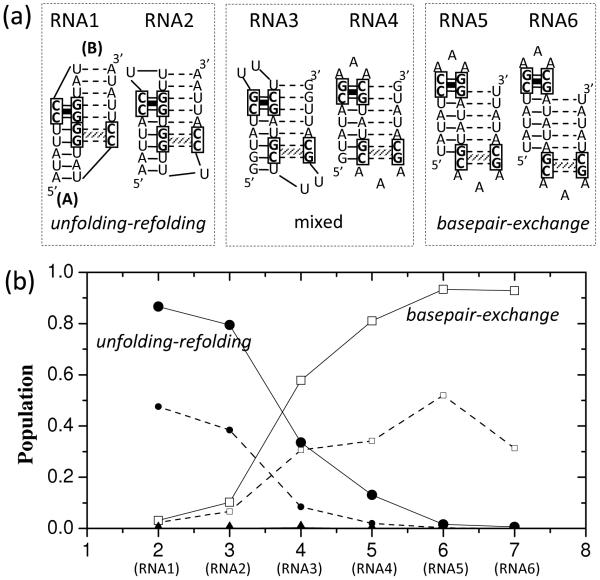
Figure 3.

(a) Six designed RNA sequences each of which folds into two bistable hairpins A and B. In both A and B, the hairpin loop is closed by a stable GC stack. The sequences are designed to have the different distances (from 2 to 7) between the loop-closing GC stacks in A and B. The base pairs in A and B are denoted by the solid and dashed lines, respectively. (b) The fractional population of pathways along the unfolding-refolding (filled circles), the basepair-exchange (empty squares) and the pseudoknot-assisted (filled triangles) pathways for the different sequences (with the different GC stack-stack distances). The smaller symbols guided by the dashed lines are the population of the corresponding pathways with the lowest energy barriers (see Fig. 4).

We found that if the distance between the GC stacks is less than 4 nucleotides (see RNA1 and RNA2 in Fig. 3a), more than 80% of the transitions would go through the unfolding-refolding pathway and less than 15% proceeds along the basepair-exchange pathway. This is because the basepair-exchange pathway here has a higher barrier as explained below. We use RNA1 as an example. A basepair-exchange pathway involves the formation of the branched structures with tandem hairpins (such as BP₂ and BP₃ in Fig. 2b). The formation of such structures requires the disruption of 5 base pairs (1A-U17, 2U-A16, 3A-U15, 4U-G14, and 5U-G13; barrier ΔG^‡₁ ≈ 4.8 kcal/mol) in the A helix and the subsequent closing of the loop in B by the GG-CC base stack (barrier ΔG^‡₂ ≈ 1.6 kcal/mol), resulting in a total barrier of ΔG^‡_{basepair-exchange} ≈ 6.4 kcal/mol, which is higher than the barrier ΔG^‡_{unfolding-refolding} ≈ 4.8 kcal/mol for the complete unfolding of helix A. The above energy barrier values are calculated for T = 310 K. Therefore, for this specific case, the free energy barrier of the basepair–exchange pathway is higher than that of the unfolding-refolding pathway and the conformational switch from A to B goes mainly through the unfolding-refolding pathway.

In contrast, for sequences (RNA5 and RNA6) with well separated GC stacks, base pairs at the helix end of A and the loop-closing GC stack of B are mutually exclusive and hence must be disrupted before the folding of B can be initiated. This involves extensive exchange between the disruption of base pairs in A and the formation of base pairs in B and a corresponding low-barrier basepair-exchange pathway (see Fig. 2b). Indeed, our simulation shows about 90% of the transitions would go through the basepair-exchange pathway (see the open squares guided by solid lines in Fig.3b) due to its lower free energy barrier than the unfolding-refolding pathway.

Furthermore, for each type of the pathways, we find the one with the lowest free energy barrier (as the dominant pathway) and estimate the fractional population that goes through the pathway (see the dashed lines in Fig. 3b). For example, for RNA1, about 50% of the population goes through a dominant unfolding-refolding pathway (see Fig. 4a). The loop-closing GC stack (as a clamp in A) causes the unfolding of A to start from the helix terminal side instead of the loop side. The process is followed by zipping of B after the first loop-closing GC stack in B is formed.

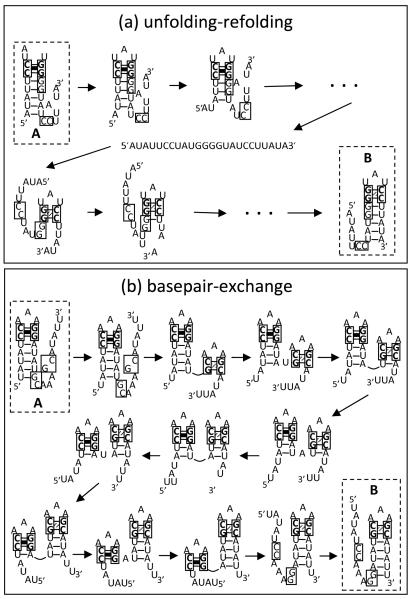
Figure 4.

(a) The dominant unfolding-refolding pathway of RNA1. (b) The dominant basepair-exchange pathway of RNA5, which involves several exchanges between the base pairs of the two bistable hairpins.

To contrast, the dominant pathway for RNA5 (Fig. 4b) starts from the disruption of the terminal base pairs of the helix in A. These base pairs are incompatible with the loop-closing GC stack in B. The partial unfolding of A is followed by the formation of the GC stack in B and the subsequent step by step exchange between the base pairs in helix A and those in helix B through the basepair-exchange pathway (Fig. 2b). The process proceeds until helix A is fully unfolded. In the above exchange process, the free energy oscillates: the free energy increases when a base stack in A is disrupted and decreases when a base stack in B is closed (see Fig. 2b).

In general, the loop-closing GC stack can effectively suppress the pseudoknot-assisted pathways, thus, the conformational switch can only go through either the unfolding-refolding pathway or the basepair-exchange pathway. The competition between the two pathways depends mainly on two factors: (a) whether the incompatible base pairs (in A) are located at the helix terminal side, and (b) how many exchanges (between base pairs in A and in B) are involved in the basepair-exchange process. If the incompatible base pairs are close to the loop and only few or no exchange happens, then the unfolding-refolding pathway becomes the only dominant pathway. Otherwise, the basepair-exchange pathway can be important.

(2) GC stack in the middle of a helix

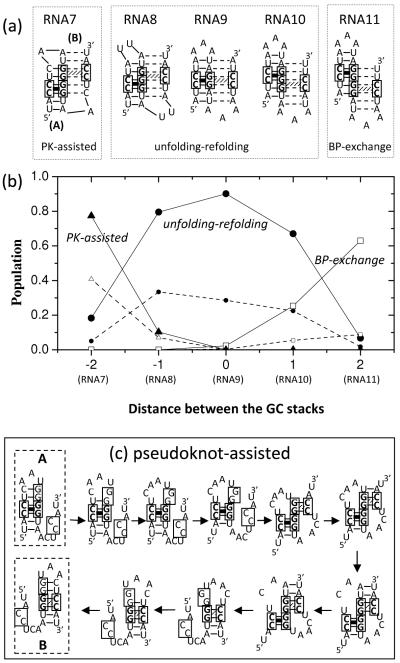
In Fig. 5a, we show five designed hairpin-forming sequences and the bistable native structures. Each bistable structure (A or B) for a given sequence contains a GC clamp in the middle of the helix. The purpose here is to investigate how the position of the GC clamps in B affect the folding pathway. As the GC stack moves to the middle of helix A (see Fig. 5a), the unfolding (of A) can be initiated from both ends of the helix. The unzipping proceeds until the GC clamp is reached. As shown in Fig. 5b, for RNA7-RNA11, the A→ B transition shows all the three types of the pathways: pseudoknot-assisted pathways for RNA7, basepair-exchange pathway for RNA11 and unfolding-refolding pathway for RNA8, RNA9 and RNA10.

Figure 5.

(a) Five RNA sequences each having two bistable hairpins with a GC stack in the middle of the corresponding helix. The sequences are designed to have the different distances between the GC stacks (from −2 to 2). (b) The fractional populations for the unfolding-refolding (filled circles), the basepair-exchange (empty squares) and the pseudoknot-assisted (filled triangles) pathways as a function of the distance between the GC stacks. Lines are a guide to the eye. The smaller symbols guided by the dashed lines are the populations of the corresponding pathways with the lowest energy barriers (see (c)). (c) The dominant pseudoknot-assisted pathway of RNA7.

For RNA8, RNA9 and RNA10, the GC stacks in A and B share one (for RNA8 and RNA10) or two (for RNA9) common (Guanine) nucleotide(s). Therefore, before the GC stack in B is formed, the GC stack in A must be disrupted, resulting in an unfolding-refolding pathway. For RNA7 and RNA11, the GC stacks in A and B have no common nucleotides. Therefore, folding of B can be initiated without first breaking the GC stack in A. For example, for RNA7 (Fig. 5c), unzipping the (non-GC) base pairs of helix A from the loop side leads to base pairing between the (enlarged) loop and the dangling end and results in a pseudoknot structure. Indeed, for RNA7, about 80% of the transitions goes through the pseudoknot-assisted pathway, less than 20% goes along the unfolding-refolding pathway, and nearly no transitions goes through the basepair-exchange pathway.

(3) GC stack at the helix terminal

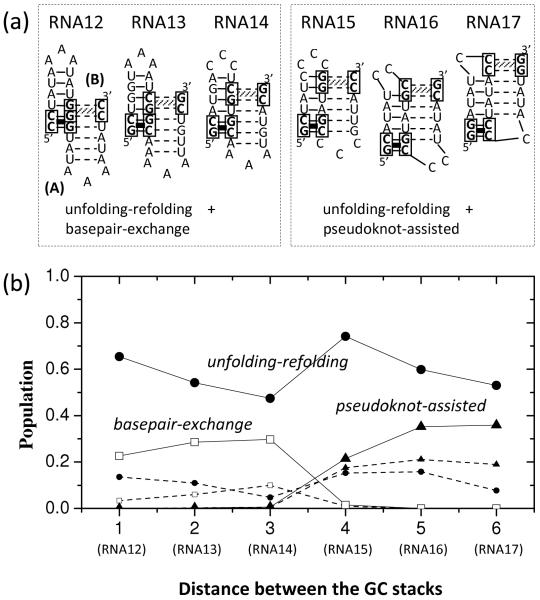
We designed six bistable hairpin-forming sequences such that each structure contains a GC clamp at the helix terminal and the relative position of the two GC clamps changes (see RNA12-RNA17 in Fig. 6a). As shown in Fig. 6b, for most sequences, more than 50% of the A→ B transitions go along the unfolding-refolding pathway and only about 30% of the events follow either pseudoknot-assisted or basepair-exchange pathway.

Figure 6.

(a) Six RNA sequences each having two bistable hairpins with a GC stack at the end of the corresponding helices. The sequences are designed to have the different distances between the GC stacks (from 1 to 6). (b) The fractional populations of the unfolding-refolding (filled circles), the basepair-exchange (empty squares) and the pseudoknot-assisted (filled triangles) pathways as a function of the distance between the GC stacks. Lines are a guide to the eye. The smaller symbols guided by the dashed lines are the population of the corresponding pathways with the lowest energy barriers.

For RNA12, RNA13 and RNA14, besides the majority population for the unfolding-refolding pathway, the rest population goes to the basepair-exchange pathway instead of the pseudoknot-assisted pathway. For RNA12 and RNA13, the basepair-exchange pathway can be quickly initiated through zipping from the loop-closing base pairs of B without breaking the base pairs in helix A. For RNA14, the basepair-exchange pathway also dominates over the pseudoknot-assisted pathway because the latter requires the disruption of base pairs U4-G12, G5-C11 and A6-U10 and the closure of the pseudoknot loop, which involves a larger entropic penalty than the closure of a hairpin loop in the basepair-exchange pathway.

In contrast, for RNA15, RNA16 and RNA17, basepair-exchange pathways are suppressed because closing the B loop requires the disruption of the GC stack (RNA15 and RNA16) or its nearby base pairs (RNA17) in A. These base pairs are located at the terminal of helix A. Breaking these stable base pairs either from the loop side or from the helix terminal side, which is clamped by the GC stack, would be slow. As a result, the A → B switch goes along either the unfolding-refolding (dominant) or the pseudoknot-assisted pathways instead of the basepair-exchange pathway.

Activation energy of the transitions

In general, the transition states are usually short lived and are rarely isolated. In addition, owing to the high free energies, the transition states have lower population in equilibrium. In experiment, it is difficult to determine the transition state and the information about the transition pathways of the folding/refolding kinetics. One of methods to probe the transition pathways is to use the Arrhenius plot.

Our calculation shows that all the conformational switches between bistable hairpins studied here are two-state processes (see SI for the detail). From the temperature dependence of the relaxation rates, we calculate the activation energy E_AB for the two-state kinetics:

$$E_{AB}=-d\text{ln}\left(k_{AB}\right)∕d(1∕k_{B}T)$$ (3)

where k_AB is the rate for the transition from A to B. The rate constant k_AB is fitted from the KMC time-dependent population for conformations A and B according to the populational kinetics for a unimolecular reaction: $p_A\left(t\right)=\frac{1}{K+1}(1+K\cdot \text{exp}(-k_{AB}t(1+\frac{1}{k})))$ and $p_B\left(t\right)=\frac{K}{K+1}(1-\text{exp}(-k_{AB}t(1+\frac{1}{k})))$,²⁴ where K is the equilibrium constant.

Another way to estimate the activation energy is to compute the enthalpy difference H _A – H^‡ between structure A and the transition state on the lowest-barrier pathway. Such an estimated barrier H _A – H^‡ is often (slightly) different from E_AB determined from Eq. 3. For instance, for RNA1, which has one dominant pathway, namely, the unfolding-refolding pathway (Fig. 4a), the activation energy at 310K from the KMC result is E_AB = 21:9 kcal/mol (see Eq. 3), which is a slightly lower than H _A – H^‡ = 26:2 kcal/mol. For RNA1, the lowest barrier unfolding-refolding pathway is shown in fig. 4a. For this pathway, the transition state is the hairpin with a single loop-closing base stack (the 6C-G12 & 7C-G11 stack). The difference between E _AB and H _A – H ^‡ arises from the non-dominant pathways (the pseudoknot-assisted or the basepair-exchange pathway). For RNA3 and RNA14, there exist multiple dominant pathways, namely, the basepair-exchange as well as the unfolding-refolding pathway.

Table 1 shows that the overall barrier E_AB lies between H _A – H^‡ of the lowest-barrier pathway for the basepair-exchange pathway (low barrier) and for the unfolding-refolding pathway (high barrier), respectively. Furthermore, the overall barrier E_AB is closer to the barrier for the pathways of large population. For example, there are two dominant pathways (the basepair-exchange and unfolding-refolding pathways) for RNA3 sequence (see Fig. 3). The basepair-exchange pathway has larger population than the unfolding-refolding pathway. As a result, the activation energy E_AB from the KMC results is closer to the barrier H _A – H^‡ of the basepair-exchange pathway.

Table 1.

Comparison of the activation energies at 310K obtained from the KMC calculations (Eq. 3) and from the pathway analysis. H_A is the enthalpy of the structure A, while H‡ is the enthalpy of the transition state in a dominant pathway with the lowest energy barrier. ‘Multiple’ refers to the case of more than one dominant pathway for the conformational switch process.

Sequence	Dominant pathway(s)	HA - H‡		EAB from KMC
		( kcal/mol )		( kcal/mol )
RNA1	Unfolding-refolding	26.2		21.9
RNA5	Basepair-exchange	2.5		5.7
RNA7	Pseudoknot-assisted	−1.7		−1.5
RNA3	Multiple	8.40	33.1	13.5
RNA14	Multiple	14.2	33.3	25.6

Comparison with experiment

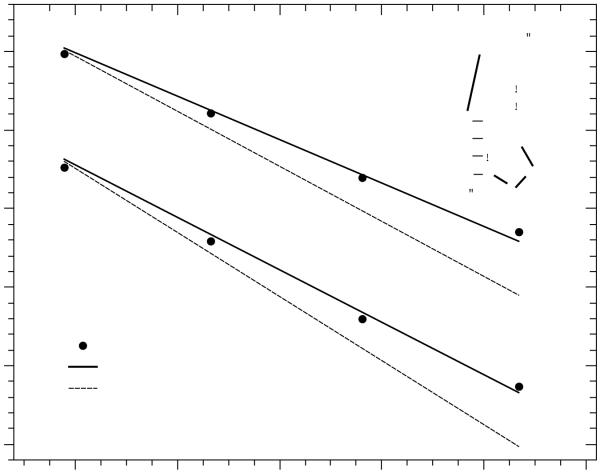
Using real-time NMR spectroscopy, Wenter et al.²⁴ measured the thermal stability, the relaxation kinetic rates and the temperature dependence of the rate constants for a 20-nt sequence 5′GACCGGAAGGUCCGCCUUCC3′. This sequence is found to fold into two alternative hairpins A and B, as shown in Fig.7. The NMR experimental data showed that the activation energy for the refolding from hairpin A to hairpin B is E_AB = 25±5 ± 3±1 kcal/mol (the respective value for the reverse transition is E_BA = 30±6 ± 3±1 kcal/mol). The activation energy amounts to about half the value for the entire enthalpy of the stable hairpin in the initial state, which is close to 49 kcal/mol according to the Turner rules and the energetic parameters for the tetraloop. The result suggests that the transition state is unlikely the fully unfolded state. Wenter et al. proposed the possibility of transient formation of pseudoknot structures in the conformational switch process.²⁴

Figure 7.

Theory-experiment comparison of the transition rates k_AB and k_BA for the A → B and B → A transitions, respectively, for a 20-nt RNA sequence that folds into two bistable hairpins (inset). The solid and dashed lines are the KMC simulation results with the conformational space including and excluding pseudoknots, respectively.

Our previous master equation-based study suggested that including or excluding pseudoknots does not cause notable differences in the predicted kinetics, although including the pseudoknots can affect the equilibrium population of the two bistable hairpins. The results raised the possibility of heat capacity induced decrease in the activation energy.⁵³ The present study, however, reveals a different scheme for the transition state and the kinetic pathways. As shown in Fig. 7, with the inclusion of pseudoknots in the conformational space, without the heat capacity effect, the activation energy from the KMC simulation agrees well with the experimental data. Moreover, the KMC calculation shows two dominant transition pathways: the unfolding-refolding pathway and the pseudoknot-assisted pathway. The experimentally observed activation energy is between the activation energy of the unfolding-refolding pathway and the pseudoknot-assisted pathway. The temperature-dependent partitioning between the two main pathways leads to the results for the overall activation energy.

The different results stem from the different rate models used in the simulation. In the previous study,⁵³ the barrier for the formation (disruption) of a base stack is assumed to be T ΔS (ΔH), where ΔS (ΔH) is the corresponding entropic decrease (enthalpic increase) in the process. The formation of a pseudoknot from a hairpin structure is accompanied by the closure of a (pseudoknot) loop and hence a large entropic decrease. Such a process is highly unfavorable in the previous rate model. In the present Metropolis rate model (Eq. 1), the rate constant is determined by the free energy change. Effectively, the unfavorable entropic penalty for the formation of a pseudoknot loop is reduced by the favorable enthalpic gain for the formation of the loop-closing base stack. As a result, the pseudoknot-assisted pathway emerges as a dominant pathway.

Conclusions

Using kinetic Monte Carlo method, we explore the kinetic mechanism for conformational switches between bistable hairpins. The competition between the three types of pathways (unfolding-refolding, basepair-exchange and pseudoknot-assisted pathways) leads to the great wealth of the different kinetics for RNA hairpin conformational switches. In general, pseudoknot-assisted and basepair-exchange pathways have much lower kinetic barrier than the unfolding-refolding pathway and hence could become a dominant kinetic pathway. The selection of the different kinetic pathway is dependent on the stability of the base pairs in structures. In particular, the location of the stable “clamping” base pairs plays a critical role in determining where and when the folding and unfolding can be initiated.

1. In the transition from hairpin A to hairpin B, the basepair-exchange pathway will be favored if (a) the loop-closing base stacks in B can be formed with the disruption of the terminal base pairs in helix A and (b) the location of the clamping base pairs allows the fast disruption of the terminal base pairs in helix A. Along the basepair-exchange pathway, the growing structure B is connected in series to the disrupting structure A (see Fig. 4b). The basepair-exchange pathway is suppressed if closing the B loop requires breaking a GC clamp in A (see RNA7 in Fig. 5a and RNA15, RNA16 and RNA17 in Fig. 6a).

2. The pseudoknot-assisted pathway dominates over the basepair-exchange pathway if (a) B can be zipped up from its helix terminal side through the disruption of the loop-closing base pairs in A and (b) the location of the clamping base pairs allows the fast disruption of the loop-closing base pairs in A. In the pseudoknot-assisted pathway, the growing helix B and the disrupting helix A coexist to form a pseudoknot structure (see Fig. 5c). A loop-closing GC clamp in A can suppress the disruption of the hairpin loop in A and hence inhibit the pseudoknot-assisted pathway (see RNA1 through RNA6 in Fig. 3a).

3. If (a) the location of the clamping base pairs inhibits fast disruption of the base pairs on either end of helix A or (b) the partial unfolding of helix A from either end is insufficient to initiate the folding of B, complete unfolding of A may be required in order to initiate the folding B. In such a case, the unfolding-refolding pathway dominates.

4. When a stable (GC) stack resides in the middle of the A helix, the A helix can be disrupted from either the loop side or the helix terminal side, which makes both the pseudoknot-assisted pathway (for unzipping of the A helix from the loop side) and the basepair-exchange pathway (for unzipping of A from the helix terminus side) possible. The actual pathways for the conformational switch depend on the relative position of the GC stacks in the A and B helices. For instance, if the formation of the stable GC stack in B requires full unfolding of the A helix, then the unfolding-refolding pathway would dominate (see RNA8, RNA9 and RNA10 in Fig. 5a)

5. Due to entropic penalties upon the formation of pseudoknot loops and the dependence of the entropy parameters on the lengths of helix stems and loops, the pseudoknot-assisted pathway may become more prominent for shorter loops and lower temperatures.

In the current study we have neglected several potentially important effects. For instance, intraloop interactions such as base stacking and pairing within a GNRA or YNMG tetraloop^57-60 can stabilize a loop structure and slow down the disruption of a loop. Furthermore, ion effects,⁶¹ such as ion concentration, charge and size, can play an important role in determining the stability and folding kinetics of nucleic acids. These effects should be considered in the future studies.

In general, the conformational transition goes through a number of pathways. The ensemble average of the pathways yields the overall transition rate, which may be close to the fastest pathway (with the lowest barrier). If folding occurs through multiple dominant pathways, the fastest pathway may provide a good estimate for the overall rate. However, the activation energy of the single lowest-barrier pathway may not provide an accurate estimate for the overall kinetics. This is because each individual dominant pathway can have a distinct activation energy.

The different rate models for the elementary kinetic moves could lead to the different kinetics. The predicted pathways and transition rates can be sensitive to the choice of how the microscopic rates are defined. For instance, the free energy-based (Metropolis) rate model and the previous (ΔH;ΔS)-based rate model give the different kinetics for the same system. With the free energy-based rate model and base stack-based move sets, the current study provides detailed insights into the kinetic mechanism for the conformational switch between bistable hairpins. The theory-experiment tests suggest that the free energy-based rate model may be valid for RNA hairpin folding kinetics (see SI). Further validation of the rate model, however, requires more detailed experimental measurements and systematic theory-experiment comparisons and calibrations. In addition to the tests with experiments, we also compare our results here with the predictions from other theories. For example, recent studies showed that pseudoknot-folding occurs through multiple pathways.^62,63 In one of the paths, tertiary interactions can be established before the formation of the secondary structures. Although a direct comparison between the kinetic mechanisms of the two different systems (hairpin switch and pseudoknot folding) is not available, the results from the different theoretical approaches point to multiple pathways for the hairpin/pseudoknot systems. Furthermore, our current results indicate that the hairpins can switch conformations through tertiary structures such as pseudoknots. In contrast to our findings about the multiple pathways, a previous master equation-based kinetic model (with the possible heat capacity effect) predicted only a single pathway (the unfolding-refolding pathway) instead of the multiple pathways.⁵³ We note that the current model, which considers pseudoknots and tandem hairpins, is based on a more complete conformational ensemble than the previous master equation-based model.⁵³ The use of the different conformational ensemble may contribute to the lack of multiple pathways (such as the pseudoknot-assisted and the basepair-exchange pathways) in the previous model. Recent experimental studies show,^64,65 multiphase kinetics even for small RNA hairpins due to the complexity of the energy landscape. The results suggest the importance of using a more complete conformational ensemble, including conformations with detailed intra-loop tertiary contacts. Moreover, we note that the heat capacity effect may cause a (small) reduction in the kinetic barrier.⁵³

In the present theory, we use the formation and disruption of a base stack/pair as kinetic move sets. The predicted kinetics could be dependent on the kinetic move set. However, such dependence can be weak if the kinetic move set can cover the conformational space and the associated rate model is properly defined. For example, the base stack/pair-based kinetic moves used in the current study are the fundamental steps at the secondary structural level. A less fundamental move set, such as the helix-based move set, may also offer reliable predictions for the kinetics if a physical model for the helix-based rate constant is used.⁴¹

In the present study, we have focused on hairpin systems with bistable states. The KMC-based method can be generalized to treat large RNAs. A possible strategy is to use the helix-based kinetic moves instead of the base pair/stack-based moves. Recently, a helix-based master equation kinetic model for RNA secondary structure folding kinetics was developed.⁴¹ In the model, each kinetic move in the model is the annihilation or creation of a helix stem instead of a base stack/pair. A low-barrier dominant pathway (namely, the basepair-exchange pathway) is selected to represent the helix-helix transition/exchange. Theory-experiment comparisons indicate that this new method is quite reliable in predicting the kinetics for RNA secondary structural folding and structural rearrangements. There, combining the helix-based method and the current KMC method may provide a useful approach for the prediction of the folding kinetics for large RNAs.