Human Intervertebral Disc Internal Strain in Compression: The Effect of Disc Region, Loading Position, and Degeneration

Abstract

The primary function of the disc is mechanical; therefore, degenerative changes in disc mechanics and the interactions between the annulus fibrosus (AF) and nucleus pulposus (NP) in nondegenerate and degenerate discs are important to functional evaluation. The disc experiences complex loading conditions, including mechanical interactions between the pressurized NP and the surrounding fiber-reinforced AF. Our objective was to noninvasively evaluate the internal deformations of nondegenerate and degenerate human discs under axial compression with flexion, neutral, and extension positions using magnetic resonance imaging and image correlation. The side of applied bending (e.g., anterior AF in flexion) had higher tensile radial and compressive axial strains, and the opposite side of bending exhibited tensile axial strains even though the disc was loaded under axial compression. Degenerated discs exhibited higher compressive axial and tensile radial strains, which suggest that load distribution through the disc subcomponents are altered with degeneration, likely due to the depressurized NP placing more of the applied load directly on the AF. The posterior AF exhibited higher compressive axial and higher tensile radial strains than the other AF regions, and the strains were not correlated with degeneration, suggesting this region undergoes high strains throughout life, which may predispose it to failure and tears. In addition to understanding internal disc mechanics, this study provides important new data into the changes in internal strain with degeneration, data for validation of finite element models, and provides a technique and baseline data for evaluating surgical treatments.

Introduction

The intervertebral disc is heterogeneous, comprised of the nucleus pulposus (NP), annulus fibrosus (AF), and endplate substructures. These tissues work together to permit flexibility of the spine and support and transfer large multi-directional loads. Intervertebral disc degeneration is a progressive, irreversible disorder that compromises structural integrity and mechanical function.^1,2 Because the primary function is mechanical, it is critical to quantify the progressive changes in disc mechanics with degeneration. While much is known about disc tissue mechanical changes with degeneration, surprisingly little is known about the change in the mechanical interactions between the AF and NP subcomponents with degeneration, due to the difficulty in measuring the internal behavior without altering the integrity of the tissue. While experimental measurements of internal pressure and displacement,^3–5 and finite element model predictions⁶ have made progress towards elucidating internal disc mechanics, there remains a need for quantitative measures of internal mechanical behavior under physiologic loading.

The intervertebral disc experiences complex loading conditions. Indeed, even simple axial compression creates complex loading throughout the disc via AF tensile hoop stresses, AF radial bulging, and mechanical interactions between the pressurized NP and the surrounding AF.^7–11 Axial compression is often combined with bending positions that are related to spine alignment and posture, resulting in altered internal disc stresses.¹² Combinations of bending with axial compression are common in activities of daily living, where both body weight and lift loads are often applied to the spine under bending postures. Therefore, it is important to evaluate the internal mechanics of nondegenerate and degenerated discs under bending conditions to better understand the mechanics leading to failure and herniation.

Internal disc deformations have been experimentally measured using radiographic or optical imaging methods.^{4,5,10,13–16} Previous studies visualized internal displacements by tracking metal beads or wires in the intact disc using radiographs.^4,5,14 These studies demonstrated that the inner and outer AF both bulge radially outward, and the NP migrates within the disc space;^5,14,17 however, they were limited by the insertion of markers or disruption of the disc structure. Physical markers may move separately from the disc material, and their insertion may alter disc deformations. Tracking the movement of stain dots provides an improvement; however, the required sagittal bisection of the disc likely depressurizes the NP and releases the AF circumferential pre-stress. Furthermore, such studies primarily evaluated displacement at the mid-disc height, with sparse data near the endplate boundaries.

NP pressure decreases with degeneration, a direct consequence of the decreased proteoglycan and water content.^18,19 Mechanical changes with degeneration reported in the literature are inconsistent, often obscured by variability among subjects.²⁰ Generally, stiffness under pure rotation or bending moments decreases with degeneration, while some studies report increased stiffness in flexion-extension bending.^21–24 The mechanics of the structural unit are complex, with six degrees of freedom, substructural interactions between the NP and AF, and load sharing with the facet joints, such that simple generalization regarding the mechanical effects of degeneration cannot be made.²⁵

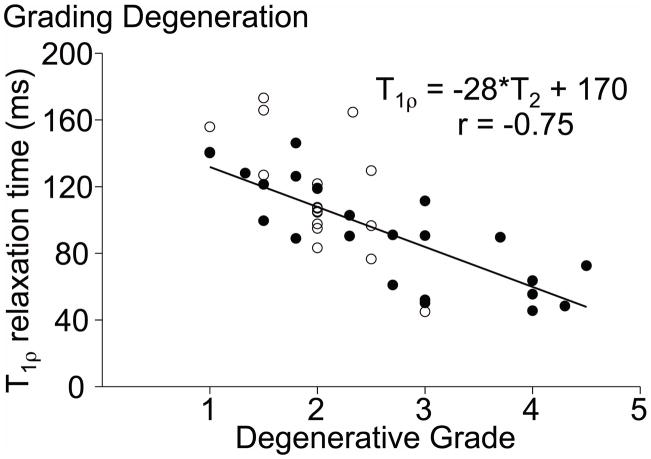
Disc degeneration has been notoriously difficult to study because there lacks a quantitative measure of degeneration with which to perform statistical analyses. Most studies used gross morphological or magnetic resonance (MR) imaging grading schemes.^26–28 While representing the current ‘gold standard’ to establish the level of degeneration, these schemes are based on integer rank assignment and are subjective. A continuous measure with little inter- or intra-observer variability can be obtained from MRI using the T_1ρ relaxation time, which is strongly correlated with NP proteoglycan content (r = 0.70), NP pressure, and the MRI-based Pfirrmann grade (r = −0.75; Fig. 1).^29–31 Therefore, a lower T_1ρ relaxation time represents a disc with lower proteoglycan content, a hallmark of degeneration.^21–24

Figure 1.

Correlation between the T_1ρ relaxation time and Pfirrmann grade for samples used in this study (filled circles) and a previous study (open circles).²⁹

Previous work in our laboratory used a high-resolution MR sequence to image the disc under axial compression.¹⁰ Texture correlation techniques were used to track internal tissue movement without the use of physical markers by matching unique pixel intensity patterns between images. Our previous study established techniques to measure 2D internal deformations of the vertebral body, NP, and AF; however, it had a small sample size which precluded statistical analysis of research questions, and it did not evaluate the internal strains in bending positions.¹⁰

The objectives of this study were two-fold: to evaluate the internal mechanics of the human disc under axial compression in combination with flexion, neutral, and extension positions by analyzing MR images to calculate strains; and to evaluate the effect of degeneration on the internal strains using a quantitative degeneration scale based on T_1ρ relaxation time. We hypothesized that the loading position (flexion, neutral, or extension) alters the interactions between the disc subcomponents and that degeneration is associated with an increased magnitude of internal strains.

Materials and Methods

Human lumbar spine sections were obtained from an approved tissue source (n = 14; NDRI, Philadelphia, PA). T₂-weighted images were obtained to determine the degenerative grade based on the Pfirrmann scale,²⁶ and a series of T_1ρ-weighted images were acquired to determine the NP T_1ρ relaxation time.²⁹ Bone-disc-bone segments were prepared by removing the muscles and facet joints from level L3-L4 and/or L4-L5 (n = 20; 22–80 years old) and potted in PMMA bone cement. The samples were wrapped in gauze, hydrated in a refrigerated PBS bath, and allowed to equilibrate to room temperature prior to testing. The gauze was kept wrapped around the disc during imaging to prevent dehydration.

Imaging under Mechanical Load

A custom-made load frame was constructed of non-magnetic materials to apply axial compressive loads to the disc while in the MR scanner, as previously described.¹⁰ Samples were constrained in the fixture to prevent bending or torsion. Imaging was acquired with a high-field 3T MR scanner (Trio, Siemens Medical Solutions). High resolution mid-sagittal MR images were acquired with T₂-weighted turbo spin-echo sequence and a custom-built 80 mm square surface coil (512 × 512 matrix size, TR = 3000 ms, TE = 113 ms, thickness = 3 mm, total scan time 12.5 min, SNR ≈ 13; resolution = 0.234 mm/pixel).¹⁰ A mid-coronal image was also acquired for samples loaded in neutral.

Each sample was tested under axial compression, with flexion, neutral, and extension positions applied in random order. Flexion and extension positions were achieved by adding a 5° plastic wedge into the loading device. The sample was preconditioned with 5 cycles from 0 to 20N compression, and a nominal 20N preload was applied for 5 mins to ensure contact with the loading platen. Preliminary studies confirmed that a 5-min preload was sufficient to reach a steady-state condition. A reference (undeformed) image was acquired while the disc was under the nominal compressive preload for each loading position. A 1000N compressive load was applied rapidly (~3 sec) and maintained for 20 mins, to allow for creep, and the imaging sequence was repeated to acquire a deformed image. Preliminary studies confirmed that 20 mins creep was sufficient to minimize tissue movement during imaging, with only 0.08 mm (< 1/3 pixel) displacement during imaging. After each test, the sample was recovered in a refrigerated PBS bath for 8 hrs, which was selected based on preliminary studies.³²

Following mechanical testing, the disc was dissected from the vertebral bodies using a scalpel, and an image was taken with a high-resolution camera. The disc edge was manually selected and the cross-sectional area was calculated using a custom Matlab program (Mathworks, Inc.).³³

Data Analysis

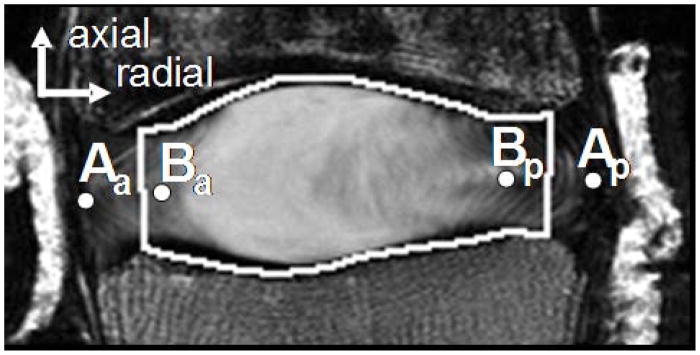
A custom Matlab program was used to calculate the average disc height in the reference and deformed images. The boundary of the superior and inferior vertebrae was selected and connected anteriorly and posteriorly to create a disc space area (Fig. 1 – white polygon). The average disc height was calculated by dividing the total disc space area by the polygon AP width at the mid-point of height.¹⁰ The axial deformation was calculated as the change in disc height between the reference and deformed image normalized by the undeformed height and represented as a percent.

Internal displacements and Lagrangian strains were calculated from the reference and deformed images using digital image correlation commercial software (Vic2D Correlated Solutions, Inc. Columbia, SC) as previously described.¹⁰ Briefly, the Vic2D algorithm analyzes the displacement of a grid of nodal points (space between nodal points = 2 pixels). The signal intensity of the pixels around each point (subset size = 31 pixels) is used to track the tissue movement for each pixel. Shear strains were reported as an absolute value. This analysis provided a resolution of 1/20^th of a pixel, or 0.01 mm. 2D strain analysis was performed in 4 disc regions: anterior AF, posterior AF, lateral AF (neutral loading position only), and NP. The coordinate system was chosen to align with the spinal axis; therefore, radial strains were oriented across lamellae, and axial strains were along the spinal axis (Fig. 2).

Figure 2.

Representative MR image of a nondegenerate sample. The dots represent the nodes from the (A) outer and (B) inner AF used to calculate the inner and outer AF radial bulge, respectively. The white polygon outlines the disc space area used to calculate the average disc height, by dividing the area by the anterior-posterior width of the polygon.

The radial bulge of the inner and outer AF was calculated as the average radial displacement of the node at the mid-disc height from the anterior and posterior AF (Fig. 2), as

$$\text{Radial}\_{\text{Bulge}}_{\mathit{OuterAF}}={1/2}^{\ast }(\mathrm{\Delta }{A}_a+\mathrm{\Delta }{A}_p)\text{and}$$ (1)

$$\text{Radial}\_{\text{Bulge}}_{\mathit{InnerAF}}={1/2}^{\ast }(\mathrm{\Delta }{B}_a+\mathrm{\Delta }{B}_p)$$ (2)

where ΔA is the radial displacement of the outer AF between the reference and deformed image, ΔB is the radial displacement of the inner AF between the reference and deformed image, and the subscripts a and p represent the anterior and posterior AF, respectively. Points A and B were defined in the reference image as the boundary of the region of interest for AF strain analysis at the mid-height. The radial bulge of the lateral AF was similarly calculated as the average displacement of the nodes at the mid-disc height in the mid-coronal plane. A positive average displacement represented an outward radial bulge.

Statistical Analyses

The median and interquartile ranges are presented, as the data did not follow a normal distribution. A Friedmann’s test with repeated measures was performed to evaluate the difference in displacement and strain across AF regions under the neutral position; a Dunn’s post hoc was performed when significance was found. In the flexion and extension positions, where only two AF regions were analyzed, a Wilcoxon matched pairs test was used to compare the strains across regions. To evaluate the effect of the loading position, a Friedmann’s test with repeated measures was performed for the change in disc height, radial bulge, and strain within each disc region. Once significance was found, a Dunn’s post-hoc test was performed to compare the flexion and extension positions with the neutral position. To evaluate the effect of degeneration, a Spearman’s correlation was performed with respect to the T_1ρ relaxation time for the actual and normalized change in disc height, the radial bulge of the inner and outer AF, and strain components. Once a significant correlation with degeneration was identified, the parameter value was calculated (based on the correlation line) for a nondegenerate disc at T_1ρ = 150 ms and for a degenerate discs at T_1ρ = 50 ms to present the relative effect of degeneration on each parameter. Significance was set at p ≤ 0.05.

Results

Representative strain maps of axial, radial, and shear strains for 3 different discs under flexion, neutral and extension loading positions are shown in the supplementary material available online. The strain distributions followed similar patterns as observed previously,⁶ where axial strains were observed as horizontal bands of both tensile and compressive strains, with large strains near the mid-transverse plane (S – Fig. 2 –1^st row). Radial strains were observed as vertical bands of tension and compression (S –Fig. 2 – 2^nd row), while shear strains were highest near the endplates (S – Fig. 2 – 3^rd row).

Effect of disc region

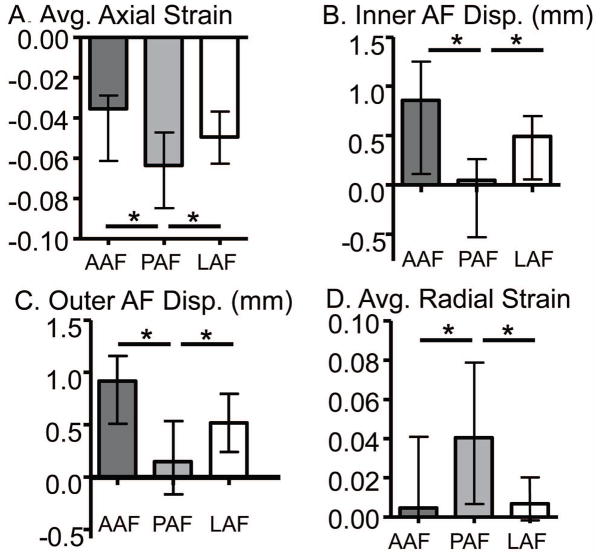
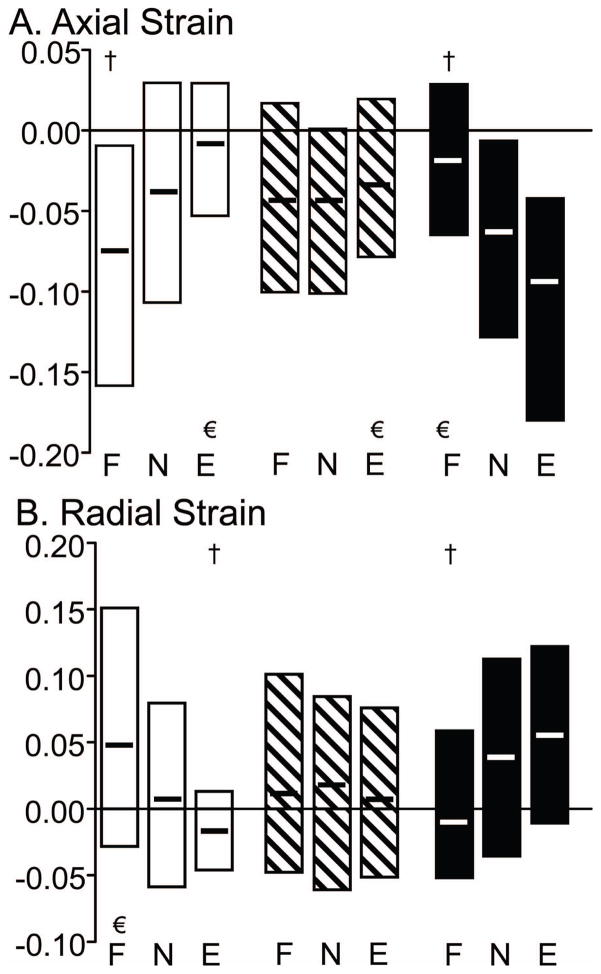
In the neutral position, the average axial strain in the posterior AF (−0.064) was compressive with a larger magnitude compared to the anterior (−0.038) and lateral AF (−0.049, p ≤ 0.04; Fig. 3A). Similarly, the maximum axial strain in the posterior AF (−0.006, interquartile range: −0.030 to 0.023) was compressive, while the maximum axial strain in the anterior and later AF was tensile (0.030 (0.000 to 0.057) & 0.042 (0.007 to 0.070), respectively; p < 0.01). No differences were observed for the minimum axial strain with AF location (p > 0.2).

Figure 3.

Internal strains and displacements across AF regions in the neutral position. A) average axial strain, B) inner AF radial displacement, C) outer AF radial displacement, and D) average radial strain in the anterior (AAF), posterior (PAF) and lateral (LAF) AF. *p< 0.05.

The radial displacement of the inner AF was not different for the anterior and lateral regions (pooled median = 0.61 mm) and was significantly lower in the posterior (0.04 mm; p < 0.01; Fig. 3B). Similarly, the outward radial displacement of the outer AF was greater in the anterior and lateral regions (p < 0.05, Fig. 3C). The average radial strain in the posterior AF (0.039) was tensile and was higher than the anterior AF (0.005) and lateral AF (0.007; p < 0.01; Fig. 3D). No differences were observed for the maximum AF radial strain with location (p = 0.07).

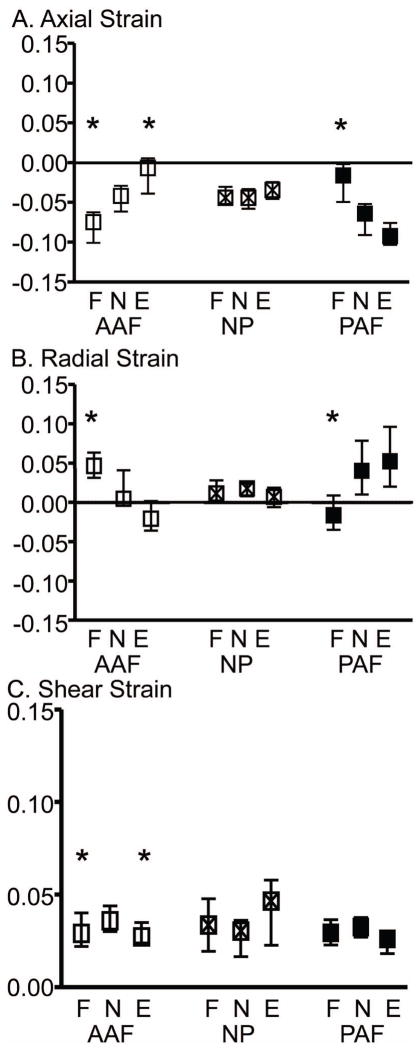
In general, in the flexion and extension position, the axial strain was more compressive and the radial strain was more tensile on the side of the applied offset compressive load (i.e. the anterior AF in flexion). In the extension position, the average axial strain was −0.094 in the posterior AF and only −0.009 in the anterior AF (i.e., 10X more compressive); in the flexion position, the average axial strain was −0.075 in the anterior AF and −0.019 in the posterior AF (i.e., 4X more compressive; p < 0.05; Fig. 4A –statistics not shown). The difference between the anterior and posterior AF radial strain was of similar magnitude for the flexion and extension positions (p < 0.01 for both, Fig. 4B – statistics not shown).

Figure 4.

The median and interquartile range of strain in the flexion (F), neutral (N) and extension (E) loading positions for the average A) axial, B) radial, and C) shear strain components for all samples (n = 20) in the anterior AF (AAF), NP, and posterior AF (PAF). * denotes significantly different from neutral position, p < 0.05.

Effect of Loading Position

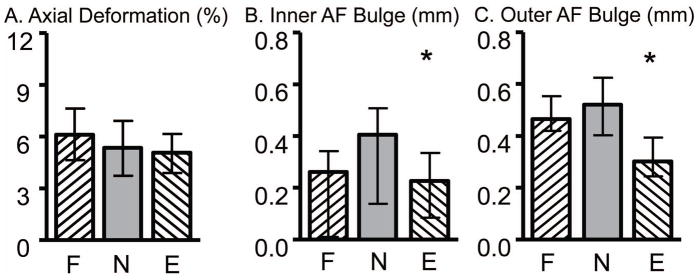
One sample had a void in the NP and was excluded from the NP strain results due to a lack of tissue for strain analysis. The axial deformation was 0.067 (0.048 to 0.099) and was not dependent on loading position (Fig. 5A).

Figure 5.

Internal displacements in the flexion (F), neutral (N), and extension (E) loading positions for A) axial deformation, B) inner AF radial bulge, and C) outer AF radial bulge. * denotes significance compared to the neutral position, p < 0.05.

Varying from a flexed to an extended position resulted in a shift in the average axial strain in the anterior and posterior AF (Fig. 4A). For example, the average axial strain in the anterior AF became less compressive from the flexed to the extended position, and the opposite behavior was observed in the posterior AF (p < 0.05; Fig. 4A). The NP axial strain was not affected by the loading position (Figs. 4A & 6A). Both the maximum and minimum AF axial strains were similarly affected (Fig. 7A).

Figure 6.

The median maximum and minimum strain for the A) axial and B) radial strain components for the anterior AF (□), NP (▧), and posterior AF (■). The interquartile range for peak strains is not shown. Significant differences with the neutral position are represented by † for the maximum strains and for the minimum strain.

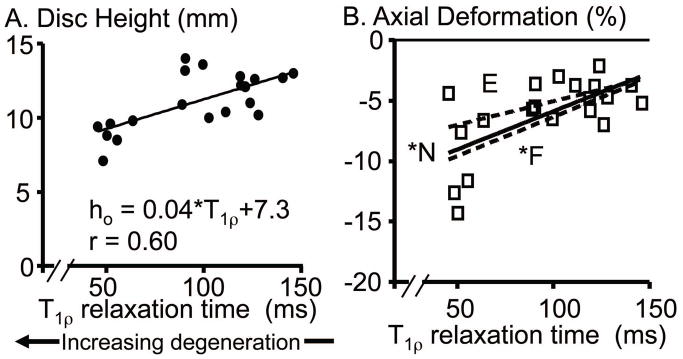
Figure 7.

A) Correlation with degeneration of the initial disc height in the reference image. B) Correlation of axial deformation with degeneration. Axial deformation data for flexion and extension are shown in the supplementary figure available online (S – Figure 7). F: Flexion position is shown as a dashed line, N: neutral position is represented by the squares with solid line, and E: extension position is shown by the dashed line. * p < 0.05.

The inner and outer AF radial bulge was calculated as the average outward radial displacement at the mid-disc height of the anterior and posterior AF and was 40% lower in the extension position than the neutral position (p ≤ 0.04, Fig. 5B & 5C). In the neutral position, the radial bulge along the mid-coronal plane was 0.41 mm (0.30 to 0.59 mm) for the inner AF was 0.48 mm (0.31 to 0.61 mm) for the outer AF; neither parameter was different from the mid-sagittal plane (p > 0.2).

Similar to the axial strain, the average and maximum AF radial strain (Figs. 4B & 6B, respectively) were altered when varying the loading position from flexion to neutral and extension. For example, in the anterior AF, the average radial strain changed from tension in the flexion position to compression in the extension position (Fig. 4B). No significant differences were found in the NP radial strains with loading position (Figs. 4B & 6B).

The average shear strain in the anterior AF was significantly greater in the neutral position than the flexion and extension positions; however, this increase was <0.01 (p < 0.05; Fig. 4C). No other differences were observed for the average or maximum shear strain across loading positions.

Effect of Degeneration

The cross sectional area of the disc was 2074 mm² (1781 to 2285 mm²) and did not depend on degeneration (p > 0.7). In contrast, the initial disc height was 11.0 mm (9.7 to 12.8 mm) and decreased with degeneration (p < 0.01, r = 0.60; Fig. 7A). The disc axial deformation was negatively correlated with degeneration for all loading positions (p ≤ 0.03, |r| ≥ 0.50; Fig. 7B & S – Fig. 7). Therefore, axial deformation was more compressive in degenerate discs (−0.09 at T_1ρ = 50 ms for the neutral position) than nondegenerate discs (−0.03 at T_1ρ = 150 ms).

The radial bulge of the inner and outer AF was independent of degeneration (p > 0.1) and was outward for the majority of discs. The inner AF bulged inward in about 10% of the discs, and, unexpectedly, across all levels of degeneration. Significant correlations for the average and maximum strains with degeneration for each disc region are shown in the Table.

Table.

Boxes with values represent significance correlations (r) for the average (top) and maximum (bottom) axial, radial, and shear strain in the anterior and posterior AF (AAF and PAF, respectively) and the NP. Values are shown for nondegenerate discs (ND, T_1ρ = 150ms) and degenerate discs (D, T_1ρ = 50ms) calculated from the correlation line.

	Average Axial			Average Radial			Average Shear
Loading	AAF	NP	PAF	AAF	NP	PAF	AAF	NP	PAF
Extension	ND = 0.023 D = −0.047 r = 0.78	ND = −0.026 D = −0.056 r = 0.49		ND = −0.051 D = 0.019 r = −0.71		ND = 0.099 D = 0.019 r=0.61		ND = 0.059 D = 0.029 r = 0.46
Neutral	ND = −2.87 D = −6.87 r = 0.45	ND = −0.030 D = −0.070 r = 0.58		ND =−0.010 D = 0.040 r = −0.60
Flexion		ND =−0.019 D = −0.069 r = 0.48

	Max Axial			Max Radial			Max Shear
Loadinq	AAF	NP	PAF	AAF	NP	PAF	AAF	NP	PAF
Extension	ND = 0.055 D = 0.015 r = 0.46			ND =−0.043 D = 0.127 r = −0.69
Neutral		ND = 0.035 D = −0.015 r = 0.59	ND = 0.032 D = −0.028 r=0.47				ND = 0.061 D = 0.131 r = −0.53
Flexion						ND = 0.014 D = 0.114 r = −0.55

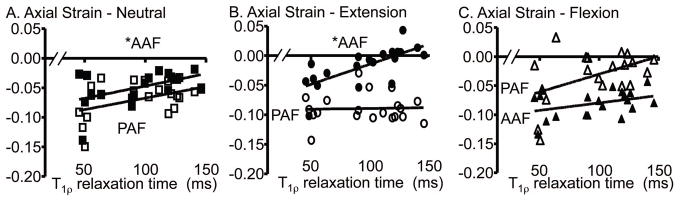
In the neutral position, the average axial strains in the anterior AF and NP were more compressive with degeneration (Fig. 8A; Table). The posterior AF followed the same pattern as the anterior AF; however, strains were not significantly correlated with degeneration (p > 0.2). The maximum axial strain correlated with degeneration in the posterior AF and the NP and was tensile in nondegenerate discs (Table).

Figure 8.

Average axial strain in the anterior AF (AAF – filled) and posterior AF (PAF – open) in the A) neutral, B) extension, and C) flexion position. * p < 0.05.

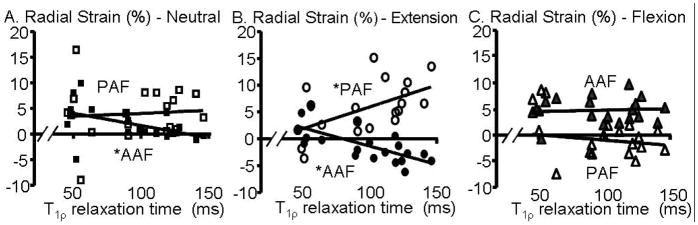
The average radial strain in the anterior AF was significantly correlated with degeneration (Fig. 9A); from slightly compressive in nondegenerate discs (−0.01) to tensile in degenerate discs (0.04; p < 0.01). The radial strain in the posterior AF and NP was not correlated with degeneration and was tensile across all levels of degeneration.

Figure 9.

Average radial strain in the anterior AF (AAF – filled) and posterior AF (PAF – open) in the A) neutral and B) extension, and C) flexion position. * p < 0.05.

In the extension position, the average axial strains in the anterior AF and NP were more compressive with degeneration with the axial strain being tensile in nondegenerate discs (0.023 at T_1ρ = 150 ms; Fig. 8B). Unlike the neutral position, the average axial strain of the posterior AF in the extension position did not follow the same pattern as the anterior AF, and the strain was highly compressive across all degeneration levels. In the flexion position, the AF axial strain was not correlated with degeneration (Fig. 8C; Table), although the patterns were similar to neutral (Fig. 8A). Similar to the extension and neutral positions, the average axial strains in the NP were more compressive with degeneration (Table).

The average radial strain in the extension position correlated with degeneration in the anterior AF (i.e. the opposite side of the loading position), where the radial strains were more tensile in degenerate discs (p < 0.01; Fig. 9B; Table). However, the posterior AF had the opposite effect and was less tensile with degeneration (p < 0.01; Fig. 9B). In the flexion position (Fig. 9C), the average radial strain did not correlate with degeneration. Only two correlations of maximum radial strain with degeneration were found: for the AF region on the opposition side of the loading position (i.e. anterior AF in the extension position), where the maximum radial strain was more tensile with degeneration (Table). For the NP, unlike the axial strain, the average and maximum radial strain in the NP was not correlated with degeneration for any loading position.

The average and maximum shear strains were 0.033 and 0.086, respectively (pooled for all regions and loading positions, n = 177). The only correlation of average shear strain with degeneration was a decrease in NP shear strain in extension, and these changes were quite small (Table). Similarly, only one condition existed in which the maximum shear strain correlated with degeneration (Table). In the neutral position, the anterior AF maximum shear strain was about 2.5X higher with degeneration from 0.061 in nondegenerate discs to 0.131 in degenerate discs.

Discussion

2D internal displacement and strain in human lumbar motion segments were calculated non-invasively using MR images of samples compressively loaded in the flexion, neutral, and extension positions. The axial compressive load of 1000 N (~1.2× body weight) corresponds to moderate physiological stresses.³⁴ While most of our measurements are the first available, the disc height loss (0.4–0.9 mm), the outer AF radial displacement (0.5 – 0.6 mm), and the normalized change in disc height (~4.5%) were similar to previous observations.^{10,13,14,20,35} The maximum shear strains (~0.09) are comparable to the maximum shear strains previously observed in the mid-transverse plane (0.05–0.14).⁴ The increase in NP compressive axial strain suggests that NP stiffness decreases with degeneration, which is consistent with the 55% decrease in the aggregate modulus observed from tissue testing.³⁶

Our results suggest that the strains in the posterior AF are high for all loading positions, regardless of degeneration level. While strains generally increased with degeneration, the posterior AF strain was not correlated with degeneration in several cases (e.g., axial strain in extension, radial strain in the neutral position (Figs. 8B & 9A; Table). Interestingly, in these cases, the strain was large for both nondegenerate and degenerated discs. Furthermore, the posterior AF exhibited higher compressive strains and higher tensile radial strains than the anterior and lateral AF. These findings may have physiological importance. First, the large strain in the posterior AF is likely a reason for the observed failure in that region – large strains sustained over the lifetime of the disc may lead to fatigue failure.^37–39 However, the absolute strain in vivo would be different due to the absence of posterior facets, which carry some of the loads. Second, it appears that NP pressure has a minimal effect on posterior AF strain, as the reduced NP pressure with degeneration did not alter these strains. In flexion, the NP moves towards the posterior,⁵ which may partially support load in this region and decrease strain. However, mechanical and structural features that tend to increase strain in the posterior AF include its lower circumferential tensile moduli^40,41 and thinner and less organized lamellae compared to the anterior AF.⁴² These factors and the observed higher strain magnitude may contribute to initiation or propagation of radial tears, leading to NP herniation.

Loading position affected both displacements and strains. This is important, as posture during lifting can be directly correlated to these positions.¹² However, the effect of loading position on strain was evaluated with different reference states, as the wedge was placed before acquiring the undeformed image. Therefore, these comparisons represent the effect of axial compression under different postures and not bending from neutral. The side of applied bending (e.g., anterior AF in flexion) had higher tensile radial strains and compressive axial strains (Figs. 4 & 6). Interestingly, in nondegnerate discs, the opposite side of bending exhibited tensile axial strains even though the disc was loaded under axial compression (Fig. 8). In flexion and extension, the inner AF radial bulge was lower than in neutral (Fig. 5), and the altered displacements likely directly affected the internal strains. The hydrated disc functions as a highly pressurized vessel,⁴³ and our results suggest that bending stresses are transferred to the opposite side of the disc through the pressurized NP.

We observed, that in most regions and loading positions, AF axial and radial strains were significantly correlated with degeneration, consistent with our hypothesis. In particular, in the anterior AF, axial strain was more compressive and radial strain more tensile with degeneration in the neutral and extension positions. These changes are consistent with a smaller disc height and reduced NP pressure in degeneration,^44–46 placing more of the applied compression directly onto the AF and thereby increasing strain. The radial strain was expected to become more tensile as reduced NP pressure places less radial constraint on the inner AF. These observations suggest that the ability of the NP to transfer compressive loads is diminished with degeneration, placing more of the compression directly onto the AF.

One advantage of our study was the use of T_1ρ relaxation time as a quantitative degeneration scale, which permits a statistically rigorous consideration of the effect of degeneration on internal disc mechanics. The T_1ρ relaxation time in the NP has a strong correlation to glycosaminoglycan content.29 Its use is not widespread, so comparison across studies may be limited; however, the relationship between T_1ρ relaxation time and the degenerative grade (Fig. 1) can be used for comparisons.

Our study has limitations, some of which were addressed previously (e.g., water movement through the image slice).¹⁰ The applied bending conditions were limited by the addition of a wedge prior to the preload, rather than a pure moment. Therefore, the bending applied here is equivalent to lifting a weight in the flexed or extended position rather than moving from neutral to flexion or extension. The applied loading conditions and 2D imaging at symmetry planes were selected so that the tissue remained within the imaging plane for both the unloaded and loaded image. Future 3D imaging will allow for more complete 3D strain analysis. The constrained loading fixture did not permit coupled motion, which may have increased internal stresses; however, this effect was likely low in the absence of facet joints. A 1000N compressive load was applied, which corresponds to an average applied stress of 0.50 ± 0.09 MPa. This stress range is responsible for some of the variability in the displacements and strains. For example, the variability in axial deformation in the neutral position was 45% (standard deviation divided by the mean); however, normalizing the deformation by the applied axial stress (1000 N/cross-sectional area) reduced the variability to 30%. Also, our loading deviates from in vivo conditions in two important ways: 1) the preload at which the reference image is acquired is low, which maximizes strain, and 2) the facet joints are missing, which transfers the entire load through the disc. As these effects were consistently applied to all conditions, the comparisons and findings are valid, though the absolute strains will not match in vivo strain magnitudes.

In conclusion, this study evaluated the effect of AF region and degeneration on internal disc deformation under physiological levels of compression in neutral, flexion, and extension positions. The posterior AF experienced higher tensile radial and compressive axial strains than the other regions, which may be a result of, or a cause for, radial tears and circumferential delamination.³⁹ The changes in AF deformations under load suggest that the load distribution mechanisms through the disc subcomponents are greatly dependent on loading position. The increase in the compressive axial strain and tensile radial strain with degeneration suggest that the load distribution mechanisms are altered, likely due to the depressurization of the NP placing more of the applied load directly to the AF. The posterior AF strain was not always correlated with degeneration, suggesting this tissue undergoes high strains throughout life, which may predispose it to failure. In addition to understanding disc internal mechanics, this study provides new data into the changes in internal disc strain with degeneration, useful data for validation of finite element models, and provides a technique and baseline data for evaluating surgical treatment, such as discectomy or implants.

Supplementary Material

Supp Fig S1. S – Figure 2.

Representative axial (1^st row), radial (2^nd row), and shear (3^rd row) strain maps of three samples under the flexion (1^st column), neutral (2^nd column), and extension (3^rd column) loading positions. The anterior AF is on the left side of each image.

Supp Fig S2. S – Figure 7.

Correlation of axial deformation with degeneration in the A) neutral, B) flexion, and C) extension loading positions. * denotes significance, p < 0.05.