Influence of Anterior Segment Power on the Scan Path and RNFL Thickness Using SD-OCT

Abstract

Purpose.

Retinal nerve fiber layer (RNFL) thickness measures with spectral domain-optical coherence tomography (SD-OCT) provide important information on the health of the optic nerve. As with most retinal imaging technologies, ocular magnification characteristics of the eye must be considered for accurate analysis. While effects of axial length have been reported, the effects of anterior segment optical power on RNFL thickness measures have not been described fully to our knowledge. The purpose of our study was to determine the influence of the optical power change at the anterior corneal surface, using contact lenses, on the location of the scan path and measurements of RNFL thickness in normal healthy eyes.

Methods.

We recruited 15 normal subjects with less than 6 diopters (D) of ametropia and no ocular pathology. One eye of each subject was selected randomly for scanning. Baseline SD-OCT scans included raster cubes centered on the optic nerve and macula, and a standard 12-degree diameter RNFL scan. Standard 12-degree RNFL scans were repeated with 10 separate contact lenses, (Proclear daily, Omafilcon A/60%) ranging from +8 to −12 D in 2-D steps. The extent of the retinal scan, and RNFL thickness and area measures were quantified using custom MATLAB programs that included ocular biometry measures (IOL Master).

Results.

RNFL thickness decreased (0.52 μm/D, r = −0.33, P < 0.01) and the retinal region scanned increased (0.52%/D, r = 0.97, P < 0.01) with increase in contact lens power (−12 to +8). The normalized/percentage rates of change of RNFL thickness (−0.11/mm, r = −0.67, P < 0.01) and image size (0.11/mm, r = 0.96, P < 0.01) were related to axial length. Changes in the retinal region scanned were in agreement with transverse scaling, computed with a three surface schematic eye (R² = 0.97, P < 0.01). RNFL area measures, that incorporated the computed transverse scaling, were not related significantly to contact lens power (863 μm²/D, r = 0.06, P = 0.47).

Conclusions.

Measurements of RNFL thickness by SD-OCT are dependent on the optics of the eye, including anterior segment power and axial length. The relationships between RNFL thickness measures and optical power are a direct reflection of scan path location with respect to the optic nerve head rim, caused by relative magnification. An incorporation of transverse scaling to RNFL area measures, based on individualized ocular biometry, eliminated the magnification effect.

Measurements of RNFL thickness by SD-OCT are dependent on the optics of the eye, including both anterior segment power and axial length. An incorporation of transverse scaling to RNFL area measures, eliminated the magnification effect.

Introduction

Glaucoma consists of a group of progressive optic neuropathies that are characterized by losses of retinal ganglion cells (RGC) and associated visual field defects. An evaluation of the retinal nerve fiber layer (RNFL), which contains axons of RGCs, provides valuable information for the management of patients with glaucoma.^1,2 Traditionally, RNFL defects have been assessed by subjective methods (ophthalmoscopy and fundus photographs),^3,4 but recently, objective measurements have become more common. For example, noninvasive, in vivo imaging technologies, such as optical coherence tomography (OCT) can be used to quantify thicknesses of retinal layers.⁵ The recent advance in this technology, spectral domain OCT (SD-OCT), captures images at higher frequencies with theoretical axial resolutions approaching 4 μm.^6–9 The standard SD-OCT scan used for evaluation of the RNFL is a circular scan, 12 degrees in diameter (nominally 3.47 mm), centered on the optic nerve head (ONH).^10,11 Thickness measures from these scans generally are presented as a continuous thickness plot following a scan path that starts on the temporal side of the ONH and progresses to the superior, nasal, inferior, and back to temporal (TSNIT plot) side, with the data presented as global and sector average RNFL thicknesses.

RNFL thickness measures with OCT technology generally are repeatable, in normal and glaucomatous eyes, with a test-retest variability of 4 to 8 μm.^12–16 However, several considerations are important in the acquisition and analyses of RNFL thickness. For example, to obtain precise and accurate measures, scans should be acquired through dilated pupils,¹⁷ be well centered on the ONH^18,19 and have a high signal-to-noise ratio.^20,21 In addition, factors, such as age,^22–24 refractive error,^25–27 and axial length,^22,28 must be taken into consideration when comparing to a normative database or evaluating variability between individuals. In general, eyes that are older, myopic or longer have thinner RNFL measures.

The systematic decrease in RNFL thickness with age is supported by histologic analysis of RGC somas²⁹ within the inner retina and axonal counts within the optic nerve.^30,31 In contrast, thinner RNFL measures in longer myopic eyes do not correspond to a decrease in neuronal content, but are thought to be a result of optical magnification. Specifically, the extent of the retinal region scanned is related to the optics of the instrument and biometry of the eye scanned.³² Hence, in longer eyes, a 12-degree circular scan path is further from the center of the optic nerve and its rim margin, where the RNFL also is thinner.^33,34 Therefore, the decrease in thickness within the peripapillary region does not reflect a change in axonal content, but rather a change in axonal density in the region.³⁵

To compensate for magnification factors, a modified Littmann formula (t = p.q.s) is used commonly to rescale RNFL thickness measures.^36,37 Using this methodology, an estimate of the RNFL thickness (t) for a 3.47 mm scan diameter can be computed from the magnification characteristics of the imaging system (P), the measured RNFL thickness using the standard scan (s), and a magnification factor (q) of the eye that incorporates axial length (q = 0.01306 × [Axial Length – 1.82]).^36,37 These methods have been used successfully to rescale RNFL thickness measures, with the assumption that the axonal content of the RNFL remains constant in the peripapillary region.^27,28,38 Although useful, the application of Littmann's formula only incorporates axial length in determining the magnification factor of the eye, assuming a constant for the position of the eye's second principal point (AP').³⁶ Hence, the method does not consider individual differences in anterior segment optics, which may be important especially for accurate measurements of RNFL thickness in patients who have had refractive and/or cataract surgery.

The influence of anterior segment power on RNFL thickness has been investigated by fitting subjects with varying powers of soft contact lenses. Although a significant relationship was not found with time domain-OCT (TD-OCT),³⁹ RNFL thickness was shown to be related to the induced refractive error for higher resolution SD-OCT⁴⁰ systems. The general relationship between RNFL thickness and refractive error was similar to that with axial length. However, an optical basis for these findings was not determined. Therefore, in the present investigation of optical scaling, the anterior segment components contributing to optical power, including corneal curvature, anterior chamber depth, and crystalline lens parameters, were included, in addition to axial length, in deriving RNFL measures from the analysis of SD-OCT images.⁴¹ Specifically, a three-surface schematic eye⁴² was used to quantify changes in the optical power of the anterior segment induced by soft contact lenses, and its influence on SD-OCT RNFL scan path length and thickness measures. Some of the results of these studies have been presented in abstract form (Patel NB, et al. IOVS 2012;53:ARVO E-Abstract 681).

Methods

Subjects

We recruited for this study 15 subjects with no history of ocular pathology. All subjects were either students or staff at the University of Houston. The study adhered to the tenets of the Declaration of Helsinki, and all aspects of the study were reviewed by the Committee for Protection of Human Subjects at the University of Houston. Before collection of data, informed consent was obtained from all subjects.

Subjects were screened using a brief medical history, autorefraction, visual acuity assessment, intraocular pressure measures, slit-lamp examination, and a dilated fundus examination to ensure good ocular health. One eye of each subject was selected randomly for data collection. To ensure a uniform focal plane and to avoid exceeding the focus range of the imaging system, only eyes with refractive errors of less than 1 diopter (D) of astigmatism and 6 D of ametropia were included.

OCT

Data were collected 30 minutes after instillation of 1% tropicamide and 2.5% phenylephrine. Baseline SD-OCT scans with the Spectralis HRA+OCT (Software version 5.3.2; Heidelberg Engineering, Heidelberg, Germany) included a 97 line raster volume scan, 20 × 20 degrees centered on the optic nerve; a 49 line raster volume scan, 20 × 20 degrees centered on the fovea; and a standard 12-degree circular scan centered on the optic nerve. Scans were acquired with eye tracking, and averaging set at 16 frames for raster scans and 40 frames for circular scans. The infrared scanning laser ophthalmoscope (IR SLO) scan angle was set at 30 degrees for all scans acquired. Scans were repeated if image overlap was noted during averaging or if the image quality was <25 dB. If scan quality was reduced due to ocular surface dryness, they were repeated at least two minutes after instilling a drop of artificial tears.

A series of 10 soft contact lenses (Proclear Daily, omafilcon A/60%; CooperVision Inc., Trumbull, CT) ranging in power from +8 to −12 D, were used to change the dioptric power of the anterior segment. To ensure adequate fit, each lens was allowed to settle on the eye for a minimum of 5 minutes and examined with slit-lamp biomicroscopy. In addition, the refractive change induced by the contact lens was assessed by autorefraction, and the SD-OCT scan focus setting. With each contact lens, a 12-degree circular RNFL scan was acquired using settings identical to those at baseline, except for the scan focus, which was adjusted to achieve a sharp fundus image. As the objective was to evaluate changes in ocular magnification, repeat /follow-up scans, that incorporate image registration, were not acquired. Instead, successive scans were centered best using landmarks within the ONH. To assess RNFL thickness repeatability, the last scan acquired was a standard RNFL scan without any contact lens. All scan data were exported in raw (“.vol”) files and analyzed using custom MATLAB (The Mathworks Inc., Natwick, MA) programs.

Ocular Biometry and Scaling

Ocular biometry, including corneal curvature, anterior chamber depth and axial length, were measured at baseline, without contact lenses, using a non-contact optical biometer (IOL Master; Carl Zeiss Meditec Inc., Dublin, CA). For scans acquired with contact lenses, the power adjustment was made by changing the radius of the anterior corneal surface. Crystalline lens parameters, including thickness and curvature, were interpolated from normative data.⁴³ The refractive indexes of the cornea, aqueous humor, and vitreous humor were adjusted for the central wavelength (870 nm) of the SD-OCT superluminescent diode.⁴⁴ Refractive index of the lens was computed with a ray tracing algorithm using the biometry and refractive data, assuming homogeneous and spherical refractive surfaces. Using these parameters a three-surface schematic eye, as described by Bennett and Rabbetts,^42,45,46 was constructed for each scan using a custom MATLAB program. Lateral or transverse scaling (μm/deg) was calculated from the second nodal point of the schematic eye, assuming a spherical retinal surface. Because axial scaling is dependent on the SD-OCT imaging system and illumination source characteristics, adjustments were not made for the different contact lenses used.

Scaling Validation

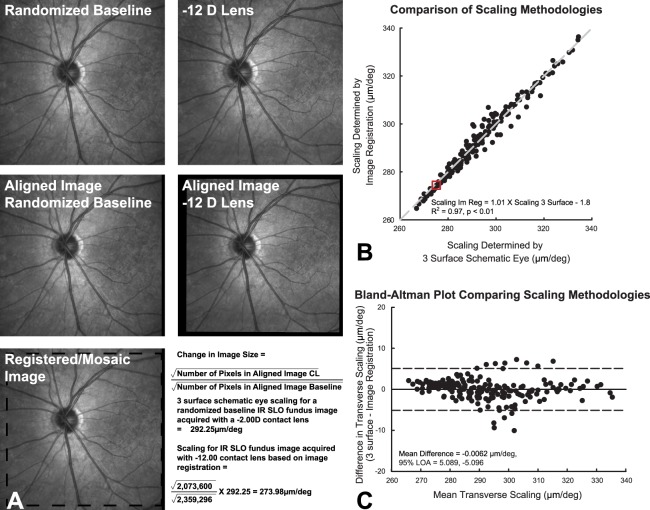
The schematic eye scaling methodology was validated with corresponding changes in retinal image size. To reduce bias, a custom automated MATLAB program was used to select randomly one of the 12 RNFL scans from each subject as a reference. The transverse scaling then was determined for this reference scan using the schematic eye paradigm. Subsequently, for each of the 12 scans in the series, the 30-degree scanning laser ophthalmoscope (SLO) fundus image was extracted from the raw data (“.vol” files) and registered to the reference fundus image using a generalized dual bootstrap, iterative closest point algorithm (i2k retina; DualAlign, LLC, Clifton, NY).⁴⁷ The resultant aligned images were used to compute a predicted/registered image scaling. Specifically, for each aligned image, the number of pixels corresponding to the fundus image was determined first (number of non-zero or black pixels). Assuming symmetrical retinal magnification the square root of the sum of “fundus pixels” in each image was used to determine the length of the aligned image in pixels. Subsequently, the lengths of the registered images, then were used to compute a predicted/registered image scaling for each scan (Equation 1, Fig. 1A).

This predicted/registered image scaling then was compared to the computed scaling. Overall, there was good agreement between retinal scaling computed using image registration and that computed using a schematic eye (Scaling_{Im Reg} = 1.01 × Scaling_{3 surface} − 1.8, R² = 0.97, Fig. 1B). A Bland-Altman analysis demonstrated a mean difference of −0.006 μm/deg, and 95% limits of agreement between −5.11 and 5.10 μm/deg. For all data analysis, the transverse retinal scaling was calculated using a schematic eye model.

Figure 1.  .

(A) For each subject all 30 degree IR SLO images from RNFL scans were registered to a baseline scan that was selected at random. As demonstrated in this example, the square root of the number of pixels for each aligned image was used to determine the scaling of each scan based on the baseline. (B) This plot illustrates the agreement between scaling determined by image registration and that computed using a three-surface schematic eye. The data point in the center of the red box is from the example shown in (A). (C) The limits of agreement determined by the 95% CI of the mean difference for retinal scaling using a schematic eye and image registration.

RNFL Segmentation and Analysis

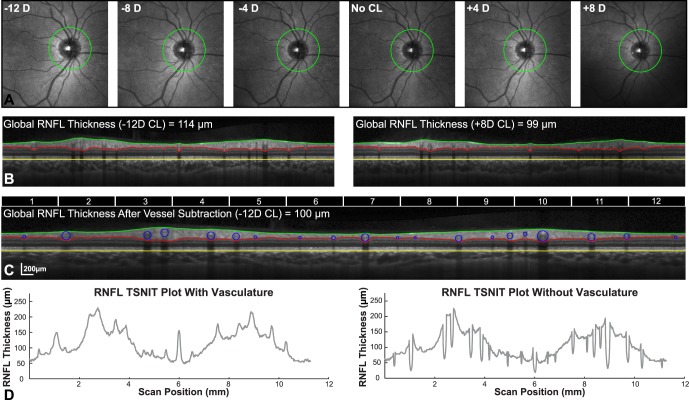
RNFL B-scans were randomized, and a custom segmentation algorithm^45,46 was used to identify the inner limiting membrane and junction between the RNFL and RGC layer. In brief, B-scan images (1536 × 496 pixels) first were de-noised using a Haar 2D stationary wavelet and convolved with a Gaussian filter (SD = 4). An iterative process then was used to identify intensity changes, corresponding to the layers of interest, within the signal profile of each A-scan. Any errors in layer identification, most commonly around shadows of major retinal vasculature, were corrected manually. To account for the nonneural retinal vasculature, B-scans first were rescaled to a 1:1 aspect ratio using the computed transverse scaling. The diameter of each major retinal vessel was determined from the corresponding shadows cast on the underlying retina (Mardin CY, et al. IOVS 2009;50: ARVO E-Abstract 3333). The center of each vessel was marked manually, and a circular region matching that of the vessel was subtracted from the RNFL thickness (Figs. 2C, 2D). RNFL thickness measures were transformed to area by multiplying the thickness for each A-scan by its calculated width. Although the SD-OCT instrument used aligns scans to the fovea, it is dependent on accurate fixation. In addition, as repeat scans were not acquired, it is possible that the alignment would be different, especially with change in magnification. Hence for improved accuracy, before calculating global, quadrant, and 30-degree sector (Fig. 2C) thickness and area measures, the start of the TSNIT plot was shifted to align with a line passing from the center of the circular scan to the anatomic center of the foveal pit (Fig. 3A). Methods used for identification of the fovea center, registration, and alignment of the TSNIT plot have been described previously.⁴⁶ In brief, the center of the fovea was identified using the total retinal thickness map of the macula cube scan. The general location of the pit was determined as the central region with thinnest retina. The center of the pit then was established as the center of concentric circles fit to iso-thicknesses planes at varying depths in this central region. The IR SLO images from the RNFL and macula scans then were registered and a reference line was fit from the center of the circular scan to the foveal pit center.

Figure 2.  .

(A) 30-degree IR-SLO fundus images with RNFL scan path illustrate an increase in retinal region scanned with increase in contact lens power. (B) The OCT B-scans acquired with a −12 D and +8 D contact lens demonstrate the change in RNFL thickness associated with scan path. (C) Retinal vasculature was subtracted from the RNFL thickness after scans were rescaled to a 1:1 aspect ratio. Top portion of the figure illustrates the 30-degree sectors used for data analysis. The 12 sectors illustrated are those used, 30-degree sectors used for data analysis are illustrated in (D). Resulting TSNIT plots with and without vasculature were used to compute average thickness and area measures.

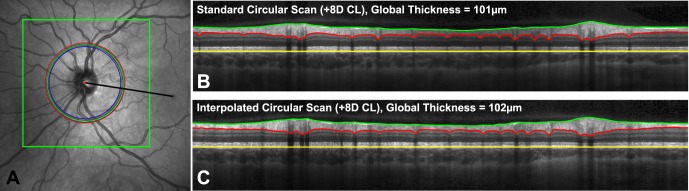
Figure 3.  .

(A) RNFL scan paths, acquired with contact lenses and at baseline, registered to the baseline 97 line raster scan (boxed region) centered on the optic nerve. The scan paths illustrated in blue, green, and red correspond to scans with a −12 D contact lens, no contact lens, and a +8 D contact lens. Black line: indicates the mean location for the line connecting the center of the optic nerve to the fovea to which TSNIT plots were aligned. (B, C) Illustrate the resultant OCT B-scans for the standard and interpolated scan with a +8 D contact lens.

Scan Path and RNFL Thickness

To investigate the relationship between scan path and RNFL thickness, paths identical to those of circular scans with contact lenses were interpolated from the baseline raster volume scan centered on the optic nerve head for each subject. The IR SLO, B-scans, and scan path locations all were extracted from raw export files (*.vol). The scan location for raster scans and RNFL scans, which are exported in mm, were converted to pixels using the instrument scaling. The IR SLO image and scan path for each RNFL scan then were registered to the IR SLO image of the baseline raster volume (Fig. 3A) using a generalized dual bootstrap, iterative closest point algorithm (i2k retina; DualAlign).⁴⁷ The image transformation was applied to the circular scan path and superimposed on the baseline raster ONH scan. Using this registered scan path, an RNFL B-scan then was constructed using bilinear interpolation from the raster volume OCT data (Fig. 3C). The resultant scans were segmented and analyzed using the same protocol as for the standard scan. To avoid bias, images were imported randomly into the program, and the user was unable to view the results of the registration process, or scan parameters used.

Results

Of the 15 subjects (mean age 24.5 ± 2.5 years) recruited, nine right eyes and six left eyes were used for data collection. All eyes were healthy as determined by best corrected visual acuity, slit-lamp biomicroscopy, intraocular pressures, and indirect ophthalmoscopy. The spherical equivalent refractive errors (range +0.62 to −5.12 D) and axial lengths (range 23.41– 26.09 mm) were distributed normally (Shapiro-Wilk, P > 0.2).

Global RNFL thickness measures without contact lenses at baseline measured 111.4 ± 9.0 μm. On repeat scan, approximately 2 hours after baseline, global RNFL thickness measured 111.1 ± 9.6 μm. The measurement error, or within subject standard deviation (S_w), was 1.19 μm. Based on this measurement error, 95% of global thickness measures should be within 1.96 × S_w (2.33 μm) of the mean. Similarly, the repeatability, or difference between any two measures is not expected to exceed √2 × 1.96 × S_w (3.31 μm) in 95% of measures.⁴⁸ Major retinal vascular contribution was 12.6 ± 1.7 μm accounting for 11.4 ± 1.6% of the global RNFL thickness. The repeatability for vascular contribution was 2.02 μm (S_w = 0.72 μm) or 1.7% of global RNFL thickness.

RNFL Thickness with Major Retinal Vasculature

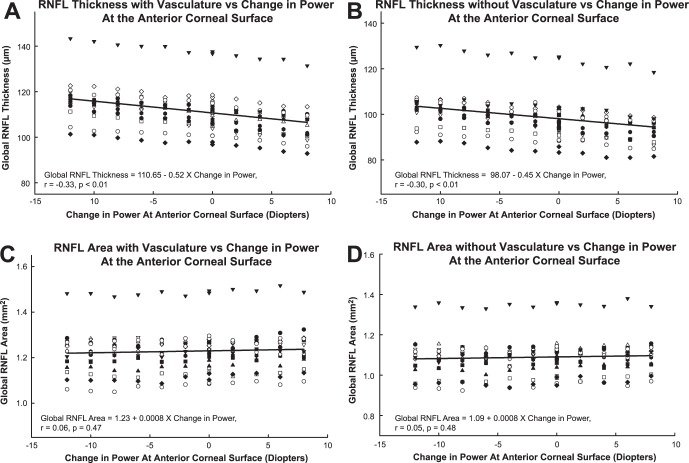
The contact lenses were effective at inducing a power change at the corneal surface as determined by autorefraction (slope −0.94, R² = 0.99, P < 0.01) and SD-OCT scan focus (slope −0.95, R² = 0.99, P < 0.01). The mean scan quality was 35.3 ± 3.2 dB, and was not significantly different for scans with and without contact lenses (P = 0.33). In addition, scan quality was not related to contact lens power (P = 0.6) or RNFL thickness (P = 0.3). Overall, the global RNFL thickness decreased linearly with increase in power (Fig. 4A, slope −0.52, 95% confidence interval [CI] −0.74 to −0.30, P < 0.01). One subject (inverted filled triangles, Fig. 4A) had significantly thicker RNFL measures, but followed trends similar to the rest of the subjects, and had no detectable pathology on ophthalmoscopic examination and visual field testing. Hence, this subject was not excluded from data analyses.

Figure 4.  .

RNFL thickness and area as a function of the nominal power of the contact lens worn during the measurement. Global RNFL thickness with standard 12-degree circular scans decrease with increasing dioptric power at the anterior corneal surface, with (A) and without (B) major retinal vasculature removal. However, there is no significant change in Global RNFL area (C, D). The different symbols represent individual subjects.

Repeated measures ANOVA with Greenhouse-Geisser correction demonstrated statistically significant differences for global, quadrant. and sector RNFL thickness measures for the range of contact lenses used (global thickness, RMANOVA F[3.9, 55.9] = 82.4, P < 0.001, Table 1). For global RNFL thickness, post hoc paired t-tests using an adjust P value of 0.004 for multiple comparisons, revealed a significant difference for contact lenses equal to or greater than +2 D and less than −4 D (Table 2). Based on the test retest repeatability for well centered scans (3.31 μm), thickness measures were significantly different for changes in anterior surface corneal power of greater than 6 D.

Table 1.  .

Mean Global and Sector RNFL Thickness Measures with Each Contact Lens

	Change in Anterior Segment Power												Test Retest	RM- ANOVA
	–12	–10	–8	–6	–4	–2	Plano	Plano	2	4	6	8
Global	116.8 ± 9.4	115.3 ± 9.6	114.6 ± 9.4	113.5 ± 9.3	112.3 ± 9.4	111.8 ± 9.0	111.4 ± 9.0	111.1 ± 9.6	109.3 ± 9.5	108.4 ± 9.0	107.0 ± 9.7	106.0 ± 8.8	3.3	<0.001
Temporal	83.8 ± 8.5	82.2 ± 8.9	81.8 ± 9.7	82.0 ± 9.0	81.4 ± 9.6	80.7 ± 8.4	80.6 ± 8.4	79.9 ± 9.1	79.9 ± 8.6	79.4 ± 8.6	78.5 ± 9.9	78.4 ± 8.7	4.7	<0.001
Superior	141.2 ± 15.9	138.9 ± 16.6	137.9 ± 16.4	136.6 ± 15.6	134.5 ± 15.4	134.0 ± 14.7	133.1 ± 14.5	133.4 ± 15.3	130.9 ± 15.2	129.2 ± 13.8	127.8 ± 14.6	126.4 ± 14.0	6.1	<0.001
Nasal	92.6 ± 13.7	92.6 ± 13.8	91.7 ± 13.1	90.2 ± 14.4	89.6 ± 13.4	90.2 ± 14.1	89.3 ± 13.2	89.3 ± 14.4	86.7 ± 14.5	86.4 ± 13.6	84.6 ± 13.2	83.5 ± 13.4	7.3	<0.001
Inferior	150.0 ± 13.3	147.9 ± 12.9	147.2 ± 13.6	145.3 ± 13.0	144.0 ± 13.2	142.7 ± 12.6	142.9 ± 13.2	142.0 ± 12.9	139.7 ± 12.7	139.1 ± 11.9	137.5 ± 12.1	135.8 ± 11.7	7.5	<0.001
S1	81.3 ± 10.6	79.6 ± 10.6	79.5 ± 11.3	79.4 ± 11.0	80.3 ± 10.6	79.5 ± 10.0	80.0 ± 10.5	78.6 ± 10.9	79.63 ± 10.2	77.9 ± 9.3	77.1 ± 10.36	77.9 ± 9.5	8	0.036
S2	119.2 ± 21.2	117.4 ± 21.9	115.7 ± 21.5	115.8 ± 21.8	115.5 ± 22.1	136.6 ± 21.6	114.7 ± 21.2	113.4 ± 20.9	113.2 ± 22.3	111.1 ± 21.2	110.7 ± 21.2	110.7 ± 19.8	6.7	<0.001
S3	168.6 ± 16.7	165.3 ± 16.8	164.5 ± 16.6	163.5 ± 17.2	161.0 ± 17.0	160.1 ± 16.4	159.1 ± 16.0	159.9 ± 17.4	157.6 ± 16.9	155.8 ± 16.0	154.6 ± 17.5	153.5 ± 17.6	10	<0.001
S4	124.6 ± 26.4	122.7 ± 27.4	121.3 ± 25.8	120.4 ± 24.6	117.3 ± 23.2	117.2 ± 22.2	116.2 ± 21.1	117.3 ± 22.4	113.9 ± 22.2	112.4 ± 19.9	109.9 ± 20.3	108.1 ± 20.3	9.2	<0.001
S5	127.3 ± 25.8	126.1 ± 24.8	124.7 ± 25.5	122.3 ± 26.2	121.6 ± 24.9	122.5 ± 23.8	119.3 ± 24.1	119.6 ± 23.9	116.8 ± 21.6	115.2 ± 23.3	112.7 ± 22.6	111.4 ± 23.8	11	<0.001
S6	91.8 ± 14.1	91.9 ± 14.3	91.2 ± 13.9	89.7 ± 14.8	89.5 ± 15.5	90.0 ± 16.7	89.9 ± 14.2	89.5 ± 15.0	86.4 ± 16.0	86.7 ± 14.4	85.3 ± 14.1	84.2 ± 15.0	10	<0.001
S7	73.9 ± 10.8	74.0 ± 11.4	73.8 ± 11.0	72.7 ± 12.8	71.9 ± 10.8	72.5 ± 11.8	72.7 ± 10.6	72.3 ± 11.6	70.6 ± 12.2	70.3 ± 11.9	69.1 ± 12.0	68.1 ± 11.6	6.2	<0.001
S8	107.7 ± 19.1	107.1 ± 18.5	107.0 ± 18.0	104.3 ± 18.6	103.4 ± 18.4	103.8 ± 18.2	102.1 ± 18.2	102.1 ± 18.6	98.1 ± 19.1	98.0 ± 17.8	95.5 ± 17.7	93.8 ± 17.5	7.9	<0.001
S9	136.8 ± 17.4	134.2 ± 17.6	134.4 ± 18.4	130.9 ± 18.2	130.3 ± 19.5	129.2 ± 17.2	128.7 ± 17.4	127.9 ± 19.3	126.7 ± 18.4	124.6 ± 16.9	123.0 ± 17.1	120.7 ± 17.6	15	<0.001
S10	182.1 ± 17.2	180.0 ± 16.5	177.3 ± 18.2	176.9 ± 17.2	174.8 ± 17.9	173.4 ± 18.3	174.4 ± 19.3	172.8 ± 18.4	169.5 ± 18.0	170.6 ± 16.2	168.3 ± 17.0	166.5 ± 17.4	12	<0.001
S11	121.8 ± 22.8	120.1 ± 24.3	120.3 ± 24.8	120.6 ± 23.3	118.9 ± 24.7	116.0 ± 23.6	117.3 ± 23.2	118.0 ± 23.8	117.2 ± 23.0	116.7 ± 23.8	116.0 ± 24.5	115.8 ± 24.7	8.4	<0.001
S12	66.8 ± 7.7	65.5 ± 7.5	65.1 ± 9.4	64.9 ± 6.7	63.2 ± 7.6	63.7 ± 7.1	62.1 ± 7.8	61.5 ± 7.7	61.6 ± 6.6	62.0 ± 7.2	62.0 ± 8.7	60.6 ± 7.8	6.5	<0.001
Vessel	13.3 ± 1.9	13.1 ± 1.3	12.8 ± 1.4	13.2 ± 1.3	13.0 ± 1.6	12.7 ± 1.6	12.6 ± 1.7	12.8 ± 1.6	12.0 ± 1.8	12.5 ± 1.6	12.3 ± 1.3	11.9 ± 1.6	2	0.001

Test-retest/repeatability measures are calculated using thickness data with no contact lenses. Significant changes in thickness were noted for each measure as indicated by repeated measures ANOVA. S1–S12 correspond to the 30-degree sectors illustrated in Figure 2C.

Table 2.  .

Mean Differences of Global RNFL Measures Compared to Baseline Scans without Any Lens

Contact Lens Power	Mean Difference (μm)	Std. Deviation (μm)	Paired t-Test, P Value
−12	5.69	2.18	<0.001
−10	4.35	1.99	<0.001
−8	3.67	1.82	<0.001
−6	2.49	1.94	<0.001
−4	1.47	1.45	0.001
−2	0.68	1.08	0.029
No lens	−0.17	0.88	0.453
2	−1.74	0.89	<0.001
4	−2.64	1.15	<0.001
6	−3.75	1.39	<0.001
8	−4.95	1.34	<0.001

Major Retinal Vascular Contribution

The RNFL thickness after removal of major retinal vasculature measured 98.5 ± 9.1 μm (S_w = 0.87 μm) without any contact lens, and decreased at a rate of 0.46 μm (95% CI, −0.67 to −0.24, P < 0.01, Fig. 4B) per diopter increase in contact lens power. Overall, the slopes for RNFL thickness change with and without retinal vasculature were not significantly different (P = 0.69). However, there was a slight, but statistically significant, decrease in the major retinal vascular thickness contribution with increase in dioptric power (slope −0.06 μm/D, R² = 0.06, P = 0.001, Table 3). The mean, maximum thickness change in vascular contribution was 1.4 μm, and less than the test-retest variability. Subsequently, the percent vascular contribution to the RNFL across the range of contact lens powers was not significantly different (RMANOVA, F[6.3, 88] = 0.965, P = 0.46).

Table 3.  .

Major Retinal Vascular Contribution in Micrometers and as a Percentage of Unscaled Global RNFL Thickness with Each Contact Lens

Contact Lens Power	Global RNFL Thickness (μm)		Major Retinal Vessel Contribution
	With Vasc.	Without Vasc	μm	% of Global
−12	116.8	103.5	13.3	11.4
−10	115.3	102.4	13.1	11.4
−8	114.6	102.0	12.9	11.3
−6	113.5	100.5	13.2	11.6
−4	112.3	99.6	13.0	11.6
−2	111.8	99.1	12.7	11.5
No lens	111.1	98.5	12.9	11.6
2	109.3	97.2	12.2	11.2
4	108.4	96.0	12.5	11.6
6	107.0	95.1	12.3	11.5
8	106.0	94.3	11.9	11.3

RNFL Circular Scan Path

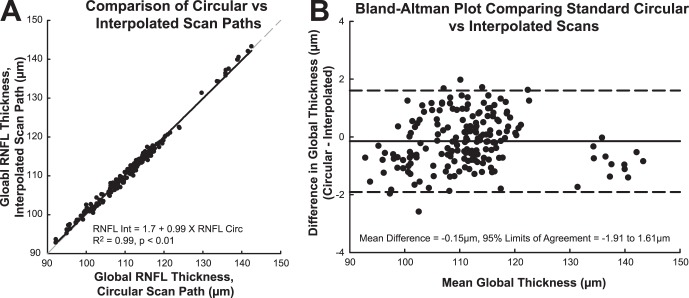
The calculated circumference of RNFL scans increased with increase in anterior surface corneal power (slope = 60.1 μm/D, R² = 0.40, P < 0.001, Table 4). The registered scan paths transferred onto their corresponding baseline raster SLO images, illustrate these changes in scan location (Fig. 2A). With an increase in scan length, there was a corresponding linear decrease in global RNFL thickness (slope −7.7 μm/mm, R² = 0.22, P < 0.001). In addition, RNFL thickness measures from interpolated B-scans, matching the registered scan paths, were in good agreement with those of the standard circular scans (Fig. 5, Mean difference = −0.15 μm, 95% LOA = 1.61 μm, −1.91 μm). The within subject standard deviation for global RNFL thickness measures from interpolated and standard scans was 0.41 μm, corresponding to a repeatability of 1.14 μm. These data provide evidence that the relationship between RNFL thickness and changes in corneal power is a result of differences in scan diameter and, consequently, scan path.

Table 4.  .

Calculated Mean Scan Circumference for the 12-Degree Circular Scan with Each Contact Lens

Change in Anterior Segment Power (D)	Scan Circumference (mm)	SD	CV (%)
−12.00	10.51	0.42	4.02
−10.00	10.59	0.43	4.03
−8.00	10.68	0.43	4.04
−6.00	10.77	0.44	4.05
−4.00	10.88	0.44	4.08
−2.00	10.99	0.45	4.10
0	11.11	0.45	4.07
+2.00	11.24	0.47	4.18
+4.00	11.39	0.48	4.23
+6.00	11.55	0.50	4.30
+8.00	11.73	0.52	4.37
Maximum change	1.22	0.11	9.02

Figure 5.  .

A comparison of the RNFL thickness measurements derived by interpolation from raster scans and direct measurements from circular scans. (A) Correlation of the thickness measures from standard circular and interpolated scans. Gray dashed line: represents a 1:1 relationship. Inset: results of a linear regression analysis. (B) Bland-Altman analysis of the limits of agreement between the thickness measures from raster scans and circular scans. Dashed lines: represent the 95% limits of agreement.

Anterior Corneal Surface Power and Axial Length

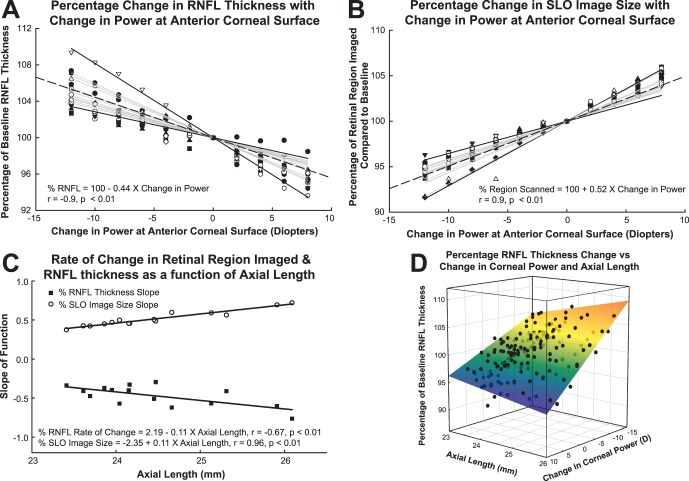
Although the trends in RNFL thickness measures were similar across subjects, there were significant inter-individual differences (Fig. 4). The inter-subject variability also is evident from the increase in standard deviations for global thickness changes with larger contact lens powers (Table 2), and the high coefficient of variation for the maximal change in scan diameter. To reduce the effects of inter-subject variability and to determine the main effects of the optical power of the cornea, the data for each subject were transformed to a percentage of baseline thickness measures (Fig. 6A). Similarly, using the same registration protocols as those for scaling validation, a percentage metric was used to describe the extent of the retinal region scanned with each contact lens using the pixel content from registered SLO images (Fig. 6B). Interestingly, the subject considered an outlier in the untransformed data (Figs. 4A, 4B) falls in the middle of the normalized data.

Figure 6.  .

When expressed as a percentage of baseline, there are significant differences in the rate of change for RNFL thickness (A) and the region of the retina scanned (B). Gray lines: linear regressions through the origin for each subject. Solid black lines in (A) and (B) represent the largest and least slope, while the dashed black fit illustrates the mean fit for the data. The rates of change (slopes of gray lines in A, B) are related linearly to axial length (C). The surface plot (D) illustrates these differences associated with axial length and change in power at the anterior corneal surface.

The data for each subject were analyzed by linear regression to obtain the slope for the best-fit line passing zero reference associated with the baseline (no contact lens) condition. The slopes of the functions ranged from −0.29 to −0.76 (Fig. 6A), with a mean slope of −0.44 (−0.47, −0.41). Data for each quadrant and clock hour sector analyzed are presented in Table 5. Similarly, the slopes for the percentage of retinal region imaged ranged from 0.38 to 0.72 (Fig. 6B), with a mean slope of 0.49 (0.47, 0.51). The slopes of the linear regression for RNFL thickness and retinal region scanned as a function of optical power were opposite in sign, but were similar in magnitude (mean difference 0.04 ± 0.08, P = 0.04). In addition, as illustrated in Figure 6C, the rates of change with axial length followed a similar trend for percent RNFL thickness (slope −0.11, R² = 0.45, P <0.02) and percent retinal image size (slope 0.11, R² = 0.92, P <0.01). Overall, changes in dioptric power at the corneal surface had a larger effect on retinal image size and RNFL thickness, in longer eyes. Equations 2 and 3 below describe the percentage change in retinal region scanned and RNFL thickness as a function of axial length (AL) and change in corneal power (ΔK) with contact lenses:

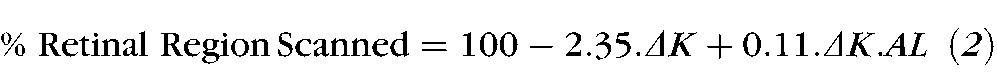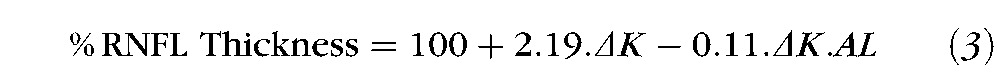Table 5.  .

Slope Values for Percent RNFL Thickness and Area Measures for Global, Quadrant, and Sector Measures with Change in Anterior Corneal Surface Power

	Slope % RNFL Thickness/D		Slope % RNFL Area/D
	Slope	95% CI	Slope	95% CI
Global	−0.45	−0.48, −0.43	0.05	0.03, 0.07
Temporal	−0.33	−0.43, −0.23	0.17	0.09, 0.24
Superior	−0.45	−0.49, −0.41	0.01	−0.03, 0.06
Nasal	−0.49	−0.56, −0.41	0.00	−0.07, 0.07
Inferior	−0.51	−0.55, −0.46	0.00	−0.04, 0.04
S1	−0.38	−0.50, −0.28	0.13	0.02, 0.24
S2	−0.33	−0.43, −0.23	0.18	0.09, 0.27
S3	−0.41	−0.47, −0.34	0.07	0.00, 0.15
S4	−0.52	−0.59, −0.44	−0.08	−0.17, 0.01
S5	−0.56	−0.64, −0.48	−0.14	−0.26, −0.03
S6	−0.47	−0.56, −0.37	0.01	−0.07, 0.11
S7	−0.38	−0.50, −0.26	0.07	−0.02, 0.17
S8	−0.65	−0.76, −0.54	−0.17	−0.27, −0.07
S9	−0.66	−0.75, −0.58	−0.14	−0.22, −0.06
S10	−0.48	−0.56, 0.41	0.02	−0.04, 0.09
S11	−0.20	−0.33, −0.08	0.26	0.15, 0.36
S12	−0.31	−0.46, −0.15	0.06	−0.09, 0.23

RNFL Area

The average global RNFL area, for the 15 subjects without any contact lenses was 1.231 ± 0.095 mm², and 1.100 ± 0.091 mm² after vessels were removed. In contrast to RNFL thickness measures, the global, quadrant and sector RNFL areas did not vary with dioptric power changes at the corneal surface (Global RNFL area, slope 0.0008 mm²/D, P = 0.47, Figs. 4C, 4D). When expressed as a percentage of baseline RNFL area, the rate of change was 0.06 ± 0.06 %/D. In addition, the relationship between individual rates of change and axial length was not statistically significant (P = 0.727).

Discussion

An accurate and precise analysis of the retinal nerve fiber layer can provide important information on the health of the optic nerve. With significant advances in noninvasive imaging technology, the RNFL can be imaged and quantified at increasingly higher resolutions, and with improved repeatability using OCT technology. However, as with most ophthalmic imaging systems, the OCT scan path is dependent on the optics of the eye and imaging device.³² For example, the RNFL circular scan path for most myopic eyes is further to the optic nerve rim margin, compared to an emmetropic or hyperopic eye. These differences in scan location can have a significant impact on the measured RNFL thickness that decreases with increasing distance from the rim margin.^34,49 Several studies in adults and children have reported a relationship between refractive error and RNFL thickness (0.9–1.6 μm/D).^22,25,26,50 Similarly, for standard RNFL scans, thickness measures decrease with increasing axial length (−2 to −3 μm/mm).^{22,25,27,28,50} As there is a strong relationship between axial length and refractive error, it is not surprising that these slopes are similar when converted using a 1 mm axial length to 3 D refractive error ratio determined using a three-surface schematic eye.⁴²

As the change in RNFL thickness for eyes with moderate ametropia is related linearly to axial length,^{22,25,27,28,50} and the distance from the rim margin, thickness measures can be rescaled to match those of an emmetropic eye. Specifically, several investigators^25,27,28 have used a modified Littmann's formula³⁶ that incorporates a magnification factor of the eye to make this correction. However, these formulas only take into account the axial length of the eye with the assumption that the inter-individual variations in optics of the anterior segment have a minimal effect on the eye's principal points.

In general, the process of emmetropization, that is changes in anterior segment optics and axial length, minimizes the effects of retinal image magnification. However, along with an increasing prevalence of myopia,⁵¹ advances in refractive^52–54 and cataract⁵⁵ surgery necessitate investigation of anterior segment power and its effect on ocular magnification and in vivo imaging. In addition, the equivalent power of the eye as determined by the cornea, crystalline lens, and the separation of the two structures,⁴² is age-dependent with possible implications on age-related changes in the RNFL.^43,56–58

Recently, using contact lenses, the effects of changes in anterior segment optics on RNFL thickness have been investigated with TD-OCT³⁹ and SD-OCT.⁴⁰ Whereas a significant relationship was not found with the time domain system, the RNFL thickness was related linearly with contact lens power (0.5 μm/D) when a spectral domain instrument was used. The discrepancy between the two studies probably is a result of differences in controlling for accommodative effects, and the axial resolution and segmentation algorithms used by the two imaging systems.^59,60

Our present study used a custom segmentation algorithm^45,46 to investigate the relationship between contact lens-associated anterior segment power changes and RNFL thickness, with and without compensation for major retinal vasculature. In general, the relationship between global RNFL thickness and dioptric power change at the cornea (−0.52 μm/D) followed similar trends to those reported previously by Lee, et al.⁴⁰ The major retinal vascular contribution for scans at baseline was 11.5 ± 1.6%, and similar to those reported previously^46,61 (Mardin CY, et al. IOVS 2009;50: ARVO E-Abstract 3333). Subtraction of this non-neuronal component did not affect significantly the relationship of the RNFL thickness with anterior segment power (−0.46 μm/D). Although not clinically significant, the decrease in the vascular thickness contribution with increase in power should be considered as imaging technology continues to improve and compensation for non-neuronal factors becomes standard in RNFL analysis.

The outcomes of our present study provided evidence that the relationship between RNFL thickness and contact lens power is a direct result of changes in ocular magnification. As illustrated by the registered scan paths used for RNFL B-scans interpolation (Fig. 2), the scan circumference became larger with increased contact lens power. The accuracy of the image registration process and subsequent scan path location was validated by the agreement and repeatability of RNFL thickness measures from the interpolated and corresponding standard circular scans (mean difference −0.15 μm, S_w = 0.41 μm). In general, the repeatability was better than that determined for the test-retest without contact lenses (mean difference 0.31 μm, S_w = 1.19 μm). Hence, these data reiterate the importance of an accurate, in registration scan placement for follow-up scans,^18,19 which was not the case for RNFL scans acquired without contact lenses. Our present findings also are in agreement with test retest RNFL thickness data from normal and glaucomatous eyes that show improved repeatability with image registration compared to using the customary, well-centered scans.¹⁵

When RNFL thickness data were expressed as a percentage of the baseline, there were significant inter-individual differences in the rate of change. Specifically, longer eyes had larger percentage deviations in RNFL thickness across the contact lens powers. This finding was supported by corresponding differences in individual rates of change for the retinal region scanned as determined by image registration. In principle, these results are in agreement with differences in image size for model eyes of varying axial length and refractive error, as imaged with a time domain system.³² Hence, the percentage change formulas (equations 2 and 3) can be used to compare intra-individual RNFL thickness measures associated with changes in dioptric power at the corneal surface. However, the formulas generated by the present data included only a narrow range of axial lengths, limited by the inclusion criteria of the study. In addition, the formulas cannot be applied for optical power changes at locations other than the anterior corneal surface, such as with cataract surgery.

An accurate measure of the scan circumference can provide useful information when comparing thickness measures between individuals or to a normative database. For this study, individualized three surface schematic eyes were used to calculate the transverse scaling and scan diameter. Overall, this method was accurate at determining changes in the retinal region imaged as illustrated by the good agreement with the registered SLO fundus images. Although the RNFL thins with increasing distance from the rim margin,³⁴ the axonal content within the peripapillary region should be relatively similar, as only a small percentage of the eyes' RGC populations reside in this region. Hence, it is not surprising that the RNFL area, calculated by multiplying thickness measures by the SD-OCT scan length, did not show any significant change across the 20 D range of contact lenses used. Subsequently, these RNFL area measures can be used to predict RNFL thickness at predetermined scan diameters. However, the relationship holds true only for a limited distance from the optic nerve. For example, in highly myopic eyes, the scan path can pass through regions with high ganglion cell densities and where RNFL thickness change is not related linearly to the distance from the rim margin. This limitation can be overcome by incorporating ocular biometry, before scan capture, and adjusting the scan angle, resulting in a fixed scan diameter at the retinal surface. Whereas these adjustments must be made before scan capture for standard circular scans, they can be made during post-processing in cases where B-scans are interpolated from volumetric raster data.

In conclusion, our study illustrates the use of image registration and retinal scaling in describing the relationship between RNFL thickness and ocular biometry. A schematic eye that includes anterior segment power and axial length can determine accurately scaling and scan dimensions. As imaging technology and RNFL segmentation algorithms improve, it is necessary to incorporate the optical properties of the patient's eye in determining the scan characteristics for thickness/area analysis.