Conduction Velocity of the Uterine Contraction in Serial Magnetomyogram (MMG) Data: Event Based Simulation and Validation

Abstract

We propose a novel approach to calculate the conduction velocity (CV) of the uterine contraction bursts in magnetomyogram (MMG) signals measured using a multichannel SQUID array. For this purpose, we partition the sensor coordinates into four different quadrants and identify the contractile bursts using a previously proposed Hilbert-wavelet transform approach. If contractile burst is identified in more than one quadrant, we calculate the center of gravity (CoG) in each quadrant for each time point as the sum of the product of the sensor coordinates with the Hilbert amplitude of the MMG signals normalized by the sum of the Hilbert amplitude of the signals over all sensors. Following this we compute the delay between the CoGs of all (six) possible quadrant pairs combinations. As a first step, we validate this approach by simulating a stochastic model based on independent second-order autoregressive processes (AR2) and we divide them into 30 second disjoint windows and insert burst activity at specific time instances in preselected sensors. Also we introduce a lag of 5 ± 1 seconds between different quadrants. Using our approach we calculate the CoG of the signals in a quadrant. To this end, we compute the delay between CoGs obtained from different quadrants and show that our approach is able to reliably capture the delay incorporated in the model. We apply the proposed approach to 19 serial MMG data obtained from two subjects and show an increase in the CV as the subjects approached labor.

I. INTRODUCTION

Premature labor and delivery is an important public health problem as it is the main cause of morbidity and mortality of newborns. One of the major challenges faced by obstetricians is a proper diagnosis of labor which could be useful especially in the prediction of labor for patients at high risk of premature delivery. To date there is no accurate and objective method to predict the onset of labor or to distinguish between false and true labors. At present, the progress of labor is monitored by recording changes in the cervical state and by measuring the rate, duration and amplitude of uterine contraction using tocodynamometer or surface electromyogram (EMG) electrodes.

The uterine contractions are a result of complex electrophysiological phenomena. It has been suggested that the uterine myometrial activity is low throughout pregnancy with significant increase during term or preterm labor [1]. The analysis of serial recordings (e.g., from gestational week 23 onwards), more precisely the analysis of the conduction velocity (CV), might help elucidate the nature of contractions and how the entire mechanism develops throughout the gestation age.

Over the past years the uterine magnetomyogram (MMG) has become one of the most promising biophysical markers for pre-term labor. The MMG recordings have important properties which makes them a suitable candidate for the investigation of the uterine activity: (i) they are independent of tissue conductivity (ii) the detection of the signal outside the boundaries of the skin is possible without making any electrical contact with the body and (iii) are independent of references, which ensures that each sensor mainly records localized activity.

In an effort to facilitate the automatic detection of uterine contractions our group has developed a method, consisting of multiple stages, to identify uterine contraction burst in the MMG signals [2].

Although this technique has the advantage of capturing the dominant frequency information, a single contraction marker is created for all sensors. This has the inconvenience that if one decides to investigate specific sensors, in some of them one might find instances labeled as contractile pattern although in reality there is no activity. Therefore, we have extended this approach to encompass all magnetic sensors, that is, for each sensor a contraction marker is computed using the power information from the respective sensor.

Early studies showed increased CV of the uterine myometrial cells before delivery and this has been attributed to the increase in the gap junction between the myometrial cells [3], [4]. In this work we develop a novel approach to compute the CV of the multidimensional MMG signals. At this time the prognostic capability of the CV has only been evaluated by means of EMG [5].

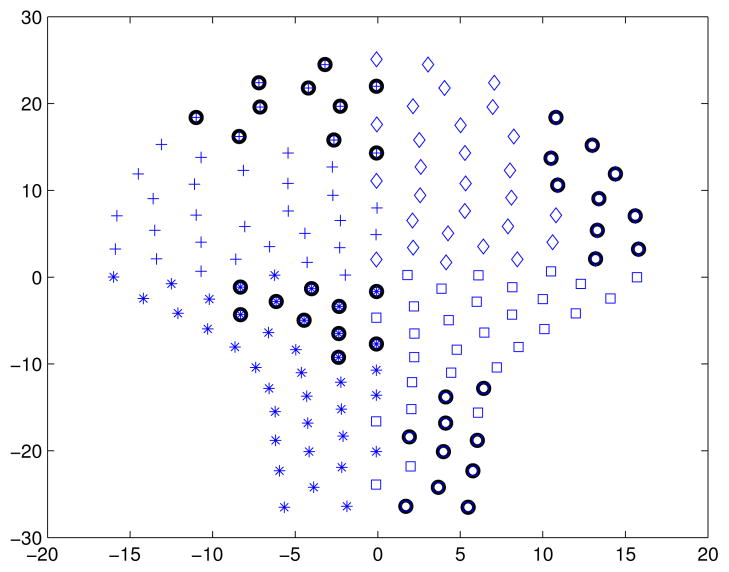
To address the issue of the CV in MMG signals, we first detect and mark the contractile patterns, within a 30 s running non-overlapping window, in each sensor using the above mentioned method. Second, we subdivide the sensor space in 4 quadrants (Q) (see Fig. 1). To study the interaction between quadrants we create pairwise combinations (e.g., Q1–2, Q1–3, Q1–4, etc.), we mark the windows where sensors (from both quadrants) are active and we compute the delay between the center of gravities (CoG) using the high order cross-correlation function. Once the delay is computed the CV can be easily calculated as the ratio between the delay and the distance between CoGs. We propose a novel way to compute the delay within multidimensional data by which we can estimate the CV of the uterine myometrial activity. We test the proposed approach on the data simulated using the model and show that our approach is able to capture the delay incorporated in the model. In the next step we apply this to 19 serial MMG data sets from two pregnant women and study the CV.

Fig. 1.

Partitioning of the sensor space in four quadrants. Diamonds, crosses, asterisks and squares are marking the sensors that belong to the first, second, third and fourth quadrant, respectively. Black circles mark sensors in which the AR2 processes are modified.

II. MATERIALS AND METHODS

A. Data Acquisition

Serial recordings, sampled at 1220.7Hz, from two healthy pregnant women were analyzed for the current study. The MMG recordings were performed at gestational age ranging between 23 and 38 weeks (a total of 19 recordings). The duration of a recording was typically around 30 minutes. Prior to any processing the data was down-sampled to 250Hz and we excluded segments with maternal movement. For this purpose, we first extracted the R peaks from the maternal magnetocardiogram (mMCG) [6]. In a next step we partitioned the signals into 3 minute disjoint windows and in each window we compute the CoG for the R peaks. We denote with m_CoG the average of the CoG in particular inspection window and with std_CoG its standard deviation. Whenever in a window

$${\mathit{CoG}}_i>m_{\mathit{CoG}}+4·{\mathit{std}}_{\mathit{CoG}}$$ (1)

the corresponding sample was marked as movement artifact. Later on in the analysis, whenever such a sample was encountered, the corresponding inspection window was discarded from further analysis. We have found that equation 1 provides a fairly good discrimination of the peaks that correspond to maternal movement. This was also in agreement with the protocol recordings that were carried out during each measurement.

The study was approved by the Ethical Review Board of the Medical Faculty, University of Tübingen. Each participant was informed about the purpose of the study and signed informed consent prior to participation.

B. Center of gravity and Hilbert amplitude

1) CoG

We denote the j-th sample of the MMG signal at k-th sensor as $S_k^j$ and the corresponding Hilbert transform is represented as $H_k^j$ where j = 1 … n with n representing the number of magnetic sensors. We define the CoG for the j-th sample as follows:

$${\mathit{CoG}}^j=\frac{{\sum }_{k=1}^n(x_k,y_k,z_k)·H_k^j}{{\sum }_{k=1}^n{H}_k^j},$$ (2)

The Hilbert transform of the MMG signal at k-th sensor is computed using the ’hilbert’ function in MATLAB (Mathworks Inc.) which yields a complex signal as a linear combination of original signal with its Hilbert transform. The magnitude of this complex signal gives the Hilbert amplitude $H_k^j$.

C. High dimension cross-correlation function

In order to calculate the delay between two CoGs (which are 3-dimensional vectors) we perform time shifted correlation analysis. For this purpose we hold CoGs from one of the quadrants constant and shift the CoGs from the second by τ samples (back in time). We discard the last τ samples from the CoGs that we hold constant in order to match the number of samples in the later. To this end the correlation coefficient is computed between these two CoGs. However, in this approach there is an element of bias as the correlation coefficient is computed for different number of samples for each shift. To avoid this bias and thereby to quantify the correlation correctly, for each shift τ we discard from both CoGs the same number of data points that corresponds to number of samples minus the maximum lag. The maximum lag up to which we would like to perform the correlation analysis is set to 15 seconds of data. For each shift, we quantify the correlation using the following correlation function [7]:

$$C=\frac{tr(X^{t}Y)}{\sqrt{tr(X^{t}X)tr(Y^{t}Y)}},$$ (3)

where X^t represents transpose of the matrix X and tr represents the trace of the matrix, i.e. the sum of diagonal elements.

D. Modeling

We propose the following stochastic model based on the second-order autoregressive process (AR2):

$$X(t)=a_{1}X(t-1)+a_{2}X(t-2)+\eta (t)$$ (4)

where the initial parameters of the AR2 process are computed as in [2]. The purpose of the proposed stochastic model is to mimic the amplitude of the MMG signals by tweaking the parameters of the model. This model is just sufficient to understand the limitation of our approach as to capture the delay between the selected sensors. Moreover, this model cannot explain the different frequency characteristic that may be present in the measured MMG signals.

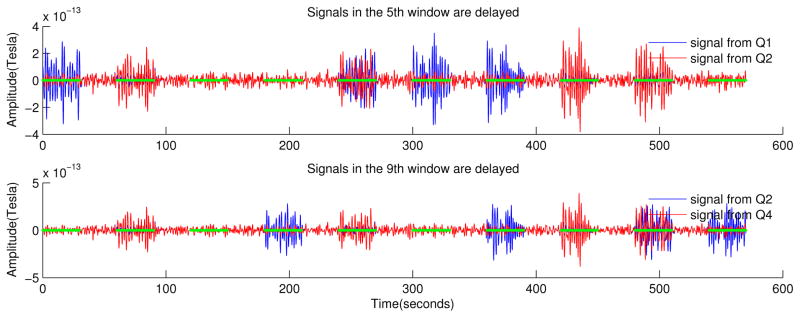
We create n realizations (to match the total number of the sensors) of the AR2 process for a duration of 9.5 minutes with a sampling frequency of 250 Hz. We divide the sensor space into four quadrants and in each quadrant we choose ten sensors where we will insert burst activity. We divide S(t) into disjoint windows and we alternate every 30 seconds between active and rest periods. During the active periods the signals in the ten selected sensors are replaced with a filtered (bandpass filter at 0.35–0.8Hz) and amplified version of the corresponding original AR2 processes. The first four active periods we modify the signal only in one quadrant, that is, in the first active period signals are modified in Q1, in the second active period in Q2, etc. Starting with the fifth active period we modify the signal in quadrant pairs, that is, in the fifth active period, signals are modified in Q1–2, in the sixth period in Q1–3, etc. In addition, whenever signals (in the ten selected sensors) are modified in quadrant pairs, a delay of 5 ± 1 seconds is introduced in the signals of the second quadrant of the pair. The duration of the delay was arbitrarily chosen and the values were drawn from a poisson random distribution. For a schematic representation of the model with the modified signals see Fig. 2.

Fig. 2.

An example of the modified signals. Top: signals belonging to Q1 (blue) and Q2 (red), note that in the fifth active window the signal in Q2 is delayed. Bottom: signals belonging to Q2 (blue) and Q4 (red), note that in the ninth active window the signal in Q4 is delayed.

III. RESULTS AND DISCUSSION

A. Event based simulation

The results of the event based simulation are summarized in Table I. The first row contains the average delay that was inserted in the preselected ten sensors of the model described in section II–D. The second row shows the delay as computed by the high-dimension cross-correlation function. We understand that the high-dimension cross-correlation function which was introduced in section II–C is able to capture the delay between the CoGs.

TABLE I.

The delay as inserted in the stochastic model and as captured by the high-dimension cross-correlation function.

Delay	Quadrant pair
	Q1–2	Q1–3	Q1–4	Q2–3	Q2–4	Q3–4
Inserted	5.09	4.90	5.04	4.93	4.98	4.98
Detected	5.31	4.91	5.13	4.75	5.09	4.94

B. MMG data

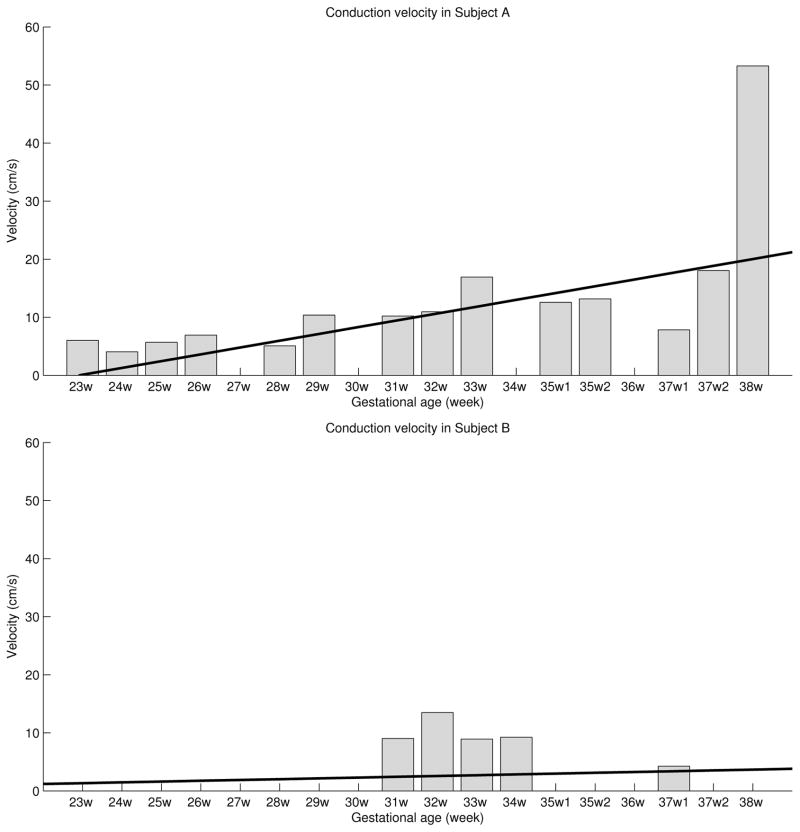
The proposed approach was applied to biological datasets as described in section II–A. Fig. 3 shows the CV in subject A (top) and subject B (bottom), obtained for each quadrant pair over the gestational age. A total of 19 datasets were investigated (14 for subject A and 5 for subject B). The values for each week were obtained as follows: for each quadrant pair in each ’active’ inspection window the delay between corresponding CoGs was computed using the high dimension cross-correlation (HDCC) function as defined in section II–C. The delay was tested for significance using a bootstrapping approach.

Fig. 3.

Conduction velocity in subject A (top) and subject B (bottom). The values for each week represent the maximum velocity that occurred in all quadrant pairs. Black thick line shows the trend in the data.

In a next step the velocity (for inspection windows that were marked ’active’) was calculated as the ratio of the distance between CoGs and the delay between the corresponding CoGs. In case of negative delay, we used the absolute value of it. Finally, for a given dataset we quantify the CV by taking its highest value from all quadrant pairs.

A recent study has shown the better performance in predicting the preterm labor using the propagation velocity in combination with the peak frequency compared to the standard clinical methods such as Bishop score, contractions, and cervical length [5].

In a previous study [8] the authors investigated several linear and non-linear signal processing methods on groups of term and pre-term delivery records recorded before and after the 26th week of gestation. The authors emphasize that their goal was not to predict the beginning of labor nor following the changes in spectra prior to delivery but to differentiate these groups early during the pregnancy. The authors conclude that when using a 0.3–3 Hz filter two methods (i) the median frequency of the power spectrum and (ii) the sample entropy provide best discrimination for the investigated groups. For their term recordings the authors observe a slight decrease in the median frequency of the power spectrum as time of gestation progresses, while other studies show an increase in the power spectra distribution [9], [10]. The decrease is later explained by the difference in the processing of the recorded data. Fele-Zorz and colleagues processed entire records, the entire electrical activity of the uterus, while in those other studies individual contractile events, i.e., the bursts associated to contractions, were processed. The authors also conclude, that if entire records are processed and records are taken more than 7 weeks prior to delivery, a slight decrease of the power spectra distribution is observed for term records. In this work we have shown that the propagation velocity is positively correlated with the gestational age in Subject A and this can be attributed to the gradual increase in the gap junction between the myometrial cells during pregnancy. Indeed this subject delivered in two weeks from the last study. In Subject B, no clear trend is seen between propagation velocity and gestational age, which could be due to the insufficient number of recordings or due to no significant change in the uterine dynamics. This subject delivered within four days from the last study but by c-section mode. Thus, in these two subjects studied there is a correlation between the CV and the outcome.

In future work this will be tested on a larger population and compare CV with the traditional used clinical measures in predicting the term/preterm labor.

IV. CONCLUSION

A novel approach to calculate the CV of the uterine contraction bursts in MMG signals has been presented.

The results are in line with those previously reported by Govindan and colleagues [11] and they indicate a faster conduction time between muscle cells as the subject approaches term.

In future work, the proposed approach will be applied to a larger amount of low-risk datasets to investigate its prediction power. The use of the current method might provide a better understanding of the electro and magnetophysiology of uterine activity and its development throughout the gestational age.