Nonlinear Analyte Concentration Gradients for One-Step Kinetic Analysis Employing Optical Microring Resonators

Abstract

Conventional methods to probe the binding kinetics of macromolecules at biosensor surfaces employ a stepwise titration of analyte concentrations and measure the association and dissociation to the immobilized ligand at each concentration level. It has previously been shown that kinetic rates can be measured in a single step by monitoring binding as the analyte concentration increases over time in a linear gradient. We report here the application of nonlinear analyte concentration gradients for determining kinetic rates and equilibrium binding affinities in a single experiment. A versatile nonlinear gradient maker is presented, which is easily applied to microfluidic systems. Simulations validate that accurate kinetic rates can be extracted for a wide range of association and dissociation rates, gradient slopes and curvatures, and with models for mass transport. The nonlinear analyte gradient method is demonstrated with a silicon photonic microring resonator platform to measure prostate specific antigen-antibody binding kinetics.

INTRODUCTION

Refractive index-based biosensors have proven to be highly useful for determining the kinetic rates of biomolecular interactions. Although the optical phenomena are distinct, the experimental design and data analysis for surface plasmon resonance (SPR),^1–4 localized surface plasmon resonance,⁵ photonic crystal,⁶ and optical microring resonator biosensors^7,8 are all similar. The success of these methods in measuring kinetic rates has been driven by the ability to monitor binding in real-time without the need for chromophoric or enzymatic labels.

Typical kinetic experiments involve immobilizing a biomolecule of interest on the biosensor surface. Analyte solution flows across the surface, and binding is monitored over time by measuring the change in refractive index within the evanescent field near the sensor surface. Kinetic experiments usually employ a stepwise titration of analyte concentrations. A constant concentration of analyte is injected for a defined period of time in the association phase, followed by the injection of a blank buffer solution to monitor the dissociation phase. The cycle of association and dissociation is repeated at multiple concentrations. Data from the concentration steps are then fit globally using numerical integration of the rate equations for a given model. Various linearization strategies can also be employed in data analysis.^9,10

The conventional stepwise titration approach has several limitations. In order to repeat the analysis at multiple concentration levels, the surface is typically regenerated before each injection. These multiple regeneration steps increase the total analysis time, consume more material, and can lead to run-to-run variability, as precise loading of the immobilized biomolecule is often difficult to achieve. Multiple regenerations are also particularly problematic for multiplexed assays where the surface is more complex.

In cases where it is difficult or impossible to regenerate the surface after each analysis, several different methods may be used to measure kinetics on a single surface by performing the titration in parallel or series. Bravman et al. have described the use of the ProteOn XPR 36 array SPR biosensor where the surface functionalization is performed orthogonal to a six-channel flow cell.¹¹ Thus, each loaded surface is split into six regions that are simultaneously and separately addressed by six concentration steps. While this method demonstrates the utility of one-shot parallel kinetic experiments for multiplexed measurements, it is limited by the complex instrumentation associated with addressing the chip in orthogonal directions.

A titration series may be also used where the surface is not regenerated after each association and dissociation cycle.¹² This method has been widely adopted, as it does not require additional instrumental components. A recent variation on this titration series method described by Rich et al. is known as a FastStep injection.¹³ This method utilizes a SensiQ Pioneeer SPR instrument with a dual syringe pump system that is able to mix analyte solution and buffer during the injection to generate defined dilutions or gradients. A FastStep injection uses the syringe mixer to increase the concentration from low to high in discrete steps. As the concentration is increased, only the association phases are monitored. The dissociation is finally measured by injecting buffer after the highest concentration step. These series methods have greatly increased the throughput of kinetic experiments.

In addition to parallel and series titrations, which utilize step concentration titrations, Shank-Retzlaff and Sligar demonstrated that a constantly increasing linear analyte gradient can be used to extract accurate kinetic rates and affinities in a single step.¹⁴ The analyte gradient method offers many of the same advantages as the FastStep method in that kinetic experiments can be performed quickly, in a single step, and by preparing only a single analyte solution. Numerical simulations showed that the linear gradient method is applicable across a wide range of kinetic rates. It can be analyzed with the two-compartment model^15,16 to account for mass transport as well as a model for heterogeneous binding sites. The linear analyte gradient method was experimentally tested by measuring the binding of cytochrome c with cytochrome b₅ using a custom-built SPR instrument with a linear gradient generated by a straight-walled gradient maker and a High Pressure Liquid Chromatography (HPLC) pump.

This report expands the theory and application of analyte gradient methods as a one-step method for kinetic experiments. We have designed a simple and scalable non-linear gradient maker that generates precise concentration gradients. This nonlinear gradient maker is more amenable to microfluidic systems than the gradient maker and HPLC pump previously used. Numerical simulations demonstrate that nonlinear gradients of different curvature offer the same capabilities as linear gradients over a wide range of kinetic rates. Furthermore, mass transport in nonlinear gradient systems can be modeled using both the two-compartment model and a temporally adjusted one-to-one interaction model. This nonlinear gradient instrumentation and theory is readily applicable to a variety of different biosensor platforms.

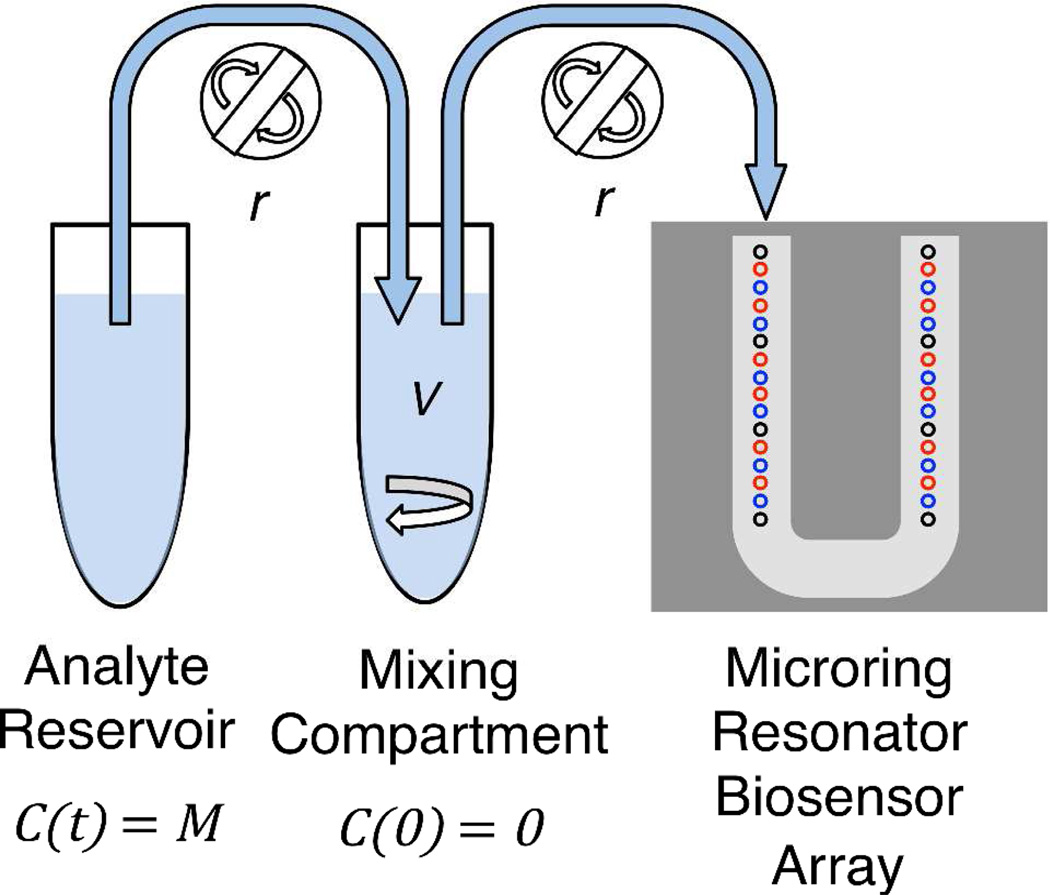
We have interfaced the nonlinear gradient maker with a microring resonator array biosensor platform.⁷ Microring resonators are refractive index-sensitive silicon photonic devices comprised of microfabricated rings arrayed on a single chip. Light couples into the microrings from adjacent linear waveguides at a particular resonant wavelength. As biomolecules bind to the microring surface, the local refractive index changes, which is detected as a shift in the resonant wavelength. The presented chip architecture positions thirty-two individually addressable rings, eight thermal controls and twenty-four active rings, sequentially along a U-shaped flow cell (see Figure 1).

Figure 1.

Schematic of nonlinear gradient maker and microring resonator array. Analyte solution with concentration M is placed in the analyte reservoir. Buffer with volume V is placed in the mixing compartment. Analyte is pumped from the analyte reservoir into the mixing tube by a peristaltic pump at flow rate r, and the gradient solution is also pumped at rate r across the microring resonator array. The microring resonator array is made up of thirty-two rings addressed via a U-channel flow cell. Black rings represent thermal controls, blue rings represent control rings (non-DNA functionalized), and red rings represent active rings (DNA functionalized).

Microring resonators have previously been used for conventional kinetic analysis⁸ as well as titration series.¹⁷ Here, we expand the utility of this platform by providing the first report of “single shot” kinetics on microring resonators. We apply this method to the binding of cancer biomarker prostate specific antigen (PSA) to an anti-PSA antibody, which is attached to the microring surface by a DNA tag. Of the twenty-four active sensor rings, twelve are left intentionally blank (non-DNA functionalized) and serve as controls for the assay, allowing us to average the binding curves from the twelve functionalized rings and perform necessary background corrections. However, different ligands can be attached to subsets of these rings for multiplexed measurements as previously demonstrated.¹⁷ This multiplexable sensor surface combined with the single run kinetics will facilitate future high-throughput kinetic studies of biomolecular interactions.

METHODS

Nonlinear Gradient Maker Design

The design for a nonlinear gradient maker is adapted from previous designs¹⁸ to facilitate easy instrumentation with microfluidic systems. A schematic is shown in Figure 1. This nonlinear gradient maker is based on a two-compartment system. An analyte solution with concentration M is placed in the analyte reservoir compartment. A peristaltic pump with flow rate r pumps solution from the analyte reservoir to the mixing compartment. Since solution is constantly removed from the analyte reservoir, it is important to have enough volume in the analyte reservoir to complete the experiment. The mixing compartment contains a blank buffer solution of volume V and is stirred by a small stir bar. Solution is pumped from the mixing compartment to the instrument at the same rate r that solution is pumped into the mixing compartment. Although the schematic depicts two peristaltic pumps for clarity, we fed both tubes through the same peristaltic pump. This both reduces the number of components and ensures that the rates to and from the mixing compartment are equal. Both compartments consisted of 1.5 mL microcentrifuge tubes with Teflon tubing for fluid delivery.

The concentration of the mixing compartment over time, C_G(t), is described by the ordinary differential equation:

$$\frac{{\mathit{\text{dC}}}_G(t)}{\mathit{\text{dt}}}=\frac{\mathit{\text{rM}}-{\mathit{\text{rC}}}_G(t)}{V}$$ (1)

where M, r, and V are defined above. Equation 1 can be analytically solved by separation of variables to yield:

$$C_G(t)=M(1-e^{-\frac{\mathit{\text{rt}}}{V}})$$ (2)

Thus, the output of the nonlinear gradient maker is determined by three independent variables, the flow rate r, the mixing compartment volume V, and the concentration of analyte in the reservoir M. Each of these variables can be easily adjusted to define the curvature and slope of the gradient profile.

To test the nonlinear gradient maker prototype, we filled the analyte reservoir with 10X Dulbecco’s Phosphate Buffered Saline (PBS) (Sigma, St. Louis, MO) and added a defined volume of deionized water into the mixing compartment. The flow rate was measured by determining the mass of water pumped over a period of time. The concentration term M was measured by introducing the PBS solution directly over the microrings and measuring the refractive index change in units of picometer shift (Δpm), the shift in the resonant wavelength of the microring resonator. The predicted gradient profile was calculated in units of Δpm by inputting the measured V, r, and M into Equation 2. The experimental response was measured by flowing the output from the gradient maker over the microring resonators and measuring the Δpm shift. Responses were tested for mixing volumes ranging from 250–1000 µL and flow rates ranging from 5–20 µL/min.

Numerical Simulations

Simulations were used to generate analyte gradient binding curves with known kinetic rates. Similar to previous studies,¹⁴ programs developed with Mathematica 8.0.4 numerically integrated a two-dimensional partial differential equations (PDE) model. This two-dimensional PDE model was derived from Glaser¹⁹ as expanded by Myszka et al.¹⁵ It accounts for diffusion parallel to the flow, the x-direction, and perpendicular to the surface, the y-direction, as well as a parabolic flow profile. A detailed description is given in the Supporting Information. The microring resonator flow cell has a height of 175 µm and a width of 500 µm with the 30 µm diameter microrings situated in the middle of the channel.⁷ Any concentration differences along the width should be neglible and were neglected. Although experiments were performed using a U-shaped flow cell,²⁰ the flow cell length was modeled as a 5 mm linear path. The flow cell was divided into a 34×34 grid, and concentration was calculated at each point on the grid over time using Equations S-1−S-5 (see Supporting Information). Unless stated differently, the diffusion constant was set to 1×10⁻⁶ cm²/s, the flow rate was set to 10 µL/min, the mixing volume was set to 500 µL, the total number of binding sites was set to 6×10⁻¹³ mol/cm², and flow cell height and length were set to 175 µm and 5 mm. Diffusion constants within an order of magnitude of this range showed very similar results. However, diffusion constants that were several orders of magnitude smaller, simulating very viscous solutions, showed much larger mass transport effects that limit the method.

The reservoir concentration was typically set to 10–25 times the equilibrium dissociation constant K_D so that the binding approached saturation at the end of the association phase. As a general guideline, we sought to ensure that the maximum concentration of the gradient was at saturating conditions at the end of the association phase so that the full range of appropriate concentrations were covered by the analyte gradient. While easy to accomplish in systems with prior knowledge of the dissociation constant, this requires some estimation in unknown experimental systems. A pilot study with a steep gradient slope is recommended to establish an appropriate estimation.

Numerical integration was performed over 7500 seconds with a time step of 0.01 seconds. The gradient concentration profile was allowed to run for 2500 seconds and was then set to zero molar to monitor the dissociation phase. The binding curves at each of the interior thirty-two grid locations were assumed to equal the response from the thirty-two microrings. We averaged the data from the thirty-two binding curves to form one averaged data set that was then fit to extract kinetic rates. All thirty-two curves can be fit individually and show similar results to the averaged curves. However, this greatly increased computation time. We also evaluated aligning the individual binding curves before averaging. This was performed by simply shifting each binding curve until it achieved maximum overlap with the first curve.

Kinetic Models

Kinetic rate constants were extracted from the simulated binding curves by fitting the association phase to the one-to-one interaction model or the two-compartment model and fitting the dissociation phase to a simple exponential decay. The one-to-one model assumes that the concentration of analyte at the surface is identical to the gradient concentration and that the binding is first order on the surface. This model is governed by an ordinary differential equation given by:

$$\frac{d{\mathrm{\Gamma }}_{\mathit{\text{bound}}}}{\mathit{\text{dt}}}=k_a{C}_G({\mathrm{\Gamma }}_{\mathit{\text{tot}}}-{\mathrm{\Gamma }}_{\mathit{\text{bound}}})-k_d{\mathrm{\Gamma }}_{\mathit{\text{bound}}}$$ (3)

where C_G is given by Equation 2 in mol/L, k_a is the association rate in M⁻¹, and k_d is the dissocation rate in s⁻¹. Γ_bound and Γ_tot are the amount of analyte bound to the surface and the total number of binding sites respectively. Both are given in mol/cm² for simulations and in Δpm for experiments.

The two-compartment model also assumes first order binding at the surface but adds an extra layer of complexity. Here, we assume that the flow cell can be divided into two regions, the flowing region and a stagnant region. The concentration in the flowing region is assumed to be equal to the gradient concentration input. Analyte diffuses between the flowing region and the stagnant region with a rate k_m. Analyte in the stagnant region can diffuse back into the flowing region or bind to the surface. This leads to a system of ordinary differential equations:

$$\frac{{\mathit{\text{dC}}}_s}{\mathit{\text{dt}}}=\frac{1}{h}(-k_a{C}_s({\mathrm{\Gamma }}_{\mathit{\text{tot}}}-{\mathrm{\Gamma }}_{\mathit{\text{bound}}})+k_d{\mathrm{\Gamma }}_{\mathit{\text{bound}}}+k_m(C_G-C_s))$$ (4)

$$\frac{d{\mathrm{\Gamma }}_{\mathit{\text{bound}}}}{\mathit{\text{dt}}}=k_a{C}_s({\mathrm{\Gamma }}_{\mathit{\text{tot}}}-{\mathrm{\Gamma }}_{\mathit{\text{bound}}})-k_d{\mathrm{\Gamma }}_{\mathit{\text{bound}}}$$ (5)

where C_s is the concentration in the stagnant layer, k_a is the association rate in M⁻¹s⁻¹, k_d is the dissociation rate in s⁻¹, k_m is the mass transport rate in cm/s, C_G is gradient concentration given by Equation 2 in mol/L, and h is the theoretical height of the stagnant layer. Γ_bound and Γ_tot are respectively the amount of analyte bound to the surface and the total number of binding sites as described above.

The dissociation phase can be modeled as a simple exponential decay. Assuming C_G(t)=0, Equation 3 becomes a simple ordinary differential equation, which solves to:

$${\mathrm{\Gamma }}_{\mathit{\text{bound}}}(t)={\mathrm{\Gamma }}_{\text{max}}{e}^{-k_{d}t}$$ (6)

where k_d is the dissociation rate in s⁻¹. Γ_bound and Γ_max are respectively the amount of analyte bound to the surface and the total number of occupied sites at the start of the dissociation, t=0, and have units described above.

Data Fitting

For the experimental data, binding curves from the active rings were corrected by subtracting the average of the control rings as well as correcting for a constantly decreasing baseline of 0.5 pm/min due to antibody falloff.¹⁷ Baseline corrected curves were normalized to correct for differences in antibody loading. Several minutes were discarded from the start of the dissociation phase to account for nonzero concentration in the flow cell. Figure 2 and S-1B demonstrate this fall time before the concentration is truly zero in the dissociation phase. The fall time depends on instrumental parameters such as flow rate and on the diffusion constant of the analyte. Rather than trying to explicitly calculate the delay or to model this effect, we simply truncated the part of the dissociation curve that appeared to be nonexponential decay, which was roughly the region before the inflection point (see Figure S-3 as an example). Note that this fall time represents an instrumental limitation for systems with fast dissociation times. Finally, association and dissociation curves from active rings were averaged. Averaging both reduces computation time and lowers the noise, allowing for a more precise fit. However, it is possible to fit each active ring individually. The median values from these individual fits are very close to the fit from the average curve, but the confidence interval is larger.

Figure 2.

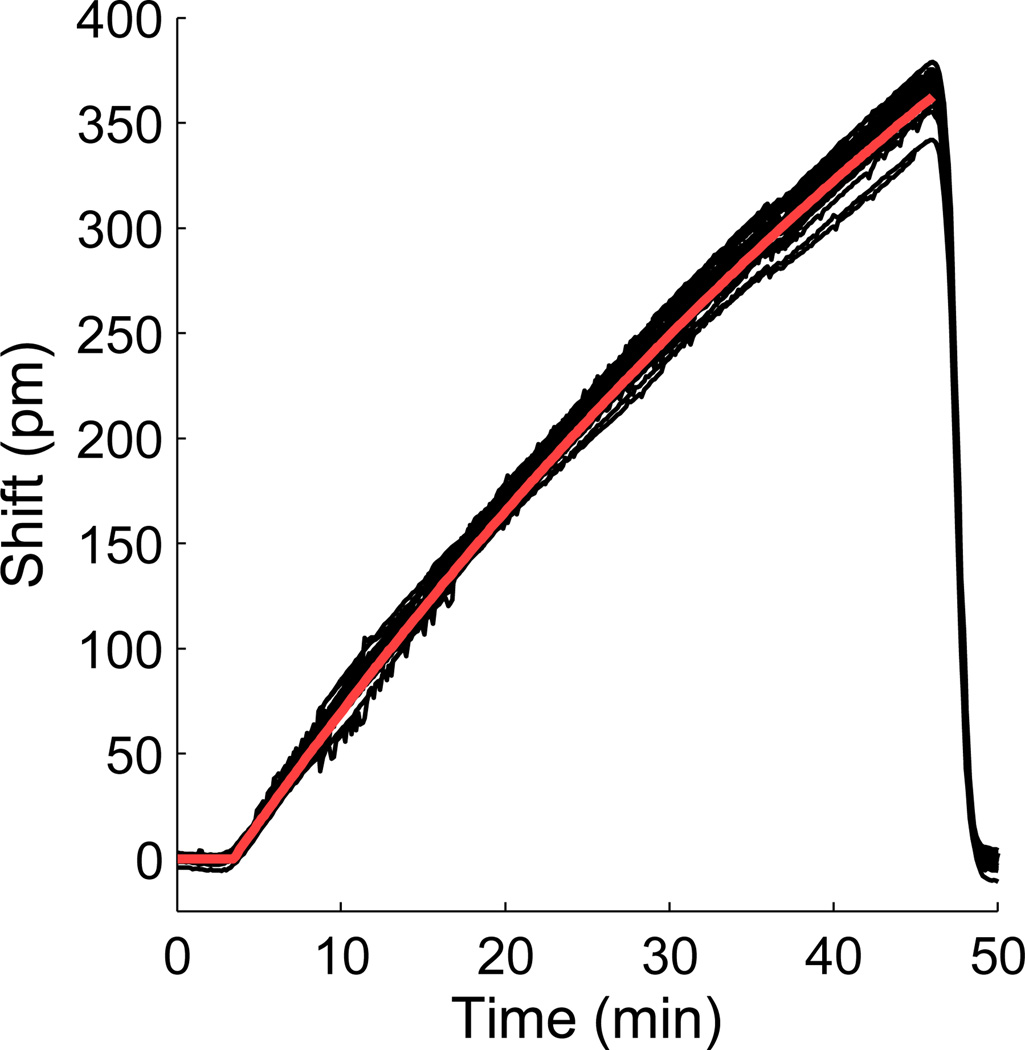
Validation of the nonlinear gradient maker. A 10X PBS buffer is used in the analyte reservoir with a 1 mL mixing volume and 13 µL/min flow rate. The maximum shift is calculated from the average maximum response from the undiluted 10X PBS buffer. The microring resonator response from all twenty-four rings is shown in black, and the predicted gradient output calculated from Equation 2 is shown in red.

Theoretical and experimental binding curves were fit to the models described above with a custom program in Mathematica 8.0.4. The general data fitting strategy employed numerical integration of the models to generate modeled curves and calculate chi-squared values.^10,14,21 The association and dissociation phases were fit globally using either the one-to-one model or the two-compartment model for the association phase and the exponential decay model for the dissociation phase. With theoretical data, the first 20 seconds of the dissociation was discarded to remove the fall time introduced by mass transport.

For both theoretical and experimental data, the reservoir concentration, mixing volume, and flow rate were manually input to calculate the gradient concentration profile. An iterative Monte Carlo routine was used to adjust the k_a, k_d, k_m, and Γ_tot to minimize the chi-squared values. Initial values were randomly generated across a range of values and evaluated. Preliminary tests demonstrated that Γ_tot values fit to within 1% of actual values in theoretical system, so Γ_tot values were manually input for theoretical binding curves to lower the computation time. However, Γ_tot was fit as an independent variable for the experimental data. Since we designed each experiment to saturate, the initial estimate for Γ_tot was the maximum picometer shift (Δpm) observed at saturation. Equilibrium constants were calculated as K_D=k_d/k_a.

The height of the stagnant layer (h) has previously been shown to have no influence on extracted association and dissociation rates.^14,15 The only parameter influenced by the value of h is k_m. We therefore set h equal to one in order to keep units consistent depending on the data set being analyzed. For simulated systems, h was set to 1 mol/cm²/M=10³ cm. For the microring resonator data, h was set to 1 Δpm/M. We have reported k_m values in terms of k_m/h.¹⁵

Due to the nonlinear nature of the model equations, confidence intervals on extracted kinetic rates were calculated by determining F-values for a combination of k_a, k_d, k_m, and Γ_tot values.²² Confidence intervals are recorded as the maximum and minimum values for each variable that were under the critical F-value. All ranges are reported in parentheses at the 95% confidence interval.

Reagents and Materials

Purified human phosphate specific antigen (PSA) and monoclonal mouse anti-human PSA antibody (clone 5G6) were purchased from Meridian Life Science, Inc. (Saco, ME). Custom DNA oligonucleotides were synthesized by Integrated DNA Technologies (Coralville, IA) and contained a 5’terminal amino group attached via a 6-carbon chain (5AmMC6). Succinimidyl 4-formylbenzoate (S-4FB), 3-N-((6-(N’-Isopropylidene-hydrazino))nicotinamide)propyltriethoxysilane (HyNic Silane), succinimidyl 6-hydrazinonicotinamide acetone hydrazine (S-HyNic), and antibody-oligonucleotide conjugation kits were purchased from SoluLink (San Diego, CA).

Zeba spin filter columns and Starting Block were purchased from Pierce (Rockford, IL). Vivaspin molecular weight cutoff filters (50,000 and 5000 Da MWCO) were obtained from GE Healthcare (Waukesha, WI). Aniline was purchased from Acros Organics (Geel, Belgium). Phosphate buffered saline, pH 7.4 (PBS, Dulbecco’s formulation) was made from 10X stock solutions (Sigma Aldrich, St. Louis, MO) for all microchip assays. The full 10X concentration was employed for salt gradient experiments. PBS with 0.05% Tween-20 (PBST) was made by adding Tween-20 to standard PBS buffer. All buffers were degassed under vacuum sonication before use in microchip assays. All other reagents were purchased from Sigma Aldrich.

Instrumentation and Chip Functionalization

Ring resonator optical scanning instrumentation, software, and chips were obtained from Genalyte, Inc. (San Diego, CA) and have been described previously.⁷ Microchip functionalization procedures including DNA functionalization and conjugation of DNA-Abs to the chip surface have also been detailed previously.¹⁷ Additional information concerning chip microfluidics, protocols for microchip functionalization, and DNA-Ab immobilization can be found in the Supporting Information.

Analyte Gradient Delivery

The gradient maker described aboved pumped fluid across the sensor surface via the same U-shaped gasket that was employed for antibody immobilization (see Figure 1) using a P625/10K.133 miniature peristaltic pump (Instech, Plymouth Meeting, PA). Tubes were prefilled with the appropriate solutions to eliminate delay due to fluid flow. Concentrated PSA was added to the analyte reservoir, and a defined volume of PBST was added to the mixing compartment. All runs were monitored in real-time and allowed to proceed until saturation conditions were met. Once the binding curve appeared saturated, the inlet from the mixing compartment was switched to buffer. PBST flow was maintained until PSA dissociation was near completion.

RESULTS AND DISCUSSION

Design and testing of nonlinear gradient maker

A key component of the analyte gradient method is the accurate and reproducible creation of a gradient concentration profile. While the previous study utilized a straight-walled gradient maker and HPLC pump,¹⁴ we sought to design a system that was more compatible with small sample volumes and microfluidic flow cells. Many commercial linear gradient makers, such as the straight-walled gradient maker, operate on the principle of a two-compartment system. One compartment, the reservoir, contains a concentrated analyte solution. The reservoir flows into the mixing compartment, which initially contains only buffer. The mixing compartment is stirred to ensure proper mixing. If the reservoir and mixing compartments drain at the same rate, the solution flowing from the mixing compartment will linearly increase in concentration over time.

Many gradient makers use gravity to drive the drainage of each compartment.¹⁸ Greater control over the flow rate can be achieved by using two peristaltic pumps to pump solution from the reservoir tube into the mixing compartment and from the mixing compartment to the instrument. However, a linear gradient maker based on this peristaltic pump design is complicated by the need for two flow rates, one from the reservoir into the mixing compartment and twice that rate from the mixing tube into the instrument, and by the constantly decreasing volume in the mixing compartment.

A nonlinear gradient maker allows for a simpler two-compartment system than a linear gradient maker. In this system, a single flow rate is used to pump from the reservoir into the mixing compartment and from the mixing compartment into the instrument. Thus, a single pump with two tubes may be used to drive the flow, and the mixing chamber remains at a constant volume. The nonlinear gradient output from this system depends on three variables, the concentration in the reservoir, the flow rate, and the volume of the mixing compartment, and is governed by Equation 2.

To test whether the nonlinear gradient maker produced the expected gradient profile, we used a concentrated phosphate buffered saline (PBS) solution in the reservoir tube and deionized water in the mixing compartment. First, the PBS solution was directly injected over the microring resonators to determine the maximum response to the refractive index difference. The gradient maker was then tested at flow rates ranging from 5–20 µL/min and mixing volumes from 250 to 1000 µL. All showed close agreement between the gradient curves predicted by Equation 2 and the refractive index shift measured by the microring resonators. A representative plot is shown in Figure 2.

A comparison of the concentration profiles generated by a step titration and the gradient titration can be found in the Supporting Information (Figure S-1). As seen in Figure S-1 and explored in recent reports,^23,24 Taylor dispersion occurring in the fluidic system upstream of the sensor surface can cause significant deviation from ideal step concentration profiles. Diffusion in the tubes from the mixing compartment to the chip surface causes significant rise and fall times on the order of minutes for the step titration (Figure S-1B). A much smaller rise time is observed for the nonlinear gradient (Figure S-1A). Fick’s first law states that diffusive flux is proportional to the concentration gradient. Since the concentration gradient is much smaller for the nonlinear gradient titration than the step titration, nonlinear gradient concentration profiles are less influenced by these fluidic diffusion effects than traditional step titrations.

Theoretical Validation of the Nonlinear Gradient Method

In order to assess whether the nonlinear gradient method offered the same capabilities as the linear gradient method, we performed numerical simulations. Numerical simulations allowed evaluation of a greater number and wider range of conditions than would have been experimentally feasible. It also allowed theoretical validation of the nonlinear gradient strategy against precisely known kinetic rates. Theoretical binding curves were generated by inputting the concentration gradient profiles, kinetic rate constants, the number of surface binding sites, flow cell dimensions, and diffusion constant into a two-dimension partial differential equation model accounting for diffusion and lateral flow. Binding at the surface was assumed to be first order. This model is governed by Equations S-1−S-5 (see Supporting Information).

Theoretical binding curves generated with the more complex two-dimensional partial differential equations model were fit to simpler models to extract kinetic rates. A range of association rates ranging from 5×10³ to 1×10⁸ M⁻¹s⁻¹ and dissociation rates from 1×10⁻⁵ to 1 s⁻¹ were examined. Fitting the theoretical curves with a simple one-to-one interaction model for the association (Equation 3) and a single exponential dissociation model (Equation 6) generally yielded fits that were accurate to within 1–3% and a confidence interval within 5 to 10% of the actual value (see Table 1). One exception was observed when dissociation rates greater than 0.1 s⁻¹ were investigated. For very fast dissociation rates, the dissociation of analyte from the surface happens on the same time scale as the diffusion of analyte. This leads to nonzero free analyte concentration levels throughout the dissociation phase that invalidate the simple exponential dissociation model. More complex models for the dissociation phase showed somewhat improved fits but were still nearly 15% from the known value. Thus, we conclude that the nonlinear gradient method is valid for association rates ranging from 5×10³ to 1×10⁸ M⁻¹s⁻¹ and dissociation rates less than 0.1 s⁻¹, ranges similar to those reported for Biacore experiments.^1,25 However, even for kinetic rates outside this range, it is possible to obtain accurate equilibrium binding constants.

Table 1.

Kinetic Rates Determined by Fitting Simulated Nonlinear Analyte Gradient Data to the One-to-One Interaction Model

Simulated Parameters		Extracted Rates One-to-One Model
ka (M−1s−1)	kd (s−1)	ka (M−1s−1)		kd (s−1)
5.00×105	1.00×100	1.35×105	(0.81–2.56)	2.75×10−1	(1.66–5.22)
5.00×105	1.00×10−1	4.47×105	(4.07–6.01)	9.17×10−2	(8.18–12.1)
5.00×105	1.00×10−2	4.86×105	(4.68–5.19)	9.94×10−3	(9.54–10.4)
5.00×105	1.00×10−3	4.92×105	(4.86–5.04)	9.99×10−4	(9.81–10.2)
5.00×105	1.00×10−4	4.96×105	(4.94–5.00)	1.00×10−4	(0.989–1.01)
5.00×106	1.00×10−2	4.86×106	(4.68–5.19)	9.94×10−3	(9.54–10.4)
5.00×104	1.00×10−2	4.95×104	(4.86–5.09)	9.96×10−3	(9.76–10.2)
5.00×103	1.00×10−2	4.95×103	(4.87–5.08)	9.96×10−3	(9.76–10.2)
5.00×104	5.00×10−4	4.94×104	(4.90–5.05)	5.00×10−4	(4.95–5.05)

While the one-to-one model generally fit well for kinetic rates within the bounds listed above, there is still some discrepancy between the actual and extracted rates that may be attributed to mass transport effects. There are several ways to account for mass transport of analyte to the biosensor surface. One commonly used approach is known as the two-compartment model.^15,16,25 The two-compartment model was used in previous theoretical studies of the linear analyte gradient method¹⁴ and has also been applied to account for spatial offsets in surface plasmon resonance arrays.²⁶ Application of the two-compartment model to the simulated nonlinear gradient binding curves yielded kinetic rates accurate to within 1% (see Table 2). Similar to linear gradients, the nonlinear gradient method shows poor confidence in the k_m value indicating that the method does not produce reliable estimates of diffusion constants.^14,15 However, the two-compartment model is significantly more accurate for association and dissection rates than the one-to-one model.

Table 2.

Kinetic Rates Determined by Fitting Simulated Nonlinear Analyte Gradient Data from Table 1 to the Two-Compartment Model

Extracted Rates Two-Compartment Model
ka (M−1s−1)		kd (s−1)		km (cm/s)
2.29×105	(2.03–2.47)	4.58×10−1	(4.06–4.93)	1.99×10−1	(1.67–2.81)
4.99×105	(4.88–5.05)	9.96×10−2	(9.76–10.1)	1.60×10−1	(1.36–2.32)
5.00×105	(4.99–5.01)	9.99×10−3	(9.98–10.0)	1.68×10−1	(1.60–1.85)
5.00×105	(4.98–5.00)	1.00×10−3	(0.997–1.00)	2.00×10−1	(1.40–2.53)
5.02×105	(5.00–5.02)	1.00×10−4	(0.995–1.00)	1.27×10−1	(0.824–1.84)
5.01×106	(4.99–5.02)	1.00×10−2	(0.998–1.00)	1.64×10−1	(1.51–1.88)
5.00×104	(4.99–5.01)	1.00×10−2	(0.998–1.00)	1.74×10−1	(1.53–2.05)
5.00×103	(4.99–5.01)	1.00×10−2	(0.998–1.00)	1.74×10−1	(1.48–2.07)
5.00×104	(4.99–5.01)	5.00×10−4	(4.99–5.00)	1.68×10−1	(1.57–1.76)

An alternative approach to the two-compartment model is to manually adjust the input into the model to account for the fact that the concentration profile seen by the surface is influenced by mass transport. For example, with FastStep injection, the instrument generates a calibration curve based on a sucrose injection before the analysis.¹³ This calibration concentration profile is used to define the analyte concentration profile in data analysis. However, mass transport has different effects in a step titration system versus a gradient system. In a step titration, the concentration changes sharply. Mass transport causes the distortion of the concentration profile at the beginning of the step but quickly reaches equilibrium.^13,15 In a gradient experiment, the concentration is constantly changing, and the concentration profile will always be in flux. When the gradient is linear or near linear, this flux is fairly constant, and mass transport may be approximated as a delay of the gradient curve rather than a distortion of the concentration profile. In our application, this delay is exaggerated by the spatial offset of microrings along the length of the flow cell. Since the concentration profile is not constant, each microring experiences a slightly different environment at any point in time. Fortunately, the spatial offset and mass transport can both be approximated as a time delay of the ideal concentration profile. This effect can be alleviated by simply shifting the binding curves on the time axis thereby temporally aligning the curves from each microring with the first curve (see Figure S-2 in Supporting Information). After aligning and averaging the curves, the one-to-one model fits nearly as well as the two-compartment model (see Table 3).

Table 3.

Kinetic Rates Determined by Fitting Simulated Nonlinear Analyte Gradient Data from Table 1 to the Temporally Shifted One-to-One Model

Extracted Rates Temporally Shifted One-to-One Model
ka (M−1s−1)		kd (s−1)
2.22×105	(1.82–3.57)	4.45×10−1	(3.65–7.17)
4.90×105	(4.78–5.17)	9.85×10−2	(9.57–10.4)
4.97×105	(4.93–5.02)	9.98×10−3	(9.90–10.1)
4.99×105	(4.97–5.00)	1.00×10−3	(0.997–1.00)
4.99×105	(4.99–5.00)	1.00×10−4	(0.998–1.00)
4.97×106	(4.93–5.03)	9.99×10−3	(9.90–10.0)
4.99×104	(4.97–5.02)	9.99×10−3	(9.95–10.0)
4.99×103	(4.97–5.02)	9.99×10−3	(9.95–10.0)
4.99×104	(4.98–5.00)	5.00×10−4	(4.99–5.01)

We have thus far evaluated two strategies to account for mass transport in a nonlinear analyte gradient experiment, the two-compartment model and temporal aligning. Although the fits from each model were similar in minimally mass transport-influenced systems, the two-compartment model gives more accurate fits in significantly mass transport-influenced systems. A key measure of the degree of mass transport influence is the ratio of k_aΓ_tot/k_m, which we will refer to as the mass transport coefficient (MTC).²⁷ Larger MTC values correspond to a greater mass transport influence on the system. To evaluate the limits of the nonlinear gradient method with regards to mass transport, we simulated binding curves for a constant K_D but with increasing association rates.²⁵ These rates were simulated at a low binding site density and at high binding site density to achieve different MTC values for the same kinetic rates. Simulated rates, extracted rates, and MTC values are given in Table 4. At low MTC values, accurate kinetic rates are extracted using the two-compartment model. However, at MTC values above about 5, the kinetic rates are no longer reliable. Although kinetic rates are not reliable for high MTC, accurate equilibrium constants may still be obtained. This agrees with previously published results²⁵ for the two-compartment model applied to step titrations. We therefore conclude that the nonlinear analyte gradient method has similar theoretical capabilities and limitations as step titrations with regards to mass transport.

Table 4.

Kinetic Rates Determined by Fitting Simulated Nonlinear Analyte Gradient Data to Two-Compartment Model

Simulated Parametersa			Extracted Rates Two-Compartment Model
ka (M−1s−1)	kd (s−1)	Γtot(mol/cm2)	ka (M−1s−1)		kd (s−1)		km (cm/s)		MTC
1.00×106	1.00×10−3	6.00×10−13	1.01×106	(0.997–1.01)	1.00×10−3	(0.995–1.01)	1.31×10−1	(0.932–2.49)	0.005
1.00×107	1.00×10−2	6.00×10−13	1.00×107	(0.999–1.00)	1.00×10−2	(0.998–1.00)	1.66×10−1	(1.58–1.82)	0.036
1.00×108	1.00×10−1	6.00×10−13	9.97×107	(9.73–10.1)	9.95×10−2	(9.72–10.1)	1.60×10−1	(1.31–2.33)	0.373
1.00×106	1.00×10−3	1.20×10−10	1.00×106	(0.998–1.01)	1.00×10−3	(0.997–1.00)	1.51×10−1	(1.21–1.97)	0.795
1.00×107	1.00×10−2	1.20×10−10	1.00×107	(0.996–1.00)	9.98×10−3	(9.95–10.0)	1.70×10−1	(1.55–2.01)	7.050
1.00×108	1.00×10−1	1.20×10−10	9.78×107	(9.57–9.90)	9.76×10−2	(9.57–9.90)	1.74×10−1	(1.51–2.47)	67.577

^aAdditional parameters used included V = 1000 µL, r = 10 µL/min, M = 25 nM. Other parameters are as stated in the text.

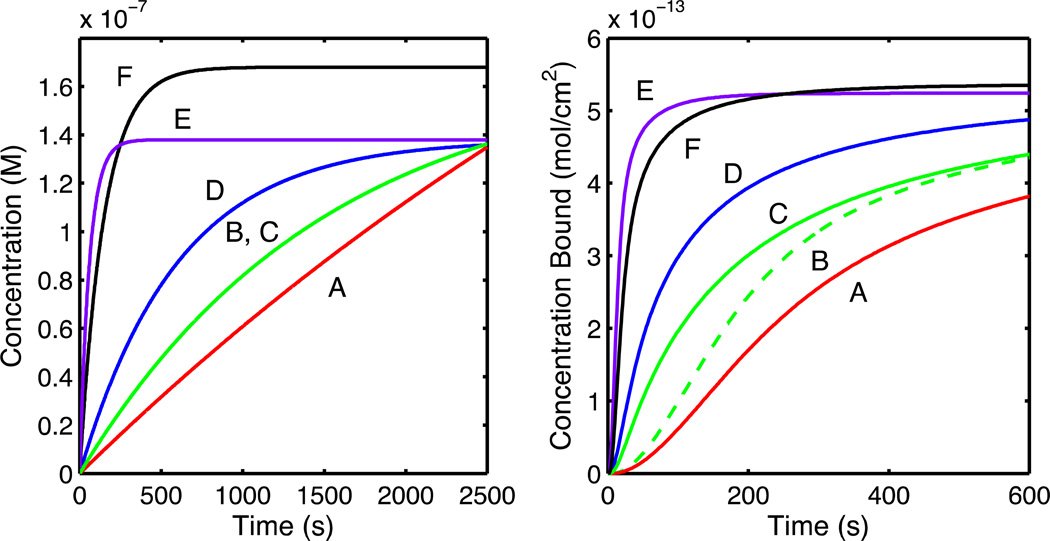
Finally, to determine if nonlinearity of the gradient slope influenced the accuracy of the extracted kinetic rates, we tested the nonlinear gradient method at a variety of flow rates and mixing compartment volumes to adjust the curvature of the gradient concentration profile. Fitting to the two-compartment model yielded kinetic rates that were accurate to within 1–2% (see Table 5). Concentration profiles and binding curves for the parameters in Table 5 are illustrated in Figure 3. These results demonstrate that the nonlinear gradient method is applicable to varying gradient slopes and curvatures. There are, however, theoretical and experimental limitations on the gradient. The primary theoretical limitation to slope is lateral mass transport effects. For a very steep slope, the spatial differences in the concentration profile will be exaggerated, and greater mass transport distortions will be introduced. Shallow slopes reduce mass transport effects but require more time. Experimentally, fast flow rates will improve mass transport but will consume more material. Larger mixing volumes will also consume more material but can be measured more precisely than small mixing volumes. Regardless, the above results demonstrate that under a range of reasonable experimental conditions the nonlinear gradient method extracts accurate kinetic rates and equilibrium binding constants.

Table 5.

Kinetic Rates Determined by Fitting Various Nonlinear Concentration Profiles to the Two-Compartment Model

	Simulated Parameters						Extracted Rates Two-Compartment Model
	ka (M−1s−1)	kd (s−1)	V (µL)	r (µL/min)	V/r (min)	M (nM)	ka (M−1s−1)		kd (s−1)
A	5.00×105	0.01	1000	10	100	396	5.00×105	(4.99–5.00)	1.00×10−2	(0.999–1.00)
B	5.00×105	0.01	250	10	25	168	5.00×105	(4.99–5.01)	1.00×10−2	(9.98–1.00)
C	5.00×106	0.1	500	20	25	168	5.01×106	(4.97–5.05)	1.00×10−1	(0.993–1.01)
D	5.00×106	0.1	500	50	10	138	5.01×106	(4.97–5.04)	1.00×10−1	(0.995–1.01)
E	5.00×106	0.1	100	100	1	138	5.03×106	(4.93–5.15)	1.00×10−1	(0.986–1.03)
F	5.00×106	0.1	100	40	2.5	168	5.04×106	(4.90–5.22)	1.00×10−1	(0.977–0.103)

Figure 3.

Concentration (left) and simulated binding curves (right) for the data in Table 5. Rows in Table 5 are shown as red (A), dashed green (B), solid green (C), blue (D), purple (E), and black (F). Solid (C) and dashed green (B) lines both derive from the green (B, C) concentration profile. Note that the time scale in the right plot has been shortened for clarity.

Application of the Nonlinear Gradient Method to Measure PSA-Antibody Binding on Microring Resonators

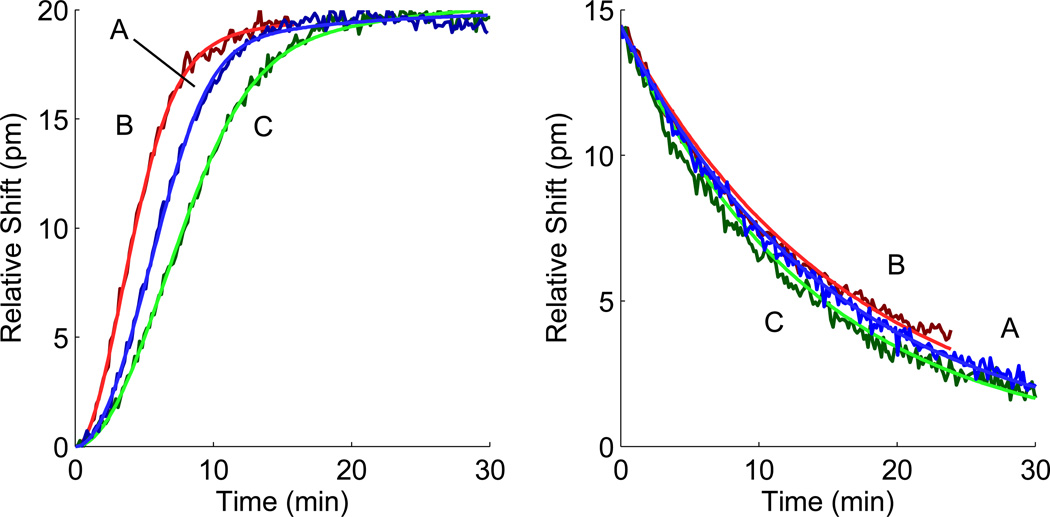
To apply the nonlinear gradient method experimentally, we interfaced the prototype nonlinear gradient maker described above with the microring resonator platform to measure the binding of PSA with an anti-PSA antibody. Of the thirty-two individually addressable microrings, eight microrings remained covered in a polymer cladding layer as thermal controls, twelve exposed microrings served as bulk index control surfaces, and twelve microrings were functionalized with ssDNA (see Figure 1 for schematic). The DNA-Ab conjugate was attached to the surface by Watson-Crick base paring. The binding response was measured in real-time for a nonlinear gradient association followed by a buffer injection to monitor dissociation. Three different gradient curvatures were tested and fit individually to determine the effects of flow rate and gradient curvature. Extracted kinetic rates are given in Table 6. Normalized association and dissociation curves as well as fits are seen in Figure 4.

Table 6.

PSA Binding to Anti-PSA Antibody with Nonlinear Gradient Method Fit to Two-Compartment Model

	Concentration Profile			Extracted Rates Two-Compartment Model
	r (µL/min)	V (µL)	M (nM)	ka (M−1s−1)		kd (s−1)		km (Δpm/Ms)
A	11.3	1000	100	9.76×105	(6.38–14.6)	1.09×10−3	(0.947–1.27)	1.32×107	(0.631–3.69)
B	18.4	1000	100	7.37×105	(5.60–9.58)	1.02×10−3	(0.898–1.20)	5.21×109	(2.61–Inf)
C	11.3	1000	50	1.00×106	(0.749–1.40)	1.20×10−3	(1.03–1.50)	4.03×107	(2.22–Inf)

Figure 4.

Microring resonator response for PSA binding to anti-PSA antibody and fits to the two-compartment model for concentration profiles detailed in Table 6. Normalized experimental association (left) and dissociation (right) curves from Table 6 are presented as dark blue (A), dark red (B), and dark green (C). Fits are presented as blue, red, and green respectively.

In all three experiments, k_a, k_d, and K_D values agree within the 95% confidence interval. The k_d values agree closely with the previously published rate for anti-PSA-5G6 and PSA measured on the same platform with a step titration series, while the k_a values are around 40% of the previously published rate.¹⁷ Of the three binding curves, only curve A with the steep gradient (concentration equal to 100 nM) and low flow rate (11.3 µL/min) shows evidence of mass transport influences. For the curves B and C with a faster flow rate (18.4 µL/min) or with a shallower slope (50 nM), fitted k_m values have no upper bound indicating an essentially infinitely fast mass transport rate (see Table 6). Moreover, fitting these two curves to the one-to-one model yields fits very similar to the two-compartment model. Conversely, curve A showed an improved fit with the two-compartment model and bounded k_m values. Thus, experimental results reinforce theoretical conclusions that shallower slopes and faster flow rates limit mass transport effects in the nonlinear gradient method. These experimental results demonstrate the utility of the nonlinear gradient method for single shot kinetic experiments on the microring resonator platform.

CONCLUSIONS

We have detailed the instrumentation, simulation, and experimental application of the nonlinear analyte gradient method for kinetics of biomolecular interactions. This represents the first application of single shot kinetic experiments on the microring resonator biosensor platform. Since the surface does not need to be regenerated, as with step-wise titrations, the analyte gradient method requires less time, materials, and sample preparation than conventional methods, and it offers increased analyte throughput. Although this experiment focused on a single ligand and analyte, future experiments making use of the multiplexing capabilities of the microring resonators will allow for single shot kinetic experiments for multiple ligands and increased assay throughput.

The principles of nonlinear analyte gradient instrumentation and experiment design are readily applicable to other refractive index-based biosensor platforms. The simplicity of the nonlinear gradient maker design makes it available to a variety of platforms and instruments. Some commercial fluidic systems have the capability to generate analyte gradients.¹³ Since the nonlinear gradient maker design detailed here could be powered by a single syringe pump with a sealed mixing compartment, we envision that existing instruments could be easily retrofitted with a gradient maker.

Finally, it is important to note that the nonlinear analyte gradient method is limited by many of the same constraints as conventional step titration experiments. Similar to step titration experiments, kinetic rates should be in the bounds detailed above. The curvature and slope of the analyte gradient profile must be reasonable as described above to avoid mass transport problems. Finally, data must be of high quality with appropriate controls to correct for baseline shifts. Despite these limitations, the nonlinear analyte gradient method is an effective alternative to conventional step-titration techniques that allows for higher throughput and single shot kinetic experiments with minimal additional instrumentation.