“Good Enough Solutions” and the Genetics of Complex Diseases

Abstract

Rationale and Objective

In this Emerging Science Review, we discuss a systems genetics strategy, which we call Gene Module Association Study (GMAS), as a novel approach complementing Genome Wide Association Studies (GWAS), to understand complex diseases by focusing on how genes work together in groups rather than singly.

Methods

The first step is to characterize phenotypic differences among a genetically diverse population. The second step is to use gene expression microarray (or other high throughput) data from the population to construct gene co-expression networks. Co-expression analysis typically groups 20,000 genes into 20–30 modules containing 10’s to 100’s of genes, whose aggregate behavior can be represented by the module’s “eigengene.” The third step is to correlate expression patterns with phenotype, as in GWAS, only applied to eigengenes instead of SNPs.

Results and Conclusions

The goal of the GMAS approach is to identify groups of co-regulated genes that explain complex traits from a systems perspective. From an evolutionary standpoint, we hypothesize that variability in eigengene patterns reflects the “good enough solution” concept, that biological systems are sufficiently complex so that many possible combinations of the same elements (in this case eigengenes) can produce an equivalent output, i.e. a “good enough solution” to accomplish normal biological functions. However, when faced with environmental stresses, some “good enough solutions” adapt better than others, explaining individual variability to disease and drug susceptibility. If validated, GMAS may imply that common polygenic diseases are related as much to group interactions between normal genes, as to multiple gene mutations.

Introduction

The Human Genome Project completed in 2001 is one of the seminal achievements in modern science, and ushered in an era of unbridled optimism about our prospects for deciphering the genetic basis of human diseases, and beyond ¹. A decade later, over a thousand genetic loci conferring increased risk of a wide variety of diseases have been identified, successfully revealing new genes and novel pathways not previously suspected to be involved ². While these findings are a major advance, associations of SNPs with common polygenic diseases, have, in some respects, been disappointing ³: generally, SNP’s typically confer only a modestly increased risk (average 1.3-fold) and explain only a small fraction of the genetic component (less than 20%). Moreover, since the loci are identified out of context, elucidating the role such genes play in disease can take years (e.g., the role of apolipoprotein E in Alzheimer’s). Even for single gene disorders (such as Huntington's disease), a mechanistic understanding of the effects of the genetic variation remains challenging. For common complex diseases such as hypertension, diabetes, atherosclerosis, heart failure, cancer and Alzheimer’s disease, SNPs associated with increased risk have small effect sizes and only account for a small fraction of the genetic risk ³. Thus, the majority of patients at risk for developing common diseases are unlikely to be identified by SNPs.

This is not really surprising, given that most common diseases are polygenic, caused by modest effects of multiple genes interacting with environmental factors. Hundreds or thousands of loci can influence common polygenic diseases and many of these loci have individual effect sizes too weak to be identified individually by Genome-Wide Association Studies (GWAS). Since GWAS focus on identifying SNPs that for the most part co-vary with single gene mutations, it is not surprising that the genetic basis of common diseases remains unsolved for the bulk of afflicted patients.

To break this impasse will require moving beyond the single gene perspective to view how groups of genes work together. A worthwhile analogy may be the similarity between a human organism and a business organization. Both have modular designs: a human is comprised of physiological modules regulating metabolism, cell cycling, apoptosis, differentiation, signaling, structural integrity, etc., whereas a large business consists of divisions, such as production, distribution, marketing, public relations, hiring, legal, etc. If you were asked to analyze why a business is failing, the equivalent to GWAS would be a bottom-up approach, reviewing the personnel file of each employee (gene), one at a time, to decide whom to pin the blame on. Occasionally, a business failure may be attributed to a single rogue employee (analogous to a monogenic disease), but most business failures are multi-factorial (analogous to complex polygenic diseases) in which key divisions are underperforming or not integrating their activities effectively with other divisions. In the human genome, there are millions of SNPs with a prevalence exceeding a few percent of the general population ². It is the combined effect of many variants which contribute to an individual’s disease risk. In principle, a bottom-up GWAS approach could be applied to analyze these SNP’s and identify the variation involved in disease. However, since each SNP involved in disease only accounts for a small fraction of the disease risk, astronomically large samples are required to identify these variants. Straightforward combinatorial mathematics illustrates the problem. To identify one SNP out of a million associated with a disease is already looking for a needle in a haystack. However, the number of ways in which a million SNP’s can be combined in pairs is approximately 500 billion¹; for triplets, this number mushrooms to 1.7×10¹⁷. For 16 SNP combinations, the number of possible combinations reaches 10⁸², greater than the estimated number of atoms in the observable universe (10⁸⁰)! As an example, GWAS performed to identify the genetic basis of coronary heart disease involved over a hundred thousand individuals, and still these studies accounted for only about 4% variance of the trait. A discussion of the lack of power of GWAS for identifying genetic interactions is presented in Zuk et al. ⁴.

If the bottom-up GWAS approach of looking at SNP (or gene) combinations to explain complex disease susceptibility has serious limitations, an alternative is to develop a top-down approach. In analyzing a business failure, this would entail a multi-step process: first, group (cluster) employees into divisions (modules); second, relate the divisions to performance measures; third, identify under-performing employees within poorly performing divisions. In this article, we provide a perspective illustrating how we might take advantage of new “–omic” technologies to view how genes work in groups, rather than as single agents, and use this information to develop an analogous top-down strategy for elucidating the genetic basis of complex polygenic diseases. In the first section, we set the stage by borrowing the “good enough solution” concept from the field of evolutionary biology ⁵, ⁶. This concept is based on the idea that in complex systems, many different combinations of the system’s parameters can produce a nearly identical output (i.e. “good enough solutions” which meet the required output specifications). Thus, a wide range of individual gene expression patterns may all be perfectly adequate for normal function, but have different abilities to adapt to an environmental stress, accounting for differential susceptibility to common diseases and drug reactions. This raises the intriguing hypothesis that susceptibility to common diseases and drug reactions may be more related to the way in which normal genes interact with each other, than to additive effects of multiple gene mutations. Following upon this rationale, we then describe how network theory can be applied to gain insight into biological systems. We explain how a randomly-interacting, growing modular network facing selection pressures naturally evolves towards a scale-free network topology conferring robustness, adaptability, and efficiency, through small world properties, to the system. We then turn to the gene networks specifically, and discuss how systems genetics approaches can be used to discover how genes are naturally grouped into modules, each containing tens to hundreds of genes, linked in an approximately scale-free modular network. We explain how the functions of these modules can often be discerned from known genes (e.g. apoptosis genes, metabolic genes, cell cycle genes) and cell markers in which they are enriched. We then illustrate how novel system genetics resources, such as the Hybrid Mouse Diversity Panel (HMDP), can be utilized to test the hypothesis that variation in gene module expression patterns between different strains of mice reflect different “good enough genetic solutions” which are all comparably adequate for normal function, but exhibit differential adaptability to disease-inducing stresses. Conceptually, this allows for a Gene Module Association Study (GMAS) to explore associations between gene module expression patterns and disease susceptibility, using the same biostatistical techniques developed for GWAS. In the final section, we discuss some possible applications of this GMAS strategy, and speculate on how this approach might be used on a broader scale involving the other “–omics,” to further elucidate the causes of common human diseases and drug reactions.

“Good Enough Solutions”

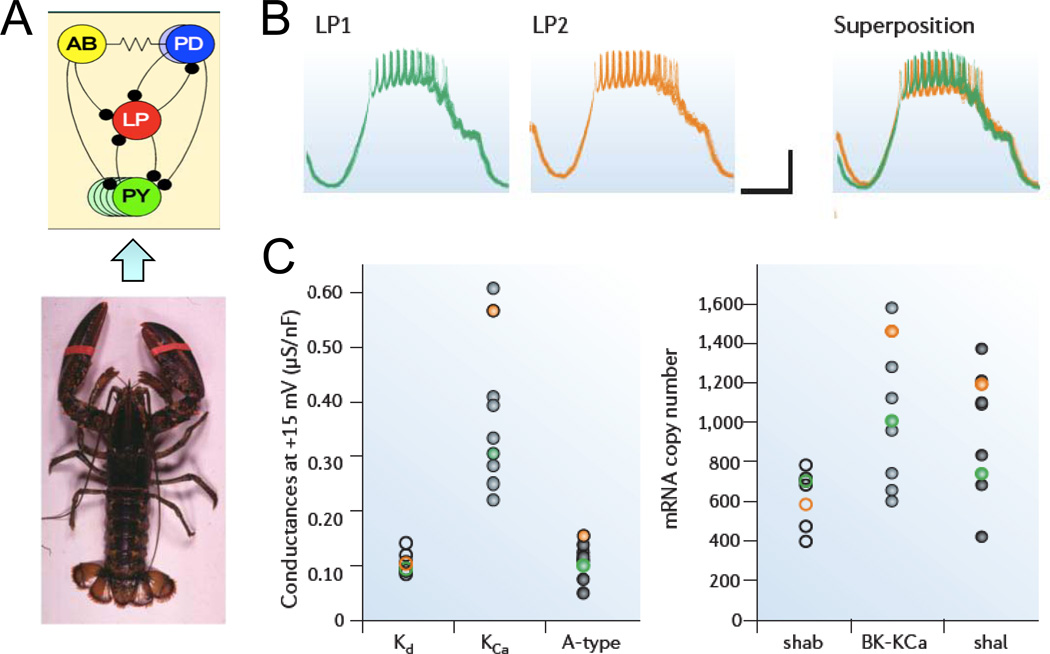
In a series of fascinating studies ⁵, neuroscientist Eve Marder and her colleagues have investigated the somato-gastric ganglion of lobsters and crabs. This ganglion, which consists of about 30 neurons with well-defined interactions, exhibits a characteristic neural bursting pattern controlling digestive activity (Fig. 1A). When Marder and colleagues analyzed the densities of various ion channels regulating the bursting activity, they were surprised to find that, despite very similar bursting patterns, the densities of the key ion channels differed substantially from lobster to lobster, which they also confirmed by measuring mRNA and protein levels ⁵. For example, some lobsters expressed Ca-activated K channels at a high level, whereas others relied on a low expression level, but both exhibited nearly identical bursting patterns under normal conditions (Fig. 1B). When subjected to an environmental stress, such as histamine exposure, however, the responses could be quite different ⁵. When they constructed a mathematical model of the bursting behavior incorporating the relevant ion channels known to be present, and performed a random search of 17 parameters to identify combinations produced similar bursting patterns, out of 594,510 models tested, they identified over a thousand “good enough solutions” that satisfied the basic requirements (Fig. 1B). Upon reflection, this is not really surprising, since it has been long appreciated that when models contain many adjustable parameters, many different combinations can be fitted to the same data (e.g. by requiring that the sum of squares of the differences between the predicted and actual data fall below some arbitrary minimum threshold). To paraphrase John von Neumann ⁷, “With four parameters, I can fit an elephant, and with five I can make him wiggle his trunk.”

Fig. 1.

“Good enough solutions” in the somato-gastric ganglia of lobsters. A. Schema of the somato-gastric ganglion (above), whose bursting pattern controls digestive activity in the lobster (below) B. All lobsters exhibit very similar bursting activities (green and orange traces). C. However, different lobsters use different combinations of ionic conductances (left) and corresponding ion channel gene expression levels (right) to produce the nearly identical bursting patterns. Adapted from Marder ⁵, with permission.

Why do different lobsters choose different “good enough solutions” for the same bursting behavior? Marder and colleagues argued that it has the evolutionary advantage of enhancing the adaptability of the lobster population as a whole to environmental stresses. For example, imagine that a toxin blocking Ca-activated K channels is dumped into the lobsters’ habitat. Those lobsters whose “good enough solutions” are highly dependent on Ca-activated K channels will be poisoned, and may die. However, lobsters whose “good enough solutions” are minimally dependent on Ca-activated K channels will be spared, so that although the lobster population will be transiently diminished, it will not be extinguished. Thus, the “good enough solution” concept resolves the paradox that a living organism must be both robust, i.e. impervious to environmental challenges, yet at the same time be able to adapt to environmental challenges. That is, the organism is resilient and stable in the face of most, but not all, environmental challenges. As long as all of the individuals in the population are not all susceptible to the same environmental challenges, this differential adaptability ensures that some individuals will survive to restore the population.

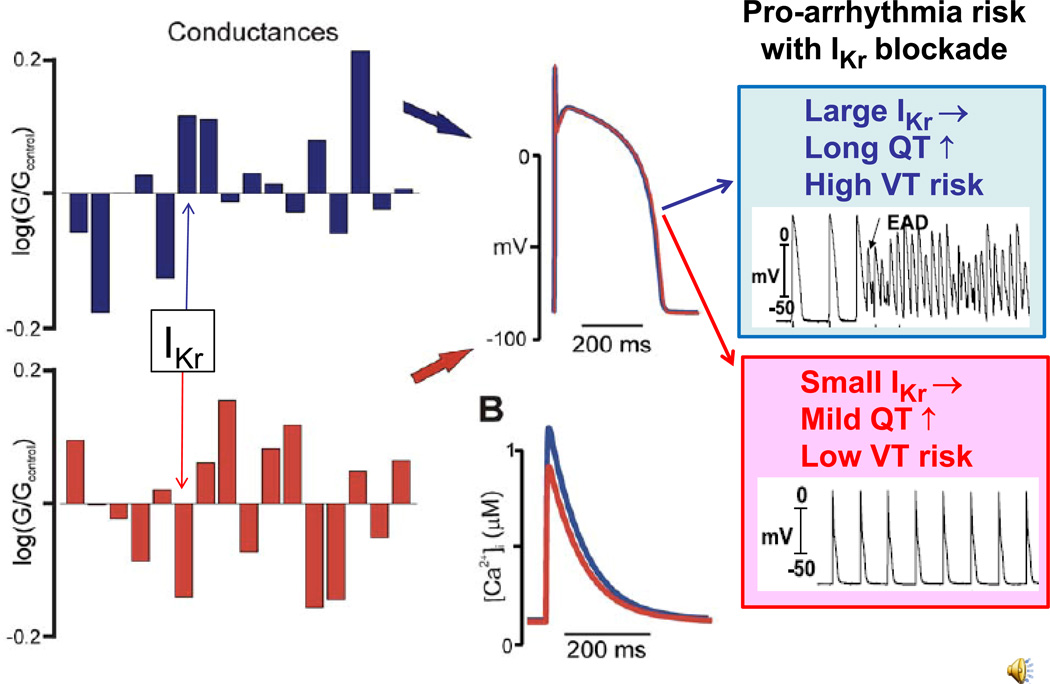
It is easy to imagine how the same principle might apply to patients in a clinical setting ⁸. For example, consider the human ventricular action potential model illustrated in Fig. 2. In this computer modeling study, Sarkar & Sobie⁹ used a human cardiac action potential model to demonstrate that many different combinations of 16 ionic current parameters all produced “good enough solutions” to generate a “normal” cardiac action potential. Fig. 2A shows two different combinations of parameters that produced nearly identical action potentials (blue and red). For the blue trace, the conductance of rapidly-activated delayed rectifier K channels (G_Kr) is much larger than for the red trace, indicating that repolarization of the blue action potential depends more strongly on G_Kr. Now imagine two patients, Tom and Jerry, whose genetically-determined cardiac action potentials correspond to the blue and red “good enough solutions” respectively. Tom and Jerry both have normal QT intervals on their electrocardiograms, since the summed ionic conductances are adequate to repolarize either action potential under normal conditions. However, suppose that Tom and Jerry develop infections, and are treated with the antibiotic erythromycin, a known G_Kr blocker. Tom’s QT interval may show dramatic QT interval prolongation, since his ventricular repolarization is strongly dependent on G_Kr. Jerry, on the other hand, may show little change, since his ventricular repolarization is relatively insensitive to G_Kr. Thus, Tom is at increased risk of developing life-threatening arrhythmias like Torsades de pointes when exposed to G_Kr blocking drugs, whereas Jerry is not.

Fig. 2.

Two sets of ionic conductances (log(G/G_control) in a human ventricular action potential model which produce nearly identical action potentials and Ca transients (middle red and blue traces, respectively), i.e. representing two “good enough solutions” for normal cardiac function. Arrows point to the conductance of I_Kr, an important current for repolarization, which is large in the blue action potential and small in the red action potential. If these action potentials corresponded to two different “good enough solutions” in real patients, the blue patient would be at greater risk for QT prolongation and torsades de pointes than the red patient if administered a drug such as erythromycin which blocks I_Kr. Adapted from Sarkar and Sobie ⁹ with permission.

If true in humans as well as lobsters and crabs, the “good enough solution” concept provides an appealing explanation for why some individuals, but not others, develop side effects from drugs, or, similarly, why only some individuals develop hypertension on a high salt diet, or atherosclerosis on a high fat diet. This raises the possibility that “modifier genes,” the traditional explanation proposed to underlie individual susceptibility to drug reactions or diseases, are really different “good enough solutions” among individuals in a population. If true, susceptibility to common diseases or drug reactions might be determined more by how normal genes are grouped, rather than by additive effects of multiple gene mutations.

Networks

To understand how our genome produces different “good enough solutions,” we need to understand how gene expression is regulated at a global level, i.e. how genes interact with each other within the context of an integrated biological network. In principle, our 23,000 genes could be individually regulated to produce a truly astronomical number of potential “good enough solutions.” However, mounting evidence indicates that biological systems are organized as modular networks, in which genes, proteins, metabolites and other factors operate in groups, rather than as single agents. For example, it is well-appreciated that many transcription factors, micro RNA’s, DNA methylation and chromatin remodeling regulate the expression of large numbers of genes in concert, consistent with genes being organized as a network of co-expression modules.

How can a gene co-expression network, if it exists, be revealed? In network theory, a complex system is represented in a highly abstract manner, dispensing with the fine details and considering the system simply as “nodes” connected by “links” or “edges”. This type of analysis has provided dramatic insights into how network structure (also called network topology) evolves in complex systems, ranging from technology and social networks to biological networks, including gene, metabolic and protein-protein interaction networks ¹⁰.

The process begins when a group of nodes form links with each other. If the process is random, then the majority of nodes will have close to the average number of links per node, and very few nodes will have many more, or many fewer, links than the average. But now suppose that the network is growing, with new nodes and new links being added over time. In this case, the original nodes, having been around longer, will have had more opportunities to capture links as they are added to the system. Thus, older nodes will have, on average, more links than newer nodes, eventually creating a small subset of the oldest nodes, called hub nodes, which are more highly connected than average node. Now imagine one more feature, that nodes which have already acquired a substantial number of links have an advantage in acquiring new links as they are added to the growing network, i.e. “the strong get stronger and the weak get weaker.” This feature, called preferential attachment, further accentuates the connectivity of the hub nodes, generating a “scale-free” network, so-called because the number of links per node follows a power law distribution.

For a self-organizing system which needs to be robust, adaptable and efficient in order to survive in a constantly changing environment full of daily stresses, such as any biological organism, the presence of highly-connected nodes in a network confers some extraordinarily useful properties. First, a network with many parallel connections between nodes has the advantage that should a link between two nodes a and b be destroyed, redundant pathways exist to allow the information to flow from a to b by an alternate route (e.g. through a node c linked to both a and b). In a typical scale-free network, for example, up to 80% of nodes and links can be randomly destroyed before the network fails catastrophically ¹¹. In contrast, a purely linear pathway (e.g. a→ b→ c → d) is disabled if even a single link or node is destroyed. Thus, the robustness of a network in the face of a constantly changing environment is a key property promoting survival.

The second key network property is the ease with which information flows quickly from one location to another. This “small world property” is conferred by hub nodes which make long range connections to other nodes, analogous to the “six degrees of separation” effect in friendship networks. The ability to access any individual node from a multitude of alternative pathways makes a scale-free network inherently adaptable to changing environmental conditions, another key priority for living systems.

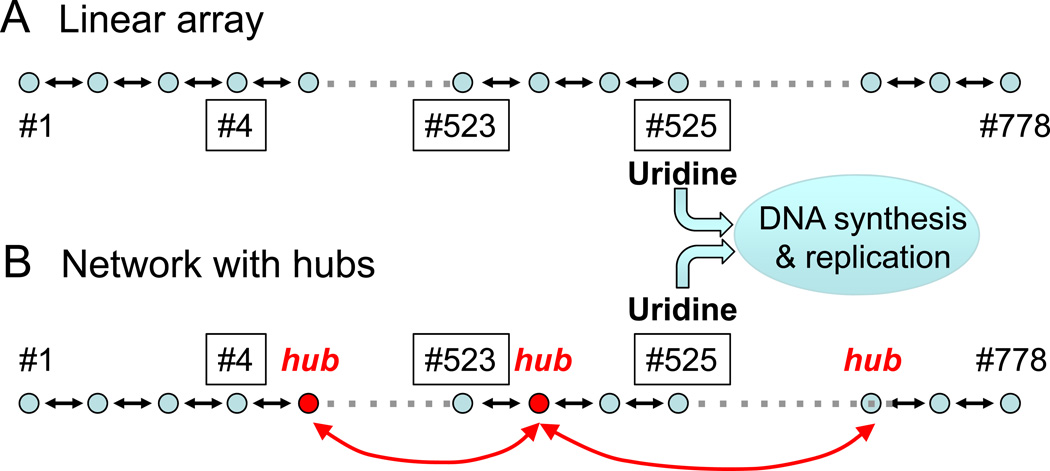
Since the properties described above involve the presence of multiple redundant pathways, one might think that a scale-free network, by favoring robustness and adaptability, sacrifices efficiency compared to a linear system in which the pathway between the input and output is very direct. This might be true if the system operated under nonvarying environmental conditions. However, to adapt to changing environmental conditions, a network is inherently more efficient than a strictly linear system. For example, consider the bacterium E. Coli, whose metabolic pathways include a total of 778 metabolites ¹². To represent metabolism as a network, each metabolite is considered a node, and each enzyme which converts one metabolite to another is a link. If, hypothetically, E. Coli’s metabolites (nodes) were arranged in a linear chain, from #1 to #778, linked by enzymes converting #1 to #2, #2 to #3, and so forth (Fig. 3A), then consider the following scenario. If metabolite #575 were a critical metabolite such as uridine, required for DNA synthesis and replication, the bacteria would thrive in a broth containing an ample supply of nearby metabolites, such as #573. However, if the supply of #573 was exhausted, and only a metabolite at the end of the chain was available, such as #4, the bacteria would now have to convert hundreds of precursor metabolites to produce uridine. This process would be slow, inefficient and energetically costly, making it unlikely that the bacteria could adapt successfully to its new environment. In contrast, in a scale-free metabolic network, the presence of hub nodes ensures that metabolites anywhere in the network can be converted to uridine in only a few steps, as illustrated in Fig. 3B (red nodes).

Fig. 3.

Small world properties in metabolic networks. A. Hypothetical arrangement of E. Coli’s 778 metabolites in a linear chain. If #525 is Uridine (required for DNA synthesis and replication), its synthesis from nearby precursor metabolites such as #523 is highly efficient, requiring only a few steps. However, if only distant precursors such as #4 are available, hundreds of steps are now required, making Uridine synthesis slow, inefficient and energetically costly. B. In contrast, highly-connected hub nodes (red) in a scale-free network allow efficient conversion of either #523 or #4 to Uridine in only a few steps.

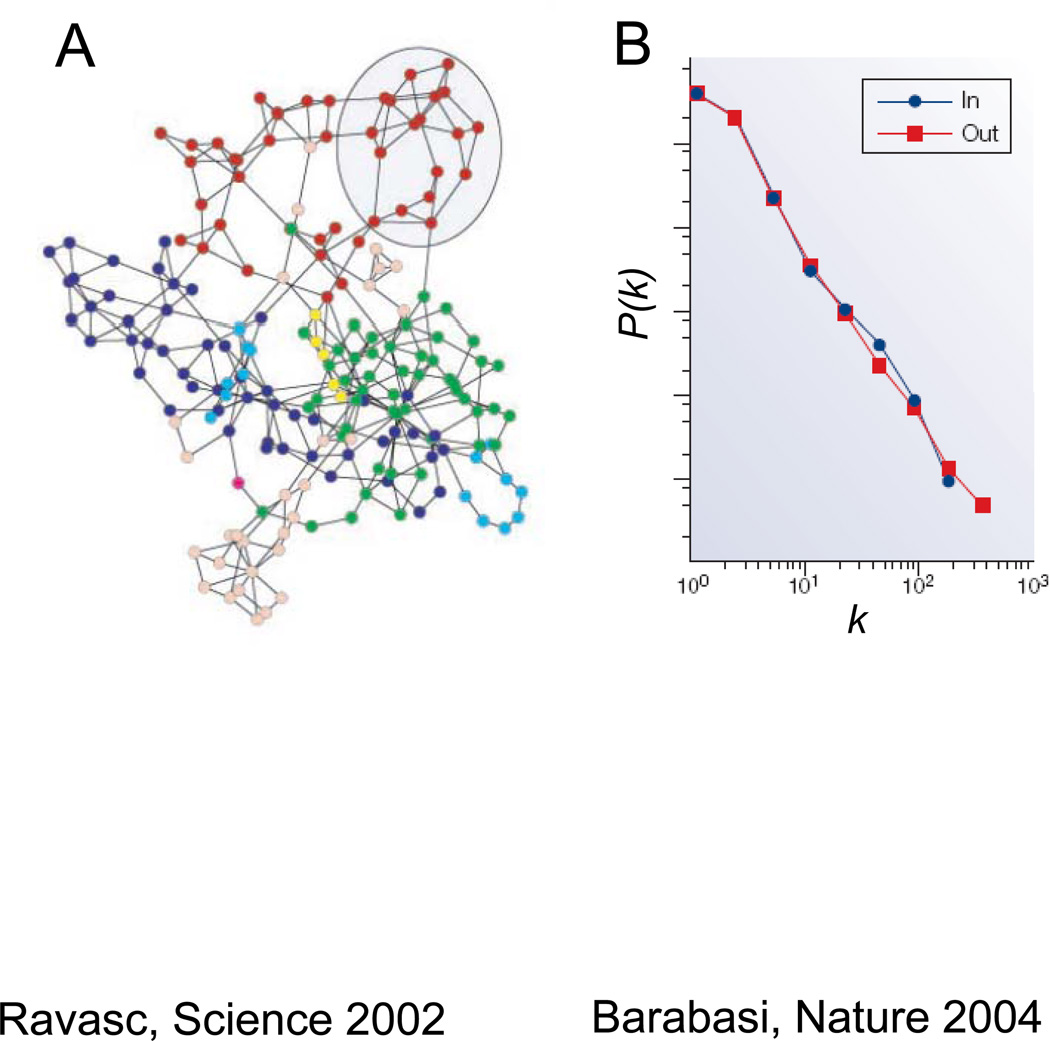
What is the evidence that scale-free topology is present in modular biological systems, such as metabolic, gene and protein networks? Directly extrapolating from technology and social networks, Barabasi and colleagues ¹² were the first to show that the metabolism of E. Coli had features of a scale-free network. Representing each metabolite as a node, and each enzyme as a link, Fig. 4A shows the E. Coli network displayed visually as a topological overlap map. Fig. 4B shows the statistical distribution of the number of links per node on a log-log scale, demonstrating the power law relationship (i.e. the defining characteristic of scale-free systems). For E. Coli, the metabolic network of 768 nodes contains 5,763 links. Due to the hub metabolites (such as ATP, pryuvate, glutamate, NADH, and others), the average number of links (distance) required to convert one metabolite to another is 3.2 ¹², i.e. less than the “six degrees of separation” characterizing many social networks. So our hypothetical E. Coli bacteria in Fig. 3 would do just fine in a culture medium containing either metabolite #573 or #4 as its only available substrate for synthesizing uridine.

Fig. 4.

A. The E. Coli metabolic network, displayed as a topological overlap map, in which metabolites are nodes (circles) and enzymes converting one metabolite to another are links (lines). Colors reflect the modules to which the nodes (metabolites) belong, corresponding to carbohydrate, protein, lipid, nucleic acid, aromatic, monocarbon and coenzyme metabolism. Adapted from Ravasc et al ²⁵, with permission. B. Log-log plot of the distribution of links per node (P(k) vs k), showing a power law distribution for both ingoing (blue) and outgoing (red) links. Adapted from Barabasi and Oltvai ⁵⁰, with permission.

Barabasi and many others have gone on to show that, in addition to metabolism, both gene co-expression networks and protein-protein interaction networks display similar power law relationships suggesting at least an approximately scale-free topology ¹⁰. Although this could be merely coincidental, the convergence of modular systems, ranging from molecular to social networks, towards scale-free topology suggests a fundamental mechanism in biological evolution for optimizing robustness, adaptability and efficiency in response to a changing environment, the essential qualities needed for a biological organism to thrive.

How to construct a gene network

We now turn to analyzing genes from a modular network perspective. We start by assuming that if genes belong to the same module, they will be co-regulated by the same factors, and therefore their expression levels should track each other. In addition, from the considerations enumerated above, we assume that this modular network is likely to exhibit, at least approximately, a scale-free topology. A number of analytical methods have been proposed to detect sets of interacting genes, including nonnegative matrix factorization ¹³, Bayesian networks ^14–17, ARACNe ¹⁸, Geronemo ¹⁹ and MINDy ²⁰ or WGCNA ^21–23. The first step is to quantify gene expression levels in a genetically diverse population, which can be achieved using gene expression microarrays or RNA sequencing. The next step is to analyze this data using an appropriate network analysis algorithm. Here we briefly summarize the approach using one of these approaches, Weighted Gene Co-Expression Network Analysis (WGCNA). WGCNA utilizes the natural quantitative variation in gene expression levels between individuals in the population to analyze how strongly each gene’s expression level correlates with every other gene’s expression level across the population. The result is a matrix containing all pair-wise Pearson correlations between all genes. These Pearson correlations are then transformed to a measure of pairwise connection strength (adjacency), which is accomplished through a soft thresholding process, accomplished by raising the correlation to a fixed power β known as the soft threshold (typically, the default β=6). This particular soft thresholding approach has several practical and theoretical advantages: i) it results in a linear relationship between adjacency and correlation coefficients on a log scale; ii) β is a single threshold parameter which is highly robust with respect to the choice of the threshold, and iii) the resulting correlation network facilitates a geometric interpretation of network statistics ²⁴.

A critical step in the network analysis is the definition of modules. Toward this end, the adjacency measure is often transformed into a more robust and biologically meaningful measure of network interconnectedness that takes into account the shared neighbors of each gene pair in the network, called topological overlap ²¹, ²⁵. From the topological overlap values calculated between each gene and every other gene, groups of genes with high topological overlap are hierarchically clustered to define modules ²¹. Modules correspond to branches of the resulting cluster tree, which are defined using dynamic tree cutting ²⁶. A gene’s connectivity is rated by the sum of all of its adjacency values (or alternatively topological overlap values) with other genes in the same module (defining its intramodular connectivity), as well as with genes in different modules (defining its intermodular connectivity). Intramodular hub genes can be identified as the most highly connected genes in each module.

Since each gene module contains tens to hundreds of genes, the next key data reduction step is to identify a reliable surrogate which expresses the aggregate behavior of each gene module in the network. In WGCNA, the method used is principal component analysis (PCA), which summarizes the expression profile of the genes inside a co-expression module by the module eigengene (the first principal component of the adjacency co-variance matrix). The module eigengene is the mathematically optimal summary of the module expression profiles, since it captures the maximum amount of variation.

It is important to emphasize that the construction of the network as outlined above is unbiased – that is, once the raw gene expression data has been processed, no assumptions are made beyond the soft threshold β used for defining the adjacency matrix. Setting a low soft threshold is more inclusive, creating a small number of highly-interlinked modules, whereas setting a high threshold is more exclusive, creating a large number of sparsely-interlinked modules with more unlinked genes. How do we choose the most appropriate soft threshold β? There is no unequivocal answer, but several independent criteria are used in practice. The primary criterion assumes that Darwinian evolution should favor a scale-free network topology, to maximize robustness, adaptability and efficiency through small world properties, as discussed earlier. Thus, a practical criterion is to select the smallest value of β that yields an approximately scale-free network topology.

Secondary criteria are based on whether the identified modules are biologically meaningful. Assuming that modules in a gene network, like divisions of a business organization, are likely to have identifiable functions, each module can be examined for the genes with known functions, to determine if the module is enriched in a particular class of genes (e.g. cell cycling, apoptosis, cytoskeleton, metabolism, signaling). Thus, from gene ontology (GO) enrichment, biological functions can often be assigned to different modules. Another strategy is to determine whether modules correlate with known cell markers, since modules sometimes correspond to different cell types within a given tissue ²⁷.

In summary, a soft threshold choice which yields a network with approximate scale-free topology containing modules with well-defined biological functions (based on gene ontology enrichment or cell marker enrichment) is biologically credible. The interested reader can access further details at: http://www.genetics.ucla.edu/labs/horvath/CoexpressionNetwork/ or in book form²⁸.

Gene networks can be constructed using gene co-expression data obtained from any population exhibiting genetic diversity. The obvious challenge, however, is to demonstrate, in an independent manner, that a modular gene network is functionally meaningful, and not just biostatistical fluke. The key functional criterion for biological validity is whether the expression of gene modules (i.e. the eigengene expression pattern) predicts phenotype. Although this aspect is still in its infancy, eigengene expression levels have been shown to correlate with traits in humans, animal models or cell lines for a variety of diseases including autism ²⁹, Alzheimer’s disease ³⁰, heart failure ³¹, obesity ³², ³³, hyperlipidemia ³⁴ and atherosclerosis ³⁵. Moreover, by associating eigengenes with specific traits, the gene module represented by the eigengene can then be broken down into its constituent submodules, which can be analyzed in detail to discover novel genes and pathways that regulate the phenotype.

Models to construct and validate gene networks

Validation of systems genetics approaches requires that both molecular phenotypes (such as global transcript levels) and clinically relevant phenotypes be concomitantly examined among the individuals of a population. What kinds of populations are available to test and validate the GMAS concept? Human studies are necessarily limited by the difficulty of accessing tissues other than blood and cell lines. Model organisms such as yeast, flies, and worms can serve as excellent resources, but their relevance to common human diseases is limited. Among mammals, rodents are currently the most well-developed models for systems genetics, since strains exhibiting wide genetic variation have been developed and there is a large body of knowledge of their physiology, genetics, and genomics. Sets of recombinant inbred rats, in particular, have proven particularly useful for systems genetic analyses of cardiovascular and metabolic traits ³⁶. The use of mice for genetic studies was facilitated historically by the popularity of breeding mice as pets, called fancy mice, which originated in China and reached its height of popularity in Europe in the late 19^th century. The genetic diversity of fancy mice spans more than a million years of murine evolution, when the ancestral Northern Asian, Southern Asian and European lines first diverged ³⁷.

To link genotype to phenotype in rodents, a typical approach is to perform genetic crosses between two strains exhibiting different phenotypic responses to an environmental stressor, such as the predisposition to obesity when placed on a high fat diet. Due to homologous recombination during cross-breeding, large regions of chromosomes are randomly swapped among progeny of the two strains, which in turn results in differences in gene expression among the progeny. Drawbacks, however, are that each progeny is genetically unique, so that the correlation between gene expression and phenotype can only be assessed once per genetically-identical individual. Also, the incidence of homologous combination in mice is low, which limits resolution.

Recently, new resources has been developed to circumvent some of these limitations ³⁸. A highly diverse set of mouse recombinant inbred strains, termed the Collaborative Cross, is now under development ³⁹. Here, we focus on a similar resource called the Hybrid Mouse Diversity Panel (HMDP) ³⁸, which consists of 100 (or more) common and recombinant inbred strains which have been either entirely sequenced or densely genotyped with over 140,000 SNPs. The HMDP strains are commercially available and thus can be assayed for multiple phenotypes by different laboratories, providing cumulative biological insights. The ability to use classic inbred strains in this manner is dependent on correction for population structure using an algorithm such as the Efficient Mixed Model Algorithm ⁴⁰. Since individuals within a given HMDP strain are genetically identical to each other, the reproducibility of gene expression and phenotype among individuals of the same strain can be assessed. Thus, intra-strain variability due to environmental factors can be separated inter-strain variability due to genetics, both with respect to gene expression and phenotypic responses to an environmental stressor. Studies to date have documented that intra-strain variability in gene expression and phenotype is much less than the inter-strain variability ³⁸. GWAS studies using the HMDP have successfully detected and finely mapped genes modulating adiposity, bone density, plasma lipids, and other complex traits ⁴¹. For example, in a network study examining the genetic basis of adiposity in mice, a set of curated pathways was shown to be enriched in genes differentially expressed between livers of fat and lean mice in a segregating mouse population ²². The identified pathways tended to center on the tricarboxylic acid cycle, which is central in energy production. Through the use of systems genetics, a set of 9 genes were predicted to be causally related to adiposity in mice ⁴². Their effects on adiposity were validated with transgenic approaches, and expression array analyses of the transgenic mice showed that the differentially regulated genes were enriched in many of the same tricarboxylic acid–centered pathways ⁴².

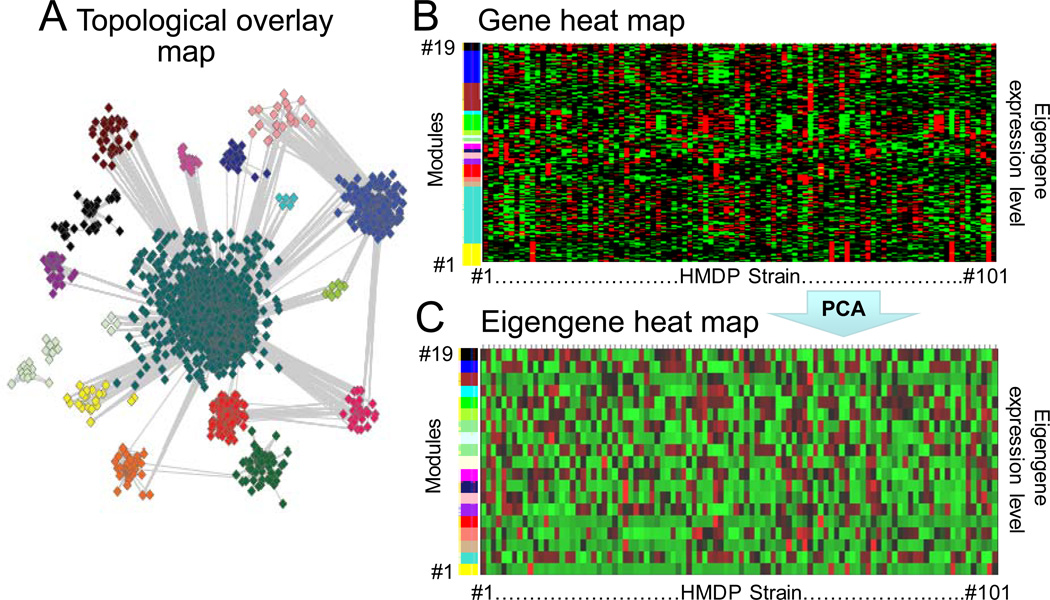
With these encouraging GWAS results, the use of HMDP for a GMAS approach designed to link groups of genes, rather than single genes, to phenotype, is now beginning to be explored. Fig. 5 shows the gene network generated from microarray analysis of heart tissue from 101 HMDP strains. Of 20,000 genes represented on the microarray chip, ~8,000 genes were expressed at significant levels in the heart. In Fig. 5A, the cardiac gene network is displayed in a topological overlap map. In this visualization, genes whose topological overlap (or adjacency) value exceeds the pre-defined threshold are defined as neighbors, which are color-coded and grouped into modules (clusters) connected by lines. Another useful display is a heat map representation shown in Fig. 5B, in which modules containing the 8,000 genes are stacked on the vertical axis, and the HMDP strains are arranged along the horizontal axis. The expression level of each gene is indicated on a red (high)-low (green) color scale. From the heat map representation, it is clear that different HMDP strains exhibit striking differences in gene expression.

Fig. 5.

A. Topological overlay map of the cardiac gene network from the HMDP. Colors indicate nodes belonging to the same gene module. B. Gene heat map of the HMDP cardiac gene network. The 8,000 expressed genes are grouped on the vertical axis according to their color-coded module (on left), with the 101 HMDP strains arranged along the horizontal axis. The expression level of each gene is indicated on a red-green color scale (red=high, black=intermediate, green=low). C. Eigengene heat map of HMDP cardiac gene network. Expression levels of individual genes in each module have been replaced by the corresponding eigengene expression level on a red-green color scale.

The patterns of gene expression within a given module in Fig. 5B are very complex. To facilitate linking gene modules to phenotype, the aggregate behavior of the individual genes within each module can be represented by an “eigengene,” derived from principal component analysis ²⁸. The eigengene is not a physical entity, like a real gene. Rather, it is a phenomenological entity representing a read-out of the aggregate behavior of all the real genes in a module, in the same sense that the blood pressure is not a physical entity, but rather is a measurement or read-out of interactions between physical entities such as the heart, blood vessels, hormone levels, blood volume, etc., or like the refractory period is a read-out of the aggregate behavior of many real ion channel proteins determining tissue excitability. Thus, of the ~20,000 individual genes in the mouse genome, a given tissue such as the heart expresses ~8,000 genes at significant levels, which can be condensed, using the WGCNA technique, into ~20 gene modules, each represented by an eigengene as the global read-out of the module’s expression level. Fig. 5C shows a heat map of eigengene expression levels for the HMDP. The eigengene heat map emphasizes even more strikingly the variation gene module expression patterns among the different HMPD stains.

Given that most of the HMDP strains were bred in captivity and selected for traits such as hair color, a natural question to ask is, why are the patterns of gene module expression so markedly different? Natural selection for most fitness genes should have been similar and traits such as hair color require only a few genes, yet the expression levels of thousands of genes differ between HMDP strains, despite only a small variation among individuals of the same strain. These markedly different gene module (eigengene) expression patterns among HMDP strains appear to be equivalently well-suited for survival in captivity, since all strains are capable of being bred and maintained. One intriguing, although still speculative, possibility is that each HMDP strain represents a different “good enough solution” for survival in captivity under normal conditions. That is, within a given strain, each mouse has roughly the same “good enough solution,” reflecting strain-specific mutations in its regulatory DNA. However, other HMDP strains, with different strain-specific mutations in regulatory DNA, manifest different eigengene patterns encoding alternative “good enough solutions.”

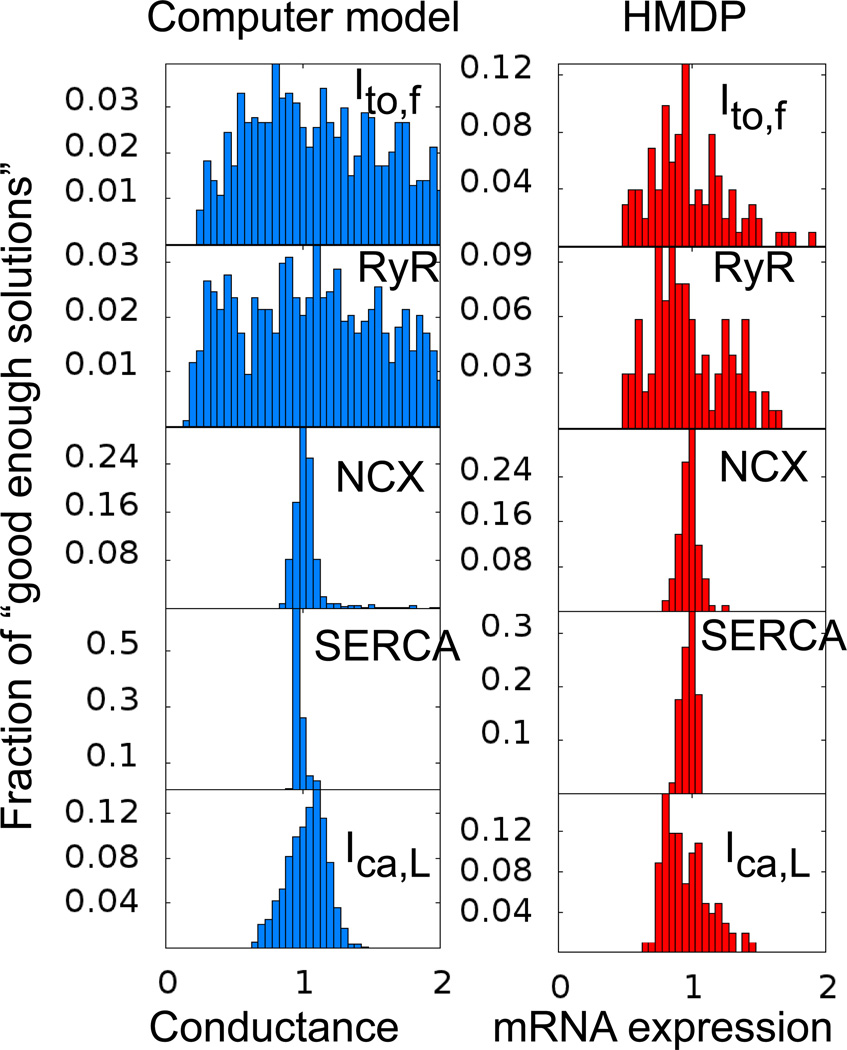
To test the feasibility of this idea, we analyzed the variation in gene expression levels observed in the microarray analysis of the HMDP for five key cardiac proteins regulating normal cardiac excitation-contraction (EC) coupling in the mouse ventricle (the transient outward current I_to,f, the ryanodine receptor RyR; the Na-Ca exchanger NCX, the sarcoplasmic-endoplasmic reticulum Ca ATPase SERCA; and the L-type Ca current I_Ca,L). The variation of mRNA expression for those five genes analyzed for one microarray (one heart) per strain for 100 strains is shown in Fig. 6A. We then compared these findings to an exhaustive computational search of “good enough solutions” in a mouse ventricular action potential model (Fig. 6B). The computational search was conducted by first generating 10,000 “trial solutions” constructed by assigning random values to the conductances corresponding to those five EC proteins, with each conductance varying from a value a few times smaller to a few times larger than its normal value. Not surprisingly, only a handful of trial solutions were good enough. To systematically find good enough solutions, we therefore used a minimization algorithm that iteratively varied all five conductances starting from the randomly chosen values until a positively defined “cost function”, which measures the departure from a normal electrophysiological phenotype (action potential and calcium transient), falls below a tolerance limit. This mathematical optimization yielded 1,952 good enough solutions from the 10,000 trial solutions with the corresponding variation of conductances shown in Fig. 6B.

Fig. 6. Correspondence between gene expression and “good enough solution” predictions.

Left panels (blue) show histograms defining the range of conductances of 5 key EC coupling proteins (transient outward current I_to,f, the ryanodine receptor RyR, the Na-Ca exchanger NCX, the sarcoplasmic-endoplasmic reticulum Ca ATPase SERCA, and the L-type Ca current I_Ca,L) among 1,952 computer-generated “good enough solutions” obtained using a mouse ventricular action potential model ⁵¹ with a mathematical formulation of Ca cycling adapted from ⁵². Right panels (red) show histograms of gene expression levels for the same 5 key EC coupling proteins among 100 HMDP strains. The reasonable agreement supports the hypothesis that gene expression variation in HMDP strains reflects multiplicity of functional “good enough solutions” for normal murine EC coupling.

Remarkably, the conductance variation of computer-generated good enough solutions matches reasonably well the variation of mRNA expression among the 100 HMDP strains. Only a rough agreement is to expected at best since functional conductances may not always correlate well with mRNA expression levels due to post-transcriptional and/or post-translational modifications ⁴³. In addition, the parameter space of good enough solutions selected by evolution need not be as large as the parameter space of all possible good enough solutions determined computationally. Despite those caveats, the comparison of Fig. 6 lends credence to the possibility that HMDP strains represent different good enough solutions for normal cardiac EC coupling. It is also consistent with the broader finding that biological circuits are generally “sloppy” ⁴⁴, i.e. tolerant to significant variations of many parameter combinations, albeit not all combinations, as exemplified here by the fact that SERCA expression is tightly constrained.

In summary, the HMDP has joined traditional genetic crosses as a powerful new resource for systems genetics studies. The genetically identical individuals within each HMDP strain can be subjected to repeated microarray analysis to confirm that variability in gene expression levels between individuals within a strain is small compared to variability between individuals from different strains. A key advantage is the increased resolution of the HMDP due to historical recombinations among classical inbred strains, allowing gene networks to be constructed with greater reliability and fidelity. Likewise, the response of each HMDP strain to an environmental stress of interest can be repeated in as many individuals from the same strain as desired to ensure that the phenotypic response is consistent. This provides an ideal model system for testing the GMAS concept.

Getting Down to Business: The GMAS Strategy

To unravel the genetic basis of common polygenic diseases, our goal is to devise a top-down strategy to analyze how genes work together in groups, rather than singly. Towards this end, the salient observations/assumptions discussed so far can be summarized as follows: 1) Applying WGCNA to the HMDP allows us to group the mouse genome of ~20,000 genes into an approximately scale-free network comprised of ~20 gene modules in a tissue such as the heart; 2) The aggregate behavior of the genes in a given module can be represented phenomenologically by the module’s eigengene, a read-out of the module’s expression level calculated from principal component analysis; 3) The expression pattern of eigengenes is very similar among individuals within a given HMDP strain, but varies considerably between different HMDP strains, reflecting the concept that evolution has generated different “good enough solutions” adequate for normal cardiovascular function; 4) When the HMDP strains are exposed to an environmental stress, however, some strains may adapt better than others, consistent with some “good enough solutions” being better suited to adjust successfully to a specific stress than others; 5) If the different eigengene expression patterns of HMDP strains truly correspond to different “good enough solutions,” then the eigengene pattern should predict the phenotypic response to the stressor.

If these observations/assumptions are valid, then the top-down strategy is straightforward: 1) Expose all of the ~100 HMDP strains to an environmental stress of interest, e.g. a high fat diet to induce atherosclerosis, chronic isoproterenol or angiotensin infusion to induce heart failure, or any stressor known to induce a disease phenotype; 2) Functionally characterize the range of phenotypes in terms of quantitative traits exhibited by the ~100 HMDP strains in response to the stressor; 3) Correlate the eigengene expression patterns of the HMDP strains with the panel of quantitative traits.

Thus, in place of the bottom-up approach of looking for associations between single genes (or SNPs) and phenotype, here we narrow the number of candidates from thousands of individual genes (or millions of SNPs) to a relatively small number of eigengenes (20–30), with each eigengene representing tens to hundreds of individual genes, depending on the size of the module. As in the case of a failing business organization, we are no longer looking one-by-one for a single rogue employee (gene) to blame, but instead are viewing how the system’s modular divisions (represented by its eigengenes) interact and adapt to the stressor. Moreover, with only 20 or so eigengenes, combinations of eigengenes are much more feasible to evaluate. That is, searching for a correlation of a single eigengene with a quantitative trait involves evaluating 20 possibilities; correlating pairs of eigengenes involves evaluating 20!/(18!×2!)=190 possible pair combinations; for triplets the corresponding number is 20!/(17! ×3!)=1,140; and for groups of 16 eigengenes, the corresponding number is 20!/(16! ×4!)=4,845, still very manageable compared to the number of possible 16 SNP combinations, which exceeded 10⁸⁰ (the number of atoms in the observable universe), using a GWAS approach.

Caveats and Challenges

In the discussion above, we have sketched out a relatively straightforward scenario for a GMAS strategy, based on the assumptions that the basal eigengene pattern encodes a “good enough solution” for normal function, and some “good enough solutions” adapt more successfully than others to environmental stress. If these assumptions are correct, then it logically follows that the eigengene pattern should predict the phenotypic response to the stressor.

The challenge, of course, will be to validate these assumptions. Models like the HMDP are valuable resources in this regard. HMDP has the advantage that the reproducibility of eigengene patterns and phenotypic response to stressors can be cumulatively tested in multiple genetically-identical individuals, in order to separate environmental influences from genetic determinants. However, the success of this approach ultimately depends on the accuracy of techniques such as WGCNA^21–23 or alternative strategies ^18–20 at deciphering biologically meaningful gene networks. In other words, to what extent are the derived gene modules real, or biostatistical flukes due to contamination by genetic noise? How does one decide on which genes to include in which module – are maximizing the scale-free topology and using gene ontology and cell marker enrichment to infer function the best criteria? Even if the gene network modular topology is accurate, are eigengenes calculated by principal component analysis the best way to represent the aggregate behavior of individual genes in a module? Both WGCNA and eigengene calculations are based on linear correlation measures. Whether more general nonlinear methods to group genes into modules or calculate eigengenes, such as mutual information testing as used in ARACNe ¹⁸ and MINDy ²⁰, or still largely unexplored methods such as maximal information nonparametric exploration (MINE)⁴⁵ or principal geodesic analysis (PGA) ⁴⁶, will improve accuracy has yet to be determined.

It is also important to recognize that eigengene patterns reflect a mixture of both genetic and environmental (epigenetic) perturbations. Co-expression modules are imperfect representations of biology. They can be refined by experimental and interactive approaches, but they are limited by the fact that they represent only one of many scales contributing to overall function, and changes in gene expression patterns reflect both genetic and environmental perturbations. Thus, it will be important to expand the approach to datasets reflecting epigenetic control (DNA methylation, chromatin structure), alternative splicing (next generation sequencing), protein localization and post-translational modification (mass spectroscopy, imaging) and metabolism (mass spectroscopy). Nevertheless, the available evidence suggests that the gene network structure is relatively invariant – that is, individual genes do not jump to different modules in response to a stressor ⁴⁷, ⁴⁸. Rather, the gene content of modules remains similar, but the expression level of the genes in the module (represented by the eigengene) changes. In this case, it may turn out that the change in the eigengene pattern, rather than the basal pattern, will be a better predictor of phenotype. These are all important issues that remain to be explored.

Clinical Implications

If the GMAS strategy outlined above for the HMDP proves successful in identifying gene module expression patterns that predict adaptability to environmental stressors, how might this help us better understand the genetic basis of common human diseases or drug reactions? With the exception of identical twins, all humans are genetically unique (i.e., each is analogous to a different HMDP strain). However, the principle is the same: if each human’s genome encodes a different “good enough solution” for survival in a “normal” human environment, then some “good enough solutions” may adapt better than others when the environment changes (e.g. from a subsistence diet to a high calorie, high fat diet, or from drug-free to a new drug state), accounting for the variable susceptibility to complex diseases. Using WGCNA, a human gene network can be constructed with microarray data from less than 100 patients ^29–31. Thus, tissue-specific human and mouse gene networks, and their corresponding eigengene patterns, can be compared between human diseases and corresponding mouse disease models to search for commonalities. For example, we might expose the HMDP strains to an arrhythmia-inducing drug to search for specific eigengene patterns associated with electrocardiographic QT interval prolongation and cardiac arrhythmias, and if so, determine whether the corresponding human eigengene patterns can be similarly identified. Moreover, novel therapies for complex diseases may be suggested if we can discover interventions which alter eigengene expression patterns, and show that this also alters diseases susceptibility. At the present time, regulation of gene module expression levels is not well-understood, but interesting candidates to evaluate include hub and driver genes ⁴⁹, microRNAs, DNA methylation or acetylation, and histone acetylation/chromatin remodeling. For example, microRNAs often coordinately regulate hundreds of individual genes. Do the genes regulated by a given microRNA belong to the same module? If so, then manipulation of specific microRNAs might provide a molecular approach to convert an eigengene pattern conferring susceptibility to a disease to one conferring resistance.

GMAS and GWAS approaches are also inherently complementary to each other. One of the major contributions of GWAS has been to identify novel pathways previously unsuspected to be involved in the pathogenesis of a disease. By linking pathways to discrete gene modules, GMAS provides an additional context for discovering how pathways are interactively linked in health and disease states. The synergy between GWAS and GMAS may thus enhance our ability to identify promising therapeutic targets among the molecular constituents of these pathways.

Realization of the potential clinical applications of GMAS will require much more work in this emerging research area which is still in its infancy. However, if a GMAS approach based on eigengene analysis or alternative strategies ultimately proves successful, then our view of how genetics influences susceptibility to common diseases and drug reactions may shift away from the traditional focus on searching for mutations, and towards studying the way in which normal genes are grouped. We already know that an identical set of genes can produce a markedly different phenotype depending on the expression pattern (e.g. the metamorphosis of a caterpillar into a butterfly). So perhaps it is not so far-fetched to imagine that whether or not an individual succumbs to a disease or drug reaction may depend more on the “good enough solution” reflected in the gene module expression pattern of completely normal genes, rather than on multiple gene mutations. Finally, gene networks are only one of many networks vital to a living organism. The ultimate and even more daunting challenge will be to map how information flows between gene networks, protein-protein interaction networks, metabolite networks, etc. The emerging science of network analysis, combined with “-omics” technologies, are powerful new tools whose further development holds great promise to meet these challenges.

Emerging Science Reviews Text Box.

Emerging Science Reviews are published on an occasional basis to highlight areas of research that are very recent and at the cutting edge of cardiovascular biology. The goal of these articles is to bring attention to promising new topics that are not yet well developed.

Nonstandard Abbreviations and Acronyms

EC coupling

excitation-contraction coupling

G_Kr

rapid component of the delayed rectifier K channel conductance

GWAS

Genome Wide Association Study

GMAS

Gene Module Association Study

HMDP

Hybrid Mouse Diversity Panel

SNP

single nucleotide polymorphism

WGCNA

Weighted Gene Co-expression Network Analysis