Biophysical Limits of Protein-Ligand Binding

Abstract

In classic work, Kuntz et al. (Proc. Nat. Acad. Sci. USA 1999, 96, 9997–10002) introduced the concept of ligand efficiency. Though that study focused primarily on drug-like molecules, it also showed that metal binding led to the greatest ligand efficiencies. Here, the physical limits of binding are examined across the wide variety of small molecules in the Binding MOAD database. The complexes with the greatest ligand efficiencies share the trait of being small, charged ligands bound in highly charged, well buried binding sites. The limit of ligand efficiency is −1.75 kcal/mol-atom for the protein-ligand complexes within Binding MOAD, and 95% of the set have efficiencies below a “soft limit” of −0.83 kcal/mol-atom. Based on buried molecular surface area, the hard limit of ligand efficiency is −117 cal/mol-Ų, which is in surprising agreement with the limit of macromolecule-protein binding. Close examination of the most efficient systems reveals their incredibly high efficiency is dictated by tight contacts between the charged groups of the ligand and the pocket. In fact, a misfit of 0.24 Å in the average contacts inherently decreases the maximum possible efficiency by at least 0.1 kcal/mol-atom.

Introduction

Protein-ligand binding is a delicate balance between the loss of entropy resulting from complexation and the enthalpy gained by forming favorable contacts with the protein ^1,2. The precise contribution of these contacts is a source of debate and has provided a significant obstacle in the ability to predict how small molecules will bind ^3–5. The interplay between entropy and enthalpy is difficult to determine since they are influenced by several factors. For entropy, binding two entities results in a loss of six degrees of freedom, and a change in the internal flexibility of the protein and ligand must be taken into account. Furthermore, the reorganization of water around the ligand and within the binding site has significant implications. In the case of enthalpy, several types of contacts can be made to varying degrees in the binding site ¹. Current thinking is that van der Waals forces are the most significant factor for binding due to tight packing between the small molecule and protein^1,6. Hydrogen-bonding and electrostatic interactions are thought to contribute more to the specificity of binding ¹. Since these interactions are also present with water and counter ions in the unbound state, they are thought to have a smaller impact on affinity ¹.

Highlighting the different interpretations regarding the drive for efficient binding, there has been contradictory evidence as to which types of interactions play the most significant roles in the binding of biotin to streptavidin, the tightest known natural complex. In 1993, Miyamoto and Kollman used free energy perturbation on biotin•streptavidin to show that the increased binding affinity for the biotin-streptavidin system can be accounted for by van der Waals contacts made in the biotin•streptavidin complex where the pocket in streptavidin is preformed as in the traditional lock-and-key theory ⁷. However, newer work has shown that networks of hydrogen bonds are responsible for the strong binding in the biotin•streptavidin complex ⁸.

A common metric to evaluate a small molecule's ability to bind is “ligand efficiency”. This metric is defined as binding affinity per number of non-hydrogen atoms ^9–11. It was first introduced by Kuntz et al. in 1999 ¹², where they analyzed 159 tightest-binding complexes and the relationship between affinities and the number of heavy (non-hydrogen) atoms present in a ligand. They showed that each heavy atom can provide at most −1.5 kcal/mol of binding affinity ¹². This maximum was consistent with their predictions of the maximum affinity obtainable by van der Waals and hydrophobic interactions ¹². Though many of the most efficient ligands were metals and small ions, electrostatics was given little attention. Even in recent investigations this class has been ignored because they are not “drug-like” ^13–15. More recently efficiency metrics have been expanded to include affinity per Ų of polar surface area (PSA).^16,17 AtlasCBS was developed to represent complexes based on pairs of efficiency indexes with the affinity per heavy atom or molecular weight being plotted versus the affinity per polar atom or affinity per PSA in order to map the “chemico-biological space (CBS)”, of known complexes.^16,17 Efficiencies have also been calculated based on the entropy per heavy atom and enthalpy per heavy atom¹⁸.

In this study, we investigated which properties lead to an optimal efficiency and what defines the physical limits of binding. To study general patterns with regard to binding affinity and efficiency, it is necessary to use a large set of protein-ligand complexes for which a structure has been solved and an experimentally-derived binding constant (K_d, K_i, or IC₅₀) has been determined. We used the largest dataset available, Binding MOAD^19,20, to explore the relationship between structure and binding affinity, extending Kuntz's examination to include all available binding events in the Protein Data Bank ²¹. By looking at the most efficient ligands and the characteristics of their binding pockets, we reveal which interactions are most important to provide the highest binding affinity and efficiency. This study explores all binding events with the goal of examining fundamental biophysical properties, rather than focusing solely on properties of drug-like chemical space.

Methods

Structural properties were derived from the complexes in our 2010 release of Binding MOAD (Mother of All Databases), which is based on all PDB entries in 2009 and earlier ^19,20. Binding MOAD is the largest database of high-resolution protein-ligand complexes annotated with binding data from the PDB ²¹ (14,720 complexes comprised of 4624 unique protein families binding 7064 unique ligands). We have compiled binding affinity data for 32% of the entries (4,782 complexes), with a preference for K_d data over K_i data over IC₅₀ data. For this study, no IC₅₀ data was used, so only the 2298 complexes with K_d and K_i data were considered. (Including the complexes with IC₅₀ data resulted in nearly identical values and did not alter the findings at all. However, their inclusion introduces too much uncertainty as the conversion to ΔG_bind is difficult to do accurately in many cases). The free energy of binding was determined directly from K_d values by ΔG_bind = RTln(K_d), and in the case K_d was not available, we approximated the free energy of binding using ΔG_bind = RTln(K_i). All structures and affinity data are freely available at http://www.BindingMOAD.org.

Coordinates of the complexes were taken from the biological unit files provided by the PDB, which display the functional form of the protein. These files were processed to remove artifacts. We specifically focused on the size of the ligand and its contact surface with the protein, so any structure with poorly defined contacts were not considered. Therefore, we excluded structures with partially occupied or missing atoms from under-resolved ligands or side chains, as well as structures with extra atoms from ligands or side chains resolved in multiple orientations. A ligand was determined to have too many or too few atoms if the number of atoms in the formula did not match the number of atoms in the coordinate section of the pdb file.

Ligand efficiency is the free energy of binding divided by the number of non-hydrogen atoms in the ligand ^9–12. Hence, a ligand with 10 atoms is twice as efficient as a ligand with 20 atoms if they bind with the same affinity. In this study, ligand efficiencies are reported as affinity per size (−ΔG_bind/atoms) and per degree of contact between the ligand and the pocket (−ΔG_bind/BSA). PyMol²² was used to make figures of the binding sites and calculate the electrostatics of the pockets using the APBS wizard²³.

Surface areas were calculated using OPLS-based radii ²⁴ with our code GoCAV which reports buried molecular surface area (BSA) of the pocket ¹⁹. Variation in BSA occurs when several examples of ligand binding occur in the biological unit (i.e., slightly different interactions for three ligands in the three binding sites of a homotrimer). This variation is represented by error bars on the graph of BSA. The exposed surface area (ESA) is also computed from the total surface area minus the BSA.

Results and Discussion

Maximum and average ligand efficiencies

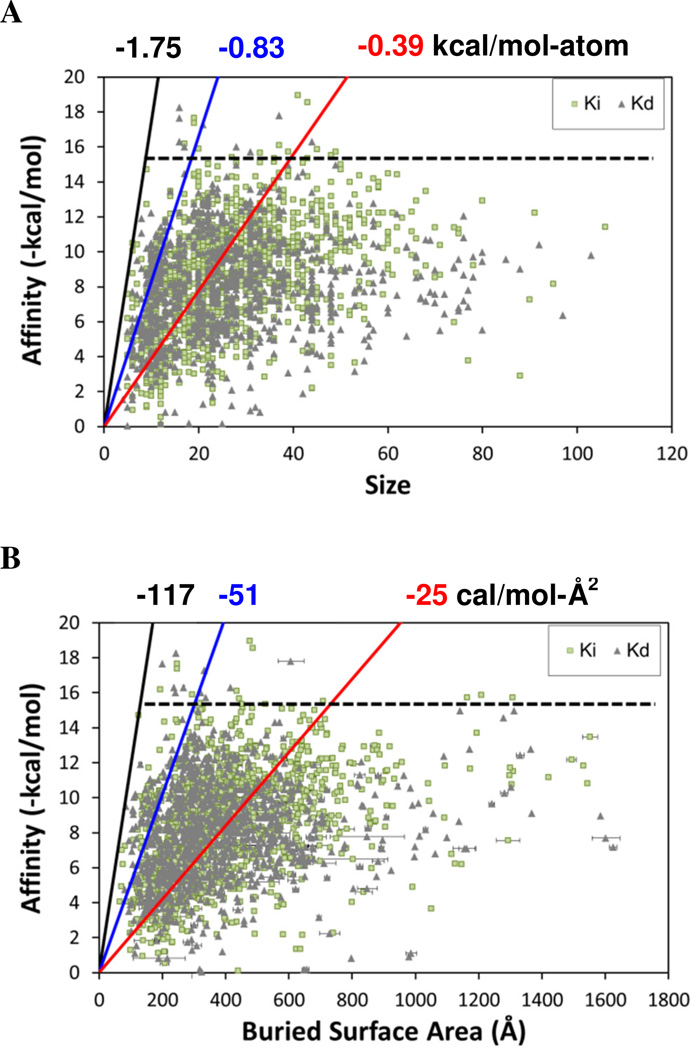
If van der Waals terms are the definitive contribution, then we may expect to see a correlation between affinity and contact surface area between the protein and ligand. However, no correlation is seen between affinity and size or contact area (Figures 1A & 1B).

Figure 1.

Plotting the affinity of the complexes versus their physical characteristics reveals the limiting cases as well as the general trends. Measurements used for affinity data are noted as K_i (light green squares) or K_d (grey diamonds). (A) Affinity versus size of the ligand, where size is given as the number of non-hydrogen atoms. (B) Affinity versus the buried surface area of the binding site. The “hard limits” of ligand efficiency are denoted with black lines and values; the “soft limits” which bound 95% of the data are denoted with blue lines and values; the average ligand efficiencies are given with red lines and values. The horizontal dashed black line denotes how few of the complexes have affinities greater than 15 kcal/mol.

Our dataset is significantly larger than that of Kuntz et al. ¹², and we find a slightly higher maximal efficiency for ligands of −1.75 kcal/mol-atom. This “hard” limit is set by several systems, but we can also designate an alternative “soft” limit of −0.83 kcal/mol-atom, which is the upper bound of 95% of the data in Figure 1. The soft limit is roughly half the value of the hard limit, and it is rather surprising to see such a dramatic change over the 115 complexes that compose the top-5% most efficient complexes. The large drop in efficiency between the two limits highlights how rare it is to find exceptional ligands and suggests that −0.83 kcal/mol-atom is a sufficient limit for most uses. In particular it would be rare to create a drug molecule with ligand efficiency in excess of the soft limit.

The average and median efficiencies of our dataset are −0.39 kcal/mol-atom and −0.34 kcal/mol-atom, respectively. These averages are in agreement with average values for ligand efficiency of −0.37 kcal/mol-atom for enzymes (median = 0.33 kcal/mol-atom) and −0.42 kcal/mol-atom for non-enzymes (median = −0.36 kcal/mol-atom), as reported in our previous work ²⁵. Accurate benchmarks for ligand efficiencies are very important because these values define physical limits of ligand binding. Furthermore, ligand efficiencies are often used to evaluate HTS data or to eliminate lead compounds during a drug development cycle ^9–11,26. Anecdotally, the best ligand efficiencies from HTS data approach −0.6 kcal/mol-atom ^9,26. Pushing for leads with ligand efficiencies near −0.3 or −0.4 kcal/mol-atom from a simple combinatorial library may be too restrictive for some systems as this is near the average for all good structures, as noted above ¹⁰. However, ligand efficiencies of candidate compounds must often be higher to allow for changes during further drug development ^26,27.

We can also define ligand efficiency in terms of BSA of the binding site. Others have proposed metrics for ligand efficiency based on free energy of binding per surface area of the ligand, but these have been based on pharmacokinetic considerations and are not equivalent to contact surface area between the ligand and its protein target ^9–11. Recently, Nissink has proposed that the maximal ligand efficiency should be proportional to protein-ligand contact area and volume ¹⁵. That work further suggests using a modified measure of ligand efficiency based on affinity/N^1/3. Based on a spherical approximation, the cubed root of N estimates the ratio of area to volume of a ligand ¹⁵. This metric is also useful for reducing the over emphasis of small ligand size that results from the traditional definition of ligand efficiency = affinity/N, where N is the number of non-hydrogen atoms ¹⁵.

Estimates based only on the ligand ignore a large portion of the interaction with the protein. Instead, we have chosen to measure the contacts directly. In our description based on the BSA of the binding site, the average efficiency is −25 cal/mol-Ų (median = −23 cal/mol-Ų). Houk and coworkers coupled structure and affinity data for a moderate set of over 1000 host-guest, 175 antibody-antigen, and 176 enzyme-inhibitor complexes to propose that affinity is proportional to BSA of the ligand ^28,29. Their data implies a relationship, equivalent to 7 cal/mol-Ų (reported as approximately 1 logK_a for every 90 Ų of buried surface). This average is approximately one-fourth of our average, but Houk's trend is for solvent accessible surface area of the ligand and ours is for molecular BSA of the binding site. Other reported values of the relationship of surface area versus free energy for transferring a hydrophobic solvent into water range from 24 to 47 cal/mol-Å^{2 30,31}, which is in excellent agreement with the range between our average and soft-limit efficiencies.

In Figure 1B, the “hard limit” for efficiency is −117 cal/mol-Ų and the soft limit that bounds 95% of the data is −51 cal/mol-Ų. We were surprised to find that the maximum efficiency with respect to BSA was in agreement with limits proposed for macromolecular binding ³². In a follow-up work examining protein-protein, protein-RNA, and protein-DNA complexes, Brooijmans et al. established the limit of 120 cal/mol for every Ų of BSA³². Macromolecular recognition generally involves large, flat regions of a protein surface ³³, but despite that large contact surface, macromolecules do not inherently bind with higher affinities than small molecule ligands ³². Keil et al. have shown that binding sites for ligands are deeper and more concave than binding sites for protein-DNA or protein-protein associations, implying a good degree of burial for small molecules despite their smaller size ³⁴. It is rather remarkable that the 120 cal/mol-Ų limit of binding efficiency appears to be universal across all varieties of binding interfaces on proteins.

Electrostatic Interactions Define Maximal Efficiency

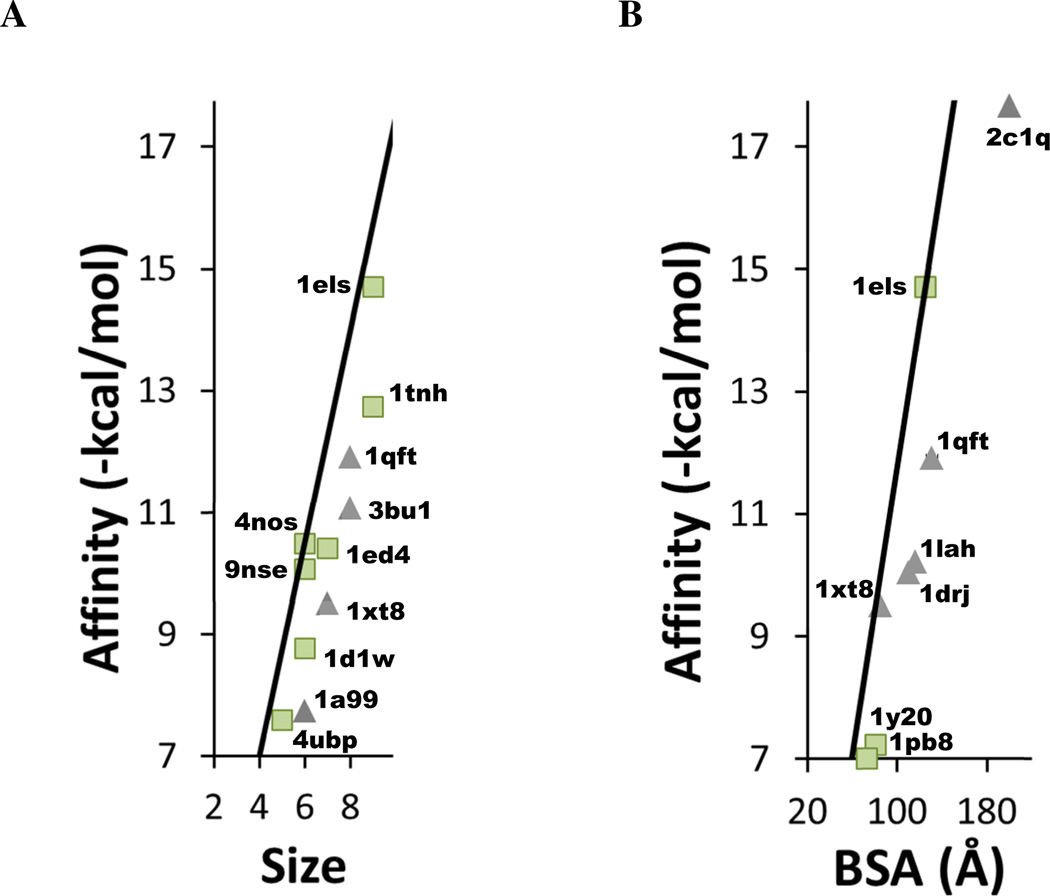
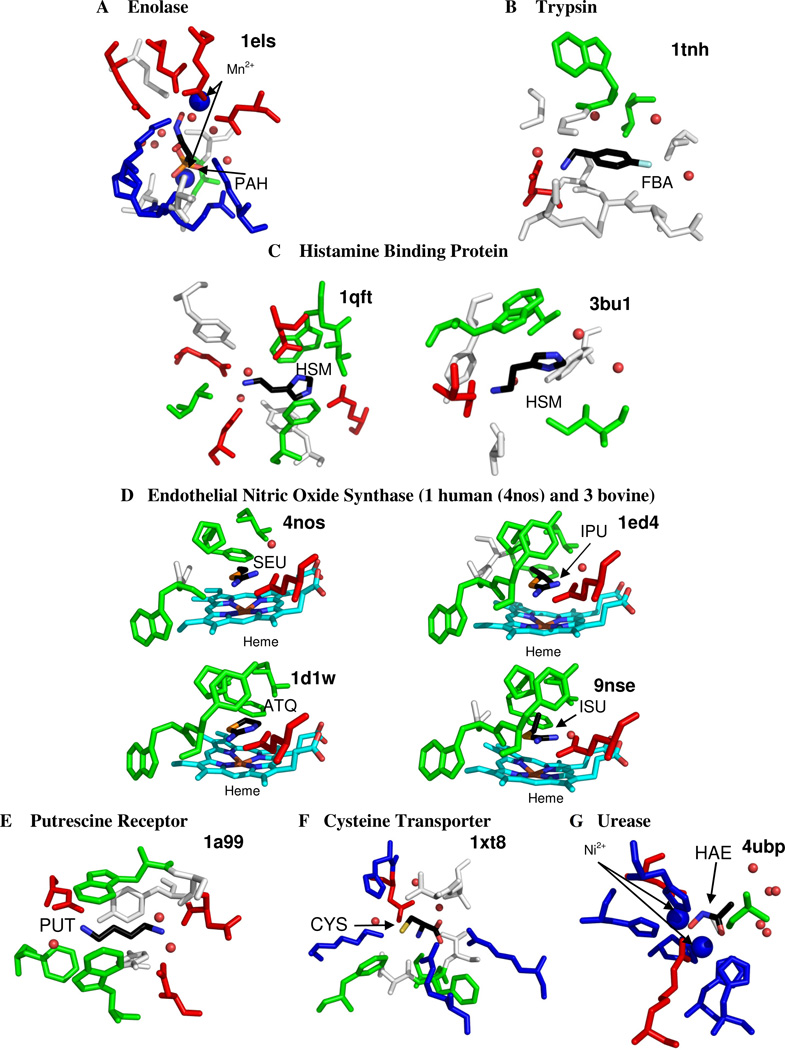
Structures which define the limit of ligand efficiency share a distinct characteristic: 90% of the systems involve a charged ligand in contact with a charged protein residue or a metal ion cofactor. In fact, many of the ligands with the best efficiencies have two or three charge centers, and they are complemented in their binding sites by several charged side chains and/or dicationic ions. Figure 2 shows the systems with the maximum efficiencies, annotated with their PDB codes. The highest efficiency is seen for a phosphonoacetohydroxamate compound with a −3 charge that is sandwiched between two dications in yeast enolase (PDB code 1els Figure 3) ³⁵. The crystal structure shows several unusually tight contacts in the chelation (2.1 Å) which create very small contact surfaces. Not only is the small molecule bound by two magnesium ions, there are two charged aspartates, two glutamates, two lysines, an arginine, and a histidine (that potentially could be charged) in the vicinity.

Figure 2.

Close up view of the complexes with the highest ligand efficiencies. (A) Affinity compared to size as in Figure 1A. (B) Affinity compared to BSA as in Figure 1B. Complexes are labeled with their PDB codes.

Figure 3.

Binding sites of the 11 most efficient complexes. Figures show all residues within 4 Å of the small molecule ligand. The ligand is colored by atom type. The water is colored red and shown in small spheres. Metal ions are shown in larger blue spheres. Acidic residues (Asp, and Glu) are colored red; basic residues (His, Lys, Arg) are colored blue; hydrophobic residues (Ala, Ile, Leu, Met, Phe, Pro, Val) are colored green; hydrophilic residues (Cys, Gly, Asn, Gln, Ser, Thr) are colored white; and Tyr and Trp are colored either green or white depending on the interaction made with the ligand. The heme is colored with C=light blue and the Iron=brown.

Other high efficiency complexes include a charged benzylamine coordinated to an acidic side chain in trypsin (1tnh) ³⁶, a dicationic histamine complexed by four acidic side chains in tick histamine-binding protein (1qft) ³⁷, a dicationic histamine which has charge-charge interactions with an acidic residue and a cation-π interaction with the aromatic ring of a Tyr residue (3bu1)³⁸, nitric oxide synthase binding +1-charged isothioureas (4nos, 1ed4, 1d1w, and 9nse - the natural substrate for this enzyme is arginine, which has a positively-charged side chain and a zwitterionic core) ^39,40, a zwitterionic cystine complexed by four charged side chains in the cystine transporter (1xt8) ⁴¹, a +2-charged 1,4-diaminobutane in the putrescine receptor (1a99) ⁴², and an anionic acetohydroxamic acid inhibitor sandwiched between two Ni⁺² in urease (4ubp) ⁴³. Each of these binding sites can be viewed in Figure 3. Even though some of these structures contain metal ions and may be considered partially covalent by some, each structure in Binding MOAD has been verified to be non-covalently bound, according to the primary citation listed in the PDB for the structure ²⁰.

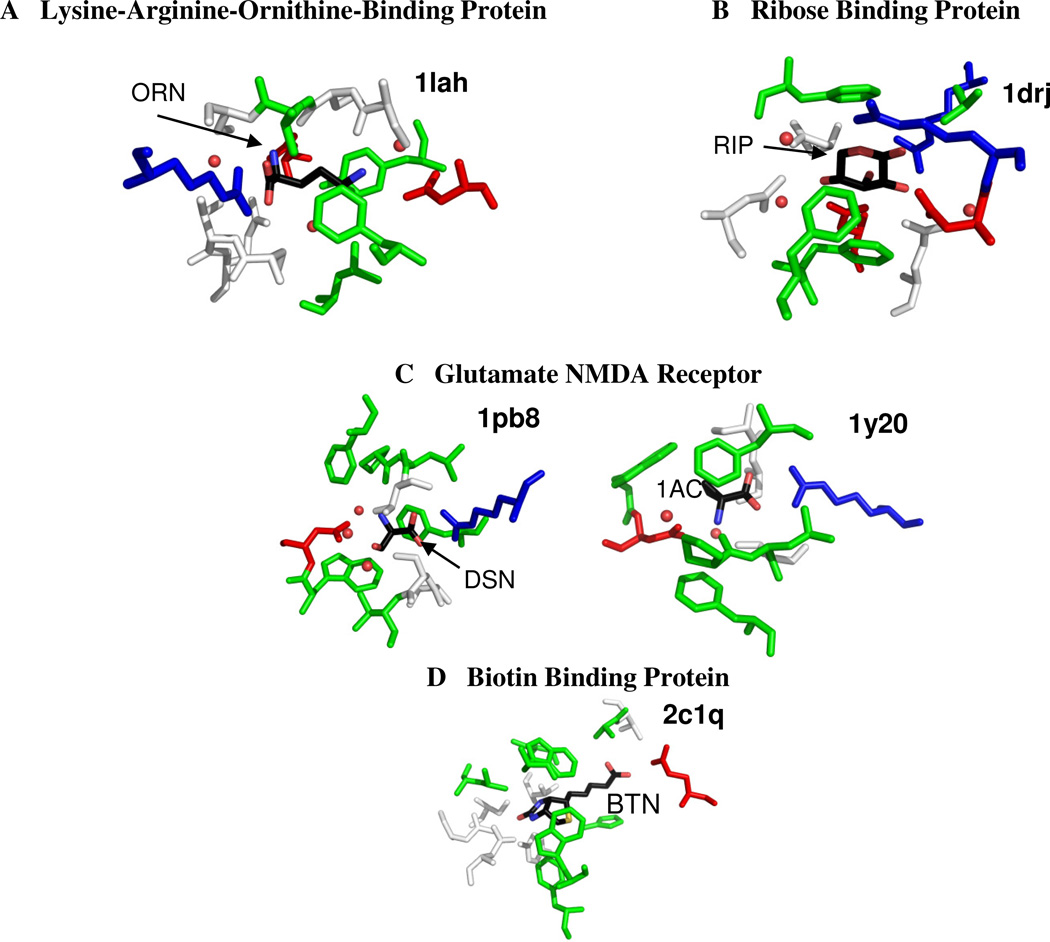
Three of the structures that are at the maximum limit of efficiency per BSA (1els, 1qft, and 1xt8 in Figure 2B) are also seen at the limits of efficiency per atom in Figure 2A. Charged ligands are seen in most of the other systems in Figure 2B, see Figure 4. These additional complexes include 1lah (an ornithine with three charge sites bound to the lysine-arginine-ornithine-binding protein)⁴⁴ and 1y20 and 1pb8 (the glutamate NMDA receptor binding a zwitterion and D-serine, respectively) ^45,46.

Figure 4.

Binding sites of highly efficient complexes (affinity per buried cavity surface area). Figures show all residues within 4 Å of the small molecule ligand. The ligand is colored by atom type. Acidic residues are colored red; basic residues are colored blue; hydrophobic residues are colored green; and hydrophilic residues are colored white as in figure 3. Water is colored red and shown in small spheres.

There are two structures involved in defining the maximal limits of ligand efficiency which do not have charge-charge interactions between the protein and the ligand. These structures are ribose bound to D-ribose-binding protein (1drj)⁴⁷ and a biotin-binding complex (2c1q)⁴⁸. Although the ligand is not charged in 1drj, the binding site in this structure contains four charged residues (two arginines and two aspartates) each making hydrogen bonds with the ribose (Figure 4B). Hydrogen bonds are very short and favorable for a hydroxyl group that glues a salt bridge together, and there are several pathways across the ribose that fill this role. This makes the packing in the site very tight and the BSA very low, which results in the exceptional ligand efficiency despite the modest affinity. As for 2c1q, biotin has a remarkably high binding affinity, but it is still not fully understood by the scientific community. We will not speculate reasons here.

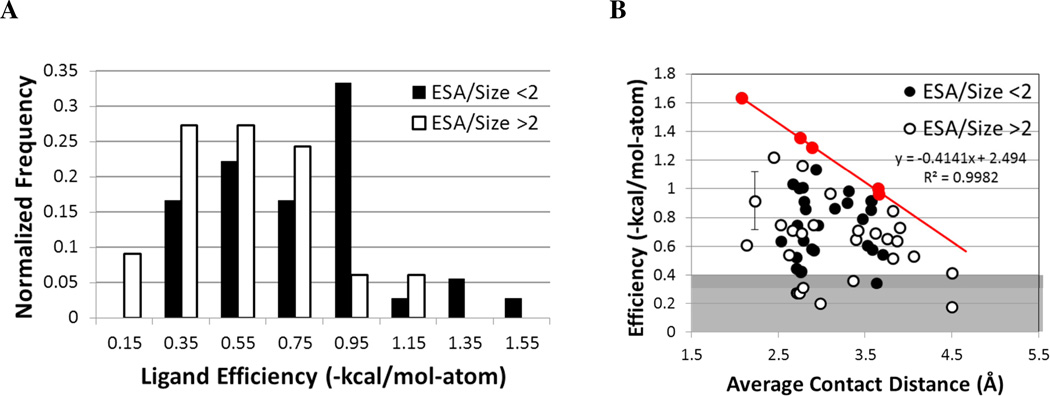
Based on the known size dependence of ligand efficiency, it is not surprising that the best ligands are small, but it is important to note that not all small, charged molecules in charged binding sites are highly efficient. To determine why all charged ligands are not highly efficient, we examined all ligands with 5–10 non-hydrogen atoms and more than one charged site (61 complexes, of which only 9 have efficiencies of −0.4 kcal/mol-atom or weaker). Note that we are using a rather high cutoff here to define “less efficient binding”; drugs often have efficiencies near this value (a 1-nM ligand with ≥31 non-hydrogen atoms has ≥400 MW and an efficiency of −0.4 kcal/mol-atom or less). We are particularly interested in the electrostatic interactions of the ligand and pocket with respect to efficiency. The Coulombic potential is dependent on distance, so we examined the minimum distance of each charge of the ligand to the charged residues of the pocket, including any metal atoms that may be present in the binding site. The contacts were determined by investigating the structure of the complex visually using MOE⁴⁹. We also calculated the exposed surface area (ESA) using our code GoCAV¹⁹, which bases ESA on the surface of the ligand that is not complemented by the protein. In this comparison, we chose to use ESA because it is a direct measure of the charged ligand’s interaction with water, rather than use BSA which is a measure of interaction with the protein. Again, we have normalized this measure by the number of non-hydrogen atoms (ESA/size). Figure 5 presents the relationship of efficiency to these metrics. It should be noted that there are five systems that are not included in Figure 5 because they do not fit our definition of multiply charged. Though each has two titratable sites, all include an amine that is tightly coordinated to a metal cofactor, making it neutral. These systems have very short average contact distances, but very poor ligand efficiencies. The binding event must include a change in ionization, which is unfavorable and leads to reduced binding. To avoid confusion, these have been excluded.

Figure 5.

Relationship between efficiency, exposure, and protein contacts for ligands with 5– 10 atoms and more than one charge site. (A) The distribution of efficiencies is compared for systems with well buried (black) versus more exposed sites (white); a cutoff of 2 Ų/atom is used to define the two sets. (B) Efficiencies are compared to the average contact distance between charged groups (black circles denote systems with ESA/size < 2 Ų/atom, and white circles are ESA/size > 2 Ų/atom). The line highlights the drop in maximal efficiency as the contacts become less favorable: roughly 0.41 kcal/mol-atom for every 1 Å increase in the average contact distance. The points used to set the line are colored red. The gray background notes systems with more modest efficiencies. The error bar indicates the standard deviation of the average of two affinity values reported in the literature ^70,71.

There is a very significant difference (two-sided Wilcoxon p-value = 0.005) in the efficiencies of complexes that are less exposed (ESA/size < 2 Ų/atom) versus those that are more exposed, Figure 5A. The 2 Ų/atom cut is chosen since it is approximately ten percent of the surface area of a water molecule. The median efficiency of well-buried ligands is −0.75 kcal/mol-atom versus a median efficiency of −0.57 kcal/mol-atom for those with ESA/size > 2 Ų/atom (mean efficiencies are−0.79 versus −0.58 kcal/mol-atom, respectively). Furthermore, if those efficiencies are compared to the average distance between charged groups (Figure 5B), it appears that longer distances severely limit the maximum efficiency possible for the system. This is in keeping with Nissink's proposal that maximal efficiency should be proportional to contacts normalized for ligand size ¹⁵.

For every increase of 1 Å in the average contact distance, the maximum efficiency drops by 0.41 kcal/mol-atom. Perhaps a more appropriate view is that a ligand's maximum efficiency is reduced by at least 0.1 kcal/mol-atom for a misfit as small as 0.24 Å in the average contacts between its charged groups and the protein's. For a 10-atom ligand, this small misfit reduces the affinity by 1 kcal/mol or more. Such significant gains/losses for such small displacements in the charges may explain why synthetic modifications to ligands that alter polarization and charge distribution can be so effective. The importance of charge interactions may support the ideas of optimizing charge complementarity that has been developed by Tidor and co-workers ^50–52. They developed an analytical solution of the Poisson-Boltzmann equation to model the electrostatics of the binding site and an analytical method of optimizing the charge profile of the ligand to match the calculated electrostatics of the binding site while also accounting for the desolvation penalty ^50–52.

The importance of charge complementarity in ligand binding can be supported by other biological binding events. The ability of salt bridges to improve the stability of protein-protein interactions in protein folding or protein-protein binding may be supportive ⁵³. Networks of salt bridges have been shown to stabilize proteins, although the majority of individual salt bridges have been shown to be destabilizing in proteins ^53,54. In a statistical study of 94 proteins from the PDB, Musafia et al. found that one-third of all residues participating in salt-bridges were involved in ‘complex’ salt bridges, which they defined as ones involving three or more amino acids ⁵⁵. Olson et al. were able to stabilize α-helical peptides by engineering multiple salt bridges and found that the amount of stability obtained was cooperative ⁵⁶. Networks of salt bridges were also found to be stabilizing by Kumar and Nussinov using continuum electrostatics to computationally determine the difference in energy of salt bridges compared to their hydrophobic isosteres, where the partial charges on the residue were set to zero ⁵⁷. They found that the stability for most salt bridges was determined largely by the desolvation penalty; however, the networked salt bridges were an exception to this phenomenon. In all cases, the networked salt bridge was found to be stabilizing, despite a large desolvation penalty ⁵⁷. These networked salt bridges are homologous to our charged ligands complemented by multiple charged residues in their binding sites. Furthermore, having a higher charge has been noted to be beneficial in metal ion binding to DNA/RNA. In these cases, the dicationic Mg²⁺ is the preferred counter ion, compared to Na⁺, for binding to and stabilizing the phosphate backbone of the nucleic acid ⁵⁸.

Coulombic forces are the strongest non-bonded interactions that can be made, and it may not be surprising that highly efficient molecules utilize the strongest forces per atom. However, it is surprising that the free energy of binding is high in these complexes because the desolvation penalty for charged molecules is significant ⁵⁹. Their relatively high affinity indicates that the penalty must be compensated in some fashion. Almost all of the structures contain water in the binding sites (Figures 3 and 4), so not all of the water molecules are displaced. This reduces the desolvation penalty.

Another reason the desolvation penalty may be lower than initially thought is that water cannot completely solvate the charges in these systems. Many have ligands and pockets with charges that are closely spaced – too close for water to pack around each charge independently. It has been shown that the multiply charged phosphate backbone of DNA, which puts charges close together, leads to “frustrated water” around the DNA. The restructuring of water was determined to dominate the interaction of polyols with DNA ⁶⁰.

It has also been shown that contact between two oppositely charged particles are stabilized by concave surfaces.⁶¹ Chrony et al. utilized molecular dynamics simulations with both explicit and implicit solvation models to create potentials of mean force for association of either a positively or negatively charged ion to an ion of opposite charge buried in a variety of hydrophobic surfaces representing multiple curvatures.⁶¹ They found that the surfaces that had positive curvature, or were “receptor” like, stabilized the state in which the ions were in contact with each other. The authors suggested this was due to an image charge formed by the surface which effectively increases the electrostatic effect. Even planar surfaces and those with slight negative curvature stabilized the ion pair, but required a water molecule to mediate the interaction.⁶¹

The limits of efficiency may be set by closely packed charged molecules because they are approaching covalent bonding. Zhang and Houk investigated 1017 enzymes-transition state complexes as well as 160 enzyme/inhibitor complexes. They found that transition states, which tend to have covalent or partially covalent bonds to the protein, had affinities of K_a = 10¹⁶ M⁻¹, while the inhibitors only bound with K_a = 10⁹ M⁻¹. Additionally, they proposed that any enzyme proficiencies and affinities of greater than 10¹¹ M⁻¹ (~15 kcal/mol) would exhibit covalent or partial covalent bonding ^28,62. At heavy atom distances less than 2.5 Å, low-barrier hydrogen bonds exhibit at least a partial covalent nature, and provide stability of 10–20 kcal/mol ^63,64. Additionally, metals have the ability to exhibit coordinate-covalent bonding to ligands ⁶⁵. In a few highly efficient complexes, we observe distances less than 2.5 Å between atoms capable of hydrogen bonding, and some cases have metals involved in coordinating the ligand. We should note that we do not believe these systems to be overly influenced by partial bonding characteristics because all are reversibly bound, many with affinities in the µM and nM range. Furthermore, in the NOS system (4nos, 1ed4, 1d1w, and 9nse) where the small molecule is near a heme, the distances to the iron are greater than 4 Å. Also, investigation of the available electron densities does not indicate partial bonding between the heme and ligand.

Maximum affinity of ligands

What defines the maximum binding affinity of ligands? Kuntz et al. found that binding affinity plateaus after ~15 atoms and little improvement is seen for larger ligands ¹². No ligand has a binding affinity of −20 kcal/mol or better. In fact, it is rare to exceed −15 kcal/mol (1.0% of the complexes in Figure 1). Kuntz and coworkers suggested that other biological factors may be the cause of the limit; for instance, molecules with too high of a binding affinity can exhibit clearance problems in the body ¹². Nature would tend to disfavor such molecules. Zhang and Houk might argue that affinities beyond −15 kcal/mol would require potential covalent binding²⁸.

Affinities better than −15 kcal/mol are so tight that a ligand will most likely never dissociate before the protein is degraded. In an investigation of reported protein half-lives, stable protein half-lives range from 16 hours to 210 hours with an average of ~105 hours or just less than four and a half days, although there are some proteins that are degraded more rapidly⁶⁶. In fact, the mean half-life of 3751 proteins in budding yeast is only 43 minutes⁶⁷. The average half-life of 100 proteins in living human cancer cells was 9 hours⁶⁸. Therefore, it is appears rare to find proteins with half-lives greater than one day. If we assume that k_on is the rate of diffusion of ~10⁶ M⁻¹s⁻¹, then an affinity of −15 kcal/mol (K_d ~ 10 pM) would correspond to an average bound lifetime of ~1 day ^66,69, but at −16 or −18 kcal/mol, the lifetimes would be approximately 6 and 187 days, respectively. However, we do not agree that clearance issues limit binding because protein binding predates complex organisms. Instead, we hypothesize that once a ligand is bound for the lifetime of a protein (~ 1 day), there is no evolutionary pressure to coax ligands and proteins to associate more tightly. Therefore, affinities beyond −15 kcal/mol are serendipitously random or man-made. They require the artificial “selective pressure” of a scientist’s goals.

Reynolds et al. have also discussed the plateau at −15 kcal/mol¹³. They noted that as size increased, the maximal efficiency would decrease. They suggested the reason for the drop in efficiency was that larger ligands would need to optimize a larger number of contacts with the protein that would lead to structural compromises and thus a reduced affinity ¹³. We acknowledge that our data could also support this proposal because significant drops in efficiency can come from rather minor misfits in charge complementarity. Also, larger sites and ligands typically have more conformational freedom through more rotatable bonds; therefore, competing entropic penalties may further limit binding efficiency.

Several other factors may also contribute to the −15 kcal/mol limit to binding. First, assays which are used to determine binding constants have inherent limitations when measuring high affinity. We do not believe that this is the cause of the limit. If it was the cause, the distribution of binding affinities would drop off sharply as one approaches the limit, providing a Poisson distribution skewed toward tight binding. However, this is not the case. The distributions in MOAD follow a near-normal distribution centered at ~9 kcal/mol. Second, our study has the limitation of examining only proteins and ligands that can be crystallized, which may bias the analysis in unknown ways. Third, most of the high-affinity complexes are man-made compounds, and ADME/Tox issues for some targets may discourage pursuing molecules that bind with affinities better than low pM. Lastly, some affinities of greater than −15 kcal/mol may be incorrectly considered covalent ^28,62. We may see a limit because Binding MOAD does not contain covalently bound ligands.

Conclusions

It is important to understand the limits of binding affinity and efficiency in order to properly describe the biophysics of protein-ligand molecular recognition. The difficulty in determining which interactions dominate free energy of binding has limited the ability of researchers to predict a priori which small molecules will bind to a target and how tightly. Our study and other recent studies have pointed to the importance of electrostatics in driving tight interactions^{50–52,55–57}. We have looked at the most efficient protein-ligand complexes and have noted that the overwhelming majority of these complexes are small molecules that have at least one charge-charge interaction, and several of them have multiple charge interactions. Although desolvation of charged molecules is a barrier to binding, it appears that the small size of the ligands and the close proximity of their charges lead to water's inability to fully solvate the ligand and its binding site. Desolvation of the cramped, charged pockets should not be as difficult to overcome as it is with widely spaced charges, and many of the examined systems even retain some water in their sites, further reducing the desolvation penalty. We highlight the importance of tightly pairing the charges of the ligand and the pocket in order to reach the biophysical limits of binding. Ligand efficiency drops by at least 0.1 kcal/mol-atom for misfits as small as 0.24 Å in average contact between charged groups of the ligand and protein (i.e., a 10-atom ligand would drop affinity by 1 kcal/mol or more).

Several points should be considered for drug development. Of course, charged moieties are disfavored in drug development, and drug-like molecules are very different that the most efficient ligands examined here. We proposed that our soft limits of −0.83 kcal/mol-atom and −51 cal/mol-Ų are reasonable upper bounds for drug development, given the less drug-like character of the top 5%. Based on the average efficiencies, we also caution that pushing for ligand efficiencies in excess of −0.4 kcal/mol-atom from a simple combinatorial library will be too restrictive for many systems. Furthermore, we stress that optimizing charge complementarity may be more important for drug design than is currently stressed, but this depends upon desolvation issues that are difficult to predict a priori.

Lastly, we suggest that the ~15 kcal/mol limit of binding may be due to the fact that there is no evolutionary pressure to create tighter binding small molecules once the bound lifetime exceeds the lifetime of the protein. In fact, most ligands with affinities in excess of −15 kcal/mol are man-made, pushed to extremes that are inaccessible by natural processes.