Abstract
Four applications of permutation tests to the single-mediator model are described and evaluated in this study. Permutation tests work by rearranging data in many possible ways in order to estimate the sampling distribution for the test statistic. The four applications to mediation evaluated here are the permutation test of ab, the permutation joint significance test, and the noniterative and iterative permutation confidence intervals for ab. A Monte Carlo simulation study was used to compare these four tests with the four best available tests for mediation found in previous research: the joint significance test, the distribution of the product test, and the percentile and bias-corrected bootstrap tests. We compared the different methods on Type I error, power, and confidence interval coverage. The noniterative permutation confidence interval for ab was the best performer among the new methods. It successfully controlled Type I error, had power nearly as good as the most powerful existing methods, and had better coverage than any existing method. The iterative permutation confidence interval for ab had lower power than do some existing methods, but it performed better than any other method in terms of coverage. The permutation confidence interval methods are recommended when estimating a confidence interval is a primary concern. SPSS and SAS macros that estimate these confidence intervals are provided.
Keywords: Mediation, Permutation test
Mediation models are often applied in psychological research to discover the mechanism by which an independent variable affects a dependent variable. A third variable—an intervening variable or mediator—intervenes between the independent and dependent variable. Methods to ascertain whether a mediating variable transmits the effects of an independent variable to a dependent variable are widely used in many substantive areas. Some examples of mediational hypotheses are that the effect of exposure to information on behavior is transmitted by understanding the information, that attitudes affect behavior through intentions, and that psychotherapy leads to catharsis that promotes mental health (MacKinnon, 2008).
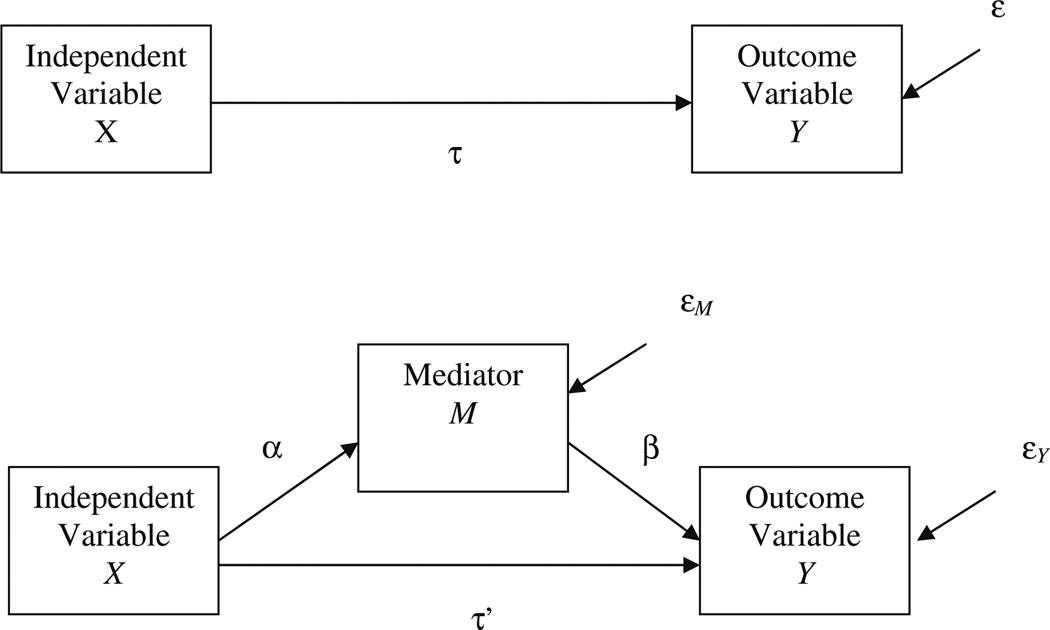
The single-mediator model is the focus of this article, as it is the simplest example of mediation. This model is depicted in a path diagram in Fig. 1 and is specified in terms of Eqs. 1, 2, and 3:
| (1) |
| (2) |
| (3) |
Fig. 1.
Path diagram for the single-mediator model
In these equations, Y is the outcome variable, X is the independent variable, M is the mediator, τ represents the total effect of X on Y, τ′ represents the relation between X and Y adjusted for M (the direct effect), β represents the relation between M and Y adjusted for X, α represents the relation between X and M, β0i is the intercept for Eq. i, and ε, εY, and εM are residuals. The mediated effect is the product of α from Eq. 3 and β from Eq. 2. The corresponding sample values for α, β, τ, and τ′ are a, b, c, and c′.
Although several outstanding methods for statistical significance testing and confidence interval estimation for mediation have been identified, even the best tests do not have ideal Type I error rates, statistical power, and confidence limit coverage. MacKinnon, Lockwood, Hoffman, West, and Sheets (2002) described 15 different tests of mediation that had been proposed at different times. They compared these methods in terms of their Type I error rates and their power to reject false null hypotheses. The tests varied in their ability to control Type I error at the nominal rate. Even those that did control Type I error often had very low statistical power. As MacKinnon et al. (2002) detailed, a major difficulty in testing for mediation is that the sampling distribution of the mediated effect, ab, is typically not normal, as many tests of mediation assume. The same is true for the c – c′ estimator of the mediated effect, which is equivalent to the ab estimator when the regressions in Eqs. 1, 2, and 3 are estimated using ordinary least squares (OLS; MacKinnon & Dwyer, 1993).
Under conditions in which the assumptions of classical statistical methods are violated, such as a nonnormal distribution, resampling methods often outperform classical methods because the resampling methods require fewer assumptions (Manly, 1997). Bootstrapping is one such resampling method that has been found to perform well in terms of Type I error control, power, and coverage, and it has therefore been widely recommended as an ideal approach to testing mediation (MacKinnon, Lockwood, & Williams, 2004; Preacher & Hayes, 2004; Shrout & Bolger, 2002), for more complex mediational models as well as for the single-mediator model (Cheung, 2007; Preacher&Hayes, 2008; Taylor, MacKinnon, & Tein, 2008; Williams & MacKinnon, 2008). Briefly, bootstrapping involves drawing many samples from the original sample with replacement (meaning that the same case may be included more than once in a bootstrap sample), estimating the mediated effect in each bootstrap sample, and using the distribution of these estimates to find a confidence interval for the true mediated effect. For the simplest bootstrap method, the percentile bootstrap, the (ω/2) × 100 and (1 − ω/2) × 100 percentiles are chosen as the limits of the confidence interval, where ω is the nominal Type I error rate. Other methods, such as the bias-corrected bootstrap, make adjustments to which percentiles from the bootstrap distribution are chosen as the confidence limits (Efron & Tibshirani, 1993; MacKinnon et al., 2004). Another resampling method that has not as yet been applied to testing for mediation is the permutation test (also called the randomization test). Like bootstrap methods, permutation tests make fewer assumptions than do classical statistical methods. MacKinnon (2008) suggested that the permutation test may be used to test mediation and described how such a test might be conducted. The purpose of this article is to describe and evaluate four permutation-based tests for mediation—the one proposed by MacKinnon (2008) and three others—and to compare them to the best-performing existing mediation tests. Two of the proposed methods also allow for the forming of confidence intervals. To the best of our knowledge, permutation-based confidence intervals have rarely been presented and have not been described for the mediated effect. To introduce permutation tests, we describe their use in comparing two means and in regression; we then describe the proposed applications of permutation tests to testing for mediation in the single-mediator model.
Permutation tests
The permutation test was proposed by Fisher (1935), who used it to demonstrate the validity of the t test. Unlike a classical statistical test, for which a test statistic calculated from the data is compared to a known sampling distribution such as a t or an F distribution, a permutation test compares the test statistic from the data to an empirical sampling distribution formed by permuting the observed scores. Like the sampling distribution used in a classical statistical test, this permutation-based distribution holds if the null hypothesis is true; if the calculated test statistic is extreme in this distribution, the null hypothesis is rejected.
Comparing two group means
The case of testing the difference between the means of two independent groups, which is typically done using an independent-samples t test, provides a straightforward example of the application of the permutation test. The test works by first finding the difference between the observed means. The data are then permuted, meaning that the cases are reallocated to the two groups in all possible combinations (with the constraint that the group sizes are held constant at their observed values). Permutation is done repeatedly to create all possible samples that could have resulted from assigning the cases to the two groups. Each sample based on reallocation provides an estimated difference between the group means that might have arisen if the null hypothesis were true. The rationale is that if the null hypothesis is true, cases in both groups come from the same population with the same group mean, so the cases could have just as easily been found in either of the two groups. The differences between group means found for each permuted sample provide estimates of differences that might arise by chance alone. In other words, they form a sampling distribution for the difference given that the null hypothesis is true. The observed difference between group means, based on the original, unpermuted data, is compared to this distribution in the same way as in any other null hypothesis test. If the observed value is extreme in the distribution, typically in the lowest or highest (ω/2) × 100% of the distribution for a two-tailed test, the null hypothesis of no difference is rejected. This permutation test is considered an exact test of the difference between two groups.
One difficulty of the permutation test is that the number of possible ways of reassigning scores to the two groups is extremely large, even for small samples. For two groups of size n1 and n2, the number of ways of reassigning the scores to the groups (i.e., the number of possible permuted samples, or Np) is equal to the number of combinations of n1 + n2, taken n1 at a time or n2 at a time:
| (4) |
For a two-group design with 10 scores in each group—for example, Np = 20!/(10!)(10!) = 184,756—calculating a test statistic for every one of these permuted samples can be quite time consuming. Therefore, rather than creating every possible permuted sample, most applications of the permutation test examine only a subset (of size np) of the possible permuted samples, Np (Edgington, 1969, 1995). Tests for which np < Np are called approximate permutation tests. Tests that use the entire set of permuted samples are called exact permutation tests. For all further applications of the permutation test, we will discuss only the approximate version.
Testing a regression coefficient
Permutation tests have been applied in several ways to tests of regression coefficients (Anderson & Legendre, 1999; Manly, 1997; ter Braak, 1992). The approach described here is known as the permutation of raw data (Manly, 1997). This application to regression analysis is similar to the two independent-group tests described above. Rather than a single variable defining group membership, there are potentially multiple predictors. In the case of a single predictor, W, predicting an outcome variable, Z, this is the regression equation:
| (5) |
To perform a permutation test of the null hypothesis that the true coefficient for W, γ1, equals zero, the model is first estimated for the original data to find g1. To form the permutation-based sampling distribution, scores on the outcome Z are then permuted and reassigned to scores on the predictor W in all possible combinations. To distinguish them from the unpermuted Z scores, the permuted scores are labeled Z+. The regression model is reestimated, predicting Z+ from W in each permuted sample; the resulting estimate of the coefficient for W in each sample is labeled g1+. The g1 coefficient from the original, unpermuted data is compared to the sampling distribution of g1+ obtained from the permuted samples to test the null hypothesis that γ1 = 0.
In multiple regression, the procedure is largely the same. The model is first estimated for the unpermuted data:
| (6) |
Scores on the dependent variable Z are then permuted and reassigned in all possible ways to unpermuted scores on the predictors W1 and W2. As the null hypothesis being tested for each predictor is that its partial association with the outcome variable is zero, it is important to maintain the associations among the predictor variables (Anderson & Legendre, 1999). Therefore, scores on the predictors are not permuted and reassigned; only the outcome variable is permuted and reassigned. The model is reestimated for each permuted sample, allowing for a null hypothesis true sampling distribution to be formed for each coefficient. Observed coefficient values based on the original data are then compared to their corresponding permutation-based sampling distributions in order to test the null hypothesis that each has a true value of zero.
A confidence interval for a regression coefficient
In addition to null hypothesis testing of regression coefficients, the permutation method can also be used to find a confidence interval for a regression coefficient (Manly, 1997). The permutation methods described above estimate a sampling distribution given that the null hypothesis is true; the observed statistic is compared to this distribution to test the null hypothesis. Creating a confidence interval, on the other hand, requires estimating the actual sampling distribution of the statistic. Because the sampling distribution to be estimated varies around the observed value of the statistic rather than around zero, permutation confidence interval estimation requires a different approach than permutation null hypothesis tests. Instead of permuting scores on the outcome variable, finding a confidence interval for a regression coefficient requires permuting residuals, an approach proposed by ter Braak (1992) for null hypothesis testing and extended to estimating confidence intervals by Manly (1997). For a one-predictor regression, the model is first estimated for the original, unpermuted data, as in Eq. 5, and the predicted values Ẑ and residuals eZ are calculated. The residuals are then permuted and reassigned to unpermuted data (which includes scores on the predictor and outcome and predicted scores), after which the residuals are labeled . This process is repeated many times to create a large number of permuted samples. Following the form of Eq. 5, new permutation-based values of the outcome variable, Z*, are calculated in each permuted sample as the original predicted score plus the permuted residual, . These permutation-based outcome variables are then regressed on the predictor in each permuted sample, yielding permutation-based estimates of the coefficient g1, labeled :
| (7) |
Note that the residuals in this regression are labeled e(Z*) to distinguish them from the original residuals eZ and the permuted residuals .
The values form an estimated sampling distribution for g1. Confidence limits for g1 are taken as the (ω/2) × 100 and (1 − ω/2) × 100 percentiles of the distribution. This confidence interval may also be used to perform a null hypothesis test: If zero is not included in the interval, the null hypothesis that γ1 = 0 can be rejected.
An iterative search for a confidence interval for a regression coefficient
Another approach to finding confidence limits for a regression coefficient, proposed by Manly (1997), requires a separate iterative search for each of the two confidence limits. We describe the process only for the upper confidence limit; it is straightforwardly generalizable to searching for the lower confidence limit. This approach is largely similar to the noniterative approach, except that it uses the current estimate of the confidence limit in place of the sample estimate of the regression coefficient to calculate the predicted values and residuals. It begins by estimating the regression model for the original, unpermuted data, and finding the usual, normal-theory upper confidence limit for g1, g1(ucl) = g1 + tω/2,(df=n−2)sg1 to use as a starting value, where sg1 is the standard error of g1. Predicted values and residuals are then calculated for the original data, but rather than finding predicted values in the usual way, using the coefficients g0 and g1, this approach uses g1(ucl) in place of g1 in the calculation. Predicted values are calculated as Ẑ(ucl) = g0 + g1(ucl) W, and the residuals are calculated as eZ(ucl) = Z − Ẑ(ucl). As for the noniterative approach, the residuals are then permuted and reassigned to unpermuted data, after which the residuals are labeled . This process is repeated many times to create a large number of permuted samples. The residuals are used, as in the noniterative approach, with the original predicted scores to calculate new outcome variable scores: . These permutation-based outcome variable scores are then regressed on the predictor in each permuted sample, as in Eq. 7:
| (8) |
When the sampling distribution is formed from the values from the different permuted samples, rather than taking confidence limits from it directly, as in the noniterative approach, this approach checks whether the estimated confidence limit g1(ucl) has the desired percentile rank of (1 − ω/2) × 100 in the permuted distribution. If it does, iteration ends, and g1(ucl) is taken as the upper confidence limit. If it does not, g1(ucl) is adjusted—downward if the percentile rank was too high, or upward if the percentile rank was too low—and another iteration is run. The process is repeated until a value of g1(ucl) is found that yields the desired (1 − ω/2) × 100 percentile rank in the sampling distribution of values of .
Permutation tests for mediation
We describe four applications of permutation tests to testing the single-mediator model. All are generalizations or extensions of the tests described above. One, the permutation test of ab, was proposed previously by MacKinnon (2008), but the other three are new.
The permutation test of ab
MacKinnon (2008, Sec. 12.6) proposed a permutation test for mediation that makes use of the permutation-of-raw-data approach described above for testing a regression coefficient (Manly, 1997). We refer to this method as the permutation test of ab. Applying this method requires, first, that the regression models in Eqs. 2 and 3 be estimated for the original, unpermuted data to find the values of a and b. Values of the outcome variable, Y, are then permuted a large number of times and reassigned to unpermuted scores on the predictor, X, and mediator, M, to created many permuted samples. The permuted Y values, labeled Y+, are then regressed on the unpermuted X and M values in each permuted sample (as in Eq. 2 above), and the coefficient for M in each permuted sample is labeled b*. Similarly, values of the mediator, M, are permuted a large number of times and reassigned to values of the predictor, X, to create many permuted samples. The permuted M values, labeled M+, are regressed on X in each permuted sample (as in Eq. 3), and the coefficient for X in each permuted sample is labeled a+. Finally, corresponding pairs of a+ and b+ values are multiplied to yield a+b+, and ab, the estimate of the mediated effect from the original data, is compared to the distribution of a+b+ to perform a test of the null hypothesis of no mediation.
The permutation test of joint significance
A second application of the permutation test to the single-mediator model is based on the joint significance test, as discussed by MacKinnon et al. (2002; see also James & Brett, 1984; Kenny, Kashy, & Bolger, 1998). The joint significance test for mediation is similar to the well-known approach proposed by Baron and Kenny (1986), except that it does not require that c, the sample estimate of τ in Eq. 1, be significant. To perform it, the regression models in Eqs. 2 and 3 are estimated; to reject the null hypothesis of no mediation, both a (the estimate of α in Eq. 3) and b (the estimate of β in Eq. 2) must be significant. The permutation test of joint significance has the same requirements to find significant mediation. It differs only in that it tests the coefficients a and b using permutation of raw data, as described above, rather than the usual t tests of regression coefficients. Practically, this means that the steps in performing this test are nearly identical to the steps for the permutation test of ab. The difference occurs in the final step, where the a+ and b+ values are used for two separate null hypothesis tests rather than being multiplied together in pairs to create a sampling distribution of a+b+. For the first test, the sample estimate a is compared against the distribution of a+. For the second, the sample estimate b is compared against the distribution of b+. If both null hypotheses are rejected, the permutation test of joint significance rejects the null hypothesis of no mediation.
A confidence interval for the mediated effect
The permutation-of-residuals method described above for finding a confidence interval for a regression coefficient may also be applied to finding a confidence interval for the mediated effect. To find the confidence interval, the method is applied separately to the regression models used to estimate the mediated effect, Eqs. 2 and 3. For Eq. 2, the model is first estimated, and predicted values Ŷ and residuals eY are calculated. The residuals are then permuted and reassigned a large number of times to unpermuted scores on X and M, after which the residuals are labeled . New permutation-based values of Y, which are labeled Y*, are calculated in each permuted sample as the original predicted score plus the permuted residual, . These permutation-based Y* values are then regressed on X and M in each permuted sample, yielding permutation-based estimates of b, labeled b*:
| (9) |
Similarly, for Eq. 3, the model is estimated, and predicted values M̂ and residuals eM are calculated. The residuals are permuted and reassigned a large number of times to unpermuted scores on X, after which the residuals are labeled . New permutation-based values of M, which are labeled M*, are calculated in each permuted sample as the original predicted score plus the permuted residual, . These permutation-based M* values are regressed on X in each permuted sample, yielding permutation-based estimates of a, labeled a*:
| (10) |
Corresponding values of a* and b* are multiplied, to yield a*b*. The distribution of values of a*b* is an estimate of the sampling distribution of ab. Confidence limits for the mediated effect are the (ω/2) × 100 and (1 − ω/2) × 100 percentiles of the distribution. The confidence interval may also be used to test the null hypothesis of no mediated effect.
An iterative search for a confidence interval for the mediated effect
The iterative-search approach to finding a confidence interval for a regression coefficient, described above, may also be extended to finding a confidence interval for the mediated effect. As in the case of the regression coefficient, a separate search is required for each of the two confidence limits. We describe the process only for the upper confidence limit. This process is largely generalizable to searching for the lower confidence limit; we will note points where the process differs for the lower limit. The regression models in Eqs. 2 and 3 are first estimated for the original, unpermuted data, and the mediated effect ab is calculated. The first-order standard error (Sobel, 1982) is used to calculate the starting value for the upper confidence limit: , where sa and sb are the standard errors of a and b. Because ab is the product of two regression coefficients rather than of a single regression coefficient, this estimate of the upper confidence limit cannot be directly used to calculate predicted scores and residuals, as in the iterative-search approach for the confidence interval for a regression coefficient. The estimated confidence limit must be analyzed into two components, one for a and one for b, which, when multiplied together, yield ab(ucl). We label these components a(ucl) and b(ucl), but note that they are not the same as the upper confidence limits for a and b. Because there are infinitely many pairs of values of a(ucl) and b(ucl) that can be multiplied to yield a particular value of ab(ucl), constraints must be applied to find a unique pair. We apply two constraints: first, a(ucl) and b(ucl) are required to be equidistant from a and b, respectively, in units of their respective standard errors. Second, for an upper confidence limit, a(ucl) and b(ucl) must be on the same side (positive or negative) of a and b, respectively. (For a lower confidence limit, a(ucl) and b(ucl) must be on opposite sides of a and b, respectively.) Although these constraints are somewhat arbitrary, the first is based on the goal of making the confidence limit be equally a function of both components, and the second is used because, for mediated effects near zero, it will correctly choose a negative value for the lower confidence limit and a positive value for the upper. These constraints yield two possible pairs of values for the components; in our application of the method, we always selected the pair that were closer to a and b. Appendix A gives details of how these constraints are used to analyze ab(ucl) into a(ucl) and b(ucl), as well as how the estimated lower confidence limit, ab(lcl), is analyzed into its components, a(lcl) and b(lcl). Once the estimated confidence limit has been analyzed into its components, the remainder of the procedure is similar to the iterative search for a confidence interval for a single regression coefficient. Each confidence limit component is used in place of its corresponding coefficient to calculate predicted values and residuals. For a(ucl), the predicted values are calculated as M̂(ucl) = b03 + a(ucl)X, and residuals are calculated as eM(ucl) = M − M̂(ucl). For b(ucl), the predicted values are calculated as Ŷ(ucl) = b02 + c′X + b(ucl)M, and residuals are calculated as eY(ucl) = Y − Ŷ(ucl). To create permuted samples, both sets of residuals are then permuted and reassigned a large number of times to their corresponding unpermuted predictors. Values of eM(ucl) are permuted and reassigned to unpermuted values of X, after which they are labeled . Values of eY(ucl) are permuted and reassigned to unpermuted values of X andM, after which they are labeled . In each permuted sample, new outcome variable scores are calculated as the sum of the original predicted value and the permuted residual. The new outcome for M is , and the new outcome for Y is . Finally, these new permutation-based outcome variables are regressed on their corresponding predictors, as in Eqs. 9 and 10:
| (11) |
| (12) |
Pairs of values of are multiplied, and the estimated upper confidence limit ab(ucl) is compared to the distribution of values of to check whether it has the desired percentile rank of (1 − ω/2) × 100. If it does, iteration ends, and ab(ucl) is taken as the upper confidence limit. If it does not, ab(ucl) is adjusted—downward if the percentile rank is too high, or upward if the percentile rank is too low—and another iteration is run.
Method
Four permutation methods for testing mediation were evaluated: the permutation test of ab, the permutation test of joint significance, the permutation confidence interval for ab, and the iterative permutation confidence interval for ab. The purpose of the present study was to examine the performance of these methods in terms of their Type I error, power, and coverage. For purposes of comparison, four of the best-performing methods of testing for mediation recommended on the basis of previous research are also included. These methods are the joint significance test, the asymmetric-distribution-of-the-product test using the PRODCLIN program (MacKinnon, Fritz, Williams & Lockwood, 2007), the percentile bootstrap, and the bias-corrected bootstrap (Efron & Tibshirani, 1993).
The eight methods of testing for mediation were evaluated in a Monte Carlo study. Data were generated and the methods of testing for mediation were performed using SAS 9.2 (SAS Inc., 2007), with the exception of the asymmetric-distribution-of-the-product test, which was done using the PRODCLIN program (MacKinnon et al., 2007). The predictor (X) was simulated to be normally distributed. The mediator (M) and the outcome (Y) were generated using Eqs. 2 and 3. Residuals were simulated to be normally distributed, and the intercepts were simulated to be zero. Four factors were varied in the study. The sizes of α and β in Eqs. 2 and 3 either were set to be zero or were varied to correspond to Cohen’s (1988) small, medium, and large effects (as in MacKinnon et al., 2002). As most methods of testing for mediation have been found to be relatively insensitive to the size of τ′, it was varied at only two levels: zero and large. Because resampling methods such as permutation tests and bootstrapping typically show the largest differences from classical methods in smaller samples, sample size was set to be 25, 50, 100, and 200 in different conditions. The entire design consisted of 128 conditions: 4 (α) × 4 (β) × 2 (τ′) × 4 (sample size). In each condition, 4,000 replications were run, and the eight methods of testing for mediation were all applied. All permutation methods were used in their approximate form, using 1,999 permuted samples for each (with the original, unpermuted data also included, for a total of 2,000 samples); for the bootstrap methods, 2,000 bootstrap samples were drawn.
The methods were compared using three criteria: Type I error, power, and coverage. The Type I error for each method was the proportion of replications in a condition for which the null hypothesis of no mediation was true (i.e., αβ = 0) yet the method rejected the null hypothesis. The power for each method was the proportion of replications in a condition for which the null hypothesis of no mediation was false (i.e., αβ ≠ 0) and the method did reject the null hypothesis. A nominal Type I error rate of ω = .05 was used for all of the hypothesis tests. Coverage was used to compare only the methods that allow for estimation of a confidence interval. This included five of the methods: the permutation confidence interval for ab, the iterative permutation confidence interval for ab, the asymmetric-distribution-of-the-product test, and the percentile and bias-corrected bootstrap methods. The coverage for each method was the proportion of replications within a condition for which the confidence interval estimated using the method included the true mediated effect αβ. A nominal coverage level of 95% was used for all confidence intervals.
Results
Across the three criteria for comparing the methods’ performance, the results were very similar for conditions in which α and β took on particular values, regardless of which coefficient took on which value. For example, the results for α = 0 and β = .14 (small) were similar to those for β = 0 and α = .14. Therefore, for simplicity, the results are presented averaging across such pairs of conditions. The patterns of results were also largely similar across the two levels of τ′, so only results for the τ′ = 0 conditions are presented. In a very small number of replications (less than 0.1%, and no more than 11 of the 4,000 in any condition), the asymmetric-distribution-of-the-product test failed to find one or both of the confidence intervals. These replications are therefore excluded in the calculation of Type I error, power, and coverage for this method.
Type I error
Type I error rates are shown in Table 1. Most methods had Type I error rates well below the nominal level when both α and β were zero. The Type I error rates increased with increasing size of the nonzero coefficient and were generally near the nominal level for conditions in which the nonzero coefficient was large. The increase from near zero to about the nominal level occurred more quickly with increasing size of the nonzero coefficient in larger samples than in smaller ones. There were two exceptions to this pattern. First, the permutation test of ab had a Type I error rate was near the nominal level when both α and β were zero, but its rate increased to far beyond the nominal level—as high as .769—as the nonzero coefficient increased from zero. Second, the bias-corrected bootstrap also had some elevated Type I error rates in smaller samples. Its rate peaked at .083, with rates of at least .070 in four other conditions. Other than these two methods, and one condition in which the rate for the asymmetric distribution of the product had a Type I error rate of .061, no method had a Type I error rate as high as .060 in any condition.
Table 1.
Type I error rates by method, sample size, and the values of α and β
| n | α and β | Permutation Test of ab |
Joint Significance |
Permutation Joint Significance |
Asymmetric Distribution of Product |
Percentile Bootstrap |
Bias-Corrected Bootstrap |
Permutation CI for ab |
Iterative Permutation CI for ab |
|---|---|---|---|---|---|---|---|---|---|
| 25 | zero, zero | .050 | .003 | .003 | .005 | .005 | .012 | .005 | .002 |
| zero, small | .079 | .004 | .005 | .006 | .005 | .015 | .006 | .002 | |
| zero, medium | .218 | .020 | .020 | .027 | .022 | .050 | .028 | .012 | |
| zero, large | .353 | .033 | .033 | .050 | .043 | .074 | .051 | .025 | |
| 50 | zero, zero | .051 | .003 | .002 | .002 | .003 | .009 | .002 | .000 |
| zero, small | .106 | .006 | .006 | .007 | .006 | .019 | .006 | .003 | |
| zero, medium | .364 | .037 | .038 | .045 | .040 | .072 | .040 | .030 | |
| zero, large | .523 | .045 | .045 | .053 | .054 | .083 | .050 | .040 | |
| 100 | zero, zero | .050 | .003 | .003 | .003 | .002 | .008 | .001 | .001 |
| zero, small | .159 | .013 | .013 | .013 | .010 | .027 | .010 | .007 | |
| zero, medium | .528 | .053 | .053 | .061 | .054 | .081 | .055 | .049 | |
| zero, large | .650 | .047 | .048 | .053 | .055 | .070 | .053 | .046 | |
| 200 | zero, zero | .057 | .004 | .004 | .004 | .002 | .008 | .002 | .002 |
| zero, small | .266 | .025 | .026 | .027 | .020 | .046 | .020 | .018 | |
| zero, medium | .659 | .047 | .046 | .053 | .051 | .066 | .051 | .047 | |
| zero, large | .769 | .052 | .051 | .054 | .058 | .065 | .054 | .050 |
The nominal Type I error rate for all methods = .05. For α and β, small = .14, medium = .39, and large = .59. τ′ = 0 in all conditions. The values for conditions other than “zero, zero” are averaged across the conditions in which the nonzero value is assigned to α and to β. For example, the values for zero, small are averages across α = zero, β = small and α = small, β = zero
The Type I error rates for each method in each condition in which the null hypothesis was true were tested against the nominal Type I error rate of .05. This was done by finding the standard error for the proportion of replications in which the null hypothesis was rejected (i.e., for the observed Type I error rate), forming a 95% confidence interval for the proportion, and checking whether .05 was in the confidence interval. As is shown in Table 2, the permutation test of ab had Type I error rates significantly above .05 in 82% of the null-true conditions, and the bias-corrected bootstrap had Type I error rates significantly above .05 in half of the null-true conditions. No other methods had difficulty with excess Type I error.
Table 2.
Percentages of conditions in which the methods performed poorly on each criterion
| Criterion | Permutation Test of ab |
Joint Significance |
Permutation Joint Significance |
Asymmetric Distribution of Product |
Percentile Bootstrap |
Bias-Corrected Bootstrap |
Permutation CI for ab |
Iterative Permutation CI for ab |
|---|---|---|---|---|---|---|---|---|
| Excess Type I error | 82 | 0 | 0 | 16 | 14 | 50 | 13 | 0 |
| Lower powera | – | 79 | 88 | 74 | 78 | 0 | 76 | 83 |
| Lower powerb | – | 50 | 67 | 0 | 40 | – | 8 | 75 |
| Low coverage | –c | –c | –c | 40 | 35 | 52 | 27 | 0 |
Excess Type I error was found by testing the observed Type I error against the nominal level of .05 for each method in each condition. Lower power was found by testing the power level for each method against the highest-power method for that condition. Insufficient coverage was found by testing the observed coverage level against the nominal level of .95 for each method in each condition
The permutation test of ab was excluded from this analysis because of its excessive Type I error rates in many conditions (see Table 1)
Both the permutation test of ab and the bias-corrected bootstrap were excluded from this analysis because of their excessive Type I error rates in many conditions (see Table 1)
This method does not produce a confidence interval, so it is excluded from the analyses of coverage
Power
Power levels are shown in Table 3. The permutation test of ab is excluded from the table because of its dramatically inflated Type I error rates. Differences between methods in power were most pronounced in conditions of midrange coefficient sizes and effect sizes. When coefficients and effects were small, all methods had low power; when they were large, all methods had high power. Across conditions, the bias-corrected bootstrap was consistently the most powerful method. The difference between its power and the power of the second most powerful method was in a few conditions larger than .050. The asymmetric-distribution-of-the-product test was usually the second most powerful method. Following it were a group of methods that performed very similarly. In descending order of power, these were the permutation confidence interval for ab, the percentile bootstrap, the joint significance test, and the permutation joint significance test. The iterative permutation confidence interval for ab nearly always had the least power of any of the tests.
Table 3.
Power levels by method, sample size, and the values of α and β
| n | α and β | Joint Significance |
Permutation Joint Significance |
Asymmetric Distribution of Product |
Percentile Bootstrap |
Bias-Corrected Bootstrap |
Permutation CI for ab |
Iterative Permutation CI for ab |
|---|---|---|---|---|---|---|---|---|
| 25 | small, small | .009 | .009 | .012 | .012 | .026 | .012 | .005 |
| small, medium | .036 | .035 | .051 | .042 | .082 | .051 | .023 | |
| small, large | .071 | .072 | .095 | .082 | .130 | .095 | .054 | |
| medium, medium | .178 | .171 | .221 | .185 | .278 | .221 | .136 | |
| medium, large | .314 | .299 | .378 | .322 | .428 | .378 | .267 | |
| large, large | .571 | .534 | .631 | .565 | .672 | .634 | .521 | |
| 50 | small, small | .025 | .027 | .027 | .023 | .054 | .024 | .017 |
| small, medium | .115 | .116 | .135 | .120 | .186 | .126 | .098 | |
| small, large | .156 | .158 | .181 | .172 | .224 | .173 | .147 | |
| medium, medium | .549 | .542 | .588 | .538 | .647 | .571 | .515 | |
| medium, large | .727 | .715 | .756 | .728 | .785 | .749 | .710 | |
| large, large | .941 | .932 | .950 | .936 | .956 | .949 | .934 | |
| 100 | small, small | .073 | .072 | .078 | .066 | .125 | .064 | .057 |
| small, medium | .271 | .272 | .295 | .279 | .353 | .276 | .258 | |
| small, large | .280 | .281 | .298 | .298 | .332 | .295 | .273 | |
| medium, medium | .936 | .936 | .944 | .933 | .956 | .939 | .933 | |
| medium, large | .966 | .964 | .969 | .965 | .971 | .968 | .963 | |
| large, large | .999 | .999 | 1.000 | .999 | .999 | 1.000 | .999 | |
| 200 | small, small | .247 | .249 | .259 | .224 | .332 | .222 | .212 |
| small, medium | .497 | .496 | .514 | .503 | .547 | .501 | .490 | |
| small, large | .501 | .499 | .510 | .506 | .523 | .509 | .491 | |
| medium, medium | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| medium, large | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| large, large | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
The nominal Type I error rate for all methods = .05. For α and β, small = .14, medium = .39, and large = .59. τ′ = 0 in all conditions. The values for conditions in which α ≠ β are averaged across the conditions in which the different values are assigned to α and to β. For example, the values for small, medium are averages across α = small, β = medium and α = medium, β = small. The permutation test of ab is not included because of its poor Type I error performance (see Table 1)
Unlike Type I error, there is not an a priori power level that methods are expected to achieve. Power performance was therefore tested by comparing the methods against each other. In each condition, the method having the maximum power was found, and all other methods’ power levels were tested against it using a z test of the difference between proportions. This comparison was done twice (see the second and third rows of Table 2). In the first comparison, only the permutation test of ab was excluded because of its excess Type I error. In the second, both the permutation test of ab and the bias-corrected bootstrap were excluded because of their excess Type I error. This was done because, although the excess Type I error for the bias-corrected bootstrap was not close to being as great as for the permutation test of ab, the method still did have Type I error rates significantly greater than the nominal level in half of the null-true conditions. In the first analysis, the bias-corrected bootstrap never had significantly less power than the most powerful method (except when more than one method had a power of 1, it was in all conditions the most powerful method). Among the remainder of the methods, the asymmetric-distribution-of-the-product test was most likely to have power not significantly lower than the most powerful method. In the second analysis, with the bias-corrected bootstrap excluded, the asymmetric-distribution-of-the-product test never had power significantly lower than the most powerful method. It was followed by the permutation test of ab, which had significantly lower power in 8% of conditions.
Coverage
Coverage is only applicable for methods used to form confidence intervals: the asymmetric-distribution-of-the-product test, the percentile and bias-corrected bootstraps, and the noniterative and iterative permutation confidence intervals for ab. For conditions in which the null hypothesis is true, coverage is simply one minus the Type I error rate when a 100 × (1 − ω)% confidence interval is used, as it was in the present study. This is true because a Type I error indicates that a confidence interval did not include zero; as zero is the true value (αβ = 0), this also indicates a failure of coverage. Coverage results are therefore inferable from the values in Table 1, and they mirror the Type I error rate results. In null-hypothesis-true conditions, all of the methods used to form confidence intervals had too high coverage (greater than .95) for the smallest nonzero coefficient sizes and sample sizes, but their coverage fell to near the nominal level for larger nonzero coefficients and sample sizes. The bias-corrected bootstrap was alone in having its coverage fall as low as .917, and below .930 in several other conditions. Among other methods, the only case of coverage falling below .940 was the one condition in which coverage for the asymmetric-distribution-of-the-product test had coverage of .939.
The coverage results for 95% confidence intervals in null-hypothesis-false conditions are shown in Table 4. Across methods, most problems with undercoverage were greater for smaller coefficient sizes and improved as the coefficient sizes increased. There was not as clear a pattern for sample size: Some undercoverage problems occurred for the smallest samples, but others appeared only in larger-sample conditions. For example, the asymmetric-distribution-of-the-product test had good coverage for the α small, β small condition with n = 25 and 50, but poor coverage (.897 and .916) for larger ns. The bias-corrected bootstrap had coverage as low as .904, with a few other conditions below .930, but had generally better coverage with increasing sample size. The other three methods—the percentile bootstrap and both of the permutation-confidence-interval-for-ab methods—had little difficulty with coverage in any condition. The iterative permutation confidence interval for ab performed particularly well, with a minimum coverage of .944.
Table 4.
Coverage of 95% confidence intervals in null-hypothesis-false conditions by method, sample size, and the values of α and β
| n | α and β | Asymmetric Distribution of Product |
Percentile Bootstrap |
Bias-Corrected Bootstrap |
Permutation CI for ab |
Iterative Permutation CI for ab |
|---|---|---|---|---|---|---|
| 25 | small, small | .978 | .991 | .974 | .992 | .998 |
| small, medium | .929 | .963 | .910 | .966 | .983 | |
| small, large | .927 | .942 | .904 | .941 | .966 | |
| medium, medium | .912 | .932 | .930 | .931 | .947 | |
| medium, large | .935 | .939 | .945 | .940 | .955 | |
| large, large | .937 | .937 | .951 | .937 | .956 | |
| 50 | small, small | .943 | .982 | .944 | .987 | .992 |
| small, medium | .924 | .943 | .914 | .944 | .954 | |
| small, large | .940 | .939 | .920 | .942 | .954 | |
| medium, medium | .932 | .937 | .945 | .939 | .948 | |
| medium, large | .942 | .940 | .947 | .942 | .951 | |
| large, large | .945 | .939 | .951 | .945 | .959 | |
| 100 | small, small | .897 | .956 | .912 | .967 | .971 |
| small, medium | .942 | .948 | .940 | .948 | .954 | |
| small, large | .942 | .940 | .933 | .943 | .949 | |
| medium, medium | .945 | .943 | .953 | .948 | .955 | |
| medium, large | .946 | .943 | .949 | .946 | .954 | |
| large, large | .947 | .943 | .947 | .947 | .951 | |
| 200 | small, small | .916 | .943 | .945 | .941 | .944 |
| small, medium | .946 | .945 | .941 | .947 | .950 | |
| small, large | .949 | .948 | .943 | .950 | .952 | |
| medium, medium | .949 | .945 | .951 | .948 | .955 | |
| medium, large | .952 | .950 | .952 | .950 | .954 | |
| large, large | .950 | .945 | .945 | .949 | .953 |
For α and β, small = .14, medium = .39, and large = .59. τ′ = 0 in all conditions. The values for conditions in which α ≠ β are averaged across the conditions in which the different values are assigned to α and to β. For example, the values for small, medium are averages across α = small, β = medium and α = medium, β = small
As with Type I error, the coverage levels for each method in each condition were tested against the nominal coverage level of .95. This was done by finding the standard error for the proportion of replications in which the confidence interval included αβ (i.e., for the observed coverage level), forming a 95% confidence interval for this proportion, and checking whether .95 was within the confidence interval. As is shown in Table 2, the two permutation confidence interval methods performed best on this criterion, with the iterative permutation confidence interval performing particularly well. The bias-corrected bootstrap performed most poorly, with coverage significantly below .95 in over half of the conditions.
Discussion
This article has introduced four methods of testing for mediation using a permutation approach and, in a Monte Carlo study, has compared their performance to that of other best-performing approaches to testing for mediation. The permutation test of ab performed poorly, with Type I error rates far beyond the nominal level in conditions in which one of α and β was nonzero. The permutation joint significance test performed similarly to, but no better than, the joint significance test. Particularly in the smallest samples and when τ′ was large, the permutation joint significance test had less power. The permutation confidence interval for ab lagged behind the two best-performing methods (the bias-corrected bootstrap and the asymmetric-distribution-of-the-product test) in power, but it had better Type I error control than the bias-corrected bootstrap, and better coverage than both. The iterative permutation confidence interval for ab had the least power of any method tested, but also the best coverage.
As in previous research (MacKinnon et al., 2004), the results of this study suggest that testing mediation is accomplished better by directly estimating the sampling distribution of the statistic being tested, rather than by estimating the sampling distribution that would hold if the null hypothesis were true and comparing the observed statistic to that distribution, as is done in most hypothesis testing. Other than the causal-step methods, such as the joint significance test, methods of testing for mediation estimate the sampling distribution of the mediated effect ab. The permutation test of ab estimates the sampling distribution of ab that holds if α = β = 0 and tests ab against that. Themethod controls Type I errorwhen α = β = 0, but when the null hypothesis is true but α or β ≠ 0, it rejects the null hypothesis at far beyond the nominal rate. In this way, it performs similarly to Freedman and Schatzkin’s (1992) approach, as tested by MacKinnon et al. (2002). Some other methods tested by MacKinnon et al. (2002), such as a test using the first-order standard error (Sobel, 1982), control Type I error but have far less power than do the best-performing methods. These methods estimate a null-true sampling distribution that holds when αβ = 0 but that gets the shape of the sampling distribution wrong when the null is false, and therefore have low power. The best-performing methods therefore do not estimate the sampling distribution of ab when the null hypothesis is true. Rather, they directly estimate the sampling distribution of ab given the observed sample value ab. The asymmetric-distribution-of-the-product test estimates the shape of the sampling distribution by taking the product of assumed normal sampling distributions for a and b. The bootstrap methods resample the data to estimate the shape of the sampling distribution. The permutation confidence interval methods permute the data to achieve this same end.
The superior performance of the methods that directly estimate the sampling distribution on the basis of the sample value ab demonstrate a case in which testing a null hypothesis with a confidence interval is superior to testing the same null hypothesis using a null-hypothesis-true sampling distribution. Confidence intervals have been widely recommended (Cohen, 1994; Wilkinson & the Task Force on Statistical Inference, 1999), and our results provide more motivation for this change in reporting research results. In most familiar cases, where only the location, but not the shape, of the sampling distribution of the statistic of interest varies with the value of the parameter (e.g., a t test for the difference between group means), a confidence interval and a test against a null-hypothesis-true sampling distribution necessarily yield the same decision regarding the status of the null hypothesis. But in situations such as mediation, where both the location and the shape of the sampling distribution of the statistic of interest vary with the value of the parameter, the conventional approach of estimating a null hypothesis sampling distribution and shifting its mean to estimate the confidence interval is not optimal. A confidence interval estimated using the shape of the sampling distribution estimated from the data is not only a superior confidence interval, it yields a superior null hypothesis test.
Recommendations
The findings of the present study echo previous research in suggesting that the distribution-of-the-product test and bootstrap tests are the best performers for testing mediation. The bias-corrected bootstrap, in particular, had the greatest power of any method tested, although it also had difficulty with excess Type I error in some conditions, again replicating previous research (Cheung, 2007; Fritz, Taylor, & MacKinnon, 2011). Among the proposed permutation methods for testing mediation, the noniterative and iterative permutation confidence intervals for ab show the most promise. Although, in most cases, researchers are likely to be more interested in a test of the null hypothesis of no mediation, in situations where estimating a confidence interval for the mediated effect is of primary interest, these permutation confidence interval methods are ideal. Setting aside the bias-corrected bootstrap because of its Type I error difficulties, the permutation confidence interval for ab was found to have less difficulty with undercoverage than any other of the most powerful methods. Specifically, although it was noticeably less powerful than the most powerful methods, the iterative permutation confidence interval for ab had the best coverage of any method. Therefore, we recommend that researchers studying mediation continue to use the distribution-of-the-product test or percentile bootstrap when a test of mediation is of primary concern, but that they use the permutation confidence interval methods when estimating a confidence interval is the major goal. To facilitate the application of these methods, we provide SPSS and SAS macros in Appendices B and C that estimate the permutation confidence interval for ab and the iterative permutation confidence interval for ab.
Limitations and future directions
Our Monte Carlo study was simplified in order to reduce the complexity of the study. For example, the predictor and the residuals of the mediator and outcome variables were all simulated to follow a normal distribution, and the data were simulated to have no measurement error. Future research should consider less optimal situations in which these simplifications are replaced by conditions more in line with typical observed data. For example, as was studied by Biesanz, Falk, and Savalei (2010), data might be simulated in which the assumption in ordinary least squares regression of the normality of residuals is violated. Such situations could actually highlight the strengths of the permutation methods introduced here, as resampling methods often outperform classical methods when assumptions are violated, although bootstrap methods would likely also perform similarly well, as Biesanz et al. found. Future research might also examine the performance of permutation methods of testing for mediation with variables having measurement error.
Appendix A
A tested confidence limit value ab(ucl) or ab(lcl) must be analyzed into two components in order to use the iterated method of finding confidence limits for the mediated effect. For the upper limit,
| (A1) |
Similarly, for the lower limit,
| (A2) |
Because many solutions are possible, two constraints are used to yield a unique solution. First, the components must be equidistant from a and b, respectively, in their respective standard error units. For the upper limit:
| (A3) |
For the lower limit, a(ucl) in Eq. A3 is replaced by a(lcl), and b(ucl) is replaced by b(lcl). Second, for the upper confidence limit, the components are required to fall on the same side of a and b, respectively:
| (A4) |
For the lower confidence limit, the components must fall on opposite sides of a and b:
| (A5) |
For the upper limit, Eq. A4 is rearranged as follows:
| (A6) |
The result is substituted into Eq. A1, yielding
| (A7) |
Equation A7 can be rearranged into a quadratic form for b(ucl), which is the only unknown in that equation:
| (A8) |
Equation A8 is then solved using the quadratic formula:
| (A9) |
This results in two solutions for ab(ucl) (because of the ± operator). The one that is closer to b is chosen. Finally, b(ucl) is substituted into Eq. A1 to find a(ucl).
For the lower confidence limit, a similar series of steps starting with Eq. A5 yields the following quadratic formula solution:
| (A10) |
As for the upper confidence limit, the solution for b(lcl) that places it closer to b is chosen and substituted into Eq. A2, to yield a(lcl).
Appendix B
This SPSS macro estimates the 95% permutation confidence interval for ab and the 95% iterative permutation confidence interval for ab. To use it, first enter and run the entire macro so that the new command “permmed” is defined. This command will be available for the duration of the SPSS session. To run the command on a data set, run the following line in SPSS:
permmed dataname = dataset x = predictor m = mediator y = outcome npermute = permutations niter = iterations seed = randomseed.
The labels in italics must be replaced by the appropriate names and values for the analysis to be run. Dataset is the name of the SPSS data set on which to run the analysis. If only one data set is open, SPSS typically names it “DataSet1.” Predictor is the name of the predictor variable. Mediator is the name of the mediating variable.Outcome is the name of the outcome variable. Permutations is the number of permutations SPSS will use in running the analysis; a large number should be used, to increase the reliability of the results. Iterations is the number of iterations SPSS will use in searching for the iterative permutation confidence limits. Typically, five iterations or fewer are sufficient. If the procedure fails to converge (the output will show the confidence limit as missing and say “not converged”), increase this value. Increase this number with caution, though, as the procedure runs all requested iterations before it completes, so large numbers can dramatically increase processing time. Randomseed is the random number seed SPSS will use in permuting the data. If a seed is chosen (it must be a positive integer <2,000,000,000), repeated runs of the procedure with the same data will produce the same confidence limits. If it is set to 0, SPSS will choose the random number seed, and repeated runs of the procedure with the same data will produce different confidence limits (because different permuted data sets are used).
DEFINE permmed(dataname = !tokens(1) / x = !tokens(1) / m = !tokens(1)/ y = !tokens(1)
/ npermute = !tokens(1) / niter = !tokens(1) / seed = !tokens(1) )
set mxloops = !npermute.
!if (!seed = 0) !then
set seed = random.
!else
set seed = !seed.
!ifend
* Make a listwise deleted dataset. *.
dataset activate !dataname.
dataset copy listwise window=hidden.
dataset activate listwise.
select if missing(!x) = 0 and missing(!m) = 0 and missing(!y) = 0.
compute x = !x.
compute m = !m.
compute y = !y.
exe.
* Find number of cases in listwise deleted dataset. *.
dataset declare nobs window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Descriptives'] subtypes = ['Descriptive Statistics']
/destination format = sav outfile = nobs.
dataset activate listwise.
descriptives variables = x
/statistics = mean.
exe.
omsend.
dataset activate nobs.
select if Var1 = 'x'.
compute nobs = N.
exe.
* Model 2: Regress y on x, m. *.
dataset declare model2 window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model2 viewer = no.
dataset activate listwise.
regression
/dependent = y
/enter x m
/save = pred(yhat) resid(yres).
exe.
omsend.
* Model 3: Regress m on x. *.
dataset declare model3 window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model3.
dataset activate listwise.
regression
/dependent = m
/enter x
/save = pred(mhat) resid(mres).
exe.
omsend.
* Gather results. *.
dataset activate model2.
dataset copy model2int window=hidden.
dataset activate model2int.
select if Var2 = '(Constant)'.
compute b02 = B.
exe.
dataset activate model2.
dataset copy model2bpath window=hidden.
dataset activate model2bpath.
select if Var2 = 'm'.
* The b path is already called B, so it does not need to be made up. *.
compute seb = Std.Error.
exe.
dataset activate model2.
dataset copy model2cprimepath window=hidden.
dataset activate model2cprimepath.
select if Var2 = 'x'.
compute cprime = B.
exe.
dataset activate model3.
dataset copy model3int window=hidden.
dataset activate model3int.
select if Var2 = '(Constant)'.
compute b03 = B.
exe.
dataset activate model3.
dataset copy model3apath window=hidden.
dataset activate model3apath.
select if Var2 = 'x'.
compute a = B.
compute sea = Std.Error.
exe.
match files
file = model2int
/rename = (B = drop1)
/file = model2bpath
/file = model2cprimepath
/file = model3int
/file = model3apath
/keep = b02 b seb cprime b03 a sea.
exe.
dataset name origresult.
compute vara = sea*sea.
compute varb = seb*seb.
compute sobelse = sqrt(a*a*varb + b*b*vara).
exe.
dataset close model2.
dataset close model2int.
dataset close model2bpath.
dataset close model2cprimepath.
dataset close model3.
dataset close model3int.
dataset close model3apath.
exe.
*** Non-iterated permutation confidence limits. ***.
* Make npermute copies of original data. *.
dataset activate listwise.
matrix.
get orig
/file = *
/variables = x, m, y, yhat, yres, mhat, mres.
compute copies = orig.
loop i = 2 to !npermute.
compute copies = {copies; orig}.
end loop.
save copies
/outfile = *
/variables = x, m, y, yhat, yres, mhat, mres.
end matrix.
dataset name origcopies.
* Get nobs into copies of original data so cases can be assinged a dataset copy
number. *.
dataset activate nobs.
compute key = 1.
exe.
dataset activate origcopies.
compute key = 1.
exe.
match files file = origcopies table = nobs
/by key
/drop = Command_ Subtype_ Label_ Var1 N Mean.
exe.
dataset name origcopiesbycopy.
dataset close origcopies.
* Assign shuffle numbers and shuffling variables to permute the residuals yres and
mres. *.
dataset activate origcopiesbycopy.
compute copynum = trunc(($casenum-1)/nobs) + 1.
compute shufflevaryres = rv.uniform(0,1).
compute shufflevarmres = rv.uniform(0,1).
exe.
* Make a dataset with yres shuffled within each dataset copy. *.
dataset activate origcopiesbycopy.
dataset copy shuffleyres window=hidden.
dataset activate shuffleyres.
sort cases by copynum shufflevaryres.
exe.
* Make a dataset with mres shuffled within each dataset copy. *.
dataset activate origcopiesbycopy.
dataset copy shufflemres window=hidden.
dataset activate shufflemres.
sort cases by copynum shufflevarmres.
exe.
* Merge shuffled residuals yres and mres with original data in each dataset copy. *.
match files
file = origcopiesbycopy
/rename (yres mres = drop1 to drop2)
/file = shuffleyres
/rename (x m y yhat mhat mres = drop3 to drop8)
/file = shufflemres
/rename (x m y yhat yres mhat = drop9 to drop14)
/keep = copynum x m y yhat yres mhat mres.
exe.
dataset name shuffled.
dataset close shuffleyres.
dataset close shufflemres.
* Calculate ystar and mstar, the new values of y and m based on shuffling the
residuals. *.
dataset activate shuffled.
compute ystar = yhat + yres.
compute mstar = mhat + mres.
exe.
* Prepare to run regressions separately within each dataset copy. *.
dataset activate shuffled.
split file by copynum.
exe.
* Model 2: Regress ystar on x, m. *.
dataset declare model2shuf window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model2shuf.
dataset activate shuffled.
regression
/dependent = ystar
/enter x m.
exe.
omsend.
* Model 3: Regress mstar on x. *.
dataset declare model3shuf window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model3shuf.
dataset activate shuffled.
regression
/dependent = mstar
/enter x.
exe.
omsend.
* Gather results. *.
dataset close shuffled.
dataset activate model2shuf.
select if Var3 = 'm'.
compute bperm = B.
exe.
dataset activate model3shuf.
select if Var3 = 'x'.
compute aperm = B.
exe.
match files
file = model2shuf
/file = model3shuf
/keep = aperm bperm.
exe.
dataset name shufresult.
dataset close model2shuf.
dataset close model3shuf.
exe.
* Include results for original data. *.
add files
file = origresult
/rename = (a,b = aperm,bperm)
/file = shufresult.
exe.
dataset name origshufresult.
compute abperm = aperm*bperm.
exe.
dataset close shufresult.
* Get confidence limits. *.
dataset declare freqout window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Frequencies'] subtypes = ['Statistics']
/destination format = sav outfile = freqout.
dataset activate origshufresult.
frequencies
variables = abperm
/percentiles = 2.5 97.5.
exe.
omsend.
dataset close origshufresult.
* Combine results for both confidence limits. *.
dataset activate freqout.
dataset copy lower window=hidden.
dataset activate lower.
select if Var2 = '2.5'.
compute permlcl = Var4.
exe.
dataset activate freqout.
dataset copy upper window=hidden.
dataset activate upper.
select if Var2 = '97.5'.
compute permucl = Var4.
exe.
match files
file = lower
/file = upper
/keep = permlcl permucl.
exe.
dataset name permcl.
formats permlcl permucl (f8.4).
dataset close freqout.
dataset close lower.
dataset close upper.
*** Iterated permutation confidence limits. ***.
* Iterate twice: 1 = lower confidence limit, 2 = upper confidence limit *.
!do !direction = 1 !to 2.
* Get initial guess as +/− 1.96 Sobel standard errors. *.
dataset activate origresult.
dataset copy clguess window=hidden.
dataset activate clguess.
!if (!direction = 1) !then
compute clab = a*b − 1.96*sobelse.
!else
compute clab = a*b + 1.96*sobelse.
!ifend
exe.
* Search for confidence limit. *.
* Set number of iterations. *.
!do !i = 1 !to !niter.
* Analyze confidence limit into its components. *.
dataset activate clguess.
compute seaoverseb = sea/seb.
compute term1 = (−1)*(a− (b*seaoverseb)).
compute term2 = (a− (b*seaoverseb))**2.
compute term3 = 4*seaoverseb*clab.
compute term4 = 2*seaoverseb.
compute term5 = (a+(b*seaoverseb)).
compute term6 = (a+(b*seaoverseb))**2.
* Find the two possible solutions for clb. *.
!if (!direction = 1) !then
compute clb1 = (term5+sqrt(term6−term3))/term4.
compute clb2 = (term5−sqrt(term6−term3))/term4.
!else
compute clb1 = (term1+sqrt(term2+term3))/term4.
compute clb2 = (term1−sqrt(term2+term3))/term4.
!ifend
* Pick the solution that puts clb closer to b. *.
compute clb1dist = abs(clb1−b).
compute clb2dist = abs(clb2−b).
do if clb1dist < clb2dist.
compute clb = clb1.
else.
compute clb = clb2.
end if.
* Get cla from clb and clab. *.
compute cla = clab/clb.
* Make merging variable so clguess can be merged with copies of
original data. *.
compute key = 1.
exe.
* Merge confidence limit components with copies of original data created
above. *.
* This will allow for new predicted values and residuals to be made based
on *.
* using the confidence limit components rather than the sample values. *.
match files file = origcopiesbycopy table = clguess
/by key
/keep = copynum x m y b02 b03 cprime cla clb yhat mhat.
exe.
dataset name origcopiesbycopyi.
* Make new residuals based on cla and clb, and sample values of other
coefficients *.
* (cprime, b02, and b03). *.
dataset activate origcopiesbycopyi.
compute yhati = b02 + clb*m + cprime*x.
compute yresi = y − yhati.
compute mhati = b03 + cla*x.
compute mresi = m − mhati.
exe.
* On the first loop, make variables for later shuffling of yresi and
mresi. *.
!if (!i = 1) !then
dataset activate origcopiesbycopyi.
compute shufflevaryresi = rv.uniform(0,1).
compute shufflevarmresi = rv.uniform(0,1).
exe.
* Save the datset for use on later loops. *.
dataset copy shufvars window=hidden.
* On subsequent loops, get back same shuffling variables made up on the
first loop. *.
!else
oms
/select all
/destination viewer = no.
match files
file = origcopiesbycopyi
/file = shufvars
/rename (x m y yhat yresi mhat mroe drop) drop1 t
/keep = copynum x m y yhat mhat shufflevarmresi
shufflevarmresi.
exe.
dataset name origcopiesbycopyi.
omsend.
!ifend
* Make a dataset with yresi shuffled within each dataset copy. *.
dataset activate origcopiesbycopyi.
dataset copy shuffleyresi window=hidden.
dataset activate shuffleyresi.
sort cases by copynum shufflevaryresi.
exe.
* Make a dataset with mresi shuffled within each dataset copy. *.
dataset activate origcopiesbycopyi.
dataset copy shufflemresi window=hidden.
dataset activate shufflemresi.
sort cases by copynum shufflevarmresi.
exe.
* Merge shuffled residuals yresi and mresi with original data in each
dataset copy. *.
match files
file = origcopiesbycopyi
/rename (yresi mresi = drop1 to drop2)
/file = shuffleyresi
/rename (x m y yhat mhat mresi = drop3 to drop8)
/file = shufflemresi
/rename (x m y yhat yresi mhat = drop9 to drop14)
/keep = copynum x m y mhat yhat mresi yresi.
exe.
dataset name shuffledi.
dataset close origcopiesbycopyi.
dataset close shufflemresi.
dataset close shuffleyresi.
* Calculate ystari and mstari, the new values of y and m based on
shuffling the residuals. *.
dataset activate shuffledi.
compute ystari = yhat + yresi.
compute mstari = mhat + mresi.
exe.
* Prepare to run regressions separately within each dataset copy. *.
dataset activate shuffledi.
split file by copynum.
exe.
* Model 2: Regress ystari on x, m. *.
dataset declare model2shufi window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model2shufi.
dataset activate shuffledi.
regression
/dependent = ystari
/enter x m.
exe.
omsend.
* Model 3: Regress mstari on x. *.
dataset declare model3shufi window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Regression'] subtypes = ['Coefficients']
/destination format = sav outfile = model3shufi.
dataset activate shuffledi.
regression
/dependent = mstari
/enter x.
exe.
omsend.
* Gather results. *.
dataset close shuffledi.
dataset activate model2shufi.
select if Var3 = 'm'.
compute bpermi = B.
exe.
dataset activate model3shufi.
select if Var3 = 'x'.
compute apermi = B.
exe.
match files
file = model2shufi
/file = model3shufi
/keep = apermi bpermi.
exe.
dataset name shufresulti.
compute abpermi = apermi*bpermi.
exe.
dataset close model2shufi.
dataset close model3shufi.
* Include current clab guess value. *.
add files
file = clguess
/rename = (clab = abpermi)
/file = shufresulti
/keep = abpermi.
exe.
dataset name origshufresulti.
formats abpermi (f8.4).
dataset close shufresulti.
* Make a frequency table with cumulative frequencies (percentile ranks)
of abpermi. *.
dataset declare freqtable window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Frequencies'] subtypes = ['Frequencies']
/destination format = sav outfile = freqtable.
dataset activate origshufresulti.
frequencies
variables = abpermi.
exe.
omsend.
* Merge current confidence limit guess, clab, with frequency table. *.
dataset activate freqtable.
compute key = 1.
exe.
match files file = freqtable table = clguess
/by key.
exe.
dataset name getptilerank.
dataset close freqtable.
* Find percentile rank of current confidence limit guess, clab in the
distribution. *.
* Do this by choosing the nearest value of abpermi (they should be equal
within *.
* rounding) and getting its percentile rank. *.
dataset activate getptilerank.
select if char.substr(Var2,1,5) ne 'Total'.
compute diff = abs(clab - number(Var2,f8.4)).
sort cases by diff.
select if $casenum = 1.
compute prankclab = CumulativePercent.
exe.
* Save results across loops. *.
!if (!i = 1) !then
dataset activate getptilerank.
dataset copy saveptilerank.
!else
oms
/select all
/destination viewer = no.
add files
file = saveptilerank
/file = getptilerank
/keep = clab prankclab.
exe.
dataset name saveptilerank.
omsend.
!ifend
dataset close getptilerank.
* Choose as the next guess for the value of the confidence limit *.
* the value of abpermi at the target percentile rank *.
dataset declare freqout window=hidden.
oms
/select all
/destination viewer = no.
oms
/select tables
/if commands = ['Frequencies'] subtypes = ['Statistics']
/destination format = sav outfile = freqout.
dataset activate origshufresulti.
!if (!direction = 1) !then
frequencies
variables = abpermi
/percentiles = 2.5.
exe.
omsend.
dataset activate freqout.
select if Var2 = '2.5'.
compute clab = Var4.
exe.
!else
frequencies
variables = abpermi
/percentiles = 97.5.
exe.
omsend.
dataset activate freqout.
select if Var2 = '97.5'.
compute clab = Var4.
exe.
!ifend
dataset close origshufresulti.
* Merge the next guess of clab back into the clguess dataset to be *.
* read at the top of the loop. *.
oms
/select all
/destination viewer = no.
match files
file = clguess
/rename (clab = drop1)
/file = freqout
/keep = a sea b seb cprime b02 b03 clab.
exe.
dataset name clguess.
dataset close freqout.
omsend.
!doend
dataset close clguess.
* Find clab that gave closest percentile rank to the target. *.
dataset activate saveptilerank.
!if (!direction = 1) !then
dataset copy loweri.
dataset activate loweri.
compute abserror = abs(prankclab - 2.5).
sort cases by abserror.
select if $casenum = 1.
compute ipermlcl = clab.
string ilowerstatus (a15).
do if abserror le 0.5.
compute ilowerstatus = '(converged)'.
else.
compute ipermlcl = number(' ',f1.0).
compute ilowerstatus = '(not converged)'.
end if.
exe.
!else
dataset copy upperi.
dataset activate upperi.
compute abserror = abs(prankclab - 97.5).
sort cases by abserror.
select if $casenum = 1.
compute ipermucl = clab.
string iupperstatus (a15).
do if abserror le 0.5.
compute iupperstatus = '(converged)'.
else.
compute ipermucl = number(' ',f1.0).
compute iupperstatus = '(not converged)'.
end if.
exe.
!ifend
dataset close saveptilerank.
!doend
dataset close origresult.
* Merge lower and upper iterated confidence limits with non-iterated confidence
limits. *.
match files
file = permcl
/file = loweri
/file = upperi
/keep = permlcl permucl ipermlcl ipermucl ilowerstatus iupperstatus.
exe.
dataset name allresult.
dataset close permcl.
dataset close loweri.
dataset close upperi.
dataset close origcopiesbycopy.
dataset activate allresult.
print
/'Permutation 95% confidence limits'
/'Lower:' permlcl (f8.3)
/'Upper:' permucl (f8.3)
/'Iterated permutation 95% confidence limits'
/'Lower:' ipermlcl (f8.3,3x) ilowerstatus *
/'Upper:' ipermucl (f8.3,3x) iupperstatus *.
exe.
dataset activate !dataname.
dataset close allresult.
exe.
!ENDDEFINE.
Appendix C
This SAS macro estimates the permutation confidence interval for ab and the iterative permutation confidence interval for ab. To use it, first enter and run the entire macro so that the new command “permmed” is defined. This command will be available for the duration of the SAS session. To run the command on a data set, run the following line in SAS:
%permmed(dataset, predictor, mediator, outcome, permutations, iterations, randomseed);
The labels in italics must be replaced by the appropriate names and values for the analysis to be run. Dataset is the name of the SAS data set on which to run the analysis. Predictor is the name of the predictor variable. Mediator is the name of the mediating variable. Outcome is the name of the outcome variable. Permutations is the number of permutations SAS will use in running the analysis. A large number should be used to increase the reliability of the results. Iterations is the number of iterations SAS will use in searching for the iterative permutation confidence limits. Typically, five iterations or fewer are sufficient. If the procedure fails to converge (the output will show the confidence limit as missing and say “not converged”), increase this value. Randomseed is the random number seed SAS will use in permuting the data. If a seed is chosen (it must be a positive integer <231 – 1), repeated runs of the procedure with the same data will produce the same confidence limits. If it is set to 0, SAS will choose the random number seed, and repeated runs of the procedure with the same data will produce different confidence limits (because different permuted data sets are used).
%macro permmed(dataname,x,m,y,npermute,maxiter,seed);
%* Make a listwise deleted dataset. ;
data listwise; set &dataname;
if (&x ne .) and (&m ne .) and (&y ne .);
rename
&x = x &m = m &y = y;
run;
%* Find number of cases in listwise deleted dataset. ;
proc means data=listwise noprint;
output out=meanout n(x) = nobs;
run;
data _NULL_; set meanout;
call symput('nobs',nobs);
run;
%* Model 2: Regress y on x, m ;
proc reg data=listwise outest=model2 tableout noprint;
model y = x m;
%* Save predicted values and residuals, which are needed for permutation tests. ;
output out=predres2 p=yhat r=yres;
run;
%* Model 3: Regress m on x;
proc reg data=listwise outest=model3 tableout noprint;
model m = x;
%* Save predicted values and residuals, which are needed for permutation tests. ;
output out=predres3 p=mhat r=mres;
run;
%* Gather results. ;
data parm2; set model2;
if _TYPE_='PARMS';
b = m; cprime = x; b02 = intercept; keep b cprime b02;
run;
data se2; set model2;
if _TYPE_='STDERR';
seb = m; keep seb;
run;
data parm3; set model3;
if _TYPE_='PARMS';
a = x; b03 = intercept; keep a b03;
run;
data se3; set model3;
if _TYPE_='STDERR';
sea = x; keep sea;
run;
data origresult; merge parm2 se2 parm3 se3;
vara = sea*sea;
varb = seb*seb;
sobelse = sqrt(a*a*varb + b*b*vara);
run;
%* Merge predicted values and residuals for models 2 and 3. ;
data predres; merge predres2 predres3;
run;
%*** Non-iterated permutation confidence limits *** ;
%* Make npermute copies of the original data. ;
proc iml;
use predres;
read all var{x m y yhat yres mhat mres} into orig;
copies = orig;
do i = 2 to &npermute;
copies = copies//orig;
end;
varnames = {'x' 'm' 'y' 'yhat' 'yres' 'mhat' 'mres '};
create origcopies from copies[colname = varnames];
append from copies;
quit;
%* Make shuffling variables to permute the residuals mres and yres. ;
data origcopiesbycopy; set origcopies;
copynum = ceil(_N_/&nobs);
shufflevaryres = ranuni(&seed);
shufflevarmres = ranuni(0);
run;
%* Make a dataset with yres shuffled within each dataset copy. ;
proc sort data=origcopiesbycopy out=shuffleyres;
by copynum shufflevaryres;
run;
%* Make a dataset with mres shuffled within each dataset copy. ;
proc sort data=origcopiesbycopy out=shufflemres;
by copynum shufflevarmres;
run;
%* Merge shuffled residual mres and yres with original data in each dataset copy. ;
data shuffled; merge origcopiesbycopy(keep=copynum x m y mhat yhat)
shuffleyres(keep=yres) shufflemres(keep=mres);
%* Find mstar and ystar, the new values of m and y based on shuffling the residuals. ;
mstar = mhat + mres;
ystar = yhat + yres;
run;
%* Model 2: Regress ystar on x, m. ;
proc reg data=shuffled noprint outest=model2shuf;
by copynum;
model ystar = x m;
run;
%* Model 3: Regress mstar on x. ;
proc reg data=shuffled noprint outest=model3shuf;
by copynum;
model mstar = x;
run;
%* Gather results. ;
data model2shuf; set model2shuf;
if _TYPE_ = 'PARMS';
bperm = m; keep bperm;
run;
data model3shuf; set model3shuf;
if _TYPE_ = 'PARMS';
aperm = x; keep aperm;
run;
data shufresult; merge model2shuf model3shuf;
run;
%* Include results for original data. ;
data origshufresult; set origresult(rename=(a=aperm b=bperm)) shufresult;
abperm = aperm*bperm;
run;
%* Get confidence limits. ;
proc univariate data=origshufresult noprint;
var abperm;
output out=permcl pctlpts = 2.5 97.5 pctlpre = perm pctlname = lcl ucl;
run;
%*** Iterated permutation confidence limits *** ;
%* Iterate twice: 1 = lower confidence limit, 2 = upper confidence limit ;
%do direction = 1 %to 2;
data clguess; set origresult;
%if &direction = 1 %then %do;
clab = a*b − 1.96*sobelse;
%end;
%else %do;
clab = a*b + 1.96*sobelse;
%end;
run;
%* Initialize loop counter and break checker. ;
%let loop = 0;
%let break = 0;
%* Search for confidence limit. ;
%do %until ((&break = 1) or (&loop = &maxiter));
%* Increment loop counter. ;
%let loop = %eval(&loop+1);
%* Analyze confidence limit into its components. ;
data clguess; set clguess;
%* Make up terms for quadratic equation solutions. ;
seaoverseb = sea/seb;
term1 = (−1)*(a− (b*seaoverseb));
term2 = (a− (b*seaoverseb))**2;
term3 = 4*seaoverseb*clab;
term4 = 2*seaoverseb;
term5 = (a+(b*seaoverseb));
term6 = (a+(b*seaoverseb))**2;
%* Find the two possible solutions for clb. ;
%if &direction = 1 %then %do;
clb1=(term5+sqrt(term6−term3))/term4;
clb2=(term5−sqrt(term6−term3))/term4;
%end;
%else %do;
clb1=(term1+sqrt(term2+term3))/term4;
clb2=(term1−sqrt(term2+term3))/term4;
%end;
%* Pick the solution that puts clb closer to b. ;
clb1dist = abs(clb1−b);
clb2dist = abs(clb2−b);
if clb1dist < clb2dist then clb = clb1;
else clb = clb2;
%* Make cla ;
cla = clab/clb;
%* Make clab into a macro parameter for easier reference ;
call symput('clab',clab);
run;
%* Merge confidence limit components with copies of original data created
above. ;
%* This will allow for new predicted values and residuals to be made
based on ;
%* using the confidence limit components rather than the sample values. ;
data origcopiesbycopyi; if _N_=1 then set clguess (keep=cla clb cprime b02
b03); set origcopiesbycopy;
%* Make new residuals based on cla and clb and sample values of
other coefficients ;
%* (cprime, b02, and b03). ;
yhati = b02 + clb*m + cprime*x;
yresi = y − yhati;
mhati = b03 + cla*x;
mresi = m − mhati;
run;
%* On the first loop, make variables for later shuffling of yresi and
mresi. ;
%if &loop = 1 %then %do;
data shufvars;
do i = 1 to &nobs*&npermute;
shufflevaryresi = ranuni(&seed);
shufflevarmresi = ranuni(0);
output;
end;
run;
%end;
%* On subsequent loops, re-use same shuffling variables made up on the
first loop. ;
%* Make a dataset with yresi shuffled within each dataset copy. ;
data shuffleyresi; merge origcopiesbycopyi
shufvars(keep=shufflevaryresi);
run;
proc sort data=shuffleyresi;
by copynum shufflevaryresi;
run;
%* Make a dataset with mresi shuffled within each dataset copy. ;
data shufflemresi; merge origcopiesbycopyi
shufvars(keep=shufflevarmresi);
run;
proc sort data=shufflemresi;
by copynum shufflevarmresi;
run;
%* Merge shuffled residuals yresi and mresi with original data in each dataset copy. ;
data shuffledi; merge origcopiesbycopyi shuffleyresi(keep=yresi)
shufflemresi(keep=mresi);
%* Calculate ystari and mstari, the new values of y and m based on shuffling the residuals. ;
ystari = yhat + yresi;
mstari = mhat + mresi;
run;
%* Model 2: Regress ystari on x, m. ;
proc reg data=shuffledi noprint outest=model2shufi;
by copynum;
model ystari = x m;
run;
%* Model 3: Regress mstari on x. ;
proc reg data=shuffledi noprint outest=model3shufi;
by copynum;
model mstari = x;
run;
%* Gather results. ;
data model2shufi; set model2shufi;
if _TYPE_ = 'PARMS';
bpermi = m; keep bpermi;
run;
data model3shufi; set model3shufi;
if _TYPE_ = 'PARMS';
apermi = x; keep apermi;
run;
data shufresulti; merge model2shufi model3shufi;
abpermi = apermi*bpermi;
run;
%* Include current clab guess value. ;
data origshufresulti; set clguess(rename=(clab=abpermi)) shufresulti;
run;
%* Make a frequency table with cumulative frequencies (percentile ranks) ;
%* of abpermi. ;
proc freq data=origshufresulti noprint;
tables abpermi /out=freqtable outcum;
run;
%* Merge current confidence limit guess, clab, with frequency table. ;
%* Find percentile rank of current confidence limit guess, clab, ;
%* in the distribution. ;
%* Do this by choosing the nearest value of abpermi (they should be equal ;
%* within rounding) and getting its percentile rank. ;
data freqtable; set freqtable;
clab = &clab;
diff = abs(clab - abpermi);
run;
proc sort data=freqtable;
by diff;
run;
data getptilerank; set freqtable;
if _N_ = 1;
prankclab = CUM_PCT;
%* Check if error is small enough to exit the loop. ;
%if &direction = 1 %then %do;
abserror = abs(prankclab - 2.5);
%end;
%else %do;
abserror = abs(prankclab - 97.5);
%end;
if abserror le 0.5 then break = 1;
else break = 0;
%* Save break as a macro variable so the loop can check its value. ;
call symput('break',break);
run;
%* If looping continutes, choose as the next guess for the value of the
confidence ;
%* limit the value of abpermi at the target percentile rank. ;
proc univariate data=origshufresulti noprint;
var abpermi;
output out=univout pctlpts = 2.5 97.5 pctlpre = clab pctlname =
lower upper;
run;
%* Merge the next guess of clab back into the clguess dataset to be ;
%* read at the top of the loop. ;
data clguess; merge clguess(drop=clab) univout;
%if &direction = 1 %then %do;
clab = clablower;
%end;
%else %do;
clab = clabupper;
%end;
run;
%end;
%* Save the confidence limit that was just found. ;
%if &direction = 1 %then %do;
data loweri; length ilowerstatus $ 15; set getptilerank;
if abserror le 0.5 then do;
ipermlcl = clab;
ilowerstatus = '(converged)';
end;
else do;
ipermlcl = .;
ilowerstatus = '(not converged)';
end;
run;
%end;
%else %do;
data upperi; length iupperstatus $ 15; set getptilerank;
if abserror le 0.5 then do;
ipermucl = clab;
iupperstatus = '(converged)';
end;
else do;
ipermucl = .;
iupperstatus = '(not converged)';
end;
run;
%end;
%end;
%* Merge lower and upper iterated confidence limits with non-iterated confidence limits. ;
data allresult; merge permcl loweri upperi;
file print;
put 'Permutation 95% confidence limits'
/'Lower: ' permlcl
/'Upper: ' permucl
/'Iterated permutation 95% confidence limits'
/'Lower: ' ipermlcl ' ' ilowerstatus
/'Upper: ' ipermucl ' ' iupperstatus;
run;
%mend permmed;
Contributor Information
Aaron B. Taylor, Department of Psychology, Texas A&M University, 4235 TAMU, College Station, TX 77843-4235, USA, aaron.taylor@tamu.edu
David P. MacKinnon, Arizona State University, Tempe, AZ, USA
References
- Anderson MJ, Legendre P. An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. Journal of Statistical Computation and Simulation. 1999;62:271–303. [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. doi:10.1037/0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Biesanz JC, Falk CF, Savalei V. Assessing mediational models: Testing and interval estimation for indirect effects. Multivariate Behavioral Research. 2010;45:661–701. doi: 10.1080/00273171.2010.498292. doi:10.1080/00273171.2010.498292. [DOI] [PubMed] [Google Scholar]
- Cheung MWL. Comparison of approaches to constructing confidence intervals for mediating effects using structural equation models. Structural Equation Modeling. 2007;14:227–246. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Cohen J. The earth is round (p < .05) American Psychologist. 1994;49:997–1003. doi:10.1037/0003-066X.49.12.997. [Google Scholar]
- Edgington ES. Approximate randomization tests. Journal of Psychology. 1969;72:143–149. [Google Scholar]
- Edgington ES. Randomization tests. New York, NY: Marcel Dekker; 1995. [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. New York, NY: Chapman & Hall; 1993. [Google Scholar]
- Fisher RA. The design of experiments. New York, NY: Hafner; 1935. [Google Scholar]
- Freedman LS, Schatzkin A. Sample size for studying intermediate endpoints within intervention trials of observational studies. American Journal of Epidemiology. 1992;136:1148–1159. doi: 10.1093/oxfordjournals.aje.a116581. [DOI] [PubMed] [Google Scholar]
- Fritz MS, Taylor AB, MacKinnon DP. Examination of two anomalous results in statistical mediation analysis. 2011 doi: 10.1080/00273171.2012.640596. Manuscript submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James LR, Brett JM. Mediators, moderators, and tests for mediation. Journal of Applied Psychology. 1984;69:307–321. [Google Scholar]
- Kenny DA, Kashy DA, Bolger N. Data analysis in social psychology. In: Gilbert DT, Fiske ST, Lindzey G, editors. The handbook of social psychology. Boston, MA: McGraw-Hill; 1998. pp. 233–265. [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Mahwah, NJ: Erlbaum; 2008. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODCLIN. Behavior Research Methods. 2007;39:384–389. doi: 10.3758/bf03193007. doi:10.3758/BF03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. doi:10.1037/1082-989X.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate Behavioral Research. 2004;39:99–128. doi: 10.1207/s15327906mbr3901_4. doi:10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manly BF. Randomization and Monte Carlo methods in biology. 2nd ed. New York, NY: Chapman & Hall; 1997. [Google Scholar]
- Preacher KJ, Hayes AF. SPSS and SAS procedures for estimating indirect effects in simple mediation models. Behavior Research Methods, Instruments, & Computers. 2004;36:717–731. doi: 10.3758/bf03206553. doi:10.3758/BF03206553. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Hayes AF. Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior Research Methods. 2008;40:879–891. doi: 10.3758/brm.40.3.879. doi:10.3758/BRM.40.3.879. [DOI] [PubMed] [Google Scholar]
- SAS Inc. SAS (Version 9.2) [Computer software] Cary, NC: Author; 2007. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7:422–445. [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology. 1982;13:290–312. [Google Scholar]
- Taylor AB, MacKinnon DP, Tein J-Y. Tests of the three-path mediated effect. Organizational Research Methods. 2008;11:241–269. [Google Scholar]
- ter Braak CJF. Permutation versus bootstrap significance tests in multiple regression and ANOVA. In: Jockel K-H, Rothe G, Sendler W, editors. Bootstrapping and related techniques. Berlin: Springer; 1992. pp. 79–86. [Google Scholar]
- Wilkinson L the Task Force on Statistical Inference. Statistical methods in psychology journals: Guidelines and explanations. American Psychologist. 1999;54:594–604. doi:10.1037/0003-066X.54.8.594. [Google Scholar]
- Williams J, MacKinnon DP. Resampling and distribution of the product methods for testing indirect effects in complex models. Structural Equation Modeling. 2008;15:23–51. doi: 10.1080/10705510701758166. [DOI] [PMC free article] [PubMed] [Google Scholar]