Gaussian mixture models for classification of neonatal seizures using EEG

Abstract

A real-time neonatal seizure detection system is proposed based on a Gaussian mixture model classifier. The system includes feature transformation techniques and classifier output postprocessing. The detector was evaluated on a database of 20 patients with 330 hours of recordings. A detailed analysis of the choice of parameters for the detector is provided. A mean good detection rate of 79% was obtained with only 0.5 false detections per hour. A thorough review of all misclassified events was performed, from which a number of patterns causing false detections were identified.

1. Introduction

Neonatal seizures are reported to manifest in 1-5% of newborns (Clancy 2006), with low birth weight and premature babies being particularly at risk (Saliba et al. 2001). These events are important to diagnose as they can represent an important sign of neurological dysfunction. In particular, neonatal seizures have been associated with hypoxic ischemic encephalopathy, central nervous system infection, intracranial haemorrhage and cerebral artery infarction (Evans & Levene 1998). Furthermore, the presence of seizure activity has been linked to poor outcome such as cerebral palsy, developmental delay, epilepsy and in severe cases, death (Legido et al. 1991).

Unlike epileptic seizures in children and adults, neonatal seizures are frequently subclinical events which exhibit no physical symptoms. Indeed, it has been reported that as many as 85% of seizures do not exhibit clinical symptoms (Bye & Flanagan 1995). Recently, Murray et al. (2008) found that only 9% of electrographic seizures were identified by staff in the neonatal intensive care unit (NICU). The study also found that a number of movement events with no associated electrographic seizure activity were considered to be seizures by the clinical staff resulting in overdiagnosis of seizures. For these reasons the electroencephalogram (EEG) is considered the gold standard for neonatal seizure detection.

The EEG is a difficult signal to interpret for non-expert users. Trained electroencephalographers are not available in all hospitals, nor are they able to provide 24 hour support in the neonatal intensive care unit. Furthermore, treatment with antiepileptic drugs (AEDs) may result in a phenomenon known as electro-clinical dissociation. This phenomenon occurs when the AEDs suppress the clinical signs of seizure, but the electrographic seizures persist (Rennie & Boylan 2007). Thus, an automated EEG-based seizure detector would prove a valuable asset to assist staff in the NICU due to the silent nature of the majority of these events.

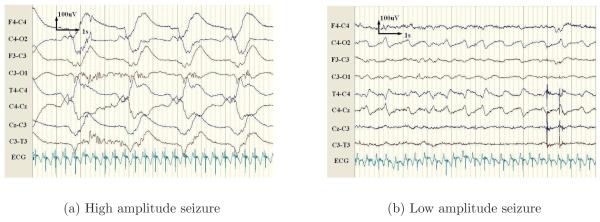
Neonatal seizures result from synchronous discharges from groups of neurons and manifest as periods of heightened periodicity in the EEG lasting for more than 10 seconds (Shellhaas & Clancy 2007). This results in a repetitive trace in the EEG with a fundamental frequency between 0.5-6Hz, examples are shown in Figure 1. Several different approaches have been proposed to quantify this increase in repetitive activity. The autocorrelation function of the EEG was investigated by Liu et al. (1992), as this gives a direct measure of repetition in a signal. Alternatively, frequency domain techniques have been proposed by Gotman et al. (1997), due to the increase in power in the delta and theta bands during seizure events. It has also been observed that the stochastic background activity is dominated by a small number of deterministic components during seizure, as exploited in the work of Celka & Colditz (2002). However, an independent review of these three algorithms by Faul et al. (2005b) concluded that the results were inadequate for integration into the NICU, due to low classification performance over an independent dataset.

Figure 1.

Example of two seizure patterns for a single patient. Here, the high amplitude seizure is generalised and manifests with a lower fundamental frequency. In contrast, the low amplitude seizure is localised to channels connected to C4 and has a higher fundamental frequency than the high amplitude seizure.

More recently, Navakatikyan et al. (2006) employed wave sequence analysis to generate features from the peaks and troughs of successive waves along with a correlation coefficient between successive waves. Initial decisions were calculated via a threshold, prior to a postprocessing routine. Another threshold based system proposed by Deburchgraeve et al. (2008) comprised of two independent routines. The first routine analysed the spikiness of the EEG, while the second analysed the EEG for repetitive activity.

Alternatively, the seizure detection problem can be treated as a pattern recognition task. Aarabi et al. (2006) selected an optimal subset of features for use in an artificial neural network (ANN), and more recently used an ANN to classify neonatal EEG into several background states and two seizure states (Aarabi et al. 2007). Zarjam et al. (2003) used wavelet analysis to obtain time-frequency features, which were classified by an ANN. Discriminant analysis was investigated by Greene et al. (2008), who compared linear, quadratic and regularised discriminants for neonatal seizure detection. Mitra et al. (2009) used neural networks as part of a neonatal seizure detector; however, a large number of heuristic rules and thresholds are also employed making it unclear which aspects of the detector contributed towards the final decision.

Gaussian mixture models (GMM) are employed here due to reported success in audio and speech recognition tasks (Reynolds et al. 2000). Additionally, GMM classifiers have been used to classify EEG in biomedical applications such as brain computer interfaces (Zhu et al. 2006, Sun et al. 2008) and person authentication (Marcel & Millan 2007). A seizure detector based on GMMs was proposed by Meng et al. (2004); however, this study was based on a different signal, electrocorticogram recordings of adult patients, with very different patterns from neonatal EEG. Thus, the underlying methodology is different from the system proposed here.

A GMM is a type of density estimator in which a probability density function (PDF) is modelled by a weighted summation of Gaussian distributions. In contrast to discriminative classifiers which focus on modelling the decision boundary between classes, GMMs are known as a generative classifier and can be used to classify data in a probabilistic framework using a model for each class. Dominant patterns in the data are captured by component distributions. It is a well-studied statistical inference technique which allows flexibility in choosing the component distributions, in obtaining density estimation for each cluster, and additionally, a soft classification can be carried out by varying the probabilistic threshold.

In this paper, the design and analysis of a GMM based seizure detection system is presented. Section 2 provides details on the dataset, algorithm and testing protocol used in this study. The results are reported in Section 3, these show the effects of the parameters for the classifier and postprocessing stage on the overall performance of the detector. This section also includes a comparison of results with other works in the literature. Finally, the results are discussed and an analysis of misclassification is presented in Section 4.

2. Methods

2.1. Dataset

Gotman et al. (1997) advise that the performance of a seizure detection algorithm can only be accurately estimated if it is tested on continuous, non-preselected files. The dataset used in this study was recorded in the NICU at Cork University Maternity Hospital over a 2 year period. During this period, 55 babies with HIE were recruited and EEGs were recorded for up to 72 hours. In this group, 17 had seizures and all seizures that developed over 72 hours after birth were captured. This reflects the real-life situation in the NICU.

The patients were full term neonates ranging in gestational age from 39 to 42 weeks. A Viasys NicOne video EEG machine was used to record multichannel EEG at 256Hz using the 10-20 system of electrode placement modified for neonates. In this study, 8 bipolar EEG channels are used (F4-C4, F3-C3, T4-C4, C4-CZ, CZ-C3, C3-T3, C4-O2, C3-O1). The dataset, shown in Table 1, contained over 267 hours of EEG. A total of 705 seizure events with a mean duration of 3.89 minutes were annotated by a neonatal electroencephalographer. This set is used for training and testing using leave one out (LOO) cross validation and is thus referred to as the LOO set (more information on this subject is provided in section 2.4).

Table 1.

EEG dataset comprising the LOO set and hold-out set.

	Patient	Record length (hours)	Seizure events	Mean seizure duration (minutes)
LOO set	1	18.2	17	1.5
	2	24.7	3	6.2
	3	24.2	149	2.3
	4	26.1	60	1.1
	5	24	49	5.9
	6	5.7	41	1.2
	7	24	6	1.1
	8	24.5	17	6
	9	24	156	5.3
	10	10	25	5.4
	11	6.2	15	5.4
	12	12	29	2.2
	13	12.1	25	4.1
	14	5.5	11	8.6
	15	12.2	59	2.1
	16	7.6	31	10.4
	17	6.6	12	8.5
	Total	267.9	705	-
Hold-out	1	14	5	8.2
	2	18.1	9	17.2
	3	29.8	41	1.6
	Total	61.9	55	-

Records for 3 new patients with seizures were subsequently obtained in 2009 at Cork University Maternity Hospital. However, these patients lack additional per channel annotations required during training and were acquired after the cross validation experiment was performed. These patients are excluded from the cross-validation set, but are used as a stand-alone data-set and are referred to as the hold-out set.

The automated system is designed to detect seizures from fullterm babies with moderate or severe hypoxic ischaemic encephalopathy (HIE) – the commonest cause of neonatal seizures. All babies were extremely sick during these events. The average seizure duration for full term babies with HIE is known to be longer than 1 minute, and in fact it is approximately 3 minutes, as outlined in Murray et al (2008), McBride et al. (2000) and Shellhaas et al. (2007). Therefore, the dataset used in this work is truly representative for the task.

2.2. Seizure detection algorithm

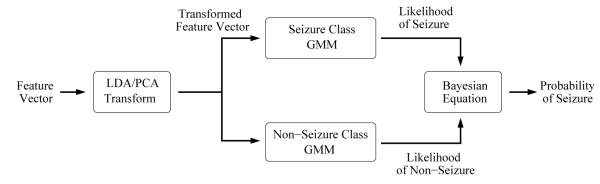
An outline of the seizure detection system is given in Figure 2. The first stage of the detector is the preprocessing step, in which the EEG is downsampled and segmented into epochs. A total of 55 features per channel are then extracted from each EEG epoch. The GMM classifier, shown in more detail in Figure 3, is composed of a feature transformation stage. The feature vectors are transformed to reduce the dimensionality of the feature space, in order to improve the classification results of the system. Linear discriminant analysis (LDA) and principal component analysis (PCA) were compared for the task of feature dimensionality reduction. The transformed feature vectors are classified by a GMM classifier, yielding a probability of seizure per channel. The GMM classifier output is filtered using a central moving average filter. The filtered probability of seizure is compared to a threshold to yield a binary decision. The single channel binary decisions are then combined into a multichannel binary decision. A final postprocessing step is the collar operation, which consists of expanding the detections forward and backward in time, thus increasing the duration of the detections.

Figure 2.

Block diagram of the neonatal seizure detector.

Figure 3.

Diagram of the GMM based classifier.

2.2.1. Preprocessing

The frequency range of neonatal seizures is 0.5-13Hz with the dominant frequency lying in the 0.5-6Hz band (Kitayama et al. 2003). The EEG is downsampled from 256Hz to 32Hz with an anti-aliasing filter having a bandwidth of 12.8Hz. Downsampling is performed to reduce the computational time and memory load of the feature extraction stage. The EEG is then segmented into 8s epochs using a sliding window with 50% overlap between epochs.

2.2.2. Feature extraction

During seizure, the EEG is characterised by heightened periodicity. The difference between seizure and non-seizure EEG can be relatively subtle, thus requiring for a large set of features to quantify the change. A set of 55 features is used in this study, see Table 2. The majority of these features are taken from three studies on features for neonatal seizure detection. Faul et al. (2005a) performed a study on the value of chaos theory and information theory based features. Greene et al. (2008) investigated the importance and compared the performance of several popular features based on time domain and frequency domain techniques. Aarabi et al. (2006) used filter techniques for feature selection from a large set of primarily time domain based features.

Table 2.

Features extracted from the EEG

Feature Type	Feature
Frequency Domain	Wavelet energy, total power, peak frequency, spectral edge frequency (80%,90%,95%), power in frequency bands of width 2Hz from 0 to 12Hz with 50% overlap, power in the normalised frequency bands
Time domain	Curve length, number of maxima and minima, root mean squared amplitude, Hjorth parameters, zero crossings, zero crossings of the 1st and 2nd derivatives, autoregressive modelling error (model order 1-9), skewness, kurtosis, nonlinear energy, variance of the 1st and 2nd derivatives
Information theory	Shannon entropy, spectral entropy, Fisher information, singular value decomposition entropy

2.2.3. Feature processing

Increasing dimensionality induces exponential growth in the number of examples required to maintain a given sampling density. High dimensions also result in the exponential growth in the complexity of the target function (a density estimate here). Two general approaches exist to reduce the dimensionality of the data: feature transformation and feature selection. The former is done by transforming the existing features into a lower dimensional space, while the latter is performed by selecting a subset of the existing features. Indeed, a feature transformation technique can be seen as a feature selection technique which uses optimization criteria such as minimizing reconstruction error (PCA) or maximizing class separability (LDA), but for classification aiming at enhancing the predictive power, rather than for the concept description aiming at preserving the topological structure of the data.

The properties of various feature transformation techniques, such as mutual orthogonality of resulting components, facilitate the subsequent density estimation problem. In other words, removing highly correlated components and features showing low separability can lead to an improvement in overall classification performance of the GMM classifier.

In this work, PCA and LDA transformations are used to increase the performance of the detector by reducing the dimensionality of the feature space. Prior to feature transformation, the features are normalised to have zero mean and unity standard deviation over the training set. The normalising template obtained during training is then applied over the test set. This step ensures that, in the PCA transform, the low eigenvalues of the covariance matrix correspond to correlations in the feature set rather than features of relatively low variance. A subspace of 30 dimensions was found to be the most discriminative for the LDA transform. For the PCA transform, 99% of the cumulative energy of the original space is retained, reducing the feature space to 32 dimensions, which is comparable to the number of dimensions preserved with LDA.

2.2.4. Gaussian Mixture Models

A Gaussian Mixture Model represents the probability density function of a random variable, $x\in {\Re }^d$, as a weighted sum of k Gaussian distributions:

$$\mathrm{p}(x\mid ϴ)=\sum _{m=1}^k{\alpha }_m\mathrm{p}(x\mid {\theta }_m),\text{where}\sum _{m=1}^k{\alpha }_m=1,\text{and}{\alpha }_m>0,\forall m$$ 1

Here Θ is the mixture model, α_m corresponds to the weight of component m and the density of each component is given by the normal probability distribution:

$$\mathrm{p}(x\mid {\theta }_m)=\frac{{\mid {\Sigma }_m\mid }^{-1∕2}}{{\left(2\pi \right)}^{d∕2}}\exp \left\{-\frac{1}{2}{(x-{\mu }_m)}^T{\Sigma }_m^{-1}(x-{\mu }_m)\right\}$$ 2

During training, the parameters α, μ and ∑ are optimised iteratively via the Expectation Maximisation algorithm (Dempster et al. 1977) in order to maximise the log-likelihood of the model.

In this study, both diagonal and full symmetrical matrices are investigated for the covariance matrix ∑ in the Gaussian distribution function. A GMM with diagonal covariance matrices typically requires less data and computational time during training than a full covariance GMM due to the lower number of parameters to be estimated. However, diagonal covariance matrices are not capable of modelling correlations among feature dimensions.

In the testing stage, a likelihood estimate is obtained for the seizure class, defined by the model Θ_s, and for the non-seizure class, defined by the model Θ_n, as shown in Figure 3. The likelihood estimates are then combined to yield the posterior probability of seizure for the sample x using the Bayesian formula:

$$\mathrm{P}(\mathrm{S}\mid x)=\frac{\mathrm{P}(x\mid {ϴ}_s)\mathrm{P}\left(\mathrm{S}\right)}{\mathrm{p}(x\mid {ϴ}_s)\mathrm{P}\left(\mathrm{S}\right)+\mathrm{p}(x\mid {ϴ}_n)\mathrm{P}\left(\mathrm{N}\right)}$$ 3

where P(S) and P(N) are the prior probabilities of the seizure and non-seizure classes respectively. The prior probabilities of each class can be obtained from the training data (Saab & Gotman 2005) or they can be set empirically to obtain the desired trade-off between good and false detections. Here however, the probabilities are compared to a threshold and it is possible to adjust the threshold rather that the prior probabilities, and for this reason the prior probabilities are kept equal. The combination of the two GMMs and the Bayesian formula in (3) is referred to as a GMM classifier hereafter.

2.2.5. Postprocessing

As can be seen in Figure 2, the postprocessing scheme consists of a moving average filter and a collar operation. The moving average filter is used as a smoothing filter, which reduces the effect of short time transients. The final stage of the detector is the collar operation. This consists in expanding the length of each positive decision from either side by a certain amount of time, determined by the collar width. Thus the decisions for all epochs neighbouring a positive decision are relabelled as positive decisions. This operation is useful to compensate for possible difficulties in detecting the start and end of seizure events.

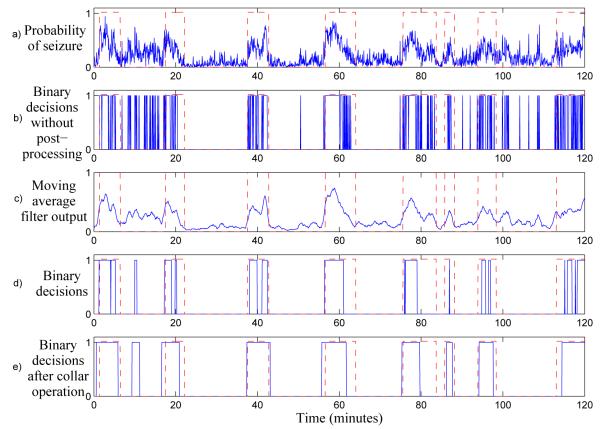
The effects of postprocessing are shown as an example in Figure 4. Without postprocessing, the number of false detections in the binary decisions is high and sensitivity is low. It can be seen that the main effects of the moving average filter is the removal of sparse short-time positive events and grouping of dense short-time positive events. The collar operation then increases the sensitivity of the system, as typically only a portion of an annotated seizure is detected.

Figure 4.

Example of the effects of postprocessing. The ground truth is shown as dashed lines, with 1 indicating a seizure. Plot a) shows the probability of seizure prior to postprocessing. Plot b) shows the resulting binary decisions when postprocessing is not used. It should be noted that short transients cause a large number of false detections. In plot c), the output of the 15 point moving average filter is shown. Plot d) shows the binary decisions resulting from the filtered probability of seizure, note that false detections have been reduced to 1 false detection seen at 10 minutes. Plot e) shows the final binary decisions after the collar operation, which increases the duration of all positive decisions. This results in higher sensitivity, but also increases the duration of the false detection.

It should be noted that the postprocessing scheme has two drawbacks. Firstly, the collar function will increase the duration of any false detections. While this is an inconvenience, the postprocessing scheme overall causes a large increase in performance resulting in a reduced number of individual false detections. Secondly, the moving average filter is implemented as a central moving average filter to prevent any phase shift between the detector output and the ground truth. Thus, in the processing stage this results in a latency of half the length of the moving average filter. For a 15 epoch moving average filter, as shown in Figure 3, this would result in a latency of 32s.

2.3. Metrics

A number of metrics are used to measure the performance of seizure detectors throughout the literature. However, as different naming conventions and rules are used by authors, it is important to define the metrics used in each study. Here, epoch based metrics are used as a stringent set of metrics. Event based metrics are also reported as they better represent the performance of the detector for clinicians.

2.3.1. Epoch based metrics

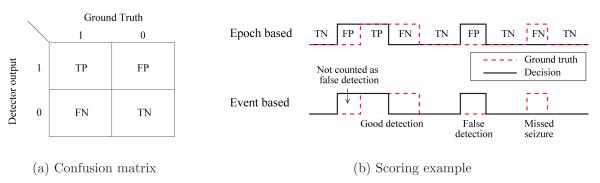
The decision vector is compared to the ground truth, and each epoch is then labelled as a True Positive (TP), True Negative (TN), False Positive (FP) or False Negative (FN) as shown in Figure 5(a). The epoch based metrics are determined from the sum of the number of epochs in each group as follows: Sensitivity corresponds to the percentage of correctly detected seizure epochs.

$$\text{Sensitivity}=\frac{\Sigma \mathit{TP}}{\Sigma \mathit{TP}+\Sigma \mathit{FN}}\times 100\%$$

Specificity is the percentage of correctly detected non-seizure epochs.

$$\text{Specificity}=\frac{\Sigma \mathit{TN}}{\Sigma \mathit{TN}+\Sigma \mathit{FP}}\times 100\%$$

The Receiver Operating Characteristic (ROC) curve is created by plotting the values of sensitivity and specificity over a range of detection thresholds. The area under the ROC curve is a useful single statistic for describing the classification performance of the system.

Figure 5.

The confusion matrix used to compute the epoch based metrics and the difference between epoch and event based metric calculations.

2.3.2. Event based metrics

Event based metrics are given for the “any overlap” grading scheme. Figure 5(b) shows the difference between the epoch and event based metrics. If any positive epoch correctly overlaps with an annotated seizure event, the entire event is considered detected. Positive epochs that precede or succeed a correct detection are not counted as false detections. Succeeding false positive epochs are grouped as a single false detection event. The Good Detection Rate (GDR) is defined as the percentage of seizure events correctly detected. False detections are reported using the False Detections per hour (FD/h) metric. The any overlap grading scheme can result in misleading results if the false detections are of an extended duration. Thus, the mean of the duration of all false detections is reported in minutes as the Mean False Detection Duration (MFDD).

2.4. Experiment setup

First, it is worth noting that the automated neonatal seizure detection system will be useful in practice only if it is patient-independent. Although the dataset consists of 705 seizures, the integrity of a patient should be preserved to avoid using the data of the same patient in training and testing.

In this work, the system is first validated using a patient independent LOO estimate over a set of 17 patients. That is, one patient is selected as the test subject with the remainder of patients constituting the training set. This procedure is repeated until each patient has been a test subject and the mean result is reported. This stage is useful as it tests not a single detector, but rather the methodology of the system and the expected performance on unseen patients. The LOO error is known as an unbiased estimator of the true generalization error (Vapnik 1982), i.e. the difference between the expected LOO error and the true error is approximately zero.

In the training stage, per channel annotations are required for the seizure class to prevent the inclusion of non-seizure exemplars. A maximum of 2 minutes of seizure data per patient are available for each training patient, this data is used to train the seizure class GMM. For the non-seizure class, per channel annotations are not required and thus all data may be used. However, to reduce the training time of the algorithm, 10% of the non-seizure data is randomly sampled and used to represent this class during training.

Additional data was subsequently obtained for three patients, which are referred to as the hold-out set. The hold-out set is classified using a single classifier trained on data from the entire LOO training set. For the hold-out set all the detector parameters are obtained over the LOO set, and thus it is possible to confirm whether the results obtained in the LOO experiment are representative of the performance of the system on unseen data.

3. Results

3.1. GMM parameters

First the choice of parameters for the GMM models is investigated on the LOO set. These parameters include the number of Gaussian distributions per class, the choice of feature preprocessing technique and the type of covariance matrix used. From the results shown in Table 3, the LDA transform leads to the highest ROC area of 95.6% and lowest standard deviation among patients of ±2.9 with 8 full covariance Gaussians.

Table 3.

ROC area results for feature preprocessing techniques using a moving average width of 15 epochs and a collar width of 40s. The standard deviation of ROC area among patients is given in parentheses

Feature Preprocessing	No. of Gaussians	No. of Features	ROC area (%) ∑ diag	ROC area (%) ∑ full
No processing	8	55	89.5 (8.7)	94.2 (5.2)
No processing	16	55	90.2 (11.5)	93.3 (5.8)
PCA	8	32	94.8 (3.5)	94.5 (4.2)
PCA	16	32	95.5 (3.2)	93.8 (6.2)
LDA	8	30	92.6 (5.3)	95.6 (2.9)
LDA	16	30	93.0 (4.7)	95.6 (3.0)

3.2. Postprocessing parameters

The impact of postprocessing on the ROC area of the system using LDA preprocessing with 8 full covariance Gaussian distributions is shown in Figure 6 for the LOO set. Without postprocessing, which is equivalent to using a moving average filter width of 1 epoch and a collar width of zero, the ROC area is 85.7% (±6.6). The largest overall ROC area of 95.6% (±2.9) is obtained using a moving average filter of 15 epochs and a collar width of 40s.

Figure 6.

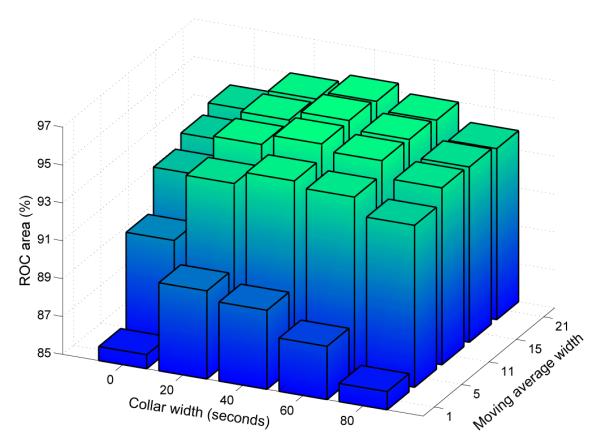
ROC area as a function of moving average and collar widths.

3.3. Performance comparison

Comparison of results with other studies is complicated by a lack of standardised metrics and databases. For reference, the database information has been tabulated for a number of recent studies in Table 4. The number of patients with seizures is relatively low for the majority of studies and thus a set of recordings without seizures are also used by some authors, these patients are shown in parentheses within the table. Any algorithm, both classifier or threshold based, should be tested on new, unseen data. Indeed, it was reported by Gotman et al. (1997b) that the performance of the system was significantly better on the training set (GDR = 71 and FD/h = 1.7) than on the test set (GDR = 66% and FD/h = 2.3). For this reason, only studies including a training and separate test set have been included. This criteria results in the exclusion of the results from Deburchgraeve et al. (2008) for which no test set is used.

Table 4.

Statistics of the test databases from various studies.

Study	Patients Seiz (+ No Seiz)	Test set duration (h) (min)	Seizure events	Seizure duration (min)
Gotman 1997	41 (+13)	237	-	-
Navakatikyan 2006	17 (+38)	24.4	97	1.94 (mean)
Aarabi 2007	10*	86	478	1.77 (mean)
Greene 2008	17	252	411	4.06 (mean)
Mitra 2009	28 (+48)	33.6	206	10s-20min

^*Only 4 patients are independent from the training set and the results are averaged over both the test and training sets.

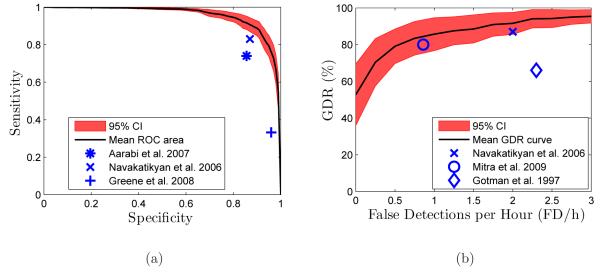
Results from previous studies are plotted against the mean ROC curve, Figure 7(a), and mean GDR vs. FD/h curve, Figure 7(b). Certain studies report only epoch or event based metrics, and as such, appear in only one figure. Leave-one-out cross validation is known to have a large variance in results, for this reason the 95% confidence interval (CI) is plotted on the curves.

Figure 7.

(a) Mean ROC curve and (b) mean GDR as a function of FD/h. These curves are obtained over the LOO set and the with 95% confidence interval is shown over all patients in the set. Also included are markers showing the reported performance from recent algorithms.

3.4. Analysis of misclassified events

In order to gain a better understanding of the system, misclassified events in the LOO set were investigated. These results are for a system with LDA preprocessing and 8 full Gaussian distributions per GMM model, the moving average filter length was set to 15 epochs and the collar length was set to 40s. The decision threshold was set to obtain 0.5 FD/h from each patient in the LOO set. At 0.5 FD/h the mean GDR was 79%, the MFDD was 2 minutes, the mean specificity was 93% and the mean sensitivity was 76%.

3.4.1. False detections

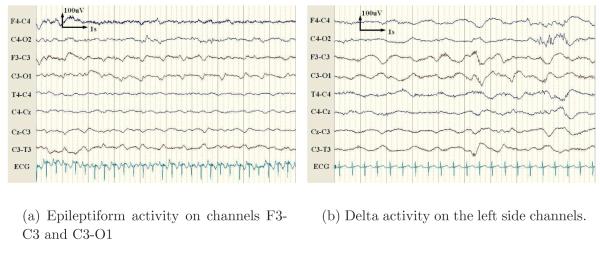
The false detections were found to occur from background activity (45%, 66/147), artefacts (43%, 64/147) and seizure-like patterns (12%, 17/147). The false alarms caused by background activity were predominantly due to short runs of ‘epileptiform’ (periodic sharp) patterns and delta activity. Epileptiform activity, as shown in Figure 8(a), is a pattern resembling a seizure but which is not prolonged (less than 10 seconds). In certain patients, the background EEG can alternate between epileptiform discharges and suppressed activity repetitively. Delta activity, as shown in Figure 8(b), was found to trigger false alarms when the background patterns became more rhythmic or spike-like.

Figure 8.

Examples of false detections occurring from artefact-free EEG.

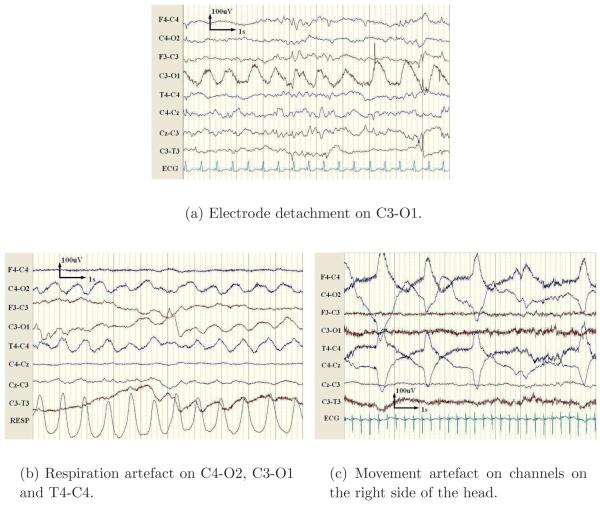
Electrode detachment was found to be the most predominant cause of false detections among artefacts. This artefact is characterised by a high power 50Hz component as the detached electrode becomes contaminated with electrical noise from the environment. The 50Hz component is removed in the proposed detector via lowpass filtering. However, oscillations caused due to motion of the detached electrode or other signals of lower frequency are preserved in the recording and may cause false alarms, as shown in Figure 9(a).

Figure 9.

Examples of the most common artefacts leading to false detections.

Respiration artefact, as shown in Figure 9(b), presents on the EEG as a pseudo-sinusoidal trace and thus is a cause of false alarms. Other artefacts emanating from movement or handling of the patient may cause high amplitude patterns in the EEG, as shown in Figure 9(c), and were found to be a source of false detections.

It was found that approximately 12% (17/147) of false detections occurred from seizure-like activity. These events can considered as “interesting detections”, that is detections that although not labelled as seizure may represent new seizures or simply sections of EEG of value to the neurophysiologist due to their similarity to seizures.

3.4.2. Missed seizures

It was found that the majority of missed seizures were seizures of short duration. Indeed, it was found that the detection rate for seizures with a duration of less than 1 minute was only 45.1%. This was significantly lower than the detection rate for seizures with a duration of over 1 minute which had a detection rate of 92.5%. In the cross-validation dataset, it was found that 144/705 seizures had a duration of less than 1 minute.

3.5. Testing on a separate dataset

A GMM classifier was trained using LDA preprocessing and 8 full covariance Gaussian mixtures per class with data from the LOO set. The postprocessing parameters were 15epochs for the moving average filter and 40s for the collar. From the results on the LOO set, the median threshold resulting in a FD/h rate of 0.5 was obtained, this threshold value was 0.775. The records of the hold-out set were then classified, the results are given in Table 5.

Table 5.

Results for the supplementary hold-out set. Also included for comparison are the results of cross validation

Patient set	GDR	FD/h
LOO set	79	0.5
Test set	74	0.39

4. Discussion

4.1. Algorithm parameters

In this study, the parameters of both the classification stage and postprocessing stage were chosen to maximize the ROC area of the system. In the classification stage, it was found that feature reduction techniques increased the ROC area. From Table 3, it can be seen that the highest ROC area obtained with no feature preprocessing (94.2%) is surpassed by both PCA (95.5%) and LDA (95.6%). However, the choice of GMM parameters (the number of Gaussians and covariance type) are dependent on the feature preprocessing technique, as full covariance matrices are required to achieve the best results for LDA, in contrast to PCA where diagonal covariance matrices lead to better results.

Without postprocessing, the ROC area shown in Figure 4 is 85.7%. The moving average filter alone results in an ROC area of 93.8%. The largest overall ROC area of 95.6% (±2.9) is obtained using a moving average filter of 15 epochs and a collar width of 40s. Thus, the duration of seizures is underestimated, requiring the addition of the collar operation in order to achieve the highest ROC area. It can therefore be concluded that the contextual information of the current epoch plays an important part in correctly classifying the EEG signal. The 15 epoch moving average filter length results in a delay of 28 seconds between a epoch being processed and a decision for that epoch being available to the clinician. This delay is considered acceptable for this particular task, as the therapeutic response to neonatal seizures is not based on isolated short seizures but rather on clusters of seizure or sustained seizure activity.

4.2. Detector performance

Comparing the performance of neonatal seizure detection systems is complicated by the different datasets and varying metrics among authors. From Table 4, it can be seen that the number of patients used for testing has a large range (10-76 patients), and that some studies recruit patients with no seizures during testing, further complicating comparison. Moreover, the length of the test sets are also very diverse, ranging from 24 to 252 hours.

Due to the probabilistic threshold utilised in this study, it is possible to obtain performance curves by varying the threshold over a range of values. These curves can then be used to facilitate the comparison of performance, as seen in Figures 7(a) and 7(b). Navakatikyan et al. (2006) provide both epoch and event based metrics. The reported sensitivity and specificity are 83% and 87% respectively, also reported are a GDR of 87% and a FD/h rate of 2. Thus, while the algorithm detects a high percentage of seizures, the false detection rate is also relatively high. Aarabi et al. (2007) report a sensitivity of 74% and a specificity of 85.6%. However the reported results correspond to the average results over both the training and test set, which implies that the results are biased and not patient-independent. Greene et al. (2008) reported a sensitivity of 33.2% and a specificity of 96%. It should be noted that despite low sensitivity, the GDR of the system was 80%. Gotman et al. (1997) obtained 66% GDR with 2.3 FD/h. Mitra et al. (2009) recently reported a GDR of 80% at 0.86 FD/h. From Figure 7, the proposed system achieves higher seizure detection scores and lower false detections, in both epoch and event metrics, than all compared studies.

Another strength of the system is the ability to detect over 50% of seizures with zero false detections. It is worth mentioning that a large factor for the widespread adoption of a new technology such as an automated seizure detector is that it does not unnecessarily increase the work of the staff in the NICU. For this reason, the false detection rate should be kept as low as possible, as otherwise the detector will contribute to more work for the NICU staff as the false detections are checked. In this respect, the system proposed here achieves 79% GDR with only 0.5 FD/h over the LOO set thus creating a potentially usable system for the NICU.

As demonstrated by the use of performance curves in this paper, the detector developed here can be set to obtain the desired trade-off between good and false detections. The ability to control the trade-off between sensitivity and specificity and between GDR and FD/h allows for the choice of a probabilistic threshold that can be optimal or at least acceptable for a particular clinical application. This is achieved due to the probabilistic decision threshold used after classification and represents a significant advantage over the multiple heuristic threshold rules used in other studies (Navakatikyan et al. 2006, Deburchgraeve et al. 2008).

It was found that the main criteria for the detector missing a seizure was the short duration of a seizure event. The choice of moving average filter length is linked with the lower sensitivity of the system with respect to seizures of duration less than one minute. The choice for the filter length is data-driven and reflects the fact that seizures of duration under a minute comprise only ~20% of the overall number of seizures in the dataset. Furthermore, every patient in the dataset presented with at least 1 seizure of duration over 1 minute. Mitra et al. (2009) included an analysis of misses and false detections, and reported that short duration events were the main cause of missed seizures. A detailed analysis of false detections is not given in most studies on neonatal seizures, thus the impact of short seizures on other systems can not be assessed.

It should be noted that premature babies were not included in this study and rather only babies that were full terms and with a diagnosis of HIE, the most common cause of neonatal seizures, were included. Some seizures in neonates can be of short duration particularly in preterm babies. However, this group was not recruited for this study, and thus the results presented here are truly representative and clinically relevant for full term babies.

Both background EEG and artefacts were found to cause false detections in the system. Certainly a dedicated artefact removal routine would improve the results despite the system being trained with artefact contaminated EEG. The problem occurs due to the downsampled EEG appearing similar to seizures during certain artefacts, in this case extra information such as a 50Hz indicator or respiration channel would be required to provide additional information to the system.

With regards to interesting detections, the system identified a small number of events which may be new seizures or be of clinical relevance. Neonatal seizures can often be difficult to distinguish from the background activity and, when multiple seizures are present, it is often difficult to clearly describe the end of one seizure and the beginning of another. To date there have not been any studies of inter-observer agreement in neonatal seizure detection.

4.3. Further validation of results

The results presented in Table 5 are indicative of the performance of the system on unseen patients once a desired operating point has been chosen. It can be seen that the results on the hold-out set (74% GDR and 0.39 FD/h) are commensurable with the results of LOO cross-validation (79% GDR and 0.5 FD/h). Indeed, the results over the hold-out set fall within the 95% CI shown in Figure 7(b). This indicates that the LOO cross-validation results are an appropriate representation of the performance of the algorithm on unseen data, which has also been confirmed more generally by Guyon et al. (2006).

The results for the LOO set are presented in the form of performance curves (Figure 7). For the hold-out set however, the system was set to a specific operating point, i.e. 0.5 FD/h. This was achieved by calculating the median threshold value over the LOO set to yield approximately 0.5 FD/h. The FD/h rate measured on the hold-out set was 0.39 FD/h, therefore it can be concluded that the desired trade-off can be selected from the performance curves of the training set and predictable performance is obtained on new unseen data.

5. Conclusion

In this study, a real-time neonatal seizure detection system is designed based on a GMM classifier. The parameters of the detector were chosen to maximise the ROC area of the system. The proposed detector was found to yield the highest performance in the field over a number of metrics. Finally, patterns in the EEG causing false detections were identified and the characteristics of missed seizures were determined. These patterns and characteristics indicate specific areas in which the detector may be improved. Elements of this system are currently being used to develop a prototype seizure detector which will be tested online in the NICU. Finally, online adaptation of the GMM classifier is under investigation which may prove to be of great importance for neonatal seizure detection by tracking slow-varying patient dependent conditions.