Toward the virtual cell: Automated approaches to building models of subcellular organization “learned” from microscopy images

Abstract

We review state-of-the-art computational methods for constructing, from image data, generative statistical models of cellular and nuclear shapes and the arrangement of subcellular structures and proteins within them. These automated approaches allow consistent analysis of images of cells for the purposes of learning the range of possible phenotypes, discriminating between them, and informing further investigation. Such models can also provide realistic geometry and initial protein locations to simulations in order to better understand cellular and subcellular processes. To determine the structures of cellular components and how proteins and other molecules are distributed among them, the generative modeling approach described here can be coupled with high throughput imaging technology to infer and represent subcellular organization from data with few a priori assumptions. We also discuss potential improvements to these methods and future directions for research.

Why do we need spatially accurate models of cell organization?

Understanding the relationship between cellular structure and function is a fundamental biological problem. Microscopy technology has progressed dramatically over recent decades and provides images with ever-increasing resolution, accuracy, and specificity. Together with these advances, several computational approaches for dealing with such data, in particular cell image data, have been described in the past 15 years [1, 2]. These are often combined to arrive at new insights about cellular and subcellular processes. Examples include understanding the differences in protein subcellular location patterns in cells obtained from normal and diseased tissues [3] or over the cell cycle [4], modeling cytoskeletal dynamics [5, 6], learning the range of possible nuclear [7, 8] and cellular [9–12] shapes, and learning the effects of gene expression changes on cellular shapes [13].

Proteomics research explores the function, structure, variability, interaction, and location of the large number of proteins expressed in cells. Due to the dependency of function and interaction on location, one of the most important tasks is to identify the subcellular locations of proteins, namely their spatial distributions in various organelles [14–16]. Indeed, some subcellular structures are defined by the locations of specific proteins, e.g. cytoskeletal structures are composed of polymerized tubulin, actin, or intermediate filament proteins that help shape, position, and even create organelles.

Results for subcellular location are typically captured in words, such as GO terms. However, this approach does not readily support realistic modeling of the influence of cell organization on behavior and is often not sensitive enough to capture changes in patterns caused by drugs or inhibitory RNAs. An important alternative is to use computational analysis of images to produce spatial models capable of encoding observed phenotypes, and the parameters of such models for different samples (e.g. in the presence of different perturbagens) can be studied and contrasted in a consistent, reproducible way. In addition, models for organelle surfaces and protein location can provide realistic geometry and molecular distribution for reaction-diffusion-type simulations (e.g. [17]) of important cellular processes in order to support or refute hypothetical mechanisms that might explain those processes. These and other kinds of simulations of cellular structures have already produced interesting insights into the workings of the cell [18–22]. Ultimately, applications of this kind of modeling might significantly affect medical diagnosis. These examples help motivate this paper’s topic.

This overview addresses current work on learning detailed models of cellular structure to support comparison and simulation studies. We describe general modeling strategy and methods for automatic learning of models of cellular shapes, organelles, and protein distributions from microscopic image data. Finally, we describe potential avenues for future research.

How do we construct models of cell structure?

Any model of cellular structures should give a description of the statistical relationship between the variables of interest, i.e. a mathematical description of the probability of any combination of values assigned to these variables. These will allow evaluation of the likely behavior of one set of variables given conditions on another. For example, the microtubule catastrophe rate might be more likely to be lower in mitosis compared to interphase, with exceptions being due to cell-to-cell variability. The model might just include the mean rates for mitosis and interphase, or it could additionally contain the standard deviation of each rate. The latter model states that the catastrophe rate of interphase cells is normally distributed with that mean and standard deviation (and similarly for mitotic cells). Note that models may not explicitly state their statistical assumptions but still have them. For example, the common differential equation-based model representing protein interactions specifies that the rate at which a particular protein’s concentration changes is solely a function of its and other proteins’ concentrations and is unaffected by random noise [23].

Models have some number of parameters, e.g. the mean catastrophe rates in interphase and mitosis, that allow them to represent a range of behaviors or patterns. A specific behavior is selected with a corresponding set of values for those parameters, e.g. lower rates in mitosis. These parameters can be chosen automatically by statistically estimating them from collected measurements (called training data) of the system of interest. Data are processed into a consistent, comparable and measurable form, usually vectors of numeric values of a specified length (called feature vectors), e.g. multiple measurements of the length of a microtubule over time (from which catastrophe rate could be inferred).

There are two major categories of statistical models, discriminative [24, 25] and generative [11, 12, 26], and both have been applied to the study of subcellular organization and protein patterns. Discriminative models only represent the probability of a feature vector being from each particular pattern and explicitly do not consider the physical or biological mechanism by which the measurements (images) were generated. We can only ask of a discriminative model: how likely is it that this feature vector comes from a particular pattern?

Generative models, on the other hand, also represent the probability of observing a particular feature vector when it comes from a particular pattern, and they even commonly contain variables that are not measured (latent variables). An example of a latent variable would be microtubule catastrophe rate in the case that the only variables measured were the lengths of the microtubules in the cell. Thus, a different query can be made of a generative model: what are examples of images I would expect for a particular protein in a given cell type under a specific condition?

As an illustrative example of the advantages of using a generative model, suppose that we wish to create a simulation in which the distributions of many proteins are represented in a single cell. We could measure this by imaging all of them simultaneously. However, technology for imaging more than a few proteins in the same sample is not available, especially for live cells. Even if we wish to build up a model from measurements of colocalization of subsets of the proteins, there are too many combinations to feasibly image (for 1,000 proteins, there are 166 million combinations of three proteins). However, generative models can approximate the colocalization of these proteins. We can build a generative model of the pattern of each protein individually that depends only on the cellular and nuclear shapes of the cell. We can then hypothesize that proteins with similar model parameters are colocalized, and can create synthetic cell images in which these proteins are placed in the same structures. This gives us an image of the same cell showing the locations of many proteins. Extending this model to include dependency on structures other than the nuclear and cell membranes, such as the cytoskeleton, would give an even more accurate synthetic cell.

Generative models can also be used to find probable values for latent variables. While a discriminative model may easily distinguish between two images of microtubules from different conditions (say wild type and treated with nocodazole, which depolymerizes microtubules), a generative model can include latent variables parameterizing the process of microtubule growth, e.g. number and average length of microtubules. Thus, unlike with discriminative models, learning the parameters of the generative model could encode the basis for the differences between patterns.

As previously proposed [11], models of cellular structures ideally should be:

1. automated: learnable automatically from images;

2. generative: able to synthesize new, simulated images displaying the specific pattern(s) learned from images;

3. statistically accurate: able to capture pattern variation between cells;

4. compact: representable by a small number of parameters and communicable with significantly fewer bits than the training images.

In the context of this paper, one key issue in building models of cells is that they need to contain modular pieces which depend on each other in order to capture correlations between structures of the cell when synthesizing an image. For example, endosomes lie between the nuclear and cell membranes, so to synthesize an image displaying an endosomal protein’s distribution pattern, one might generate a nuclear shape, then, given that the cell membrane is always outside the nuclear membrane and their orientations are correlated [11], generate a cell shape whose probability distribution depends on the selected nuclear shape, and finally generate endosome-shaped objects so that they lie between the two shapes. Combined together, these pieces produce a generated image which is analogous to a real multichannel microscope image. Open source software components that can learn such conditional models and synthesize instances as images are available at http://CellOrganizer.org.

One important issue in modeling is the balance between accuracy and precision and how it is affected by model complexity, i.e. the number of parameters. We want to choose a level of complexity that will allow the model to generate images resembling real ones while maintaining computational feasibility. For example, a nuclear shape approximated by an ellipse could not incorporate bends or blebs, but a model using polygons with thousands of vertices might take hundreds of thousands of images to have its parameters properly estimated.

Parametric models can be built for nuclear shape

A cell’s nuclear and plasma membranes form the largest partitions of cellular material and so are the first structures to model. We start by modeling nuclear shape as the foundation for the rest of the cell in two-dimensional (2D) and three-dimensional (3D) images, and then we model cell shape as statistically dependent or constructed upon nuclear shape (but dependency in the other direction would also be reasonable).

By images of nuclei, we mean images where the inside of the nucleus is marked by a fluorophore and so has a higher intensity than the outside of the nucleus, whether what is marked is DNA, histone, or something else. Since the nuclear envelope breaks down and chromatin condenses during mitosis, our model is restricted to interphase nuclei. The shape of the imaged nucleus is represented as a binary image or mask, i.e. a 2D or 3D array of pixels with each pixel being one or zero, or part of the shape or not. To get a shape image, the raw image is binarized by, e.g. selecting a threshold intensity value and setting pixels in the shape image to one if the corresponding pixels in the raw image are greater than that threshold and setting them to zero otherwise.

2D nuclear shapes

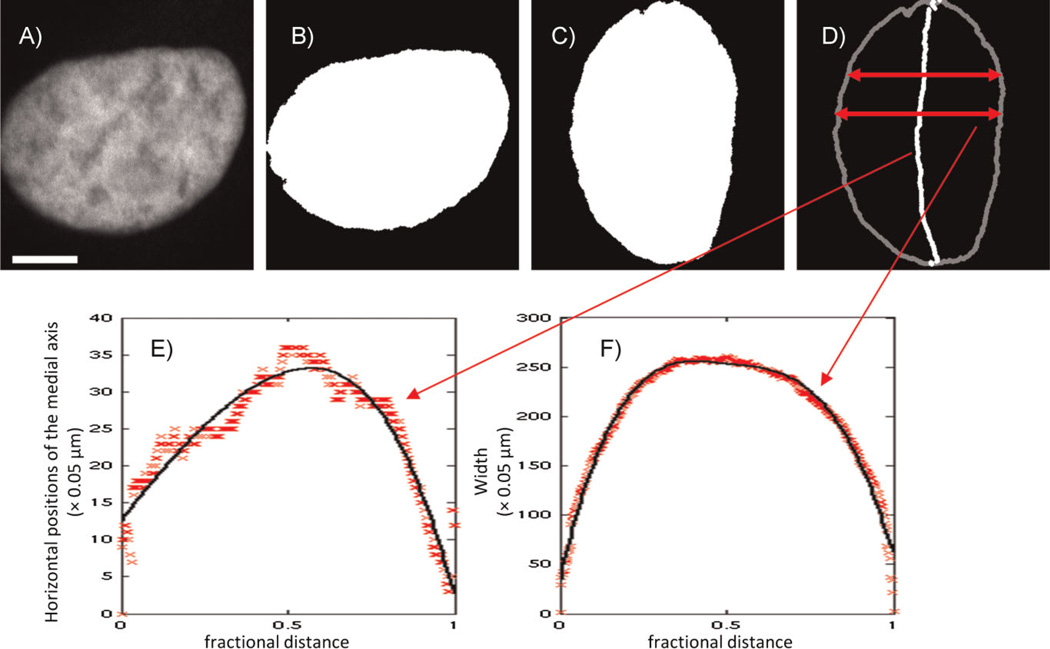
An initial parametric nuclear shape model was built from 2D images [11]. Nuclear shapes were captured well using two simple curves that together defined the region of the 2D plane occupied by the shape. If the nuclear shapes were approximated by an ellipse, the major and minor axes of that ellipse could be considered the axes of a coordinate system for these curves. One curve encoded bending of the nucleus to either side of the major axis (the bent axis is called the medial axis), and the other represented the width of the nucleus at every point along that bent axis. The procedure is illustrated in Fig. 1. Each curve was represented as a B-spline with five parameters. Another parameter was added for the overall length of the nucleus along the major axis, bringing the total number of parameters to 11. Variation between all the individual nuclei’s parameters was modeled as two multivariate Gaussian distributions, one for each curve, and thus could be sufficiently summarized using just the mean vectors and covariance matrices of those distributions. Generation of new nuclear shapes can be done simply by randomly sampling curve parameters from the learned distributions and drawing the nuclear image using those curves. Thus, a large set of realistic nuclear shapes can be represented, compared, and synthesized with a model that is not much more complicated than one representing the nucleus as an ellipse.

Figure 1.

Illustration of medial axis model fitted by B-splines for nuclear shape. The original nuclear image (A) was processed into a binarized image (B), in which the nuclear object consists of the white area. The nuclear object was rotated so that its major axis is vertical (C) and then converted into the medial axis representation (D). The horizontal positions of the medial axis as a function of the fractional distance along it are shown by the symbols in (E), along with a B-spline fit (solid curve). The width as a function of fractional distance is shown by the symbols in (F), along with the corresponding fit (solid curve). Scale bar: 5 µm. (From [11]).

3D nuclear shapes

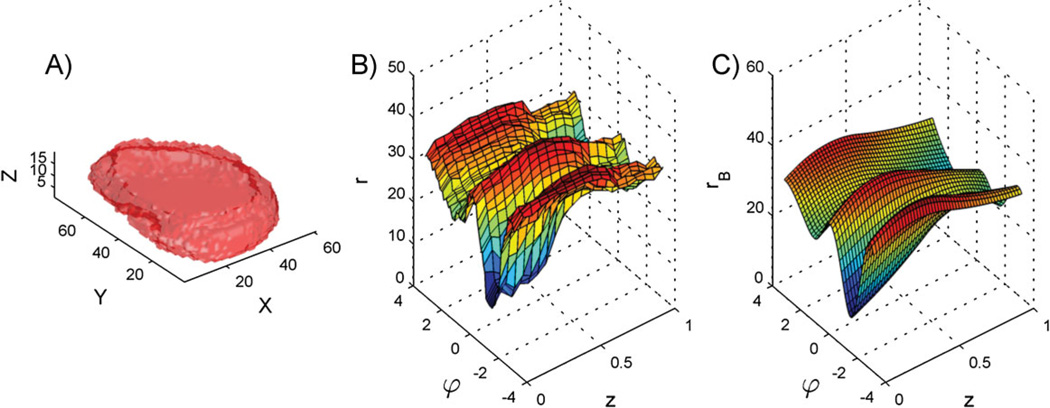
Real nuclei are 3D, however, and the 2D nuclear shape model has been extended to 3D [12]. To do this, the 3D nuclear shape was modeled as a mesh defined in cylindrical coordinates. By mesh, we mean a set of 3D vertices connected by polygons to form a surface without holes (this is the 3D analog of a polygon in 2D). This mesh’s vertices were placed on the boundaries of the shape image in a grid pattern, so the vertices were positioned at a set of fixed angles (with angle being in the plane of the bottom of the cell) and at a set of fixed heights above the bottom. The model encoded the distance of each vertex from the center of the nucleus, with distance being measured in the horizontal plane. A smooth surface (analogous to the curves in the 2D case) was then fitted to the mesh to represent it with a few parameters (i.e. 562) rather than with all the distance values (i.e. 6,480). This also served to remove high frequency variation in the boundary due largely to measurement noise (observable as small bumps in Fig. 2A). The top and bottom of the surface were kept flat. The distribution of all of these parameters was again shown to be captured well by a multivariate Gaussian. Figure 2 illustrates the generative process using a real nuclear shape. Having learned that probability distribution, we can sample from it to generate new nuclear surfaces.

Figure 2.

Nuclear shape representation. A: Surface plot of a 3D HeLa cell nucleus. B: Unfolded surface of the nuclear shape in a cylindrical coordinate system. The surface plot shows the radius r as a function of azimuth u and height z. C: B-spline surface fitted to the unfolded nuclear surface. (From [11] and [12]).

Parametric models concisely capture cell shape

The next component of the generative framework is the shape of the plasma membrane, hereafter referred to as the cell shape, and it will be conditioned on the nuclear shape generated by the models in previous section. These models work well for 2D and 3D images of cultured cells with fibroblastic shapes.

2D cell shapes

As previously stated, a nuclear shape fits within its cell shape, and their orientations are correlated, so a conditional relationship between the models for each shape is required to encode these effects. One approach [11] was to rotate each nuclear and cell shape pair so that the nuclear major axis was vertical and if necessary flip the shapes so that the majority of the nuclear shape’s pixels was on the same side of the major axis for all cells. The first operation allows the model to capture correlation due to orientation, as without this alignment orientation-related effects would cancel out each other. The second operation will capture correlations between lateral asymmetry of nuclei and their cell shapes. Cell shape was then modeled as a polygon defined in polar coordinates with the origin at the nuclear center and with vertices at angles with one-degree increments (like a 2D version of the 3D nuclear shape model). In order to make the cell’s size relative to the nucleus’ size, the value modeled at each angle was the ratio of the cell radius at that angle to the nuclear radius. Thus, each cell shape was represented as a vector of length 360.

Recalling the accuracy versus precision trade-off, a covariance matrix encoding how each of the vertices correlates with the others would require 64,980 values to be estimated. With far too few cells (perhaps a few hundred) to estimate all of these, only the largest modes of variation in the cell boundary were estimated using principal component analysis (PCA). PCA rotates a set of multidimensional points so that the new first dimension contains as much of the variance in the points as possible, the new second dimension contains the plurality of variance left in the data, and so on. The 10 largest modes captured 90% of the total variation in all of the original cell shapes, and these feature vectors of length 10 were again modeled with a multivariate Gaussian. A new cell shape can be generated from the statistical model by sampling from that normal distribution and reversing the transformations listed above to retrieve a full cellular shape polygon.

3D cell shapes

The cell shape model was also extended to 3D [12]. As with the 3D nuclear shape model, cell boundaries were modeled as meshes defined in cylindrical coordinates. Distances were represented by a set of ratios as with the 2D cell shape model to ensure that the cell contained the nucleus, but with one ratio at each height and angle pair. PCA needed 20 modes to capture 90% of the total variation.

Nonparametric models capture more complex shapes and relationships

Almost any parametric model involves enough simplification to have trouble representing all the complexities of the objects being modeled. Different types of cells may drastically differ in their shapes: neurons have a branching structure, neutrophils have wrinkled surfaces, and epithelial cells can be anywhere from column-like with microvilli to goblet cells with large invaginations to quite flat. So far, we have focused on cells having fibroblast-like, “fried egg” shapes such as those of cultured HeLa cells. The 2D model of the cell’s outline assumes that any point on a shape’s boundary is visible from the center of the cell. Such an assumption does not hold in many cases for cells having branching or bottlenecked (like pseudopodia) projections on their boundaries. Additionally, the above dimensionality reduction tends to discard small details.

An alternative to parametric modeling is the nonparametric approach, i.e. to let the shape representation and probabilistic model grow in detail with the number of data available rather than compute a fixed set of summarizing statistics from the data [7, 8]. The set of possible shapes is defined as any shape that can be formed by interpolating between shapes observed in real images, and the probability of observing any shape is related to how much it resembles those observed shapes.

By shape interpolation, we mean creating a new shape from two others that appears to be somewhere between the two and takes on some of the character of either. For example, consider interpolating between the shape of a round nucleus and that of an elongated, bent nucleus. As with linear interpolation between two real values, the shape would be rounder (more like the first image) the closer the interpolation factor is to zero and more elongated and bent the closer it is to one. The interpolation process also produces a measure of the distance between the two shapes [27].

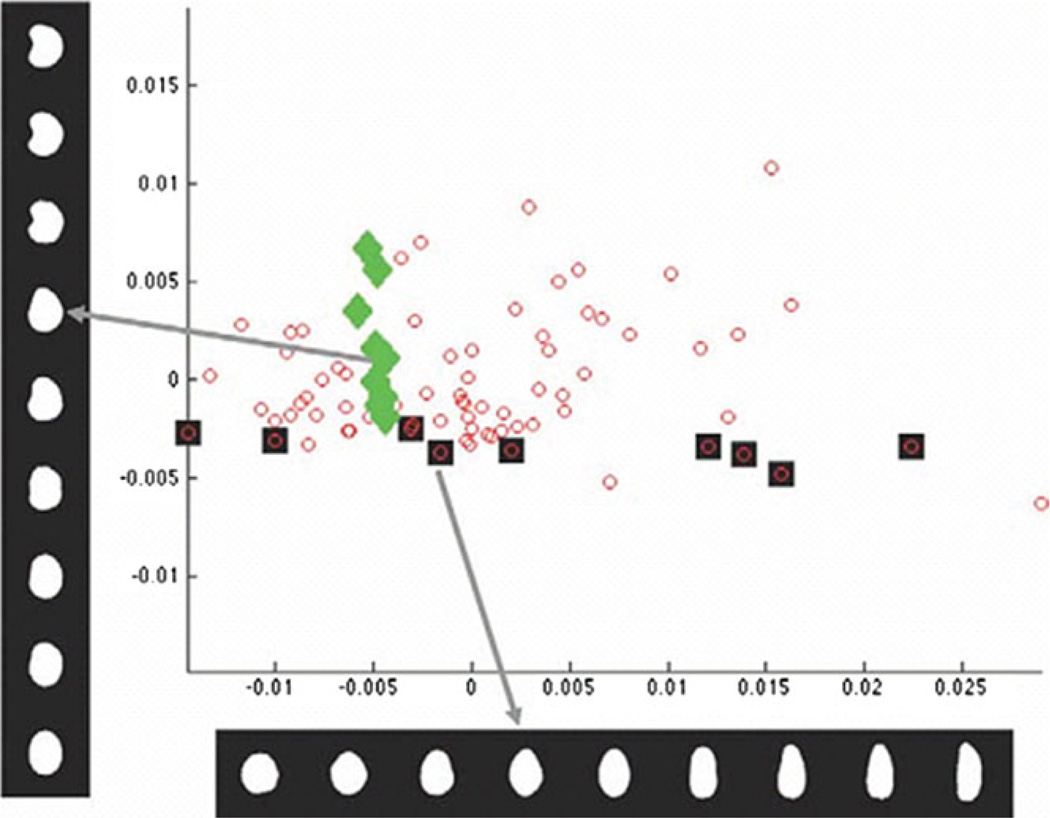
A distance matrix can then be computed using the distances between every pair of shapes. From this matrix a set of points representing the observed images can be derived using multidimensional scaling (which is like PCA where the input is a distance matrix). This arrangement of points is termed a shape space. We show an illustration of a shape space in Fig. 3. Because this space is defined using the interpolation-based distance measure, images of shapes can be synthesized from any point in the shape space using the same image interpolation method.

Figure 3.

Plot of the first two components of the low-dimensional representation of the nuclear shape computed by the shape interpolation method discussed in the text. Each small circle corresponds to one nuclear image. Images associated with specific data points are shown on the left (diamonds) or across the bottom (squares). Each dark square corresponds to each image shown in the horizontal bottom series of images. Likewise, each light diamond corresponds to each image stacked vertically. Note that the method separates different modes of shape variation (bending and elongation) into separate coordinates (vertical and horizontal) (from [7]).

As can be seen, the above approach does not make any assumptions about the shapes (other than that each is a single, connected shape). The probability distribution is defined using all of the input data. In order to assign a probability to each point in the shape space, including points representing unobserved shapes, we set the probability to be proportional to the sum of a set of small Gaussians, with each Gaussian’s mean at an observed shape (this is called kernel density estimation). As a result, the probability of a shape is higher near a higher density of observed shapes.

The shape and probability models together allow one to synthesize new examples of plausible nuclear or cellular shapes even given a number of images that would be considered too low to estimate a parametric model with this level of detail. However, this model is very large in terms of memory: it stores all the observed shapes as part of the model (this problem can be reduced by only saving the most important examples).

Models of vesicular organelles can be learned directly from images

The most difficult and important piece in the generative framework is the representation of subcellular components and accounting for protein spatial distribution patterns within a cell. Much work has been done, but this area is wide open due to the complexity and intricacy of both membrane-bound and structural subcellular components.

2D objects

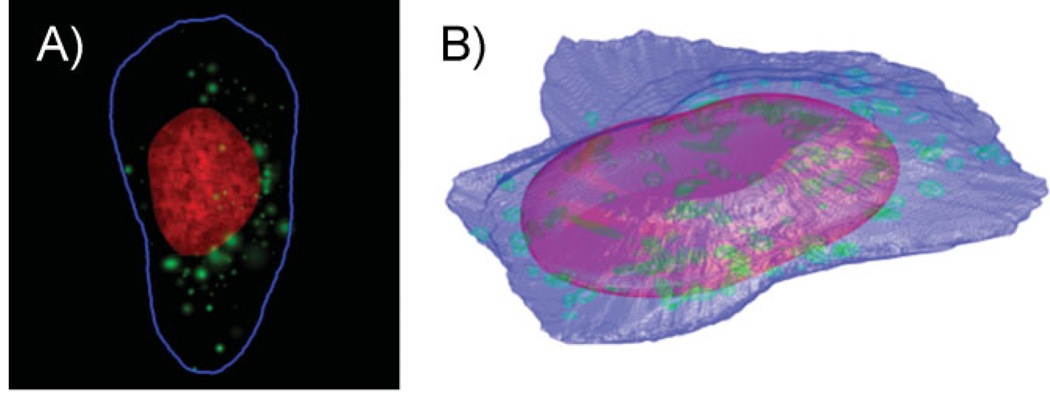
Granular and discrete vesicular organelles like endosomes, lysosomes, and peroxisomes are approximately ellipsoidal or bead-like and appear as small objects in, e.g. fluorescent confocal images of cells labeled for a vesicular protein. We have therefore previously built object-based models from 2D images [11]. An object was detected as a contiguous region of high-intensity pixels in a cell image that was surrounded by lower-intensity pixels. A vesicle’s appearance can be approximated as a 2D Gaussian distribution because a 2D image of protein inside a vesicle would show intensity decreasing with the distance from the center of the vesicle, as expected if the intensity in a given pixel were proportional to the volume that underlies that pixel. Since vesicles were often touching or overlapping, regions of high-intensity pixels might have contained multiple objects, so we separated them as a preprocessing step. Probability distributions were then fitted to the number of vesicles in a cell and the size, intensity, and position of each vesicle. The position of each object was represented in polar coordinates, with the angle being between the object’s position and the major axis of the nucleus and the radial distance being relative to the nearest points on the nucleus and the cell membrane. With these four distributions, it is simple to synthesize a new vesicular pattern by first sampling the number of objects and then, for each object, sampling its size, intensity, and position. Figure 4A displays an example of a synthesized image showing a lysosomal pattern.

Figure 4.

Example synthetic images generated by models learned from images of the LAMP2 (lysosomal). A: A 2D image generated by 2D modeling. The DNA distribution is shown in red, the cell outline in blue, and the lysosomal objects in green. B: A 3D image generated by 3D modeling. The nuclear surface is shown in red, the cell surface in blue, and the lysosomal objects in green. (From [12]).

Extension to 3D

The 2D object-based models were easily extended to 3D [12]. An example of a synthesized 3D image showing a lysosomal pattern is displayed in Fig. 4B.

Indirect learning can model complex network structures

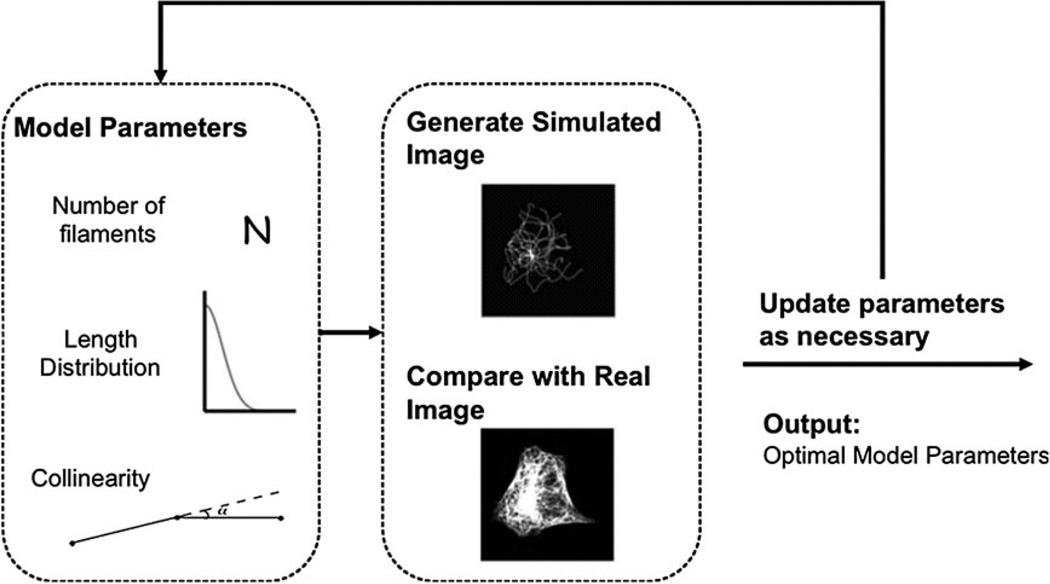
Object-based models are inappropriate for proteins that form network distributions such as tubulin. However, microtubules often cross and pile up near the center of the cell, so, unlike with vesicles, individual microtubules cannot be easily detected. As a result, it becomes difficult to directly estimate parameters for their distributions except in special circumstances (e.g. speckle microscopy [28]) that do not apply on a proteome scale because they require suitable polymerization and depolymerization rates. On the other hand, indirect learning, a form of automated guess-and-check, provides an alternative for parameter estimation. Its principle is to generate a library of synthetic images from a model with various values for those parameters and estimate the model parameters corresponding to real images as those from the synthetic image that most closely resembles the real images. This resemblance is measured using another set of features that can be readily computed from both images and does not depend on identifying the microtubules.

3D microtubules

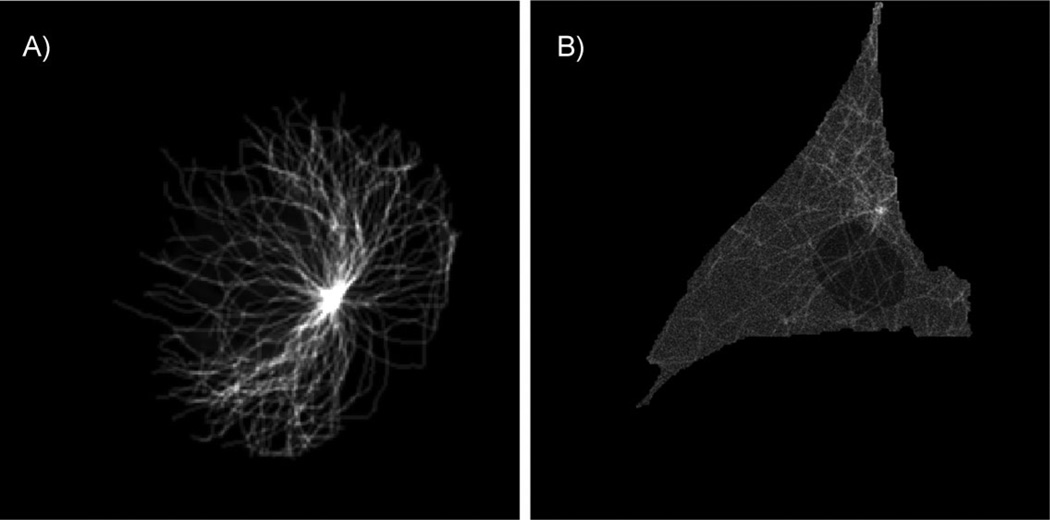
Indirect learning has been used to learn the parameters of a model of 3D microtubule distributions from images of fixed cells [5]. The parameters of this model were the number of microtubules, their lengths, and the degree to which they grew in the same direction (collinearity). Synthesis of a microtubule image from this model is straightforward and is inspired by a growth process in real cells. First the number of microtubules is sampled, then the length of each microtubule is sampled individually, and lastly collinearity is sampled. A centrosome location is chosen and the microtubules grow from it. Small line segments representing newly grown portions of the microtubule are added incrementally, and their tendency to grow in the same direction as previous segments is controlled by the collinearity parameter. Once a microtubule’s desired length has been reached, the simulation for that microtubule ends. Finally, synthetic images are blurred with a microscope’s point spread function to emulate the appearance of a real image. The features used to compare real and synthetic images included ones that described intensity histograms and intensity as a function of distance from the estimated centrosome position. The entire process is illustrated in Fig. 5, and a 2D slice from a generated 3D image is shown in Fig. 6A.

Figure 5.

Overview of the approach to indirectly learning parameters of microtubule distribution (from [5]).

Figure 6.

A: A 2D slice example with the maximum plane intensity from generated 3D image using microtubule model. B: A 2D slice example with the maximum plane intensity from generated 3D image using microtubule model plus free tubulin model.

Addition of free tubulin

The above model of microtubule distributions has been extended to model the distribution of free tubulin monomers [6]. To do so, we estimated histograms of free tubulin intensities from pixels a distance away from the high-intensity microtubules in images of live cells (fixed cells lose free tubulin during permeabilization). Synthetic images of free tubulin were added to synthetic microtubule images to make a complete synthetic tubulin distribution. Figure 6B is a 2D slice of such an image.

Models can be combined to build more detailed models

A major goal of work in this area is to develop cell models that incorporate realistic spatial subcellular distributions for many or most proteins. It is difficult to imagine using multicolor microscopy when the number of proteins is on the order of thousands. An alternative is to combine generative models learned from separate sets of images. Unfortunately, this procedure assumes that these distributions are independent. However, endosomes are closely dependent on microtubules during transport, and lysosomal proteins may be present together in the same vesicles. This introduces the need for learning the conditional structure of these patterns. Given the large number of possible combinations that need to be explored, generative models can be an important tool for learning the conditional structure by testing in silico which conditional relationships make accurate predictions about cell behavior.

Making generative models dynamic is the next step

A natural next step in modeling cellular and nuclear shapes is to consider temporal evolution. In recent work (Buck, Rohde & Murphy, in preparation), we have used the nonparametric shape representation to produce a random walk-based simulation of both cellular and nuclear shapes over time and in 3D. The simulation iteratively moves through the shape space by Brownian motion. Further work is needed to evaluate this model by comparing the shape-space trajectories of time-series images of real cells with synthetic trajectories. The dynamic behavior of subcellular components like tubulin distributions [29, 30] can be added and moved along with cell and nuclear boundaries and, later on, influence evolution of shape.

How about models of other cellular components?

Aside from vesicular components and microtubule networks, there are many other complex cellular components whose distributions need be modeled. The actin filament network is one; although it is also a network distribution and might be modeled and learned inversely as were microtubules, it lacks a well defined organizing center (like the centrosome for microtubules) and has more complex processes such as bundling and branching. Therefore, a more intricate model might be needed to represent actin networks. Partial attempts to do so have been made [20, 22]. Taking a hint from the nonparametric shape space representation of cellular and nuclear boundaries and another from the implicit solvent concept in models of protein dynamics (which represents the mass action of solvent rather than the small effects of many individual water molecules and ions), we may see in certain applications a sophisticated prediction of probable actin network structure and force generation across the cell membrane rather than an explicit representation of each molecule or filament composing it. There has also been extensive work on learning polymerization models from movies of moving cells [31]. Other filament networks and their interactions with membranes have been modeled as well [32].

Gaussian-shaped object models are inappropriate for organelles such as the ER, and building a learnable generative model for reticular compartments has not yet been described. One might represent the general membrane shape as a surface with flexible parameterization (e.g. a mesh or shape image) that could be directly repositioned at any point due to specific applied forces, e.g. the cytoskeleton or membrane proteins. Another representation might use a statistical description of membrane evolution akin to [33].

Ultimately, the membrane model should permit topological changes due to budding, fusion, and even cell division. This would introduce the challenge of producing forces to move simulated molecules away from the neck of a budding vesicle or the interface of a fusing vesicle. Probabilistic modeling of a changing number of entities where the interactions between the entities influences the change in number may prove difficult, but this could lead to the creation of new statistical representations or the adoption of unused ones.

Much remains to be done

In this paper, we have discussed the need for and reviewed methodological approaches to creating models of cells and their components. Such generative models complement the traditional discriminative method, which excels at differentiating between patterns, by modeling the process from biology and physics to visible data (e.g. microscopy images) and so better explaining the causes of pattern differences.

In the future, given the ability to learn parameters of these models, it will be important to investigate quantitative differences in the patterns between cell types and conditions as these will correspond to differences in cellular function. Furthermore, synthesizing instances of cells from models to initialize simulations will allow making predictions and, coupled with proper experimental design, validating or refuting them, increasing our confidence in our understanding of biology and ultimately expediting development of medical interventions. While much work remains to be done, the possibility of deep, comprehensive, and quickly accumulating understanding of cellular organization and behavior seems within reach.

Abbreviations

2D

two-dimensional

3D

three-dimensional

PCA

principal component analysis