In Vivo Glucose Monitoring Using Dual-Wavelength Polarimetry to Overcome Corneal Birefringence in the Presence of Motion

Abstract

Objective

Over the past 35 years considerable research has been performed toward the investigation of noninvasive and minimally invasive glucose monitoring techniques. Optical polarimetry is one noninvasive technique that has shown promise as a means to ascertain blood glucose levels through measuring the glucose concentrations in the anterior chamber of the eye. However, one of the key limitations to the use of optical polarimetry as a means to noninvasively measure glucose levels is the presence of sample noise caused by motion-induced time-varying corneal birefringence.

Research Design and Methods

In this article our group presents, for the first time, results that show dual-wavelength polarimetry can be used to accurately detect glucose concentrations in the presence of motion-induced birefringence in vivo using New Zealand White rabbits.

Results

In total, nine animal studies (three New Zealand White rabbits across three separate days) were conducted. Using the dual-wavelength optical polarimetric approach, in vivo, an overall mean average relative difference of 4.49% (11.66 mg/dL) was achieved with 100% Zone A+B hits on a Clarke error grid, including 100% falling in Zone A.

Conclusions

The results indicate that dual-wavelength polarimetry can effectively be used to significantly reduce the noise due to time-varying corneal birefringence in vivo, allowing the accurate measurement of glucose concentration in the aqueous humor of the eye and correlating that with blood glucose.

Introduction

The disease diabetes mellitus currently affects over 346 million people worldwide and nearly 25.8 million adults and children in the United States.^1,2 Diabetes and its associated complications are ranked as the seventh leading cause of death in the United States.^1,2 Based on findings released by the National Institutes of Health, it has been shown that improved glycemic control can significantly reduce the risk of many secondary microvascular-associated complications such as kidney failure, heart disease, gangrene, and blindness.^1,2 It has been shown that proper self-management and education of the disease such as accurate monitoring of blood sugar, healthy eating, and being active can significantly improve health outcomes and the quality of life in people with diabetes.² The current commercial methods of sensing are invasive, requiring a finger or forearm stick to draw blood each time a reading is needed or by using an implanted sensor for continuous glucose monitoring. These approaches are painful, raise concerns about bloodborne pathogens, and can be cumbersome and embarrassing. The continuous glucose monitoring also requires calibration with the finger stick devices one or more times daily. Thus, unfortunately, it is frequently difficult to obtain the appropriate motivation and dedication on the part of the patients, suffering from diabetes, for them to commit to an intensive program of blood sugar monitoring.

Over the past few decades there has also been significant research performed in the development of noninvasive optical methods, including near-infrared absorption and scatter spectroscopy,^3–7 Raman inelastic scatter spectroscopy,^8,9 optical coherence tomography,^10,11 photoacoustic spectroscopy,^12,13 and polarimetry.^14–21 The Raman, optical coherence tomography, near-infrared absorption and scatter spectroscopy, and photoacoustic spectroscopy-based techniques hold some promise but suffer primarily from a lack of specificity.^22–24

The development of a polarimetric glucose sensor as a noninvasive monitor for the determination of blood glucose levels would greatly facilitate patient compliance by eliminating the invasive nature of current glucose monitoring techniques. As mentioned, each optical technique for noninvasive measurement of glucose has its own advantages and disadvantages; however, the polarimetric approach has the advantage of being highly specific to changes in glucose while remaining completely noninvasive to the subject.²⁵ The use of optical polarimetry for the detection of sugar concentrations has its origins in the late 1800s, when it was used in the sugar industry for monitoring the production processes of sugar.^26–29 However, it was not until the early 1980s when the use of polarized light had began to focus on physiological glucose measurement. Rabinovich et al.^14,15 first proposed the application of optical polarimetry to measure the glucose level in the aqueous humor of the eye as a way to noninvasively sense blood glucose levels. Although these previous polarimetric glucose techniques using a single wavelength have shown good repeatability in vitro and in having submillidegree sensitivity, they lack in vivo sensitivity mainly due to varying birefringence of the cornea caused by motion artifact.^14–17 To date, dual-wavelength polarimetry using a closed-loop approach has been shown to have some success in measuring glucose concentrations in the presence of motion-induced birefringence within a cuvette, in vitro with a plastic eye phantom, and ex vivo with excised New Zealand White (NZW) rabbit corneas.^18–21

In this article, we report, for the first time, the ability to obtain accurate in vivo glucose monitoring results in NZW rabbits using a dual-wavelength polarimetric glucose sensing system that can significantly reduces the noise due to corneal birefringence in the presence of motion.

Research Designs and Methods

Optical polarimetry approach

The polarimetric detection of molecules is based on the fact that the molecule of interest is a chiral molecule, which means it does not have a structural plane of symmetry. All chiral molecules will cause linearly polarized light to rotate upon contact and are known as optically active molecules. Glucose is a chiral molecule, which allows for it to be detected through the use of polarimetry.^26–29 The equation used to describe the rotation of linearly polarized light in the presence of an optically active compound is shown in Eq. 1:

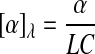(1)

where [α]_λ is the specific rotation of light dependent on wavelength (λ), α is the observed rotation, C is the concentration of the optically active material, and L is the path length of the sample. Using this equation it is possible to determine the concentration of an optically active sample if the path length is known. The concentration of glucose in the anterior chamber of the eye can then be used to determine the blood glucose levels. A correlation between blood and aqueous humor glucose levels has previously been identified, by Cameron et al.,³⁰ with a time delay of less than 5 min.

Dual-wavelength optical polarimeter

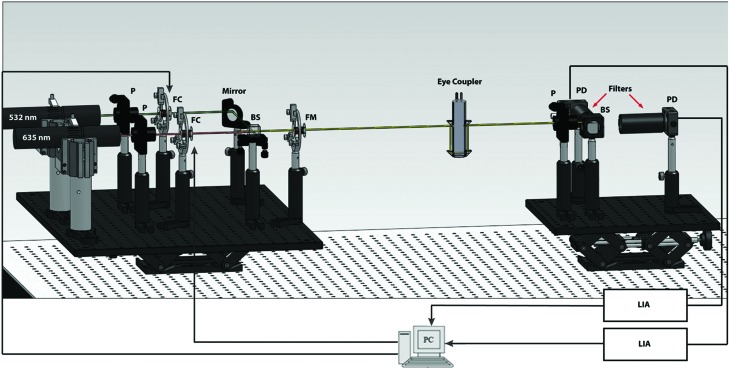
The optical setup is illustrated in Figure 1 in the form of a computer-aided design rendering. The system components are the same as described recently by our group.²¹ In brief, the optical setup consists of two platforms: the source (left) and detection (right) sides with the sample placed in between the two platforms via an eye coupling device. The source side of the system consists of two lasers of different colors (one red and one green), as shown on the left in Figure 1. The light emitted from these two lasers is combined and modulated using a series of electro-optical components. The beam of light is then passed through the sample via the eye coupling device, separated into respective colors, and then collected by the two detectors shown on the collection side of the optical setup. The sample causes the signal at the detector to change, which includes information about both the amount of glucose present in the sample (aqueous humor) and the noise associated with the signal (such as birefringence). The relationship between the noise present in the two respective signals remains constant and, therefore, can be minimized using a multiple linear regression (MLR) analysis of the signals. A MLR analysis is essentially a scaled subtraction of the two signals wherein it removes the common noise and detects the signal variation caused by the change in glucose concentration only.

FIG. 1.

Computer-aided design of the in vivo dual-wavelength polarimetric glucose detection system. Note that the rabbit's eye was coupled to the system via the refractive index matching eye coupling device shown after the Faraday modulator (FM). The two ports on the top of the eye coupling device are used to fill in the device with phosphate-buffered saline solution in order to achieve index matching between the air and cornea. BS, beam-splitter; FC, Faraday compensator; FM, Faraday modulator; LIA, lock-in amplifiers; P, polarizer; PD, photodetector. Color images available online at www.liebertonline.com/dia

More specifically, the optical sources used in the system consists of two laser diodes: a 635 nm wavelength module (Power Technology, Inc., Little Rock, AR) emitting at 7 mW and a 532 nm wavelength diode-pumped solid-state module (Aixiz LLC, Houston, TX) emitting at 10 mW. Glan–Thompson linear polarizers (Newport, Irvine, CA) convert the beams from an unpolarized to horizontally linearly polarized state. The individual beams then pass through respective Faraday rotators that operate as rotational compensators in order to achieve closed-loop feedback control of the system. The Faraday rotators are constructed of inductive solenoid coils with a terbium-gallium-garnet optical crystal rod wrapped within the center. The terbium-gallium-garnet crystals (Deltronic Crystals Inc., Dover, NJ) have a high Verdet constant designed to achieve the desired optical rotation for the magnetic field generated. The Faraday compensation coils are driven by current amplifiers to create a magnetic field required to produce the necessary compensation in optical rotation. The two beams are then overlaid on top of each other using a beam-splitter/combiner (Optosigma Corp., Santa Ana, CA). The combined beam then passes through a Faraday rotator set to modulate at 1.09 kHz with a modulation depth of approximately±1°, which modulates the direction of linear polarization. The combined light beams are then passed through the aqueous humor of an NZW rabbit using a custom-built index matched eye coupling device shown in Figure 1 and shown being coupled to a rabbit in Figure 2. A linear polarizer is positioned perpendicularly to the initial polarizers to act as an analyzer to the optical beam. The beam then passes through a 50/50 beam-splitter. The beams are then separated using bandpass filters at each of the wavelengths (635 nm and 532 nm) before being converted into electronic signals using two PIN photodiodes (Thorlabs, Newton, NJ). The signal from each of the diodes then passes through wide-bandwidth current amplifiers (CVI Melles Griot, Albuquerque, NM). Noise reduction in the output signal from the amplifiers is accomplished through the utilization of lock-in amplifiers (Stanford Research Systems, Sunnyvale, CA) to minimize the noise from outside the frequency band of interest. The lock-in amplifiers then produce DC signals, which serve as inputs to a proportional-integral-derivative controller programmed in LabVIEW version 8.9 (National Instruments, Austin, TX). The outputs of this controller are then passed through a driver circuit, which in turn is used to drive the two compensating Faraday rotators. Real-time response of the system is essential in order to overcome motion artifacts. The respiratory cycle (approximately 1.5 Hz) and the cardiac cycle (approximately 3.4 Hz) are the primary contributors to the motion-induced corneal birefringence artifact in vivo.³¹ To date our current proportional-integral-derivative control feedback mechanism reaches stability in about 100 ms, which is sufficient for analyte detection in the presence of motion artifacts in the eye due to the respiratory and cardiac cycles. As previously reported the dual-wavelength polarimetric system described above can achieve an accuracy of less than 0.4 millidegrees, which corresponds to glucose measurements of less than 10 mg/dL.¹⁸

FIG. 2.

Photograph of the eye coupling device used during in vivo New Zealand White rabbit experiments. The rabbit's eye was coupled to the system via the eye coupling device; the glass test tube was filled with phosphate-buffered saline solution to accomplish refractive index matching. The rabbits were placed in a custom-built rabbit holder to provide comfort and rabbit orientation, which allowed for repeatable positioning of the rabbit to achieve eye coupling. Color images available online at www.liebertonline.com/dia

Theoretical description of overcoming corneal birefringence in the presence of motion using dual-wavelength optical polarimetry

The postprocessing for our current dual-wavelength system starts with the voltage collected on the detectors as depicted in Figure 1 because this voltage is proportional to the glucose concentration for each wavelength. Mathematically, the operation of the single-wavelength system is based on Eq. 2, where θ_m is the depth of the Faraday modulation, ω_m is the modulation frequency, and φ represents the rotation due to the optically active sample. From Equation 2, it is evident that the signal from our single-wavelength polarimeter is based on three terms: a DC term, a fundamental frequency term, and a double frequency term. It is the second, the fundamental frequency term, that contains the glucose information, φ. Without an optically active sample and with the DC term removed, the detected signal only consists of the double modulation frequency (2ω_m) term because the rotation, φ, due to glucose is zero. However, when an optically active sample is present, such as glucose, the detected signal then becomes an asymmetric sinusoid, which contains both the fundamental (ω_m) and the 2ω_m modulation frequency terms. By locking into this fundamental term the signal is proportional to glucose:

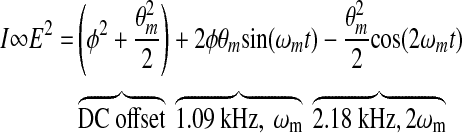(2)

In Eq. 2 it is assumed that the rotation, φ, is due to glucose only, which is valid when there is no motion artifact or Faraday compensation. However, in the dual-wavelength system with an in vivo sample both Faraday compensation and motion artifact exist. In a recent publication,²¹ it has been shown that when birefringence and Faraday compensation are added, for the limited range of motion observed in vivo, it affects the azimuth angle only. Hence, the change in ellipticity of the state of polarization for this case can be ignored, and the signal can be represented as a sum of terms, namely, φ=φ_g, φ_b, and φ_f represent optical rotations due to glucose, corneal birefringence, and the Faraday compensator, respectively. For the dual-wavelength system, the single frequency components for the two signals at the respective photodetectors can be represented as

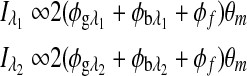(3)

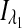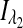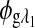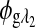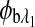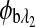where and are the respective detected intensities, and are the respective rotations due to glucose, and and are the respective rotations due to the sample birefringence. The optical rotation due to the Faraday compensator, φ_f, is known so it can be easily removed. The optical retardation for a birefringent sample is a function of both the wavelength and the birefringence |n_o−n_e|. In case of the cornea, the birefringence quantity |n_o−n_e| is known to be constant with wavelength, a behavior attributed to the form birefringence of the cornea.^32–34 However, both the rotation due to glucose and the rotation due to the birefringence are wavelength dependent, but the relationship between 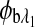and 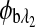is fixed as long as the wavelengths are known (635 nm and 532 nm in the case of our preliminary results). Using the MLR scaled subtraction methodology, the known scaled change in rotation due to the birefringence can be accounted for with respect to wavelength, and, furthermore, MLR can be used to extract the glucose concentration as shown in Eq. 4:

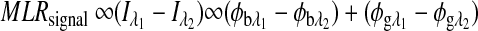(4)

The first term on the right-hand side is a constant, and the second term varies as a function of glucose concentration. Thus, Equation 4 can be represented as:

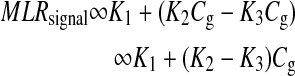(5)

where 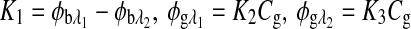, and C_g is the glucose concentration. The MLR analysis accommodates the offset K₁ due to birefringence and normalizes for the slopes K₂ and K₃ as a function of wavelength for a given glucose concentration.²¹

During each in vivo rabbit trial the output voltages from the lock-in amplifiers and compensation voltages required to null the system, for each wavelength, were collected at a sample rate of 5 ms over the duration of the trial via the LabVIEW VI software on the PC shown in Figure 1. The compensation voltage data for each wavelength were then averaged over a minute around the time of each blood draw, and the calculated values were used for both the individual linear regression analysis and the dual-wavelength MLR analysis. A glucose prediction model was created for each individual rabbit trial. The known glucose concentration was determined from the collected blood samples using a YSI 2300 STAT Plus™ biochemistry analyzer (YSI Life Sciences, Yellow Springs, OH) at the time of each study. For the individual regression models, the predicted glucose concentrations were calculated using an equation of the form Glucose_pred=m*[V(t)]+b, where V(t) is the averaged compensation voltage signal for the individual wavelengths and m and b are calibration coefficients calculated by the regression models. The MLR-predicted concentrations for each individual rabbit were determined from models of the form Glucose_pred=m₂*[V₂(t)]+m₁*[V₁(t)]+b, where V₁(t) and V₂(t) are the time-averaged compensation voltages required to null the system for each individual wavelength and b, m₁, and m₂ are calibration coefficients calculated by the MLR model. The predictive measurements used in the individual rabbit trials were calculated without accounting for the time delay associated with the glucose concentration of aqueous humor. Because of the variability in the position of the entrance beam on the cornea between rabbit trials, the regression analyses used for predicting glucose concentration were calculated individually for each rabbit trial. Because of the changes in light coupling between rabbit trials, quantitative real-time glucose measurements were not calculated. Rather, all predicted glucose measurements were calculated retrospectively during postprocessing of the data.

Animal protocol

In total, three NZW rabbits weighing between 2.2 and 3.8 kg were used during the in vivo experiments. Each rabbit was tested three times over a period of 5 months. The rabbits were anesthetized using an intramuscular injection of ketamine, xylazine, acepromazine, and saline solution combination. The combination resulted in a 21-mL cocktail consisting of 42.9 mg/mL ketamine, 8.6 mg/mL xylazine, 1.4 mg/mL acepromazine, and 7.2 mL of saline solution. The cocktail was administered at a dose of 1 mL/1.5 kg of body weight intramuscularly. Once the rabbit was anesthetized it was placed into a custom-built rabbit mold, and the eye coupling mechanism was coupled to the eye as shown in Figure 2. Saline solution was added to the eye coupling device to act as an index matching solution. Data were obtained from the system, and blood was collected from the animal throughout the experiment. Approximately 1 mL of blood was collected every 10 min and placed into a heparin/fluorite (Becton Dickinson, Sparks, MD) blood collection tube to prevent the blood from clotting. After each blood draw a combination of 1 mL of heparin saline was used to flush through the catheter tubing in order to reduce the risk of clotting. The heparin saline syringe and blood collection syringes were connected to a 19–21-gauge SURFLO^® winged infusion set (Terumo, Somerset, NJ) that was inserted into the central auricular artery of the rabbit's left ear for blood collection via a standard-bore three-way stopcock (Baxter^®, Deerfield, IL). Glucose induction was achieved via two methods. Initially, blood glucose was elevated through the use of the xylazine in the anesthetic cocktail. Xylazine has been shown to block the pancreatic insulin release via stimulation of parasympathetic receptors.^35,36 The resulting effect creates a temporary rise in the blood glucose level and also in the aqueous humor of the eye.^35,36 This side effect is beneficial in our particular case because it provided for fairly large changes in glucose without having to induce diabetes in the animal. Blood samples were collected from the rabbits using a 19-gauge needle and syringe every 10 min until the anesthetic began to wear off, at approximately 45 min. A second method to increase glucose levels used bolus injections of 25% glucose solution. The glucose solution was administered using a 22–24-gauge intravenous catheter (Terumo) inserted into one of the marginal ear veins on the rabbit's left ear. After blood collection, the blood glucose was measured using AlphaTRAK™ (Abbott, Abbott Park, IL) and Aviva ACCU-CHEK^® (Roche, Basel, Switzerland) handheld meters along with a YSI 2300 STAT Plus biochemistry analyzer for comparison with the acquired signal. The blood glucose level ranged from 70 mg/dL to an upper limit near 320 mg/dL based on the measurements obtained using the YSI analyzer. Note that most commercially available handheld glucose monitors are made to work within this range of glucose concentrations with target accuracy of within 20% of a laboratory standard measurement.^37,38

Results

The results of the dual-wavelength polarimetric system for determining glucose concentration inside the anterior chamber of the NZW rabbits are shown in Figures 3–5. After a series of initial tests to establish the procedure for blood collection and eye coupling, the experiments were repeated a total of nine times using three NZW rabbits (n=3) across multiple days. For each rabbit trial, data were collected continuously over a period of approximately 45 min, which allowed for maximum change in the glucose concentration due to the anesthesia.^35,36 For analysis of the data, the voltage required to null the compensating Faraday rotators within the system for each of the individual wavelengths was averaged over a 1-min period around the time of the blood collection. The dashed line in Figures 3–5 represents the ideal result where predicted glucose concentration is the same as the actual glucose concentration over the ranges measured in the animal trials.

FIG. 3.

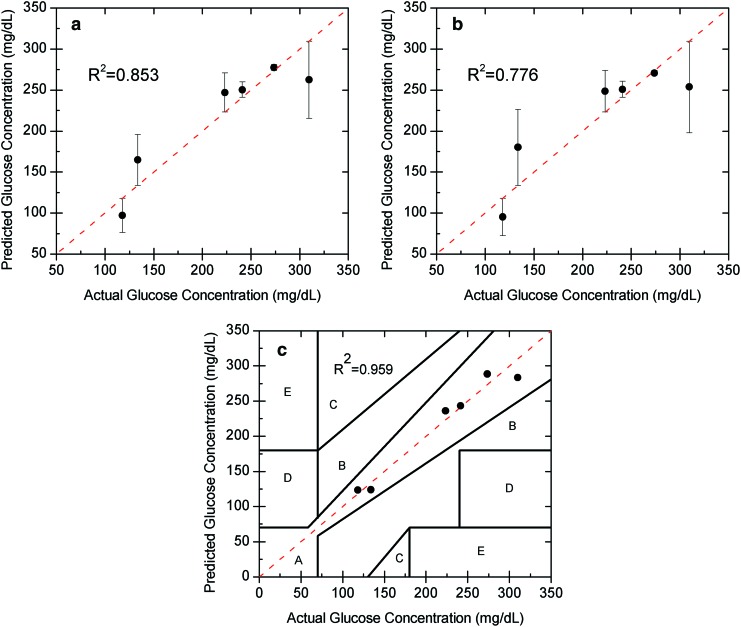
In vivo glucose estimation for a single day using a linear regression model for (a) the individual 532 nm laser, (b) the individual 635 nm laser, and (c) the combined laser wavelengths shown on a Clarke error grid. Note the large error (above 30 mg/dL) and mean absolute relative difference (above 10%) for each of the individual wavelengths because of the motion, due to cardiac cycle and respiration, but that the error and mean absolute relative difference are significantly reduced (20 mg/dL and 5.4%, respectively) relative to the individual wavelength models when both wavelengths are used. Color images available online at www.liebertonline.com/dia

FIG. 5.

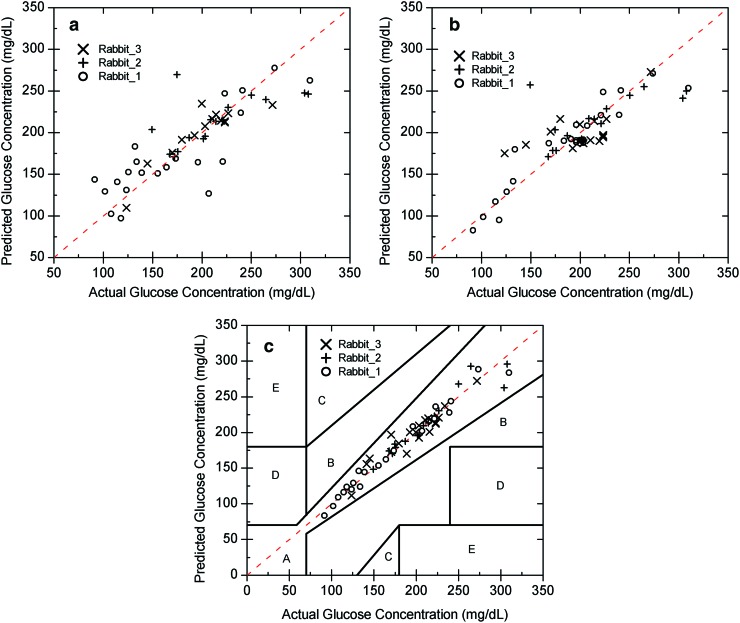
In vivo glucose prediction within rabbits across multiple days using the linear regression model for the individual wavelengths (a) 532 nm and (b) 635 nm as well as the (c) dual-wavelength data using multiple linear regression shown on a Clarke error grid. Note the large errors within each rabbit (20–35 mg/dL) for each single wavelength because of the motion but that the error is reduced (9–14 mg/dL) relative to the single-wavelength models when both wavelengths are used. Color images available online at www.liebertonline.com/dia

Results within a rabbit on a single day

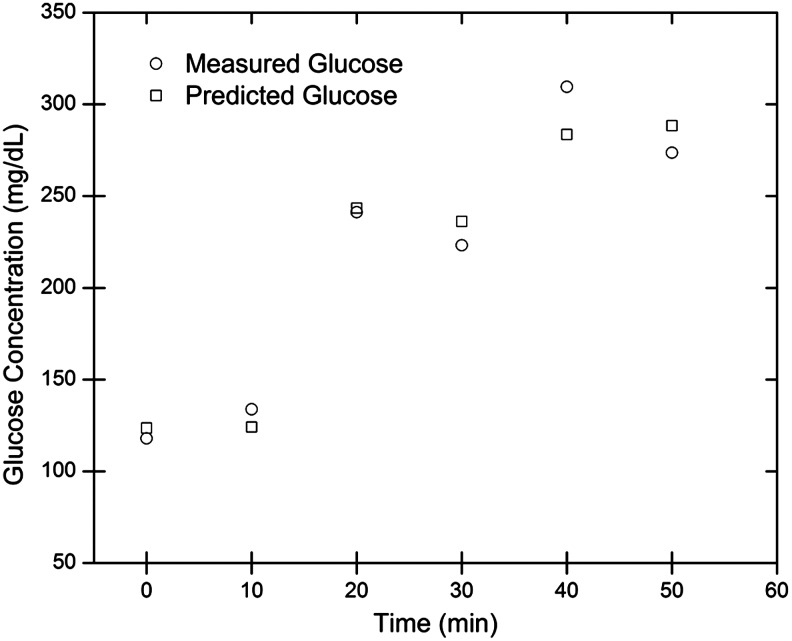
The individual glucose predictions are depicted in Figure 3a and 3b for one rabbit on a single day for the 532 nm (left) and 635 nm (right) wavelengths using a standard linear regression analysis. As shown the mean absolute relative difference (MARD) within a rabbit on a single day was calculated to be 12% (32.7 mg/dL SE) and 14.7% (40.4 mg/dL SE) at the respective wavelengths. In addition, the correlation coefficients for the 532 nm and 635 nm wavelength data were 0.853 and 0.776, respectively, using a linear regression approach. As shown, the single-wavelength data are unable to accurately predict the glucose concentration in vivo in the presence of birefringence with motion. Although the data from each wavelength had large errors, those errors showed a trend with each other (i.e., common mode noise at each wavelength due to motion), and thus, by using the two wavelengths with an MLR model, the accuracy improved tremendously to a MARD of 5.4% (19.9 mg/dL SE). In addition, the data were more linear with a correlation coefficient of 0.959 and, when plotted on a Clarke error grid, showed 100% in Zones A+B as depicted in Figure 3c. The time profile for the predicted glucose concentration and measured glucose concentration of an individual rabbit trial is depicted in Figure 4.

FIG. 4.

In vivo time profile of measured and predicted glucose concentrations for an individual rabbit trial.

Results within each rabbit across multiple days

The results within a rabbit (n=3) across 3 days are shown in Figure 5 for Rabbit 1, Rabbit 2, and Rabbit 3. For this comparison the regression models were again formed using the data collected for each individual trial separately, and then the overall SE in estimation was calculated for the individual rabbits (n=3). Rabbit 1 resulted in MARDs of 16.95% and 8.53% (33.08 mg/dL and 22.06 mg/dL SEs) for the individual wavelength regression models of the 532 nm and 635 nm wavelengths, respectively. Using dual wavelengths and the MLR analysis provided a MARD of 4.08% (9.35 mg/dL SE). The MARDs for Rabbit 2 were 10.32% and 10.47% (35.26 mg/dL and 35.78 mg/dL SEs) for the respective 532 nm and 635 nm individual wavelength models. The dual-wavelength MLR model resulted in a reduction in the MARD to 3.58% (14.14 mg/dL SE). For Rabbit 3, the MARDs using individual 532 nm and 635 nm wavelengths were 8.50% and 11.73%, respectively (20.58 mg/dL and 25.31 mg/dL SEs). The dual-wavelength MLR approach for Rabbit 3 resulted in a reduction of the MARD to 5.13% (11.34 mg/dL SE), which is at the accuracy limit of the system. Note that when the dual-wavelength data in Figure 5c were placed on a Clarke error grid, 100% of the data were within Zones A+B for all three rabbits (Rabbit 1, Rabbit 2, and Rabbit 3) across days. All three rabbits showed 100% of data within Zone A.

Results for all three rabbits across multiple days

The linear regression analyses for the individual 532 nm and 635 nm wavelengths for all nine trials are represented in Figure 5a and b, respectively. The MARDs for the 532 nm and 635 nm single-wavelength models were calculated to be 12.05% and 10.47% (29.87 mg/dL and 27.34 mg/dL SEs), respectively, over all trials. Using individual dual-wavelength MLR analysis for each trial and then comparing MARD across all the trials produced a MARD of 4.49% (11.66 mg/dL SE) as depicted in Figure 5c. As shown in Figure 5a and b the individual wavelength linear regression models appear to once again present a poor prediction model around the actual glucose measurement line as shown by the dashed line. The MLR analysis for all nine studies is illustrated in Figure 5c. The data demonstrate that dual-wavelength polarimetry can effectively predict glucose concentrations within the aqueous humor in the presence of motion-induced corneal birefringence given the position of the beam remains relatively the same. In Figure 5c, it is clear that the combined MLR analysis provides a much tighter grouping of predicted glucose concentrations with respect to the actual glucose concentrations over the entire rabbit study with an MARD of 4.49% (11.66 mg/dL SE). In addition, as depicted in Figure 5c, when plotted on a Clarke error grid, 100% of the points were in Zones A+B with 100% of the hits falling in Zone A.

Conclusions

In summary, we have presented, for the first time, that dual-wavelength polarimetry can be used in vivo with NZW rabbits to significantly reduce the noise due to corneal birefringence in the presence of motion and provide accurate glucose concentration predictions. The results show MARDs with the dual-wavelength system of less than 4.49% across animals and across days and that we can plot the data on a Clarke error grid and obtain 100% within Zones A+B, which is within the range of current commercial glucose meters. Although the results presented show that dual-wavelength polarimetry has the ability to measure glucose concentration within the aqueous humor in the presence of motion-induced time-varying birefringence, there are still limitations to this optical approach that will need to be overcome prior to use in preclinical trials. One limitation in the in vivo data presented was that, although the prediction analysis could be done across animals and across days, it required that within-individual trial calibrations be done due to changes in the location of the entrance and exit beam on the cornea across days. Thus, the results are not based on a universal calibration because the current eye coupling device does not allow a means to determine beam entrance location on the cornea, which imposes offset constraints within and across rabbits. Future work will focus on the development of a better coupling system to allow for the creation of a universal calibration model that works at least within a subject across days and possibly across subjects over several days. Further work will focus on developing an algorithm for quantitative real-time glucose measurements as opposed to the retrospective calibrations used in this study. In addition, animals induced with diabetes will be used to enable larger dynamic glucose ranges from 50 to 600 mg/dL.

Acknowledgments

This work was supported by grant RO1 DK076772 from the National Institutes of Health. The authors would like to thank Tony Akl, Ph.D. student in the Optical Biosensing Laboratory, for his technical assistance and helpful discussions and Dr. Mike McShane, Associate Professor of Biomedical Engineering at Texas A&M University, for the use of his YSI biochemistry analyzer.

Author Disclosure Statement

No competing financial interests exist. C.W.P. and B.H.M. built the optical system, performed the experiments, and analyzed the data. G.L.C. conceived the project, designed the instrumentation, and contributed to discussion of experiments and data processing. V.C.G. contributed to the animal model and contributed to the discussion of animal studies. C.W.P. wrote the manuscript. G.L.C., V.C.G., and B.H.M. reviewed/edited the manuscript.