Abstract
With the advance of modern radiation therapy technique, radiation dose conformation and dose distribution have improved dramatically. However, the progress does not completely fulfill the goal of cancer treatment such as improved local control or survival. The discordances with the clinical results are from the biophysical nature of photon, which is the main source of radiation therapy in current field, with the lower linear energy transfer to the target. As part of a natural progression, there recently has been a resurgence of interest in particle therapy, specifically using heavy charged particles, because these kinds of radiations serve theoretical advantages in both biological and physical aspects. The Korean government is to set up a heavy charged particle facility in Korea Institute of Radiological & Medical Sciences. This review introduces some of the elementary physics of the various particles for the sake of Korean radiation oncologists' interest.
Keywords: Proton, Neutron, Carbon ion, Particle therapy
Introduction
The modern radiation therapy has evolved to the state-of-the-art with the advances in imaging and dose conformation techniques. Over the past decades, those techniques have yielded substantially improved local control and survival of the cancer patients. However, the improvement in the benefits of radiation therapy mostly comes from the dose conformation of photons, which are main source of radiation therapy currently in use rather than radiobiological effectiveness. It now appears that such technology may be approaching a ceiling because of the inherent limitation of the photon. The next step in this natural evolution might be the use of particles rather than photons which have higher RBE. Among the particles, protons are currently being most intensely investigated. By the time of July 2010, five heavy ion therapy centers (three in Japan, two in Germany) and 29 proton therapy centers are operating worldwide [1]. Also, 23 proton or carbon therapy centers are under construction [2]. Until the end of 2009, 78,275 patients were treated with hadron therapy. Most of them were treated with proton (67,097), followed by carbon (7,151), helium (2,054), pion (1,100) and other ions (873) [3].
In Korea, one proton therapy facility is currently operating in National Cancer Center. And a carbon beam facility is under process by Korea Institute of Radiological & Medical Sciences (KIRAMS). But still, many of the radiation oncologists in Korea are not interested in the particle therapy, which have vast potential for the intractable radioresistant tumors. Thus, a basic understanding of the surging technology and in depth knowledge of the clinical benefits is needed. The authors are trying to review the issues into three categories; physics, biology, and clinical field with the intent to bring the particle therapy close to Korean Radiation Oncologists' Society.
Basic Particles in Therapy
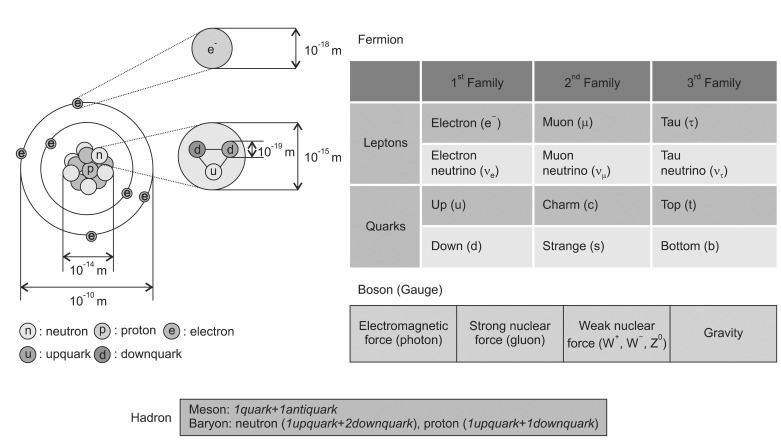
The term radiation applies to the emission and propagation of energy through space or a material medium, whereas the particle radiation means the energy propagated by traveling corpuscles that have a definite rest mass and a definite momentum [4]. To explain the relationship of these particles, the Standard Model of fundamental particles is suggested. It may not be a complete theory, but it serves important theoretical and experimental advances. The model explains a theory concerning the electromagnetic, weak, and strong nuclear interactions which mediate the dynamics of the known subatomic particles. In the Standard Model, the elements of the atom are classified into fermions and bosons (Fig. 1). The fermions are considered to be the constituents of matter while bosons are the force carriers the transmit interactions. The former is characterized by spin in odd half-integer quantum units of the angular momentum (1/2, 3/2, 5/2) while the latter has a spin of an integer number (0, 1, 2) [4]. There are two types of elementary fermions: quarks and leptons. The Standard Model distinguishes twenty four different fermions: six quarks and six leptons, each with a corresponding antiparticle. The antiparticles have the same mass as its particle but opposite charge. The fermions are classified into three generations. Between the generations (or families), they differ only by their mass, and all interactions and quantum numbers are identical. There are two classes of leptons exist: charged leptons (also known as the electron-like leptons) and neutral leptons (known as neutrinos better). The most well-known lepton is the electron.
Fig. 1.
Standard Model of particles. Hadron is particles composed of quarks; meson has two quarks (quark and antiquark) and baryon has three quarks (up and down quarks).
The observed elementary bosons, named after physicist S. N. Bose, are all gauge bosons: photons, W and Z bosons, and gluons which are mediating electromagnetism, the strong nuclear force, the weak nuclear force and the gravity possibly. The Higgs boson is a hypothetical massive elementary particle which is not discovered yet. The words hadron comes from the Greek word hadrós (stout, thick), leptons from leptos (fine, small, thin), baryons from barys (heavy) and meson from mesos (intermediate) respectively. A hadron is a particle made of quarks held together by the strong force which is categorized into two families: baryons (made of three quarks, spin 1/2) and mesons (made of one quark and antiquark, spin 0). The protons and neutrons, which are both baryon and hadron, lumped together as 'nucleons' to compose atomic nuclei. A proton is made up of two up-quarks and one down-quark so that their charges are +2/3, +2/3 and -1/3 to make total +1. A neutron is made up of one up-quark and two down-quarks which are +2/3, -1/3, -1/3 to make total charge 0. The best-known mesons are the pion and the kaon, but a great number of them are continued to be discovered. Leptons also constitute matter. However, an electron, a representative lepton, is a light particle so that it is not discussed in the 'particle therapy' categories.
In general, the term particle therapy is a collective word to indicate the hadron and the heavy particle therapy. A charged particle therapy is used to cover the both proton therapy and heavy ion therapy (note that neutron is not charged). By the definition, a charged particle is called as 'heavy' if its rest mass is larger compared to the rest mass of the electron. The muons (M = 207 me), pions (M = 270 me), kaons (M = 967 me), protons (M = 1,836 me), alpha particles, deuterons, tritons, fission fragments, and other heavy ions are all heavy-charged particles. However, the terms of light and heavy particles are sometimes used differently in radiation biology, which is the heavy particles are referred to the particles heavier than α particle [5]. Such a concept of the term 'heavy' in radiation therapy is not defined by physical unit. In this article, we restricted the term heavy charged particle to the charged particles with masses heavier than protons. Other word to describe the heavy ion is HZE particles' (high atomic number 'Z' and energy 'E').
Protons have advantages with excellent depth-dose distributions but have similar RBEs with photons. Neutrons have no dose distribution advantage over photons but are likely to have very high RBEs. The heavy ions have better dose distribution and higher RBEs than photons. However, the biological effectiveness depends on the type of particles. For example, the Argon ions have a high LET and RBE. Since they would break up so readily in practice, the only limited penetration can be obtained [5]. Currently, particles heavier than carbon are not well investigated for clinical purpose because a tail in dose distribution downstream of the Bragg peak increases with Z which may increase a dose to normal tissues [6].
Interactions of Particles with Matter
Particles can only interact if the total charges and quantum numbers are conserved. A simple notation is used to describe an interaction. If a neutron n impinges on a target nucleus T, forming a resultant nucleus R and the release of an outgoing particle g, this interaction is shown as T(n,g)R. Only the portion in parentheses is used in the interaction which does not involve nucleus: (n,n) - elastic scattering; (n,γ) - radiative capture; (n,n') - inelastic scattering; (n,p), (n,α) and etc. - charged particle emission; and (n,f) - fission. For example, an nuclear capture reaction (n,nγ) of 238U can be described as follow:
![]()
However the modes of interaction in the matter are quite different so that the dosimetric characteristics are unique along with the particles. Protons and heavy charged particles have a characteristic build-up region whereas the neutrons' depth dose profile is similar to the photons. Furthermore, the modes of energy transfer according to the particles are quite different from their interactions with the target. The complexity of particle beams renders these treatments cost a great expense. Considering that the cost of the proton therapy was found to be 2.4 folds higher than of the photons [7], the cost of heavy particle therapies must be greater.
1. Interactions of neutron
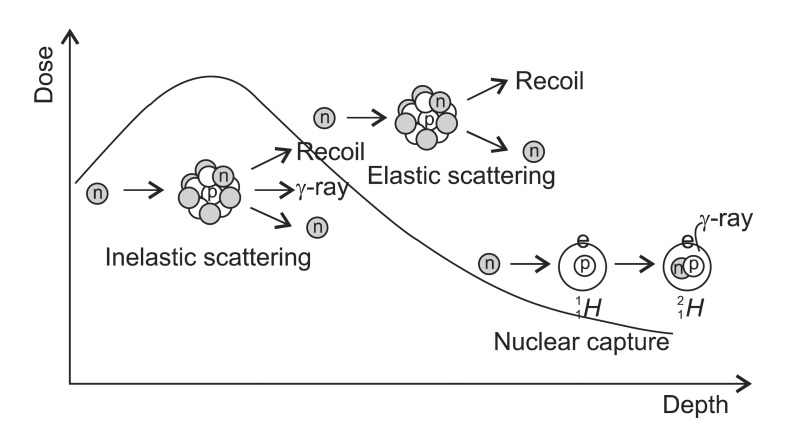
The neutron has a mass of 1.675 × 10-27 kg and a half-life of 885.7 ± 0.8 second with no charge. Since a neutron has no charge and does not interact with orbital electrons, it can easily pass through the target nucleus to cause various reactions. However, not all the possible reactions contribute to the dose distribution equally. The degree of importance of the reactions depends on the target nucleus and the energy of neutron. The hydrogen, carbon, oxygen and nitrogen atoms which compose the most of human soft tissue (H,10.5%; C, 22.6%; O, 63.7%; N, 2.34%) interact differently with neutron [8]. For instance, the elastic collision is related to the atomic weight, and thus hydrogen does not have elastic scattering interaction. Therefore, with the higher hydrogen content, the dose absorbed in fat exposed to a neutron beam is about 20% higher than in muscle, because the dose deposited in tissue from a high energy neutron beam is contributed predominantly by recoil process [4]. The neutron beam is divided into three categories by energy: below 0.5 eV as thermal neutrons, above 0.5 eV up to 10 keV as intermediate and above 10 keV as fast neutrons. Low energy neutron results neutron capture interactions to cause γ-rays while high energy neutron interacts elastic scattering in the matter. In a dosimetrical aspect, the dose in the human body is dominated by the contribution of recoil protons resulted from elastic scattering of hydrogen nuclei above 10 keV below which γ-rays resulted from thermal neutron capture interaction dominates.
1) Elastic scattering (n,n): Elastic scattering occurs when a neutron strikes a nucleus and rebounds elastically (Fig. 2). The amount of kinetic energy transferred depends upon the angle of impact and hence the direction of motion of the neutron and nucleus after the collision. When a neutron hits a nucleus, it may rebound completely or bounce off in different directions. In the former interaction, the kinetic energy is conserved completely. In the latter interaction, the large amount of kinetic energy is transferred to the nucleus so that the recoiling nucleus becomes ion pairs to lose energy through the excitation and ionization. This interaction is important at lower energy region up to 10 MeV and not effective above 150 MeV. The fast neutrons are thermalized by elastic scattering interactions. The elastic scattering interaction is related closely with the atomic weight of the target. The relationship of a neutron mass 1 with the initial kinetic energy E0 hits a nucleus mass A to the final kinetic energy E1 is: [(A - 1)/(A + 1)] ≤ (E1/E0) ≤ 1. When a neutron hits the nucleus of hydrogen (A = 1), the energy spectrum of scattering neutron varies from 0 to E0 whereas the spectrum varies from 0.176E0 to E0 if it hits the carbon. In average, the kinetic energy of a neutron E encountering a nucleus of atomic weight A, the energy loss is 2EA/(A + 1)2. Thus to reduce the energy of neutrons with the fewest number of elastic collisions target nuclei with small A should be used. For example, to reach to the thermal equilibrium (0.025 eV: most probable energy for neutrons at 293°K), hydrogen atom needs only 18 collisions whereas carbon atom needs 110 collisions.
Fig. 2.
Interaction of neutrons. Elastic scattering: a neutron hits nucleus and bounce off in a different direction. Target nucleus gains energy from neutron and then increases speed. Inelastic scattering: a neutron hits a nucleus and is temporarily absorbed, forming a compound nucleus. An excited nucleus de-excites by emitting another neutron of lower energy and γ-ray. Nuclear capture: This is the most common nuclear reaction. The product nucleus becomes an isotope with increased mass. The interaction emits only γ-ray (no particles are emitted).
2) Inelastic scattering (n,n'): The interactions of fast neutrons of the therapeutic range energy are dominated by this interaction, which in turn causes the emission of photons, neutrons, and charged particles [4]. Non-elastic scattering differs from inelastic scattering by only that the secondary particles are not neutrons (e.g., 12C(n,α)9Be Eγ = 1.75 MeV). A neutron may strike a nucleus and be absorbed momentarily, which is forming an excited state nucleus releasing radiation eventually. When a neutron hits and enters into a nucleus, the nucleus is excited into an unstable condition. After then, the excited nucleus returns to the stable state by emitting γ-ray (e.g., 14N(n,n')14N Eγγ = ~10 MeV). Thus, the average energy loss depends on the energy levels within the nucleus. If all the excited states of the nucleus are too high, inelastic scattering does not occur so that this interaction happens only when high energy neutrons interact with heavy nuclei. For the hydrogen, its nucleus does not have the excited state thus only elastic scattering happens. A variety of emissions, however, may follow if the energy of neutron and the atomic mass are high enough. If more than one neutron is emitted, nuclear fission will occur.
![]()
3) Neutron capture (n,γ): The neutron may be captured by the nucleus of absorbing matter, and only the absorbing atom emits γ-ray. The interaction is the same as nonelastic scatter, but this occurs only at the low energy levels. This process leads to disappearance of neutron. The result of this interaction is an isotope of the same element as the original nucleus with the increased mass number. The probability of this interaction is inversely proportional to the energy of the neutron. The scattered neutron lost its energy is captured by a specific nucleus so that the probability is called as "Capture Cross Section." The probability of a specific nucleus capture is differed from target nucleus and its energy. It varies from almost 0 for 4He, 0.0035 for 12C, 0.33 for 1H, and 1.70 for 14N Barns (10-28 m2). The neutron capture interaction accounts for a significant fraction of the energy transferred to tissue by neutrons in the low energy ranges (e.g., 1H(n,γ)2H Q = 2.2 MeV Eγ = 2.2 MeV and 14N(n,p)14C Q = 0.626 MeV Ep = 0.58 MeV). The hydrogen capture reaction is the major contributor to dose in the tissue from thermal neutrons.
2. Interactions of proton
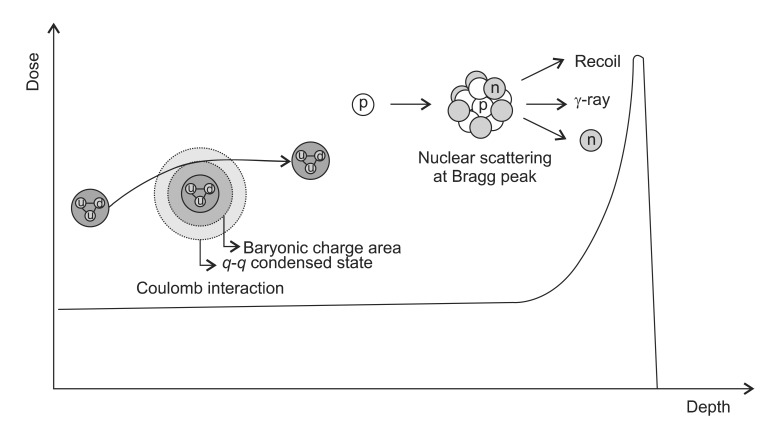
The proton has a mass of 1.67-27 kg with a positive charge having a half-life of 1035 years. The advantage of proton beam over the photon comes from the both of the high energy and low energy interactions. For the protons with a higher energy, the several processes of energy transfer such as direct inelastic collisions by proton, inelastic collisions by delta rays, and elastic and non-elastic nuclear reactions may occur. The secondary particles are also important, because they can be scattered to a considerable range. By these interactions, it shows characteristic depth dose curve of low dose at the entry region and high dose at a specific depth. Unlike photons or neutron, it has a short build up region followed by a maximum energy deposition region near the end (the Bragg peak). As they move through target material, they interact by electronic or nuclear reaction. The electronic interactions are ionization and excitation of atomic electrons whereas the nuclear reaction interactions are Coulomb scattering, elastic collision and non-elastic nuclear collision.
1) Coulomb scattering: At the entry region, the primary protons lose their energy mainly by Coulomb interactions with the outer shell electrons to cause excitation or ionization (Fig. 3). Inelastic collision may occur without loss of energy in this region. But the energy loss per interaction is small so that there is no significant deflection of proton at this area. The range of secondary electrons is less than 1 mm and the most of the dose is absorbed locally. As the protons travel through tissue, the energy get lowered so that the number of ionization events rapidly increases and reaching its apex known as a Bragg peak. Shortly after the Bragg peak, the number of ionizations quickly diminishes to zero. The energy loss of the proton beam is constantly related with the elementary component of the body which is known as the ping power. It depends on the charge and velocity of the projectile charged particles and the atomic number and electron density of the target material according to the simplified Bethe formula:
Fig. 3.
Interaction of protons. The Coulomb interaction slows the velocity of protons before Bragg peak. As the stopping power increases, the energy of proton lowers at the Bragg peak where the proton interacts with nucleus to emit secondary neutron and γ-rays.
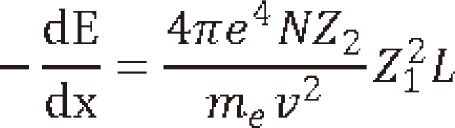
Where N is the target density, Z2,, me, v, Z1, and L are referred as target atomic number, the electron the mass, the velocity, the charge and the stopping function. As the energy lowers, the velocity lowers to 0, causing a peak (the Bragg peak) to occur. The width of peak depends on range straggling in medium and initial energy spectrum while the peak to plateau ratio depends on the width of energy spectrum. However, the Bethe-Bloch model becomes invalid at the low energies (<10 MeV/A).
Usually, the values of stopping powers are obtained from experiments and simulations and are similar to cross-sections in the sense that they are natural properties of the materials [9]. The stopping powers for various materials are given in International Commission on Radiation Units and Measurements report 49 [10]. Mass stopping power is energy loss per unit path length in g/cm2. Therefore, the low atomic number (Z) materials have the greater mass stopping power than high-Z materials. For example, the stopping power for a 1 MeV proton is 25.4 MeV/kg/m2 in water and 6.39 MeV/kg/m2 in lead. High Z materials scatter the proton at a larger angle without much energy loss so that those materials are used to spread out the beam.
2) Non-elastic scattering (p,d,p',n,γ): Non-elastic interactions with protons occur at higher energies and produce secondary particles which usually stop in the vicinity of the interaction and have a relatively high biological effectiveness. Primary protons are lost in non-elastic nuclear interactions. The contributions to the absorbed dose by non-elastic scattering are about 5% in 100 MeV, 10% in 150 MeV, and 20% in 250 MeV [11]. With 250 MeV energy, about 20% of the incident protons show a non-elastic nuclear interaction with the target nuclei to generate charged particles such as proton (p,p), deuteron (p,d), alpha particles (p,α) or recoil protons (p,p'). These secondary products are absorbed locally. The interaction may generate non-charged particle such as neutron (p,n) or γ-rays (p,γ) (i.g., 12C(p,γ)13N). These non-charged particles can pass a relatively longer ranged to be absorbed by surroundings (Fig. 3). Numerous neutrons are produced by nuclear interaction of protons, thus the neutron induced interactions should be examined in detail for the actual proton therapy. Behind the distal endpoint of the Bragg peak, the absorbed dose by the n-secondary particles due to neutrons went up to about 70-80% of the total absorbed dose, the contributions to which were the n-secondary protons produced by the (n,p) reaction and the n-secondary alpha particles (n,α). Therefore, though the dose contribution of low energy protons less than a few hundred keV is about 5%, the biological implications of this interaction are not that simple. The endpoint processes transfer electrons mainly through ionization collisions to generate many ions and radicals.
3) Electron exchange: As the proton slows down, it causes increased interaction with orbital electrons to make maximum interaction at the end of range. Finally, at the end of interactions, the energy is lowered below the proton's stopping power so that they exchange electrons with hydrogen atoms of the target. This is called charge-changing process [12,13]. Both electron capture process p + H2O → H + H2O+ and electron loss process H + H2O → p+e- + H2O occur. The ions and radicals induce biological damage in the bio-cells effectively despite of the slight dose contribution [14]. These electrons can move only a few micrometers at the most, which is almost the same scale as a chromosome in the cell nucleus [14]. The advantage of low energy proton beams are from the spatial distribution of ions and radicals which may form clusters and attack bio-molecules such as DNA [15]. Thus, the RBE increases in a depth beyond the endpoint of the Bragg peak [16]. Matsuzaki et al. [14] reported that the effective dose for each secondary particle by multiplying the absorbed dose by the factor, and the ratio of the effective dose was found to be increased to 20:140:180 for electrons, protons and alpha particles, respectively. According to the radiation weighting factors defined in the International Commission on Radiological Protection (ICRP) 2007 recommendation [17], these factors for electrons, protons, and alpha particles are 1, 2, and 20, respectively. This result suggests that the proton dosimetry beyond the Bragg peak is difficult to evaluate accurately.
3. Interactions of heavy charged particles
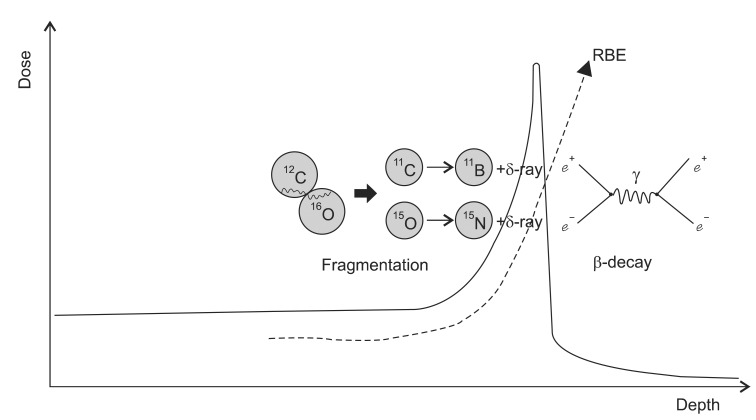
1) Electron collision: Though the charged particles are still losing their energy by the interactions with atomic electrons at the entry region, the angular and energy straggling is much lower than protons as the heavy particles have much larger mass [18]. In the energy interval of therapeutic interest, heavy charged particles show diverse interactions from pure fragmentation at high energy levels to Rutherford scattering and inelastic scattering interactions in low energy levels depending on the nuclear structure of target matter (Fig. 4). Except at low velocities, the heavy charged particles lose a negligible amount of energy in nuclear collisions. Also, heavy charged particles colliding with electrons will lose only a small fraction of their energy per collision (usually about 25 eV, but on the average 100 eV and at most >> 4 mE/M) [19]. Thus, the heavy particles have much larger relative dose in the Bragg peak and small lateral scattering than protons and they offer an improved dose conformation as compared with photon and proton beam. Another characteristic of heavy charged particle beam is that by the lower-charge fragments, they produce considerable dose tails after the Bragg peak.
Fig. 4.
Interaction of carbon. Carbon hits oxygen and both atoms are fragmented into boron and nitrogen generating delta radiation. The delta radiations decay to emit gamma radiation which can be used as the source of PET-CT in treatment field. Due to locally absorbed radiation around and after the Bragg peak, relative biological effectiveness (RBE) increases abruptly.
2) Nuclear collision: Nuclear interactions of heavy particles are occurred by either gazing or head-on collisions. Unlike gazing collisions, the head-on collisions occurs less frequently but these interactions transfer large energy to cause projectile breaks into many small pieces, and no high-velocity fragment survives. Heavy ions having gazing interactions with nuclei may result in fragmentation of the incident ions or target nucleus. The resultant charged fragments of the target nuclei that interpenetrate undergo significant interactions. In the interaction, evaporated nucleons (changing the characteristics of the nucleons) and light clusters are produced. The importance of the fragments depends upon how it affects the absorbed dose distribution in linear energy transfer (LET) which in turn depends upon the nature of the medium, ion type and its energy [20]. Further, these effects increase as a function of the beam energy. For example, for a 12C beam at 200 MeV/n about 30% of the primary carbon ions are involved in nuclear reactions and do not reach the Bragg maximum at about 8.6 cm depth in water, whereas at 400 MeV/n only the 30% of the primary particles reach the Bragg peak at about 27.5 cm depth in water since 70% of 12C are absorbed by nuclear reactions [21]. The interactions may serve advantages for the therapy verification with the similar mechanisms as positron emission tomography (PET) imaging. Verification of dose delivery to the tumor is possible by taking advantage of the property of positrons in producing 511 keV annihilation gamma photons [22,23]. These isotopes travel almost the same velocity as the main beam and stop in almost the same place and they emit gamma rays to be detected in a conventional PET scanner. As a consequence the location of the spread out Bragg peak and therefore the high dose treatment volume is visualized [24]. The production yield of some positron emitter nuclide such as 11C and 10C has been studied using GEANT4 (GEometry ANd Tracking-4) computer code [25]. The secondary positron emission is exploited for visualizing the dose distribution during irradiation in hadron therapy and consequently allowing a safer irradiation of the tumor volume by supplying sufficient quality for monitoring in head and neck cancer treatments [26].
3) Nuclear fusion: While the fragments lighter than 12C, such as for example 11B, are mainly produced by projectile and target fragmentation, the occurrence of fragments heavier than 12C is also very significant because they are found in a considerable amount with rather low energies which may contribute to the increase of the RBE of the carbon beam (Fig. 5) [21]. The interactions such as complete fusion and/or break-up fusion produce these fragments as evaporation residues. For example, at the low energy threshold of about 5 MeV/n, a complete fusion interaction of 12C + 12C → 24Mg may occur. As a result, many radioactive and stable isotopes may be produced in interaction between heavy ion beam and the elements of soft tissues [27]. In a calculation model for the carbon therapy, the 12C interact with the elements 16O, 12C, 14N and 1H, which are the most abundant nucleus in fat and muscle tissue, produce isotopes such as: 12C + 12C → 6Li + 18F, 12C + 12C → 5Li + 19F, 12C + 12C → 4Li + 20F, 12C + 14N → 24Na + (α,d, p), and 12C + 16O → 24Na + (α,d, p). The 18F and 24Na have a half-life of 110 minutes and 15 hours respectively. Thus it is inferred that after carbon ion therapy the patient must be quarantined [27]. Still, thorough studies of the nuclear interactions of the heavy particles in the therapeutic energy range are needed before their clinical applications.
Fig. 5.
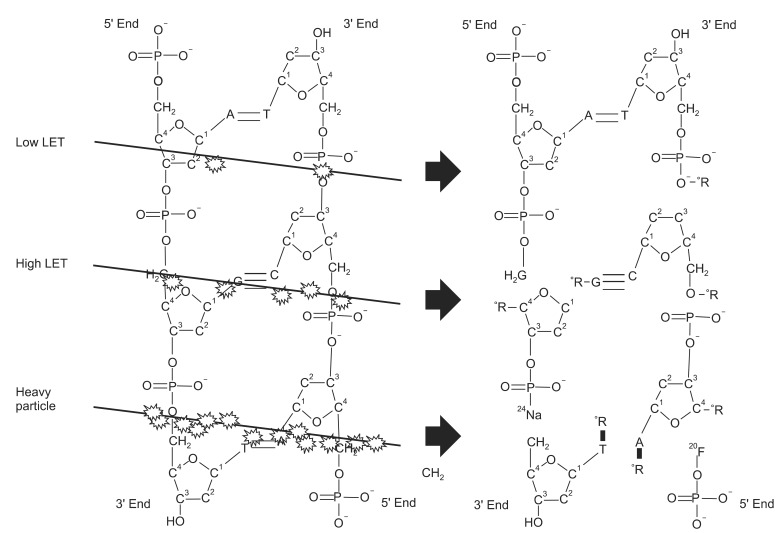
Interactions of low linear energy transfer (LET), high LET and heavy particles with DNA. The low LET radiation generates radicals to cause single strand break while the high LET radiation causes multiple lesions to cause double strand break. During the heavy particle interactions, the fragmentation of elements atoms occur resulting isotopes (e.g., 12C + 12C → 4Li + 20F and 12C + 16O → 24Na + (α , d, p)). (The base image of DNA structure is from Wikimedia Commons. Permission is granted to copy under the terms of the GNU Free Documentation License).
LET and RBE of Charged Particles
LET is the function of the energy loss per unit distance (dE/dx) as an ionizing radiation travels through the matter, and it correlates with RBE. It is similar to the stopping power except that it does not include the effects of radiative energy loss (i.e., Bremsstrahlung or delta-rays). The LET below 10 keVµm-1 is regarded as low LET radiation while above 10 keVµm-1 is high LET radiation. Typical LET values for the radiations are; 250 kVp X rays 2 keV/µ m, Cobalt-60 γ-rays 0.3 keV/µ m, 3 MeV X rays 0.3 keV/µ m, 1 MeV electrons 0.25 keV/µ m, 14 MeV neutrons 12 keV/µ m, 1 keV electrons 12.3 keV/µ m, and 10 keV electrons 2.3 keV/µ m. The LET values of heavy charged particle beams reach up to few hundred keV/µ m. When Zirkle and Tobias [28] introduced the term LET, it was regarded to be a universal parameter for radiobiological effects. The relative RBE, which is the dose of a reference radiation to achieve the same biological effect of photon, shows dependency on LET. The relation between LET and RBE indicates that an optimum value for RBE occurs at 100 keV/um for LET [24]. It is well known that the high LET radiation has definite biological differences from low LET radiation. The high LET radiations show less dose fractionation effect for they have higher α/β ratios than low LET radiation. Of the note, the LET is a macroscopic physical parameter that cannot be directly translated to the biological effectiveness. Therefore, different ions of the same LET may have different RBE because the track diameter and ion density are not in proportion to LET. For example, 10Ne, 18Ar and 26Fe have same LET around 800 keVµ-1 [29]. And the RBE-LET relationship depends on the type of radiation, dose fractionation, and biologic endpoint. In a recent report, RBE for charged particles has calculated utilizing initial slopes of V79 Chinese hamster cell line survival curves. Plots between RBE and Zeff (effective charge) for 2H and 3He particles indicated that two different RBE peaks were observed from 2H and 3He particles at 10 and 83, and these values correspondences for LET values of 7 keVµ-1 and 55 keVµ-1 [30]. The results indicate that the amount of energy deposited in biological entities is not appropriate measure of the effectiveness of charged particle especially at lower dose region. Thus, the relationship of the LET and RBE of the particles must be considered separately according to the particles.
1. Proton
Protons are regarded as having slightly higher relative biological effectiveness (RBE) than photons. The generic RBE of proton in current radiation therapy is 1.1, which is based on the use of a single RBE value [16]. The generic RBE cannot be the true RBE for each treatment because the variability of RBE in clinical situations is believed to be within 10-20% [31,32]. Further, the generic RBE is not considering various physical and biological properties such as energy, fractional dose or particular tissues. As mentioned above, the RBE is certainly higher than 1.1 at the area distal to the Bragg peak [16,33]. In this part of the depth-dose curve, the average proton energy decreases rapidly, leading to an increased LET. Recently, Grassberger et al. [34]. have shown that the LET distributions in actual patients undergoing proton therapy significantly differs from analytical techniques when they include secondary particles into account. In their report, passive scattering and three-dimensional intensity-modulated proton therapy (3D-IMPT) led to largely comparable LET distributions, whereas the distal edge tracking IMPT (DET-IMPT) plans resulted in considerably increased LET values in normal tissues and critical structures. Because in the brainstem, dose-averaged LET values exceeding 5 keV/µm were observed in areas with significant dose (>70% of prescribed dose). This suggests that if a critical structure is located distal to target, the generic LET of proton is not apt to be applicable making the dosimetric optimization become very complicated. As the principal concern of radiation oncologists to use RBEs is that to benefit from the large pool of clinical results obtained from photon beams, the large variations of LET in proton beam distal to the Bragg peak cause a lot of stresses to the physicians. The proton therapy planning systems are using an electron density image obtained by the calibration and conversion of an X-ray computed tomography (CT) images, but it has been pointed out that this method can induce up to 2% proton range error [35]. Thus, it has been suggested that the proton therapy planning needs a more accurate way of acquiring an electron density on images or proton stopping power on images. The proton CT (pCT) is a potential candidate for accomplishing this [36,37].
Moreover, the issues concerned about secondary cancers, especially in pediatrics are discussed. Paganetti [16] reported that the biological effect downstream of the target caused by neutrons was analysed using a radiation quality factor of 10. Even though the biological dose was found to be below 0.5% of the prescribed target dose (for a 3 × 3 × 3 cm3 spread out Bragg peak [SOBP]), he pointed out that this dose should not be significant with respect to late effects, e.g. cancer induction. The contribution of neutron to the effective dose which is produced by proton beams when treated with 72 Gy by passive beam modulator was reported about 100 mSv [38]. For a cured patient who underwent treatment at age 60, this corresponds to an estimated lifetime cancer risk of about 0.5% but for a cured 10 year old, this corresponds to a lifetime cancer risk of about 3% [39]. In another study to predict risks of second malignant neoplasm incidence and mortality due to secondary neutrons in a girl and boy receiving proton craniospinal irradiation showed that the risks of a fatal SMN were 5.3% and 3.4% for the girl and boy, respectively [40]. Hall [41] pointed out that many proton facilities use passive method to produce a field of sufficient size, but the use of a scattering foil produces neutrons, which results in an effective dose to the patient higher than that of IMRT. Therefore the benefit of protons is only achieved if a scanning beam is used in which the doses are 10 times lower than with IMRT. In reply to Gottschalk's comments [42] that "However, neutron dose is rarely, if ever, the main concern," E. J. Hall again emphasized that "just how uncertain our knowledge really is of the cancer risks from low doses of neutrons". Based on these considerations that the variation of proton LET across the SOBP region is small but it is significant at the terminal end of a SOBP. This measurable increase in LET over the terminal few mm of the SOBP results in an extension of the biologically effective range [31]. The avoidable lifetime cancer risks may be lower in actively scanning method rather than passive method [43].
2. Heavy charged particles
The heavy charged particle beams show very diverse RBEs as they travel through the matter. While the protons are producing relatively localized biological damage according to the dose, the heavy particles are producing many ion tracks around the path so that they cause locally multiplied damages [44]. Thus simple dose scaling or plotting of dose from a reference depth dose is not appropriate. To understand the models of heavy charged particles, it is needed to understand ion track and track structures. Actually, it is the track structure rather than LET which implicate radiobiologic effect for the heavy particle beams.
The expression 'track structure' refers to an 'event-by-event' description of the physical processes following irradiation, represented as a matrix Sn (i,X,E), where i is the interaction type, X is its position, and E is the deposited energy [44]. In comparison with the photon beam, which is sparsely ionizing radiation, the particle beams produce dense ionization tracks with more 'clustered damage' [45]. The mechanism of producing clustered damage is that the particle beams have very complex track structures characterized by energy depositions along with the primary particle path and radially projecting secondary beams so called 'delta-rays'. A delta ray is characterized by very fast electrons produced in quantity by alpha particles or other fast energetic charged particles knocking orbiting electrons out of atoms. Collectively, these electrons are defined as delta radiation when they have sufficient energy to ionize further atoms through subsequent interactions on their own. Delta rays appear as branches in the main track. These branches will appear nearer the start of the track of a heavy charged particle, where more energy is imparted to the ionized electrons. With the assumption that biological damage is determined by locally ejected δ-electrons, increased effectiveness of particle radiation can be described by a combination of the photon dose response and microscopic dose distribution. For this purpose, a local effect model (LEM) has been suggested which showed that the predictions of the LEM are in good agreement with clinical data [46,47]. The input parameters of this model are radial dose distribution, size of cell nucleus and X-ray sensitivity (α/β ratio) [48] to determine local damage probability of microscopic track structure by calculating the dose in small compartments by the reference of X-rays.
The biological damages such as DNA double strand break (DSB) or fragmentation are significantly related with beam quality. Recently, a radial energy deposition distribution, the distribution of DNA strand breaks and their yields were simulated by Monte Carlo track structure simulation for C and Ne ions with the same LET around 450 keV/µm [49]. The radial DNA damage distribution shows different pattern for C and Ne ions. DSB are mostly formed in the central area, while the single strand break tends to spread to the surrounding area. Though both of the ions are high LET radiation, C and Ne ion showed a different pattern of DNA damage [49].
Unlike low LET radiation, a significant non-random contribution to the number of DSBs after irradiation with high-LET was confirmed [50,51]. In a recent report, the prediction of whole-genome simple chromosome exchanges (dicentric plus reciprocal translocations) was possible with the PARTRAC code based on ion track structure model [44]. In this report, Ballarini et al. [44] predicted premature chromatic condensation (PCC) by using various charged particles. The predicted PCCs of 1 GeV 56Fe beams for the 0.2, 1.0 and 2.0 Gy were 13.2, 64.4 and 115.6 respectively, which showed considerable linear relationship with the chemically induced PCCs of 16.6 ± 2.5, 76.3 ± 12.9 and 114.3 ± 19.9 respectively. Qualitatively, the dose response was basically linear both for fragments smaller than 1 kbp, which is critical to a higher RBE value. This reflects the role of radiation track-structure, which for high-LET radiation is particularly effective at producing clustered energy depositions and thus very small DNA fragments. Thus the statistical difference of the DSB induction among the low LET and high LET radiation may important contributions with the aim of performing reliable predictions of the consequences of heavy-ion irradiation.
Outlook
With the development of new technologies, including beam application and treatment planning, there will likely be a broader implementation of particle beam therapies within a very recent future. As we have only one proton center, the Korean radiation oncology society is not paying their attentions on the particle beams. The authors hope this contribution may provoke some interests for the Korean radiation oncologists' society on the particle therapies and may help them to prepare the tsunami of paradigm shift in radiation therapy.
Acknowledgments
This work was supported by Development of Heavy Ion Medical Accelerator Programof Ministry of Education, Science & Technology (MEST) (grant code: 2011k000567).
Footnotes
No potential conflict of interest relevant to this article was reported.
References
- 1.Hirao Y, Ogawa H, Yamada S, et al. Heavy ion synchrotron for medical use: HIMAC project at NIRS-Japan. Nucl Phys A. 1992;538:541–550. [Google Scholar]
- 2.Particle Therapy Co-operative Group. Particle Therapy Co-operative Group; 2011. [cited 2011 Mar 20]. Particle therapy facilities in a planning stage or under construction [Internet] Available from: http://ptcog.web.psi.ch/newptcentres.html. [Google Scholar]
- 3.Jermann M. Patient statistics per end of 2010: Hadron therapy patient statistics. Particle Therapy Co-Operative Group; 2011. [cited 2011 Mar 20]. Available from: http://ptcog.web.psi.ch/patient_statistics.html. [Google Scholar]
- 4.Khan FM. The physics of radiation therapy. 4th ed. Philadelphia: Lippincott Williams & Wilkins; 2009. pp. 6–7. [Google Scholar]
- 5.Van der Kogel AJ, Joiner MC. Basic clinical radiobiology. 4th ed. London, UK: Hodder Arnold; 2009. p. 68. [Google Scholar]
- 6.Amaldi U. Hadrontherapy in the world and the programmes of the TERA Foundation. Tumori. 1998;84:188–199. doi: 10.1177/030089169808400216. [DOI] [PubMed] [Google Scholar]
- 7.Goitein M, Jermann M. The relative costs of proton and X-ray radiation therapy. Clin Oncol (R Coll Radiol) 2003;15:S37–S50. doi: 10.1053/clon.2002.0174. [DOI] [PubMed] [Google Scholar]
- 8.International Commission on Radiation Units and Measurements (ICRU) Tissue substitutes in radiation dosimetry and measurement. ICRU Report 44. Bethesda, MD: ICRU Pub.; 1989. [Google Scholar]
- 9.National Institute of Standards and Technology. Gaithersburg, MD: National Institute of Standards and Technology; 2011. [cited 2011 Jun 20]. Stopping power and range tables for protons [Internet] Available from: http://physics.nist.gov/PhysRefData/Star/Text/PSTAR.html. [Google Scholar]
- 10.International Commission on Radiation Units and Measurements (ICRU) Stopping powers for protons and alpha particles. ICRU Report 49. Bethesda, MD: ICRU Pub; 1993. [Google Scholar]
- 11.International Commission on Radiation Units and Measurements (ICRU) Nuclear data for neutron and proton radiotherapy and for radiation protection. ICRU Report 63. Bethesda, MD: ICRU Pub; 2000. [Google Scholar]
- 12.Uehara S, Toburen LH, Wilson WE, Goodhead DT, Nikjoo H. Calculations of electronic stopping cross sections for lowenergy protons in water. Radiat Phys Chem. 2000;59:1–11. [Google Scholar]
- 13.Dingfelder M, Inokuti M, Paretzke HG. Inelastic-collision cross sections of liquid water for interactions of energetic protons. Radiat Phys Chem. 2000;59:255–275. [Google Scholar]
- 14.Matsuzaki Y, Date H, Sutherland KL, Kiyanagi Y. Nuclear collision processes around the Bragg peak in proton therapy. Radiol Phys Technol. 2010;3:84–92. doi: 10.1007/s12194-009-0081-2. [DOI] [PubMed] [Google Scholar]
- 15.Nikjoo H, Goodhead DT. Track structure analysis illustrating the prominent role of low-energy electrons in radiobiological effects of low-LET radiations. Phys Med Biol. 1991;36:229–238. doi: 10.1088/0031-9155/36/2/007. [DOI] [PubMed] [Google Scholar]
- 16.Paganetti H. Nuclear interactions in proton therapy: dose and relative biological effect distributions originating from primary and secondary particles. Phys Med Biol. 2002;47:747–764. doi: 10.1088/0031-9155/47/5/305. [DOI] [PubMed] [Google Scholar]
- 17.The 2007 Recommendations of the International Commission on Radiological Protection. ICRP publication 103. Ann ICRP. 2007;37:1–332. doi: 10.1016/j.icrp.2007.10.003. [DOI] [PubMed] [Google Scholar]
- 18.National Research Council. Studies in penetration of charged particles in matter. Nuclear science series report 39. Washington, DC: National Academy of Sciences-National Research Council; 1964. [Google Scholar]
- 19.Lyman JT, Awschalom M, Berardo P, et al. Protocol for heavy charged-particle therapy beam dosimetry: a report of Task Group 20 Radiation Therapy Committee American Association of Physicists in Medicine. AAPM Report 16. New York, NY: American Institute of Physics for the American Association of Physicists in Medicine; 1986. [Google Scholar]
- 20.Bichsel H, Hiraoka T, Omata K. Aspects of fast-ion dosimetry. Radiat Res. 2000;153:208–219. doi: 10.1667/0033-7587(2000)153[0208:aofid]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 21.Mairani A. Nucleus-nucleus interaction modelling and applications in ion therapy treatment planning. Sci Acta. 2007;1:129–132. [Google Scholar]
- 22.Enghardt W, Fromm WD, Manfrass P, Schardt D. Limited-angle 3D reconstruction of PET images for dose localization in light ion tumour therapy. Phys Med Biol. 1992;37:791–798. doi: 10.1088/0031-9155/37/3/021. [DOI] [PubMed] [Google Scholar]
- 23.Ponisch F, Parodi K, Hasch BG, Enghardt W. The modelling of positron emitter production and PET imaging during carbon ion therapy. Phys Med Biol. 2004;49:5217–5232. doi: 10.1088/0031-9155/49/23/002. [DOI] [PubMed] [Google Scholar]
- 24.Hall EJ, Giaccia AJ. Radiobiology for the radiologist. 6th ed. Philadelphia, PA: Lippincott Williams & Wilkins; 2006. pp. 410–411. [Google Scholar]
- 25.Pshenichnov I, Mishustin I, Greiner W. Distributions of positron-emitting nuclei in proton and carbon-ion therapy studied with GEANT4. Phys Med Biol. 2006;51:6099–6112. doi: 10.1088/0031-9155/51/23/011. [DOI] [PubMed] [Google Scholar]
- 26.Crespo P, Shakirin G, Enghardt W. On the detector arrangement for in-beam PET for hadron therapy monitoring. Phys Med Biol. 2006;51:2143–2163. doi: 10.1088/0031-9155/51/9/002. [DOI] [PubMed] [Google Scholar]
- 27.Sardari D, Verga N, Saidi P. Estimation of the radioactivity produced in patient tissue during carbon ion therapy. Mod Appl Sci. 2010;4:26–28. [Google Scholar]
- 28.Zirkle RE, Tobias CA. Effects of ploidy and linear energy transfer on radiobiological survival curves. Arch Biochem Biophys. 1953;47:282–306. doi: 10.1016/0003-9861(53)90467-6. [DOI] [PubMed] [Google Scholar]
- 29.Chatterjee A, Schaefer HJ. Microdosimetric structure of heavy ion tracks in tissue. Radiat Environ Biophys. 1976;13:215–227. doi: 10.1007/BF01330766. [DOI] [PubMed] [Google Scholar]
- 30.Yousif A, Bahari IB, Yasir MS. Physical quality parameters affect charged particles effectiveness at lower doses. World Appl Sci J. 2010;11:1225–1229. [Google Scholar]
- 31.Paganetti H, Goitein M. Radiobiological significance of beamline dependent proton energy distributions in a spreadout Bragg peak. Med Phys. 2000;27:1119–1126. doi: 10.1118/1.598977. [DOI] [PubMed] [Google Scholar]
- 32.Paganetti H. Significance and implementation of RBE variations in proton beam therapy. Technol Cancer Res Treat. 2003;2:413–426. doi: 10.1177/153303460300200506. [DOI] [PubMed] [Google Scholar]
- 33.Robertson JB, Williams JR, Schmidt RA, Little JB, Flynn DF, Suit HD. Radiobiological studies of a high-energy modulated proton beam utilizing cultured mammalian cells. Cancer. 1975;35:1664–1677. doi: 10.1002/1097-0142(197506)35:6<1664::aid-cncr2820350628>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 34.Grassberger C, Trofimov A, Lomax A, Paganetti H. Variations in linear energy transfer within clinical proton therapy fields and the potential for biological treatment planning. Int J Radiat Oncol Biol Phys. 2011;80:1559–1566. doi: 10.1016/j.ijrobp.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schaffner B, Pedroni E. The precision of proton range calculations in proton radiotherapy treatment planning: experimental verification of the relation between CT-HU and proton stopping power. Phys Med Biol. 1998;43:1579–1592. doi: 10.1088/0031-9155/43/6/016. [DOI] [PubMed] [Google Scholar]
- 36.Penfold SN, Rosenfeld AB, Schulte RW, Schubert KE. A more accurate reconstruction system matrix for quantitative proton computed tomography. Med Phys. 2009;36:4511–4518. doi: 10.1118/1.3218759. [DOI] [PubMed] [Google Scholar]
- 37.Wang D, Mackie TR, Tome WA. Bragg peak prediction from quantitative proton computed tomography using different path estimates. Phys Med Biol. 2011;56:587–599. doi: 10.1088/0031-9155/56/3/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jiang H, Wang B, Xu XG, Suit HD, Paganetti H. Simulation of organ-specific patient effective dose due to secondary neutrons in proton radiation treatment. Phys Med Biol. 2005;50:4337–4353. doi: 10.1088/0031-9155/50/18/007. [DOI] [PubMed] [Google Scholar]
- 39.Committee to Assess Health Risks from Exposure to Low Levels of Ionizing Radiation, National Research Council. Health risks from exposure to low levels of ionizing radiation: BEIR VII Phase 2. Washington, DC: National Academy Press; 2006. [PubMed] [Google Scholar]
- 40.Taddei PJ, Mahajan A, Mirkovic D, et al. Predicted risks of second malignant neoplasm incidence and mortality due to secondary neutrons in a girl and boy receiving proton craniospinal irradiation. Phys Med Biol. 2010;55:7067–7080. doi: 10.1088/0031-9155/55/23/S08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hall EJ. Intensity-modulated radiation therapy, protons, and the risk of second cancers. Int J Radiat Oncol Biol Phys. 2006;65:1–7. doi: 10.1016/j.ijrobp.2006.01.027. [DOI] [PubMed] [Google Scholar]
- 42.Gottschalk B. Neutron dose in scattered and scanned proton beams: in regard to Eric J. Hall (Int J Radiat Oncol Biol Phys 2006;65:1-7) Int J Radiat Oncol Biol Phys. 2006;66:1594. doi: 10.1016/j.ijrobp.2006.08.014. [DOI] [PubMed] [Google Scholar]
- 43.Ares C, Hug EB, Lomax AJ, et al. Effectiveness and safety of spot scanning proton radiation therapy for chordomas and chondrosarcomas of the skull base: first long-term report. Int J Radiat Oncol Biol Phys. 2009;75:1111–1118. doi: 10.1016/j.ijrobp.2008.12.055. [DOI] [PubMed] [Google Scholar]
- 44.Ballarini F, Alloni D, Facoetti A, Ottolenghi A. Heavy-ion effects: from track structure to DNA and chromosome damage. New J Phys. 2008;10:1–17. [Google Scholar]
- 45.Goodhead DT. Initial events in the cellular effects of ionizing radiations: clustered damage in DNA. Int J Radiat Biol. 1994;65:7–17. doi: 10.1080/09553009414550021. [DOI] [PubMed] [Google Scholar]
- 46.Scholz M, Matsufuji N, Kanai T. Test of the local effect model using clinical data: tumour control probability for lung tumours after treatment with carbon ion beams. Radiat Prot Dosimetry. 2006;122:478–479. doi: 10.1093/rpd/ncl426. [DOI] [PubMed] [Google Scholar]
- 47.Elsasser T, Kramer M, Scholz M. Accuracy of the local effect model for the prediction of biologic effects of carbon ion beams in vitro and in vivo. Int J Radiat Oncol Biol Phys. 2008;71:866–872. doi: 10.1016/j.ijrobp.2008.02.037. [DOI] [PubMed] [Google Scholar]
- 48.Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy: the model and its approximation. Radiat Environ Biophys. 1997;36:59–66. doi: 10.1007/s004110050055. [DOI] [PubMed] [Google Scholar]
- 49.Watanabe R, Wada S, Funayama T, Kobayashi Y, Saito K, Furusawa Y. Monte Carlo simulation of radial distribution of DNA strand breaks along the C and Ne ion paths. Radiat Prot Dosimetry. 2011;143:186–190. doi: 10.1093/rpd/ncq539. [DOI] [PubMed] [Google Scholar]
- 50.Hoglund E, Blomquist E, Carlsson J, Stenerlow B. DNA damage induced by radiation of different linear energy transfer: initial fragmentation. Int J Radiat Biol. 2000;76:539–547. doi: 10.1080/095530000138556. [DOI] [PubMed] [Google Scholar]
- 51.Lobrich M, Cooper PK, Rydberg B. Non-random distribution of DNA double-strand breaks induced by particle irradiation. Int J Radiat Biol. 1996;70:493–503. doi: 10.1080/095530096144680. [DOI] [PubMed] [Google Scholar]