Mathematical modeling of a survey-meter used to measure radioactivity in human thyroids: Monte Carlo calculations of the device response and uncertainties

Abstract

This paper presents results of Monte Carlo modeling of the SRP-68-01 survey meter used to measure exposure rates near the thyroid glands of persons exposed to radioactivity following the Chernobyl accident. This device was not designed to measure radioactivity in humans. To estimate the uncertainty associated with the measurement results, a mathematical model of the SRP-68-01 survey meter was developed and verified. A Monte Carlo method of numerical simulation of radiation transport has been used to calculate the calibration factor for the device and evaluate its uncertainty. The SRP-68-01 survey meter scale coefficient, an important characteristic of the device, was also estimated in this study. The calibration factors of the survey meter were calculated for ¹³¹I, ¹³²I, ¹³³I, and ¹³⁵I content in the thyroid gland for six age groups of population: newborns; children aged 1 yr, 5 yr, 10 yr, 15 yr; and adults. A realistic scenario of direct thyroid measurements with an “extended” neck was used to calculate the calibration factors for newborns and one-year-olds. Uncertainties in the device calibration factors due to variability of the device scale coefficient, variability in thyroid mass and statistical uncertainty of Monte Carlo method were evaluated. Relative uncertainties in the calibration factor estimates were found to be from 0.06 for children aged 1 yr to 0.1 for 10-yr and 15-yr children. The positioning errors of the detector during measurements deviate mainly in one direction from the estimated calibration factors. Deviations of the device position from the proper geometry of measurements were found to lead to overestimation of the calibration factor by up to 24 percent for adults and up to 60 percent for 1-yr children. The results of this study improve the estimates of ¹³¹I thyroidal content and, consequently, thyroid dose estimates that are derived from direct thyroid measurements performed in Belarus shortly after the Chernobyl accident.

1. Introduction

The radiation exposure of the thyroid, primarily due to intakes of ¹³¹I by children and adolescents, is one of the most important consequences of the Chernobyl accident (WHO, 2006). To evaluate the thyroid exposure, wide-scale monitoring of ¹³¹I content in thyroids was conducted among the residents of contaminated areas of Belarus during the first few weeks after the accident (Gavrilin et al., 1999), Ukraine (Likhtarev et al., 1993), and the Russian Federation (Bratilova et al., 2003). Several readily available devices were used for measurements, including some that were not designed to measure radioactivity in humans, like SRP-68-01. This device is a scintillation survey meter that was commonly used in the former Soviet Union for geological exploration to detect uranium and thorium deposits by measuring environmental exposure rates.

The thyroid monitoring was conducted in May–June 1986, shortly after the Chernobyl accident. These “direct thyroid measurements”, as they are called, provide a time-specific estimate of an individual’s thyroid activity, which can be used as the basis for estimating the radiation dose to the thyroid. The U.S. National Cancer Institute and the Ministry of Health of Belarus are collaborating to conduct a cohort study of thyroid cancer and other thyroid diseases in Belarus (Stezhko et al., 2004). Dose estimates for about 11,800 study subjects are based upon the direct thyroid measurements made in 1986. Measurements of thyroid activity in about 4900 of the subjects were made using the SRP-68-01 survey meter.

The purpose of this paper is to estimate the uncertainties of the ¹³¹I activity in the thyroid derived from direct measurements made with the SRP-68-01 device. These uncertainties are due to

• variability of the device scale coefficient (counts s⁻¹ μR⁻¹ h);

• deviations from the proper detector positioning made by the persons who conducted measurements and were not thoroughly trained or experienced;

• variability in the size (mass) of the thyroid gland;

• presence of radiation sources other than ¹³¹I in the thyroid, e.g. external contamination of the human body and clothing by radionuclides, internal contamination of the human body by cesium radioisotopes.

The first three sources of uncertainty are considered in this paper. The complexities of the device response to radiation sources other than radioiodines in the thyroid are considered in a separate paper.¹ Similar assessments will be reported for the DP-5 instrument, which was used to measure exposure rates near the thyroids for most of the other study subjects.

To estimate the uncertainty associated with the measurement results, this study developed and verified a mathematical model of the SRP-68-01 survey meter. A Monte Carlo method of numerical simulation of radiation transport has been used to calculate the calibration factor of the device (i.e., the activity of ¹³¹I in the thyroid per unit exposure rate measured near the thyroid gland, Bq μR⁻¹ h) and evaluate its uncertainty. It should be noted that considerable work on modeling the SRP-68-01 device was done by Ulanovsky et al. (1997, 2004). However, the task of estimating thyroidal content of ¹³¹I from measurements of the exposure rate near the neck was broader than it was initially expected and, therefore, further calculations have been performed.

2. Determination of ¹³¹I in thyroid from exposure rate measurements near thyroid gland

The activity of ¹³¹I in the thyroid is calculated from results of measurements of the exposure rate made with the SRP-68-01 survey meter located near the thyroid gland using the following equation:

$$A=(P_{\mathit{meas}}-P_{\mathit{bg}})\times \mathit{CF}=P_{\mathit{thyr}}\times \mathit{CF},$$ (1)

where A is the activity of ¹³¹I in the thyroid (Bq); P_meas is the exposure rate measured near the thyroid gland (μR h⁻¹); P_bg is the contribution to the measured exposure rate of radiation sources other than ¹³¹I in the thyroid (μR h⁻¹); CF is the calibration factor (Bq μR⁻¹ h) relating the activity of ¹³¹I in the thyroid to the net thyroidal exposure rate (P_thyr).

The calibration factor of the device is defined as the “true” activity content of ¹³¹I in the thyroid per unit exposure rate measured by the device near the thyroid and can be estimated as

$$\mathit{CF}=\frac{k}{\eta },$$ (2)

where k is the scale coefficient of the device (counts s⁻¹ μR⁻¹ h). The parameter η is the total efficiency of the SRP-68-01 device to gamma rays emitted from ¹³¹I located in the thyroid. It is the ratio of the photon count rate to the emission rate from ¹³¹I in the thyroid (counts s⁻¹ Bq⁻¹).

As seen in Eqs. (1) and (2), in order to reconstruct the activity of radionuclides in the thyroid from the exposure rate, it is necessary to know the scale coefficient of the device, k, and the device total efficiency, η. The sections below describe experimental evaluation of the scale coefficient and Monte Carlo calculations of the total efficiency of the device. Although ¹³¹I is the principal radionuclide of interest, Eqs. (1) and (2) can be applied to other iodine isotopes accumulated in the thyroid gland.

3. Characteristics of the SRP-68-01 survey meter

Fig. 1 is a photograph of the SRP-68-01 survey meter probe and readout device, which are connected by a cord that extends through the handle of the probe. The radiation detector is located at the left end of the probe, which is about 53 cm long. The detector is a cylindrical NaI(Tl) crystal 30 mm in diameter and 25 mm long. Fig. 2 illustrates the materials of construction components that surround the detector, including the photomultiplier tube, which is not shown completely. Both the detector and the photomultiplier tube are enclosed in iron and aluminum tubes. A rubber cap, with a diameter of 5.4 cm, covers the end of the assembly.

Fig. 1.

SRP-68-01 survey meter.

Fig. 2.

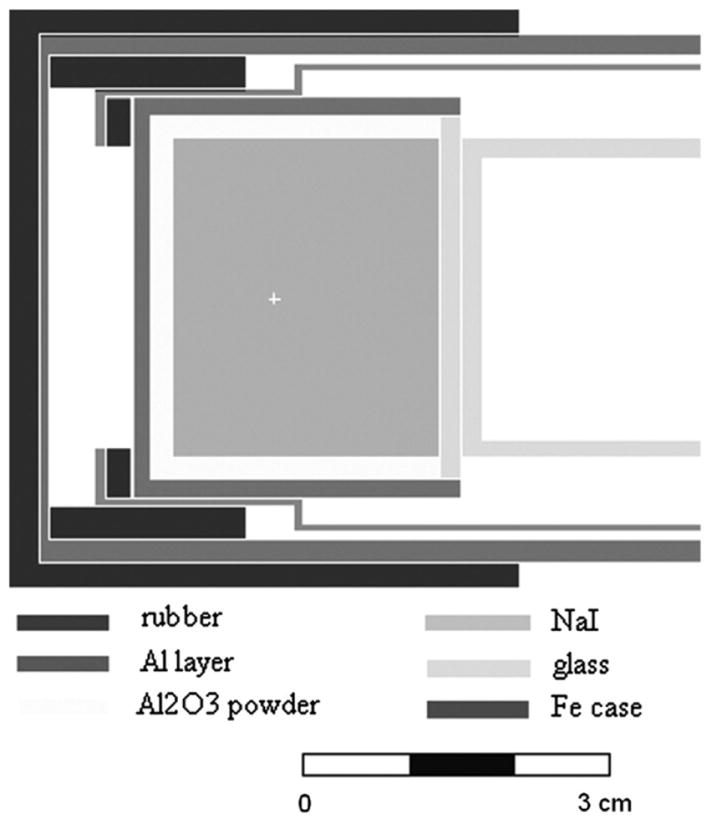
Materials and dimensions of the detector of the SRP-68-01 survey meter.

The operation of the device is based on the detection of the pulses received from the scintillation detector. The analog readout has two graduated scales to indicate the pulse count rate (0–10,000 counts s⁻¹) or the exposure rate (0–3000 μR h⁻¹). In 1986, operators recorded the exposure rate measured near the thyroid gland in μR h⁻¹.

The SRP-68-01 device registers photons in the energy region (E_c, E_max). For a specific photon energy of the source, E_s, the total efficiency of the detector, η(E_s), is caused by the total number of photons registered in the energy region (E_c, E_max)

$$\eta (E_s)={\mathit{\int }}_{E_c}^{E_{\mathit{max}}}s(E,E_s)\mathit{dE},$$ (3)

where s(E,E_s) is the detector efficiency as a function of energy E that is present in the spectrum produced by the source of photons with energy E_s; E_c = 0.025 MeV and E_max = 3 MeV are the lower discrimination threshold and the upper detection threshold of the SRP-68-01 device,² respectively.

For a radionuclide with complicated gamma-spectrum, the total efficiency of the detector, η, can be written as the sum of energy-specific efficiencies, η(E_s), corresponding to all photons emitted by the radionuclide:

$$\eta =\sum _{s}p(E_s)\eta (E_s),$$ (4)

where p(E_s) (unitless) is the yield of photons with energy E_s, based on the information update (ICRP, 2003) in ICRP Publication 38 (ICRP, 1983). Only photons with energies greater than 25 keV are included in the summation in Eq. (4).

From Eqs. (1), (2) and (5), the activity of ¹³¹I in the thyroid can be calculated as

$$A=k\frac{P_{\mathit{thyr}}}{\sum _{s}p(E_s)\eta (E_s),}$$ (5)

The efficiency of the detector, η(E_s), for each photon emitted with energy E_s is calculated using MCNP v.4B (Briesmeister, 1997). The scale coefficient is the count rate per unit exposure rate registered by the device; it is not the same for each SRP-68-01 instrument. Determination of the average scale coefficient is one of the goals of this work. According to the survey meter user manual, the scale coefficient is greater than 2.4 counts s⁻¹ μR⁻¹ h, which is not very definitive. Experimental evaluation of the SRP-68-01 scale coefficient is described in the following section.

3.1. Scale coefficient

To determine the scale coefficient, k, both the count rate and exposure rate must be measured. The scale coefficient is determined only by the electronic scheme of the device and does not depend on either the gamma-ray energy or the measurement geometry. The scale coefficient was first determined for the SRP-68-01 device over a range of exposure rates using a ²²Na source, which emits gamma rays with 0.511 and 1.275 MeV energies. To cover the entire range of the device scale, a 740-kBq ²²Na source was placed at different distances from the detector. Count rates and exposure rates measured by the device are given in Table 1. The scale coefficient was found to be 3.68 ± 0.04 counts s⁻¹ μR⁻¹ h for the instrument tested. This value is higher than the value of 3.33 counts s⁻¹ μR⁻¹ h that was previously used by Ulanovsky et al.³ for this device type. Relative uncertainty associated with the evaluation of the single instrument’s mean scale coefficient was found to be 0.01.

Table 1.

Count rate and exposure rate measured by the SRP-68-01 device for ²²Na radiation source and the corresponding values of the scale coefficient.

Parameter	Background	Result of measurement for 22Na
Count rate (counts s−1)	43	78	82	210	275	800	810	1950	2000	2050
Exposure rate (μR h−1)	11.5	21	22.5	58	75	215	220	530	550	550
Scale coefficient, k (counts s−1 μR−1 h)	3.74	3.71	3.64	3.62	3.67	3.72	3.68	3.68	3.64	3.73

3.1.1. Variability of the scale coefficient

It is obvious that there is a variability of scale coefficients between different devices of the same model. To directly evaluate the variability of scale coefficients, the count rate and exposure rate readings must be obtained for a number of the SRP-68-01 devices. Because SRP-68-01 is no longer in general use, a supply of these instruments was not available for this study. Indirect evaluation of the variability of scale coefficient between devices was based on the available results of historical measurements of the responses for many SRP-68-01 instruments to a ²²⁶Ra radiation source. These measurements were performed during routine calibration of sixty-six SRP-68-01 devices from different organizations in Belarus.⁴ The exposure rate was measured by all devices under the same conditions. The gamma flux density at the instrument location was the same for all instruments. The distribution of the relative exposure rate reading for the devices (Fig. 3) can be described by a normal distribution with a mean equal to 1 and standard deviation equal to 0.05.

Fig. 3.

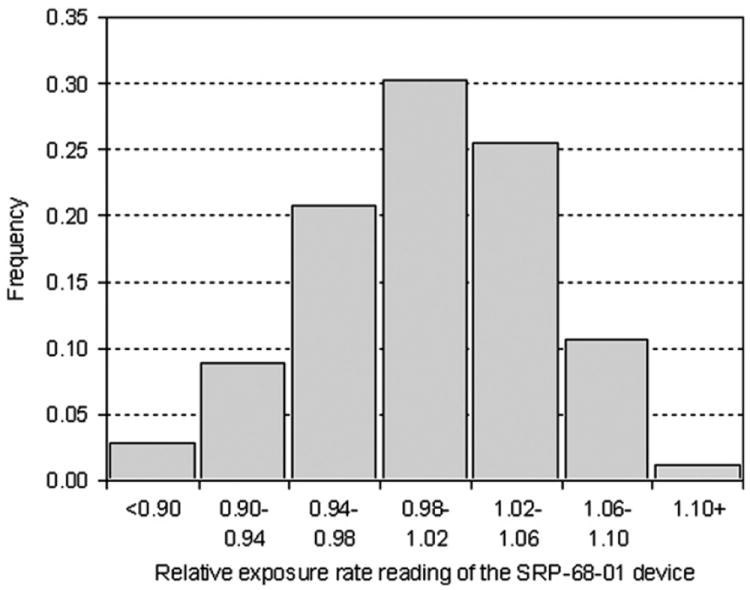
Variability of relative exposure rate readings for sixty-six SRP-68-01 instruments exposed to the same radiation field.

Relative variability of 0.05 in measured exposure rate reading of 66 devices combined with relative uncertainty associated with determining the mean scale coefficient of 0.01 resulted in total relative variability of the scale coefficient of 0.05.

3.2. Verification of the mathematical model of the device

To verify the MCNP model of the SRP-68-01 device, the known activity of the reference point gamma radiation sources was compared with the activity of that source calculated from the measured exposure rate using Eq. (5) and the scale coefficient k = 3.68 counts s⁻¹ μR⁻¹ h determined above.

Exposure rates from reference point gamma radiation sources of ²⁴¹Am, ⁵⁷Co, ¹³³Ba, ¹³⁹Ce, ¹³⁷Cs, ²²⁸Th, ¹⁵²Eu were measured for distances of 0.15 and 10 cm between the source and the detector. The Monte Carlo simulations of the device’s total efficiency, η, for each radionuclide of interest were performed in accordance with Eq. (4). Table 2 provides a comparison of reference activities and activities calculated from the measured exposure rates. As seen in Table 2, the errors in estimation of activities for a majority of the measurements do not exceed 13 percent, which is the typical 1-sigma uncertainty in a measurement made by the instrument.⁵

Table 2.

Comparison of activities of point radiation sources: reference values and those calculated with the detector model from background subtracted measurements of exposure rate.

Isotope	Reference activity—R (kBq)	d = 0.15 cm			d = 10 cm
		Backgrounda subtracted measurement of exposure rate (μR h−1)	Calculated activity—C (kBq)	Relative error (C–R)/R (%)	Backgroundb subtracted measurement of exposure rate (μR h−1)	Calculated activity—C (kBq)	Relative error (C–R)/R (%)
241Am	108.4	1188	122.4	12.9	44.5	121.2	11.8
57Co	41.0	1138	40.6	−1.0	46.5	36.8	−10.2
133Ba	53.7	2138	56.5	5.2	102.5	58.3	8.6
139Ce	16.7	508	16.8	0.6	23.5	17.0	1.8
137Cs	126.9	1238	122.2	−3.7	63.5	112.3	−11.5
228Th	35.1	1088	31.0	−11.7	52.5	30.8	−12.3
152Eu	45.2	1538	44.2	−2.2	70.5	42.6	−5.8

^aBackground exposure rate was equal to 12 μR h⁻¹.

^bBackground exposure rate was equal to 12.5 μR h⁻¹.

4. Evaluation of measurement geometry

To perform a Monte Carlo simulation of radiation transport during measurement of the exposure rate near the thyroid gland, a family of Oak Ridge National Laboratory (ORNL) phantoms (Cristy, 1980; Cristy and Eckerman, 1987) was used. The phantoms represent a newborn; children aged 1, 5, 10, 15 years; and adults. Ulanovsky and Eckerman (1998a) modified the ORNL phantoms to make them anatomically more realistic in the neck area. In the current calculations, the internal structure of phantoms (except the thyroid gland) was not taken into account and, therefore, it was assumed that phantoms have uniform density.

4.1. Extension of the neck length

The neck length in phantoms for the newborn and young children (<5 yr) is comparable to the diameter of the SRP-68-01 device, while, for older children and adults, there is enough space for the detector to be located near the thyroid. Such disproportion led to a psychological reaction of the measured person of young age when a big device is moved to the neck: the person instinctively moves the head back to allow the operator to touch the neck and to measure the exposure rate near the thyroid.⁶ Moving the head during the thyroid measurement effectively extended the neck length. Fig. 4 shows two scenarios of thyroid measurement with the survey meter for a one-year-old phantom: the neck is normal, but the device does not touch the neck; and the neck is extended.

Fig. 4.

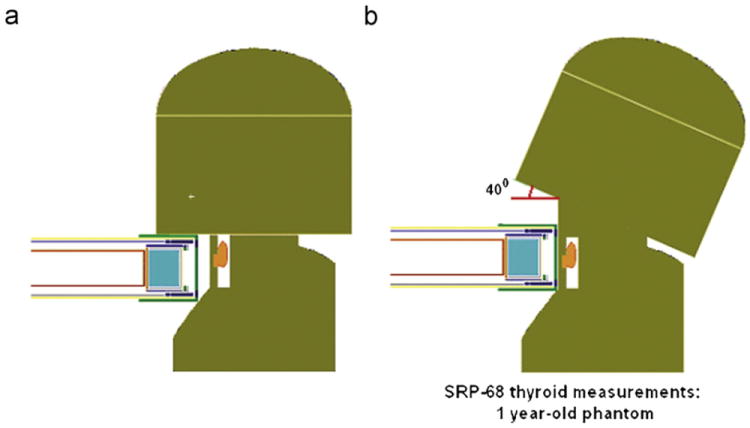
Two scenarios of the thyroid measurement with the SRP-68-01 device for 1-yr phantom: (a) the device does not touch “normal” neck; (b) “extension” of the neck allows contact.

The coefficient of neck extension was determined as

$$K_{\mathit{ext}}=\frac{L_{\mathit{ext}}-L_{\mathit{norm}}}{L_{\mathit{norm}}}=\frac{R_{\mathit{neck}}}{L_{\mathit{norm}}}\times \tan (\alpha )-1,$$ (6)

where L_ext and L_norm are the lengths of the extended and normal neck (cm), respectively; R_neck is the radius of the neck (cm); and α is the angle of head movement.

The angle of head movement during the thyroid measurement with the SRP-68-01 device was assumed to be the same as when drinking water. The neck extension coefficient, K_ext, was found to be the same for adults, both males and females, and equal to 0.37 ± 0.04. This value corresponds to the angle of head movement α ≈ 40°, which was assumed to be the same for all ages. Table 3 contains the neck length, radius, and neck extension for phantoms of newborns and young children measured as illustrated in Fig. 4(b).

Table 3.

Age-dependent length, radius and extension of the neck when the head is tilted 40-degrees as in Fig. 5(b).

Neck parameter	Newborn	1 yr	5 yr
Length (cm)	3.1	4.3	5.5
Radius (cm)	2.8	3.6	3.8
Extension (cm)	2.3	3.0	3.2

The SRP-68-01 response was calculated for two scenarios of thyroid measurements corresponding to the “normal” and “extended” neck. We assumed that the thyroid gland did not move from its “normal” position while the head was tilted. Fig. 5 illustrates the device response for newborn, 1- and 5-year-old phantoms for two scenarios. There is a significant difference in the survey meter response between the two scenarios of thyroid measurement for newborns and children aged 1 year. The device response is much lower in measurements with the “normal” neck (when the head does not move back and the device does not touch the neck) than in measurements with the extended neck when the detector is located close to the neck. The neck extension does not change the device response for 5-year-old and older phantoms. For newborns and 1-year-old children, the scenario illustrated in Fig. 4(b) was considered to represent the most likely geometry for direct thyroid measurements.

Fig. 5.

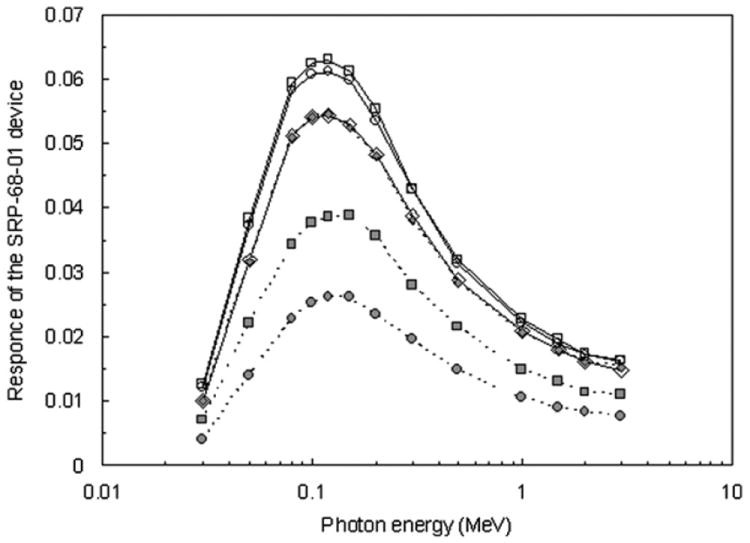
Comparison of the SRP-68-01 response for newborn (circles), 1 yr (squares), and 5 yr (diamonds) phantoms for two scenarios of the thyroid measurements: normal (filled markers) and extended (open markers) neck.

4.2. Position of the detector

During the measuring campaign in May–June 1986, it was recommended⁷ to use the following position of SRP-68-01: the lower point of the detector should touch the lower point of the neck. For phantoms representing persons of different ages, the detector center is located in different positions relative to the thyroid center during the measurement in such geometry:

• the centers of the detector are 0.55 and 0.05 cm above the centers of the thyroid for newborns and children aged 1 yr, respectively; and

• the centers of the detector are 0.17, 1.05, 1.8, and 2.6 cm below the centers of the thyroid for children aged 5, 10, 15 yr, and adults, respectively.

For 1- and 5-year-old phantoms, it is recommended to place the center of the detector very close to the thyroid center (TC). For newborns, it is not possible to align the center of the detector with the TC.

4.2.1. Uncertainty in the position of the detector

During real thyroid activity measurements, it is difficult to exactly position the lower edge of the detector at the lower point of the neck. For that reason and because some operators who performed measurements were not thoroughly trained or experienced, we considered uncertainties associated with positioning the detector. For each phantom, the response of the device was calculated assuming placement in the recommended position. Additionally, the response was averaged over a range of possible detector positions from the lower point of the neck to 1 cm upward along the neck. For the phantom of a newborn, the detector just fits into the space available when the neck is extended and movement of the detector along the neck is not possible. Calculation of the calibration factor of the SRP-68-01 device and evaluation of other uncertainties associated with positioning are described in the following section.

5. Calibration factor

The calibration factor of the device is defined as “true” activity in the thyroid per unit exposure rate measured by the device near that organ. From Eq. (2), the calibration factor is the ratio of the scale coefficient of the device to the device efficiency to the radionuclide accumulated in the thyroid.

The total efficiency of the device located near the thyroid, η, was calculated by MCNP-4B code (Briesmeister, 1997) using the phantoms and geometry of measurement described in the sections above. The calculated calibration factors for SRP-68-01 (with E_c = 0.025 MeV) for ¹³¹I, ¹³²I, ¹³³I, and ¹³⁵I in the thyroid gland are presented in Table 4. Calibration factors were also calculated for detector thresholds of 0.02 and 0.03 MeV. Differences between these two sets of estimates and the calibration factors presented for ¹³¹I are small, within −0.7 to 0.9 percent. This was expected because the device total efficiency, η(E), is significantly lower in the energy range of 0.02–0.03 MeV (Fig. 5) compared to that for the main photon energy (0.364 MeV) of ¹³¹I.

Table 4.

Age-dependent calibration factors for radioiodines for standard position of the SRP-68-01 device.

Age group	Calibration factor (Bq μR−1 h)
	131I	132I	133I	135I
Newborn	98	46	120	120
1 yr	100	46	118	120
5 yr	110	52	133	135
10 yr	126	62	158	163
15 yr	147	73	187	190
Adult	167	86	220	223

Most direct thyroid measurements of cohort members with the SRP-68-01 device were made after 8 May 1986. By that time, radioactive decay had removed the short-lived radioiodines (¹³²I, ¹³³I, and ¹³⁵I). For that reason, only the calibration factor for ¹³¹I is considered in the following sections.

5.1. Random uncertainty and bias in the calibration factor

Two types of errors in the calibration factor were considered in this study:

1. Random uncertainty due to (a) variability of the scale coefficient for the SRP-68-01 device, (b) variability in the thyroid mass of a measured person; and (c) statistical uncertainty of Monte Carlo calculations of the device calibration factor;

2. bias due to possible deviations of the device position from the proper geometry of measurements.

5.1.1. Random uncertainty

Table 5 summarizes sources of random uncertainty in the SRP-68-01 calibration factor. As discussed above, variability of the scale coefficient is characterized by a mean of one and a standard deviation of 0.05. Uncertainty in the calibration factor due to variability of the thyroid mass was evaluated by Monte Carlo simulations of the SRP-68-01 response performed for persons of the same age with different thyroid masses. The distribution of thyroid mass for each age was assumed to be log-normal with a geometric mean representing a standard thyroid mass for a phantom of given age and a geometric standard deviation (GSD) of 1.4 (Skryabin et al., 2010). The calibration factor was calculated for the following sizes of the thyroid mass: the standard for a given age (m), m/GSD, m × GSD, m/GSD², and m × GSD². Statistical uncertainty of Monte Carlo simulation of calibration factors was estimated to be in the range between 1 percent for newborn and 2 percent for adult.

Table 5.

Contribution of various sources of error to random uncertainty and to bias of the SRP-68-01 calibration factor for ¹³¹I in thyroid.

Source of error	Standard deviationa for age group
	Newborn	1 yr	5 yr	10 yr	15 yr	Adult
Random uncertainty
Variability of scale coefficient	±0.05
Variability of thyroid mass	+0.03/−0.06	+0.04/−0.04	+0.05/−0.08	+0.09/−0.05	+0.08/−0.03	+0.07/−0.03
Statistical uncertainty	±0.01	±0.01	±0.01	±0.01	±0.02	±0.02
Overall uncertainty due to all sourcesb	0.08	0.06	0.09	0.10	0.10	0.09
Bias due to errors in geometry of measurement
Shift away from the neck	+0.31	+0.32	+0.31	+0.27	+0.23	+0.18
Vertical shift along the neck	+0.03c	+0.03	+0.03	−0.02	−0.06	−0.07
Inclination in the vertical planed	+0.12	+0.16	+0.14	+0.13	+0.10	+0.08
Inclination in the horizontal plane	+0.05	+0.09	+0.04	+0.03	+0.04	+0.05
Overall bias due to all sources	0.51	0.60	0.52	0.41	0.31	0.24

^aRelative to a mean of 1 for each source of error.

^bMaximal error due to variability of thyroid mass was used to calculate overall uncertainty.

^cError was assumed to be the same as that for age 1 yr.

^dError is slightly asymmetrical relative to the “normal” position of the detector. Value averaged over position in both directions is given.

To estimate overall random uncertainty in the survey meter calibration factor for a given age group, all considered above errors were combined assuming that they are statistically independent. The resulting standard deviation, σ_overall, is calculated as

$${\sigma }_{\mathit{overall}}^2=\sum _i{\sigma }_i^2,$$ (7)

where σ _i is the standard deviation due to i-th source of error.

The estimated random uncertainties of the calibration factors for different ages are given in Table 5. Overall uncertainty is characterized by the standard deviation 0.08 for newborns; 0.06, 0.09, 0.1, 0.1 for children aged 1, 5, 10, 15 yr, respectively, and 0.09 for adults (Table 5).

Likhtarev et al. (1995) also considered variability in overlying tissue thickness (distance between the edge of the isthmus and the entrance surface of the detector) as a source of uncertainty of the device calibration factor. According to Ulanovsky and Eckerman (1998b), the thickness of overlying tissue in the ORNL phantom series is slightly dependent on the phantom age and is equal to 0.4 cm for phantoms representing a newborn and children aged 1 and 5 yr. For children aged 10 and 15 yr, the thickness is 0.5 and 0.55 cm, respectively, and 0.6 cm for adults. Although this source of uncertainty is not trivial (ranged from 0.05 to 0.1, according to Likhtarev et al. (1995)), it was not considered in this study.

5.1.2. Bias in the calibration factor due to deviation from the proper geometry of measurements

To evaluate the influence of measurement geometry on the calibration factor, the following positional deviations of the detector were considered:

• shift in the horizontal direction away from the neck (y-shift): 0.25, 0.5, 0.75 and 1 cm;

• shift in the vertical direction along the neck (z-shift from the position when the lower edge of the detector is at the bottom of the neck).

The range of possible z-shift values depends on the age:

• Newborns—no possibility for shifting;

• 1-year-old children: 0.5, 0.94 (middle of extended neck) and 1.5 cm;

• 5-year-old children: 0.17 (TC), 0.5, and 1.63 cm;

• 10-year-old children: 0.5, 1.05 (TC), and 2.0 cm;

• 15-year-old children: 0.5, 1.0, and 1.8 cm (TC);

• adults: 0.5, 1.0, and 2.0 cm.

The following angular deviations were also considered:

• inclination of the detector in the vertical plane, a_v (vertical inclination): ± 5°, ± 10°, and ± 15°;

• inclination in the horizontal plane close to the neck, a_h (horizontal inclination): ± 5° and ± 10°.

This study considered the error of the device calibration factor averaged over a range of possible deviations from the proper geometry. Calibration factors were calculated for all vertical and horizontal shifts listed above. The estimated error of the device calibration factor is the average for each age group over the same deviation range: 1 cm from the position when the bottom of the detector was at the bottom of the neck. The same procedure was applied to angular deviations. Within the range considered, equally possible positions of the detector were assumed in estimation of the average error. The relative error RE in the calibration factor was calculated using the following equation:

$$\mathit{RE}(z)=\frac{\sqrt{\frac{1}{z}{\mathit{\int }}_0^z{(\mathit{CF}(u)-\mathit{CF}(0))}^2\mathit{du}}}{\mathit{CF}(0)},$$ (8)

where CF(u) and CF(0) are the calibration factors calculated for deviation u (cm or degree) and for the “normal” position of the detector, respectively, (Bq μR⁻¹ h); z is the possible deviation from the proper geometry of measurements (cm or degree).

The estimated biases in the SRP-68-01 calibration factor due to deviation of the detector position from the recommended geometry of measurements are given in Table 5. As seen from the table, the horizontal movement of the detector away from the neck is the most important geometry-related source of error that causes a bias in the result; the larger the separation the lower the detector response and, consequently, the higher the calibration factor. The relative error due to that source varies from 0.32 for children aged 1 yr to 0.18 for adults. Likhtarev et al. (1995) and Ulanovsky et al. (1997) also found that movement of the detector away from the neck was the most important type of mistake that may have occurred during direct thyroid measurements.

A vertical shift of 1 cm or less of the detector along the neck has a small influence (2–3 percent) on the device response for children aged less than 10 years because, for the “standard” geometry of measurements, the center of the detector is located above or close to the thyroid center (see Section 4.2). Because the center of the detector is already above the thyroid for the phantoms of a newborn and 1-yr old child, moving it upward produces a negative bias in the detector response and, consequently, a positive bias in the calibration factor. For the phantom of a 5-yr old child, the detector is slightly (1.7 mm) below the thyroid center when in the standard position. Moving it upward by 2 mm, the detector response increases slightly; however, further upward movement produces a negative bias in the detector response. For older children and adults, the detector starts out below the center of the thyroid, and upward movement of the detector will produce a set of positive biases in the detector response (and negative biases in the calibration factor) with respect to the response in the standard position.

The relative errors due to positioning mistakes listed in the table are not standard deviations of normal distributions; they are biases that move the estimated calibration factors mainly in one direction. Therefore, overall error due to all geometry factors is a sum of biases that are one-way shifts in the calibration factor. For the three youngest phantoms, all the shifts are positive, which means that the calibration factor could be overestimated by a total of 51–60 percent. For the phantoms of the three older ages (10 and 15 years, and adult), the vertical positioning error produces a negative bias, which compensates somewhat, and the overestimations are about 41, 31, and 24 percent, respectively.

5.2. Comparisons with results of other studies

The calibration factors for ¹³¹I that have been estimated in this study were compared with those measured experimentally by Gavrilin et al. (1992) and Kaidanovsky and Dolgirev (1997). The results were also compared with results of other Monte Carlo calculations reported by Ulanovsky et al. (2004). Results of those comparisons are discussed below.

5.2.1. Comparison with calibration factors derived from measurements of people

Calibration factors for the SRP-68-01 device were determined experimentally by Gavrilin et al. (1992) and Kaidanovsky and Dolgirev (1997). These results provide an important test of the validity of calculations done in this study.

In 1988–1989, Gavrilin et al. (1992) measured thyroidal content of ¹³¹I administered to 110 adults in Hospital No. 6 in Moscow (Russia). During the measurements, the SRP-68-01 detector was placed in the lower point of the neck; the same position of the detector is used in the present study. The calibration factor for adults of 174 Bq μR⁻¹ h given in Table 6 is the arithmetic mean of a log-normal distribution of 110 estimates with geometric mean of 170 Bq μR⁻¹ h. Variability of calibration factors among the measured individual subjects is characterized by geometric standard deviation of 1.23. The corresponding standard deviation of 35 Bq μR⁻¹ h is also shown in the table.

Table 6.

Comparison of the SRP-68-01 device calibration factors for ¹³¹I in thyroid measured by Gavrilin et al. (1992), Kaidanovsky and Dolgirev (1997); calculated by Ulanovsky et al. (2004) and calculated in this study.

Reference	Calibration factor for 131I (Bq μR−1 h)
	Newborn	1 yr	5 yr	10 yr	15 yr	Adult
Measurements of people, lower point of neck
Gavrilin et al. (1992)	–	–	–	–	–	174±35
Kaidanovsky and Dolgirev (1997)a	–	136±26b		158±26c		180±29d
Calculated in this studye
Point estimate at lower point of neck	97±8f	94±6	106±10	133±13	165±17	193±17
Averaged over 1 cm interval	98g±8	100±6	110±10	126±13	147±15	167±15
Monte Carlo calculations, center of thyroid
Ulanovsky et al. (2004)h	98	101	108	128	140	163
Ulanovsky et al. (2004)i	108	112	119	141	155	180
This study	–j	–j	105±9	127±13	149±15	158±14

^aScale coefficient k=3.68 counts s⁻¹ μR⁻¹ h was used to re-calculated calibration factor given in kBq counts⁻¹ s.

^bMean and standard error of values for a group of 12 children aged 1–8 yr.

^cMean and standard error of values for a group of 24 children aged 8–16 yr.

^dMean and standard error of values for a group of 45 persons older than 16 yr.

^eCalculation was done for scenario of measurements with extended neck.

^fMean and 1-sigma random uncertainty (see Table 5).

^gPoint estimates as movements of the detector along the neck are not possible.

^hScale coefficient k=3.33 counts s⁻¹ μR⁻¹ h was used by Ulanovsky et al. (2004).

ⁱAdjusted to the scale coefficient k=3.68 counts s⁻¹ μR⁻¹ h obtained in this study.

^jPhysically impossible to place detector against the center of thyroid without extension of the neck.

Kaidanovsky and Dolgirev (1997) provide calibration factors (kBq counts⁻¹ s) derived from the results of measurements of ¹³¹I in thyroids for 12 children aged 1–8 years, 24 persons aged 8–16 years, and 45 persons older than 16 years. The measurements were performed in St. Petersburg in the laboratory of the radioisotope diagnostics. The calibration factors estimated by Kaidanovsky and Dolgirev (1997) in kBq counts⁻¹ s and the scale coefficient k=3.68 counts s⁻¹ μR⁻¹ h obtained in this study were used to obtain calibration factors that could be compared with our calculations. The mean calibration factors for each group and the standard errors are given in Table 6. Only random uncertainties for calibration factors calculated in this study are shown in Table 6. Uncertainties due to geometry deviations are not included for calibration factors calculated in this study as the measurements of people in hospitals with administrated ¹³¹I (Gavrilin et al., 1992; Kaidanovsky and Dolgirev, 1997) have been done by well-trained staff in a uniform manner.

For adults, the values calculated in this study are in good agreement with those determined experimentally in the other two studies. The age groups of children studied do not exactly match the ages of the phantoms, but there appears to be reasonably good agreement between the calibration factors of the SRP-68-01 device measured in individuals of different ages and those calculated in this study.

5.2.2. Comparison with other Monte Carlo calculations

Calibration factors for the SRP-68-01 device calculated by Ulanovsky et al. (2004) are for the detector placed against the center of the thyroid. Table 6 compares these calibration factors with calibration factors calculated for the geometry of measurements of Ulanovsky et al. (2004) using a mathematical model of the SRP device developed in this study. Calculations were done for phantoms of all ages except newborns and children aged 1 year because, for these ages, it is physically impossible to place the detector against the center of thyroid without extension of the neck. Ulanovsky et al. (2004) did not consider extension of the neck; so, the results of both studies were compared only for children aged 5, 10, 15 years, and for adults. As mentioned above, the value of the scale coefficient used in calculations by Ulanovsky et al. (2004) was 3.33 counts s⁻¹ μR⁻¹ h while the scale coefficient of 3.68 counts s⁻¹ μR⁻¹ h was used in this study. For comparison purposes, the calibration factors calculated by Ulanovsky et al. (2004) were adjusted to the value of scale coefficient obtained in this study. Both the original and adjusted calibration factors are shown in Table 6 together with our estimates for the same geometry. As can be seen, there is a good agreement between the two sets of calculated calibration factors of the SRP-68-01 device.

6. Conclusions

In this work, a mathematical model of the SRP-68-01 survey meter was developed and used to calculate the device calibration factors and the possible effects of mistakes in positioning the detector during direct thyroid measurements. The MCNP model of the device was verified by means of comparisons of the known activities of reference gamma radiation sources and calculated activities of those sources based on the exposure rate measurements. The SRP-68-01 survey meter scale coefficient, a characteristic defining the device response, was also measured as part of this study.

The mathematical model was used to estimate the calibration factors of the SRP-68-01 survey meter for ¹³¹I, ¹³²I, ¹³³I, and ¹³⁵I content in the thyroid gland for six age groups: newborns; children aged 1, 5, 10, 15 years; and adults. A realistic scenario of direct thyroid measurements with an “extended” neck was suggested to calculate the SRP calibration factors for newborns and 1-yr old children.

Uncertainties in the device calibration factors due to variability of the device scale coefficient, variability in thyroid mass and statistical uncertainty of Monte Carlo method were evaluated. The uncertainties in calibration factor estimates were found to be from 0.06 for children aged 1 year to 0.1 for 10-yr and 15-yr old children. The positioning mistakes of the detector during the measurement bias the estimated calibration factors mainly in one direction. Deviations of the device position from the proper geometry of measurements were found to lead to overestimation of the calibration factor by up to 24 percent for adults and up to 60 percent for 1-year old children. The main source of possible bias in the calibration factor was found to be movement of the detector away from the neck; it might overestimate the calibration factor by 32 percent for younger children and by 18 percent for adults. The results of this study improve the estimates of ¹³¹I thyroidal content and, consequently, thyroid doses due to ¹³¹I intake derived from direct thyroid measurements performed in Belarus shortly after the Chernobyl accident.