Mystery of FliK in Length Control of the Flagellar Hook

INTRODUCTION

A long history of the long hook: the first paper regarding hook length control in the flagellum appeared about 40 years ago. Silverman and Simon (1972) found that a flaE (the previous name of fliK in Escherichia coli) mutant produced extraordinarily long hooks, which they named polyhooks, and concluded that the flaE gene “functions to control the length of the hook” (22). Around the same time, Patterson-Delafield et al. (1973) found that a flaR (the previous name of fliK in Salmonella enterica serovar Typhimurium) mutant similarly produced extraordinarily long hooks, which they named superhooks (20). “Polyhook” connotes a repeated end-to-end polymer of the hook, whereas “superhook” simply connotes a long hook. Retrospectively, “superhook” might have been the proper name, since there is no evidence so far to show that the lengths of long hooks occur as integral multiples of the wild-type hook length. But we respect history and call it a polyhook today. Ironically, later on, we found extraordinary long polyhooks and named them super-polyhooks (19).

Because this topic has a long history and has involved contradictive explanations of similar data from many research groups, it is not easy to present all experimental data in chronological order. Many ideas and models have come and gone, but none of them is fully satisfactory. In this article, I discuss the currently most popular model from other laboratories and present our new model, which naturally opposes the current model. Because of limited space, I have to skip most of the biochemical and genetic data (Kelly Hughes may discuss these aspects in his paper) (7, 8) and also skip studies done with the needle complex of pathogenic bacteria (I see more similarities than differences between the two systems). Instead, I focus on physical aspects of the hook length control and begin with the statistics of hook length.

AN IMPORTANT MESSAGE FROM LENGTH DISTRIBUTION

In order to discuss length, it is crucial to begin with quantitative measurements of the hook length. Since the hook has a characteristically curved shape, it was difficult to measure the length of the hooks even with computer software for measuring curves without introducing errors. To make matters worse, the hook is thick (20 nm) in comparison with its length (55 nm), which would have caused further errors in measurements. Thus, it was desirable to measure straightened hooks. We modified the usual method of preparation of hooks for electron microscopy by staining grids using phosphotungstic acid at pH 4, because low pH and low temperatures cause a polymorphic transition of the hook shape from curved to straight.

The length distribution of the wild-type hook is rather broad, with an average of 55 nm and a standard deviation of 6 nm (5). This standard deviation is not a result of measurement errors. We find hooks as long as 80 nm, or as short as 30 nm, indicating that control of hook length is not tight at all. Furthermore, the broad, symmetric shape of the distribution suggests a stochastic process like diffusion rather than a deterministic one as seen with a physical ruler. Despite the large standard deviation, people tend to use the averaged value of length only, claiming that hook length is “well-controlled” at ca. 55 nm. The claim is misleading.

FliK IS THE KEY FACTOR IN HOOK LENGTH CONTROL

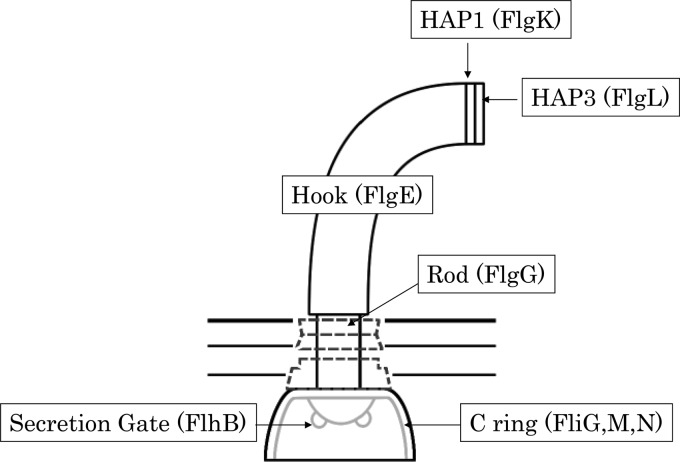
Since 1972, we have found all the proteins that play a role in hook length control. They are FlgE, FlgG, FlgK, FlgL, FliG, FliK, FliM, FliN, and FlhB (3, 5, 12, 19, 23, 25) (Fig. 1). FliK is the most mysterious among them. (i) FliK is not incorporated into the flagellar structure, while the others are structural proteins of the flagellum (1). (ii) FliK is soluble and secreted (13). When it is properly secreted, the average length of the hook is kept to ca. 55 nm. When it is not properly secreted, hook length is uncontrolled and increases. (iii) FliK is bifunctional, controlling the hook length and changing secretion substrates (so-called substrate specificity switching) (6, 25). (iv) The most striking feature of FliK is that the molecular size of FliK is proportional to the hook length (21). These facts urge people to believe that the FliK molecule directly measures the length of a growing hook as if it were a physical ruler.

Fig 1.

Schematic diagram of the flagellar hook-basal body. The component proteins of each substructure are indicated in parentheses.

In addition to the unique features, FliK has a characteristic structure. (v) The N-terminal half of FliK (FliK_N) is largely unstructured, while the C-terminal half (FliK_C) contains a compactly folded domain that interacts with FlhB to switch the secretion modes (16). These distinct structures are responsible for two separate functions: FliK_N is directly involved in length control, while FliK_C controls the hook length only by switching the substrate specificity of the secretion apparatus. It should be noted that these two functions are not independent of each other. When FliK_C is absent, the hooks keep elongating into polyhooks even in the presence of FliK_N. In contrast, as long as FliK_C is present, the hooks elongate to produce polyhooks with filaments attached, the so-called polyhook-filament phenotype. Moreover, when FliK_N is absent, overproduction of FliK_C fragments gives rise to shorter hooks in the polyhook filaments (6). Therefore, it seems that FliK_C plays a crucial role in ending hook elongation. What then is the role of FliK_N?

CRITICISM OF THE PHYSICAL RULER MODEL

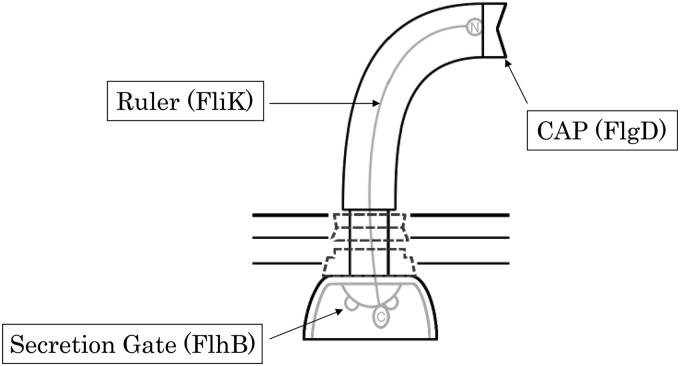
The physical ruler model claims that the FliK molecule measures hook length per se (4, 9, 17, 24). It works like this: FliK_N goes through a channel of the flagellar filament and interacts with FlgD, the cap protein of a growing hook, while FliK_C forms a globular structure and stays in the cytoplasm (Fig. 2). When FliK_N reaches its maximum length, a signal is transmitted to FliK_C to interact with FlhB, the secretion gate, at which point a conformation change occurs to switch the substrate specificity (15).

Fig 2.

The physical ruler model. The N terminus of FliK (circled “N”) binds to the cap protein (FlgD), while FliK_C stays in the cytoplasm. When FliK_N reaches the “mature” length, FliK_C interacts with FlhB to switch the substrate specificity.

The physical ruler model is popular at the moment, perhaps because the mechanism is simple and easily grasped. However, the physical ruler model goes against my understanding of the physical properties of proteins and peptides. First, it is difficult for me to imagine a stretched peptide working outside and inside the cell at the same time, and FliK_N is not large enough to be a sensor on the order of, e.g., chemoreceptors in the membrane. Second, there is inconsistency in the proposed mechanism; when a growing hook is still shorter than the FliK_N length, FliK_C must not work, and instead FliK may be exported and another FliK molecule may wait for the hook to reach a proper length. But when a growing hook is at the proper length relative to the length of FliK_N, FliK_C must act immediately to stop the hook elongation. This activity of FliK_C is thus purposely altered according to hook length. People who favor the ruler model often use phrases such as “when the hook reaches its mature length of 55 nm” or “when the hook elongates to its defined length” (14). The phrases do not really explain the model, because they do not say how the proper length is detected. Indeed, it is impossible for a FliK molecule to detect the hook length before it is secreted in this model.

The molecular clock model (17) is a variant of the physical ruler model. Length (L) and time (T) are independent parameters in physics. However, in our case, hook length L (in nanometers) and time T (in seconds) are intricately related to each other by the equation L = v′T, where v is the growth rate of the hook (in nanometers per second). The rate is possibly time-dependent, as we have previously shown by a statistical method (11). We cannot yet measure the length of time it takes each hook to grow. For now, let us stick to measurable length rather than introducing immeasurable time (2).

HOW MANY FliK MOLECULES ARE SECRETED?

It is important to know the number of FliK molecules secreted during assembly of a mature hook. In the original ruler model, FliK is assumed to be secreted several times until the hook length comes close to the FliK_N length. I and others previously showed that a FliK variant which lacked the FliK_N and thus did not secrete FliK_C at all produced normal hook lengths when the variant was overproduced (6). We also showed that amounts of the FliK variants, which have small deletions at various points in FliK_N, vary from an undetectable level (probably one FliK molecule per hook) to a very high level, although all the variants give rise to controlled hook lengths (21).

PROBLEMS WITH THE MEASURING-CUP MODEL

We previously proposed a model in which the C ring measures the amount of FlgE and subsequently determines hook length (12). Remember that a mutant devoid of the fliK gene produces polyhooks. The length distribution of polyhooks, however, shows a peak at 55 nm with an exponentially decreasing tail. Analysis of the two-phase curve suggested that hooks quickly grow to a length of ca. 55 nm and then continue to grow at a low but constant rate (11). If FliK were sporadically secreted, the likelihood would be high for FliK to go through the gate when the hook length is around 55 nm, and whether it does so could be determined by the amount of FlgE initially accumulated in the cup.

To test if the C ring could form a measuring cup, we constructed mutants lacking each component of the C ring. The mutants cannot form an intact C ring and thus cannot produce intact flagella. They, however, can produce a few intact flagella, if FliI (ATPase for secretion) is overproduced, which would enhance the secretion of flagellar proteins. The hook lengths in the C-ring mutants with overproduced FliI range from 10 nm to more than 100 nm in the presence of the intact FliK. The average length is ca. 65 nm (10). These data suggest that the C ring is necessary for tight control of the hook formation but not for determination of the hook length itself, arguing against the measuring-cup model.

THE WAITING-ROOM MODEL

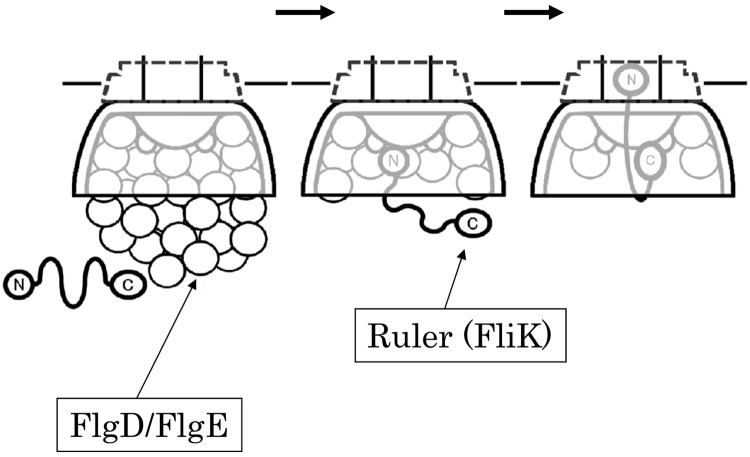
On proposing a new model, I would like to make one assumption, namely, that flagellar proteins accumulate within and around the C ring prior to secretion (Fig. 3). It is likely that the flagellar proteins to be secreted are localized at the basal area of the flagellum, because each flagellum grows independently from others in peritrichously flagellated bacteria. The C ring may act as the docking station for the soluble export proteins. In addition, we remember several facts: (i) FliK_N interacts with FlgD and FlgE (13); (ii) FliK_N is necessary for secretion (6, 14), (iii) the C terminus of FliK is necessary for completing the whole process (6, 15), and (iv) FliK_C interacts with FlhB (18).

Fig 3.

The waiting-room model. The N and C termini of FliK are indicated (circled “N” and circled “C”). FliK_N is indicated by a thick line. Empty circles represent FlgD or FlgE. FliK_C is anchored at FlhB. The N terminus of FliK is covered with FlgD/FlgE in the beginning. When FliK_N becomes free from FlgD/FlgE, FliK_N bends to allow access to the secretion gate.

When the basal area is filled with FlgD/FlgE, the N terminus of FliK (circled “N” in Fig. 3) cannot reach the secretion gate because it is held back by binding to FlgD/FlgE. The C terminus of FliK (circled “C” in Fig. 3) is anchored at FlhB in the C ring. FliK_N is covered with bound FlgE which is surging to the gate. When amounts of FlgD/FlgE decrease or are emptied from the basal area, then the N terminus of FliK has a chance to access the gate. When FliK_N enters the gate, FliK_C has a chance to bind to the FlhB of the gate. When FliK_N goes through the channel, FliK_C is pulled and detached from FlhB, which switches the substrate specificity. In this model (which I have named the waiting-room model), only one FliK molecule needs to detach from one FlhB to switch the secretion modes. Unbound FliK molecules may be secreted without affecting the state of FlhB, explaining the discrepancy in the numbers of secreted FliK molecules.

A SHORT CONCLUSION

To be honest, I am not sure about this new model. We have much more circumstantial than direct evidence; we know neither the number of FlhB subunits nor the ratio of FlgE to FliK accumulated at the base. However, I strongly believe that the hook length control is a cytoplasmic event and that the hook length is a result of the secretion of FlgE accumulated at the base. But I could be wrong in the details again. All in all, FliK may be secreted just to guarantee its efficient interaction with FlhB, which is hidden in the deepest location in the C ring; otherwise, the probability of the interaction would be far lower.