Weak Selection and Protein Evolution

Abstract

The “nearly neutral” theory of molecular evolution proposes that many features of genomes arise from the interaction of three weak evolutionary forces: mutation, genetic drift, and natural selection acting at its limit of efficacy. Such forces generally have little impact on allele frequencies within populations from generation to generation but can have substantial effects on long-term evolution. The evolutionary dynamics of weakly selected mutations are highly sensitive to population size, and near neutrality was initially proposed as an adjustment to the neutral theory to account for general patterns in available protein and DNA variation data. Here, we review the motivation for the nearly neutral theory, discuss the structure of the model and its predictions, and evaluate current empirical support for interactions among weak evolutionary forces in protein evolution. Near neutrality may be a prevalent mode of evolution across a range of functional categories of mutations and taxa. However, multiple evolutionary mechanisms (including adaptive evolution, linked selection, changes in fitness-effect distributions, and weak selection) can often explain the same patterns of genome variation. Strong parameter sensitivity remains a limitation of the nearly neutral model, and we discuss concave fitness functions as a plausible underlying basis for weak selection.

UNDER the neutral model, newly arising mutations fall into two major fitness classes: strongly deleterious and selectively neutral (Kimura 1968; King and Jukes 1969). The first class is well supported by mutation accumulation experiments (reviewed in Simmons and Crow 1977; Halligan and Keightley 2009) and early DNA sequence comparisons (Grunstein et al. 1976; Kafatos et al. 1977) and is shared among competing evolutionary models. The novel and controversial aspect of the neutral theory was the proposition that, among mutations that go to fixation, the vast majority are selectively neutral. Advantageous substitutions, although important in phenotypic evolution, are sufficiently rare at the molecular level that they need not be considered to adequately model the process. Under the neutral theory, within- and between-species variation sample two aspects of a process of origination by mutation and changes in gene frequency dominated by drift and, for some mutations, negative selection (Kimura and Ohta 1971a). In contrast, polymorphism and divergence may be “uncoupled” under selection models (Gillespie 1987).

Protein polymorphism and the neutral model: invariance of heterozygosity

Clear predictions for levels of polymorphism within populations and divergence among species are appealing aspects of the neutral model. However, within a few years of its proposal, the notion of drift-dominated evolution was challenged by overall patterns of allozyme polymorphism and contrasts between DNA and protein divergence.

Although evolutionary geneticists were generally surprised by the extent of naturally occurring variation revealed by allozyme gel electrophoresis in the 1970s (Lewontin 1991), the lack of species with high polymorphism levels became a central problem for proponents of the neutral theory (Robertson 1968; Maynard Smith 1970a; Lewontin 1974). The neutral model makes a simple prediction for protein heterozygosity, a summary statistic for levels of naturally occurring variation. Heterozygosity, H, is defined as the probability of randomly sampling different alleles from a population in two independent trials. Kimura and Crow (1964) determined expected heterozygosity for neutral alleles in an “idealized” population of constant size with random mating among hermaphroditic individuals. Generations are nonoverlapping in this scenario, and offspring are generated by randomly sampling gametes from the parents. Under such conditions, referred to as a Wright–Fisher population, and in the absence of mutation, genetic drift leads to a loss of heterozygosity at a rate inversely related to the population size. If new mutations arise in each generation, heterozygosity will reach an equilibrium between mutational input and loss by drift:

$$H=4Nv/\left(1+4Nv\right),$$

where v is the per-generation mutation rate to new, neutral alleles, and N is the number of diploid individuals in the population. If all amino acid changes are either strongly deleterious or selectively neutral, v can be replaced with the product of the fraction of neutral mutations (f_n) and the total mutation rate (u). To employ results for Wright–Fisher populations to predict heterozygosity (and other aspects of genetic drift) in populations that violate assumptions of the model, N is replaced by the “effective” population size (N_e) (see Charlesworth 2009). Incorporating both substitutions gives an expected heterozygosity of H = 4N_e f_nu/(1 + 4N_e f_nu).

Heterozygosity under the neutral model can be predicted given values for mutation rate and effective population size. Estimates for both parameters are crude, but Maynard Smith (1970b) and Nei and Graur (1984) predicted that levels of protein heterozygosity in large natural populations should approach the upper limit of 1. Although some species show close to zero allozyme variation, very few studies found H > 0.30. Species such as humans, Drosophila melanogaster, and Escherichia coli show roughly similar levels of protein polymorphism although their historical population sizes presumably differ greatly. This “invariance of heterozygosity” (Lewontin 1974) was argued as strong evidence against the neutral model.

Protein divergence and the neutral model

The neutral model also makes simple predictions for evolutionary divergence. For proteins, new mutations fall into two main fitness classes: strongly deleterious mutations that natural selection quickly eliminates from populations and neutral mutations that drift to fixation with probabilities equal to their initial frequency. Neutral mutations have smaller fixation probabilities in larger populations than in smaller populations, but this difference is exactly matched by the higher mutational input in larger populations, and the expected rate of neutral divergence is simply the mutation rate (and is independent of population size) (Wright 1938).

The initial motivation for Kimura’s proposal of the neutral theory was absolute rates of protein evolution that appeared to violate theoretical upper limits for adaptive fixations (Kimura 1968), but the molecular clock was quickly adopted as one of the strongest pieces of evidence supporting neutral evolution (Kimura and Ohta 1971a). The clock-like nature of protein evolution (Zuckerkandl and Pauling 1965) was considered to be in accord with the neutral theory’s prediction of lack of dependence on population size and inconsistent with adaptive models that predict rate dependence on both population sizes and the particular ecology of species. To account for the molecular clock, Kimura and Ohta (1971a,b) proposed that mutation rates are approximately constant per year. In addition, they suggested that the fraction of neutral mutations varies among proteins (this explains the among-protein rate variation) but remains relatively constant over time (this explains the clock-like divergence for each protein) (Kimura and Ohta 1971b). Kimura’s views on the importance of weakly selected mutations fluctuated over his career (Kimura and Takahata 1995); we will refer to the initial formulation discussed above as the “neutral model.”

Contrasting patterns of protein and DNA divergence forced a reconsideration of the fit of protein molecular clocks to the strict neutral model (Ohta 1972a). DNA divergence, accessed through DNA–DNA hybridization (Laird and McCarthy 1968; Kohne 1970), appeared to show a generation time effect (greater divergence in lineages experiencing larger numbers of generations per year) in contrast to the absolute-time dependence of protein evolution. The ratio of DNA to protein divergence varied considerably (>10-fold) among lineages. Under the neutral model, this ratio gives an estimate of 1/f_n for proteins (assuming f_n = 1 for DNA divergence), and such variation violated a tenet of the neutral model (Kimura and Ohta 1971a).

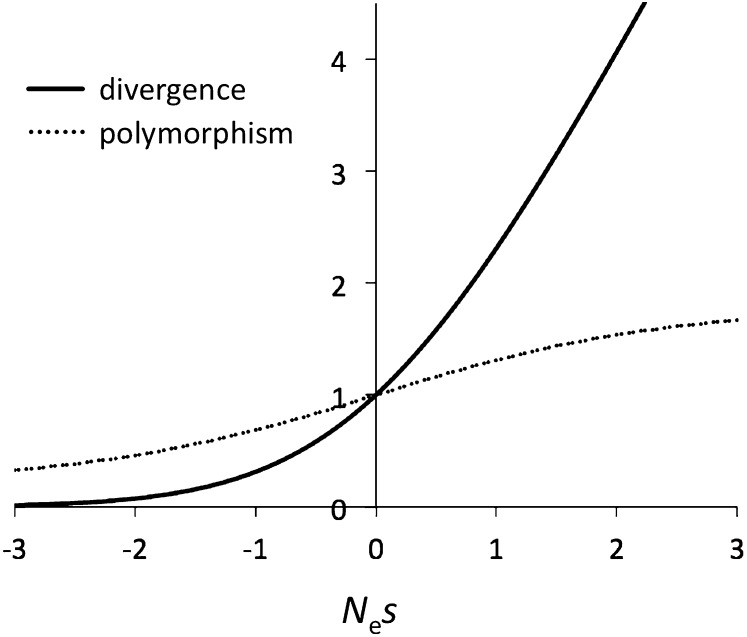
Ohta proposed that “nearly neutral” mutations could explain both the upper limit of protein heterozygosity and excess variation in protein divergence scaled to DNA divergence. The efficacy of selection depends on the product of selection coefficient and effective population size (N_es), referred to as “selection intensity” or “scaled selective effect.” The model assumes a large fraction of newly arising mutations with “borderline” fitness effects between clearly deleterious (N_es << −1) and selectively neutral (|N_es| << 1). Amino acid changes with subtle effects on protein folding could fall into this category (Barnard et al. 1972; Ohta 1973). For mutations in the nearly neutral range, the balance between the influence of genetic drift and natural selection is strongly dependent on effective population size. Figure 1 shows expected levels of within- and between-species variation for mutations with small fitness effects. Positive and negative selection increase and decrease expected levels of polymorphism and divergence, respectively, but the impact of selection is greater on divergence than on polymorphism. Interestingly, the rate of increase in polymorphism declines with the magnitude of positive selection. Although more strongly selected advantageous alleles have a reduced probability of loss by drift, they also show a shorter transit time within populations (and thus have a smaller probability of being sampled). Slightly deleterious mutations, N_es ≈ −1, have non-negligible probabilities of being sampled within populations and going to fixation relative to neutral mutations, but fixation probabilities drop to essentially zero for N_es < −3. Ohta defined nearly neutral mutations as those “whose selection coefficients are so small that their behavior is not very different from strictly neutral mutants. Operationally, this is defined by |N_es| < 1 (Ohta 1972b). The relative strengths of selection and genetic drift shift gradually near |N_es| ≈ 1, so “near neutrality” cannot be precisely defined (especially for s > 0). In this section, we employ Ohta’s definition of effectively neutral mutations in the range |N_es| < 1 and consider only deleterious mutations.

Figure 1 .

Polymorphism and divergence under weak selection. Expected levels of nucleotide diversity and DNA divergence (each relative to neutral mutations) are shown. The dotted line represents nucleotide diversity (probability of observing a polymorphism at a given nucleotide site in a pair of randomly chosen chromosomes) and is calculated using sampling formulas from Sawyer and Hartl (1992), assuming an infinite-sites mutation model and constant N_e. The solid line shows the fixation probabilities of mutations (Kimura 1962). The plots assume directional (genic) selection with fitness values 1, 1 + 1/2s, and 1 + s for the homozygote for the ancestral allele, heterozygote, and homozygote for a new mutation, respectively. The plots assume independent evolution among sites and are based on Kimura (1983, p. 44).

Under weak selection, expected heterozygosity becomes H ≈ 4N_e f′_nu/(1 + 4N_e f′_nu), where f_n from the neutral model is substituted by the fraction of nearly neutral mutations (f′_n). f_n is assumed (under the original neutral model) to be generally constant among lineages but f′_n is very sensitive to effective population size. For nearly neutral mutations, f′_n decreases as N_e increases; thus, heterozygosity increases more slowly as a function of population size than for neutral alleles (Ohta 1974; Ohta and Kimura 1975). Excess rare (low frequency) variants observed for allozyme data in a number of species (Latter 1975; Ohta 1975; Chakraborty et al. 1980) are consistent with slightly deleterious protein polymorphism.

Neutral and adaptive scenarios were also proposed to account for the invariance of allozyme heterozygosity. The expected relationship between H and N_e assumes that populations have reached a steady-state level of polymorphism. Nei and Graur (1984) developed a demographic hypothesis to explain the upper limit on heterozygosity; population sizes may fluctuate considerably on evolutionary timescales, and effective population size is especially sensitive to strong reductions. Consistently low heterozygosities result from bottlenecks during glaciation events; current population samples for many species reflect the recovery of neutral variation in expanding populations since the last glaciation. The approach to equilibrium heterozygosity can require 4–8N generations after population size changes (Nei and Graur 1984; Tajima 1989), and frequency spectra will be skewed toward rare polymorphisms during the recovery phase. Maynard Smith and Haigh (1974) showed that adaptive fixations can cause bottleneck-like reductions in variation and excess rare variants at neutral sites that are genetically linked to advantageous mutations, a process termed “genetic hitchhiking.” Deleterious mutations also reduce levels of neutral variation at linked sites (Charlesworth et al. 1995). Population bottlenecks and linked selection may contribute to the upper limit of heterozygosity for neutral variation, but weak selection in protein evolution also predicts differences in ratios of protein to synonymous polymorphism among populations (see below).

Nearly neutral mutations were also invoked to explain variation in rates of protein evolution. As noted above, DNA divergence appeared to be reduced in lineages with long generation times whereas protein evolution showed a more clock-like dependence on absolute time. Ohta and Kimura (1971) and Ohta (1972a) postulated an inverse relationship between generation time and effective population size to explain this discordance [e.g., among mammals, humans and elephants have longer generation times and presumably smaller population sizes than rodents (see Chao and Carr 1993)]. If mutation rates are expressed in units of generations, then the rate of protein divergence (nonsynonymous substitutions per site) in absolute time is f′_n ug, where u is the mutation rate per generation and g is the number of generations per year. An inverse relationship between f′_n and g can produce clock-like protein evolution if f′_n g is roughly constant. Because lineages that undergo fewer generations per year also experience less effective negative selection against slightly deleterious mutations, the ratio of protein to DNA divergence is positively correlated with generation time.

Structure of the Nearly Neutral Model

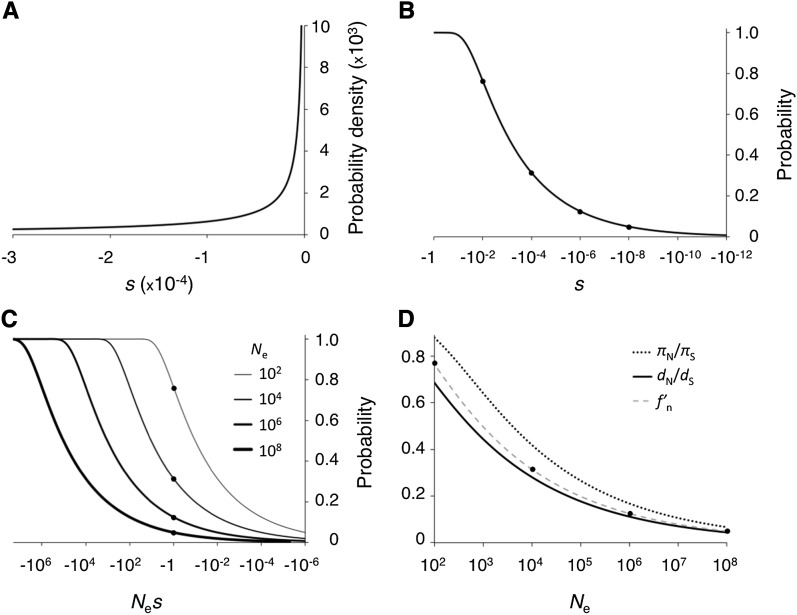
The nearly neutral model posits a distribution of selection coefficients with a large fraction of new mutations with fitness effects near the reciprocal of population sizes found in nature. This section will give an illustration of the model and its predictions. Figure 2A shows an example of the probability distribution of selective effects (DSE) of new mutations that puts a substantial density in the nearly neutral range for a wide range of population sizes, 10² < N_e < 10⁸. Initially, we considered only deleterious mutations. It is important to note that “weakly selected” refers to the magnitude of N_es rather than to the functional or fitness effects of mutations. This distinction is critical because empirical studies define “strong” and “weak” effects relative either to an absolute scale or to the sensitivity of the assays used. The limit of detection for laboratory studies, even in large-scale fitness assays for microbes, is usually s > 0.001 (e.g., Dykhuizen and Hartl 1983; Lind et al. 2010; Hietpas et al. 2011). “Weakly selected” alleles in such studies would be well outside the nearly neutral range in many natural populations; mutations of |N_es| ≈ 1 in populations with effective sizes N_e > 10⁴ may be undetectable in fitness and phenotype assays.

Figure 2 .

Example evolutionary patterns under slightly deleterious mutations. (A) A probability density function for negative selection coefficients (gamma distribution with shape parameter 0.2 and scale parameter 0.05). The area under the curve gives the proportion of mutations in a given fitness range. This distribution of s was chosen to allow substantial increases in the effectively neutral proportion for population sizes in the range 10²–10⁸ and is assumed in plots in B, C, and D. Under this distribution of selective effects (DSEs), <25% of newly arising mutations have s < −0.01 and <2% of mutations have s < −0.1. (B) Cumulative distribution function for selective effects of new mutations. y-axis values are the total areas under the curve in A for x < s < 0. f′_n, the proportion of “effectively neutral” mutations, −1 < N_es ≤ 0, for a given population size is the y-axis value at x = 1/N_e (values are marked for N_e of 10², 10⁴, 10⁶, 10⁸). (C) Cumulative distribution function for N_es. y-axis values are the areas under the DSE curve for x < N_es < 0 in A. Curves are shown for N_e of 10², 10⁴, 10⁶, and 10⁸ (thicker lines represent larger population sizes). f′_n values are indicated (as solid circles) for each population size. (D) Polymorphism and divergence as a function of N_e. Expected DNA diversity (π_N/π_S, dotted line) and divergence (d_N/d_S, solid line) are shown. The dashed line shows f′_n, and values for N_e of 10², 10⁴, 10⁶, and 10⁸ are marked. Expected divergence is smaller than f′_n because selection reduces fixation rates for slightly deleterious mutations within this range. π_N/π_S values are higher than f′_n because mutations in the range N_es < −1 contribute to polymorphism (Figure 1). These plots assume independent evolution among sites.

Figure 2B shows the cumulative distribution function for the DSE shown in Figure 2A. Expected levels of polymorphism and divergence are functions of scaled selective effects, N_es (Figure 1), and Figure 2C shows the cumulative distribution functions for N_es across a range of population sizes. Many mutations that fall into the “effectively neutral” range in small populations are strongly selected in larger populations, and f′_n varies considerably as a function of N_e. Expected polymorphism and divergence patterns under this DSE are shown in Figure 2D. Polymorphism is less reduced under weak selection than divergence but both decrease at substantial rates over a wide range of N_e.

In the analyses above, we have assumed no new mutations that enhance fitness, s > 0. Adaptive evolution may often occur in response to environmental change. Because slightly deleterious fixations go to fixation at appreciable rates, nearly neutral models must allow for slightly advantageous mutations, including back mutations and compensatory mutations (Ohta 1972b, 1973; Latter 1975; Ohta and Tachida 1990), even in the absence of pressure for novel function. Compensatory evolution retards the slow decline in fitness by slightly deleterious fixations and will be more effective if some compensatory mutations have large positive fitness effects (i.e., if they can compensate for multiple deleterious fixations).

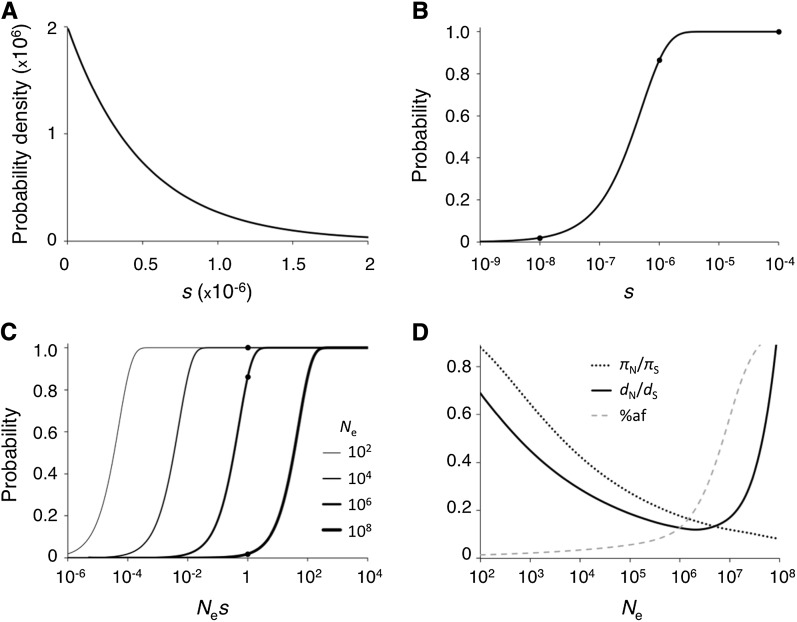
Figure 3A shows an example DSE for advantageous mutations. Even a small fraction of such mutations can have a substantial impact on divergence (we assume that 99% of new mutations are drawn from the deleterious DSE shown in Figure 2A and that 1% of mutations are drawn from the DSE shown in Figure 3A). Expected polymorphism and divergence under the combined deleterious and adaptive DSE are shown in Figure 3D. Advantageous mutations contribute little to polymorphism, and DNA diversity shows a negative relationship with N_e similar to the deleterious mutations case. However, larger populations have smaller proportions of deleterious, and larger proportions of adaptive, fixations. The fixation rate of new mutations begins to increase as a function of population size when the proportion of effectively selected positive mutations (N_es > 1) becomes large. The effect of population size on expected polymorphism and divergence can be highly sensitive to the particular DSE; we present a single example to illustrate relationships among DSEs, population size, and evolutionary patterns under the nearly neutral model.

Figure 3 .

Example evolutionary patterns for slightly deleterious and advantageous mutations. (A) Probability density function for positive selection coefficients (gamma distribution with shape parameter 1 and scale parameter 5 × 10⁻⁷). (B) Cumulative distribution function for selective effects of new mutations. y-Axis values are the total areas under the curve for 0 < s < x in A. f′_n for a given population size is the y-axis value at x = 1/N_e (values are marked for N_e of 10⁴, 10⁶, 10⁸). Almost all beneficial mutations are effectively neutral in N_e of 10² and 10⁴, and almost none are effectively neutral in N_e of 10⁸. (C) Cumulative distribution function for N_es or scaled selective effects. y-Axis values are the areas under the DSE curve for 0 < N_es < x in A. Curves are shown for N_e values of 10², 10⁴, 10⁶, and 10⁸ (thicker lines represent larger population sizes). f′_n values are shown as solid circles for each population size. (D) Polymorphism and divergence as a function of N_e for a distribution of fitness effects that combines the density functions in Figure 2A (99% of new mutations) and Figure 3A (1% of new mutations). The dashed line shows the proportion of advantageous fixations. Expected DNA diversity (π_N/π_S, dotted line) and divergence (d_N/d_S, solid line) are shown. These predictions assume independent evolution among sites.

Evidence for Weak Selection in Protein Evolution

Both DNA variation data and statistical methods for testing evolutionary mechanisms have proliferated tremendously in the past decade, and we summarize key findings related to the nearly neutral model below.

Population size and rates of evolution

Negative relationships between rates of protein evolution and population size are a clear prediction of near neutrality; Ohta (1972a) showed such correlations in Drosophila and mammals. Although generation time may be a noisy predictor of N_e and DNA–DNA hybridization gives only rough measures of distance, Ohta's study is notable for introducing an early form of comparison of nonsynonymous and putatively neutral divergence to test evolutionary models. More recent analyses often employ the ratio of nonsynonymous to synonymous DNA divergence per site (d_N/d_S) to estimate f_n or f′_n under the neutral and nearly neutral models, respectively.

Several genome-scale comparisons support the weak-selection prediction of inverse relationships between d_N/d_S and population size. Faster protein evolution in primates compared to rodents was observed in early studies limited to small numbers of genes (Li et al. 1987; Ohta 1995), and the pattern has been confirmed in larger-scale analyses (Chimpanzee Sequencing and Analysis Consortium 2005; Rhesus Macaque Genome Sequencing and Analysis Consortium et al. 2007). In addition, substitutions among amino acids with greater physicochemical differences have been more frequent in primates than in rodents (Zhang 2000; Eyre-Walker et al. 2002; Hughes and Friedman 2009). Analyses of nuclear genes in a broader range of mammals revealed a twofold variation in d_N/d_S and negative relationships between d_N/d_S and estimates of population size (Lindblad-Toh et al. 2005; Kosiol et al. 2008; Ellegren 2009). Wright and Andolfatto (2008) noted that such a relationship extends to comparisons among pairs of bacteria, Drosophila, plants, and mammals. The relationship is strong, but DSEs may not be conserved across distantly related organisms.

Independent comparisons between host-dependent bacterial lineages and their free-living relatives show consistently faster evolution in endosymbionts (Moran 1996; Wernegreen and Moran 1999) as well as pathogens (Andersson and Andersson 1999; Warnecke and Rocha 2011). Wernegreen (2011) also noted a higher ratio of radical-to-conservative amino acid replacement changes in insect symbionts relative to free-living relatives. Vertically transmitted symbionts, such as Buchnera in aphids, experience population bottlenecks during transmission from parent to embryo as well as population-size fluctuations of the host species. In addition, symbiont genomes experience limited opportunities for recombination; genetic linkage among selected mutations reduces the efficacy of natural selection in a manner similar to reduced N_e (Hill and Robertson 1966; Felsenstein 1974; Birky and Walsh 1988; Charlesworth 1994; Barton 1995). Low heterozygosity at synonymous positions is consistent with small population sizes of bacterial endosymbionts (Funk et al. 2001; Abbot and Moran 2002; Herbeck et al. 2003).

Because reduced N_e is associated with the ecology of host dependence, shifts in DSEs should also be considered as a cause of elevated protein divergence. In particular, “relaxed selection,” an increased density of mutations with very small effects, is plausible in an intracellular environment that may be more stable than environments of free-living microbes (especially for insect and animal hosts) and from which many metabolites can be obtained directly (Moran 1996). In this scenario, an increase in the density of mutations with fitness effects in the range −1 < N_es < 0 reflects an elevated proportion of amino acid changes with smaller selection coefficients rather than (or in addition to) a reduced N_e. Interestingly, several fast-evolving endosymbiont lineages show high expression of heat-shock proteins (McCutcheon and Moran 2011). GroEL, an ATP-dependent bacterial chaperonin that assists in protein folding, is among the most abundant proteins in independently derived endosymbionts. Elevated heat-shock protein expression may be part of a compensatory response to slightly deleterious fixations that destabilize proteins (Moran 1996; van Ham et al. 2003; Fares et al. 2004) and could be an example of a relatively small number of adaptive changes counteracting a much larger number of deleterious fixations. GroEL overexpression can enhance growth rates of laboratory strains of bacteria that have accumulated mutations but show a cost in the ancestral strains (Moran 1996; Fares et al. 2002). Interestingly, this cost is apparent only when ancestral strains are grown in amino-acid-limited environments. Elevated heat-shock protein expression may be favored in endosymbiont lineages that have accumulated destabilizing mutations. Enhanced protein folding should reduce the fitness effects of further destabilizing amino acid changes (i.e., shift the distribution of selection coefficients) (Tokuriki and Tawfik 2009a). Thus, elevated heat-shock protein expression and accumulation of destabilizing mutations may form a positive feedback loop until the benefits of further chaparonin overexpression no longer outweigh the costs.

A number of cases of accelerated divergence in small populations have been documented for proteins encoded in mitochondrial genomes. Island bird species show elevated rates of protein evolution relative to their mainland counterparts (Johnson and Seger 2001), and similar patterns hold for other vertebrates as well as invertebrates (Woolfit and Bromham 2005). Higher d_N/d_S in obligately asexual lineages than in sexual lineages of Daphnia (Paland and Lynch 2006) and freshwater snails (Johnson and Howard 2007; Neiman et al. 2010) is consistent with elevated Hill–Robertson interference with reduced opportunities for recombination [between mitochondrial DNA (mtDNA) and nuclear genomes] and/or greater frequencies of founder events in asexual lineages (Glémin and Galtier 2012). However, asexual lineages are often short-lived, tip branches on the phylogeny, and d_N/d_S for these lineages may include a greater fraction of polymorphic mutations than in sexual lineages. Both d_N/d_S and ratios of radical-to-conservative amino acid fixations are positively correlated to body mass for mtDNA-encoded proteins (13 genes) among >100 species of mammals (Popadin et al. 2007). If body mass and N_e are inversely related (Damuth 1981), these patterns support slightly deleterious fixations in large mammals. In many of the examples above, lineages that are thought to differ in N_e also differ in their ecology; differences in DSEs remain a plausible alternative, or a contributing factor, to heterogeneity in protein divergence. In addition, Bazin et al. (2006) found little evidence for positive correlations between mtDNA heterozygosity and proxies for effective population size (allozyme and nuclear DNA variation) across a wide range of taxa. They suggested that complete genetic linkage in mtDNA genomes and recurrent positive selection (Gillespie 2001) may underlie such patterns. However, within-taxa comparisons show positive correlations between mtDNA heterozygosity and nuclear genome variation in mammals (Mulligan et al. 2006; Nabholz et al. 2008) and other animals (Piganeau and Eyre-Walker 2009). Variation in mutation rates, adaptive evolution, and/or biased transmission may contribute to within- and between-taxa differences for mtDNA polymorphism.

Within-genome comparisons can also test for relationships between N_e and protein evolution. Near neutrality predicts faster protein evolution in regions of reduced recombination, and such patterns have been confirmed in yeast (Connallon and Knowles 2007; Weber and Hurst 2009) and Drosophila (Campos et al. 2012; Mackay et al. 2012). Because these studies compare evolutionary rates among different genes, differences in DSEs may contribute to heterogeneity. Such differences may be related to the functional categories of genes that reside in regions of low recombination and/or to their expression level. Interestingly, in Drosophila, subsets of loci such as male-biased genes (Betancourt and Presgraves 2002; Presgraves 2005; Zhang and Parsch 2005) and D. melanogaster lineage accelerated genes (Larracuente et al. 2008) show the opposite trend: positive correlations between recombination and d_N/d_S consistent with limits to adaptive evolution under low recombination. Primates show no correlation between d_N/d_S and the rate of recombination (Bullaughey et al. 2008), but relationships between local recombination rates and DNA diversity in the human genome are weak (Hellmann et al. 2005).

Interpretations of among-lineage and within-genome d_N/d_S tests of near neutrality are complicated by recent evidence that a majority of protein changes are adaptively fixed in many species (reviewed in Fay 2011). Advantageous mutations go to fixation at higher rates in larger N_e when they are weakly selected and when adaptive evolution is mutation-limited. In such cases, d_N/d_S can show positive relationships with N_e (Figure 3D) even in the presence of slightly deleterious mutations.

Population size and protein polymorphism

Several assumptions are necessary when attributing variation in protein divergence to near neutrality. Advantageous substitutions should be rare, and DSEs must remain constant among the lineages compared. In addition, relative ancestral effective population sizes must be known. Some studies assume relationships between N_e and the ecology of organisms (e.g., host-cell dependence, island habitats), and other studies estimate N_e from current polymorphism levels. The former approach leaves open the possibility of associations between the “life style” of organisms and their DSEs. The latter method allows inference of N_e in roughly the last 4N generations. In most cases, molecular divergence measured by d_N/d_S occurred at a much deeper time scale. Finally, inferring f′_n from d_N/d_S requires an assumption of neutral divergence at synonymous sites and accurate estimation of d_S. Both natural selection (reviewed in Akashi 2001; Chamary et al. 2006; Hershberg and Petrov 2008; Plotkin and Kudla 2010) and biased gene conversion (reviewed in Birdsell 2002; Marais 2003; Duret and Galtier 2009) can cause fixation biases in synonymous divergence. In addition, estimates of d_S can differ considerably among methods when base composition is biased and/or when divergence is large (Dunn et al. 2001; Bierne and Eyre-Walker 2003; Aris-Brosou and Bielawski 2006).

Weak selection also predicts inverse relationships between polymorphism levels (scaled to neutral values) and N_e (see Figures 2 and 3). The DNA analog of heterozygosity in allozyme data is “nucleotide diversity,” the number of differences (per nucleotide site) in a randomly selected pair of chromosomes from a population (π). Under neutral protein evolution, equilibrium DNA diversity at nonsynonymous sites is

$${\mathit{\pi }}_{\mathrm{N}}=4N_{\mathrm{e}}{f}_{\mathrm{n}}u,$$

where u is the total mutation rate (Kimura 1969; Watterson 1975; Tajima 1983). If all synonymous mutations are neutral, π_N/π_S provides an estimate of f_n, which, under the neutral model, should be generally constant among species. Under near neutrality, π_N/π_S gives an estimate of f′_n, the proportion of effectively neutral mutations that are strongly dependent on N_e [note that f′_n estimates from polymorphism include mutations with a larger range of selection intensities than f′_n estimated from divergence (see Figure 1)]. Fluctuations in population size and/or linked selection may contribute to the invariance of allozyme heterozygosity, but such factors do not affect expected π_N/π_S for neutral protein polymorphism.

Tests of weak selection that compare polymorphism among populations are robust to some of the assumptions required in divergence tests. Estimates of population size from present-day populations should be more accurate for the relevant N_e. Since advantageous mutations make small contributions to polymorphism (under directional selection), comparisons of π_N/π_S are less affected by adaptive evolution than divergence (Figure 3). In addition, although neutrality at synonymous sites (or other control classes such as introns) may not be strictly valid, weak selection in the control class will have less impact on polymorphism than fixation. Finally, π_N/π_S comparisons can be performed among closely related species (or even among populations of the same species if they are evolving independently). The critical assumption of DSE identity is more likely to hold among closely related organisms than among more distantly related species.

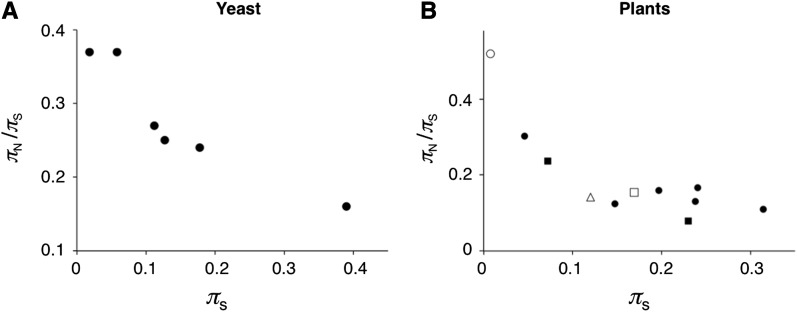
Elyashiv et al. (2010) found negative relationships between π_N/π_S and estimates of population size among closely related yeast species. π_S varies roughly 10-fold among essentially independently evolving populations of Saccharomyces cerevisiae and S. paradoxus, suggesting similar variation in N_e. Although data were available for only six populations, π_N/π_S varies considerably among populations (from 0.16 to 0.37) and shows a negative correlation with π_S. Piganeau and Eyre-Walker (2009) showed negative correlations between π_N/π_S and π_S for mtDNA genes across more distantly related species within several taxa (they examined >1700 species including fish, birds, mammals, insects, and mollusks).

π_N/π_S ratios for mammal and plant nuclear genes also show negative associations with estimates of population size. In comparisons limited to a small number of genes, Satta (2001) found higher π_N/π_S in humans than in chimps; this difference has been confirmed in genome-scale analyses (Hvilsom et al. 2012). π_N/π_S is also higher in humans (0.35) than in mice (0.19; Halligan et al. 2010) and rabbits (0.05; Carneiro et al. 2012), which is consistent with substantial differences in f′_n. Among a larger number of plant species, π_N/π_S varies by roughly fourfold among species and is inversely related to estimates of N_e (which ranges from ∼3 × 10⁴ to ∼7 × 10⁵) (Gossmann et al. 2010; Slotte et al. 2010; Strasburg et al. 2011).

Figure 4 shows protein polymorphism comparisons among yeasts and plants. Both yeast and plants show negative relationships between π_N/π_S and π_S as predicted under weak selection. π_N/π_S is lower among Drosophila species than among mammals (both overall and among homologous genes involved in the metabolic process) (Petit and Barbadilla 2009), but patterns within Drosophila are unclear (the numbers of sampled populations is low; see supporting information, Table S1). Polymorphism patterns for individual species can be attributed to differences in DSEs rather than population size [e.g., high π_N/π_S in humans has been attributed to relaxed selection (Takahata 1993; Satta 2001)]. Sampling species with a breadth of population sizes in a larger number of taxa will be necessary to establish N_e as a key factor determining the proportions of weakly and strongly deleterious mutations and to test whether near neutrality underlies the invariance of protein heterozygosity.

Figure 4 .

Levels of nonsynonymous and synonymous DNA polymorphism among populations. DNA diversity for nonsynonymous mutations (scaled to DNA diversity for synonymous mutations) is plotted against DNA diversity for synonymous mutations (an estimate of population size). π_S is a proxy for population size if mutation rates are similar among the species compared. Note that statistical analyses of such data must account for the contribution of π_S to both axes (Piganeau and Eyre-Walker 2009; Elyashiv et al. 2010). Common symbols in each plot indicate the same set of genes compared among species. Data are shown for taxa for which six or more independent populations have been sampled for ≥20 nuclear genes. See Table S1 for species names, sample numbers, number of loci, and references (as well as data for a more limited number of Drosophila species).

Within-lineage contrasts of polymorphism and divergence

The examples above employed mostly among-lineage contrasts in the evolutionary dynamics of protein and DNA mutations to test mechanisms of molecular evolution. Within-lineage comparisons offer an alternative approach to test for natural selection acting at its limit of efficacy. We first consider approaches restricted to polymorphism data. As discussed above, frequency spectra for allozyme variation are often skewed toward an excess of rare (low frequency) variants in mammals and Drosophila (Latter 1975; Ohta 1975; Chakraborty et al. 1980). These studies compared data for a single class of mutations to a theoretical expectation for neutral alleles at steady state (see also Watterson 1977); rejection of the null hypothesis is consistent with either selection or departures from equilibrium. Bulmer (1971) took a different approach in directly comparing observed frequency distributions among classes. At loci segregating for more than two alleles, common allozyme variants consistently showed intermediate electrophoretic mobility whereas rare alleles tended to show extreme (both slow and fast) mobility. The statistical approach compared patterns for within-locus mutation classes and rejected equal fitness effects among mobility classes (the neutral model predicts no association between frequency and mobility) in favor of natural selection. Because electrophoretic mobility is primarily dependent on the overall charge of proteins, Bulmer’s findings are consistent with stronger deleterious effects of radical amino acid mutations relative to conservative changes.

Comparisons among functional categories of mutations that are interspersed in DNA can resolve overlapping predictions for demographic and selection scenarios in tests of the neutral model. Sawyer et al. (1987) proposed direct comparisons between the site frequency spectra for nonsynonymous and synonymous DNA polymorphisms (interspecific data were not available). Their study showed an excess of rare amino acid variants among naturally occurring alleles of an E. coli gene. Sawyer et al. (1987) argued that inference of natural selection from direct comparisons among classes of mutations from the same gene is robust. Because factors that affect variation in a given genetic region (e.g., demographic history or genetic linkage to selected sites) have similar impacts on synonymous and nonsynonymous mutations, differences in their frequency spectra can be attributed to differences in their fitness effects. A similar argument for robustness applies to the Bulmer test discussed above.

McDonald and Kreitman (1991) included divergence data in direct comparisons of mutation classes interspersed in DNA. Their test divides variable sites into two classes (polymorphic mutations are pooled into a single class and compared to fixed differences). The test relies on the sensitivity of the ratio of the numbers of polymorphic-to-fixed differences (r_pd) to even very weak selection (Figure 1). Slightly deleterious amino acid polymorphisms elevate nonsynonymous r_pd, whereas adaptive protein evolution has the opposite effect.

We will refer to the general category of approaches that compare frequency spectra and fixations between classes of mutations interspersed in DNA as “population genetics of interspersed mutations” (PGIM) tests. Numerous studies have reported PGIM patterns consistent with slightly deleterious amino acid changes. Excess rare polymorphisms and higher r_pd for nonsynonymous compared to synonymous variation appear to be general patterns in viral (Edwards et al. 2006; Pybus et al. 2006; Hughes 2009) and bacterial genomes (Hughes 2005; Charlesworth and Eyre-Walker 2006; Rocha et al. 2006; Hughes et al. 2008) as well as in animal mtDNA (Ballard and Kreitman 1994; Nachman et al. 1996; Rand and Kann 1996; Hasegawa et al. 1998; Wise et al. 1998; Weinreich and Rand 2000; Gerber et al. 2001; Subramanian et al. 2009). Similar patterns have been noted in nuclear genes from yeast (Doniger et al. 2008; Liti et al. 2009), Drosophila (Akashi 1996; Fay et al. 2002; Loewe et al. 2006; Begun et al. 2007; Shapiro et al. 2007; Haddrill et al. 2010; Andolfatto et al. 2011), humans (Cargill et al. 1999; Sunyaev et al. 2000; Hughes et al. 2003; Williamson et al. 2005; Boyko et al. 2008; Keightley and Halligan 2011; Subramanian 2012), mice (Halligan et al. 2010), and plants (Bustamante et al. 2002; Nordborg et al. 2005; Foxe et al. 2008; Fujimoto et al. 2008; Gossmann et al. 2010; Slotte et al. 2010; Branca et al. 2011; Strasburg et al. 2011). Excess rare polymorphism could reflect very strongly deleterious mutations if the number of sampled chromosomes is very high, but sample sizes in most of these studies do not approach such levels. Interpretations of PGIM patterns often assume random sampling from a panmictic population, but some of the studies above are likely to include alleles from structured populations; in such cases, local adaptation could contribute to excess protein polymorphism. Balancing selection, more generally, is consistent with high nonsynonymous r_pd and, under some conditions, with excess rare variants (Gillespie 1994a). Genome scans have detected little evidence for major contributions of long-term balancing selection in humans (Andrés et al. 2009) and Drosophila (Wright and Andolfatto 2008), but the genomic signal for other forms of balancing selection may be more subtle (Charlesworth 2006).

The null hypothesis of PGIM tests is identical distributions of selection intensities among classes of DNA mutations. Additional information, such as an assumption of neutral mutations for one of the classes, allows inference of the sign of selection coefficients. The statistical power to detect selection can be improved by including both frequency spectra and divergence data [i.e., by combining the Sawyer et al. (1987) and McDonald and Kreitman(1991) approaches] and by inferring frequencies for newly arisen polymorphisms (Akashi 1999a; Bustamante et al. 2001). Such information also allows inference of the relative contributions of slightly deleterious, effectively neutral, and advantageous substitutions to genome evolution (Charlesworth 1994; Akashi 1999b; Fay et al. 2001; Bustamante et al. 2002; Smith and Eyre-Walker 2002; Sawyer et al. 2003, 2007). Recent approaches jointly estimate demographic parameters (e.g., population size changes) and distributions of N_es (Williamson et al. 2005; Keightley and Eyre-Walker 2007; Boyko et al. 2008; Eyre-Walker and Keightley 2009; Schneider et al. 2011; Wilson et al. 2011). Although the number of taxa that have been examined remains limited, current findings are generally consistent with an N_e effect on the efficacy of negative selection on nonsynonymous polymorphism (discussed above). The proportion of adaptive protein fixations among lineages also shows some indications of a positive association with population size (Gossmann et al. 2012). Such associations are expected for both weakly selected beneficial alleles and more strongly selected alleles when rates of adaptive evolution are mutation-limited. Among mammals, PGIM studies support ∼60% adaptive protein fixations in mice and rabbits (Halligan et al. 2010; Carneiro et al. 2012) compared to a point estimate of 0% (and a rough maximum estimate of ∼40%) in humans (Eyre-Walker and Keightley 2009). Adaptive proportions range from 0 to 50% among sunflower species and show positive relationships with estimates of N_e (Strasburg et al. 2011). Several studies estimate >50% adaptive evolution in three Drosophila species believed to have large population sizes (Smith and Eyre-Walker 2002; Bierne and Eyre-Walker 2004; Welch 2006; Maside and Charlesworth 2007; Haddrill et al. 2008; Schneider et al. 2011; Wilson et al. 2011), but adaptive proportions are also high in a species with a substantially lower estimate of N_e (Bachtrog 2008).

McDonald and Kreitman (1991) discussed a potential caveat in PGIM inference of adaptive protein evolution. Spurious evidence for positive selection can arise from a combination of weakly deleterious mutations and changes in population size (see also Ohta 1993; Eyre-Walker 2002; Hughes 2008). Current approaches to estimate selection intensity assume that N_es has remained constant over the period that sampled polymorphisms and fixed differences have arisen. However, consider a case where fixed differences accumulate in a small population that subsequently increases so that the sampled polymorphisms come from the larger population whereas a large proportion of the fixed differences occurred in the smaller, ancestral N_e. In our example (Figure 2), a population size of 10² has a >2.5-fold higher d_N/d_S than a population of 10⁴. Under such a scenario, an excess of slightly deleterious fixations will reduce nonsynonymous r_pd relative to the constant population size case. This pattern would be interpreted as evidence for adaptive evolution under assumptions of constant DSE and effective population size. Current approaches to jointly estimate demographic parameters and distributions of N_es do not attempt to adjust for excess amino acid fixations in cases of smaller ancestral populations.

Slightly deleterious fixations in ancestral populations remain a viable alternative explanation for excess replacement fixations in PGIM tests. McDonald and Kreitman (1991) argued that such scenarios require extensive parameter tuning (particular combinations of DSE, population sizes, and timing of population size change) and favored the simpler explanation of adaptive evolution. Fay et al. (2002) claimed that considerable among-gene variation in nonsynonymous r_pd favors adaptive evolution rather than slightly deleterious fixations. This argument assumes similar DSEs among genes, but the basis for this assumption is unclear. DSEs are likely to be determined by structural features of proteins (e.g., ratio of solvent exposed to buried residues) as well as their expression patterns, and both factors may vary widely among genes. Eyre-Walker and Keightley (2009) suggested that the scenario of deleterious fixations in small ancestral populations is unlikely to explain low protein r_pd across multiple lineages. This argument is valid if high rates of adaptive protein evolution are consistently found among species with independent population histories but does not address evidence for high rates of adaptive protein evolution in particular lineages or cases where support for adaptive evolution varies among species (e.g., plants). Incorporating a model of codon bias evolution in tests of positive selection at other site classes may help to distinguish between deleterious and adaptive fixations (Akashi 1999a).

Compensatory Protein Evolution

Determining the contribution of alleles of small effect in adaptive evolution is a challenge for polymorphism/divergence analyses. The notion that adaptive evolution should “advance by the shortest and slowest steps” (Darwin 1859) remains a central assumption in many theories of adaptation (reviewed in Orr 2005). Further developments in statistical approaches may provide a means to infer DSEs among positively selected mutations, but disentangling the proportion of adaptive fixations and the magnitude of their effects may prove difficult (Boyko et al. 2008; Schneider et al. 2011).

Weakly beneficial mutations may include compensatory changes that maintain fitness in the face of abundant slightly deleterious fixations. The term “compensatory” has been used in a number of contexts, and we will first attempt to clarify some terminology. Kimura (1985) focused on scenarios of simultaneous substitutions of relatively strongly deleterious and compensatory mutations. Because fitness remains constant and genetic drift drives double-mutant substitution, we refer to such cases as “compensatory neutral” (CN). Weakly deleterious mutations can go to fixation at appreciable rates, and we refer to the restoration of fitness by subsequent, positively selected mutations as “compensatory weak selection” (CWS) (Osada and Akashi 2012). Note, however, that such mutations can confer large fitness benefits if they compensate for multiple deleterious fixations. Finally, several studies of artificial protein evolution have found that adaptive amino acid fixations are followed by beneficial fixations that restore pleiotropic deleterious effects of the initial substitution (reviewed in Andersson and Hughes 2010). The latter class often includes mutations that elevate protein stability (Wang et al. 2002; Ortlund et al. 2007; Tokuriki et al. 2008). If the initial substitution is positively selected (s > 0 despite pleiotropic effects), we refer to subsequent beneficial fixations as “compensatory modifiers” (CM). The distinction among classes of compensatory evolution is important because, under CWS, weak deleterious fixations create a necessity for positive selection even in the absence of environmental change.

Compensatory substitutions may be prevalent in genome evolution. Co-evolution at nucleotide sites that correspond to paired regions in RNA stem structures supports both CN and CWS (Chen et al. 1999; Meer et al. 2010). PGIM comparisons between translationally preferred and unpreferred synonymous codons are consistent with CWS in the maintenance of Drosophila and yeast codon bias (Akashi 1995; Liti et al. 2009), and similar contrasts between putative fitness classes suggest CWS maintenance of nucleosome occupancy patterns in yeast (Kenigsberg et al. 2010). Conserved expression patterns despite gain and loss of binding sites in regulatory regions (Ludwig et al. 2000; reviewed in Weirauch and Hughes 2010) and turnover of splicing enhancers in mammals (Ke et al. 2008) have been attributed to mutation-selection-drift balance (CWS).

Laboratory studies support an abundance of epistatic mutations that can restore loss of fitness in proteins (Burch and Chao 1999; Moore et al. 2000; Poon 2005; Poon et al. 2005), but identifying compensatory evolution in nature has proven challenging. Charlesworth and Eyre-Walker (2007) tested for CWS by comparing rates of evolution (mostly mtDNA-encoded proteins) among pairs of species that inhabit mainlands and islands. They found higher rates of protein evolution in mainland relative to island populations in cases where the mainland populations are thought to be derived from island populations. Such patterns are consistent with compensatory evolution in larger (mainland) populations following an accumulation of slightly deleterious fixations in smaller (island) populations. However, such patterns could also reflect population size effects on mutation-limited adaptive evolution in novel habitats.

Co-evolutionary patterns can reveal compensatory protein evolution (Haag 2007). Mutations that are strongly deleterious in one species can be fixed in a different genetic background (presumably containing compensatory mutations) in other species. Patterns consistent with such a scenario have been documented in mammals (Kondrashov et al. 2002) and insects (Kulathinal et al. 2004). Several early studies identified within-protein correlations among amino acid positions but did not account for phylogenetic relationships (Korber et al. 1993; Neher 1994). More recent studies have identified co-occurring substitutions within a phylogeny (Pollock 1999; Fukami-Kobayashi et al. 2002; Dimmic et al. 2005; Dutheil et al. 2005; Yeang and Haussler 2007). Such patterns support within-protein epistatic interactions but do not distinguish among CN, CM, and CWS scenarios. Mapping the temporal order of substitutions (given dense sampling of species) can identify sequentially occurring substitutions consistent with CM or CWS (Bazykin et al. 2006; Kryazhimskiy et al. 2011; Osada and Akashi 2012), but distinguishing between these scenarios may be limited to particular biological contexts.

The difficulty of predicting fitness effects of amino acid changes has been a major limitation to testing compensatory evolution. The notion that protein evolution may, in large part, reflect mutation-selection-drift balance among slightly deleterious destabilizing and weakly beneficial, stabilizing amino acid changes (Tokuriki and Tawfik 2009b; Goldstein 2011; Wylie and Shakhnovich 2011) may allow tests of CWS if mutations falling into these fitness classes can be predicted.

Concave Fitness Functions and the Paradox of Near Neutrality

Most of this review has focused on patterns of protein and DNA variation that test weak selection. However, one of the strongest objections to the nearly neutral model has been a theoretical one—its reliance on a particular distribution of selective effects. We show an example of a DSE (Figure 2A) that gives nearly neutral dynamics over a wide range of population sizes (Figure 2D). However, such dynamics hold only for a specific range of shape parameters; small changes in the DSE can cause a lack of dependence of polymorphism and divergence on population size and/or a complete lack of evolution in large populations (Nei and Graur 1984; Gillespie 1987; Takahata 1993). Thus, support for weak selection among classes of mutations and across taxa is paradoxical. Population sizes and ecological circumstances vary widely among species, and relationships between DNA mutations and fitness are determined by different factors for different types of mutations. Why should DSEs in nature so often show the precise characteristics required for nearly neutral evolution?

Linked selection may constrain effective population sizes in natural populations. Larger populations experience a higher input of non-neutral mutations (reduced f′_n and elevated within-population mutation rate to advantageous alleles). Depending on recombination rates and DSEs, levels of neutral polymorphism at sites linked to selected sites may show little relationship with population size (Gillespie 2000). Although the number of species for which both direct estimates of mutation rates and measures of DNA diversity in natural populations are available is small, estimates of N_e range over three orders of magnitude (Charlesworth 2009). Linked selection is likely to constrain among-lineage variation in N_e (especially in regions of limited recombination) but does not appear to be sufficient to account for the paradox of near neutrality.

General properties of phenotype–fitness relationships may underlie weak selection. Wright (1929, 1934) proposed that diminishing returns in fitness as phenotypes approach optima explain the prevalence of genetic dominance among wild-type alleles and recessive effects of newly arising mutations. His model examined relationships between the catalytic activity of an enzyme (a phenotypic value) and flux through a biochemical pathway (directly related to fitness) and showed that the fitness benefit for a given increase in activity is greater for low-activity alleles than for alleles functioning close to an optimum. Kacser and Burns (1981) confirmed hyperbolic relationships between activity and flux under enzyme kinetic models and gave supporting evidence from biochemical studies. The Kacser–Burns model applies only to particular scenarios of enzyme catalysis (Savageau 1992; Wilkie 1994; Omholt et al. 2000), but concave fitness functions may hold more generally. Classic studies by Crow and co-workers showed an “inverse heterozygous-homozygous effect” for deleterious mutations in Drosophila; deleterious mutations of large effect tend to be recessive (large s, small h) whereas alleles of small effect tend to show heterozygous effects (small s, large h) (Greenberg and Crow 1960; Simmons and Crow 1977). Such patterns are consistent with diminishing returns because fitness vs. phenotype relationships are close to linear (additive) within restricted ranges of phenotypic values but show strong nonlinearity over wider ranges. Gene-deletion studies in yeast support inverse relationships between fitness (growth rate) and heterozygous effects across functional categories of genes (Phadnis 2005; Agrawal and Whitlock 2011). Gene knockouts were tested (missense mutations may not show the same associations), but the findings are consistent with concave fitness functions for a variety of traits (including noncatalytic functions). Non-additive relationships between protein stability and fitness (Bershtein et al. 2006; Tokuriki and Tawfik 2009b; Wylie and Shakhnovich 2011) could underlie diminishing returns epistasis.

Hartl et al. (1985) related concave fitness functions to mechanisms of molecular evolution. Under diminishing returns, DSEs change as character values approach optima. Changes in activity will have smaller fitness effects (both positive and negative) as enzymes approach optimum activity, and Hartl and co-workers predicted that characters in natural populations should be on plateaus of concave fitness functions. Gillespie (1994b) found that concave fitness functions can lead to phenotypic values close to their optima and to dynamics indistinguishable from neutral evolution when phenotypes of new mutations are normally distributed around parental values (i.e., equal proportions of positively and negatively selected mutations). However, if mutations often have small phenotypic effects and tend to be deleterious, then characters will evolve to equilibrium values below their optima (Akashi 1996; Hartl and Taubes 1998). Smaller populations will evolve to lower equilibrium values than larger populations, and a wide range of population sizes could show a balance among weak selection, drift, and mutation; i.e., DSEs will evolve in different population sizes to a point where many mutations show |N_es| ≈ 1 (Figure 5). Such a scenario has been proposed to account for patterns of codon usage bias (Li 1987; Akashi 1995; Kondrashov et al. 2006). The correlation between evolutionary rate and population size can be weak under concave fitness relationships but will depend on how DSEs change with phenotypic values (Cherry 1998). Concave fitness functions are an appealingly simple explanation for widespread weak selection, but evidence for this form of epistasis remains mixed. Some mutation accumulation studies support increasing negative effects with declining fitness whereas others support the opposite pattern (reviewed in de Visser et al. 2011).

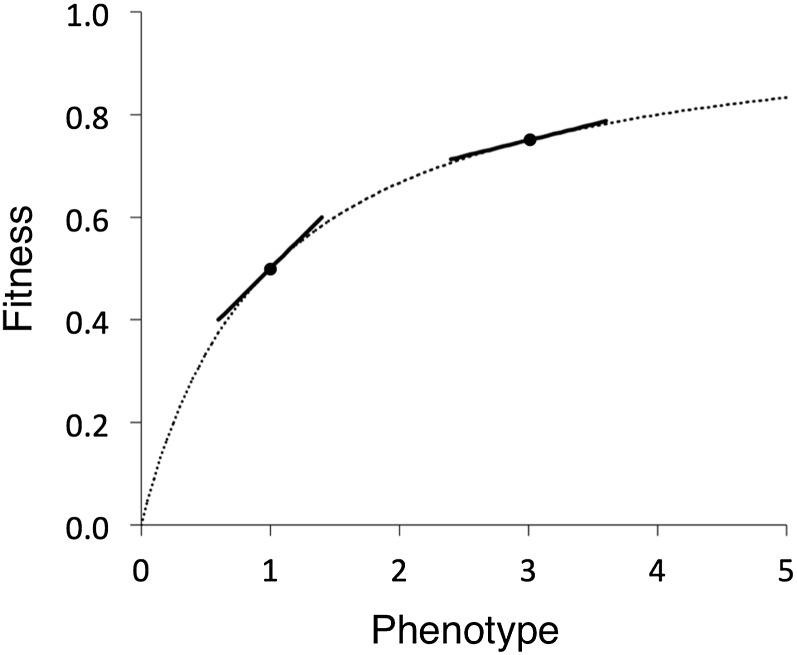
Figure 5 .

Concave fitness functions and near neutrality. The curve y = x/(1 + x) shows a hypothetical relationship between fitness and phenotypic values of a trait. The slope of the curve at a given point determines the fitness effect of small phenotypic changes (slopes are shown for phenotypic values of 1 and 3). The slope decreases as a function of the phenotypic value (i.e., the distribution of s changes with character values). If a large fraction of mutations have small phenotypic effects and if the rate of mutation to deleterious alleles is higher than the rate to advantageous mutations, populations will evolve to a point on the curve where slightly deleterious mutations that move the population away from the optimum will be balanced by weak positive selection. The left and right points marked in the figure correspond to equilibrium points in species with small and large population sizes, respectively (this assumes constant mutation rates and population sizes).

Discussion

Although support for weak selection in protein evolution has accumulated in diverse taxa, adaptive protein evolution and changes in the distribution of fitness effects can often make predictions that overlap those of near neutrality. Within-population comparisons (excess rare amino acid variants) provide some of the strongest evidence for weak selection because positive, directional selection should have little impact on polymorphism data. Associations between levels of protein polymorphism and estimates of N_e among closely related populations also support weak selection because DSEs are likely to be conserved on relatively short time scales.

Distinguishing adaptive, neutral, and nearly neutral modes of molecular evolution remains challenging. All three mechanisms enjoy sufficient support to be considered among potential explanatory factors in almost all studies that infer mechanisms of genome evolution. For polymorphism analyses, near neutrality can cause differences in levels of variation and in frequency spectra among functional categories of mutations or among populations. In among-species comparisons, weak selection may underlie considerable variation in rates and patterns of divergence. Slightly deleterious amino acid mutations can reduce the power to detect adaptive protein evolution but can also generate a false signal of adaptive fixations under particular scenarios of population size change. Weak selection in the comparison class in tests of adaptive protein evolution (often synonymous DNA changes) can also contribute to false signals of positive selection (Akashi 1999a).

Compensatory evolution, and small fitness effects in adaptive evolution more generally, may be important factors in protein evolution but have been difficult to test. Evidence for such factors is stronger at synonymous sites, in RNA genes, and in noncoding DNA than in protein evolution in part because functional and fitness effects of mutations can be predicted (e.g., translationally preferred vs. unpreferred synonymous changes, destabilizing and stabilizing changes in RNA stem structures). Further incorporation of biophysical principles may be essential for advancing our understanding of protein evolution. Models of protein evolution that account for both stability and activity effects have the potential to predict fitness effects of amino acid changes (Depristo et al. 2005; Bloom et al. 2007b; Tokuriki and Tawfik 2009b; Wilke and Drummond 2010; Goldstein 2011; Wylie and Shakhnovich 2011) and may help to determine the proportion of compensatory subsitutions among adaptive fixations. This information, in combination with experimental approaches (e.g., Bershtein et al. 2006; Bloom et al. 2007a; Araya and Fowler 2011), will allow tests of Ohta’s (1973) prediction of fundamental relationships among protein primary structure, folding, and weak selection.