iAK692: A genome-scale metabolic model of Spirulina platensis C1

Abstract

Background

Spirulina (Arthrospira) platensis is a well-known filamentous cyanobacterium used in the production of many industrial products, including high value compounds, healthy food supplements, animal feeds, pharmaceuticals and cosmetics, for example. It has been increasingly studied around the world for scientific purposes, especially for its genome, biology, physiology, and also for the analysis of its small-scale metabolic network. However, the overall description of the metabolic and biotechnological capabilities of S. platensis requires the development of a whole cellular metabolism model. Recently, the S. platensis C1 (Arthrospira sp. PCC9438) genome sequence has become available, allowing systems-level studies of this commercial cyanobacterium.

Results

In this work, we present the genome-scale metabolic network analysis of S. platensis C1, iAK692, its topological properties, and its metabolic capabilities and functions. The network was reconstructed from the S. platensis C1 annotated genomic sequence using Pathway Tools software to generate a preliminary network. Then, manual curation was performed based on a collective knowledge base and a combination of genomic, biochemical, and physiological information. The genome-scale metabolic model consists of 692 genes, 837 metabolites, and 875 reactions. We validated iAK692 by conducting fermentation experiments and simulating the model under autotrophic, heterotrophic, and mixotrophic growth conditions using COBRA toolbox. The model predictions under these growth conditions were consistent with the experimental results. The iAK692 model was further used to predict the unique active reactions and essential genes for each growth condition. Additionally, the metabolic states of iAK692 during autotrophic and mixotrophic growths were described by phenotypic phase plane (PhPP) analysis.

Conclusions

This study proposes the first genome-scale model of S. platensis C1, iAK692, which is a predictive metabolic platform for a global understanding of physiological behaviors and metabolic engineering. This platform could accelerate the integrative analysis of various “-omics” data, leading to strain improvement towards a diverse range of desired industrial products from Spirulina.

Background

Spirulina (Arthrospira) platensis is a filamentous non-N₂-fixing cyanobacterium that has become important as a source for commercially produced nutraceutical compounds, as this cyanobacterium utilizes sunlight and CO₂ to produce chemical compounds that are essential for life. Spirulina has been consumed as a protein source for many years by North Africans and Mexicans [1] because it contains high amounts of healthy nutritional molecules such as beta-carotene, phycocyanin, vitamins, trace minerals, and polyunsaturated fatty acids [2]. Recently this cyanobacterium has played an important role in a wide range of applications in the nutraceutical industry, including human food supplements and animal feed [3]. Moreover, many scientific articles have reported the therapeutic benefits of this microorganism, such as helping to prevent heart disease, cancer, and diabetes [4]. Furthermore, S. platensis is potentially one of the algae capable of producing bioenergy and renewable energy, which could help to decrease the effects of global-warming [5]. Among the diverse range of cyanobacterial species, S. platensis is capable of growing in outdoor environments at a high rate [6]. In terms of cellular capacities, many of its bioactive compounds could be inexpensively produced by photosynthesis. These facts plus its nutritional value make S. platensis an attractive photobiological cell factory.

The growing availability of genomic sequences and software technologies has made it possible to reconstruct genome-scale metabolic networks of various organisms. Genome-scale metabolic models come from the systematic reconstruction of all cellular biochemical reactions according to the genetic information of a given organism [7]. A vast number of applications of a reconstructed metabolic network have been reported and include such possibilities as genome annotation and metabolic engineering [7]. Knowledge of the presence or absence of specific pathways in a given organism can help to improve the quality of genome annotation [8]. Furthermore, after the metabolic pathways are initiated, this reconstructed metabolic network becomes a useful tool for applications in the area of metabolic engineering, the general goal of which is to redistribute fluxes within a metabolic network towards a desired goal [9]. Reconstruction of the metabolic network is also necessary for in silico predictions of gene functions and the metabolic capabilities of an organism [10]. By applying flux balance analysis (FBA) technique [11,12], the metabolic network may be converted to a genome-scale model, allowing a qualitative assessment of the relationship between genotypic and phenotypic behaviors, and a global estimation of flux distributions within the metabolism of an organism, which cannot possibly be measured using a standard experimental design. Currently, one popular tool for investigating complex stoichiometric metabolic models is the constraint-based reconstruction and analysis (COBRA) toolbox [13,14] with MATLAB. This technique relies on linear programming (LP) and a given set of various appropriate constraint parameters known from experiments. Numerous successes have been reported using these methods as the tools to elucidate in silico models (virtual organisms) [15-17].

Various genome-scale metabolic models of many organisms are currently available [18]. However, of cyanobacterium, only Synechocystis sp. PCC6803 has been developed by independent research teams around the world [19-21]. Each proposed model provides informative knowledge on rational bioenergy production by Synechocystis sp. PCC6803 as a photobiological cell factory. With such an impressive advantage of S. platensis, especially as a nutraceutical, as previously mentioned, S. platensis has become one of the preferred choices for a sustainable photobiological cell factory. Unfortunately, there have only been a limited number of attempts to computationally analyze the metabolism of Spirulina. A simple metabolic flux model of S. platensis consisting of 22 reactions was proposed by Meechai et al[22]. This model was used to predict rate limiting enzymes for the production of gamma-linolenic acid. A larger metabolic network of S. platensis comprising 121 reactions and 134 metabolites was formulated by Cogne and his team [23]. This model accounted for central metabolic pathways, anaplerotic reactions, energy metabolism reactions, anabolic reactions, synthesis of macromolecules, biomass and growth-associated exopolysaccharides (EPS). However, these two models did not provide the whole-cell characteristics and metabolic capabilities of S. platensis. Recently, the genome sequence of S. platensis C1 became available [24], together with an increasing number of studies of its physiological and molecular levels. These data have enabled a genome-scale metabolic model reconstruction of S. platensis.

This paper presents the first genome-scale metabolic model of S. platensis (i.e., iAK692), representing global growth behaviors under three different growth conditions: autotrophic, heterotrophic, and mixotrophic. The metabolic network is based on the S. platensis C1 genome, a collective knowledge base, and extensive manual curation. Computational simulation was performed using COBRA toolbox [13,14]. The results from in silico predictions were further validated with experimental evidence. Various analyses of the iAK692 model were performed to identify active reactions and essential genes under each growth condition. Moreover, phenotypic phase plane (PhPP) [25] analysis was carried out to predict the metabolic states of iAK692 during autotrophic and mixotrophic growths. The iAK692 model not only provides further physiological knowledge of the cellular system, but is also a valuable platform for integrating multilevel “-omics” data, which could provide further insight towards increasing the number of desired industrial bioproducts from Spirulina.

Results and discussion

Metabolic model reconstruction

Reconstruction of a draft model

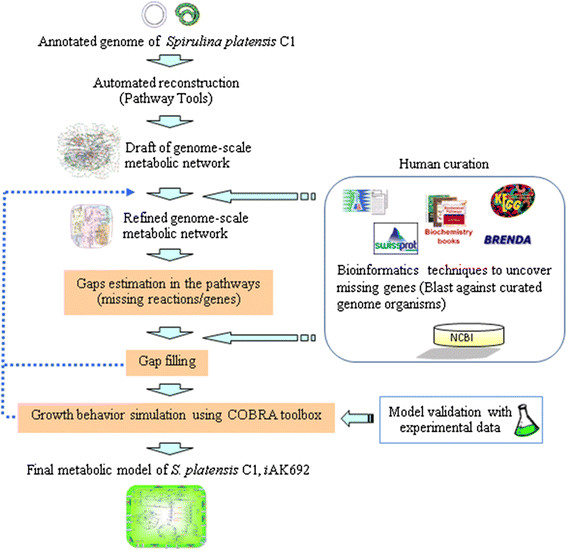
In order to build a genome-scale metabolic model of S. platensis C1, the genome-scale metabolic network was reconstructed according to a series of extensive refinements (Fig. 1 and see also Materials and Methods). The genome of S. platensis C1 is deposited in the GenBank Database (NCBI ID 67617) [24]. The estimated genome size for the 63 DNA scaffolds is approximately 5.9 Mb. A total of 6,176 open reading frames (ORFs) were predicted; 3,759 ORFs (61 %) were well annotated with gene functions; and 2,372 ORFs (38 %) were identified as putative or hypothetical proteins (Table 1). Reconstruction of the model was initiated with automated construction using Pathway Tools software [26,27]. Using this fully computational procedure, a draft metabolic network, called the “Draft model”, was generated based on the annotated genome data. This automated process facilitates the top-down reconstruction approach, giving an overview network and visualization; therefore, it provides the maximum possible number of pathways, each of which has different numbers of reactions and genes.

Figure 1.

The iterative procedure used to reconstruct the genome-scale metabolic model ofS. platensisC1. The draft of the metabolic network was automatically established using Pathway Tools software. The manual curation was performed based on a combination of Spirulina-related journal publications and biochemical books and databases. Missing reactions in the pathway were manually estimated and filled. Blast program was used in order to find a potential corresponding gene. The accepted network was further studied via a structural analysis and simulation based on the COBRA toolbox [13,14.]

Table 1.

Characteristics of model size after each reconstruction step

Features	Numbers
Genome information
Genome size (bp)	5,934,248
Open reading frames(ORFs)	6,176
Annotated genes	3,759
Reconstruction metabolic model	Draft model	Refined model	Final model
Genes
ORFs	575	692	692
% ORF of genome	9.3	11.2	11.2
Reactions	1,661	688	875
Internal enzymatic reaction	1,661	688	699
Gene-associated	849	650	650 (93 %)
No gene association	812	38	49 (7 %)
Exchange reaction	0	0	176
Metabolites	1542	658	837

The Pathway Tools software [26,27] predicts the metabolic network for S. platensis C1 based on the gene name or EC number matching method. This preliminary model accounted for 102 pathway frames (including a number of pathway variants), 557 genes corresponding to 1,661 biochemical reactions, and 1,542 metabolites. A summary of the draft model is shown in Table 1. The pathways were also predicted and a large number of the pathway reactions were obtained. We also found that one gene could participate in more than one reaction of different pathways. Thus, this process built 102 candidate pathways and 812 out of 1,661 reactions were presented and showed no gene association. However, the quality of the predicted large-scale reconstructed network depends on the quality of the initial annotated data. Furthermore, the reconstructed network must express the biology and physiology of S. platensis C1; for instance, whether or not the predicted pathways or reactions present in S. platensis C1 and the numbers of incomplete pathways (missing gene and reaction) indicate a disconnection in the network. Hence, manual-intensive curation was subsequently performed to increase the accuracy of the draft auto-generated network.

Metabolic network refinement

Biochemical information about cyanobacteria was obtained from the literature and biochemistry textbooks, and online biochemical databases were used to research several iterative methods of reconstruction and were used to refine the draft model; this is referred to as the “Refined model”. In more detail, the predicted pathways/reactions that have not been reported for Spirulina physiology, such as cholesterol biosynthesis I, II, and III pathways, were eliminated from the network. Pathway Tools mapped only one gene, crtB, encoding phytoene synthase, onto two reactions out of twenty-two reactions in these pathways for the draft model. However, we found that the phytoene synthase enzyme was involved in the presence of the carotenoid biosynthesis pathway. Since carotenoid is an important molecule in photosynthesis, the synthesis pathway of this compound was retained.

Then the Blast algorithm [28,29] and the tool for the protein domain prediction against pfam databases [30] were used to determine the enzymatic gene functions needed to complete the pathways where no gene could be found in the automated metabolic reconstruction. A total of 135 genes were annotated and added to the network. Missing reactions (referred to as gaps) that resulted in dead-end metabolites and prevented the computational simulation of cell growth were identified and filled in. This procedure was continued until all of the biomass components in Table 2 were included. After manually updating the gap filling process, we also attempted to search for the genes in the genome, which can be associated with the added reactions. A total of 35 reactions from closely related organisms were added to complete the connectivity of the network. The refined model contains 692 metabolic genes, 658 metabolites, and 688 biochemical reactions (Table 1). The number of many-to-many relationships between reactions and genes presented in the network is 207 reactions.

Table 2.

iAK692 biomass composition equation

Component	Molar ratio	Component	Molar ratio
Carbohydrate (16 %)*	0.1230
CMP-N-acetylneuraminate	0.0220	Glycogen	0.0430
Cyclitol	0.0510	Peptidoglycan	0.0300
dTDP-rhamnose	0.7320	UDP-D-glucose	0.1240
Protein (68 %)*	0.8404
Alanine	0.1010	Lysine	0.0360
Arginine	0.0530	Methionine	0.0180
Aspartate	0.0980	Phenylalanine	0.0390
Cysteine	0.0070	Proline	0.0380
Glutamate	0.1320	Serine	0.0540
Glycine	0.0860	Threonine	0.0540
Histidine	0.0140	Tryptophan	0.0090
Isoleucine	0.0580	Tyrosine	0.0330
Leucine	0.0940	Valine	0.0760
Lipid (11 %)*	0.0182
DGDG	0.1310	SQDG	0.1470
MGDG	0.3200	Triglyceride	0.1860
Glycerol	0.2160
DNA (0.88 %)*	0.0039
dATP	0.2790	dGTP	0.2220
dCTP	0.2220	dTTP	0.2790
RNA (3.12 %)*	0.0130
ATP	0.2620	GTP	0.3220
CTP	0.2000	UTP	0.2160
Antenna chromophore (1 %)*	0.0016
Cholorophyll a	0.0016

* % total dry weight of major cellular composition estimated from S. platensis cell grown under autotrophy [23]. The stoichiometric coefficient of each building block was retrieved and expressed on the basis of one mole of dry cell. DGDG: digalactosyldiacylglycerol; MGDG: monogalactosyldiacylglycerol; SQDG: sulfoquinovosyldiacylglycerol.

Generation of the computational genome-scale model (iAK692)

In order to make the computation-ready model, referred to as the “Final model”, the balance between each element, including metabolites and protons (H⁺), reaction directionality, transport reaction, and the completely characterized biomass equation were curated and added to the refined model. We checked the balance of protons in a reaction and also found that different databases contain some contradictory information. In this reconstruction, we used Metacyc [31] as the key reference for H⁺ balancing. Additionally, the stoichiometry and reversibility of the reactions were manually verified and assisted by biochemical reaction databases such as KEGG [32] and Brenda [33]. We also considered the direction of the reaction on the basis of thermodynamics. If the reaction consumed high-energy compounds such as ATP, the reaction was designated irreversible. Considering only the internal reactions of the model, there are 558 irreversible and 317 reversible reactions. The cofactors, i.e, NADPH, and NADH involved in the reactions were manually curated based on information from literature [7] and the published genome-scale model of Synchocystis sp. PCC6803 [19]. The system boundary was defined across the cytoplasmic membrane and environment in terms of transport reactions. Diffusion was assumed to be the mechanism for transporting nutrients between cytoplasm and extracellular environment. Thus, transporter genes were not assigned in this first large-scale model of S. platensis. Instead, a total of 88 exchange reactions were included in the model to ensure that organic nutrient metabolites (i.e., amino acid and sugar), inorganic nutrient metabolites (i.e., phosphate, sulfate, nitrate, and potassium), gaseous metabolites (i.e. O₂ and CO₂), photons, and water could enter and leave the system in response to the physiological state. We are aware that the transport mechanisms across the cell membrane should be considered in this study because of their possible effect on the model. This is an issue that we will address in a future study.

In order to determine the capability of a genome-scale model, the most popularly used objective function in FBA is normally the biomass objective function (BOF). A biomass equation represents all necessary precursors that form the cellular biomass. Thus, 14 reactions with no gene association were added for the synthesis of intermediate macromolecules, i.e. proteins, carbohydrates, lipids, RNA, DNA, and chlorophyll, which are considered to form the major composition of biomass. The biomass formation equations were obtained based on data from different sources of experimental efforts for S. platensis under autotrophic conditions [23] (Table 2). Moreover, the net reaction for all light-dependent reactions was obtained from a previous report [34]. All reactions in the reconstructed metabolic network are listed and shown in Additional file 1: Table S1.

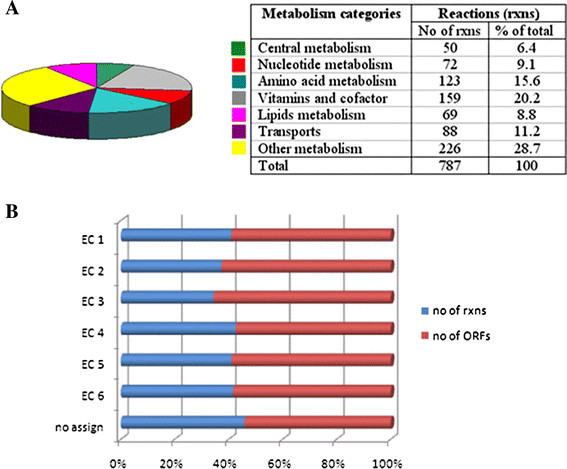
The different methods of reconstruction resulted in the final model, iAK692, and account for 692 metabolic genes, 837 metabolites, 176 exchange reactions, and 699 internal biochemical reactions, including 650 gene-associated reactions and 49 with no gene association (Table 1). A total of 875 reactions included in the model were designated as belonging to the high level of metabolism (Fig. 2A). The functional classification of the ORFs included in the reconstruction is summarized in Figure 2B, based on the Enzyme Commission (EC) number [35]. The majority of ORFs are associated with the transferase enzyme (EC 2).

Figure 2.

Classification of metabolic reactions in theS. platensisC1 model. (A) Distribution of each metabolic reaction; the table shows the numbers for the total reaction. (B) Percentage of reactions and genes classified based on the EC number. EC 1: oxidoreductases; EC 2: transferases; EC 3: hydrolases; EC 4: lyases; EC 5: isomerases; EC 6: ligases.

Network topology of iAK692

The structural organization of iAK692 was characterized by an analysis of metabolic connectivity via reactions within the network. Most of the metabolites in the network have few connections, whereas a few metabolites participate in a large number of reactions. The top 10 most highly connected metabolites are ATP, ADP, phosphate, diphosphate, NADP, NADPH, CO₂, NAD, NADH, and O₂. These frequently used metabolites were found to be involved in energy metabolism, such as ATP and ADP, and in redox metabolism, such as NADPH and NADP (Table 3). These metabolic hubs serve as key compounds related to the core metabolism of the organism in transferring specific biochemical groups such as phosphate groups, redox equivalents, amino groups and acetyl groups. In addition, connectivity was compared to other genome-scale models, including Synechocystis sp. PCC6803 (iSyn669) [20], Escherichia coli (iAF1260)[36], and yeast (iFF708) [37]. It was found that iAK692 has a similar network topology and metabolite hub to these models (Table 3). It should also be noted that these metabolites are involved in energy and redox metabolism, representing the currency of biological life. The topology also indicates that in the organization of the network a few hubs dominate the overall connectivity of the network and the network eventually disintegrates into isolated clusters. These characters show to what degree different components of the cellular metabolism are interconnected. Perturbations in cellular behavior, such as changing a few fluxes in metabolism, can affect the entire metabolism. Hence, studying the structural organization of the network provides hints for discovering corresponding regulatory mechanisms of the cell.

Table 3.

Numbers of metabolite connectivity of top 10 metabolites in theiAK692 metabolic network compared to those in other published models

Metabolite	Connectivity
	iAK692	iSyn669	E.coli	yeast
ATP	134	144	338	166
ADP	92	103	253	131
PI	92	108	81	113
PPI	84	97	28	-
NADP+	84	64	39	61
NADPH	83	63	66	57
CO2	72	72	53	66
NAD+	70	46	79	58
NADH	69	42	75	52
O2	57	36	40	31

Validation of iAK692

S. platensis C1 naturally grows under autotrophic conditions using carbon dioxide as a carbon source and converting light as cellular energy, like other cyanobacteria. Several strains of these microalgae, including S. platensis, were recently researched for their potential to grow under heterotrophic and mixotrophic environments [38]. However, there have been no reports of either mode of cultivation in the S. platensis strain C1. Thus, we investigated the cellular properties of heterotrophic and mixotrophic growth in order to gain more basic physiological knowledge of S. platensis C1. Subsequently, we validated the reconstructed metabolic network by comparing the predicted results from in silico simulations with the experimental results. The measured maximum specific growth rates of S. platensis C1 under the three growth conditions are summarized in Table 4. More details of the results are shown in Additional file 2: Table S2.

Table 4.

Constraints for metabolite uptake rates used for model simulation, and the comparison of the predicted growth rate by thein silicomodel and observed growth rate from the experiments in each growth condition

Growth conditions	Constraints of consumed metabolites (mmol/mmol dry cell/h)					Maximal specific growth rate (1/h)
	Bicarbonate	Phosphate	Nitrate*	Sulfate*	Glucose**	In silico	In vivo
Autotrophic	0.20	0-0.0056	0-0.040	0-0.0014	0	0.0257	0.0255
Heterotrophic	0	0-0.0056	0-0.040	0-0.0014	0.017	0	0
Mixotrophic	0.20	0-0.0056	0-0.040	0-0.0014	0.017	0.0334	0.0262

* data from ref. 38.

** data from ref. 39.

The basic capabilities of iAK692 were evaluated based on constraint-based modeling using the FBA technique [11,12] to quantitatively predict growth under the three metabolic modes. Assuming a steady state, FBA simulates the mass balance of all metabolites derived from the stoichiometric reactions together with constraints and the objective function. In this study, we set the biomass flux as the objective function.

For autotrophic growth, cells synthesize organic molecules for biomass formation from inorganic compounds and sunlight. The maximum specific growth rate of S. platensis C1 was demonstrated in batch cultivation (Table 4). The uptake rates of the main metabolites, bicarbonate and phosphate, were measured and used as the constraints of the simulation. In order to assess the predictive potential of the model, we simulated the in silico model based on minimal media consumption, as shown in Table 4. The constraints of certain metabolite uptake rates were obtained from the literature [38,39]. The photon flux was set to be between zero and 100 μEinstein/m²/s with a fixed uptake rate of 0.20 mmol/mmol dry cell/h of bicarbonate. The results show that the maximum in silico-specific growth rate was similar to the maximum specific growth rate measured from the experiments. The experimentally determined value and the computationally predicted value were 0.0255 and 0.0257 1/h, respectively. On the other hand, when the photon flux was omitted (i.e., set to 0 μEinstein/m²/s), the in silico cell could not grow (i.e., the maximum specific growth rate was 0 1/h. This simulation results show a consistency with the control experiment, in which no growth was found.

For the heterotrophic mode, S. platensis C1 was cultivated on glucose in the dark. The results show that the cell failed to grow heterotrophically (Table 4). In the simulation, we set the glucose uptake rate equal to 0.017 mmol/mmol dry cell/h with no light. The predicted value of growth was zero (Table 4), showing an agreement between in vivo and in silico conditions. Considering the genomic data, S. platensis C1 has the hex gene encoding the hexokinase enzyme, which converts glucose molecules into glucose-6-phosphate. This is the first important step in the glycolysis pathway, which allows cells to metabolize glucose as a carbon source. However, a lack of the ability to utilize sugar in the dark was recently reported in some strains of Spirulina[40]. Therefore, this agreement in the results may stem from no or a loss of function of the gene product when growing for a long period of time under autotrophic conditions in the laboratory. Moreover, the glucose concentration had no effect on the growth of S. platensis under the heterotrophic conditions reported in a previous study [41].

In the mixotrophic mode with carbon dioxide and glucose as carbon sources and light as the energy source, the measured growth rate under this condition was found to be slightly higher than that of the autotrophic mode (Table 4). The model simulation under mixotrophic conditions also showed a higher growth rate (0.0334 1/h), although to a different extent. Interestingly, this growth rate corresponds to that of an increase in biomass formation during the mixotrophic cultivation of another Spirulina strain by Lodi and his team [39]. They suggested that the mixotrophic culture had the highest growth rate because the heterotrophic and autotrophic metabolism processes might be active in parallel. However, the current experimental study for S. platensis C1 has showed that the mixotrophic growth rate (0.0262 1/h) is only slightly higher than the autotrophic growth rate (0.0255 1/h) (Table 4). We also modeled the hex gene knockout that results in zero flux of this reaction. The results show that the growth rate decreased from 0.0334 1/h to 0.0257 1/h (data not shown). Therefore, the different growth behaviors found for the different physiological properties and in silico predictions might require further experimental verification in order to discover further explanations and make new discoveries. All profiles of the flux distributions of the three growth conditions are presented in Additional file 2: Table S2.

Reaction activity and flux variability analyses

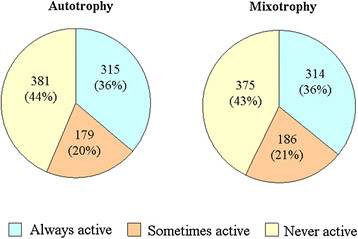
The result validation demonstrates that the in vivo growth rates of iAK692 are consistent with the experimental growth rates found under the three different modes. In order to investigate the flux distributions in terms of active reactions, this model was only used for the simulation of autotrophic and mixotrophic growths because the cells failed to grow under heterotrophic conditions. The flux results show that iAK692 had 322 (41 %) and 307 (39 %) active reactions under the autotrophic and mixotrophic conditions, respectively. These two numbers of active reactions are close to those found in previous studies of other genome-scale models such as those for Clostridium beijerinckii[42], E. coliStaphylococcus aureusHelicobacter pylori and yeast [43], which comprise around 300 active reactions. For a more precise determination of active reactions in each growth condition, we performed flux variability analysis (FVA) [44] to determine possible ranges of fluxes of all reactions that still satisfy the same optimal growth. Here, we classify the reaction activity into 3 categories based on the FVA results: (i) a reaction is considered “always active” if min/max flux values are non-zero with the same sign, (ii) a reaction is considered “sometimes active” if the range of possible fluxes contains zeroes, and (iii) a reaction is considered “never active” if min/max flux values are equal to zero during optimal growth. To satisfy the optimal autotrophic growth, we found that 315 (36 %) reactions are always active; 179 (20 %) reactions are sometimes active, and 381 (44 %) reactions are never active (Fig. 3). On the other hand, to achieve its optimum growth in mixotrophic condition 314 (36 %) reactions are always active; 186 (21 %) are sometimes active, and 375 (43 %) are never active for the S. platensis (Fig. 3). It is noted that there is a total of 494 and 500 “active reactions” (both sometimes and always active) for autotrophic and mixotrophic conditions, respectively. It was observed that all the 494 reactions found active under the autotrophic growth are also active under the mixotrophic growth. The six remaining reactions that are found active only under the mixotrophic growth are shown in Table 5. These reactions belong to the pathways involving glucose exchange, glycolysis, arginine and proline metabolism, and cofactor and prosthetic group biosynthesis. We think that these pathways are necessary for the conversion of external glucose to intermediates in the synthesis of macromolecules needed for mixotrophic cell growth. All profiles of FVA of both growth conditions are presented in Additional file 3: Table S3.

Figure 3.

Comparison of predicted active reactions under different growth conditions. (A) autotrophy, (B) mixotrophy.

Table 5.

List of reactions found active only iniAK692 grown under mixotrophic condition

Reaction ID	Reaction name	Reactiuon equation	Pathway	Responsible gene
SP0001	glucokinase	Alpha-D-glucose + ATP -- > alpha-D-glucose-6-phosphate + ADP + H+	Glycolysis	SPLC1_S271400
SP0111	ornithine acetyltransferase	L-glutamate + acetyl-CoA -- > N-acetyl-L-glutamate + coenzyme-A + H+	Arginine and proline metabolism	SPLC1_S202710
SP0267	glutamate-cysteine ligase	L-cysteine + L-glutamate + ATP -- > L-gamma-glutamylcysteine + phosphate + ADP + H+	Cofactor and prosthetic group biosynthesis	SPLC1_S361150
SP0268	glutathione synthetase	glycine + L-gamma-glutamylcysteine + ATP -- > reduced-glutathione + phosphate + ADP + H+	Cofactor and prosthetic group biosynthesis	SPLC1_S531620
LGLUCtex	Glucose transport	alpha-D-glucose < −− > alpha-D-glucoseXT	D-glucose exchange
LGLUCtexX	Glucose transport	alpha-D-glucoseXT < −− > alpha-D-glucoseXTX	D-glucose exchange

Metabolic gene essentiality analysis

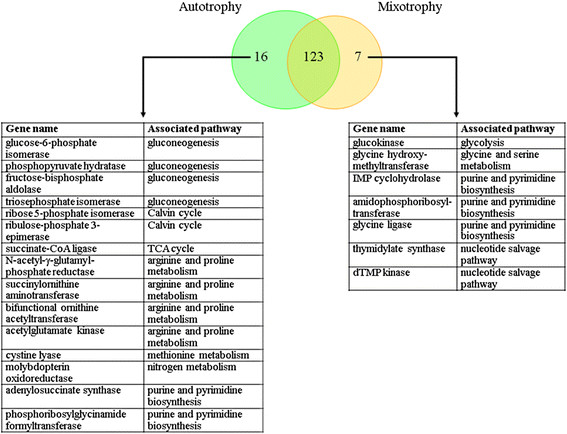
The capacity of iAK692 for predicting the growth behavior when it suffers gene deletion was evaluated. Like many other constraint-based models [45], the iAK692 model contains a list of gene-protein-reaction interactions indicating which genes are connected with each reaction in the metabolic network. The essentiality of each gene can be determined by constraining its associated reaction not to carry flux. Therefore, the network reaction(s) associated with each gene was deleted, one by one, by setting both the upper and lower bounds of a reaction to zero and optimizing for the biomass formation. In this study, the iAK692 model accounting for 875 biochemical reactions and 837 metabolites was employed to identify the essential genes for survival under autotrophic and mixotrophic growth conditions using the MOMA platform [46]. It was found that 139 and 130 genes were essential for the growth of iAK692 under autotrophic and mixotrophic conditions, respectively (Fig. 4). A list of these essential genes can be found in the Additional file 4: Table S4. The total number of 130 essential genes for the mixotrophy was about 19 % (130 of 692) of the total genes. This number is close to those found in other published models -- 15 % (187 of 1,260 genes) in E. coli (iAF1260) [36], and 10 % (148 of 708 genes) in yeast (iFF708) [37]. It is noted that there were 123 common essential genes between the two growth conditions. These common genes can be considered core metabolic genes for the growth of iAK692. Fig. 4 also shows a list of unique essential genes for each growth condition. Not surprisingly, the unique essential genes for autotrophy were the genes associated with the Calvin cycle and gluconeogenesis pathways that are responsible for photosynthesis and glucose formation, respectively.

Figure 4.

Comparison of essential genes under different growth conditions.

Phenotypic phase plane analysis

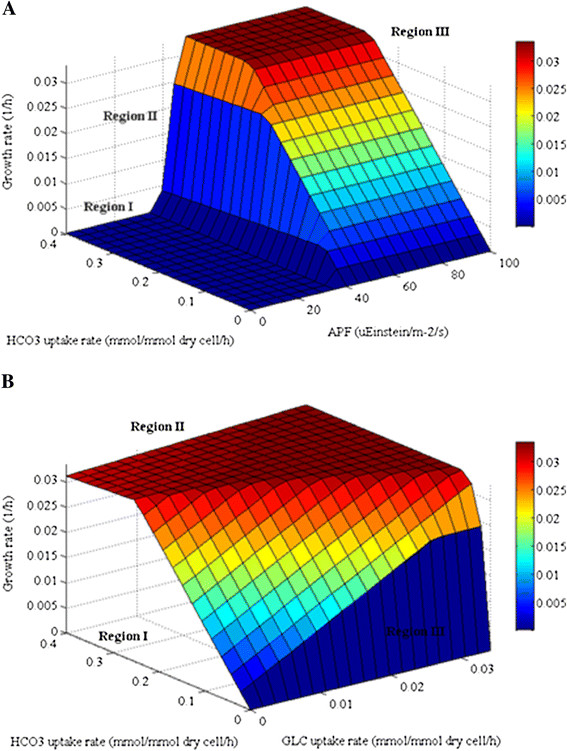
Phenotypic phase plane (PhPP) analysis is a useful approach for examining the steady-state solution space when two variables of interest are varied [25]. We employed PhPP to demonstrate the effect of light and bicarbonate ions on the growth of iAK692 under autotrophic condition. Within the metabolic network, inorganic carbon was transported from the medium as bicarbonate ions into cells. The intracellular bicarbonate was then dehydrated via carbonic anhydrase enzyme to become CO₂. The intensity of light input was represented by absorbed photon flux (APF). The surface of a three-dimensional PhPP corresponding to the predicted maximal growth rate as a function of the photon flux (0 – 100 μEinstein/m²/s) and the bicarbonate uptake rate (0–0.4 mmol/mmol dry cell/h) was plotted (Fig. 5)A. It was found that the cells exhibited distinct phenotypes depending on the amounts of bicarbonate and light fluxes. It is apparent that the cell growth rate is zero in Region I where the APF is below 40 μEinstein/m²/s. It is possible that there is not enough light intensity to generate sufficient amount of ATP required for cell growth in this region. At the APF between 40 and 45 μEinstein/m²/s (Region II), the maximal growth was found to be linearly dependent on both the absorbed light and bicarbonate availability. At the APF above 45 μEinstein/m²/s (Region III), the cell growth is limited by the bicarbonate ion availability. It is noteworthy to mention that our model fails to describe the photoinhibition at high APFs, although it has been well documented that photoinhibition is observed in autotrophic cultures of Spirulina. This is another issue that we will address in a future study.

Figure 5.

Phenotypic phase planes for autotrophic and mixotrophic growths ofS. platensisC1 metabolic network. (A) autotrophy, the estimated maximal biomass formation rate as a function of light and bicarbonate uptake. (B) mixotrophy, the estimated maximal biomass formation rate as a function of bicarbonate and glucose uptake. HCO3: bicarbonate; GLC: glucose.

Furthermore, PhPP for the case of iAK692 grown under varying bicarbonate and glucose uptake rates in the presence of constant APF (46.7 μEinstein/m²/s) was performed to investigate the relationship between photosynthesis and respiration growth of iAK692 during mixotrophy. The PhPP plot shows three distinct regions describing different growth phenotypes (Fig. 5B). In region I where the glucose uptake flux equals zero, iAK692 is able to grow using bicarbonate ion as a sole carbon source via photosynthetic pathways. This region can be characterized as autotrophy. In region II, the optimal growth of iAK692 was linearly dependent on both bicarbonate and glucose uptake fluxes. However, such dependency does not exist at high uptake rates as the carbon nutrients become saturated. Both photosynthetic and respiratory pathways are active in this region. In region III, we observed that iAK692 fails to grow in the absence of bicarbonate ion regardless of the amount of glucose availability. This implies that the respiratory pathways in the iAK692 strain could be triggered only if the photosynthetic pathways are active during the mixotrophic growth.

Conclusions

Herein, we reconstructed a genome-scale metabolic network of the cyanobacterium S. platensis C1, which is valuable both scientifically and economically. The network was constructed using i) automatic reconstruction by Pathway Tools software [26,27]; and ii) iterative processes of extensive manual curation based on genomic and bibliome data (Fig. 1). The curated network accounts for 771 metabolic genes, 712 metabolites, and 868 reactions. More than 85 % of the total reactions were associated with genes.

We used the COBRA toolbox [13,14] to investigate the global metabolic capability of S. platensis C1. This approach allowed an estimation of the flux distribution of the entire metabolism. The simulated results were validated by experimental evidence and showed satisfactory agreement under three different growth conditions; namely, autotrophic, heterotrophic, and mixotrophic. Analyses of the iAK692 model enabled us to gain insights into the metabolic phenotypes and essential genes of S. platensis C1 grown under these conditions. With a growing Spirulina community, the proposed model would not only be useful for studying cellular phenotypes but it could also serve as a platform for “-omics” data integration in order to achieve the beneficial stage of model-driven discovery in Spirulina systems biology [8].

Methods

Culture conditions and sample analysis

S. platensis strain C1 was used in this study. Cells were grown at 35 °C in 1,000 ml Erlenmeyer flasks with a culture volume of 500 ml and continuous stirring. Autotrophic and mixotrophic cultures were grown under fluorescent light at 100 μEinstein/m²/s. Zarrouk’s medium [47] was used for autotrophic growth and Zarrouk’s medium with glucose at a final concentration of 20 mM was used for the mixotrophic cultures. For the aerobic-dark cultures (heterotrophic), the flasks were wrapped with aluminum foil and incubated in the dark and sodium bicarbonate in Zarrouk’s medium was substituted by 20 mM of glucose. The control culture was not provided with a carbon source. In this heterotrophic cultivation using various organic or inorganic compounds as a carbon source, the cultures were cultivated in 250 ml flasks containing 100 ml of each tested medium, with three replicates.

The maximum growth rates under autotrophic, heterotrophic, and mixotrophic growth conditions were measured by the optical density at 560 nm and compared with the standard curve. The results from these three conditions are shown in Table 4. For autotrophic growth, the amount of bicarbonate was determined by titration with 0.1 N H₂SO₄[48]. The level of phosphate was measured as described elsewhere [49]. The maximum uptake rates of both substrates were calculated as 0.20 and 0.0056 mmol/mmol dry cell/h, respectively, in the exponential phase.

Metabolic network reconstruction

A metabolic network of S. platensis C1 was formulated using a combination of two procedures: automatic and manual reconstruction (see Fig. 1). In order to accelerate the process of metabolic network reconstruction, the annotated data of the draft genome sequence of S. platensis C1 (NCBI ID 67617) [24] were used as the input for the Pathway Tools software version 13.0 [26,27], which can automatically generate a preliminary gene-protein-reaction (GPR) association in the network. The PathoLogic algorithm embedded in the software performs the inference process from the entire sequence and functional annotations of S. platensis C1 by comparing the data to the MetaCyc database [31] as a key reference. The initial metabolic network consists of connections between the gene sequences, enzymes, metabolites, reactions, and biochemical pathways. Then, the manual reconstruction procedure was performed. Biochemical information related to Spirulina from the literature, books and published databases, such as KEGG [32], Brenda [33], CyanoBase [50] and updated Metacyc [31], were used as manually curated data for each pathway, reaction and gene product (enzyme): i) presence/absence pathway and reaction, ii) metabolite and cofactor specificity, iii) directionality of reactions, and iv) GPR association and location. The exchange reactions that allow specific molecules through the system and environment were included in the model according to TransportDB [51]. The Pathway Tools software cannot automatically provide information about protein complexes or isoenzymes. Published information must be used to determine the type of enzyme relationship, which is assumed to be an AND or OR relationship, where the AND relationship indicates cooperation between subunits in protein complexes and the OR relationship indicates the existence of isoenzymes. BLAST [28,29] was used for assigning enzymatic functions of the missing genes by searching nucleotide sequences against NCBI’s database using the expectation value (E-value) of less than e-5 and the similarity and identity score of 50 %. The top best hits were taken to check for the protein domain against pfam database [30] , if it contains the conserved domain, gene are assumed to be functional orthologues. However, the no gene-association reactions were presented in the refined network, although we could not annotate the corresponding gene sequence in the S. platensis C1 genome via the homology search because of its physiological evidence. During the manual curation, iterative modeling was performed using FBA for checking the completeness and consistency of the model and experiment. Some reactions were added to fulfill the system connection based on reactions present in closed organisms. The process of curation is iterative until the gaps in a draft metabolic network are filled [52,53]. An accepted metabolic network of S. platensis C1 was further used to predict growth behavior under autotrophic, heterotrophic, and mixotrophic conditions. Since no biomass composition data for S. platensis C1 are available, the stoichiometry of the biomass formation reaction used in this study was obtained from the work of Cogne et al[23].

Topology analysis

In order to analyze the metabolites connected within the network, we formulated a stoichiometric matrix S, derived from reaction lists of S. platensis C1. The column and row represent a reaction and a metabolite, respectively; each element is a stoichiometric coefficient. For each network, metabolite connectivity is defined as the number of metabolites that participate in any given reaction. The number of occurrences of each metabolite was calculated to reveal the highly connected metabolites of the reconstructed network. We also compared the metabolite connectivity pattern between the published genome-scale metabolic networks of Synechocystis sp. PCC6803 (iSyn669) [20], E. coli (iAF1260)[36], and yeast (iFF708) [37].

Flux balance analysis (FBA)

Flux balance analysis is a modeling technique that requires a developed stoichiometric metabolic network and a list of constraint parameters of biochemical reactions [11,12]. A set of metabolic reactions are converted into a mathematical stoichiometric format or an S (m × n) matrix, where the rows indicate the metabolites, m, and the columns represent the reactions, n. Based on a pseudo-steady state assumption, the change in growth rate is much smaller than the change in metabolite concentration and flux. Thus, the model could be written as S x v = 0, where v corresponds to a vector of all reaction fluxes in the network. Since the metabolic networks usually possess higher the number of independent reactions than the number of metabolites, the rank of a developed stoichiometric matrix is thus less than the number of reactions fluxes, giving rise to an underdetermined system. Using linear programming, the flux vector can be found by specifying an objective function (z) that can be minimized or maximized. In the case of minimization, the linear equation can be written as min z = c^Tv , where c is a row vector representing the influence of individual fluxes on the objective function. The metabolic flux distributions of the network are estimated under given conditions. In addition, the constraint parameters indicate the allowable range of flux values and are needed for convex solution space. The constraints for the upper and lower boundaries of reversible and irreversible reactions were defined as -∞ ≤ v_i ≤ ∞ and 0 ≤ v_i ≤ ∞, respectively. More details on the FBA approach have been described elsewhere [54,55].

Minimization of metabolic adjustment (MOMA)

The algorithm of minimization of metabolic adjustment was introduced by Segre et al[46]. This approach uses quadratic programming to search for a point in the feasible solution space of the mutant, which is nearest to an optimal point in the wild-type feasible solution space. The minimal distance is evaluated from the closest point and defined as the Euclidian distance. MOMA is also based on the same stoichiometric constraints as FBA, but it relaxes the assumption of optimal growth flux for the mutants. This method displays a suboptimal flux distribution that is intermediate between wild-type optimum and mutant optimum. In this study, we used the MOMA algorithm available in the COBRA toolbox [13,14] to carry out the gene essentiality analysis.

Model simulation

In this work, we used the COBRA toolbox [13,14] with the Systems Biology Markup Language (SBML) Toolbox v2 [56] on MATLAB to automatically construct the stoichiometric matrix of the reconstructed metabolic network. This tool uses FBA, which uses glpk (http://www.gnu.org/software/glpk/) as the linear programming solver to estimate the optimal flux distributions under the maximized biomass objective. Simulations of three different growth conditions: heterotrophic (with glucose, aerobically in the dark), autotrophic (without glucose in the light) and mixotrophic (with glucose in the light) were performed according to the minimal growth-dependent medium. The uptake rates of carbon, nitrogen, phosphate, and sulfate sources were set and varied under each condition as shown in Table 4. The minimal medium of heterotrophic and mixotrophic growth was supplemented with glucose as the other carbon source. The light reaction was lumped and the photon flux was constrained between zero and 100 μEinstein/m²/s for autotrophic and mixotrophic conditions, while it was set to zero for heterotrophic cell growth. The other external metabolites involved in transport reactions such as H₂O, Na⁺, Mg²⁺, H⁺, Zn²⁺, and Fe²⁺ (see Addition file 1), except for the substrates, were allowed to freely enter or leave the system. The uptake rates of all metabolites absent in the medium were set to zero. The flux values were expressed in mmol/mmol dry cell/h. All the three models in SBML format are provided in Additional files 5-7.

Active reaction determination

In order to investigate the system-level change in response to the growth conditions we identified modes of metabolic operation under autotrophy and mixotrophy in terms of active reaction presented the non-zero flux value of the simulations. The different in silico constraints of the simulation were set according to the carbon source utilized, as described above.

Flux variability analysis (FVA)

Flux variability analysis is used to examine the full range of numerical values for each reaction flux in the metabolic system while still satisfying the given constraints set and optimizing for a particular objective [44]. Determining the range of flux values (v) through each reaction, maximum value of the biomass objective function (z) is first computed and is used as s further constraint with multiple optimizations to minimize and maximize flux values of every reaction through FBA. The mathematical equation can be written as max(z^Tv). The difference between the calculated minimum and maximum values for each flux defines the flux variability of that reaction. In this study, we used the COBRA toolbox [13,14] to perform FVA.

Gene essentiality analysis

The effect of genetic changes such as gene deletion can be simulated by constraining reactions associated to gene of interest to be zero [45]. To determine the effect of genetic perturbation, all reactions associated with each gene in the iAK692 model were individually removed while still optimizing the growth rate. This in silico analysis was performed using the MOMA algorithm running through the COBRA toolbox [13,14] under autotrophic and mixotrophic conditions. An essential gene (lethal gene) was defined if no positive flux value for biomass formation could be obtained for a given mutant.

Phenotypic phase plane (PhPP)

A robustness analysis was performed to determine the sensitivity of the predicted growth in changing the fluxes through a pre-defined range. Phenotypic phase plane is the method which has been used to obtain the sensitivity analysis as a function of dual variables [25]. PhPP analysis was done by varying two particular reactions of interest and iteratively calculating the objective function. The shadow prices of the dual fluxes were evaluated for each solution. In metabolic network, a shadow prices is the rate at which the objective function (z) changes in response to an increase availability of each metabolite. Mathematically equation used to calculate the shadow price can be written as: γ_i = dz/db_i where γ_i is the ith shadow price and b_i is the ith metabolite of the metabolic network. In this study, we performed PhPP using the COBRA toolbox [13,14]. The simulation was carried out with autotrophy by setting the boundaries of the absorbed photon fluxes between zero to 100 μEinstein/m²/s; and of the bicarbonate uptake rates between zero to 0.4 mmol/mmol dry cell/h. For mixotrophy, PhPP analysis was performed by varying the boundaries of the glucose uptake rates between zero to 0.034 mmol/mmol dry cell/h and the bicarbonate uptake rates between zero to 0.4 mmol/ mmol dry cell/h.

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

AK performed the reconstruction of the genome-scale metabolic model and the network analysis and wrote the manuscript; AK, AP, and AM designed the study and were involved in model simulation and evaluation. AK, AP, and CK performed the Spirulina cell cultivation experiments. All authors read and approved the final manuscript.

Supplementary Material

Additional file 1

Additional file 1iAK692 model. Excel file containing a list of the biochemical reactions in the final version of the metabolic network reconstruction, iAK692.

Additional file 2

Additional file 2: Fluxome distribution under three different growth simulations. This Excel file contains a list of all flux distribution (in mmol/mmol dry cell/h) profiles under the autotrophic, heterotrophic, and mixotrophic culture conditions.

Additional file 3

Additional file 3: Flux variability analysis. Excel file contains flux variability of the entire metabolic network for autotrophic and mixotrophic growths.

Additional file 4

Additional file 4: Gene deletion analysis using MOMA approach inS.platensisC1 metabolic model. Excel file contains the grRatio, grRateKO and grRateWT values for S. platensis C1 single gene deletion during autotrophic and mixotrophic growths.

Additional file 5

Additional file 5: SBML Model for the autotrophic simulation.This file contains the stoichiometric iAK692 model in the SBML format with all of the constraints needed for simulation using the COBRA toolbox.

Additional file 6

Additional file 6: SBML Model for the autotrophic simulation.This file contains the stoichiometric iAK692 model in the SBML format with all of the constraints needed for simulation using the COBRA toolbox.

Additional file 7

Additional file 7: SBML Model for the autotrophic simulation.This file contains the stoichiometric iAK692 model in the SBML format with all of the constraints needed for simulation using the COBRA toolbox.

Acknowledgements

The authors would like to thank Dr Intawat Nookeaw (Chalmers University, Sweden) for his help in modeling and all the staff at the Algal Technology Laboratory at King Mongkut’s University of Technology Thonburi (KMUTT) for their assistance in Spirulina cell cultivation. The authors also thank anonymous reviewers for their valuable discussions and comments on this manuscript. This work was supported by grants from the Thailand government’s annual budget 2009 and the Platform Technology program of the National Center for Genetic Engineering and Biotechnology.