Abstract
Human skeletal muscles have different fiber types with distinct metabolic functions and physiological properties. The quantitative metabolic responses of muscle fibers to exercise provide essential information for understanding and modifying the regulatory mechanisms of skeletal muscle. Since in vivo data from skeletal muscle during exercise is limited, a computational, physiologically based model has been developed to quantify the dynamic metabolic responses of many key chemical species. This model distinguishes type I and II muscle fibers, which share the same blood supply. An underlying hypothesis is that the recruitment and metabolic activation of the two main types of muscle fibers differ depending on the pre-exercise state and exercise protocols. Here, activation measured by metabolic response (or enzymatic activation) in single fibers is considered linked but distinct from fiber recruitment characterized by the number (or mass) of each fiber type involved during a specific exercise. The model incorporates species transport processes between blood and muscle fibers and most of the important reactions/pathways in cytosol and mitochondria within each fiber type. Model simulations describe the dynamics of intracellular species concentrations and fluxes in muscle fibers during moderate intensity exercise according to various experimental protocols and conditions. This model is validated by comparing model simulations with experimental data in single muscle fibers and in whole muscle. Model simulations demonstrate that muscle-fiber recruitment and metabolic activation patterns in response to exercise produce significantly distinctive effects depending on the exercise conditions.
Keywords: computational modeling, skeletal muscle, fiber types, metabolism, exercise
Introduction
Skeletal muscle is a heterogeneous tissue with different fiber types(8; 48; 53). Metabolic responses of the muscle fibers during exercise can reveal regulatory mechanisms that govern metabolism in skeletal muscle in health and disease states. Under normal physiological conditions, exercise performance (19) and fat transport and metabolism in skeletal muscle(10; 36) are affected by fiber type distribution. Under pathophysiological conditions, abnormalities in size and distribution of type 1 and type 2 muscle fibers have been associated with mitochondrial respiratory chain dysfunction (13). Another study in insulin resistance and type 2 diabetic rats concluded that muscle fiber type I seems much more susceptible to the development of insulin resistance than muscle fiber type II (7). These findings underline the importance of fibers-type distribution in determining the muscle metabolic response to different stimuli. However, in vivo metabolic responses of these fibers during exercise have not been distinguished and evaluated, nor accurately related to the whole body response. In the transition from rest to exercise, muscle blood flow increases and muscle fibers are recruited to match the required energy demand (9). During exercise, when the rate of ATP turnover rapidly increases, intracellular metabolic processes associated with ATP synthesis in recruited muscle fibers need to be activated simultaneously to meet the energy demand. Although magnetic resonance imaging (MRI) can be used to quantify the increased volume of active skeletal muscle(12; 43), it cannot distinguish the recruitment pattern of the different muscle fiber types. For this purpose, the depletion pattern of glycogen and phosphocreatine (PCr) in the muscle fibers has been used to detect the activation in single muscle fibers during the transition from rest to exercise with increased energy expenditure (16; 17; 22; 27; 28). However, these measurements do not provide enough information to distinguish the extent of involvement of fiber type I and II during exercise. Although metabolite concentration changes cannot be directly related to the number of recruited fiber, they provide qualitative information of the fiber types involvement. Therefore, a quantitative characterization of the fiber activation includes not only the determination of metabolite and enzyme changes, but also a measure of the number of recruited fibers (i.e. type I and II). The metabolic and motor nerve responses to exercise determine the recruitment of the muscle fibers (30). Thus, in this work, the recruitment and metabolic activation of muscle fibers that are commonly and interchangeably used to refer to the fiber activation are considered as two distinct processes.
The quantitative contributions of fiber type I and II to the energy demand and detailed dynamics of metabolic responses of muscle fibers in response to different exercise intensities are unknown. Indeed, accurate measurements to quantify the recruitment and metabolic activation of muscle fibers in vivo have not been possible to date. To preferentially engage type I and II fibers during exercise with either metabolic activation or recruitment muscle fibers or both, experimental approaches have tried neuromuscular blockade agents (26) or pre-exercise glycogen depletion (27). However, these experimental conditions did not produce quantitatively distinct contributions of recruitment and metabolic activation of type I and II fibers on the metabolic response in the whole working muscle.
Quantitative analysis of experimental data and simulation of the dynamics of metabolic and physiological changes in tissue metabolism under different conditions requires a, computational model of skeletal muscle (e.g., vastus lateralis muscle)(33). Such a model, which incorporates type I and type II muscle fibers, is developed here based on a previous model that lacks this information (33). An underlying hypothesis is that the recruitment and metabolic activation of the two main types of muscle fibers differ depending on the pre-exercise state and exercise protocols. Here, activation measured by metabolic response in single fibers is considered distinct from fiber recruitment characterized by the number (or mass) of each fiber type involved during a specific exercise. Each of the two parallel fiber compartments of the model, which share the same blood supply, is divided into cytosolic and mitochondrial domains. Mass transport and reaction fluxes of key chemical species are distinguished in each fiber type. To simulate the skeletal muscle fibers metabolic response to moderate intensity exercise protocols using bicycle and knee extension, the model incorporates time-dependent rate coefficients that allow for changes in effective volumes and metabolic rates of each fiber. The metabolic and transport fluxes respond to exercise by a parallel activation mechanism (23-25; 33; 52).
For this study, most model parameter values were similar to those previously published(33). Values of other model parameters, viz., activation coefficients, were estimated based on optimal fitting of model-simulated outputs to experimental data (26; 27; 37; 39; 42; 51). Consequently, this model can simulate in vivo dynamic responses of intracellular metabolism in single fiber types during exercise that cannot be evaluated otherwise. Based on experimental data, the metabolic status of the two types of muscle fibers in the resting state are nearly the same. In exercising skeletal muscle, however, the recruitment and metabolic activation patterns of the muscle fiber types are different. Model simulations were performed to investigate these different roles under several experimental conditions.
Methods
Overview
A mathematical model was developed to quantitatively evaluate the in vivo effects of type I and type II fibers in human skeletal muscle in response to short-term, moderate-intensity exercise. For each fiber type, the model represents the same metabolic pathways that include glycolysis/glycogenolysis, lipid metabolism, β-oxidation, tricarboxylic acid (TCA) cycle, oxidative phosphorylation and special reactions associated with high-energy phosphate metabolism. Protein metabolism was not considered because it is a much less important energy source for skeletal muscle during short-term exercise in normal, healthy subjects. In the resting state, the metabolism of the fiber types (indicated by ATP turnover) does not differ statistically(50). Consequently, in the resting steady state for this model, the volumes and metabolic states of the two fiber types are the same. During the transition from rest to exercise, however, the fibers types undergo different recruitment and activation. In our description of the development of this model we present the basic components of the model and the strategy for quantifying the characteristics (viz. activation coefficients) of the fiber types based on several different experimental protocols (Table 1).
Table 1.
Experimental conditions associated with model simulations.
| Experiment | Condition | Protocol | Recruitment & Metabolic deactivation/activation | Reference |
|---|---|---|---|---|
| 1 | Control | Cycling (50%VO2max) | Type I fiber Activation | (27) |
| 2 | Pre-exercise glycogen depletion | Cycling (50%VO2max) | Type II fiber Activation | (27) |
| 3 | Control | Cycling (60% VO2max) | Type I fiber Activation | (37; 39; 42; 51) |
| 4 | Control | Knee-extensor (50%VO2max) | Type I fiber Activation | (26) |
| 5 | Neuromuscular Blocking Agent | Knee-extensor (50%VO2max) | Type I fiber Deactivation | (26) |
Model Development
Model structure
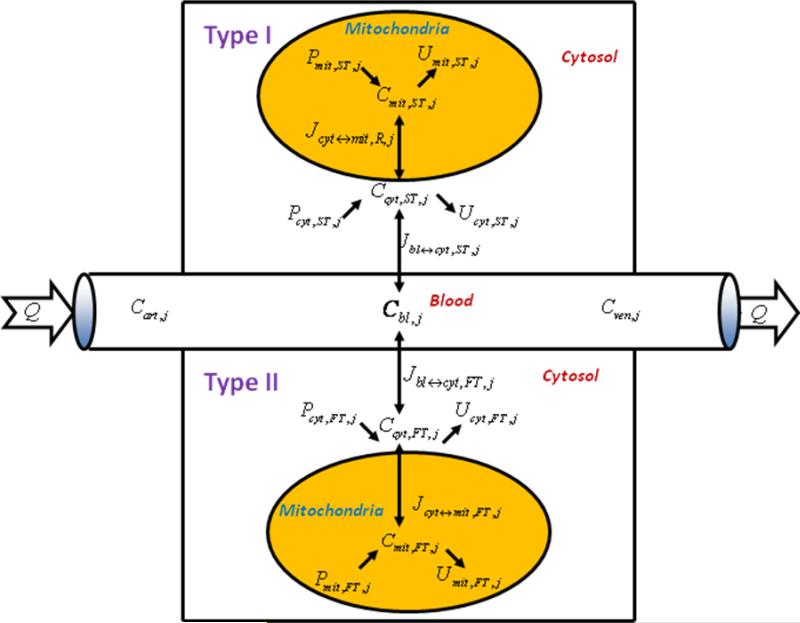
This model groups muscle fibers into two main classes: type I (slow-twitch, aerobic, red) and type II (fast-twitch, anaerobic, white)(22; 38). Here type II muscle fibers include type IIa (fast–oxidative) and type IIb (fast-glycolytic). In human skeletal muscle, e.g., vastus lateralis, different muscle fiber types and their related capillaries exist in close proximity(47). Therefore, the fiber types share a common blood supply that affects the transport processes of chemical species between blood and muscle fiber types. Within each fiber type, the model distinguishes the cytosolic and mitochondrial compartments with respect to intracellular species transport and metabolism (Fig. 1).
Figure 1.
Schematic diagram of model structure. Whole skeletal muscle is composed of one blood domain and two tissue domains, corresponding to each muscle fiber, respectively. The fluid volume consists of capillary blood and interstitial fluid (ISF). Both muscle fiber types share a common blood supply. Each muscle fiber is compartmentalized as cytosol and mitochondria. Transport fluxes exist between blood and cytosol, and between cytosol and mitochondria. The species concentrations in tissue depend on reaction and transport fluxes.
Dynamic mass transport balances
In capillary blood, the concentration of a chemical species j is determined by the dynamic mass balance equation for type I-red (R) and type II-white (W) fiber types(33; 34):
| (1) |
where Cart,j is the arterial species concentration; Vbl is the total effective volume of capillary blood and interstitial fluid (ISF) space; Q is the blood flow; is the net mass transport flux between blood and cytosol of each fiber type, F ∈ (R,W). These transport processes can be passive (k=p) or facilitated (k=f).
The concentrations CX,F,j of species j in the cytosol (X=cyt) and mitochondria (X=mit) are determined by the dynamic mass balance equations(33; 34):
| (2) |
| (3) |
where VX,F is the effective volume of the cytosol or mitochondria in each muscle fiber; is the net mass transport flux between the cytosol and mitochondria; RX,F,j is the net metabolic reaction rate in each fiber:
| (4) |
where ϕX,F,S↔P is the reaction flux involving substrate (S) and product (P); βF,j,S↔P is the corresponding stoichiometric coefficient. The specific mass balance equation of each species is given in the online supplemental material (Part B).
Metabolic reaction flux relations
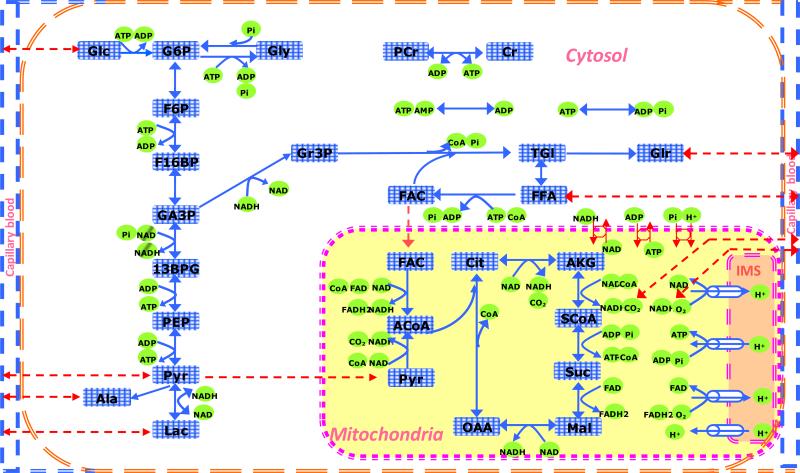
The metabolic pathways common to both fiber types are shown in Fig. 2. In the cytosol and mitochondria, the reaction fluxes of Eqs. (2) and (3) are typically expressed by reversible enzyme kinetics(33; 34):
| (5) |
where γ(A, I) is a controller function for activation (A) or inhibition (I); [SF,q] and [PF,l] are concentrations of substrates and products with stoichiometric coefficients mq and nl; and are Michaelis-Menten equilibrium constants of forward and backward reactions with the same values in both fibers. The maximal forward and backward reaction rate coefficients, and , are related by equilibrium coefficients(33; 34):
| (6) |
The reaction flux equations in the cytosol and mitochondria are given in online supplemental materials (Part C).
Figure 2.
Schematic diagram of the biochemical pathways depicting species and metabolic pathways of the cytosol and mitochondria of skeletal muscle. The chemical species are Glc: glucose, Gly: glycogen, G6P: glucose-6-phosphate, F6P: fructose-6-phosphate, F16BP: fructose-1,6-bisphosphate, GA3P: glyceraldehyde-3-phosphate, 13BPG: 1,3-biphosphate glycerate, PEP: phosphoenolpyruvate, Pyr: pyruvate, Lac: lactate, Ala: alanine, Gr3P: glycerol-3-phosphate, Tgl: triglycerides, Glr: glycerol, FFA: free fatty acid, FAC: fatty acyl-CoA, ACoA: acetyl-CoA, Cit: citrate, AKG: α-ketogluterate, SCoA: succinyl-CoA, Suc: succinate, Mal: malate, Oxa: oxaloacetate, CoA: coenzyme-A (free), PCr: phosphocreatine, Cr: creatine, Pi: inorganic phosphate, CO2: carbon dioxide, O2: oxygen, NADH: reduced nicotinamide adenine dinucleotide, NAD+: oxidized nicotinamide adenine dinucleotide, FADH2: reduced flavin adenine dinucleotide, FAD: oxidized flavin adenine dinucleotide, ATP: adenosine triphosphate, ADP: adenosine diphosphate, AMP: adenosine monophosphate, H+: hydrogen ions (protons).
Transport flux relations
The governing equations of passive and facilitated transport fluxes have the following general forms:
| (7a) |
| (7b) |
where λx↔y,F,j is the effective permeability-surface area product for passive diffusion between domains: x ↔ y ∈{bl ↔ cyt, cyt ↔ mit} of each fiber type; Tx↔y,F,j is the maximal transport rate for facilitated transport; Mx↔y,j is the phase equilibrium constant assumed to be the same in both fibers. The transport flux equations of each species are given in online supplemental material (Part D).
Muscle recruitment and metabolic activation functions
Often, in exercise physiology literature the muscle fiber recruitment and metabolic activation are used as synonymous terms. However, in this work, we distinguish these two terms. Here, muscle recruitment is associated with an increase in flow and volume parameters, while metabolic activation is associated with an increase in transport and metabolic rate coefficients. This terminology will be used in every section of the manuscript.
In response to an increase in work rate, muscle blood flow (Q) and effective volumes of blood (Vbl) and fibers (VR,VW) increase. In this model, the dynamics of these muscle properties are described by a generalized enhancement function, RFk ∈(Q,Vbl,VR,VW) characterized by responses to a step increase in work rate starting at time t0 (33):
| (8) |
where are the variable values at resting, steady state; εk is the recruitment coefficient for muscle volumes and blood flow; τεk is the time constant.
Most transport and metabolic reaction fluxes change at the onset of muscle contraction according to a parallel-activation hypothesis (23; 24; 33). The corresponding activation rate coefficients AFk ∈(λ,Tmax,Vmax) are represented by a generalized activation function:
| (9) |
where represents the parameters at resting steady state; αk is an activation coefficient; τα is a time constant. αk is distinguished between muscle fibers according to the activation patterns under different physiological conditions.
Evaluation of model parameters and initial conditions
To evaluate the many parameters and initial conditions of the variables in this complex systems model is a challenge. In absence of specific transport and metabolic properties of type I and II fibers, we assumed similar characteristics for both muscle fiber types. The blood supply and metabolite concentrations at resting state for whole tissue are obtained from the literature as our previous model (33). Since this model is based on an earlier validated model of whole skeletal muscle metabolism, the values of many variables/parameters (e.g., Mx↔y,j in transport, , in reaction) and initial conditions are essentially the same. Some parameters associated with muscle activation in exercise, e.g., time constant τεk, τα and recruitment coefficient εk, can be derived from literature (5; 15; 33; 43). In this study, the unknown parameters that were determined are those activation coefficients αk incorporated in the specific reaction and transport fluxes under different physiological conditions.
Volume
Skeletal muscle volume (Vmus) is the sum of the effective volumes of blood (Vbl )(including capillary blood and interstitial fluid-ISF space) and muscle cells in the tissue (Vtis)(33; 34):
| (10) |
The volume of muscle cells can be further divided into fiber volumes F ∈{R,W} as well as volumes of cytosol and mitochondria:
| (11) |
The intracellular proportions in skeletal muscle are (33; 34):
| (12) |
For vastus lateralis muscle of healthy human subjects, the type I and II fiber volumes are estimated by(3; 21; 41; 46; 53)
| (13) |
Because type I fibers have a greater number of mitochondria, and assuming that the cytosol is 88% of type I fiber volume, we calculated the relative volume of the cytosol and mitochondria in type II fibers as:
| (14) |
| (15) |
The values of the volumes in each muscle fiber are summarized in Table 2.
Table 2.
Volume components of skeletal muscle at resting steady state under different experimental conditions.
| Symbols | Components | % of whole muscle | Exp. 1,2 & 3 | Exp. 4 & 5 |
|---|---|---|---|---|
| Volume (L) | Volume (L) | |||
| Vmus | Whole skeletal muscle | 100 | 5† | 2‡ |
| Vbl | Blood | 20 | 1 | 0.4 |
| VR | Type I muscle fibers | 40 | 2 | 0.8 |
| VW | Type II muscle fibers | 40 | 2 | 0.8 |
| Vcyt,R | Cytosol of Type I muscle fibers | 35.2 | 1.76 | 0.704 |
| Vmit,R | Mitochondria in Type I muscle fibers | 4.8 | 0.24 | 0.096 |
| Vcyt,W | Cytosol in Type II muscle fibers | 36.8 | 1.84 | 0.736 |
| Vmit,W | Mitochondria in Type II muscle fibers | 3.2 | 0.16 | 0.064 |
Note:
1)Volume distribution of muscle fibers corresponds to the human vastus lateralis muscle.
2)Vbl is the effective volume of capillary blood and interstitial fluid (ISF). We assume the two domains are in equlibrium.
3) Muscle in two legs are involved in cycling exercise, we assumed the effective volume at rest is 5L.
4) Part of muscle in one leg is involved in knee-extensor exercise, we assume the effective volume at rest is 2L.
Species concentrations at resting steady state
Species concentrations in the two muscle fiber types can be estimated using whole muscle concentrations. Species mass (j) in the fibers must sum to species mass of the tissue:
| (16) |
At resting steady state, we assume that the masses of most intracellular metabolites are the same within the two fiber types: . From these relationships, most concentrations in each type of muscle fiber can be calculated. Experimental data show however, that concentration differences of some metabolites between two types of muscle fibers are significantly different, which are related to the metabolic characteristics of the muscle fiber types. For the following chemical species, the relative concentrations in the fiber types are estimated from experimental data: high-energy phosphate compounds, e.g., PCr(2; 11; 45; 46; 49), ATP(11; 45), ADP(11) and several other metabolites - G6P(49), Ala(14), Gly(11; 49), TGl(18; 35; 45), NADH and NAD+ (44).
The species concentration in the cytosol and mitochondria in each fiber are determined by mass balances:
| (17a) |
The species (j) concentration in the cytosol and mitochondria of each fiber type are summarized in Table 3 including the relative mass concentrations of the species:
| (17b) |
Table 3.
Species concentrations in whole muscle tissue and in the cytosol and mitochondria of each muscle fiber type at resting steady state.
| Species j | Muscle Tissue † [mmol/kg ww] | Relative mass ωR,j (%) |
Type I muscle fiber CR,j
‡
|
Type II muscle fiber CW,j
‡
|
||||
|---|---|---|---|---|---|---|---|---|
| Relative mass θR,j (%) | Relative mass θW,j (%) | |||||||
| Glc | 0.5 | 50 | 100 | 0.568 | 0 | 100 | 0.543 | 0 |
| Pyr | 0.05 | 50 | 95 | 0.0540 | 0.0208 | 95 | 0.0516 | 0.0312 |
| Lac | 0.78 | 50 | 100 | 0.886 | 0 | 100 | 0.848 | 0 |
| Ala | 1.3 | 40 | 100 | 1.182 | 0 | 100 | 1.69 | 0 |
| Glr | 0.065 | 50 | 100 | 0.0738 | 0 | 100 | 0.0707 | 0 |
| FFA | 0.45 | 50 | 100 | 0.455 | 0 | 100 | 0.435 | 0 |
| CO2(F) | N/A | N/A | N/A | 1.403 | 1.525 | N/A | 1.403 | 1.525 |
| O2(F) | N/A | N/A | N/A | 0.0338 | 0.027 | N/A | 0.0338 | 0.027 |
| G6P | 0.25 | 40 | 100 | 0.227 | 0 | 100 | 0.326 | 0 |
| Gly | 95 | 40 | 100 | 86.364 | 0 | 100 | 123.91 | 0 |
| F6P | 0.044 | 50 | 100 | 0.05 | 0 | 100 | 0.0478 | 0 |
| F16BP | 0.06 | 50 | 100 | 0.0682 | 0 | 100 | 0.0652 | 0 |
| GA3P | 0.08 | 50 | 100 | 0.0909 | 0 | 100 | 0.0869 | 0 |
| 13BPG | 0.08 | 50 | 100 | 0.0909 | 0 | 100 | 0.0869 | 0 |
| PEP | 0.0049 | 50 | 100 | 0.00557 | 0 | 100 | 0.00533 | 0 |
| Tgl | 15 | 70 | 100 | 23.86 | 0 | 100 | 9.783 | 0 |
| Gr3P | 0.15 | 50 | 100 | 0.17 | 0 | 100 | 0.163 | 0 |
| FAC | 0.0035 | 50 | 95 | 0.00378 | 0.00146 | 95 | 0.00361 | 0.00219 |
| PCr | 20 | 45 | 100 | 20.45 | 0 | 100 | 23.91 | 0 |
| Cr | 10.5 | 42 | 100 | 10.02 | 0 | 100 | 13.24 | 0 |
| ATP | 6.2 | 45 | 84.8 | 5.38 | 7.07 | 95 | 7.09 | 4.667 |
| ADP | 0.8 | 70 | 11 | 0.14 | 8.307 | 40 | 0.209 | 3.6 |
| AMP | 0.04 | 36 | 100 | 0.0329 | 0 | 100 | 0.0555 | 0 |
| Pi | 2.75 | 50 | 95 | 2.97 | 1.146 | 95 | 2.84 | 1.72 |
| CoA | 0.02 | 50 | 80 | 0.018 | 0.033 | 80 | 0.0174 | 0.05 |
| NADH | 0.05 | 60 | 0.5 | 3.41E-4 | 0.498 | 0.5 | 2.17E-4 | 0.498 |
| NAD | 0.45 | 60 | 30 | 0.184 | 3.156 | 30 | 0.117 | 3.15 |
| ACoA | 0.002 | 50 | 0 | 0 | 0.0167 | 0 | 0 | 0.025 |
| Cit | 0.095 | 50 | 0 | 0 | 0.792 | 0 | 0 | 1.187 |
| AKG | 0.013 | 50 | 0 | 0 | 0.108 | 0 | 0 | 0.163 |
| SCoA | 0.13 | 50 | 0 | 0 | 1.083 | 0 | 0 | 1.63 |
| Suc | 0.095 | 50 | 0 | 0 | 0.792 | 0 | 0 | 1.19 |
| Mal | 0.095 | 50 | 0 | 0 | 0.792 | 0 | 0 | 1.19 |
| Oxa | 0.0024 | 50 | 0 | 0 | 0.02 | 0 | 0 | 0.03 |
| FADH2 | 0.024 | 50 | 0 | 0 | 0.2 | 0 | 0 | 0.30 |
| FAD | 0.212 | 50 | 0 | 0 | 1.767 | 0 | 0 | 2.65 |
| H+ | N/A | N/A | N/A | 7.94E-05 | 2.51E-05 | N/A | 7.94E-05 | 2.51E-05 |
Concentrations in whole tissue obtained from experimental data.
Concentrations in muscle fibers calculated from model equations (Eqs.16-17).
Species transport fluxes and parameters at resting steady state
To determine the resting steady state fluxes, we applied the steady state mass balances from Eqs. 1-4 with the muscle uptake (or release) rate of the species(33; 34):
| (18) |
In the cytosol, the flux balance is
| (19) |
and in the mitochondria, the flux balance is
| (20) |
As in our previous work, the basis of flux balance analysis is the and . However, these values cannot be directly measured and only is available. For the target muscle, the vastus lateralis in this study, the metabolic status of the two muscle fiber types, e.g., ATP turnover(50) and respiratory quotient (RQ), only have minor differences at basal state. Therefore, we simplified this system and assumed that the relative flux distributions of in the two muscle fibers are the same,
| (21) |
The values of and are normalized by the volume of each fiber type (Table 4).
Table 4.
Blood species concentrations and transport rates between blood and tissue for whole muscle and for muscle fibers at rest.
| Species (j) | Cart,j [mmol/min] | Cven,j [mmol/min] | [mmol/min] | † [mmol/min/kg fiber] |
|---|---|---|---|---|
| Glc | 5.0 | 4.7833 | 0.195 | 0.0488 |
| Pyr | 0.08 | 0.0667 | 0.012 | 0.003 |
| Lac | 0.5 | 0.6 | –0.09 | -0.0225 |
| Ala | 0.25 | 0.322 | –0.065 | -0.0163 |
| Glr | 0.04* | 0.0489 | –0.008 | -0.002 |
| FFA | 0.7* | 0.619 | 0.073 | 0.0183 |
| CO2 (T) | 23.405 | 25.5 | –1.885 | -0.47 |
| CO2 (F) | 1.22 | 1.329 | N/A | N/A |
| O2 (T) | 9.235 | 6.548 | 2.418 | 0.605 |
| O2 (F) | 0.135 | 0.049 | N/A | N/A |
| H+ | 3.98E-5 | 4.78E-5 | –7.25E-6 | -1.81E-6 |
Transport flux values for each type of muscle fibers are assumed same at rest, which is normalized based on the volume of muscle fiber, respectively.
From values of the transport rates and species concentrations (Tables 3 and 4), the transport rate coefficients related to fiber type (λx↔y,F,j, Tx↔y,F,j) can be uniquely determined according to the governing equations of species transport (Eq.7) by satisfying the constraint of resting steady state. Here we assume that the values of Mx↔y,j in the carrier mediated transport flux between both blood and cytosol and between cytosol, and mitochondria are the same in the two muscle fiber types and correspond to our previous model. The values of the parameters in the transport fluxes are shown in the supplemental materials Table A1.
Species metabolic fluxes and rate parameters at resting steady state
Based on the transport fluxes between blood and each fiber and under resting steady state conditions, the reaction fluxes in type I and II fibers was determined by flux balance analysis. In the current model, (Table 5). From species concentrations (Table 3) in each fiber at rest, the maximal reaction rate coefficients of Eqs. 5-6 can be evaluated (Supplemental material Table A2). As in our previous model, the values of , were kept the same for both fiber types.
Table 5.
Reaction fluxes at rest and estimated activation coefficients αk,F for type I and type II fibers F ∈{RW} associated with reaction fluxes under experimental conditions 1 and 2.
| Reaction flux | † [mmol/min/kg fiber] | Type I & II* [-] |
|---|---|---|
| Hexokinase | 0.0489 | 0 |
| Glycogen synthase | 0.25 | 0 |
| Glycogen phosphorylase | 0.25 | 32.96 |
| Phosphoglucose isomerase | 0.0488 | 25.68 |
| Phosphofructokinase | 0.0488 | 25.68 |
| Aldolase +TPI | 0.0488 | 25.68 |
| GA3P dehydrogenase | 0.0955 | 25.68 |
| Phosphoglycerate kinase | 0.0955 | 25.68 |
| Pyruvate kinase | 0.0955 | 25.68 |
| Lactate dehydrogenase | 0.0225 | 0 |
| Lipases | 0.002 | 47.50 |
| Gr3P dehydrogenase | 0.002 | 0 |
| Acyltransferase | 0.02 | 0 |
| Acyl-CoA synthetase | 0.0243 | 47.52 |
| ATPase | 2.69 | 76.63, 23.25 |
| Adenylate kinase | 0 | 0 |
| Creatine kinase | 0 | 0 |
| Alanine aminotransferase | 0.0163 | 0 |
| Pyruvate dehydrogenase | 0.0598 | 7.01, 278.7 |
| β-Oxidation | 0.0183 | 47.52 |
| Citrate Synthase | 0.206 | 101.1 |
| Isocitrate dehydrogenase | 0.206 | 101.1 |
| AKG dehydrogenase | 0.206 | 101.1 |
| SCoA synthetase | 0.206 | 101.1 |
| Succinate dehydrogenase | 0.206 | 101.1 |
| Malate dehydrogenase | 0.206 | 101.1 |
| Complex I+III+IV | 0.876 | 484.16, 6.28 |
| Complex II+III+IV | 0.334 | 484.16, 6.28 |
| ATP synthase | 2.69 | 11.13 |
Flux values are normalized to the volume of each type of muscle fibers, which are same.
In case of only one value the activation coefficient of type I fibers was assumed the same as that of type II fibers in both experiments 1 and 2. Otherwise, first and second values are associated with type I and II fibers, respectively, and were estimated using the data set of the experiment 1 and 2, respectively.
Dynamic characteristics of model parameters
In response to a step increase in work rate, changes in the transport and metabolic rate coefficients are described by an activation function AFk ∈(λ, Tmax, Vmax) given by Eq. 9, which is characterized by αk, a magnitude coefficient, and τα, a time constant. The values of the activation coefficients αk (Tables 5-6), distinguished in muscle fibers at different physiological states were estimated by least-square matching of model outputs to experimental data of subjects during moderate-intensity exercise. We assumed τα = τεk for flow and muscle volume activation, which is the same for all chemical species (Table 7).
Table 6.
Estimated activation coefficients αk,F for type I and type II fibers F ∈{R.W} associated with transport fluxes under experimental conditions 1 and 2.
| Species | Type I & II* |
|---|---|
| Blood-Cytosol, αk,F | |
| Glc | 2.51 |
| Pyr | 20.94 |
| Lac | 20.94 |
| Ala | 7.78 |
| Glr | 0 |
| FFA | 3.39 |
| CO2 | 34.11 |
| O2 | 34.11 |
| H+ | 3.39 |
|
Cytosol-Mitochondria, αk,F | |
| Pyr | 23.26 |
| Pi | 18.41 |
| ATP - ADP | 18.41 |
| NADH - NAD | 14.77, 114.23 |
| FAC | 6.28 |
| CoA | 11.13 |
| O2 | 34.11 |
| CO2 | 34.11 |
| H+ | 11.13 |
In case of only one value the activation coefficient of type I fibers was assumed the same as that of type II fibers in both experiments 1 and 2. Otherwise, first and second values are associated with type I and II fibers, respectively, and were estimated using the data set of experiment 1 and 2, respectively.
Table 7.
Recruitment parameter values for flow and muscle volume for Experimental 1 and 2.
| Parameter | Experiment 1 & 2* | |
|---|---|---|
| Q | [L min-1] | 0.9 |
| τ ε k | [min] | 0.42 |
| ε Q | [-] | 7.784 |
| ε VBl | [-] | 0.56 |
| ε VR | [-] | 1.12, 0 |
| ε VW | [-] | 0, 1.12 |
In case of only one parameter value, this was used in both experiments 1 and 2. Otherwise, first and second values are derived from experiment 1 and 2, respectively.
The dynamics of muscle blood flow and effective volumes of associated with muscle recruitment are described by a recruitment function, RFk (t) k ∈ (Q,Vbl,VR,VW) given by Eq. 8, which is characterized by εk, a magnitude coefficient, and τεk, a time constant. The values depend on the conditions of Experiments 1 and 2 (Table 7). In Experiments 1 and 2, τεk is associated with blood flow dynamics and εQ is obtained experimentally (5). The recruitment coefficient of the blood volume change εVBl is assumed to be that of whole muscle as determined in vivo using NMR (12; 43). At steady state, the volume coefficients for type I and type II fibers are assumed equal, εVR = εVW. With no recruitment of type II fibers during exercise, , and from Eqs. (8), (10) and (11):
| (22) |
During exercise, type I and II muscle fibers undergo different recruitment and activation controls, which depend on exercise and physiological states of skeletal muscle as determined by the experiment. To simulate data from experiment 1, type I fibers are primarily activated without additional recruitment of type II fibers at the onset of exercise. To simulate data from experiment 2, type II fibers are primarily activated without additional recruitment of type I fibers (Table 7) at the onset of exercise.
Simulation strategy
During exercise, type I and II muscle fibers undergo different recruitment and activation, which depend on exercise and physiological states of skeletal muscle as determined by the experiment. First, we established values of the model parameters, metabolite concentrations and fluxes at resting, steady state. Then, according to different experimental conditions, model parameter values were changed to simulate the experimental responses. Unknown parameters of the model were optimally estimated by least-squares fitting of model outputs to data from Experiments 1 and 2. Parameter values were changed to predict the metabolic response to exercise from Experiments 3, 4 and 5 according to the prevailing conditions (Table 8).
Table 8.
Model parameter values related to the additional recruitment (RF) and metabolic activation (AF) functions of type I and type II fibers under different experimental conditions.
| Simulation | Experiment | Type I Fibers | Type II Fibers | ||
|---|---|---|---|---|---|
| Muscle Recruitment | Metabolic Activation | Muscle Recruitment | Metabolic Activation | ||
| ε VR | α k,R | ε VW | α k,W | ||
| Validation | 1 | 1.12 | Table 5,6 | 0 | 0 |
| “ | 2 | 0 | Table 5,6 | 1.12 | Table 5,6 |
| Prediction | 3 | 1.12 | Table 5,6 | 0 | 0 |
| “ | 4 | 1.12 | Table 5,6 | 0 | Table 5,6 |
| “ | 5 | 0 | Table 5,6 | 1.12 | Table 5,6 |
| “ | 5 | 0.42 | Table 5,6 | 1.12 | Table 5,6 |
Experiment 1
From the study by Krustrup et al. (27), data for the control group (cycling at 50% VO2max) includes [ATP], [Gly] and [PCr] in single muscle fibers and [PCr], [Gly] and [Lac] from whole muscle. For comparison to the experimental data at the onset of exercise, model simulations assumed only type I fibers were recruited and activated. The transport and reaction flux activation coefficients of type I fibers (αk,R) were estimated with the data from Experiment 1.
Experiment 2
From the same study by Krustrup et al.(27), data are available for the same exercise protocol, but applied to subjects with pre-exercise glycogen depletion. Under this condition, both type I and II muscle fibers are metabolically activated, but only type II fibers have an additional recruitment at the onset of exercise (Table 2 and 7). For model simulations, the activation coefficients for type I fibers are the same as in Experiment 1 (except zero for measured glycogen utilization-phosphorylation) (Table 5-6). While most activation coefficients for type II fibers (αk,W) have the same values as αk,R obtained in Experiment 1, those activation coefficients most likely to be affected by different experimental conditions were estimated by optimal fitting of model outputs to experimental data from Experiment 2 (Table 5-6).
Experiment 3
Other independent studies (37; 39; 42; 51) with a similar protocol to the study of Krustrup et al.(27) report data from an exercise protocol at moderate intensity (cycling at 60% VO2max). These data included [Gly] and [ATP](42), [Glc], [G6P], [F6P], [Pyr] and [Lac](37), [PCr] and [Cr](51), and NADH/NAD+ (39) for whole muscle. For model simulations, we used the same enhancement and activation coefficients as Experiment 1 (only type I fibers are metabolically activated with an additional recruitment at the onset of exercise) (Table 2, 5 and 6, 7). The outputs of these simulations were compared with the experimental data for independent model validation.
Experiment 4
From a study by Krustrup et al (26), data are available for a 10-min protocol that required knee-extension exercise of one leg at moderate exercise intensity (~50% VO2max) using normal subjects as a control group. Because less muscle is recruited during knee extensor exercise compared to cycling exercise, the effective volume at rest was assumed as 2L (Table 2). For simulation purposes, at the onset of exercise only type I fibers were considered to have an additional recruitment but both fiber types were assumed to be metabolically activated based on PCr data. Values of the activation coefficients for each fiber type were the same as those from Experiments 1 and 2.
Experiment 5
From a study by Krustrup et al.(26), data are available for a 10-min protocol with a knee-extension exercise of one leg at moderate exercise intensity (~50% VO2max) for a group of subjects who had taken blockade agent, which blocks the activity of type I fibers (e.g. no additional recruitment). Based on PCr data, we assumed that both fiber types were metabolically activated. The activation coefficients for these fiber types were assumed to be the same as those from Experiment 1 and 2. In this case, the effects of fiber recruitment were investigated independent of changes in fiber metabolic activation.
Numerical methods
For model simulations, the differential equations were solved numerically (‘ode15s’, MATLAB, The MathWorks Inc). The optimal values of activation coefficients αk were obtained using a generalized reduced gradient algorithm (33).
Results
For validation and prediction purposes, model simulations were compared with published experimental data in exercising skeletal muscle during short-term, moderate-intensity exercise. The experimental data consisting of species concentrations and transport rates were obtained from biopsy measurements from whole muscle or from single muscle fibers. A strategy was developed to distinguish the recruitment function (RF) from the metabolic activation function (AF) of type I and type II muscle fibers by model simulation of exercise under several different experimental conditions (Table 8). In the recruitment function (RF) should be noted that when εVR or εVW is zero both fibers type are still recruited but there is no additional recruitment of type I or II fibers at the onset of exercise, respectively.
Experiment 1
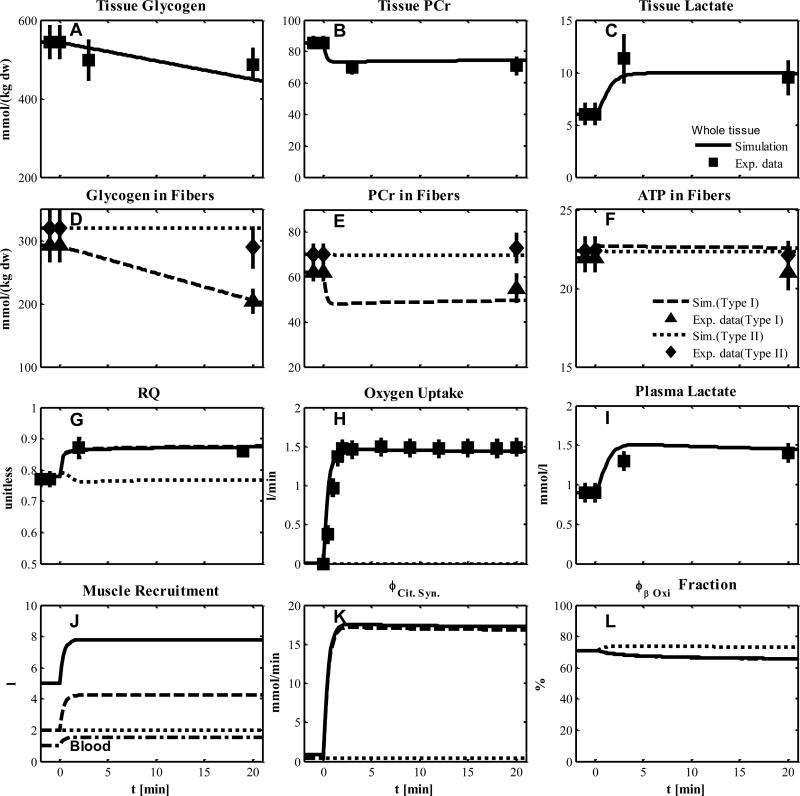
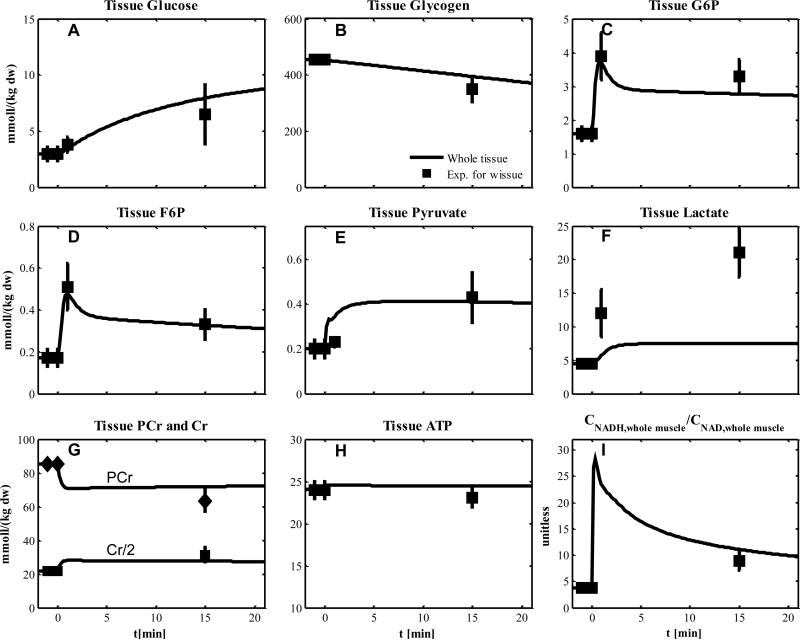
We compared our model simulations with experimental data from human skeletal muscle that was obtained during short-term cycle ergometer exercise at moderate intensity (~50% VO2max, (27)), (Fig.3). The simulated metabolic responses match the corresponding data in whole tissue (solid lines: tissue glycogen, lactate and PCr in Figs.3A-C respectively; plasma lactate in Fig. 3I) and in single type I fibers (glycogen, PCr and ATP in Fig. 3D-F, respectively). Under this condition, only type I fibers are activated with an additional recruitment at the onset of exercise (Table 8). The values of activation coefficients of type I fibers (αk,R) for the transport and reaction fluxes were optimally estimated (Tables 5 & 6), while the recruitment of type I fibers was simulated according to muscle flow and volume characteristics (Table 2 and 7). During exercise, skeletal muscle is mainly responsible for the O2 and CO2 dynamic responses of the whole body. For this simulation, the measured whole body respiratory exchange ratio (RER) is assumed to be the same as the respiratory quotient RQ in exercising muscle, which corresponds to the simulated RQ (Fig. 3G). Assuming that exercising muscle accounts for 75% of the change in pulmonary oxygen uptake, the simulated increase in oxygen uptake in the muscle was comparable to the experimentally derived increase in pulmonary oxygen uptake (Fig. 3H). The effects of recruitment of type I fibers and blood flow on the volume components are simulated in Fig. 3J. The increase of citrate synthase flux with exercise in whole tissue is mainly due to type I fibers (Fig. 3K) in which the contributions of β-oxidation and pyruvate dehydrogenase flux are 65.6% (Fig. 3L) and 34.4 %, respectively.
Figure 3.
Simulated dynamics and experimental data for intracellular species concentrations in skeletal muscle in response to an increased work rate equivalent to cycle ergometer exercise at 50% VO2max for subjects corresponding to Experiment 1: (A) Glycogen, (B) Phosphocreatine (PCr), (C) Lactate in tissue; (D) Glycogen, (E) PCr and (F) ATP in type I and II fibers; (G) Respiratory quotient (RQ); (H) Oxygen Uptake; (I) Plasma Lactate; (J) Effective volume change of whole muscle, type I and II fibers and blood domain; (K) Citrate Synthase flux; (L) β oxidation contribution to the citrate synthase flux. The lines represent model simulations of whole muscle (—), type I fibers (---) and type II fibers (. . .). Experimental data are means ± standard error. Solid squares for whole tissue; upper triangles for type I fibers; diamonds for type II fibers.
Experiment 2
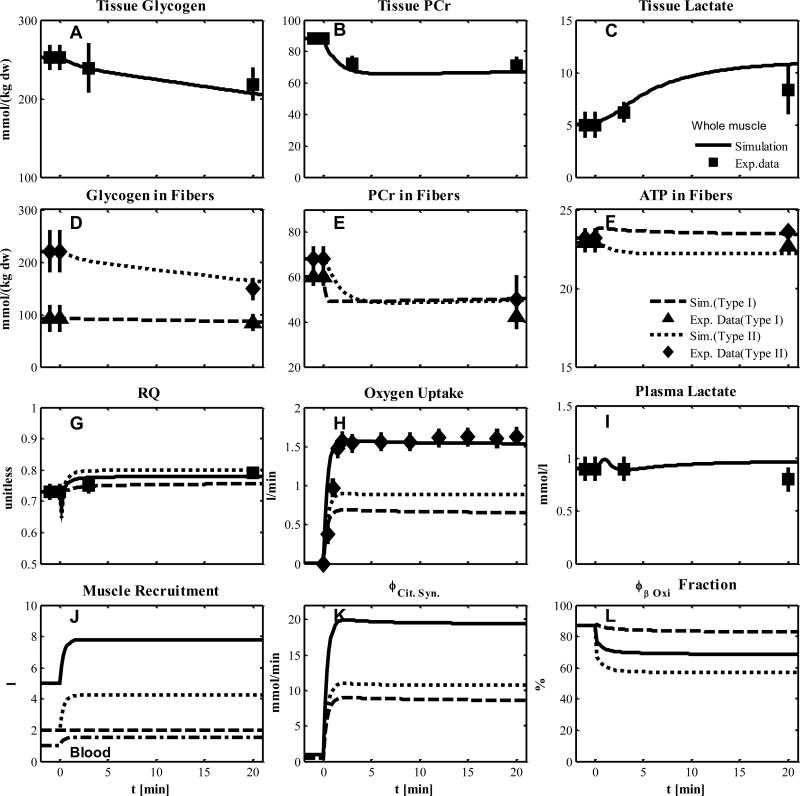
In this experiment we used data from subjects who had undergone muscle glycogen depletion before exercise as described in the protocol of Experiment 1 (27). This experimental paradigm allowed greater metabolic activation and recruitment of type II fibers. The simulated metabolic responses were found to match the corresponding data for whole muscle tissue as represented by tissue glycogen, lactate and PCr (Figs. 4A-C), and RQ, oxygen uptake, and plasma lactate (Figs. 4G-I). The simulation also successfully matched glycogen, PCr and ATP (Figs. 4D-F) data for single fibers. In these simulations, type I fibers were activated without additional recruitment at onset of exercise. The metabolic activation coefficients αk,R had the same values as in Experiment 1. Values of the transport and reaction flux activation coefficients of type II fibers (αk,W) were estimated (Table 5-6) by fitting model outputs to the data (Fig. 4). The recruitment of type II fibers was simulated with muscle flow and volume characteristics similar to those for recruitment of type I fibers (Table 2 and 7) for Experiment 1. If skeletal muscle accounts for 75% of the increase in pulmonary oxygen uptake during exercise, then we find that the simulated oxygen uptake change of muscle is comparable to the experimental change in pulmonary oxygen uptake (Fig. 4H). With recruitment and metabolic activation of type II fibers, muscle oxygen uptake was higher than that measured in Experiment 1. The contribution of type II fibers to the muscle oxygen uptake (Fig. 4H, dashed line) was greater than that of type I fibers, which is also evident from the simulated changes of effective volumes (Fig. 4J). The increase of citrate synthase flux in whole tissue is equally distributed to both muscle fibers (Fig. 4K) while the contribution of β-Oxidation and pyruvate dehydrogenase flux to the citrate synthase is 68.5% (Fig. 4L) and 31.5 % during exercise, respectively.
Figure 4.
Simulated dynamics and experimental data for intracellular species concentrations in muscle in response to an increased work rate equivalent to cycle ergometer exercise at 50% VO2max for subjects with pre-exercise glycogen depletion corresponding to Experiment 2: (A) Glycogen, (B) Phosphocreatine (PCr), (C) Lactate in tissue; (D) Glycogen, (E) PCr and (F) ATP in type I and II fibers; (G) Respiratory quotient (RQ); (H) Oxygen Uptake; (I) Plasma Lactate; (J) Effective volume change of whole muscle, type I and II fibers and blood domain; (K) Citrate Synthase flux; (L) β oxidation contribution to the citrate synthase flux. The lines represent model simulations of whole muscle (—), type I fibers (---) and type II fibers (. . .). Experimental data are means ± standard error. Solid squares for whole tissue; upper triangles for type I fibers; diamonds for type II fibers.
Experiment 3
The experimental protocol was similar to that of Experiment 1, but the exercise intensity was a little higher (60% VO2max). For model simulations, values of the recruitment and metabolic activation coefficients were the same as those of Experiment 1. The simulated outputs match the data for glucose, glycogen, G6P, F6P, pyruvate, PCr, Cr, ATP, redox state in whole muscle tissue (Fig. 5). For lactate, however, model simulation underestimates tissue lactate changes (Fig. 5F).
Figure 5.
Simulated dynamics and experimental data for intracellular species concentrations in whole muscle in response to an increased work rate equivalent to cycle ergometer exercise at 60% VO2max: for subjects corresponding to Experiment 3 (A) Glucose; (B) Glycogen; (C) Glucose-6-phosphate (G6P); (D) Fructose-6-phosphate (F6P); (E) Pyruvate, (F) Lactate; (G) Phosphocreatine and creatine, the experimental data and simulation of Cr were divided by 2 to distinguish the response of PCr and Cr; (H) ATP; (I) Tissue redox state (NADH/NAD+ ratio). Experimental data are means ± standard error for whole tissue.
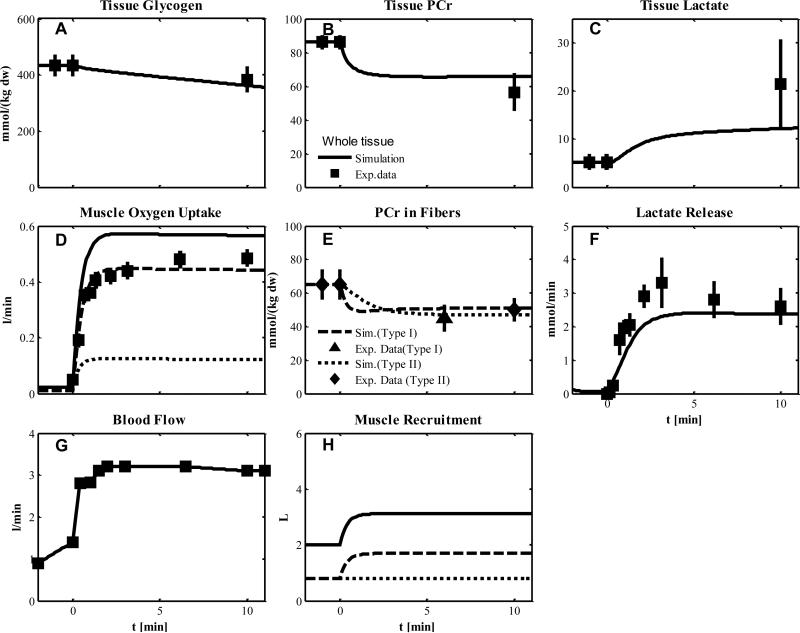
Experiment 4
The one-leg, knee-extensor exercise at moderate intensity of this experiment involves less skeletal muscle than with typical cycling, which is accounted for by muscle volume characteristics (Table 2). In model simulations, we assumed a metabolically activation of both type fibers with an additional recruitment of only type I fibers at the onset of exercise (Fig. 6H) according to the flow and volume characteristics reported in Table 2 and 7. The measured blood flow for local muscle was an input for simulation (Fig. 6G). The simulated outputs match the metabolite responses represented by glycogen, PCr, lactate concentration in tissue (Fig. 6 A-C) and PCr concentration in fibers (Fig. 6E). The simulated outputs in comparison to the corresponding data were higher with respect to muscle O2 uptake (Fig. 6D) and lower with respect to lactate release (Fig. 6F). As indicated by PCr data (Fig. 6E), both types of muscle fibers can be metabolic activated and values of activation coefficients were those from Experiments 1 and 2.
Figure 6.
Simulated dynamics and experimental data for intracellular species concentrations in muscle in response to an increased work rate equivalent to one-leg knee-extensor exercise at 50% VO2max for subjects corresponding to Experiment 4: (A) Glycogen; (B) Phosphocreatine (PCr); (C) Lactate in tissue; (D) Muscle oxygen uptake; (E) PCr in type I and II fibers; (F) Lactate release; (G) Blood flow (Q); (H) Effective volume change of whole muscle, type I and II fibers and blood domain. The blood flow curve was obtained by data interpolation. Lines represent model simulations of whole muscle (—), type I fibers (- - -), and type II fibers (. . .). Experimental data are means ± standard error. Solid squares for whole tissue; upper triangles for type I fibers; diamonds for type II fibers.
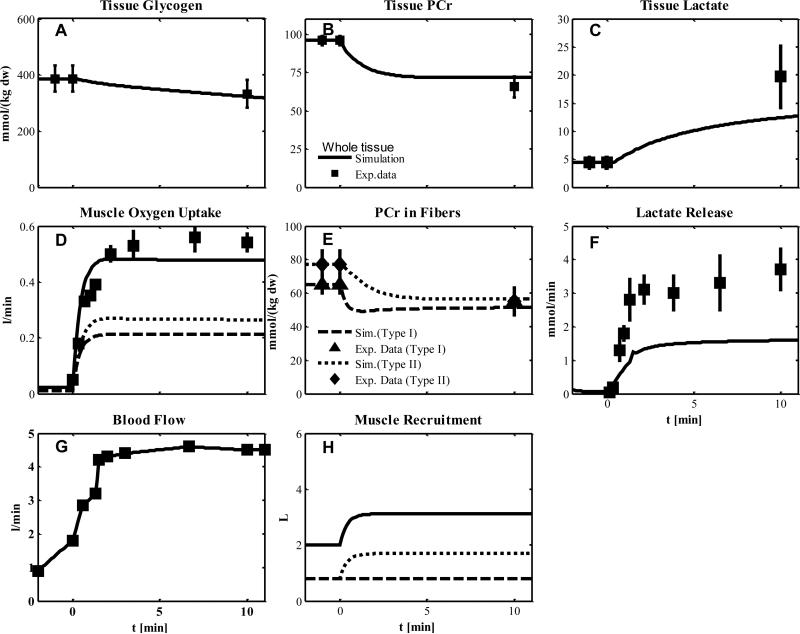
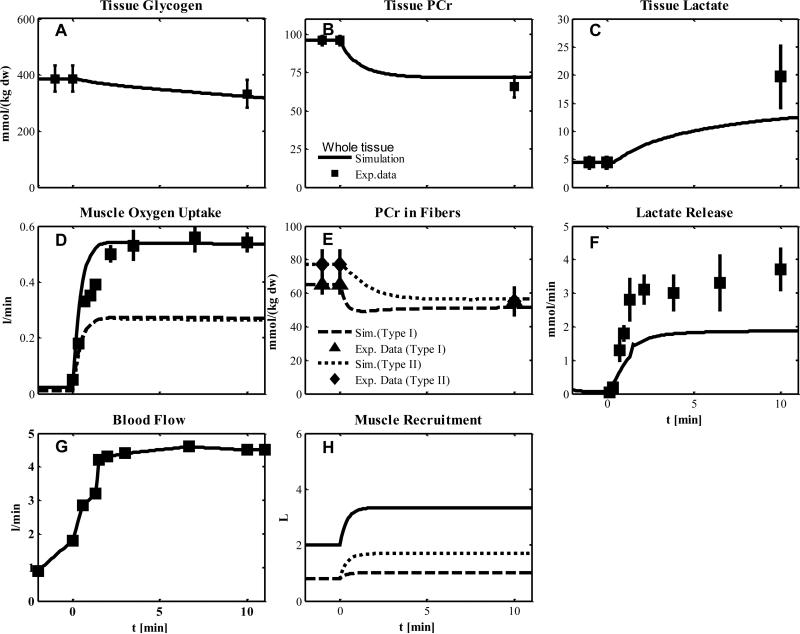
Experiment 5
In this experiment, subjects were injected with a blockade agent (CUR) to deactivate type I fibers before knee-extensor exercise as in Experiment 4. Although CUR is a blocking agent of type I fibers, the PCr data (Fig. 7E) indicate incomplete blocking. Therefore, we assumed that both muscle fiber types were metabolically activated with values for simulation estimated from Experiments 1 and 2 (Table 5-6). To account for the effect of the blockade agent on the recruitment of type I fibers (Table 2 and 7), we considered two cases: (a) no additional recruitment (Fig. 7) or partial additional recruitment (Fig. 8). The metabolite responses of glycogen, PCr, lactate in tissue and PCr in fibers were similar under these two conditions (Fig. 7A-C, E and Fig.8A-C, E). The simulation of muscle O2 uptake, however, with partial additional recruitment (Fig. 8D) match the data and is higher than with no additional recruitment (Fig. 7D). For both conditions (a) and (b), the simulated lactate release was lower than the data (Fig. 8F and Fig. 7F).
Figure 7.
Simulated dynamics and experimental data for intracellular species concentrations in muscle in response to an increased work rate equivalent to one-leg knee-extensor exercise at 50% VO2max for subject received blocking agent cisatracurium corresponding to Experiment 5: (A) Glycogen; (B) Phosphocreatine (PCr); (C) Lactate in tissue; (D) Muscle oxygen uptake; (E) PCr in type I and II fibers; (F) Lactate release; (G) Blood flow (Q); (H) Effective volume change of whole muscle, type I and II fibers and blood domain. The blood flow curve was obtained by data interpolation. Lines represent model simulations of whole muscle (—), type I fibers (- - -), and type II fibers (. . .). Experimental data are means ± standard error. Solid squares for whole tissue; upper triangles for type I fibers; diamonds for type II fibers.
Figure 8.
Simulated dynamics and experimental data for intracellular species concentrations corresponding to Experiment 5. Model simulation assumes more recruitment of type I fibers compared to the model simulation of Figure 7.
Discussion
Overview
The overall goal of this study was to develop a mathematical model to quantify the contributions of type I and type II fibers to the metabolic response of human skeletal muscle during short-term, moderate-intensity exercise. The metabolic differences between the two fiber types became evident during exercise where there was a distinctive recruitment and metabolic activation pattern of muscle fibers. Our mathematical model simulations were able to quantify the contributions of the recruitment and metabolic activation of each fiber type to the dynamic metabolic responses of skeletal muscle during exercise.
The focus of this study is related to the recruitment and metabolic activation of muscle fibers during moderate-intensity exercise (~50-60% VO2max) performed with a cycle-ergometer (27; 37; 39; 42; 51) or knee-extensor protocol(26). We used five distinct sets of data (Experiments 1-5) obtained under different muscle conditions to test the model. Experimental data and model simulations indicate that type I fibers have primary importance in the energy metabolism in skeletal muscle under control conditions of Experiments 1, 3, and 4. Experiments 2 and 5 indicated that type II fibers contribute to the metabolic response. Inferences on the engagement of type I and II fibers during exercise were based on changes in glycogen and phosphocreatine content of muscle fibers and whole muscle tissue, as well as of pulmonary oxygen uptake and respiratory exchange ratio (RER). The experimental data alone cannot quantitatively distinguish the recruitment and metabolic activation of each fiber type, or their effects on the metabolite content and metabolic flux changes during exercise. However, these limitations were overcome when the experimental data were combined with simulations using the mechanistic, mathematical model presented in this study.
Effects of muscle fiber type activation on metabolic response
The effect of recruitment and metabolic activation of muscle fibers on the metabolic response during exercise was investigated by either excluding or including the contributions of the muscle fibers (according to the strategy summarized in Table 8). The parameters of muscle fiber recruitment and metabolic activation were optimally estimated using data from subjects performing the cycle-ergometer protocol that was used in Experiment 1(27). These data were then used to predict the metabolic response to the cycle-ergometer and knee-extensor protocol that were used in Experiments 3 and 4, respectively. These simulations were performed independently. Assuming only type I fibers are activated with an additional recruitment at the onset of contraction (Table 8), simulations match most experimental data associated with metabolite concentration changes in whole muscle (Fig. 3A-C, Fig. 5) and in single fibers (Fig. 3D-F). The simulated RQ and muscle oxygen uptake changes are also consistent with the experimental RER and pulmonary oxygen uptake measurements (Fig. 3G-H). The assumption that muscle oxygen uptake accounts for 75% of the change in pulmonary oxygen uptake during exercise is consistent with previous data (32; 40). One exception is the higher tissue lactate concentration during simulations compared to experimental data under Experiment 3 (Fig. 5F). This may reflect differences in fitness, body composition, or muscle fiber type between the subjects involved in the different studies.
According to the data from Experiment 2(27), the skeletal muscle metabolic response to cycle-ergometer exercise is sensitive to pre-exercise glycogen depletion in type I fibers. Under this experimental condition, glycogen content changes were observed only in type II fibers (Fig. 4D), while phosphocreatine concentration decreased in both muscle fiber types (Fig. 4E). In Experiment 1, the negligible glycogen and phosphocreatine changes in type II fibers were assumed to indicate no metabolic activation and no recruitment of these fibers. In Experiment 2, the engagement of type I fibers is more difficult to characterize because glycogen was not utilized, but phosphocreatine was significantly decreased during exercise. To account for a partial engagement of type I fibers, these fibers were considered metabolically activated with no recruitment at the onset of exercise. With recruitment of only type II fibers, but metabolic activation of both fiber types (Table 8) during exercise, the simulations of this metabolic response match the experimental data (Fig. 4).
While the relative decreases of glycogen concentration in whole muscle were similar with or without pre-exercise glycogen depletion (~11% in Exp 1, Fig. 3A vs. ~13% in Exp 2, Fig. 4A), the simulated respiratory quotient (RQ) of skeletal muscle was lower under experimental conditions 2 (Fig. 4G. vs. Fig. 3G). This reduced RQ appears consistent with higher rates of β-oxidation and a reduced contribution of glycolysis according to the lower plasma lactate concentration under experimental condition 2 (Fig. 4I) compared to those of Experiment 1 (Fig. 3I). The greater increase in muscle oxygen uptake under Experiment 2 compared to Experiment 1 (Fig. 4H vs. Fig. 3H) is related to the higher β-oxidation required in the presence of low glycogen levels within the muscle (68.5%, Fig. 4L vs. 65.6%, Fig. 3L). The metabolic fluxes of the TCA cycle (e.g. citrate synthase) closely match the total contribution of β-oxidation and pyruvate dehydrogenase fluxes during steady-state exercise.
Based on the metabolic activation characteristics from Experiments 1 and 2 as well as the recruitment characteristics of Experiment 2 (Table 8), model simulations predicted the metabolic response to knee-extensor exercise with type I fiber deactivation (Experiment 5, Fig.7). Even in this case, the model assumption of metabolic activation of both fiber types was consistent with experimental glycogen phosphocreatine changes (Fig. 7A, B and E). The higher oxygen uptake change simulated for Experiment 2 (Fig. 4H) compared to that of Experiment 5 (~0.5L/min vs. 1.5L/min, Fig. 7D) was related to the increased muscle mass engaged in knee-extensor relative to cycle-ergometer exercise (~8L vs. ~3L, Table 2, Fig.4J vs. Fig.7H).
Under Experiment 5, the model simulation underestimates the lactate release (Fig. 7F). This discrepancy may be related to the lactate transport parameters estimated for the subjects performing exercise under Experiment 2. The estimated parameters indicate a negligible plasma lactate release during cycle-ergometer exercise (Fig. 4I), which may be significant during knee-extensor exercise (Fig. 7F).
Effects of muscle fiber type recruitment on metabolic response
The effects of muscle fiber recruitment on the metabolic response during exercise are indicated in Figs. 7 and 8. Simulations of the responses to the knee-extensor exercise model do not predict higher muscle oxygen uptake changes with deactivation of type I fibers (Experiment 5, Fig. 7D) compared to the control case (Experiment 4, Fig. 6D). The underestimation of muscle oxygen uptake could be related to the assumption of no additional recruitment of type I fibers despite metabolic activation during exercise (Table 8). Indeed, muscle oxygen consumption is proportional to the muscle mass engaged regardless of the specific metabolic activation changes during exercise. Thus, during submaximal exercise, when muscle fiber recruitment is higher, muscle oxygen consumption is greater. In fact, phosphocreatine changes in the type I fibers (Fig. 7E) indicate additional recruitment of type I fibers during exercise despite blocking agent effect. Under Experiment 5, the potential recruitment of type I fibers was quantified with simulations shown in Fig. 8 (Table 6). The greater recruitment of type I fibers during exercise increased muscle oxygen uptake (Fig.7D vs. Fig. 8D), but had little effect on metabolite concentration changes (Fig. 7 vs. 8 A, B, C, E and F). Therefore, glycogen and phosphocreatine measurements are important to detect activation of muscle fibers, but these data alone do not provide a measure of the mass of fibers engaged during exercise.
Regulation of skeletal muscle fiber recruitment and metabolic activation
Fiber recruitment varies with hierarchical order of fiber activation with increasing exercise intensities (6; 17; 20). Specifically, during low and moderate intensity exercise, metabolic changes occur primarily in type I fibers(17; 27) while recruitment of type II fibers is more evident at higher intensity exercise. Fiber recruitment during exercise has been studied by muscle contraction frequency changes(1; 4), metabolic stress represented by alteration of muscle glycogen(29), or thigh occlusion(30). However, a quantitative relationship between muscle fiber type distribution and whole muscle metabolic response during exercise was not fully established.
Inferences from these experimental approaches rely on measurement of glycogen or PCr depletion in isolated single fibers and plasma metabolite contents. Also, muscle and pulmonary oxygen uptake kinetics link information at different levels from fibers to the whole body. However, quantitative information about the concentration changes of key metabolites in each fiber type cannot be directly related to the metabolic fluxes. Furthermore, species concentration changes do not reveal the activated fiber density (volume/muscle mass), which is essential to quantify muscle fiber recruitment.
In this mathematical model, the metabolic fluxes are normalized relative to the volume of each muscle fiber type. The effective volume of activated muscle fibers is an important factor that determines total fluxes, e.g. oxygen consumption rate. Under different physiological conditions, recruitment and metabolic activation have distinct effect on recruitment patterns of t muscle fiber types on the metabolic response to exercise. Recruitment patterns of the muscle fiber type are related not only to the metabolic response, but also the motor-nerve response to exercise(30). For similar exercise workloads, metabolic activation (e.g. ATP and CP depletion in both slow and fast fibers) during thigh occlusion was greater than that obtained without thigh occlusion (30). However, metabolic activation obtained with thigh occlusion during exercise was similar to that obtained without occlusion but at higher exercise intensity and with more muscle groups recruitment. This experimental evidence is consistent with results shown in Fig. 7 and 8. In this case, the additional muscle recruitment (Fig. 7H vs. 8H) has a major effect on the muscle oxygen consumption (Fig. 7D vs. 8D) and negligible effects on the metabolic changes (Fig. 7B vs. 8B, 7C vs. 8C, 7E vs. 8E).
Our analysis suggests that metabolic activation and recruitment of muscle fibers are closely related, but the degree of metabolic activation (Eq. 9) inferred from metabolite changes may differ from that of the fiber recruitment (Eq. 8). Activation as measured by metabolic response in single fibers is distinct from fiber recruitment that is characterized by the number (or mass) of each fiber type involved during a specific exercise. The regulation processes of activation and recruitment of muscle fibers, which are highly dependent on exercise conditions, require new techniques for in vivo measurement. Such experimental techniques could be used in combination with our computational model to investigate the relationships between the extents of metabolic activation, number of fibers recruited, and muscle groups engaged at different intensity exercise.
Model limitations
The results from our study underline the need for critical experiments that measure fiber recruitment and metabolism in order to simulate and quantify the contributions of type I and II fibers to the regulation of energy metabolism. In the absence of data on fiber recruitment under the experimental conditions, the model incorporated the same recruitment pattern for type I and type II fibers. Also, we assumed that the fiber-recruitment pattern for cycle-ergometer and knee-extensor exercise was the same. Without appropriate data, simulations one cannot distinguish recruitment patterns associated with pre-exercise glycogen depletion, a blocking agent, or exercise protocol (cycle-ergometer vs. knee-extensor).
The recruitment patterns of muscle fiber types to exercise have not been experimentally determined. Consequently, model assumptions must be inferred based on limited data. The estimated activation parameters were obtained for Experiments 1 and 2 under the assumptions of specific recruitment patterns. However, one cannot exclude the possibility that other recruitment patterns could take place under these experimental conditions. Therefore, the estimated activation parameters could have been affected by muscle recruitment. This possibility cannot be quantified without a combination of muscle recruitment and metabolic activation measurements.
Furthermore, the sparse metabolic data for type I and II muscle fibers limit the evaluation of activation coefficients using model simulations. Without sufficient biochemical and biophysical data on muscle fiber types, key characteristics of both fiber types cannot be differentiated. Nevertheless, parameters estimated for this model led to simulations that predict the metabolite change in whole tissue and in single fibers for different exercise protocols of independent experiments.
From experimental studies (Krustrup et al., (26; 27)), the higher muscle oxygen uptake associated with type II fibers in response to cycling (Fig. 3H vs. 4H) and knee-extensor (Fig 6D vs. 7D) exercise were attributed to lower energetic efficiency compared to type I fibers. In particular, an increase in oxygen consumption for the same energy demand could be related to a lower P/O ratio (i.e., moles ATP generated per mole oxygen consumed) in type II fiber than in type I fibers(31). Also, the higher consumption of oxygen could be explained by a switch in substrate utilization since the P/O ratio for fat is lower than that of carbohydrate metabolism. Model simulations were based on similar metabolic oxygen efficiencies for both fiber types. Therefore, under-estimation of the simulated muscle oxygen uptake under Experiment 5 (Fig. 7D) could be related to lower energy efficiency of type II fibers.
Another limitation of this mathematical model is that it does not distinguish between type II fibers, viz., type IIa (fast twitch-oxidative) and IIb (fast twitch-glycolytic)(53). However, distinct metabolic responses of these fiber types during exercise are even more difficult to obtain experimentally. When more experimental data become available these data could be used to enhance the current model in order to distinguish all three muscle fiber types and simulate their metabolic response to exercise.
Conclusions
Simulations with a mechanistic, mathematical model together with key experimental data permitted the evaluation of functional and structural properties of type I and II fibers from responses of whole skeletal muscle under different physiological conditions. This study focused on simulations that quantify the contributions of recruitment and metabolic activation of type I and II fibers to the skeletal muscle energy metabolism during moderate exercise. Muscle recruitment and metabolic activation have different effects on changes in metabolite and metabolic flux during exercise. A combination of recruitment and metabolic measurements are required to accurately quantify type I and II muscle fiber activation during exercise. We conclude that experiments are needed to provide critical data on skeletal muscle fiber characteristics under a range of physiological conditions. With such data, this mathematical model could be extended to obtain more distinctive simulations of metabolic responses to exercise. Such an approach is likely to generate novel insights into human physiology and metabolism that would not be possible solely from experimental data.
Supplementary Material
Acknowledgments
We acknowledge the contribution of Dr. Ranjan Dash to our previous model of skeletal muscle energy metabolism and muscle fiber composition; many of the model features of this previous model were used in the present study. This study was supported in part by grants (P50 GM-66309, K25AR057206 and 1F31 GM084682) from the National Institute of General Medical Sciences (NIH), and by a grant (NNJ06HD81G) from the National Aeronautics and Space Administration NASA.
Reference List
- 1.Ahlquist LE, Bassett DR, Jr., Sufit R, Nagle FJ, Thomas DP. The effect of pedaling frequency on glycogen depletion rates in type I and type II quadriceps muscle fibers during submaximal cycling exercise. Eur J Appl Physiol Occup Physiol. 1992;65:360–364. doi: 10.1007/BF00868141. [DOI] [PubMed] [Google Scholar]
- 2.Altenburg TM, Degens H, van Mechelen W, Sargeant AJ, de Haan A. Recruitment of single muscle fibers during submaximal cycling exercise. J Appl Physiol. 2007;103:1752–1756. doi: 10.1152/japplphysiol.00496.2007. [DOI] [PubMed] [Google Scholar]
- 3.Ball-Burnett M, Green HJ, Houston ME. Energy metabolism in human slow and fast twitch fibres during prolonged cycle exercise. J Physiol. 1991;437:257–267. doi: 10.1113/jphysiol.1991.sp018594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barstow TJ, Jones AM, Nguyen PH, Casaburi R. Influence of muscle fiber type and pedal frequency on oxygen uptake kinetics of heavy exercise. J Appl Physiol. 1996;81:1642–1650. doi: 10.1152/jappl.1996.81.4.1642. [DOI] [PubMed] [Google Scholar]
- 5.Barstow TJ, Lamarra N, Whipp BJ. Modulation of muscle and pulmonary O2 uptakes by circulatory dynamics during exercise. J Appl Physiol. 1990;68:979–989. doi: 10.1152/jappl.1990.68.3.979. [DOI] [PubMed] [Google Scholar]
- 6.Beltman JG, de HA, Haan H, Gerrits HL, van MW, Sargeant AJ. Metabolically assessed muscle fibre recruitment in brief isometric contractions at different intensities. Eur J Appl Physiol. 2004;92:485–492. doi: 10.1007/s00421-004-1105-6. [DOI] [PubMed] [Google Scholar]
- 7.Bonen A, Holloway GP, Tandon NN, Han XX, McFarlan J, Glatz JF, Luiken JJ. Cardiac and skeletal muscle fatty acid transport and transporters and triacylglycerol and fatty acid oxidation in lean and Zucker diabetic fatty rats. Am J Physiol Regul Integr Comp Physiol. 2009;297:R1202–R1212. doi: 10.1152/ajpregu.90820.2008. [DOI] [PubMed] [Google Scholar]
- 8.Bottinelli R, Reggiani C. Human skeletal muscle fibres: molecular and functional diversity. Prog Biophys Mol Biol. 2000;73:195–262. doi: 10.1016/s0079-6107(00)00006-7. [DOI] [PubMed] [Google Scholar]
- 9.Brown SP, Miller WC, Eason JM. Exercise Physiology: Basis of Human Movement in Health and Disease. Lippincott Williams & Wilkins; 2006. [Google Scholar]
- 10.Budohoski L, Gorski J, Nazar K, Kaciuba-Uscilko H, Terjung RL. Triacylglycerol synthesis in the different skeletal muscle fiber sections of the rat. Am J Physiol. 1996;271:E574–E581. doi: 10.1152/ajpendo.1996.271.3.E574. [DOI] [PubMed] [Google Scholar]
- 11.Edstrom L, Hultman E, Sahlin K, Sjoholm H. The contents of high-energy phosphates in different fibre types in skeletal muscles from rat, guinea-pig and man. J Physiol. 1982;332:47–58. doi: 10.1113/jphysiol.1982.sp014399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Endo MY, Kobayakawa M, Kinugasa R, Kuno S, Akima H, Rossiter HB, Miura A, Fukuba Y. Thigh muscle activation distribution and pulmonary VO2 kinetics during moderate, heavy, and very heavy intensity cycling exercise in humans. Am J Physiol Regul Integr Comp Physiol. 2007;293:R812–R820. doi: 10.1152/ajpregu.00028.2007. [DOI] [PubMed] [Google Scholar]
- 13.Enns GM, Hoppel CL, DeArmond SJ, Schelley S, Bass N, Weisiger K, Horoupian D, Packman S. Relationship of primary mitochondrial respiratory chain dysfunction to fiber type abnormalities in skeletal muscle. Clin Genet. 2005;68:337–348. doi: 10.1111/j.1399-0004.2005.00499.x. [DOI] [PubMed] [Google Scholar]
- 14.Essen-Gustavsson B, Blomstrand E. Effect of exercise on concentrations of free amino acids in pools of type I and type II fibres in human muscle with reduced glycogen stores. Acta Physiol Scand. 2002;174:275–281. doi: 10.1046/j.1365-201x.2002.00942.x. [DOI] [PubMed] [Google Scholar]
- 15.Ferreira LF, Townsend DK, Lutjemeier BJ, Barstow TJ. Muscle capillary blood flow kinetics estimated from pulmonary O2 uptake and near-infrared spectroscopy. J Appl Physiol. 2005;98:1820–1828. doi: 10.1152/japplphysiol.00907.2004. [DOI] [PubMed] [Google Scholar]
- 16.Gollnick PD, Armstrong RB, Sembrowich WL, Shepherd RE, Saltin B. Glycogen depletion pattern in human skeletal muscle fibers after heavy exercise. J Appl Physiol. 1973;34:615–618. doi: 10.1152/jappl.1973.34.5.615. [DOI] [PubMed] [Google Scholar]
- 17.Gollnick PD, Piehl K, Saltin B. Selective glycogen depletion pattern in human muscle fibres after exercise of varying intensity and at varying pedalling rates. The Journal of Physiology. 1974;241:45–57. doi: 10.1113/jphysiol.1974.sp010639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.He J, Watkins S, Kelley DE. Skeletal muscle lipid content and oxidative enzyme activity in relation to muscle fiber type in type 2 diabetes and obesity. Diabetes. 2001;50:817–823. doi: 10.2337/diabetes.50.4.817. [DOI] [PubMed] [Google Scholar]
- 19.Holloszy JO, Coyle EF. Adaptations of skeletal muscle to endurance exercise and their metabolic consequences. J Appl Physiol. 1984;56:831–838. doi: 10.1152/jappl.1984.56.4.831. [DOI] [PubMed] [Google Scholar]
- 20.Iaia FM, Perez-Gomez J, Thomassen M, Nordsborg NB, Hellsten Y, Bangsbo J. Relationship between performance at different exercise intensities and skeletal muscle characteristics. J Appl Physiol. 2011;110:1555–1563. doi: 10.1152/japplphysiol.00420.2010. [DOI] [PubMed] [Google Scholar]
- 21.Jones AM, Campbell IT, Pringle JS. Influence of muscle fibre type and pedal rate on the VO2-work rate slope during ramp exercise. Eur J Appl Physiol. 2004;91:238–245. doi: 10.1007/s00421-003-0971-7. [DOI] [PubMed] [Google Scholar]
- 22.Kirwan JP, Costill DL, Mitchell JB, Houmard JA, Flynn MG, Fink WJ, Beltz JD. Carbohydrate balance in competitive runners during successive days of intense training. J Appl Physiol. 1988;65:2601–2606. doi: 10.1152/jappl.1988.65.6.2601. [DOI] [PubMed] [Google Scholar]
- 23.Korzeniewski B. Regulation of ATP supply during muscle contraction: theoretical studies. Biochem J. 1998;330(Pt 3):1189–1195. doi: 10.1042/bj3301189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Korzeniewski B, Liguzinski P. Theoretical studies on the regulation of anaerobic glycolysis and its influence on oxidative phosphorylation in skeletal muscle. Biophys Chem. 2004;110:147–169. doi: 10.1016/j.bpc.2004.01.011. [DOI] [PubMed] [Google Scholar]
- 25.Korzeniewski B, Zoladz JA. A model of oxidative phosphorylation in mammalian skeletal muscle. Biophys Chem. 2001;92:17–34. doi: 10.1016/s0301-4622(01)00184-3. [DOI] [PubMed] [Google Scholar]
- 26.Krustrup P, Secher NH, Relu MU, Hellsten Y, Soderlund K, Bangsbo J. Neuromuscular blockade of slow twitch muscle fibres elevates muscle oxygen uptake and energy turnover during submaximal exercise in humans. J Physiol. 2008;586:6037–6048. doi: 10.1113/jphysiol.2008.158162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krustrup P, Soderlund K, Mohr M, Bangsbo J. Slow-twitch fiber glycogen depletion elevates moderate-exercise fast-twitch fiber activity and O2 uptake. Med Sci Sports Exerc. 2004;36:973–982. doi: 10.1249/01.mss.0000128246.20242.8b. [DOI] [PubMed] [Google Scholar]
- 28.Krustrup P, Soderlund K, Mohr M, Bangsbo J. The slow component of oxygen uptake during intense, sub-maximal exercise in man is associated with additional fibre recruitment. Pflugers Arch. 2004;447:855–866. doi: 10.1007/s00424-003-1203-z. [DOI] [PubMed] [Google Scholar]
- 29.Krustrup P, Soderlund K, Mohr M, Gonzalez-Alonso J, Bangsbo J. Recruitment of fibre types and quadriceps muscle portions during repeated, intense knee-extensor exercise in humans. Pflugers Arch. 2004;449:56–65. doi: 10.1007/s00424-004-1304-3. [DOI] [PubMed] [Google Scholar]
- 30.Krustrup P, Soderlund K, Relu MU, Ferguson RA, Bangsbo J. Heterogeneous recruitment of quadriceps muscle portions and fibre types during moderate intensity knee-extensor exercise: effect of thigh occlusion. Scand J Med Sci Sports. 2009;19:576–584. doi: 10.1111/j.1600-0838.2008.00801.x. [DOI] [PubMed] [Google Scholar]
- 31.Kushmerick MJ, Meyer RA, Brown TR. Regulation of oxygen consumption in fast- and slow-twitch muscle. Am J Physiol. 1992;263:C598–C606. doi: 10.1152/ajpcell.1992.263.3.C598. [DOI] [PubMed] [Google Scholar]
- 32.Lai N, Zhou H, Saidel GM, Wolf M, McCully K, Gladden LB, Cabrera ME. Modeling oxygenation in venous blood and skeletal muscle in response to exercise using near-infrared spectroscopy. J Appl Physiol. 2009;106:1858–1874. doi: 10.1152/japplphysiol.91102.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li Y, Dash RK, Kim J, Saidel GM, Cabrera ME. Role of NADH/NAD+ transport activity and glycogen store on skeletal muscle energy metabolism during exercise: in silico studies. Am J Physiol Cell Physiol. 2009;296:C25–C46. doi: 10.1152/ajpcell.00094.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Li Y, Solomon TP, Haus JM, Saidel GM, Cabrera ME, Kirwan JP. Computational model of cellular metabolic dynamics: effect of insulin on glucose disposal in human skeletal muscle (used with permission). Am J Physiol Endocrinol Metab. 2010;298:E1198–E1209. doi: 10.1152/ajpendo.00713.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Malenfant P, Joanisse DR, Theriault R, Goodpaster BH, Kelley DE, Simoneau JA. Fat content in individual muscle fibers of lean and obese subjects. Int J Obes Relat Metab Disord. 2001;25:1316–1321. doi: 10.1038/sj.ijo.0801733. [DOI] [PubMed] [Google Scholar]
- 36.Marotta M, Ferrer-Martnez A, Parnau J, Turini M, Mace K, Gomez Foix AM. Fiber type- and fatty acid composition-dependent effects of high-fat diets on rat muscle triacylglyceride and fatty acid transporter protein-1 content. Metabolism. 2004;53:1032–1036. doi: 10.1016/j.metabol.2004.03.011. [DOI] [PubMed] [Google Scholar]
- 37.Parolin ML, Spriet LL, Hultman E, Hollidge-Horvat MG, Jones NL, Heigenhauser GJF. Regulation of glycogen phosphorylase and PDH during exercise in human skeletal muscle during hypoxia. Am J Physiol Endocrinol Metab. 2000;278:E522–E534. doi: 10.1152/ajpendo.2000.278.3.E522. [DOI] [PubMed] [Google Scholar]
- 38.Pette D. Metabolic heterogeneity of muscle fibres. J Exp Biol. 1985;115:179–189. doi: 10.1242/jeb.115.1.179. [DOI] [PubMed] [Google Scholar]
- 39.Phillips SM, Green HJ, Tarnopolsky MA, Heigenhauser GJ, Grant SM. Progressive effect of endurance training on metabolic adaptations in working skeletal muscle. Am J Physiol. 1996;270:E265–E272. doi: 10.1152/ajpendo.1996.270.2.E265. [DOI] [PubMed] [Google Scholar]
- 40.Poole DC, Gaesser GA, Hogan MC, Knight DR, Wagner PD. Pulmonary and leg VO2 during submaximal exercise: implications for muscular efficiency. J Appl Physiol. 1992;72:805–810. doi: 10.1152/jappl.1992.72.2.805. [DOI] [PubMed] [Google Scholar]
- 41.Pringle JS, Doust JH, Carter H, Tolfrey K, Campbell IT, Sakkas GK, Jones AM. Oxygen uptake kinetics during moderate, heavy and severe intensity “submaximal” exercise in humans: the influence of muscle fibre type and capillarisation. Eur J Appl Physiol. 2003;89:289–300. doi: 10.1007/s00421-003-0799-1. [DOI] [PubMed] [Google Scholar]
- 42.Putman CT, Jones NL, Hultman E, Hollidge-Horvat MG, Bonen A, McConachie DR, Heigenhauser GJ. Effects of short-term submaximal training in humans on muscle metabolism in exercise. Am J Physiol Endocrinol Metab. 1998;275:E132–E139. doi: 10.1152/ajpendo.1998.275.1.E132. [DOI] [PubMed] [Google Scholar]
- 43.Ray CA, Dudley GA. Muscle use during dynamic knee extension: implication for perfusion and metabolism. J Appl Physiol. 1998;85:1194–1197. doi: 10.1152/jappl.1998.85.3.1194. [DOI] [PubMed] [Google Scholar]
- 44.Ren JM, Henriksson J, Katz A, Sahlin K. NADH content in type I and type II human muscle fibres after dynamic exercise. Biochem J. 1988;251:183–187. doi: 10.1042/bj2510183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rowell LB, Shepherd JT. Handbook of Physiology Section 12 Exercise: Regulation and Integration of Multiple Systems. 1996.
- 46.Sahlin K, Soderlund K, Tonkonogi M, Hirakoba K. Phosphocreatine content in single fibers of human muscle after sustained submaximal exercise. Am J Physiol Cell Physiol. 1997;273:C172–C178. doi: 10.1152/ajpcell.1997.273.1.C172. [DOI] [PubMed] [Google Scholar]
- 47.Saltin B, Henriksson J, Nygaard E, Andersen P, Jansson E. Fiber types and metabolic potentials of skeletal muscles in sedentary man and endurance runners. Ann N Y Acad Sci. 1977;301:3–29. doi: 10.1111/j.1749-6632.1977.tb38182.x. [DOI] [PubMed] [Google Scholar]
- 48.Scott W, Stevens J, Binder-Macleod SA. Human skeletal muscle fiber type classifications. Phys Ther. 2001;81:1810–1816. [PubMed] [Google Scholar]
- 49.Tsintzas K, Williams C, Constantin-Teodosiu D, Hultman E, Boobis L, Clarys P, Greenhaff P. Phosphocreatine degradation in type I and type II muscle fibres during submaximal exercise in man: effect of carbohydrate ingestion. J Physiol. 2001;537:305–311. doi: 10.1111/j.1469-7793.2001.0305k.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vinnakota KC, Rusk J, Palmer L, Shankland E, Kushmerick MJ. Common phenotype of resting mouse extensor digitorum longus and soleus muscles: equal ATPase and glycolytic flux during transient anoxia. J Physiol. 2010;588:1961–1983. doi: 10.1113/jphysiol.2009.185934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Watt MJ, Howlett KF, Febbraio MA, Spriet LL, Hargreaves M. Adrenaline increases skeletal muscle glycogenolysis, pyruvate dehydrogenase activation and carbohydrate oxidation during moderate exercise in humans. J Physiol. 2001;534:269–278. doi: 10.1111/j.1469-7793.2001.t01-1-00269.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhou L, Cabrera ME, Huang H, Yuan C, Duda M, Sharma N, Bian F, Stanley WC. Parallel Activation of Mitochondrial Oxidative Metabolism with Increased Cardiac Energy Expenditure is Not Dependent on Fatty Acid Oxidation. J Physiol. 2006 doi: 10.1113/jphysiol.2006.123828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zierath JR, Hawley JA. Skeletal muscle fiber type: influence on contractile and metabolic properties. PLoS Biol. 2004;2:e348. doi: 10.1371/journal.pbio.0020348. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.