Abstract
To better understand the biomechanical mechanisms underlying the association between hyperkyphosis of the thoracic spine and risk of vertebral fracture and other degenerative spinal pathology, we used a previously validated musculoskeletal model of the spine to determine how thoracic kyphosis angle and spinal posture affect vertebral compressive loading. We simulated an age-related increase in thoracic kyphosis (T1-T12 Cobb angle 50° to 75°) during two different activities (relaxed standing and standing with 5 kg weights in the hands) and three different posture conditions: 1) an increase in thoracic kyphosis with no postural adjustment (uncompensated posture), 2) an increase in thoracic kyphosis with a concomitant increase in pelvic tilt that maintains a stable center of mass and horizontal eye gaze (compensated posture), and 3) an increase in thoracic kyphosis with a concomitant increase in lumbar lordosis that also maintains a stable center of mass and horizontal eye gaze (congruent posture). For all posture conditions, compressive loading increased with increasing thoracic kyphosis, with loading increasing more in the thoracolumbar and lumbar regions than in the mid-thoracic region. Loading increased the most for the uncompensated posture, followed by the compensated posture, with the congruent posture almost completely mitigating any increases in loading with increased thoracic kyphosis. These findings indicate that thoracic kyphosis and spinal posture both influence vertebral loading during daily activities, implying that thoracic kyphosis measurements alone are not sufficient to characterize the impact of spinal curvature on vertebral loading.
Keywords: Kyphosis, Spinal Loading, Posture, Biomechanical Model, Vertebral Fracture
Introduction
Thoracic kyphosis refers to forward curvature of the thoracic spine in the sagittal plane. Exaggerated thoracic kyphosis, or hyperkyphosis, is common in the elderly, and this age-related increase in thoracic kyphosis has been attributed to the presence of vertebral fractures (1–3), intervertebral disc degeneration (2, 3), loss of spinal muscle strength (4, 5) and degeneration of the intervertebral ligaments (6). In addition to being caused by vertebral fractures, hyperkyphosis is also a strong risk factor for incurring new vertebral fractures, independent of bone mineral density (7, 8). This increased risk of vertebral fractures may be due to an anterior shift in body mass that effectively increases the moment arm between the spine and the superincumbent body mass that it supports (9, 10). This increased moment arm would lead to higher spinal moments and trunk muscle forces that would increase spinal compressive loading and vertebral fracture risk. However, the precise relationship between thoracic kyphosis angle and spinal compressive loading has not been systematically explored. Specifically, it is not known how much a given increase in thoracic kyphosis angle increases vertebral compressive loading, and whether this increase is large enough to contribute to the increased fracture risk associated with hyperkyphosis.
In addition to thoracic kyphosis, other postural and morphological parameters can influence the distribution of body mass and therefore the biomechanical environment of the spine. For instance, in response to an age-related increase in thoracic kyphosis a person can make various postural adjustments to maintain a stable center of mass and horizontal eye gaze (11–15). These postural adjustments include posterior tilting or translation of the pelvis, hip extension, knee flexion, and dorsiflexion of the ankles, all of which act to counter the anterior shift in body mass associated with increased thoracic kyphosis (11, 12). The postural adjustment strategy that an individual employs, and the degree to which they are able to adjust, will affect the biomechanical environment of the spine, but how these different parameters interact with thoracic kyphosis angle to affect spinal compressive loading is poorly understood.
Another factor that interacts with the thoracic kyphosis angle to influence vertebral compressive loading is whether one’s posture is “congruent” (16), meaning that the thoracic curvature is proportional to and balances the lumbar lordosis. Congruency is necessary for maintenance of an upright posture, and the degree to which someone’s posture is congruent will influence body mass distribution and the biomechanical environment of the spine. An age-related increase in thoracic kyphosis, without a concomitant change in lumbar lordosis, leads to an “uncompensated incongruent posture” (16), where the thoracic and lumbar regions no longer have complementary amounts of curvature and upright posture is therefore diminished. However, as discussed above, it is possible to make a postural adjustment, such as tilting the pelvis back, to stabilize the body’s center of mass. When this occurs, the individual will have a “compensated incongruent posture” (16) since some adjustment was made to correct balance and redistribute body mass, but the thoracic and lumbar curves are still not balanced.
Our overall objective is to understand the contribution of spine biomechanics to spine-related pathologies, including vertebral fractures. The goals of this study were to systematically investigate the effect of thoracic kyphosis angle and whole-body posture on vertebral compressive loading. We used a musculoskeletal model of the spine to examine how vertebral loading at the mid-thoracic and thoraco-lumbar regions changes with a simulated increase in thoracic kyphosis during three postural conditions: 1) an increase in thoracic kyphosis with no postural adjustment (uncompensated posture), 2) an increase in thoracic kyphosis with a concomitant increase in pelvic tilt that maintains a stable center of mass and horizontal eye gaze (compensated posture), and 3) an increase in thoracic kyphosis with a concomitant increase in lumbar lordosis that also maintains a stable center of mass and horizontal eye gaze (congruent posture). (Figure 1). We hypothesized that spinal loading would be minimally affected by changes in thoracic kyphosis for a congruent posture and most affected for an uncompensated posture.
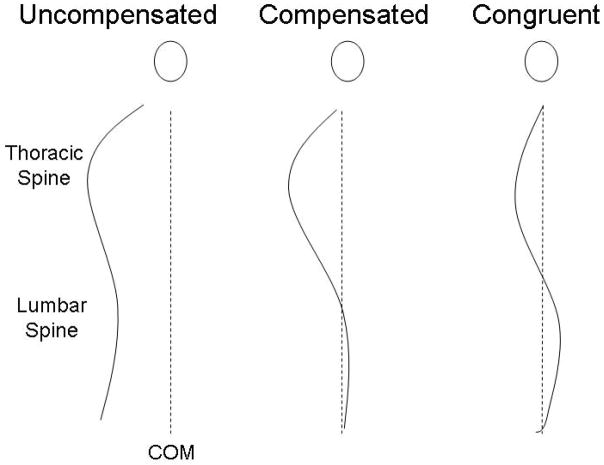
Figure 1.
Illustration demonstrating the sagittal spinal profiles associated with an uncompensated posture, a compensated posture (in this case tilting the pelvis posteriorly), and a congruent posture.
Materials and Methods
Musculoskeletal Spine Model
We used a static musculoskeletal model of the spine (17) to estimate compressive force on the T6 through L5 vertebral bodies of a representative 65 year old woman during a simulated increase in thoracic kyphosis. Our spine model has been previously validated against in vivo measurements of trunk muscle myoelectric activity and intervertebral disc pressures in the thoracic and lumbar spine during a variety of activities, including relaxed standing, trunk lateral bending, trunk flexion/extension, and standing with a 10kg load and elbows flexed 90° (17). For the purposes of the current study, vertebral compressive force was estimated for three different posture conditions (described later) and for two different activities: 1) relaxed standing with arms hanging down and 2) standing with elbows flexed 90° and 5 kg weights in each hand (Figure 2).
Figure 2.
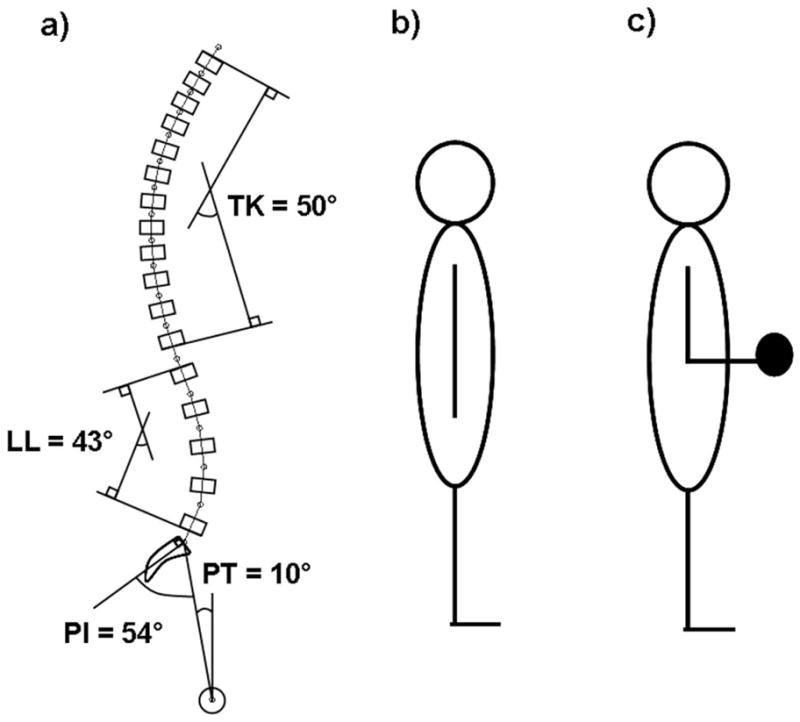
a) Sagittal view of the baseline spinal curvature and pelvic orientation used in the biomechanical model, showing the degree of thoracic kyphosis (TK), lumbar lordosis (LL), pelvic incidence (PI), and pelvic tilt (PT); b) cartoon of the first activity modeled: standing upright with the arms hanging straight down at the sides; c) cartoon of the second activity modeled: standing upright with the elbows flexed 90° and 5 kg weights in each hand. Both activities were modeled in 3D and were sagittally symmetric.
Our musculoskeletal model operates on principles similar to those used in previously published biomechanical models of the lumbar spine (18–20), except that it also estimates vertebral loading in the thoracic spine by taking into account the mechanical contribution of the ribs and sternum (17). In brief, the body was modeled as a series of linked-segments, and for this study the weight, length, and center of mass position for each segment was estimated for a 65 year old woman (height = 1.61 m, weight = 70.31 kg) using published anthropometric data (21–25). The center of mass of each thoracic and lumbar trunk segment (T1 through L5) was positioned anterior to the vertebral body centroid using data from Pearsall and colleagues (23). Muscles present in the model included pectoralis major, rectus abdominus, serratus anterior, trapezius, latissimus dorsi, external oblique, internal oblique, sacrospinalis, transversospinalis, psoas major, and quadratus laborum. Trunk muscle cross-sectional areas and moment arm lengths in the medial-lateral and anterior-posterior directions were estimated using regression equations relating these properties to age, sex, height, and weight (26). The forces and moments applied to each vertebral body due to the weight and position of superincumbent body mass, as well as the weights being held in the hands, were calculated for each activity. Muscle forces required to balance the moments and maintain static equilibrium were determined using a static optimization algorithm that minimized the sum of cubed muscle intensities (17). The maximum allowable muscle stress was limited to 1 MPa (27) to keep solutions within a physiologically acceptable range. Compressive force on the vertebral body was the sum of the superincumbent weight and muscle loading acting in the axial direction of the vertebral body.
Baseline Spinal Curvature and Pelvic Orientation
The baseline spinal curvature and pelvic orientation for the model were created using average values from the literature (Figure 2) (28, 29) as follows: T1-T12 Cobb angle = 50°, L1-L5 Cobb angle = 43°, pelvic incidence = 54°, pelvic tilt = 10°, sacral slope = 44°, and L5-S1 intersegmental angulation = 21°.
Thoracic Kyphosis Sensitivity Analysis
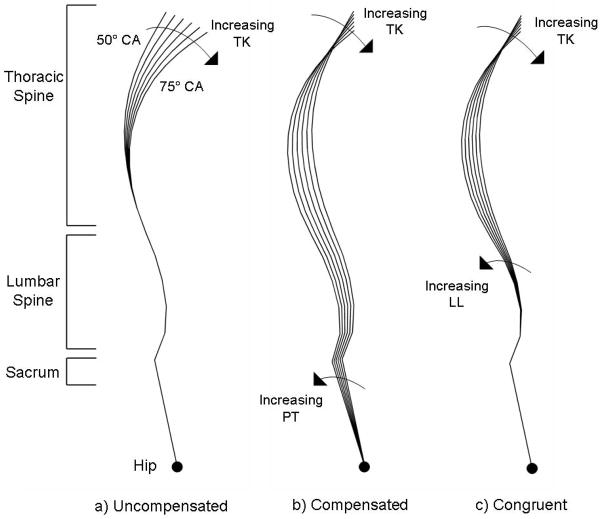
To determine the effect of increasing thoracic kyphosis on spinal compressive loading, we started with our baseline spinal model, which represents a congruent posture, and increased the T1-T12 Cobb angle from 50° to 75° in 1° increments (Figure 3) to simulate an age-related increase in thoracic kyphosis (30). Adjustments to the T1-T12 Cobb angle were evenly added to the different vertebral levels to achieve the desired Cobb angle. For example, to achieve a 75° T1-T12 Cobb angle, the baseline thoracic curvature of 50° was increased 25° by adding 25/11 ≈ 2.27° to each of the 11 intersegmental angles between T1 and T12. For each T1-T12 Cobb angle, we estimated vertebral compressive loading for the two different activities and three different postural conditions: 1) uncompensated posture, 2) compensated posture and 3) congruent posture. For the uncompensated posture condition, the T1-T12 Cobb angle was varied from 50° to 75° while all other spino-pelvic parameters remained fixed at their baseline values. For the compensated posture condition, pelvic tilt was varied (10° to 15.31° in 0.23° increments) concomitantly with the T1-T12 Cobb angle (50° to 75° in 1° increments) to maintain the sagittal alignment of the head and neck directly above the hip joint. For the congruent posture condition, the L1-L5 Cobb angle was varied (43° to 52.10° in 0.36° increments) concomitantly with the T1-T12 Cobb angle (50° to 75° in 1° increments) to maintain the sagittal alignment of the head and neck directly above the hip joint.
Figure 3.
Schematic representation of the range of spinal curvatures modeled in this study, starting with a) uncompensated posture, b) compensated posture, and c) congruent posture. The T1-T12 Cobb angle was varied from 50° to 75° in 1° increments, but for clarity the images above show only the 5° increments with the extreme spinal curves labeled.
Compressive force on the T6 through L5 vertebral bodies was calculated for each T1-T12 Cobb angle during the three posture and two activity conditions. Detailed force versus Cobb angle results are presented for T8 and T12, the most common sites for osteoporotic vertebral fracture (31, 32). Least-squares linear regressions were fitted to the load versus Cobb angle data for each of the vertebral bodies between T6 and L5 in order to determine the increase in vertebral compressive force for every 1° increase in Cobb angle.
We also explored how subject height and weight might interact with posture, thoracic kyphosis, and activity to influence spinal loading at T12. We varied the height and weight of our subject using values ranging between the 5th and 95th percentiles for US women above age 20 (33) (Figure 6). While varying height, weight was held fixed at the 50th percentile value for women (71 kg) and when varying weight, height was held constant at the 50th percentile value for women (1.62 m).
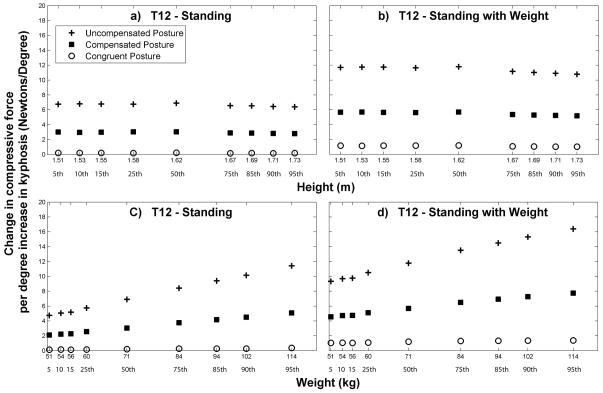
Figure 6.
Increase in T12 compressive loading for every 1° increase in the T1-T12 Cobb angle. These values are the slopes of least-squares linear regressions fitted to the load versus Cobb angle data at T12 for each height/weight combination. Note that when the subject’s height was varied, subject weight was held constant at 71 kg (the 50th percentile value for females) and when the subject’s weight was varied, subject height was held constant at 1.62 m (the 50th percentile value for females).
Results
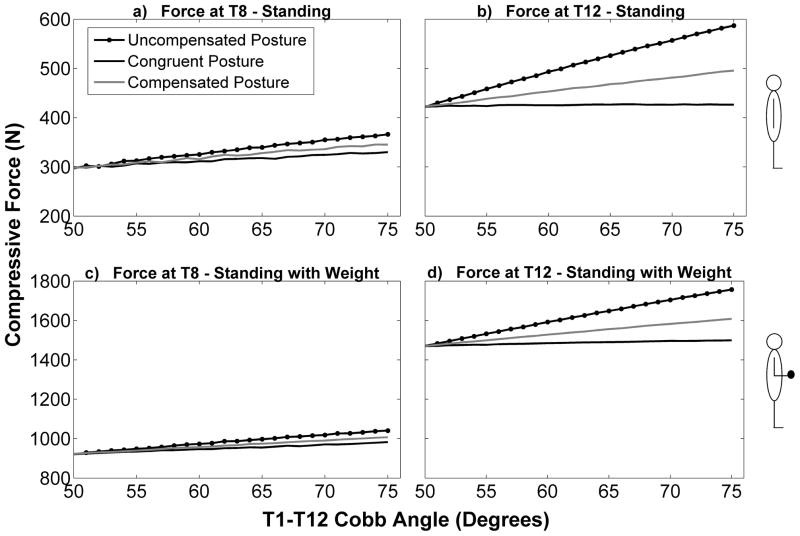
Vertebral compressive force was higher at T12 than T8 and higher for standing with weight in the hands than standing with no weight (Figure 4). At the baseline condition (thoracic kyphosis = 50°) the spino-pelvic parameters for the three different posture conditions (uncompensated, compensated, and congruent) were the same, meaning that the shape of the spine and the orientation of the pelvis were identical for all three postures, as were vertebral compressive forces. For this baseline condition the compressive force at T8 was 297 N for standing and 921 N for standing with elbows flexed and weight in the hands, whereas the compressive force at T12 was 422 N for standing and 1471 N for standing with elbows flexed and weight in the hands. At T8, compressive loading increased with increasing thoracic kyphosis for each of the three postures, with the increase in loading being greatest for the uncompensated posture, followed by the compensated posture, and finally the congruent posture (Figure 4). A similar trend was observed at T12 except that the differences in loading between the different postures at a given thoracic kyphosis angle were greater than those observed for T8.
Figure 4.
Compressive force (Newtons) on T8 and T12 as a function of T1-T12 Cobb angle (degrees) for the two activities, as well as the three different postures.
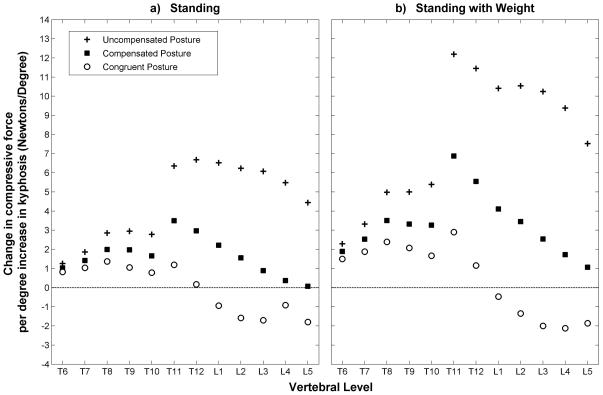
The uncompensated and compensated postures in general caused greater increases in loading in the lumbar and thoracolumbar regions than in the thoracic spine. The congruent posture appeared to mitigate kyphosis-related increases in loading at all vertebral levels, and even caused loading to decrease with increasing Cobb angle in the lumbar spine (Figure 5).
Figure 5.
Increase in compressive loading for every 1° increase in the T1-T12 Cobb angle. These values are the slopes of least-squares linear regressions fitted to the load versus Cobb angle data for each vertebral body.
For a given posture and thoracic kyphosis angle, the magnitude of vertebral compressive loading was higher when subject height or weight was increased, which was expected (data not shown). Varying subject height had minimal to no effect on the load versus Cobb angle trends already observed at T12 (Figure 6). That is, subject height did not affect the change in compressive force per 1° increase in kyphosis. Increasing subject body weight caused larger kyphosis-related increases in loading for the uncompensated and compensated posture conditions (Figure 6). Interestingly, the congruent posture condition prevented this interaction of subject weight and thoracic kyphosis angle.
Again, all three postures showed an increase in spinal compressive loading with increasing thoracic kyphosis, but the increase was greatest for the uncompensated posture, followed by the compensated posture, and finally the congruent posture.
Discussion
We used a musculoskeletal model of the spine to investigate the effect of increasing thoracic kyphosis on vertebral compressive loading under three different postural conditions (uncompensated, compensated, and congruent) and two different activities (relaxed standing and standing with weight in the hands). We found that an uncompensated increase in thoracic kyphosis resulted in the largest increases in spinal loading, whereas maintenance of a congruent posture minimized the increases in loading. Use of a postural compensation technique also reduced kyphosis-related increases in loading, but not to the same extent as the congruent posture. The differences in loading between the three posture conditions were greater in the thoracolumbar and lumbar regions than in the thoracic region. Varying subject height did not affect kyphosis-related increases in loading. However, increasing subject weight resulted in larger kyphosis-related increases in loading for the uncompensated and compensated postures, but did not have an effect for the congruent posture.
Vertebral fractures are most common at the mid-thoracic and thoracolumbar regions (31, 32), and therefore these are the most relevant spinal locations in terms of understanding how excessive thoracic kyphosis might increase vertebral fracture risk. Higher loads at T12 compared to T8 were expected considering that T12 is located inferior to T8 and therefore carries a higher percentage of the body’s weight. In addition, load sharing with the ribs and sternum likely reduced the compressive force exerted on T8 (17). In general, we found that the thoracolumbar and lumbar regions of the spine experienced greater kyphosis-related increases in loading then the thoracic region, which is most likely due to the fact that for a given increase in thoracic curvature, lower sections of the spine see a proportionally greater amount of body mass shifted anteriorly. Additionally, the ribs and sternum in the thoracic region likely share a proportion of the increased load. Together, these two effects might explain the marked increase in loading that occurs between the lower-thoracic and thoracolumbar regions (Figure 5).
As body weight increased, the kyphosis-related increase in loading was greater for both the uncompensated and compensated postures, presumably because a greater amount of body mass was being shifted anteriorly, whereas in the congruent posture this additional body mass was more efficiently distributed around the trunk such that increasing thoracic kyphosis did not significantly change the moment arm between the body mass and the T12 vertebral body.
The results of our simulations are largely consistent with prior biomechanical modeling studies (10, 34, 35). Briggs and colleagues found that during upright standing osteoporotic individuals with a vertebral fracture had higher estimated vertebral compressive loading between T7 and L5 than individuals with no vertebral fracture, and that these differences in loading were due to subtle differences in spinal curvature (34). Furthermore, during relaxed standing, estimated vertebral compressive forces between T7 and L5 are reported to be up to 14% greater in elderly subjects with high versus low thoracic kyphosis, and an increased thoracic kyphosis angle increased loading more so at T12 than at T8 (10).
In our study, increasing thoracic kyphosis increased spinal compressive loading more in the uncompensated condition than in the compensated or congruent conditions because it shifted a greater amount of body mass forward. This generated higher flexion moments which required larger muscle forces to equilibrate, elevating compressive loads on the vertebral bodies. The congruent and compensated posture conditions countered the anterior shift in body mass associated with an increasing thoracic kyphosis, with the congruent posture condition being more effective. The clinical implication is that some older individuals who have very high thoracic kyphosis may not have increased vertebral loading and be at an elevated risk for fracture because they have congruent posture. In comparison, those who have an age-related increase in thoracic kyphosis and do not have a congruent spinal configuration may have a greater risk for fracture than someone with the same thoracic kyphosis angle but who maintains a congruent posture.
In support of this concept, Keller and colleagues (36) applied a biomechanical model to a large group of young asymptomatic subjects to investigate how various spinal morphology parameters influence loading of the intervertebral disc. Whereas they found a positive correlation between compressive forces on thoracic vertebrae and forward sagittal balance (anterior shift in the center of mass position), they found no association between thoracic compressive forces and any sagittal spinal angles, despite a high variation in thoracic kyphosis angle among the subjects (T1-T12 Cobb angle ranged between 16.3° and 71.5°). The lack of association between thoracic kyphosis angle and thoracic spine compressive forces supports the notion that other postural parameters play a significant role in determining body mass distribution and therefore the spine’s biomechanical environment. These results are consistent with the current study’s findings that postural congruency and the use of a compensation technique can act to mitigate any increases in compressive loading associated with an elevated thoracic kyphosis angle. The asymptomatic subjects in the Keller study (mean age = 26.7 years) may have exhibited highly congruent postures because of their young age and the notion that congruency is indicative of a healthy spine (16). Taken together, these observations suggest that thoracic kyphosis measurements alone are not sufficient to characterize the impact of spinal curvature on vertebral loading, and that whole body postural alignment likely needs to be taken into consideration.
Despite age-related increases in the thoracic kyphosis angle, people are generally able to maintain their center of mass in a narrow range by employing various postural compensation strategies (11–15). For instance, Schwab and colleagues (12) found that thoracic kyphosis increased with advancing age but that center of mass was maintained at a constant distance from the heel due to posterior translation of the pelvis and an increase in pelvic tilt. Similarly, patients with a variety of degenerative spinal pathologies, including vertebral fracture, spondylolisthesis, lumbar spinal canal stenosis, disc pathology, sciatica, degenerative lumbar scoliosis, and spondylodiscitis, maintain their center of mass in a tight range similar to that of healthy controls (13). Therefore, it seems unlikely that a fully uncompensated increase in thoracic kyphosis, like that modeled in the current study, would actually occur. Rather, it seems that individuals will always attempt some form of compensation, with the degree and effectiveness of that compensation depending on the severity of the thoracic kyphosis deformity and characteristics of the individual. For instance, individuals with a larger pelvic incidence appear better able to compensate for thoracic kyphosis deformities and sagittal imbalance because they can tilt their pelvis back more than individuals with a smaller pelvic incidence (11). Understanding the factors that affect one’s ability to make postural adjustments is an area that needs further investigation.
The current study examined the effect of spinal curvature and posture on the net compressive load carried by each vertebral body, but did not look at how these factors might affect the spatial distribution of loading on the vertebral body. This was beyond the capability of the current musculoskeletal model, but is an important topic for future investigations. For instance, a majority of vertebral fractures are classified as anterior wedge compression fractures, meaning that the anterior portion of the vertebral body has been reduced in height significantly compared to the posterior and middle sections. It is important to understand what role posture and spinal curvature might play in changing the patterns of stresses and strains within the vertebral body. For instance, compared to flexed postures, upright and extended postures result in increased load transfer through the facet joints (37, 38). Further, the presence of intervertebral disc degeneration dramatically increases load transfer through the facets and stress-shields the anterior vertebral body (39, 40). This may cause a reduction in BMD in the anterior vertebral body, predisposing to anterior wedge fractures during forward flexion (39, 40). It is essential for future studies to investigate how thoracic kyphosis angle and overall sagittal alignment might interact with factors such as intervertebral disc degeneration to affect the distribution of loading throughout the spinal column. For instance, although a particular posture may reduce the total load on the vertebral body, it might concentrate load in some regions and stress-shield others, predisposing to injury despite the fact that the total load has been decreased.
A limitation of this study was that it only investigated one possible compensation strategy, namely coordinated changes in spinal curvature, whereas there are many other compensation strategies, and combinations of strategies, that an individual could employ to counter an anterior shift in body mass (11). Further research is required to understand how effective these various strategies are at restoring postural stability and mitigating increases in spinal loading. Another limitation was that our baseline spinal geometry for the model was derived from average values found in the literature, and we increased the thoracic kyphosis angle by uniformly adding to this curvature. However, spinal geometry is highly variable and two individuals with the same thoracic kyphosis angle can have spines that are shaped very differently (41, 42). Future studies should investigate the role of posture and thoracic kyphosis angle on spinal loading within the context of population variability. Finally, loading was only examined in two sagittally symmetric, static activities. Future studies should examine how thoracic kyphosis affects spinal compressive loading for a variety of static and dynamic activities, including those that are not sagittally symmetric.
In conclusion, there is evidence linking hyperkyphosis of the thoracic spine to vertebral fractures and other spinal degenerative diseases. It is thought that excessively stooped posture increases the forces applied to various spinal tissues to a level capable of causing pathology and degeneration. However, we suggest that the current theory ascribing increased spinal loading to greater amounts of thoracic kyphosis is overly simplistic as it does not take into account other postural adjustments that accompany age-related increases in thoracic kyphosis, and which act to modulate any increases in loading. Our results indicate that in addition to measuring thoracic kyphosis angle, it is also necessary to evaluate overall posture and spino-pelvic alignment when assessing one’s risk for degenerative spinal pathology due to altered spine biomechanics, such as vertebral fractures. Further, when treating spinal deformities, clinicians should strive to restore congruent posture because of its positive effects on spinal loading, balance, and eye gaze.
Acknowledgments
This work was supported by grants from the National Institutes of Health (R01AR053986, R01AR/AG041398, T32AG023480, T32AG023480-07, 1F31AG041629-01), and by the National Heart, Lung, and Blood Institute (NHLBI) Framingham Heart Study (NIH/NHLBI Contract N01-HC-25195). The contents are solely the responsibility of the authors, and do not necessarily represent the views of the NIH.
Footnotes
Disclosures
All authors state that they have no conflicts of interest.
Authors’ roles: Study design: AB, DA, MB. Study conduct: AB, DA, JD, MB. Data collection: AB, DA, JD. Data analysis: AB, DA, MB. Data interpretation: AB, DA, MB. Drafting manuscript: AB. Revising manuscript content: AB, DA, JD, MB. Approving final version of manuscript: AB, DA, JD, MB. All authors take responsibility for the integrity of the data analysis.
References
- 1.Milne JS, Williamson J. A Longitudinal Study of Kyphosis in Older People. Age and Ageing. 1983 Jan 1;12(3):225–33. doi: 10.1093/ageing/12.3.225. [DOI] [PubMed] [Google Scholar]
- 2.Goh S, Price RI, Leedman PJ, Singer KP. The relative influence of vertebral body and intervertebral disc shape on thoracic kyphosis. Clinical Biomechanics. 1999;14(7):439–48. doi: 10.1016/s0268-0033(98)00105-3. [DOI] [PubMed] [Google Scholar]
- 3.Manns RA, Haddaway MJ, McCall IW, Cassar Pullicino V, Davie MWJ. The relative contribution of disc and vertebral morphometry to the angle of kyphosis in asymptomatic subjects. Clinical Radiology. 1996;51(4):258–62. doi: 10.1016/s0009-9260(96)80342-4. [DOI] [PubMed] [Google Scholar]
- 4.Katzman W, Cawthon P, Hicks GE, Vittinghoff E, Shepherd J, Cauley JA, Harris T, Simonsick EM, Strotmeyer E, Womack C, Kado DM. Association of Spinal Muscle Composition and Prevalence of Hyperkyphosis in Healthy Community-Dwelling Older Men and Women. The Journals of Gerontology Series A: Biological Sciences and Medical Sciences. 2012 Feb 1;67A(2):191–5. doi: 10.1093/gerona/glr160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mika A, Unnithan VB, Mika P. Differences in Thoracic Kyphosis and in Back Muscle Strength in Women With Bone Loss due to Osteoporosis. Spine. 2005;30(2):241–6. doi: 10.1097/01.brs.0000150521.10071.df. [DOI] [PubMed] [Google Scholar]
- 6.Birnbaum K, Siebert CH, Hinkelmann J, Prescher A, Niethard FU. Correction of kyphotic deformity before and after transection of the anterior longitudinal ligament – a cadaver study. Archives of Orthopaedic and Trauma Surgery. 2001;121(3):142–7. doi: 10.1007/s004020000193. [DOI] [PubMed] [Google Scholar]
- 7.Huang M-H, Barrett-Connor E, Greendale GA, Kado DM. Hyperkyphotic Posture and Risk of Future Osteoporotic Fractures: The Rancho Bernardo Study. Journal of Bone and Mineral Research. 2006;21(3):419–23. doi: 10.1359/JBMR.051201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Roux C, Fechtenbaum J, Kolta S, Said-Nahal R, Briot K, Benhamou C-L. Prospective assessment of thoracic kyphosis in postmenopausal women with osteoporosis. Journal of Bone and Mineral Research. 2010;25(2):362–8. doi: 10.1359/jbmr.090727. [DOI] [PubMed] [Google Scholar]
- 9.Briggs A, Greig A, Wark J. The vertebral fracture cascade in osteoporosis: a review of aetiopathogenesis. Osteoporosis International. 2007;18(5):575–84. doi: 10.1007/s00198-006-0304-x. [DOI] [PubMed] [Google Scholar]
- 10.Briggs AM, van Dieën JH, Wrigley TV, Greig AM, Phillips B, Lo SK, Bennell KL. Thoracic Kyphosis Affects Spinal Loads and Trunk Muscle Force. Physical Therapy. 2007 May;87(5):595–607. doi: 10.2522/ptj.20060119. [DOI] [PubMed] [Google Scholar]
- 11.Roussouly P, Nnadi C. Sagittal plane deformity: an overview of interpretation and management. European Spine Journal. 2010;19(11):1824–36. doi: 10.1007/s00586-010-1476-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schwab F, Lafage V, Boyce R, Skalli W, Farcy J-P. Gravity Line Analysis in Adult Volunteers: Age-Related Correlation With Spinal Parameters, Pelvic Parameters, and Foot Position. Spine. 2006;31(25):E959–E67. doi: 10.1097/01.brs.0000248126.96737.0f. [DOI] [PubMed] [Google Scholar]
- 13.Geiger E, Müller O, Niemeyer T, Kluba T. Adjustment of pelvispinal parameters preserves the constant gravity line position. International Orthopaedics. 2007;31(2):253–8. doi: 10.1007/s00264-006-0157-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lafage V, Schwab F, Skalli W, Hawkinson N, Gagey P-M, Ondra S, Farcy J-P. Standing Balance and Sagittal Plane Spinal Deformity: Analysis of Spinopelvic and Gravity Line Parameters. Spine. 2008;33(14):1572–8. doi: 10.1097/BRS.0b013e31817886a2. [DOI] [PubMed] [Google Scholar]
- 15.Schwab F, Lafage V, Patel A, Farcy J-P. Sagittal Plane Considerations and the Pelvis in the Adult Patient. Spine. 2009;34(17):1828–33. doi: 10.1097/BRS.0b013e3181a13c08. [DOI] [PubMed] [Google Scholar]
- 16.Knight R, Jackson R, Killian J, Stanley E, Lowe T, Winter R. Scoliosis Research Society. 2003. White Paper on Sagittal Plane Alignment. accessed from SRS.org. [Google Scholar]
- 17.Iyer S, Christiansen BA, Roberts BJ, Valentine MJ, Manoharan RK, Bouxsein ML. A biomechanical model for estimating loads on thoracic and lumbar vertebrae. Clinical Biomechanics. 2010;25(9):853–8. doi: 10.1016/j.clinbiomech.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bean JC, Chaffin DB, Schultz AB. Biomechanical model calculation of muscle contraction forces: A double linear programming method. Journal of Biomechanics. 1988;21(1):59–66. doi: 10.1016/0021-9290(88)90192-3. [DOI] [PubMed] [Google Scholar]
- 19.Brown SHM, Potvin JR. Constraining spine stability levels in an optimization model leads to the prediction of trunk muscle cocontraction and improved spine compression force estimates. Journal of Biomechanics. 2005;38(4):745–54. doi: 10.1016/j.jbiomech.2004.05.011. [DOI] [PubMed] [Google Scholar]
- 20.Schultz AB, Andersson GBJ. Analysis of Loads on the Lumbar Spine. Spine. 1981;6(1):76–82. doi: 10.1097/00007632-198101000-00017. [DOI] [PubMed] [Google Scholar]
- 21.Contini R. Body Segment Parameters, Part II. Artificial Limbs. 1972;16(1):1–19. [PubMed] [Google Scholar]
- 22.Liu YK, Laborde JM, Van Buskirk WC. Inertial properties of a segmented cadaver trunk: their implications in acceleration injuries. Aerospace Medicine. 1971;42(6):650–7. [PubMed] [Google Scholar]
- 23.Pearsall D, Reid J, Livingston L. Segmental inertial parameters of the human trunk as determined from computed tomography. Annals of Biomedical Engineering. 1996;24(2):198–210. doi: 10.1007/BF02667349. [DOI] [PubMed] [Google Scholar]
- 24.de Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics. 1996;29(9):1223–30. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- 25.Winter DA. Biomechanics and Motor Control of Human Movement. 4. Hoboken, NJ: John Wiley & Sons; 2009. [Google Scholar]
- 26.Anderson DE, D'Agostino J, Bruno AG, Manoharan RK, Bouxsein ML. Regressions for estimating muscle parameters in the thoracic and lumbar trunk for use in musculoskeletal modeling. Journal of Biomechanics. 2012;45:66–75. doi: 10.1016/j.jbiomech.2011.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Narici M. Human skeletal muscle architecture studied in vivo by non-invasive imaging techniques: functional significance and applications. Journal of Electromyography and Kinesiology. 1999;9(2):97–103. doi: 10.1016/s1050-6411(98)00041-8. [DOI] [PubMed] [Google Scholar]
- 28.Bernhardt M, Bridwell KH. Segmental Analysis of the Sagittal Plane Alignment of the Normal Thoracic and Lumbar Spines and Thoracolumbar Junction. Spine. 1989;14(7):717–21. doi: 10.1097/00007632-198907000-00012. [DOI] [PubMed] [Google Scholar]
- 29.Kuntz C, Levin LS, Ondra SL, Shaffrey CI, Morgan CJ. Neutral upright sagittal spinal alignment from the occiput to the pelvis in asymptomatic adults: a review and resynthesis of the literature. Journal of Neurosurgery: Spine. 2007;6(2):104–12. doi: 10.3171/spi.2007.6.2.104. [DOI] [PubMed] [Google Scholar]
- 30.Vialle R, Levassor N, Rillardon L, Templier A, Skalli W, Guigui P. Radiographic analysis of the sagittal alignment and balance of the spine in asymptomatic subjects. The Journal of Bone and Joint Surgery. 2005;87-A(2):260–7. doi: 10.2106/JBJS.D.02043. [DOI] [PubMed] [Google Scholar]
- 31.Ismail AA, Cooper C, Felsenberg D, Varlow J, Kanis JA, Silman AJ, O’Neill TW the European Vertebral Osteoporosis Study G. Number and Type of Vertebral Deformities: Epidemiological Characteristics and Relation to Back Pain and Height Loss. Osteoporosis International. 1999;9(3):206–13. doi: 10.1007/s001980050138. [DOI] [PubMed] [Google Scholar]
- 32.Melton LJ, Lane AW, Cooper C, Eastell R, O'Fallon WM, Riggs BL. Prevalence and incidence of vertebral deformities. Osteoporosis International. 1993;3(3):113–9. doi: 10.1007/BF01623271. [DOI] [PubMed] [Google Scholar]
- 33.McDowell MA, Fryar CD, Ogden CL, Flegal KM. US Department of Health and Human Services CfDCaP, National Center for Health Statistics. Anthropometric Reference Data for Children and Adults: United States, 2003–2006. 2008. [PubMed] [Google Scholar]
- 34.Briggs A, Wrigley T, van Dieën J, Phillips B, Lo S, Greig A, Bennell K. The effect of osteoporotic vertebral fracture on predicted spinal loads in vivo. European Spine Journal. 2006;15(12):1785–95. doi: 10.1007/s00586-006-0158-0. [DOI] [PubMed] [Google Scholar]
- 35.El-Rich M, Shirazi-Adl A, Arjmand N. Muscle Activity, Internal Loads, and Stability of the Human Spine in Standing Postures: Combined Model and In Vivo Studies. Spine. 2004;29(23):2633–42. doi: 10.1097/01.brs.0000146463.05288.0e. [DOI] [PubMed] [Google Scholar]
- 36.Keller TS, Colloca CJ, Harrison DE, Harrison DD, Janik TJ. Influence of spine morphology on intervertebral disc loads and stresses in asymptomatic adults: implications for the ideal spine. The Spine Journal. 2005;5(3):297–309. doi: 10.1016/j.spinee.2004.10.050. [DOI] [PubMed] [Google Scholar]
- 37.Adams M, Hutton W. The effect of posture on the lumbar spine. J Bone Joint Surg Br 1985. 1985 Aug 1;67-B(4):625–9. doi: 10.1302/0301-620X.67B4.4030863. [DOI] [PubMed] [Google Scholar]
- 38.Adams M, Hutton W. The effect of posture on the role of the apophysial joints in resisting intervertebral compressive forces. J Bone Joint Surg Br 1980. 1980 Aug 1;62-B(3):358–62. doi: 10.1302/0301-620X.62B3.6447702. [DOI] [PubMed] [Google Scholar]
- 39.Adams MA, Pollintine P, Tobias JH, Wakley GK, Dolan P. Intervertebral Disc Degeneration Can Predispose to Anterior Vertebral Fractures in the Thoracolumbar Spine. Journal of Bone and Mineral Research. 2006;21(9):1409–16. doi: 10.1359/jbmr.060609. [DOI] [PubMed] [Google Scholar]
- 40.Pollintine P, Dolan P, Tobias JH, Adams MA. Intervertebral Disc Degeneration Can Lead to “Stress-Shielding” of the Anterior Vertebral Body: A Cause of Osteoporotic Vertebral Fracture? Spine. 2004;29(7):774–82. doi: 10.1097/01.BRS.0000119401.23006.D2. [DOI] [PubMed] [Google Scholar]
- 41.Gelb DE, Lenke LG, Bridwell KH, Blanke K, McEnery KW. An Analysis of Sagittal Spinal Alignment in 100 Asymptomatic Middle and Older Aged Volunteers. Spine. 1995;20(12):1351–8. [PubMed] [Google Scholar]
- 42.Hammerberg EM, Wood KB. Sagittal Profile of the Elderly. Journal of Spinal Disorders & Techniques. 2003;16(1):44–50. doi: 10.1097/00024720-200302000-00008. [DOI] [PubMed] [Google Scholar]