Identification of phosphorus emission hotspots in agricultural catchments

Abstract

An enhanced transport-based management approach is presented, which is able to support cost-effective water quality management with respect to diffuse phosphorus pollution. Suspended solids and particulate phosphorus emissions and their transport were modeled in two hilly agricultural watersheds (Wulka River in Austria and Zala River in Hungary) with an improved version of the catchment-scale PhosFate model. Source and transmission areas were ranked by an optimization method in order to provide a priority list of the areas of economically efficient (optimal) management alternatives. The model was calibrated and validated at different gauges and for various years. The spatial distribution of the emissions shows that approximately one third of the catchment area is responsible for the majority of the emissions. However, only a few percent of the source areas can transport fluxes to the catchment outlet. These effective source areas, together with the main transmission areas are potential candidates for improved management practices. In accordance with the critical area concept, it was shown that intervention with better management practices on a properly selected small proportion of the total area (1–3%) is sufficient to reach a remarkable improvement in water quality. If soil nutrient management is also considered in addition to water quality, intervention on 4–12% of the catchment areas can fulfill both aspects.

Highlights

► The enhanced P emission model PhosFate was applied in two hilly catchments. ► A new optimization method that identifies the most effective sources is presented. ► Only a few percent of the total area generates the majority of the river loads. ► An effective management can be achieved by selecting the highly contributive areas. ► Implementation of the local practices should still rely on on-site experiences.

1. Introduction

Diffuse phosphorus (P) emissions are almost immeasurable at source and consequently it is hard to identify their area of origin. Management of diffuse P pollution is complicated to implement due to the spatial and temporal variability of the emissions, their different transport pathways and complex and strong relations to hydrology and soil properties. Because of these characteristics, cost-effective management of the diffuse P pollution requires watershed level approximation and model simulations (Campbell et al., 2004) unless a strong emission-based principle is applied (e.g. emission regulations), which might be costly and of limited acceptance. Model simulations are especially necessary to understand processes taking place in the catchment if the river monitoring system is underdeveloped or water quality data are scarce. Besides the assessment of existing pollution patterns, mathematical models can be used to assist in the evaluation of management practices to be applied in the catchment (Mostaghimi et al., 2001). Lumped screening models are able to identify the sub-catchments. These models show a clear water quality problem related to diffuse emissions, and they can evaluate the role of different pathways and sources of pollution. However, more detailed examinations on the spatial distribution of the emissions and local planning of management practices are limited due to the spatial aggregation used in these models. Spatially distributed catchment models, which divide the study area into small elementary units, focus more detail on the local variations of the catchment properties, the contaminations and their management alternatives within the watershed.

The application of models with different spatial scales depends on the management goals. Strategic analyses and decisions related to national water quality management programs or management plans of larger river basins are usually based on larger scale models (Schreiber et al., 2003; ICPDR, 2009; Schilling et al., 2011; Zessner et al., 2011). Local water quality investigations and implementation of practical measures rely on field studies and smaller scale modeling results (field scale models, e.g. CREAMS, Knisel, 1980 or EPIC, Williams et al., 1983). Watershed scale water quality models (e.g. WEPP, Flanagan and Livingston, 1995; EUROSEM, Morgan et al., 1998; ANSWERS-2000, Bouraoui and Dillaha, 2000; AnnAGNPS, Bingner and Theurer, 2003; SWAT, Neitsch et al., 2002) usually use the principles of the process-based field scale models by extending them to complex land use and management situations (Shirmohammadi et al., 2001). The so called index-based approaches attempt to identify the critical pollution areas within the catchment. These pollution screening assessments are often followed by field scale model applications to determine best management practices for the polluted areas (Shirmohammadi et al., 2001).

In case of a distributed parameter model, the selected element (grid) scale can significantly influence the model performance. A major source of error in catchment models comes from the incompatibilities between model scale, database scale and the scale of the heterogeneity of the environmental processes (Zhang et al., 2004). The most common issue is that the parameters or input data are measured at one particular scale (or more) and then they are inputs into a model constructed at another scale. Therefore, some assumptions on the upscaling are needed. The choice of the grid scale (resolution) determines how the variability is represented in the model (Grayson and Blöschl, 2000). Differences from element to element are represented explicitly, whilst heterogeneity within an element is represented implicitly. Fluxes generated in a single element can be explicitly routed in the catchment, however, the related model variables in a grid are affected by the fluxes of the surrounding cells besides the local characteristics (Zhang et al., 2004). Sub-element (implicitly represented) variables can be conceptualized in four ways: (i) assuming zero variation of the parameter values, (ii) using effective parameters, which reproduce the bulk behavior of the cell, (iii) applying distribution functions rather than a single value and (iv) direct parameterization of sub-grid variability (Blöschl and Sivapalan, 1995).

Recent model applications to assess spatial variability of the soil loss or P emissions or spatial risk assessments often rely on the Universal Soil Loss Equations (USLE, Wischmeier and Smith, 1978) or its improved versions (e.g. the Revised USLE, (RUSLE), Renard et al., 1997). Van Rompaey et al. (2001) developed a new model (SEDEM) to calculate annual sediment yield of river systems, which contains the RUSLE approach (for erosion rates) and a routing function (for sediment transport). They concluded that accuracy of sediment yield predictions using distributed model is significantly higher than that of a lumped regression model. De Vente et al. (2008) applied and compared three sediment yield models with different basic concepts (empirical, physically based and index-based) at regional scale. They state that for the prediction of erosion rates at the regional scale, the use of simple models with limited data requirements seems preferable and provides the best results. Tetzlaff et al. (in press) presented an application of an adopted version of USLE extended with a sediment delivery ratio to identify areas having risk potential for sediment input to surface waters. The paper suggests that based on the results, delineation and ranking of sub-areas vulnerable to soil loss and sediment transfer become feasible, followed by target-oriented investment to conduct detailed studies and programs of measures.

Another direction in this research field is to focus on the transport efficiency of the areas and the possible transport routes of the sediment within a catchment under different land use and topographic conditions. These approaches examine the connectivity of the hydrological (sediment transport) systems and determine spatial linkages between the sediment source areas and the recipients through catchments. Using connectivity analyses the effective catchment area can be determined, which has a contribution to the river loads. Examples of this approach can be found in e.g. Fryirs et al. (2007), Borselli et al. (2008) or Aurousseau et al. (2009). Phosphorus Index approaches attempt to identify the areas within the catchment, which have potential risk of P movement to water bodies (Campbell and Edwards, 2001). The index is determined by assessing different factors on P availability at the sources (e.g. fertilizer and manure rates and application forms, availability for plants), transport possibilities (e.g. runoff and soil loss rates, travel distance) and the affecting management properties. P-Index model applications are presented by e.g. Bechmann et al. (2007), Drewry et al. (2011) or Ulén et al. (2011).

Water quality targets that are used to evaluate the pollution status of water bodies are usually related to in-stream concentrations (e.g. requirements based on the European Water Framework Directive (EU WFD), OJEC, 2000). The overall results of the watershed management can be realized as river load (concentration) reductions at several stream monitoring gauges. However, the required management practices to reduce river loads have to finally be addressed to relevant sources within the watershed. Emission reductions with the same rate in the whole catchment or areas having emissions (or soil loss rates) over a certain threshold value would be an equitable solution, but it surely would not provide a cost-effective management with respect to river water quality. Not all of the source areas effectively contribute to the river loads and the extent of their contribution depends on the transport efficiency of the emitted pollutants within the catchment and toward the outlet. Thus, management efforts to reduce water pollution should be selective if costs are also considered. Interventions should be concentrated on the critical source and/or transfer areas where the highest fluxes to the river net come from and/or where significant direct transfers of pollutants from land to water probably occur (Campbell et al., 2004). Therefore, only a transport-based management approach can be environmentally and economically effective. Besides this, persuasion of the local stake-holders on the necessity of the management actions and the practical execution of the management plans including adequate technical implementation and financial subsidies can probably be realized on a smaller proportion of the catchment area.

Since P usually moves from the sources toward the water bodies in particulate form via overland sediment transport generated by runoff (Campbell and Edwards, 2001), the paper concentrates on the fate of suspended sediment (SS) and particulate phosphorus (PP) within the catchment. The paper presents an enhanced catchment-scale modeling approach by improving its earlier versions. The new model functions focus on SS and PP transport modeling and their optimized management. The model is able to find the most significant source areas contributing to the river loads and provides an optimized, cost-effective management alternative to reduce P emissions. The advantage of the model as compared to other more complex approaches is that information requirements are restricted to data easily available in many countries throughout Europe and beyond and application is neither limited by time and money consuming data acquisition nor calibration procedures. The simple, well-structured methodology contains sets of empirical and physically-based equations with limited number of variables and parameters. Although the model is not able to follow P load time-dynamics by focusing on the spatial variability of the emissions and loads within the catchment, it is easy to recognize likely hot-spot regions and evaluate efficiency of management practices. The model was applied to test the improved algorithms in two pilot areas, which have similar catchment properties (topography, soil, land use, climate), however, they show different SS and PP load observations. Comparative study was executed in respect to the river loads, spatial distribution of the emissions and management scenarios to reduce SS and PP fluxes.

2. Case study areas

The study was performed in two hilly catchments with significant agricultural coverage and dominance of diffuse P emissions. The Wulka River is located in the eastern part of Austria, whilst the Zala River catchment can be found in Western-Hungary (Fig. 1). Both watersheds are well monitored (many monitoring stations at high frequency), which provided a proper data set for the model calibration and validation. Since both of the rivers are the main inflows of high-priority lakes (Wulka: Lake Neusiedler, Zala: Lake Balaton), examination of PP river loads is of high concern due to the remobilization capability of the PP settled in the lake. The main watershed characteristics are summarized in Table 1. Long-term average (between 1994 and 2000, omitting data of the extreme years) PP concentrations of Wulka and Zala are 0.24 mg P l^− 1 and 0.19 mg P l^− 1, respectively. Total phosphorus (TP) values are 0.39 mg P l^− 1 (Wulka) and 0.28 mg P l^− 1 (Zala). Since these measured PP and TP concentrations are high in comparison to any water quality standards, reduction of PP river loads is a reasonable management task. Further reason of selection of these two areas was that despite the general properties of the catchments their measured area-specific SS loads show a clear difference, which encourages executing a comparative assessment.

Fig. 1.

Location of the case study areas (circles and triangles indicate the catchment outlets and upstream gauges, respectively).

Table 1.

Main characteristics of the Wulka and the Zala catchments.

Attribute	Unit	Wulka	Zala
Area	km2	373	1480
Mean slope	%	8.0	6.5
Dominant soil type	–	Silty, loamy soil	Loamy soil
Share of cropland	%	54	49
Share of pastures	%	12	9
Share of forests	%	28	36
Average precipitation	mm a− 1	625	658
Long-term P surplus	kg P ha− 1	615	490
Mean discharge	m3 s− 1	1.1	5.6
Mean SS load	t SS ha− 1 a− 1	0.13	0.07
Mean PP load	kg P ha− 1 a− 1	0.23	0.23
Mean TP load	kg P ha− 1 a− 1	0.37	0.33

3. Methods

3.1. The PhosFate model

The catchment-scale P emission model PhosFate (Kovacs et al., 2008) was developed for watershed management purposes. It is appropriate to support decision-making in watershed management. It allows planning best management practices (BMPs) in catchments and simulating their possible impacts on the phosphorus loads based on the critical source area concept. PhosFate is a semi-empirical, long-term average, distributed parameter model. Its spatial units are raster cells (with a size of e.g. 50 × 50 m), the time scale is one year or more. It was originally planned to evaluate the point/non-point ratio of the P emissions and to assess the efficiency of different management scenarios in comparison to the present state. The model computes the main elements of the hydrologic cycle, soil erosion, local P emissions and P transport in the terrestrial areas and throughout the stream network. The model was validated in several types and sizes (from a few to ten thousands of km²) of well-monitored catchments in Central Europe (Hungary, Kovacs et al., 2008; Honti et al., 2010, Albania, Kovacs et al., 2012, Austria and Switzerland, ongoing research projects). Model applications showed good performance in both arid and wet regions.

The recent version of the model builds on the earlier attempts (Kovacs and Honti, 2008; Kovacs et al., 2008) by either adapting or improving their algorithms. However, significant extensions have been recently implemented in the model as well. PhosFate includes water balance modeling and flow routing, enhanced calculation of emissions and transport of SS, PP and dissolved P (DP), calculation of impacts of point sources and reservoirs and an optimization algorithm to reveal relevant emission sources. Since the paper focuses on the fate of the SS and PP fluxes, only the relevant parts of the whole methodology are presented. The scheme of the SS and PP transport calculations is demonstrated in Fig. 2. The overall model concept is to build up the catchment from elementary cells to represent the spatial heterogeneity of the watershed. Sub-grid variability is conceptualized by either assuming no variability in the cells or applying effective parameters. Soil loss rates (with USLE) and PP emissions (based on agricultural P surplus data and the soil loss) are computed for every single cell independently according to their own properties. Then the individual cells are connected by the flow tree and a cumulative transport is calculated with an explicit routing using mass balance equations. SS and PP retention is calculated as a function of the cell residence time.

Fig. 2.

Scheme of the transport algorithm.

A detailed methodology of the model is described in Appendix A. The most important modifications of the emission and transport modeling are the introduction of a dual function (riparian zone and water body) for the channel cells, the enhanced calculation of the SS and PP retention in the terrestrial areas and the separation of the field and in-stream retention parameters. Main inputs of the model are digital maps (elevation, soil type, land use and humus content), statistical data (agricultural P surplus), meteorological data (rainfall records) and point information (reservoir volume). Results of the calculations are the spatial distribution of the soil loss and PP emissions, the SS and PP load values at any arbitrary point within the catchment, the SS and PP retention patterns of the catchment and the cell residence time and travel time values to the outlet.

The optimization algorithm – as the most important model improvement in comparison to the earlier versions – is presented in the following.

3.2. Hot spot identification and optimization

To achieve an optimal management (high reduction in PP and SS exports from the catchment at low intervention cost), not all emission source areas have to be addressed by the interventions because they contribute differently to the river loads. PhosFate calculates all processes in a spatially explicit manner. In this way, any modeled quantity can be monitored with the resolution of the input data. Each cell has its contribution to the total river loads and some cells transport remarkable mass fluxes coming from their upstream neighbors in the hydraulic hierarchy. Tracking the transport pathways from each cell, the most promising locations for an intervention can be selected. The selection is driven by the load contribution efficiency of the cells determined by the model. Those cells, which succeed to send the biggest amount of emitted material to the stream network, can be considered as ideal subjects to source control (reduction of local emission via e.g. land use change or erosion protection). On the other hand, there are cells that transport significant amounts of P to the rivers coming from their immediate vicinity (even though they can have low rate of own emission). These are the best places for transport control, i.e. to establish forest or grassy retention zones (mostly along streams). Some of the cells produce and transmit considerable fluxes as well (e.g. arable land adjacent to a stream). The optimization can be governed by two objective functions. The first option is cost efficiency at fixed pollution limit, i.e. how to reduce the amount of PP transport into the stream network to a prescribed limit with the most effective intervention methods (covering as few cells as possible). The second one is load reduction efficiency at fixed available cost, i.e. how to intervene on a specified number of cells with the biggest gain in load reduction.

The selection method of the hot spots is based on the transport algorithm. Assuming a unit emission value (e.g. 1 kg P a^− 1) in each cell and routing the emissions to the outlet, the proportion of the local emissions that can reach the outlet can be determined. Similarly, the transportable amount of the inflowing flux of the cells can be calculated, i.e. what flux can be conveyed from the entering flux of the given cell to the outlet. Although the cumulative relative retention downstream of a local cell is the same for the emission and the inflowing flux, the retention in the cell itself is different (Eq. (A.6)), which makes it reasonable to differentiate between the two relative contributions. Since the equations are linear for the absolute fluxes, multiplying these relative loads with the cell emission and inflowing flux values, absolute transportable fluxes can be generated. Since these processes are executed for each cell, they result in two new layers called the “source load” map and “transfer load” map. Optimization is based on these two maps by estimating the achievable load reductions on both layers if an intervention is implemented. Utilizing the source load and transfer load maps the impact of a local intervention on the load at the outlet can be directly and locally evaluated. Ranking the cells according to their achievable load reduction (gain) caused by an intervention, a priority sequence of the cells can be derived for the interventions, which forms the basis for an optimized watershed management.

The calculation of the achievable gain is the most performance-demanding part of the algorithm. We assigned a possible intervention type to all non-urban field cells of the catchments. This assignment could theoretically consider the present land use, slope and soil conditions and management practices, but the high number of the applicable alternatives at a specific location would highly complicate the procedure. Therefore, for the optimization we selected two specific options, managed grasslands without over-grazing for any arable land and forestation for everything else. These measures can be considered as almost ideal management practices with high soil loss reduction efficiency and increased roughness. Therefore, we do not specify whether it is source or transport control, simply a potential measure (land use change) is applied that is able to reduce both source and transfer loads. As a first step, we calculated the alternative local SS and PP emissions for each cell based on its intervention land use category. Knowing the (usually decreased) local load and the (usually higher) Manning's coefficient in case of intervening at a specific cell enables us to estimate the exact improvement in the source load and transfer load maps based on Eq. (A.6). The relative retention (deposition related to the inflowing load or the local emission) after an intervention can be computed as a function of the present relative retention and the Manning's coefficients:

$$1-re{t}_{SS,i,m}=\left(1-re{t}_{SS,i,o}\right)\cdot exp\left(-k_{\mathit{SS}}\cdot K_{topo,i}\cdot \left(n_{i,m}-n_{i,o}\right)\right)$$ (1)

where ret_SS,i,m is the modified relative retention at cell i after an intervention [−], ret_SS,i,o is the original relative retention at cell i [−], k_SS is the sediment deposition rate [s^− 1], K_topo,i is a topographic constant at cell i as a function of the cell flow length, slope and hydraulic radius [m^1/3], n_i,m is the modified Manning's coefficient at cell i [s m^− 1/3] and n_i,o is the original Manning's coefficient at cell i [s m^− 1/3].

This procedure results in new source load and transfer load maps that show the transportable amount of the local emissions/inflowing fluxes of a single cell if the local emission and the roughness is modified according to the management practice applied in the specific cell. The modified maps are compared to the original ones by calculating their differences, which define the possible gain of each cell. Finally, the two difference maps are summed to get the total achievable gain (amount of PP load reduction at the outlet via source and transport control together). Since the two gains are summed, there is no differentiation between the two kinds of control means (source and transport), their aggregated impact on the river loads is the decisive factor. Intervention is executed in that cell with the highest total gain. Channel cells (with grassy riparian zones) are not involved in the procedure. Since intervening in a cell affects the future possible gain in the connected field cells both upstream (through the improvement in retention from the passing PP and SS flux) and downstream (through the decrease in the local PP and SS loads), the modified source load, transfer load and gain maps need to be updated in these regions after carrying out the actual intervention in the cell with the best gain. These sequential updates make the procedure iterative. Since the change of the source load and transfer load values can be finally traced back to that of the Manning values (Eq. (1)), the calculation is relatively fast. Unit-costs of the interventions are not differentiated, the number of cells (the area) designated for interventions simply determines the costs. Cells designated by the algorithm are the possible hot-spots in the catchment where further management efforts should focus on.

The iterative algorithm of calculation is then the following:

• 1.Estimate the achievable gain for each cell.
• 2.Intervene (change land use) in the cell with the biggest possible gain.
• 3.Actualize the model calculations in the affected region (up- and downstream neighbors of the intervention cell).
• 4.If the budget (maximum area for interventions) is spent or the load target is achieved, finish the procedure, else repeat from the beginning (1).

It is possible to refine the method by differentiating between various land use conversions in respect to specific costs. Designating advisable land use classes at certain locations of the catchment (e.g. vulnerable soils, steep slopes, riparian zones or fertile soils) for particular conversions (e.g. erosion protection in arable land, change of arable land to grassland, pasture to forest or riparian zone to forest) with different area-specific costs the optimization can be executed more specifically. In this case, the total achievable gain of a cell has to be divided by the costs defined for the conversion applied in order to get gain values related to unit costs (e.g. kg P a^− 1 load reduction per €).

3.3. Evaluation of the river monitoring data

SS and PP river fluxes generated by soil erosion were determined by analyzing the measured discharge and concentration time series of the gauging stations. At the outlets where daily discharge and water quality data were available, the simple annual averages closely represented the mean loads. However, they still included the fluxes from point sources and autochthonous materials transported by base flow. Applying the flow separation technique mentioned before (Arnold et al., 1995) for the daily discharge time series, the river fluxes at base flow conditions were analyzed. The relationship found between the base flow rates and river mass fluxes was extended to the periods with surface runoff contribution as well. In this way, base load contribution was assigned to every day. Then the determined “base loads” were subtracted from the total measured values resulting in “event loads”, and finally the daily values were summed up to annual ones. Annual average event loads were considered as soil erosion induced fluxes for the model calibration. At the other upstream stations having weekly, biweekly or monthly values, the simple annual means are highly uncertain due to the insufficient number of the samples. Thus, separation of the base loads was executed only for a long-term period to provide enough number of observations and the derived long-term event loads at the upstream cross-sections were applied to check the spatial plausibility of the model.

3.4. Definition of water quality targets

According to the implementation of the EU WFD in Austria and Hungary, the bioregion-related, type-specific environmental quality standard of the good status for orthophosphate-P (PO4-P) is 0.2 mg P l^− 1 (BMLFUW, 2010) and 0.05 mg P l^− 1 (in case of a downstream lake, VM, 2010), respectively (the Austrian value refers to the 90th percentile, whilst the Hungarian to the mean). However, there is no standard value of the PP, which would be necessary for a management strategy of it. Therefore a PP concentration limit was introduced to provide target value for the management. Assuming same proportion of PO4-P and PP in the long-term TP concentration, the PP criteria is equal to that of the PO4-P (as it is set in the Hungarian regulation). Applying both the national PO4-P criteria values (the Austrian one has to be converted to an annual mean that is approx. 0.15 mg P l^− 1) and their average, three mean PP criteria values were determined (scenario 1: 0.15 mg P l^− 1, scenario 2: 0.10 mg P l^− 1 and scenario 3: 0.05 mg P l^− 1). Multiplying these concentration criteria values with the mean discharge rates, mean PP load criteria were calculated.

Assuming no change in the long-term hydrologic cycle and base load characteristics, the separated base load values of PP can be kept fixed independently on the management practices implemented. Subtracting these base values from the mean total load criteria numbers, target values for the event loads were determined which should be met after the management actions.

3.5. Model application

Digital maps of the pilot catchments were collected from open data sources and national data sets. Elevation models were available for both watersheds at 50 m grid size. Land use maps were clipped from the Corine Landcover map (100 m × 100 m raster, EEA). Soil maps were generated by combining national topsoil data and a European soil database (1 km × 1 km raster, EC JRC). P surplus data were taken from former scientific projects related to nutrient management (daNUbs Project, IWAG, 2005, STOBIMO Project, BMLFUW, 2011). They were distributed to the agricultural fields (arable land, orchard, vineyard and pasture) of the catchments. Meteorological, hydrological and water quality observations were collected from the national monitoring databases. Spatial interpolation of the rainfall gauges was executed using the Thiessen-polygon technique. All input maps were finally converted to 50 m gird size (spatial units of the calculations).

Exact determination of the R-factor requires precipitation records at high (at least hourly) frequency. Since such data were not easily available for the pilot areas, the annual R-factors were related to the annual surface runoff volumes as proxies of the high intensity rainfall events instead of rainfall intensities. Long-term average R-factor was estimated from the summer half-annual rainfall volume according to Strauss et al. (1995), and annual values were simply estimated from the long-term one using the relative differences of the annual and long-term surface runoff amounts. Surface runoff volumes were determined by applying a base flow separation method analyzing the measured daily discharge time series (Arnold et al., 1995). It provides base flow time series from the total discharge data at daily time step using an automated frequency signal analysis technique. Since CM-factor is a highly time-varying parameter (especially for agricultural land), its annual average value was calculated as a weighted mean of CM-factors for summer and winter conditions (representing high and low soil protection by vegetative cover, respectively). Proportions of the summer and winter half-annual surface runoff volumes on the total one were considered as weighting factors.

The model was applied in the test watersheds for different simulation periods (1992–2000 for the Wulka watershed, 1994–2003 for the Zala watershed). Accuracy of the modeled channel was checked by visual inspection of satellite pictures on the spring sections in Google Maps. Calibration of the model was executed for long-term average SS and PP loads at the outlets. During the model calibration, the field and in-stream retention parameters of the two catchments were set as similar as possible due to the strong similarity of the watershed characteristics. To ensure the consistency of the parameters, calibration in both catchments was done for the overlapping simulation period (1994–2000). The extremes (high load in 1996 in Wulka, low load in 2000 in Zala) were not taken into account in the averages, because they were not considered representative for long-term means. Subsequent spatial validation was done at upstream cross sections for the averages (1994–2000). Additionally, the annual variability of the simulation periods was examined at the outlet for individual years (including the extremes). However, since calibration was performed for the overlapping period, only the years outside the calibration period (Wulka: 1992–1993, Zala: 2001–2003) can be considered as independent validation years. The model results for the single years within the calibration period (1994–2003) contain only the random errors of the computations, the systematic error was eliminated by the calibration.

Based on the calibrated model, management scenarios were evaluated for long-term average conditions according to different management strategies. In the first step, the source areas were managed (soil nutrient management) only by implementing managed grasslands in areas with soil loss higher than 10 tons SS per hectare and year (that is around a generally suggested maximum tolerance limit for soil loss, Morgan, 2005). Since a certain amount of the calculated local gross soil loss is deposited at the source cells, the tolerance limit applied for management was related to the net soil loss values (exported flux out of the cells, i.e. gross soil loss minus deposition). In the next step, the areas with the highest gain in respect to water quality at the outlet were selected and managed using the optimization algorithm (water quality management). Starting always at the cell with the highest gain and covering more and more parts of the catchment with interventions, the decreased PP loads and the load reduction efficiencies of the specified intervention areas were calculated. Additionally, the area demand of the scenarios was determined. Finally, a combinative management procedure that considers both water quality and soil nutrient management together was executed.

4. Results and discussion

4.1. Event load separation and load targets

Separation of the base loads in the Wulka catchment resulted in long-term SS and PP event loads of 0.09 t SS ha^− 1 a^− 1 and 0.15 kg P ha^− 1 a^− 1, respectively. Share of the event SS and PP loads from the total amounts (presented in Table 1) is 67% and 66%, respectively. It varies among the simulation years between 60% and 88% for SS and 51% and 91% for PP. In the Zala catchment, the determined SS and PP event loads are 0.06 t SS ha^− 1 a^− 1 and 0.14 kg P ha^− 1 a^− 1, respectively. The proportion of the event loads are 82% and 59%. Lower share of PP event loads in Zala is a consequence of the fact that considerable loads from point sources contribute to the total PP loads. Variability between the simulated years is wider and ranges from 36% to 89% and from 6% to 66%. This is due to the stronger meteorological fluctuations of the simulation period modeled in Zala.

Mean total PP load targets (determined from the mean discharge and criteria concentrations) are reported in Table 2. Subtracting the base load values (0.07 kg P ha^− 1 a^− 1 and 0.09 kg P ha^− 1 a^− 1 in the Wulka and Zala catchments, respectively) from the total load criteria numbers resulted in event load target values of 0.07 kg P ha^− 1 a^− 1 and 0.09 kg P ha^− 1 a^− 1 (scenario 1) and 0.02 kg P ha^− 1 a^− 1 and 0.030 kg P ha^− 1 a^− 1 (scenario 2). These targets were used for quality evaluation and management planning of PP event loads in the Wulka and Zala catchments, respectively. PP event load reduction is needed by 55% and 86% in the Wulka catchment and by 36% and 80% in the Zala catchment according to scenarios 1 and 2, respectively (Table 2). In case of scenario 3 (the most rigorous limit), the calculated targets became negative (Table 2), which indicates that management of erosion induced event loads without involving the base load regulation (e.g. point sources) is not enough to meet the 0.05 mg P l^− 1 mean concentration limit. Therefore, only scenarios 1 and 2 were henceforward examined in this study.

Table 2.

Target criteria values (concentrations and loads) and necessary event load reductions for the watershed management.

Scenario	Target	Unit	Wulka	Zala
–	Base load	kg P ha− 1 a− 1	0.07	0.09
1	Concentration	mg P l− 1	0.15	0.15
	Total load	kg P ha− 1 a− 1	0.14	0.18
	Event load	kg P ha− 1 a− 1	0.07	0.09
	Reduction	%	55	36
2	Concentration	mg P l− 1	0.10	0.10
	Total load	kg P ha− 1 a− 1	0.09	0.12
	Event load	kg P ha− 1 a− 1	0.02	0.03
	Reduction	%	86	80
3	Concentration	mg P l− 1	0.05	0.05
	Total load	kg P ha− 1 a− 1	0.05	0.06
	Event load	kg P ha− 1 a− 1	− 0.02	− 0.03
	Reduction	%	118	124

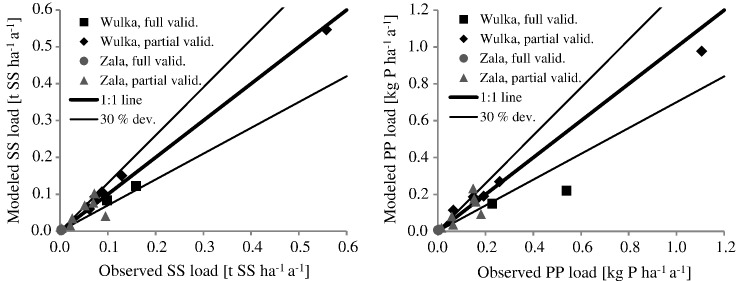
4.2. Model calibration and validation

Figs. 3 and 4 show the comparison of the modeled and measured SS and PP loads. Long-term averages at the outlets could be almost perfectly calibrated (Fig. 3). Checking the results at the upstream stations, the simulated fluxes fit the measured long-term averages. Model errors are usually lower than 30%. There are two outliers in both catchments with an error of more than 30%, which are smaller tributaries. These more significant deviations in tributaries are probably caused by the some specific local conditions, which are not caught by the model (neither the input data nor the methodology). They usually have stronger influence on the transport at smaller scale than at larger one.

Fig. 3.

Observed and modeled long-term average (1994–200, without extremes) SS (on the left) and PP (on the right) event river loads at the monitoring stations of the Wulka and the Zala rivers (one dot represents one station, outlet: calibration, upstream gauges: validation).

Fig. 4.

Observed and modeled SS (on the left) and PP (on the right) event river loads of individual years at the outlet of the Wulka (1992–2000) and the Zala (1994–2003) catchments (one dot represents one year).

Regarding the annual loads at the two outlets (Fig. 4), small modeling errors for SS can be recognized. In Wulka, all deviations are less than 30%, whilst in Zala there are two years with remarkable errors (60% and 82%). This can be explained by analyzing the SS load-surface runoff relationships. In Wulka, there is a strong relationship (direct proportionality) between the SS load and the runoff volume, thus the model is reasonably able to estimate the observed values since R-factor of USLE was estimated from the runoff volumes. However, the relationship of SS load and runoff is more complicated in Zala where despite the generally existing direct proportionality there are remarkable exceptions with even reverse proportionality. That means in these years the R-factor can only uncertainly be estimated from the runoff volume only. This uncertainty is caused by the simple approach for the R-factor estimation, which does not take into account the impact of the rainfall intensities. Coefficient of determination (R²) of the SS-results is 0.97. For PP, the deviations are a bit higher, which is a consequence of the constant enrichment ratio applied and the cumulative computation errors (R-factor, SS transport and P enrichment). Nevertheless, there is a reasonable fit between the simulated and observed values. Deviations from the observed values are usually lower than 30% except the problematic years discussed by SS loads and some individual years with unexpected measured PP fluxes. These latter probably represent measuring inaccuracies and cause lower R² value of 0.89 for P. Thus, acceptable model performance can be achieved by calibrating a few model parameters.

4.3. Catchment scale results

From Figs. 3 and 4 it is obvious that the area-specific SS and PP event loads are higher in the Wulka catchment, although the local specific soil loss rates are lower. This phenomenon indicates significant sediment and PP retention in the Zala watershed, which was also found by Zessner et al. (2005) based on water quality data analysis during high flow events. Table 3 summarizes the calculated long-term average local emission rates, the transported fluxes (yields) entering the main channel network (taking into account field retention) and the exported fluxes (loads) out of the watershed (considering in-stream retention). About two and a half times higher average soil loss and PP emission rate were calculated for the Zala catchment (5.69 t SS ha^− 1 a^− 1 and 4.34 kg P ha^− 1 a^− 1, respectively) than that of the Wulka (2.15 t SS ha^− 1 a^− 1 and 1.89 kg P ha^− 1 a^− 1). This significant difference is more surprising if we consider that the mean slope is larger in the Wulka than in the Zala catchment. Since the meteorological factors are very similar, the difference is mainly caused by inadequate agricultural practices paired with unfavorable slope and soil conditions in the Zala watershed. Analysis of the slope distribution of the arable lands shows that the area proportion of fields at slopes higher than 12% is two times higher in the Zala catchment (15% in Zala, 7% in Wulka). These fields are responsible for the highest soil loss rates.

Table 3.

Long-term average, area-specific SS and PP fluxes of the Wulka and the Zala catchments.

Component	Unit	Wulka	Zala
Soil loss	t SS ha− 1 a− 1	2.15	5.69
Field retention	t SS ha− 1 a− 1	2.06 (95.5%)	5.61 (98.6%)
Sediment yield	t SS ha− 1 a− 1	0.10	0.08
In-stream retention	t SS ha− 1 a− 1	0.01 (11.8%)	0.02 (25.0%)
Sediment event load	t SS ha− 1 a− 1	0.09	0.06
PP emission	kg P ha− 1 a− 1	1.89	4.34
Field retention	kg P ha− 1 a− 1	1.71 (90.7%)	4.16 (95.8%)
PP yield	kg P ha− 1 a− 1	0.18	0.18
In-stream retention	kg P ha− 1 a− 1	0.02 (11.7%)	0.04 (25.0%)
PP event load	kg P ha− 1 a− 1	0.16	0.14

Similarly, high differences can be seen by the absolute field retention values, thus, the sediment yields of the two areas are close to each other. Retention is more intense in the Zala catchment. It can be explained by analyzing the land use forms of the riverside zones. They were defined as 100 m wide corridors in both perpendicular directions from the channel cells. In the Zala catchment, these corridors show a dominance of natural vegetation (55% of the zone area) and less arable land coverage (35%). In the Wulka catchment, the situation is the opposite. The higher share of natural vegetation of the riverside zones in the Zala catchment is a reasonable explanation why the area-specific retention values are differing. In relative terms, 95.5% and 98.6% of the eroded soil material is retained in the catchments of Wulka and Zala, respectively. During the model calibration process the field and in-stream retention parameters were set as similar as possible due to the strong similarity of the pilot areas. Thus, higher retention in the Zala catchment is a consequence of its catchment properties, such as the natural vegetative zones around the channel network, longer surface runoff lengths and the higher threshold value of drained cells, which defines a stream. This latter is an a priori decision of the modeler and the higher value for Zala (400 cells or 100 ha) has been justified by the visual checking in Google Maps. Nevertheless, using the same threshold value for the Zala catchment than that of the Wulka (200 cells), the model computes significantly lower field retention and higher sediment yield entering the river network. This would lead to a necessity to raise the in-stream retention parameter in Zala, which would cause remarkable in-stream retention of SS and would not fit the measured values at the upper stations. Therefore different threshold values and similar retention parameters were set which ensure reasonable fits to the measured loads. The higher threshold value of Zala indicates that the initial stretches of the tributaries are at natural conditions, not or only slightly regulated and convey a little water permanently or only the surface runoff, thus, their retention capability is higher than that of a stretch downstream having permanent flow. Because of the high sensitivity of the river threshold value on the results, it is crucial to determine the threshold value as precise as possible. However, further investigations are needed to absolutely clarify the retention nearby the watercourses and to more explicitly define stream channels in the model.

Comparing the in-stream retention values, considerable difference can be found between the catchments. In the Zala catchment, 25% of the suspended solids remain in the system with a majority of it in the small reservoirs located on the tributaries. In the Wulka catchment where no considerable reservoir exists (except one sediment detention basin near the outlet, but it seems to be less effective based on the analysis of measured water quality data up and downstream), the retention is less (11.7%). In total, only 4% (0.09 t SS ha^− 1 a^− 1) and 1% (0.06 t SS ha^− 1 a^− 1) of the total soil loss can be transported out of the Wulka and Zala catchments, respectively. Even though SS load of the Wulka catchment is one and a half times higher than that of the Zala catchment, there is almost no difference between their PP loads. For P, the retention values are lower and the exported proportion is higher (8% and 3%, respectively) due to the P enrichment in the suspended solids. Enrichment is more intense in the Zala catchment, which resulted in almost the same area-specific PP load (0.16 P kg ha^− 1 a^− 1 and 0.14 P kg ha^− 1 a^− 1).

The calculated sediment delivery ratios (SDR) are low (Wulka: 4% and Zala: 1%), but they still lie in the ranges reported by the literature. For example, a catchment area-SRD function was published by Novotny (2003) based on analysis of watersheds with various sizes. For catchments of a size between 100 km² and 1000 km², SDR values of 3%–20% are shown. SDR is decreasing with the increasing size of the drainage area. De Vente et al. (2008) evaluated 61 catchments (30 km²–13,000 km², the mean size is 1000 km²) and computed SDR ratios (with a combined RUSLE-sediment transport approach) between 0.4% and 55% (most of them are lower than 10%). Tetzlaff et al. (in press) computed an SDR range of 0.5%–78% (mean: 18%) for 450 sub-catchments of a large catchment. These approaches have similar soil erosion algorithm (USLE or its revised versions) as compared to the PhosFate model, however, they contain different sediment delivery methods (sediment transport capacity by De Vente et al. (2008), sediment delivery area concept by Tetzlaff et al. (in press), retention calculation based on residence time in PhosFate).

4.4. Spatial distributions of the emissions

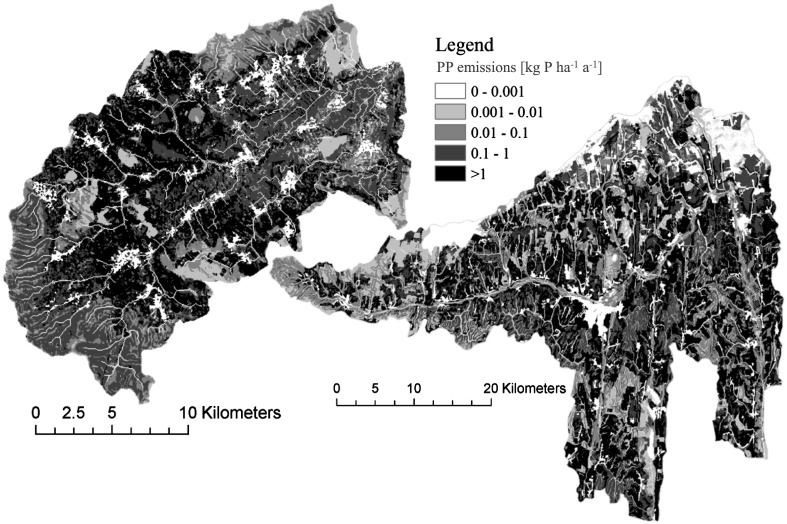
Spatial distribution of the long-term average PP emissions is demonstrated in Fig. 5, which highlights the most important source regions within the catchments. The middle part of the Wulka catchment produces the highest local emissions via soil erosion. South-western regions are mainly covered by forests, whilst agricultural fields on moderate slopes can be found in the east. In the Zala watershed, the source areas are mostly located in the middle and in the southwest. However, they are more evenly distributed within the catchment. 4.8% of the catchment area of Wulka has higher gross (locally mobilized) soil loss value than the selected threshold value of 10 tons SS per hectare and year. These source areas produce 49% of the total PP emissions within the catchment. Changing the threshold value to 2 tons SS per hectare and year (typically suggested for sensitive areas with highly erodible soils, Morgan, 2005), the proportion of the catchment area exceeding the limit is 26%. The share from the total emitted PP amount is 87%. In the Zala catchment, 13% of the total area generates higher soil loss than the limit value of 10 tons SS per hectare annually and it has a share of 85% from the catchment-wide PP emissions. In case of the lower threshold value, the area proportion is 29% and the relative contribution to the total emissions is 97%. That means, only a few percent of the catchment territory is responsible for a remarkable share of the soil loss of the catchment that is associated with the highest PP emissions as well. Only about 30% of the catchment area produces almost the total P emissions generated by soil erosion. This highly indicates how important the recognition of the source areas within the catchment is. Identification of the local hotspots has an important role in resource management planning in order to reduce nutrient losses from the soils.

Fig. 5.

Long-term average area-specific local PP emissions via soil erosion in the Wulka (on the left) and the Zala (on the right) catchments.

As it was discussed before, pollution problems cannot be described with the local emission rates only. The transport of pollutants within the catchment also plays a key role in assessing and managing water quality. Fig. 6 shows the long-term average contributions of the local cells to the river loads (source loads) or in other terms the remaining fluxes of the cell emissions passed the transmission which can be exported out of the catchment (sum of the cell values is equal to the load at the outlet). The most effective source areas are mainly located along the channel network and in the closer neighborhood of the channels. Comparing the emission and source load maps only a small proportion of the black areas (high rates) of the emission maps are shown as black on the source load maps as well. That means only that those cells are effective sources which are located in the direct vicinity of channels or are lying farther on and have sufficiently high emission rates to produce load contributions and/or the retention along the overland flow pathways is less intense.

Fig. 6.

Local contributions to the long-term average PP event river loads at the outlet (source loads) in the Wulka (on the left) and the Zala (on the right) catchments.

In the Wulka catchment, only 2.8% of the catchment area transports 75% of the total loads at the outlet (cell loads higher than 1 kg P ha^− 1 a^− 1), whilst only 12% of the territory is responsible for 96% of the transported flux (cell loads higher than 0.1 kg P ha^− 1 a^− 1). In Zala, these numbers are 2.2%–88% and 6.1%–98%. These values – in comparison to the proportion values reported by the emission rates – emphasize that recognition of the effective source areas is crucial toward an efficient watershed management. These really active source areas – together with the transfer areas – are decisive factors for water quality management to achieve good status of the water bodies.

4.5. Results of the management strategies

Management of the source areas (soil nutrient management) affected 2.5% and 11.7% of the total area of the Wulka and the Zala catchments, respectively. Since net soil loss is considered, the proportions of the areas with an erosion rate over the threshold are lower than it was before in the case of gross erosions. Source controlling based on soil loss tolerance limit resulted in a PP load reduction at the outlet of 52% and 88% in the Wulka and the Zala watersheds, respectively. That means, both management scenarios (36% and 80% PP load reduction desired) are executable in the Zala catchment via source controlling in 11.7% (17,328 ha) of the total area. In Wulka, only the higher concentration limit that needs a PP load decline of 55% can be nearly achieved via management of the erosive areas. However, it would affect a smaller agricultural area (2.5% or 948 ha) only.

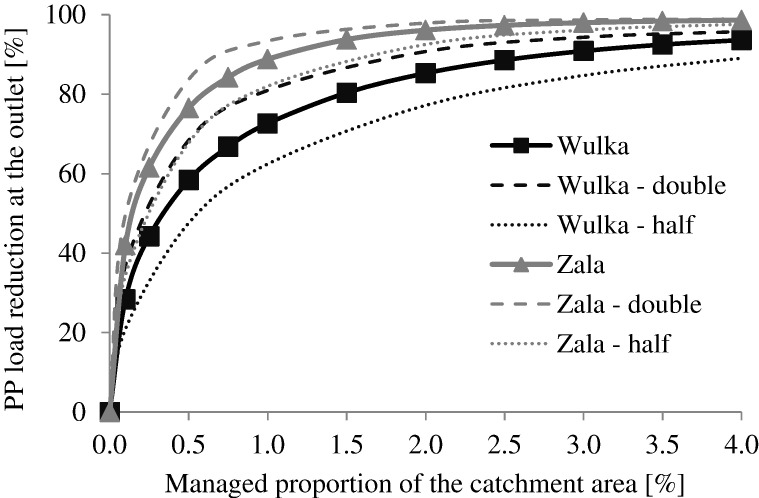
Fig. 7 shows the achievable highest PP load reduction at a specific intervention area as a result of the optimized water quality management. In managing a few, but properly selected cells, remarkable decline in PP loads can be realized. As the intervention area increases, the specific efficiency decreases since the cells with the highest gain have already been managed (the shape of the area-load reduction function is a saturation type curve). Management can be more effective in the Zala catchment, 36% reduction (scenario 1) can be already attained with management on 0.1% of the catchment area (148 ha), whilst intervening on 0.75% of the total area (1110 ha) causes a reduction higher than 80% (scenario 2). In the Wulka catchment, 0.5% of the area (186 ha) is necessary to attain 55% reduction (scenario 1) and management of 2.5% catchment area (932 ha) can produce 86% load decrease (scenario 2). Intervention applied on 3% (1119 ha, Wulka) and 1.5% (2220 ha, Zala) of the catchment area would bring a PP load decline of 90%. That means, the same high load reduction (about 90%) can be achieved at much smaller intervention area, if optimized transport and source control are applied together (e.g. 1.5% instead of 11.7% in the Zala catchment). Sensitivity of the emission calculations is presented in Fig. 7, where the dashed lines correspond to load reduction curves if the original emission values of the entire catchments are doubled and halved. Load reduction efficiencies are minimally changing as consequences of these modifications, the maximum deviation is 10%. That means, despite the remarkable change of the emissions, the achievable flux reductions are slightly varying, hence the area demand of the interventions and the designation of the hot-spots are less sensitive to the precision of the emission calculations (if the distribution of the emissions are not changing).

Fig. 7.

Achievable reductions of PP event river loads at the outlet at different intervention areas in the Wulka and the Zala catchments (dashed lines represent values for halved and doubled emissions).

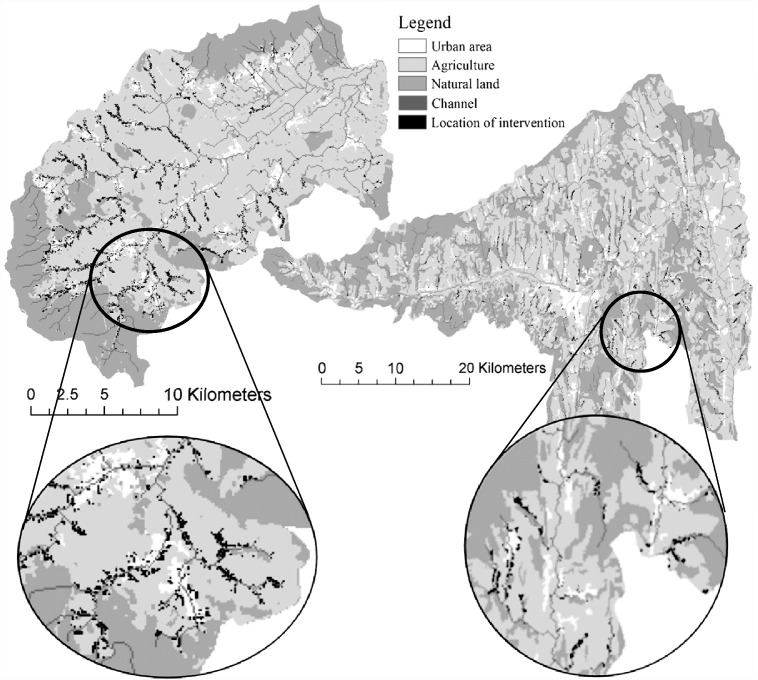
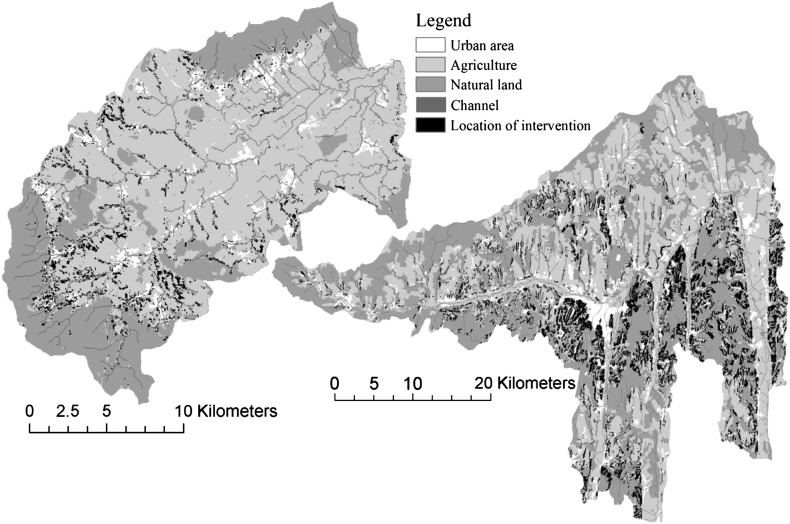
Fig. 8. presents the location of the necessary interventions with respect to water quality targets (according to scenario 2). Hot-spots lie most frequently along the channels (buffer zones) passing the erosive regions of the catchments and additionally some highly erosive slopes are also intervened (source control). Almost all of the designated cells are arable lands or orchards. Since their share on the total area is about 50% in both areas, approx. the double values of the catchment proportions are valid for the cropland.

Fig. 8.

Suggested areas (indicated by black color on the original land use maps) for intervention in order to fulfill water quality management (pollution control) goal according to scenario 2 in the Wulka (on the left) and the Zala (on the right) catchments.

Combinative management was possible in the Wulka watershed only, because in the Zala catchment soil nutrient management accomplishes the water quality targets as well (on 11.7% of the total area). However, in the Wulka catchment, the lower water quality criteria (scenario 2) cannot be met via source controlling alone. Applying source controlling (soil nutrient management) at 2.5% of the total area (as it was evaluated before) and executing an additional optimized management of the effective hot-spots, the stricter water quality limits can also be fulfilled. This resulted in an additional 1.5% of the catchment area that should be managed. Thus, in total, intervention on 4% of the catchment area of the Wulka catchment can realize the water quality goal as well. Fig. 9. shows the recommended areas for an intervention (Wulka: 4% or 1492 ha, Zala: 11.7% or 17,328 ha), which can ensure the realization of both management aspects. Relating the area demand to the arable lands, 7.4% (Wulka) and 23.9% (Zala) are concerned.

Fig. 9.

Suggested areas (indicated by black color on the original land use maps) for intervention in order to fulfill both water quality and soil phosphorus management goals in the Wulka (on the left) and the Zala (on the right) catchments.

Table 4 summarizes the main results of the management strategies. Soil nutrient management (over 10 tons SS per hectare and year net erosion rate) is quite effective regarding water quality management as well. However, it would need high area demand where the original land use should be managed to reduce soil (and phosphorus) losses. If soil nutrient losses are generally not concerned and water quality improvement is the main management goal, impressive river load reductions can be achieved with relatively few intervention cells. However, in this case, higher amount of the phosphorus stock of the topsoil is mobilized and transported from the fields. The combinative approach can fulfill both management purposes with reasonable area demand.

Table 4.

Area demand and event load reductions of the Wulka and the Zala catchments according to different management strategies.

Management	Component	Unit	Wulka	Zala
Soil nutrient management	Area	ha	948	17,328
	Load reduction	%	52	88
Water quality management	Area (scen. 1)	ha	186	148
	Load reduction (scen. 1)	%	55	36
	Area (scen. 2)	ha	932	1110
	Load reduction (scen. 2)	%	86	80
Combined management	Area (scen. 2)	ha	1492	Not necessary
	Load reduction (scen. 2)	%	86	Not necessary

Other studies focus also on the hot-spot identification. Drewry et al. (2011) evaluated the risk of P-losses of a catchment using a P Index approach. About 33% of total area is considered to be at moderate risk, whilst only 0.03% of the catchment was characterized as an area with high risk. Bechmann et al. (2007) tested a P-Index model at a sub-catchment scale and they found relatively acceptable correlation between the P-indices and the measured river concentrations of the-sub-catchments. Using a catchment-scale sediment connectivity approach, Fryirs et al. (2007) concluded that the proportion of the effective catchment area (with a potential to contribute to sediment river loads) on the total area is between 3% and 73% for the different pilot sub-catchments, and the proportion depends on the spatial distribution of the buffers and barriers within the sub-catchments.

The novelty of the PhosFate model in comparison to the other approaches, which attempt to identify hot-spots or risk areas, is that it contains the advantages of both the index-based and connectivity procedures. Direct modeling of the emissions (source factors) and the explicit routing of the fluxes (transport factors and connectivity) with simple distributed parameter approach allow one to find the effective areas within the catchment. In addition, the model produces comparable results (loads) to the observations and the impact of the improved management practices on the critical areas can directly be related to water quality improvements. Finally, the optimization procedure ranks the hot-spot cells according to their gain if an intervention occurs, which enables us to select the most effective intervention areas within the catchment and minimize the intervention area. Lumped or semi-distributed parameter models are widely used for water quality assessments as well (e.g. SWAT application by White et al., 2010), but they cannot show the possible location of the hot-spots within the sub-catchment or hydrological response units.

Theoretically, the selected critical areas (either source or transmission areas) could be verified by some additional monitoring investigations at hillslope or sub-regional scale (e.g. sediment yield measurements at hillslope scale or water quality sampling of the upstream tributaries). Temporal and financial limitations of this study did not allow us to execute detailed measuring programs. However, despite the limitations of the applied soil loss model (USLE), its improved or revised forms are widely used as long-term or annual soil loss estimator and engineering tool for evaluation management actions to control erosion, especially at regional or hillslope scale (Nearing et al., 2001; Novotny, 2003).

4.6. Uncertainties of the results

Model results are likely sensitive to the accuracy of the input data. Data inaccuracies and low resolution of some of the input data (e.g. missing spatial objects, aggregated soil or land use classes with average parameter values or estimated management practices) as well as uncertainties in the model structure can lead to uncertainties in runoff pathways, emission rates and consequently, retention parameter values. These can result in uncertain load reduction efficiencies and hot-spot identification. Also, the model does not account for the time-dependency of the emissions and the transport. In addition, the scale problem may confound the results as many of the processes occur at the sub-grid scale (e.g. rill flow hydraulics, rill detachment, sediment resuspension). Representation of the sub-grid variability by either assuming zero variability (e.g. soil properties or topography) or applying effective parameter values (e.g. roughness or crop management factors) is also uncertain. Resolution of the data is probably not the main source of the inaccuracies (except some spatial data at low resolution). Amorea et al. (2004) applied the USLE and the WEPP models for different catchments at hillslope scale with different subdivision of the hillslopes. They concluded that a finer subdivision, even though it approximates better the field scale conditions, is not necessarily needed for a better model performance.

Because of the presented uncertainties, many of which are local, we consider the present modeling study as a screening procedure at regional (catchment) scale. The results of the optimization can help identify the most important regions within a catchment in respect to water quality management. These are possible hot-spots or critical areas of the catchment, where practical management activities could be of interest. However, the results do not specify the precise location and kind of the necessary management practices within the screened critical areas. For the possible hot-spots identified by the procedure it may be useful to conduct more detailed, process-based modeling supported by field experiments. Investigations at local scale can ascertain what practical management actions are needed at a particular location. Nevertheless, screening procedures can effectively support national or basin scale management programs, which can concern many smaller water bodies with limited financial funds, by determining priority areas for the management actions.

5. Conclusions

The enhanced version of the catchment-scale P emission model PhosFate was successfully applied in two hilly medium-sized catchments with significant agricultural coverage. Even though the model does not specifically address the dynamics of the mass fluxes, it is able to reasonably simulate the annual SS and PP loads. Cross-validation for several upstream gauges was also acceptably executed. Besides river load modeling, a new optimization algorithm is presented. It attempts to identify the most effective source and transmission areas, which probably have the highest load reduction efficiency if an intervention is implemented.

The main finding is that despite the high proportion of emission source areas only a few percent of the total area is responsible for the majority of the river loads. This small proportion can be further reduced if the most important transfer areas are revealed as well. The area demand of the interventions can be minimized by managing those parts with the strongest possibility to reduce river loads (either source or transfer areas). That means if intervention measures are indeed concentrated on the highly contributive areas, a highly effective management can be achieved without having to transform the overall land use practice on most of the catchments. Introducing BMPs on a carefully selected few percent of the total area can significantly cut the total amount of emissions and also the transported material fluxes. Combining source controlling with the optimization algorithm, goals of both soil nutrient and water quality management can be simultaneously fulfilled at a reasonable proportion of the catchment area.

The presented modeling study is considered as a screening procedure at regional (catchment) scale. The model is able to identify the possible hot-spots where improved management activities may be of interest. In a next step it may be beneficial to perform more detailed analyses (field scale modeling and field experiments) to determine what management options are necessary at local scale.

Appendix A. Methodology of the PhosFate model

A.1. Erosion modeling

Gross soil loss is estimated using an adapted version of the USLE approach:

$$S{L}_i=R_i\cdot K_i\cdot L{S}_i\cdot C{M}_i\cdot S{P}_i$$ (A.1)

where SL_i is the annual gross soil loss rate of cell i [t SS ha^− 1 a^− 1], R_i is the annual rainfall energy factor of cell i [t SS ha^− 1 a^− 1], K_i is the soil erodibility factor of cell i [−], LS_i is the topographic factor (slope and slope-length factors together) of cell i [−], CM_i is the crop management factor of cell i [−], SP_i is the erosion protection factor of cell i [−] and i is the cell index [−].

Parameters of USLE can be derived from meteorological data and various digital maps of catchment properties (elevation, soil, land use). The parameter values are set according to the literature (Novotny, 2003; Randle et al., 2006). The rainfall energy factor (R-factor) is related to the rainfall distribution within the simulation period. The slope factor is determined from the local cell slope values. Slope-length factor is computed with an assumed constant slope length (cell size). The soil erodibility factor is a function of the physical topsoil type, the humus content of the topsoil and the slope. The crop management factors (CM-factor) are assigned to the land use classes. Finally, the erosion protection factor is related to the applied management practice and the slope.

A.2. PP emission modeling

PP content of the topsoil consists of three different pools in the model:

$$C_{PPtot,i}=C_{PP,i}+C_{PP,org,i}+C_{PP,sta,i}$$ (A.2)

where C_PPtot,i is the total PP content of the topsoil at cell i [μg P g^− 1], C_PP,i is the active inorganic PP concentration of the topsoil at cell i [μg P g^− 1], C_PP,org,i is the organic PP concentration of the topsoil (mainly in the humus layer) at cell i [μg P g^− 1] and C_PP,sta,i is the stable inorganic PP concentration of the topsoil at cell i [μg P g^− 1].

Inactive inorganic phase is related to the clay content of the soil (Behrendt et al., 1999). Organic phase is calculated from the humus content assuming fixed organic material–organic carbon and organic carbon–organic P ratios (Neitsch et al., 2002). Active inorganic pool is determined from the long-term agricultural P surplus and the cultivated soil depth. Agricultural surplus is a direct modeling input, it has to be calculated using statistical data on the amounts of applied fertilizer and manure, added crop residue and waste water and the harvested crops over the last 50 years. Atmospheric deposition and humus mineralization can also be taken into account. P surplus is then divided to dissolved and particulate phases using a partition function. Langmuir-type adsorption equation is used for the partitioning:

$$\frac{SU{R}_{P,i}\cdot {10}^2}{z_{\mathit{soil}}}=C_{PP,i}\cdot {\rho }_S\cdot \left(1,-,{\Theta }_{s,i}\right)+C_{DP,i}\cdot {\Theta }_{S,i}=\frac{Q_{0,i}\cdot b_i\cdot C_{DP,i}}{1+b_i\cdot C_{DP,i}}\cdot {\rho }_S\cdot \left(1,-,{\Theta }_{s,i}\right)+C_{DP,i}\cdot {\Theta }_{S,i}$$ (A.3)

where SUR_P,i is the long-term accumulated agricultural P surplus of the topsoil at cell i [kg P ha^− 1], z_soil is the depth of the cultivated soil [0.3 m], ρ_S is the soil particle density [2700 kg m^− 3], C_DP,i is the dissolved P concentration of the topsoil porewater at cell i [μg P l^− 1], Θ_S,i is the porosity of the topsoil layer at cell i [m³ m^− 3], Q_0,i is the adsorption maxima at cell i [μg P g^− 1] and b_i is the adsorption energy coefficient at cell i [l μg^− 1].

Parameters of the isotherm (adsorption maxima and energy coefficient) are related to soil features (clay and humus content, pH value) according to Novotny (2003). PP emissions via soil erosion of the elementary cells are simply calculated as a product of the soil loss, the cell area and the PP concentration of the topsoil:

$$E_{ER,i}=S{L}_i\cdot A_{\mathit{cell}}\cdot C_{PPtot,i}\cdot {10}^{-3}$$ (A.4)

where E_ER,i is the annual PP emission via soil erosion at cell i [kg P a^− 1] and A_cell is the cell area [ha].

A.3. Sediment transport modeling

SS transport is computed by connecting the individual cells to each other. Transport modeling of the local mass fluxes within the catchment is cumulative according to the flow tree. Flow tree is determined from the slope map using the classic D8 routing scheme (O'Callaghan and Mark, 1984). It conveys the water flow from each cell always to only one of the eight neighborings, to which the given cell has the highest elevation gradient (slope). Every cell is characterized as either field or channel cell based on a threshold value of upstream located cells which is minimally necessary to form a channel. The channel cells have dual functions, they route flow and mass fluxes downstream as parts of a watercourse (channel function) and also convey loads coming from their neighboring field cells through riparian zone (field function). The riparian zones are characterized by a hypothetical land use (grassed soil) in the vicinity of the channel. Their local emissions are neglected, however, they have a limited retention capability with respect to the passing flux. Mass balance equation is solved at each cell. The outflowing flux is the sum of the inflowing flux, the gross soil loss and the sediment retention via settling (negative value):

$$OU{T}_{SS,i}=I{N}_{SS,i}+S{L}_i\cdot A_{\mathit{cell}}-RE{T}_{SS,i}$$ (A.5)

where OUT_SS,i is the outflowing sediment load of cell i [t SS a^− 1], IN_SS,i is the inflowing sediment load of cell i [t SS a^− 1] and RET_SS,i is the sediment deposition at cell i [t SS a^− 1].

Sediment deposition is computed from the inflowing load and local soil loss values with an exponential function of the cell residence time:

$$RE{T}_{SS,i}=I{N}_{SS,i}\cdot \left[1-exp\left(-k_{\mathit{SS}}\cdot t_{cell,i}^{*}\right)\right]+S{L}_i\cdot A_{\mathit{cell}}\cdot \left[1-exp\left(-k_{\mathit{SS}}\cdot t_{cell,i}^{*}\cdot 0.5\right)\right]$$ (A.6)

where k_SS is the sediment deposition rate [s^− 1], t^⁎_cell,i is the residence time of flow at cell i [s].

The passing flux is experiencing full-scale retention during its travel through the cell. Residence time depends on the average flow velocity and the flow path length. Flow velocity is calculated for both overland and channel flow with the Manning's equation (Liu and De Smedt, 2004):

$$v=\frac{1}{n_i}\cdot H{R}_i^{\frac{2}{3}}\cdot S_i^{\frac{1}{2}}$$ (A.7)

where n_i is the Manning's roughness coefficient at cell i [m^− 1/3 s], HR_i is the average hydraulic radius at cell i [m] and S_i the slope at cell i [m/m].

The average hydraulic radius is estimated with a power function of the upstream catchment area of the given cell (Molnar and Ramirez, 1998; Liu and De Smedt, 2004):

$$H{R}_i=a_P\cdot A_{drain,i}^{b_P}$$ (A.8)

where A_drain,i is the total drained area upstream of the cell i [km²] and a_P, b_P model parameters related to the discharge frequency [−].

The Manning's roughness parameter is related to the land use classes (Fread, 1993; Liu and De Smedt, 2004). For each cell two flow path lengths are considered: one for the inflowing fluxes and one for the local emissions. Cell flow path length is identical to the cell size for the inflowing SS fluxes, whilst the half of the cell size is set for the local emissions (hence the factor of 0.5 in the second part of Eq. (A.6)). In channel cells, half of the cell size is set as terrestrial flow path length (width of the riparian zone) for the inflowing fluxes assuming that the channel is located on the cell centerline and it covers negligible proportion of the cell size (including bank slopes).

Different deposition parameters are used for the terrestrial and in-stream transport, whereas the latter represents net deposition rate. Thus, the sediment load can be calibrated with two adjustable parameters (field and in-stream retention parameters), which should be adapted to local conditions. Reservoirs are considered for the channel transport as well, whereas reservoir residence time is calculated from the inflowing discharge and the operation volume. Discharge is calculated by the hydrological sub-model of PhosFate that is an adapted version of the long-term water balance model WetSpa (Batelaan and Woldeamlak, 2004; Honti et al., 2010). SS fluxes via resuspension from the bottom sediment are neglected. They are indirectly included into the net channel deposition parameter.

A.4. PP transport modeling

The PP transport is described by equations similar to Eqs. (A.5) and (A.6) used for SS substituting the gross soil loss with the PP emission. Retention parameters applied for the SS transport are utilized without any change. The single but remarkable difference is the introduction of the enrichment ratio. The mass balance for PP is:

$$OU{T}_{PP,i}=\left(I{N}_{PP,i}+E_{ER,i}\cdot c{}_{enr,i}-RE{T}_{PP,i}\right)\cdot c_{enr,adj}$$ (A.9)

where OUT_PP,i is the outflowing PP load of cell i [kg P a^− 1], IN_PP,i is the inflowing PP load of cell i [kg P a^− 1], c_enr,i is the local enrichment ratio at cell i [−], RET_PP,i is the PP deposition at cell i [kg P a^− 1] and c_enr,adj is an adjustment factor [−].

The PP retention is the following:

$$RE{T}_{PP,i}=I{N}_{PP,i}\cdot \left[1-exp\left(-k_{\mathit{SS}}\cdot t_{cell,i}^{*}\right)\right]+E_{ER,i}\cdot c_{enr,i}\cdot \left[1-exp\left(-k_{\mathit{SS}}\cdot t_{cell,i}^{*}\cdot 0.5\right)\right]\text{.}$$ (A.10)

The enrichment parameter is the ratio of the PP concentration of the suspended sediment to that of the parent soil. This enrichment is a consequence of the selective sediment transport, i.e. the fine particles have higher proportion in the suspended sediment than that of the coarse ones. Since fine particles usually have high adsorption capacity (specific surface), the selective transport is accompanied with an enrichment of the P. Values of the enrichment ratio are related to the clay content of the soil and calculated with an exponential function for each cell (Novotny, 2003). Besides this, a general adjustment factor can be set to adjust the original values. When PP transport is calculated, local PP emissions are multiplied with the location dependent cell values and the net outflowing flux is additionally multiplied with the constant adjustment factor. Since in the recent version, there is no direct transformation between the dissolved and particulate phases after separating them in the topsoil, these processes are indirectly aggregated into the enrichment parameter as well.