Parametric modulation of an atomic magnetometer

Abstract

The authors report on a rubidium atomic magnetometer designed for use in a shielded environment. Operating in the spin-exchange relaxation-free regime, the magnetometer utilizes parametric modulation of the z-magnetic field to suppress noise associated with airflow through the oven and to simultaneously detect x- and y-field components, using a single probe beam, with minimal loss of sensitivity and bandwidth. A white noise level of 60 fT/(Hz)^1/2 was achieved.

Measurement of extremely weak magnetic fields is essential in several important areas of physics and medicine, such as fundamental symmetry tests^1,2 and magnetoencephalography.³ Due to their high sensitivity, superconducting quantum interference devices (SQUIDs) traditionally have been the detectors of choice; however, recent advances in atomic magnetometers^4,5 have made them an attractive alternative due to the lack of helium cryogenics and the potential for cost reduction and increased sensitivity. Among the atomic magnetometers developed to date, the spin-exchange relaxation-free (SERF) magnetometer of Kominis et al. has achieved the highest magnetic field sensitivity, rivaling that of SQUIDs.⁵ Using a longitudinally spin-polarized alkali vapor, the SERF magnetometer detects the transverse spin polarization induced by weak magnetic fields. For highest sensitivity, the SERF magnetometer requires careful nulling of external magnetic fields, which can be achieved with magnetic shielding;⁵ however, operation in an unshielded environment has also been reported.⁶

In this letter, we describe operation of a SERF magnetometer in a commercial two-layer high-magnetic permeability shielded room (MSR) (Lindgren RF Enclosures, IL) designed for biomagnetism applications. Our magnetometer utilizes parametric modulation that suppresses sources of nonmagnetic technical noise and allows for multicomponent field measurements using a single probe laser. A sensitivity of 60 fT/(Hz)^1/2 was achieved, probably limited by pump laser intensity fluctuations.

Our Rb SERF magnetometer is similar to the K magnetometer of Seltzer and Romalis:⁶ a circularly polarized laser beam (795 nm, 15 W, 4 nm full width at half maximum) optically pumps the atoms along the z direction, while an unstabilized probe laser (782.9 nm) traveling along the x direction provides a Faraday rotation detection signal⁷ after passing sequentially through the Rb cell, a 780±2 nm bandpass filter, a half wave plate, a beam splitter, and two subtraction photodiodes. The cell (r=2.5 cm, t=2.2 cm) contains 1 atm of ³He and 6 Torr of N₂ in addition to a small amount of Rb metal. It was heated with flowing hot air to a temperature as high as 188 °C inside a single-layer oven. To maintain the magnetometer in the SERF regime we constructed a three-dimensional Helmholtz coil system to null the 0.5 mG residual field inside the MSR.

For a pump beam oriented along the z direction and a probe laser beam oriented along the x direction, a well-nulled SERF magnetometer detects the x component of the electron spin S according to

$$S_x=S_0{\mathrm{\Omega }}_y/\mathrm{\Gamma }\prime ,$$ (1)

where Ω=g_sμ_BB/ℏ is the Larmor precession rate about the magnetic field B, R is the optical pumping rate, Γ is the spin-relaxation rate, Γ′ = R+Γ, and S₀=R/2Γ′ is the z component of the spin polarization produced by optical pumping. We refer to this unmodulated operation of the SERF as the “dc mode.”

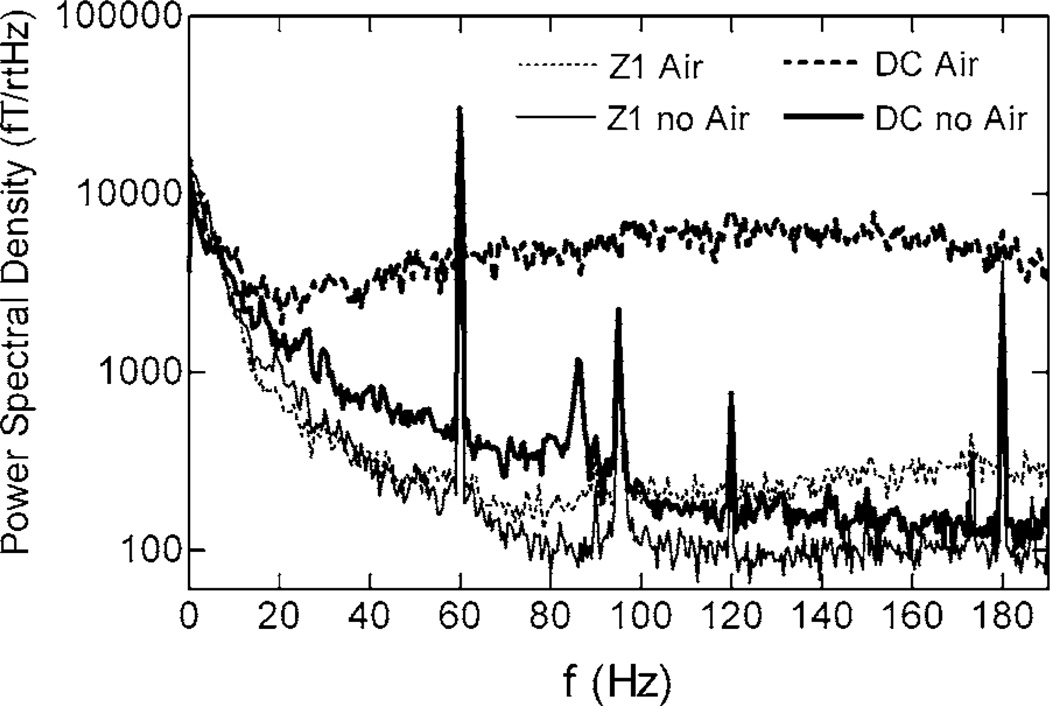
Ideally, the noise floor for the magnetometer should be set by the residual field fluctuations in the MSR. We found, however, that the noise performance was degraded by fluctuating index gradients in the flowing hot air—as was verified by momentarily turning off the airflow—that produced additional noise due to the motion of the probe laser on the photodiodes. To overcome this problem, we applied a large, oscillating magnetic field at several kilohertz along the z direction and used phase-sensitive detection to extract the signal of interest, based on the fact that index fluctuations at such a high frequency are negligible. As shown in Fig. 1, this operating mode, which we refer to as “z mode” mode, suppressed air noise greatly.

FIG. 1.

Elevated magnetic field spectral noise density due to air noise in dc mode and its suppression in Z1 mode.

The z mode works by forcing transverse spin components to oscillate at a high frequency due to precession about the oscillating longitudinal magnetic field, as illustrated in the inset of Fig. 2. Defining Ω=(Ω_x(t), Ω_y(t), Ω₀ cos(ω_zt)), S₊ = S_x + iS_y, and Ω₊=Ω_x+iΩ_y, then in the spin-temperature limit the transverse spin obeys (1+ε)dS₊/dt=−S₊[Γ′−iΩ₀ cos(ω_zt)]−iS_zΩ₊, where 1 + ε is the “slowing-down” factor that accounts for angular momentum storage in the Rb nucleus.⁸ The z component of spin produced by optical pumping is much larger than any magnetic-field-induced changes, so we approximate S_z ≈ S₀ = R/(2Γ′). For large Ω₀ the strongest torque on the transverse spin is due to the oscillating field, so it is convenient to make the ansatz S₊(t) = A₊(t)e^iϕ(t), where A₊(t) is a slowly varying amplitude and ϕ(t)=Ω₀ sin(ω_zt)/[(1 + ε)ω_z]. The above equation then becomes

$$(1+\epsilon )\frac{{\mathit{\text{dA}}}_{+}}{\mathit{\text{dt}}}=-A_{+}\mathrm{\Gamma }\prime -i{\mathrm{\Omega }}_{+}{S}_0{e}^{-i\varphi (t)}\approx -A_{+}\mathrm{\Gamma }\prime -i{\mathrm{\Omega }}_{+}{S}_0{J}_0(u).$$ (2)

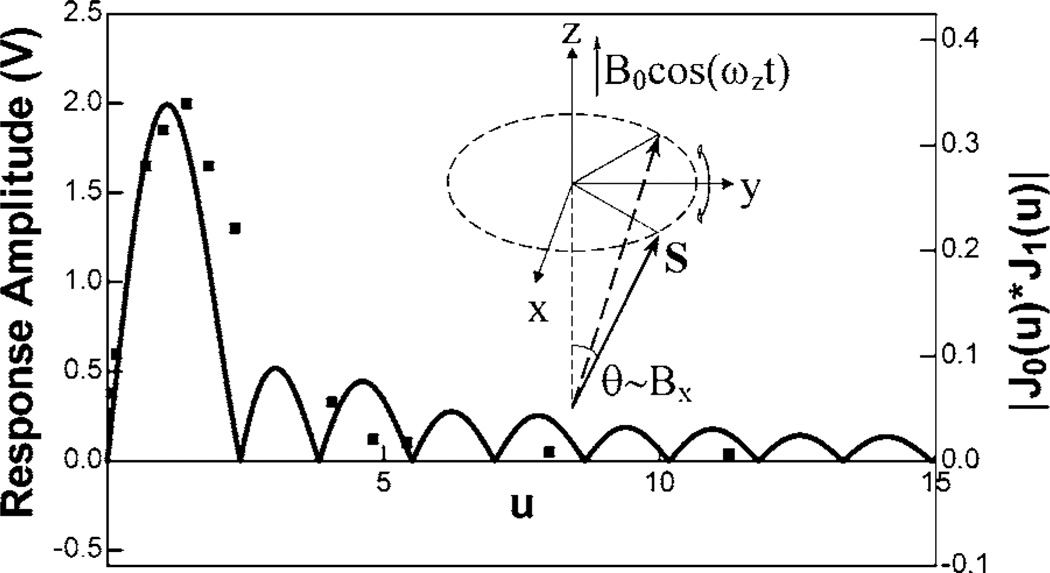
FIG. 2.

Measured Z1-mode sensitivity as a function of normalized modulation field amplitude u=Ω₀/[(1+ε)ω_z], showing comparison with the approximate theoretical response function [Eq. (3)]. The inset depicts the spin dynamics for a z-mode magnetometer. An applied magnetic signal, B_x, rotates the spin polarization into the y-z plane. The oscillating z-field (z-modulation) B₀ causes the spin to oscillate along an arc. Maximum sensitivity to B_x is achieved by adjusting B₀ to make the arc approximately semicircular. Notice that the x polarization oscillates at frequency ω_z and the y polarization oscillates at 2ω_z.

Since ϕ(t) is oscillating very rapidly on the time scale of A₊, we have replaced the exponential by its average value e^−iϕ(t) → J₀(u), where J_m(u) is the Bessel function of order m of the first kind whose argument is u=Ω₀/[(1 + ε)ω_z]. Since Eq. (2) is the same, up to the factor J₀, as the dc-mode SERF, it follows that the z mode retains the full SERF bandwidth. For a slowly changing Ω₊, the part of S₊ oscillating at ω_z has a real part

$$S_x({\omega }_z)\approx \frac{{\mathrm{\Omega }}_x{S}_z}{\mathrm{\Gamma }\prime }2J_0(u)J_1(u)\text{sin}({\omega }_{z}t).$$ (3)

Comparison to Eq. (1) shows that the z-mode magnetometer has nearly the same sensitivity as the dc mode when the modulation field strength is optimized to maximize J₀(u)J₁(u).

In addition to noise suppression, the z-mode magnetometer operating at high modulation frequency (ω_z ⪢ Γ′/(1 + ε)) can simultaneously detect two orthogonal magnetic field components: the portion of S₊ that oscillates at 2ω_z has a real part

$$S_x(2{\omega }_z)\approx \frac{{\mathrm{\Omega }}_y{S}_z}{\mathrm{\Gamma }\prime }2J_0(u)J_2(u)\text{cos}(2{\omega }_{z}t).$$ (4)

Thus the first harmonic signal (Z1-mode signal) is proportional to B_x and the second harmonic signal (Z2-mode signal) is proportional to B_y. Again, the full magnetometer bandwidth is maintained.

This type of longitudinal parametric modulation has not been used before in magnetometry. It has the desirable feature that in the absence of low-frequency transverse fields, the modulation field produces no signal and does not affect the optical pumping process. In contrast, conventional transverse parametric modulation^9,10 introduces large even harmonic signals, which must be isolated from the odd harmonic signals of interest. Similarly, resonance magnetometers⁴ require stable rf and bias magnetic fields. The longitudinal parametric oscillation method is background-free and so the stability constraints on the oscillating fields and phase-sensitive detectors are greatly reduced. It also reduces low-frequency probe noise, thereby reducing the need for probe polarization modulation.

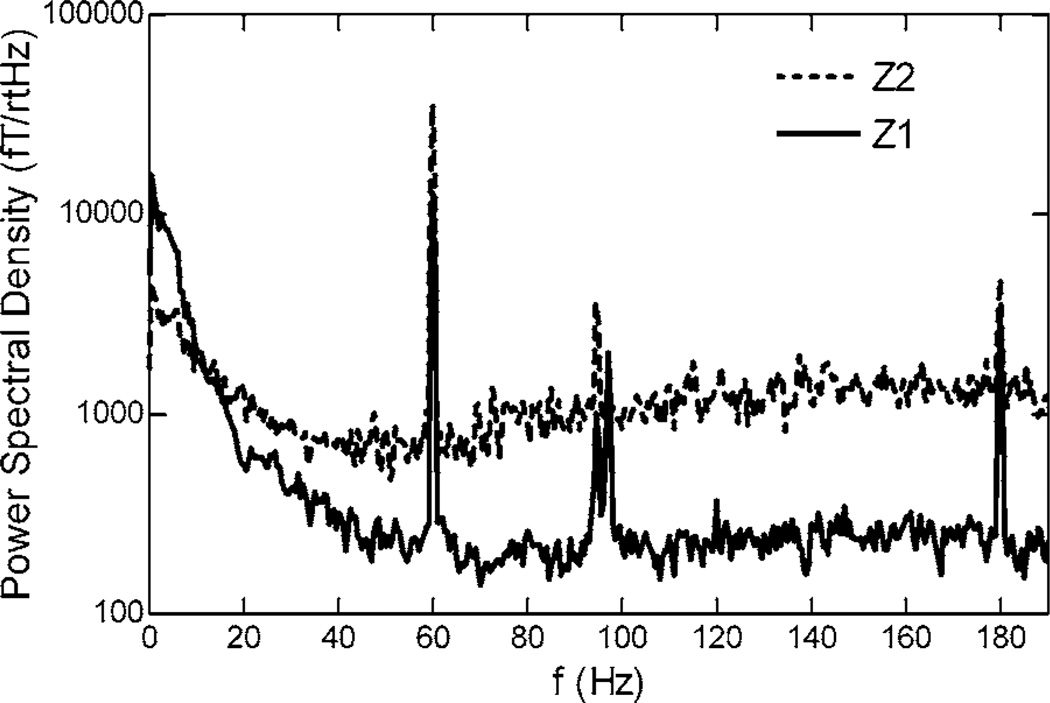
To illustrate the properties of the z-mode SERF magnetometer, we measured the relative sensitivity of the Z1 mode as a function of modulation field strength and simultaneously measured two components of the magnetic field. The results (Fig. 2) show the expected dependence on field strength except at high fields where the SERF assumption begins to break down and neglected higher order Bessel terms should also be included. Figure 3 shows the power spectra of simultaneous detection of two magnetic components. There was a modest cross-talk between the two channels; we obtained 9.3% leakage into B_y when applying a B_x field and an 8.5% leakage into B_x when applying a B_y field.

FIG. 3.

Magnetic field spectral density in the nonoptimized Z1 mode and Z2 mode for simultaneous measurement of the residual B_x and B_y magnetic fields inside our MSR. The modulation field has a frequency of 1553 Hz and a peak-to-peak amplitude of 6.5 mG.

Seltzer and Romalis⁶ previously demonstrated a multicomponent SERF magnetometer using low-frequency, low-amplitude modulation; however, the requirement of quasi-steady state operation limited the bandwidth. In contrast, the z-mode SERF described here retains the full SERF bandwidth.

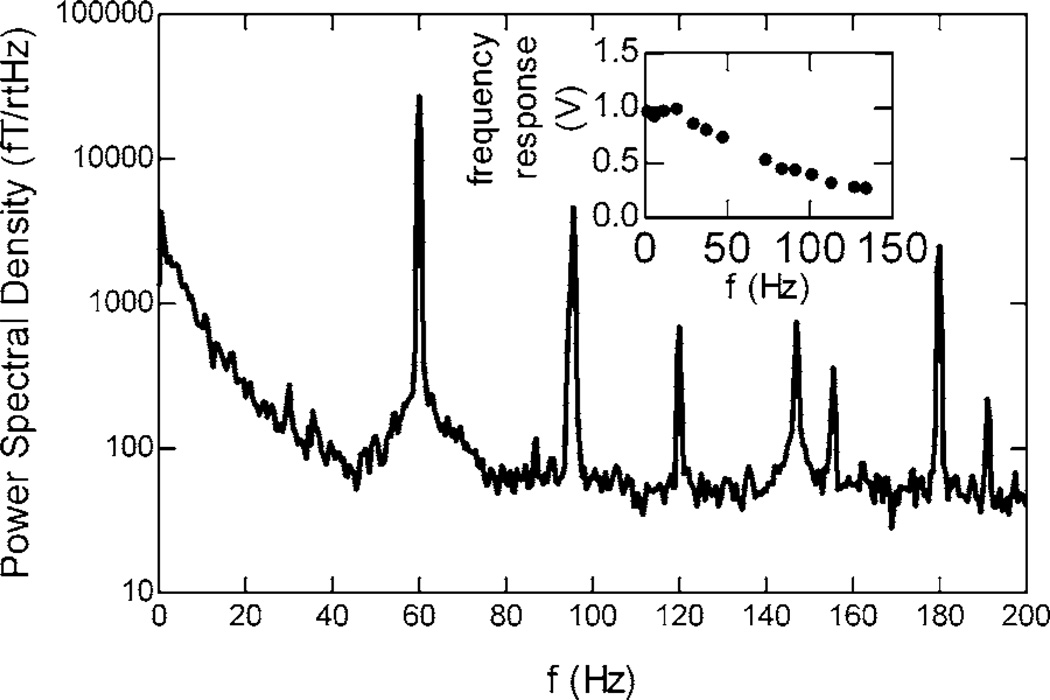
With further optimization of the pump and probe laser (changing to a stabilized laser, 1.7 nm detuned from D2 line, 0.84 mW) we were able to achieve a bandwidth of 31 Hz and a white noise level of 60 fT/(Hz)^1/2 in Z1 mode, only about a factor of 2 higher than the ambient noise in our MSR (see Fig. 4).

FIG. 4.

Magnetic field spectral density in Z1 mode after optimization of the probe beam. The inset shows the frequency response.

While the SERF sensitivity at low frequencies is maximized by using a weakly relaxing atom such as K, the sensitivity-bandwidth product is roughly independent of the spin-relaxation rate and, therefore, the species. The higher bandwidth of a Rb SERF is attractive for biomagnetism applications.

In conclusion, we demonstrated a SERF magnetometer detection scheme that utilizes longitudinal high-frequency magnetic field modulation. Not only does this method suppress sources of nonmagnetic noise but it also enables simultaneous detection of two orthogonal magnetic components with a single probe beam without sacrificing bandwidth. A bandwidth of 31 Hz and a white noise level of 60 fT/(Hz)^1/2 were achieved when operating inside our MSR.