Collective Dynamics of Elastically Coupled Myosin V Motors

Background: Collective myosin Va functions are important to various transport processes in eukaryotes.

Results: Strain coupling between myosins affects multiple motors velocities and run lengths.

Conclusion: The large step size and small stall force of myosin Va yields a dependence of multiple myosin behaviors on the structural and mechanical properties of cargos.

Significance: The properties of myosin V motors lead to unique cooperative behaviors compared with other motor types.

Abstract

Characterization of the collective behaviors of different classes of processive motor proteins has become increasingly important to understand various intracellular trafficking and transport processes. This work examines the dynamics of structurally-defined motor complexes containing two myosin Va (myoVa) motors that are linked together via a molecular scaffold formed from a single duplex of DNA. Dynamic changes in the filament-bound configuration of these complexes due to motor binding, stepping, and detachment were monitored by tracking the positions of different color quantum dots that report the position of one head of each myoVa motor on actin. As in studies of multiple kinesins, the run lengths produced by two myosins are only slightly larger than those of single motor molecules. This suggests that internal strain within the complexes, due to asynchronous motor stepping and the resultant stretching of motor linkages, yields net negative cooperative behaviors. In contrast to multiple kinesins, multiple myosin complexes move with appreciably lower velocities than a single-myosin molecule. Although similar trends are predicted by a discrete state stochastic model of collective motor dynamics, these analyses also suggest that multiple myosin velocities and run lengths depend on both the compliance and the effective size of their cargo. Moreover, it is proposed that this unique collective behavior occurs because the large step size and relatively small stalling force of myoVa leads to a high sensitivity of motor stepping rates to strain.

Introduction

The ATP-dependent transport of vesicles, organelles, and other cellular commodities by cytoskeletal motor proteins is central to a variety of mechanisms that regulate the internal organization of eukaryotic cells. These processes influence how subcellular materials are imported and exported, delivered to and from different intracellular compartments, and ultimately are distributed throughout the cytoplasm. This key role in eukaryotic cell physiology has motivated numerous biochemical and single-molecule studies aimed at understanding the fundamental properties of individual motor proteins (1–6). However, the transport of intracellular cargos is most commonly driven by teams of motor proteins composed of multiple copies of the same motor that share the responsibility of cargo transport and even mixtures of different motor types that compete to drive cargo motion. In the latter case, the different motor teams on the same cargo may step at different rates (7), in opposite directions (8–11), or along different types of cytoskeletal filaments. Collective motor functions are therefore believed to influence cargo velocities and run lengths, their net directionality as well as how they switch between microtubule- and actin-dependent transport modes. Nevertheless, despite increased attention to these problems, many aspects of multiple-motor dynamics remain poorly characterized.

Studies of collective motor functions have been advanced significantly by the recent development of biosynthetic techniques that allow collections of motors to be organized on a common scaffold or cargo (12–16). These methods can facilitate much more detailed and reliable analyses of multiple motor behaviors because they provide precise control over the number of motors on a cargo, their structural arrangement, as well as the elastic properties of the linkages that connect the motors together. Complexes containing two-kinesin motors have also been self-assembled using engineered DNA-protein conjugates and a single DNA duplex as a molecular scaffold (13). In vitro assays of their transport along microtubules in the absence of an applied load have shown that elastically coupled kinesins step asynchronously but move with near-identical average velocities compared with single kinesin motors. More importantly, even though these complexes were designed intentionally to be mechanically compliant, two-kinesin run lengths were only slightly longer than those of a single kinesin molecule, and much less than model predictions that assume the motors do not interact with one another during cargo transport (17). This comparison therefore clearly shows that interactions between kinesins can have a significant impact on their collective behaviors.

The weak dependence of multiple kinesin run lengths on motor number can be explained by a discrete state stochastic model that accounts for alterations in the free energy of a motor complex due to tension development between the motors that results from asynchronous motor stepping and the associated stretching of the elastic linkages of a motor complex (17). Overall, this model predicts that even very weak elastic coupling between kinesins (〈κ_complex〉 ∼ 0.01 pN/nm) can reduce cargo-microtubule affinities significantly due to strain-dependent attenuation of motor filament binding rates and acceleration of motor detachment. In turn, such effects decrease collective kinesin run lengths by reducing the probability that both kinesins will remain bound to the microtubule simultaneously.

Two-kinesin behaviors generally are much more rich and complex in the presence of an applied load. However, force assays using an optical trapping instrument (14, 18) and the subsequent mechanical modeling (19) also have uncovered analogously weak enhancements of multiple kinesin velocities, run lengths, and detachment forces. Under these conditions, a combination of strain coupling and other kinetic constraints, associated with spatial and temporal dependence of applied loads, tend to reduce the time-averaged number of kinesins that contribute productively to cargo motion (18, 19). These observations are significant considering that weak dependences of cargo run length and velocity to variation in kinesin number has been also found in vivo (20). Such behavior has been attributed previously to unknown factors within cells that are not present during in vitro experiments. However, the above in vitro studies show these responses potentially can be derived from the intrinsic dynamic properties of multiple kinesin complexes themselves without evoking additional regulation. Furthermore, the negative cooperative behavior of kinesins will likely influence transport processes involving multiple antagonistic motors because any reduction in the average number of engaged kinesin motors naturally will affect how they compete with other types of motors.

Many aspects surrounding the net negative cooperative behaviors of multiple kinesins are likely generic and will to some extent apply to a variety of multiple motor complexes containing other types of processive motors. The mechanical properties of different classes of molecular motors can, however, vary appreciably. For example, myosin Va (myoVa)⁴ is a processive, double-headed motor that transports cargos directionally along actin filaments (3). Single myoVa molecules move with roughly similar velocities as kinesin, but they have a smaller stalling force (2–3 pN) and a much larger step size (36 nm) (21, 22). These properties may yield an even stronger sensitivity of multiple myosin dynamics to the strain-dependent coupling between motors than is found with multiple kinesins. Because collective motor dynamics ultimately depends on the intimate interplay between motor filament affinity, stepping and strain, these expectations must ultimately be tested directly.

Here, we explore these issues by examining the transport properties of individual, structurally defined motor complexes containing precisely two myoVa motors that are linked together by two different types of molecular scaffolds. The incorporation of myosin motors that are labeled individually with different color quantum dots (Qdots) into these complexes allows the stepping dynamics and relative positions of each motor domain to be monitored with nanometer scale precision. Experimental analyses and theoretical modeling of these motor systems show that weak elastic coupling can influence both multiple myoVa run lengths and velocities. Moreover, this unique negative cooperative behavior also is predicted to be influenced by the effective size of the scaffold/cargo and to largely stem from the large step size and relatively small stalling force of a single myoVa motor.

MATERIALS AND METHODS

Proteins

A heterodimeric myoVa was engineered so that only one of the two heavy chains contained a biotin tag at the N terminus for conjugation to streptavidin Qdots. One heavy chain contained myoVa coding sequence (amino acids 1–1098), followed by a C-terminal FLAG tag. The other heavy chain contained an N-terminal biotin tag, amino acids 1–1098 of myoVa, a 43-amino acid acidic leucine zipper (Z_E) (see supplemental Methods for sequence), and a C-terminal His₆ tag. The acidic zipper dimerizes with the corresponding basic zipper sequence (Z_R) on the DNA scaffold. The N-terminal biotin tag consists of 87 amino acids residues (Met⁷⁰–Glu¹⁵⁶) from the Escherichia coli biotin carboxyl carrier protein, which is biotinylated at a single lysine during expression in Sf9 cells (23). The two myoVa heavy chain constructs were co-expressed with a calcium-insensitive calmodulin (CaMΔall) (24). The heterodimeric construct was expressed in Sf9 cells and purified essentially as described previously (25). The cell lysate containing the heterodimer was passed first through an anti-FLAG column (Sigma-Aldrich) and then through a His-SELECT nickel affinity column (Sigma-Aldrich), with the final elution consisting of the heterodimeric motor.

DNA Scaffold

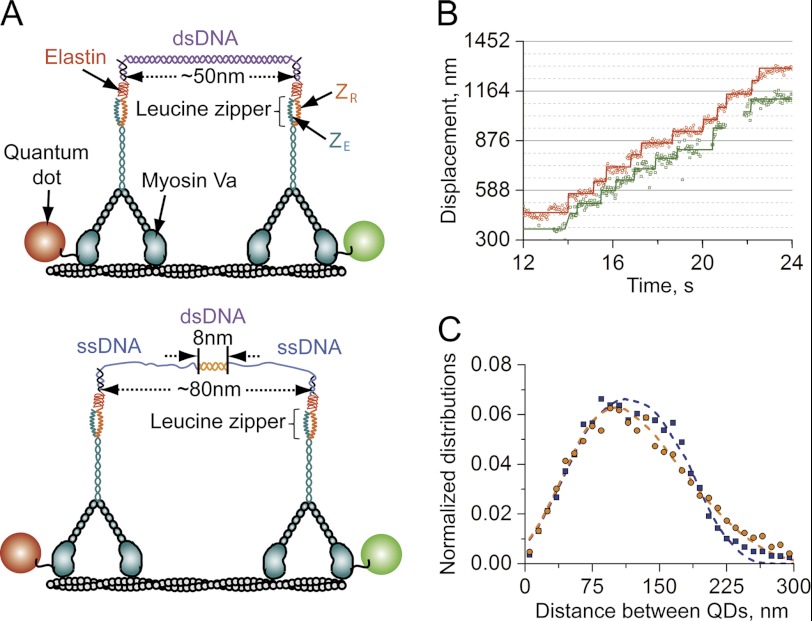
The synthesis of the DNA scaffolds and the artificial protein linker polymers (Z_RELS₆-ssDNA) were prepared according to the procedures described in Refs. 13 and 26. For the present study, two different DNA scaffolds were prepared that contained the same total number of base pairs along their lengths, but whose central duplexes were either 8- or 50-nm-long (Fig. 1A). The sequence of the oligonucleotides used to construct the two scaffolds is given in the supplemental Methods.

FIGURE 1.

Transport of two-myoVa motors in the absence of an applied load. A, illustrations of two-myoVa complexes assembled using DNA scaffolds with central duplexes that were either 50- (top) or 8-nm (bottom) in length. B, characteristic trajectories at 2 μm ATP produced by a complex assembled using the 50-nm DNA scaffold, showing the positions of both the red and green Qdots (QD) attached to one motor domain of each of the two motors in the complex. C, measured (blue and orange symbols) and calculated (dashed lines) distributions of Qdots separation distances for the 50 (blue) and 8 (orange) nm scaffolds. κ_complex and k_on⁰ were the only parameters varied in the model calculations. The remaining parameters were treated as constants whose values were estimated from existing experimental data (see Table 1). Statistical tests of the calculated Qdot spacing distributions for 8- and 50-nm yield reduced Chi-squared statistic (χ²/ν) values of 1.13 and 1.29, respectively, for each non-linear/non-Gaussian distribution (ν = (30 data points − 2 variable parameters − 1)). Moreover, analogous tests show that each calculated distribution is statistically different from the other (i.e. χ²/ν = 12.5 if calculated distributions for the 8 nm scaffold is used to approximate the 50-nm scaffold data and 6.6 if the 50 nm distribution is used to fit the 8 nm data).

Two-myosin Complex Formation

DNA-templated myoVa complexes incorporating two Qdot-labeled motors were prepared by first incubating the motors separately with either green or red Qdots. Specifically, 0.5 μl of 1 μm streptavidin-655 Qdot (Invitrogen) was mixed with 1 μl of 0.56 μm heterodimeric myoVa for 10 min at room temperature. At the same time, 0.5 μl of 1 μm streptavidin-565 Qdot (Invitrogen) was incubated with 1 μl 0.56 μm heterodimeric myoVa. The two solutions were then added to 0.5 μl of 0.9 μm DNA scaffolds that were preassembled with the Z_RELS₆-ssDNA polymers and incubated for 15 min to facilitate full complex formation.

Experimental Procedure and Data Acquisition

For the total internal reflection fluorescence (TIRF) motility experiments, the complex consisting of two Qdot-labeled motors attached to the DNA scaffold was diluted 900–1600 times into a solution containing 25 mm imidazole, pH 7.4, 25 mm KCl, 4 mm MgCl₂, 1 mm EGTA, 1 mm DTT, 1 mm ATP, and 0.1 mg/ml CaMΔall, the calcium-insensitive CaM mutant (24). The protein-DNA complex was perfused into a flow cell in which Alexa 635 phalloidin (Invitrogen) labeled-actin was adhered to the coverslip surface by N-ethylmaleamide-inactivated myosin, an ATP-insensitive sulfyhydryl-modified myosin. No oxygen scavenger was used to intentionally allow the actin filaments to bleach after a few seconds, which facilitated subsequent red channel acquisition. The run length and velocity for the single myosin Va heterodimer were determined by the same procedure but without adding DNA scaffold. For the experiment to determine whether the two motors synchronized their steps, a lower concentration of 2 μm ATP was used.

To image the complex moving on actin filaments, the flow cell was placed on the stage of a TIRF microscope, based on a Nikon TE2000 inverted microscope equipped with a PlanApo 1.45 numerical aperture objective. The Qdot fluorescence was imaged by TIRF using a 488-nm argon ion laser for excitation (Spectra Physics, Santa Clara, CA). The fluorescent images of 655 and 565 Qdot were separated by an image splitter (Optical Insights LLC, Santa Fe, NM) and projected side by side onto an intensified CCD camera (XR-Mega S30; Stanford Photonics, Stanford, CA) and recorded as a TIFF stack using Piper Control software (Agile Automation, Inc., Union City, CA) at 10 frames/second. The effective pixel resolution at 2 × 2 binning was 117 nm/pixel. Typically, 1000 frames were recorded for each TIFF stack.

Data Analyses

Analysis of two-myoVa transport events were restricted to trajectories where the red and green Qdots moved together along the actin filaments. The red and green channels images were overlapped in ImageJ software and inspected manually to locate events in which red and green Qdot-labeled myoVa moved together. Events where the complexes reached the end of the actin filament prior to detachment also were discarded. The remaining trajectories were analyzed using custom software routine written in MATLAB that calculates the center position of each Qdot by fitting their intensity profile to a two-dimensional Gaussian function (16). At our experimental integration time of 0.1 s, this procedure yields Qdot localization accuracies of 6 nm (28).

Distributions of Qdot separation distances during two-myoVa transport were calculated as follows. After calibrating the registry between the two image channels of the microscope, the trajectories of the red and green Qdots were aligned using the matrix transform procedure as described in supplemental Methods. The red-green Qdot separation distances were then calculated frame by frame from the trajectories using a custom Excel macro. The Qdot position traces with 2 μm ATP in the buffer were analyzed by an objective step finding algorithm to determine the step size and dwell time of a step (29).

Two-myoVa run lengths are reported as the total distance traveled by the motor complexes. Average velocities were calculated by dividing this distance by the total time the complex remained bound to the filament. Run length distribution histograms were fit with p(x) = Ae^−x/λ, to determine the characteristic run length λ, where p(x) is the relative frequency of the motor traveling a distance x along a track and A is a constant. The rates at which complexes transition between single- and two-motor bound configurations were determined via analyses of the appearance and disappearance of individual Qdots within two-myoVa trajectories. Considering the length of an individual myosin motor (∼30 nm), and the length of the scaffolds (8 and 50 nm), Qdots connected to the motor domain of an unbound mysosin should be able to move to a z-position above the actin filament where the TIRF excitation intensity is minimal (the end-to-end length of the complexes is at least 68 and 110 nm for the 8 and 50 nm assemblies, respectively). Moreover, the diffusive motions of the Qdots on dissociated motors will further decrease their intensities and contribute to their disappearance. The present mechanical analyses of complex elasticities suggest such motions will be appreciable.

To account for Qdot blinking in these analyses, the time that individual Qdots remain in a dark state was examined separately using immobilized Qdots, which most commonly disappeared for only a single frame. Consequently, the disappearance of either Qdot within a trajectory was attributed to the partial detachment of a motor complex only if a Qdot was absent for two or more frames (t ≥ 200 ms). Partial assembly binding rates (k_on[1→2]) and detachment rates (k_off[2→1]) were approximated by fitting distributions of the times that the complexes remained in single- or two-motor-bound configurations to an exponential function.

Transition Rate Modeling

Two-myoVa behaviors were analyzed using the discrete-state stochastic model developed by Driver et al. (17). In this model, the rates two-motor complexes transition between single- and a range of two-motor-bound configurations where the motors are bound to different filament lattice sites are assumed to depend on the development and release of strain between the motors during each respective transition. The complexes can exchange between different filament-bound configurations via motor binding, stepping, and detachment. In each case, configuration-dependent strain energy changes are determined by the elastic properties of a complex (κ_complex) and the distances they stretch during each transition. The dependences of κ_complex on motor separation distances were determined from analyses of Qdot separation distances as described in the “Results.”

Motor stepping rates were calculated as described in Refs. 17 and 30. Microscopic binding and detachment transitions where a second myoVa attaches and releases from the actin filament are parameterized using the following expressions,

where k_on⁰ and k_off⁰ are the microscopic binding and unbinding rates for a single (non-interacting) motor. The parameter F(i) is the effective internal force imposed on each motor due to the stretching of the assembly by a distance corresponding to i actin lattice sites, and F_d is the critical detachment force (F_d = k_BT/d), which characterizes the sensitivity of motor detachment to strain (see Ref. 17). E(i) and E₁ correspond to the strain energy of the complex when both motors are bound and when only a single motor is bound respectively (E₁ = 0). Note that the two above relations satisfy detailed balance, which naturally dictates that k_on[1→2],i and k_off[2→1],i are both influenced by the strain. Accordingly, because experimental calculations of motor-filament binding rate, 〈k_on[1→2]〉, correspond to an average strain-dependent transition rate, these rates were modeled by choosing a value for k_on⁰ that provides reasonable agreement between theory and experiments when inputted into Equation 2. Average detachment transition rates, 〈k_off[2→1]〉 as well as two-myoVa velocities and run lengths were calculated from the steady-state solution of the model using this approximation of k_on⁰ without further adjustment. Other model parameters employed in these calculations are provided in Table 1.

TABLE 1.

Comparison of experimental and theoretical transport parameters

V_single, V_assembly, RL_single, and RL_assembly are the average velocities and run lengths of a single- myoVa and two-myoVa assembly, respectively. k_off[1→0] is the detachment rate of a single motor. 〈k_on[1→2]〉 is the average strain-dependent rate that a complex will transition from a single- to a two-motor-bound configuration. 〈k_off[2→1]〉 is the average myosin detachment rate during transition from two- to single-motor bound configurations. P₂-bound myoVa is the average probability that both motors in an assembly will be filament-bound.

	Experimenta			Modelb
	Single myoVa	8-nm scaffold	50-nm scaffold	8-nm scaffold	50-nm scaffold
Vsingle	0.24 ± 0.14 μm/s
RLsingle	0.64 μm
Vassembly		0.13 ± 0.11 μm/s	0.18 ± 0.11 μm/s	0.22 μm/s	0.21 μm/s
RLassembly		1.24 ± 0.11 μm	1.0 ± 0.11 μm	1.2 μm	1.2 μm
koff[1→0]	0.375 1/s	0.375 1/s	0.375 1/s	0.375 1/s	0.375 1/s
kon[1→2]		2.36 ± 0.06 1/s	2.67 ± 0.05 1/s	2.4 1/s	2.6 1/s
koff[2→1]		1.08 ± 0.05 1/s	0.97 ± 0.05 1/s	0.91 1/s	0.91 1/s
P2-bound myoVa		0.65	0.55	0.55	0.57

^a Average values were calculated from n = 96, 70, and 137 trajectories for the single myoV, and the 8- and 50-nm myoV complexes, respectively. Values are presented as mean ± S.E.

^b myoV stepping rates are approximated using the formalism described in Refs. 30 and 17 and the following parameters: θ × d_step = 0.3 × 36 nm; v_forward^o = 7.5 steps/s; v_backward^o = 1.8·10⁻⁷ steps/s, F_d = 3 pN.

RESULTS

Stepping Dynamics of Elastically Coupled Myosin V Motors

Here, we characterize how multiple myoVa motors function collectively by examining the stepping dynamics of individual myosin molecules within a multiple motor complex. Motor complexes were created using a duplex of DNA as a molecular scaffold that both defines the number of motors within a complex and their nominal, unstrained separation distance (13). Two different complexes were created. The total number of bases in the DNA scaffolds was held constant, but the central duplexed portion of the scaffold contained different numbers of matched based pairs, yielding dsDNA domains that were either 8 or 50 nm in length (Fig. 1A). MyoVa motors incorporating a C-terminal acidic leucine zipper peptide (Z_E) were linked to each end of the scaffold via a DNA-conjugated protein polymer (Z_R-ELS₆-ssDNA) that contains a complementary basic zipper peptide (Z_R). The myoVa constructs were engineered as heterodimers so that only one of the motor domains contained an N-terminal biotin tag. This approach simplifies subsequent analysis by allowing only one head of each myoVa to be labeled with a Qdot.

Complexes containing two Qdot-labeled myoVa molecules were prepared as described under “Materials and Methods” and tracked as they moved on actin filaments using TIRF microscopy. Only those complexes that contained one motor with a red Qdot, and the other with a green Qdot were analyzed. This approach not only confirms the incorporation of two motors into the complex but also allows us to distinguish transport events where the complex is associated with a single versus a two-motor bound configuration. The positions of one head domain of each motor can also be monitored in time as the complex steps processively along an actin filament, allowing variations in the separation distance between the motors to be examined.

A characteristic trajectory of a two-myosin complex assembled with a 50 nm DNA scaffold is shown in Fig. 1B. In these traces, the stepping of each motor is signified by discrete 72-nm displacements of its corresponding Qdot. Trajectories of individual motors were often broken up into multiple segments due to the dissociation and subsequent rebinding of one motor of the complex. The motors were also found to step asynchronously, which leads to time-dependent changes in the separation distance between the Qdots (Fig. 1C). Moreover, relatively large Qdot separation distances of >200 nm are commonly observed, which corresponds to a 200 ± 36 nm spacing between the center of mass of the two motors. Observations of such large scaffold extensions naturally indicate that the two-myosin complexes are mechanically compliant over these distances.

Two-myosin Complexes Are Mechanically Compliant but Influenced by Volume Exclusion and Strain-induced Stiffening

Histograms of the distance between the Qdots show the ability of the complex to adopt bound configurations in which the motors are spaced relatively far apart on the actin filament (Fig. 1C). Regardless of whether the central duplex of the scaffold was 8- or 50-nm-long, measured distributions of Qdot spacings were quite broad compared with the DNA scaffold length and contained considerable amplitude at Qdot spacings ranging between 75 and 200 nm. The amplitude of this distribution drops off rapidly below 75 nm, suggesting that there is a minimum distance that the motors can be separated on the actin filament, potentially due to steric factors. In contrast, the probability that the complex was bound with a particular spacing decreases much more slowly as the Qdot spacing increases from 75 and 200 nm. Considering that myoVa has a relatively low stall force (∼2 pN), this observation suggests that the myosins can stretch their elastic linkages relatively easily over these distances. However, very few transport events were observed once the Qdots were spaced >200 nm apart, especially when the 50-nm scaffold was employed. Taken together, these results suggest that the mechanical properties of myoVa complexes are influenced by volume exclusion and that their elastic spring constants (κ_complex) increase non-linearly with respect to their end-to-end extension.

To gain further insight into the mechanical (elastic) properties of the myoVa complexes, we next calculated Qdot separation distributions using a discrete-state stochastic modeling procedure used previously to examine the dynamics of analogous two-kinesin complexes in the absence of an applied load (17). This model is useful for the present analyses because it accounts for the mechanical properties in binding/unbinding and stepping transitions between distinct track-bound configurations of a two-motor complex, in which the motors are bound to a range of different filament lattice sites. The core features of this model are described in Ref. 17 and under “Materials and Methods.” To capture the mechanical properties of the myoVa complexes suggested by the Qdot distance distributions, the mechanical treatments of our original model was modified as follows. The joints between the motors and the DNA scaffolds are expected to be flexible and able to rotate relatively freely as they incorporate an unhybridized domain. The ELS₆ polymers should also contribute to this flexibility. Thus, we assumed that the Z_RELS₆/motor component of the complex at each end of the scaffold has an effective length of 30 nm and that these elements can rotate without introducing strain. We also consider the excluded volume of the motors and do not allow the complexes to adopt configurations where the center positions of the motors are separated by ≤36 nm. To account for the non-linear elasticity of the scaffolds that is implied in the Qdot separation distance distribution at large Qdot distances and was observed in prior optical trapping studies of analogous complexes (14), we assumed the complexes are compliant at intermediate extensions (κ_complex ∼ 0.001 pN/nm) and stiffen at large extensions (κ_complex = 0.1 pN/nm). Overall, the combination of these constraints yield non-linear force extension profiles where the complexes are incompressible at small separation distances, relatively compliant at intermediate separation distances, and very rigid at large extensions (supplemental Fig. S1).

Calculated Qdot distance distributions are presented in Fig. 1C (dashed lines). In general, we find that the treatment of volume exclusion and the non-linear elasticity of the scaffold due to its strain-induced stiffening are both necessary to reproduce the measured distributions of Qdot separation distances (supplemental Fig. S2). Moreover, only slight modifications to the elastic behavior of the complex are needed to reproduce the different widths and shapes of the Qdot distance distributions produced in assays using the 8- and 50-nm scaffolds. In particular, approximating the 8-nm scaffold distribution required assumptions that these complexes are compliant over a somewhat larger range of scaffold extension distances compared with the 50-nm scaffolds (250 and 180 nm for the 8- and 50-nm scaffolds, respectively). There are two reasons for this distinction. First, the small length of the 8-nm duplex dictates that the myosins will experience tension at smaller separation distances. This property leads to the asymmetric shape of the 8-nm scaffold distribution. Second, both DNA scaffolds incorporate the same total number of nucleotides. Yet, because the contour length of ssDNA is longer than that of dsDNA (31), strain-induced stiffening of the 8-nm scaffold will occur at slightly larger extension distances; hence, the tail of the 8-nm scaffold distribution extends to larger separation distances.

Coupled myoVa Motors Exhibit Attenuated Run Lengths and Velocities

The observations that complexes are mechanically compliant at intermediate extensions of the scaffold lead to expectations that multiple myosins will function productively as a team, yielding long run lengths compared with single myoVa molecules and negligible reductions in transport velocities. Both forms of the two-myoVa complexes produced longer average run lengths than a single myoVa (Table 1 and supplemental Fig. S3), but the run length enhancement of the two-myoVa complex is much smaller than predicted by models that assume that motors do not interact during transport (27). Moreover, the average velocities of both two-myoVa complexes were ∼25–45% lower than the velocity of a single myoVa motor. In contrast to observations of multiple kinesin behaviors (13), even relatively weak coupling between the myosins reduces both cargo run lengths and velocities in the absence of an applied load.

Modeling Two-myosin Dynamics via Direct Analyses of Motor-filament Binding and Detachment Transitions

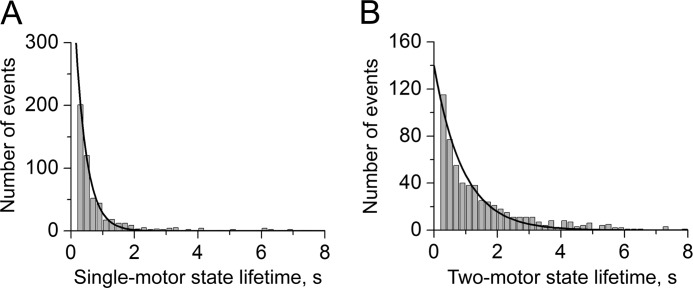
The proportion of time that the complexes associate with actin filaments in a one versus two-bound motor configuration and how rapidly they transition between these states via binding and detachment events were characterized. Both motors were assumed to be engaged in transport only if the red and green Qdots were both detected within a frame. Average partial assembly attachment and detachment rates (〈k_on[1→2]〉 and 〈k_off[2→1]〉, respectively) were estimated via exponential fits to distributions of the times that one or both motors were actin-bound (Fig. 2, A and B). Overall, these analyses indicate that both the 8- and the 50-nm complexes spent the majority of their time (>55%) moving along actin filaments with two engaged motors (Table 1; Fig. 2, A and B). Consistent with this behavior, binding transition rates (〈k_on[1→2]〉) were found to be slightly greater than twice the rate at which a complex partially detaches from actin.

FIGURE 2.

Distribution of the average time that motors within a 50-nm DNA complex spend associated with the filament via a single (A) or both motors (B) bound to the filament. Exponential fits to each distribution are indicated by the solid line. These fits yield average lifetimes of single and two-motor-bound configurations of 0.36 ± 0.01 s and 1.03 ± 0.05 s, respectively. Corresponding values from fitting lifetime distributions for the 8-nm scaffolds were 0.42 ± 0.01 s and 0.93 ± 0.04.

The ability to characterize the rate at which the complexes transition between different classes of motor-bound configurations offers a unique opportunity to parameterize transition rate models of multiple motor dynamics by providing additional metrics to gauge model predictions. When motor filament binding rates are determined from experimental measurements of k_on[1→2], transition rate modeling yields relatively small run length enhancements and reduced two-myosin velocities compared with a single myoVa motor (Table 1, and supplemental Fig. S4, A and B). Calculations of both the percentage of time that the complex associates with actin through both myosin molecules, and partial complex detachment rates (〈k_off[2→1]〉) also show similar agreement with the experimental data. The largest deviation between theory and experiment occurred in calculations of the average velocities produced by complexes formed using the 8-nm scaffolds. As discussed below, this likely stems from our simple treatment of their strain-induced stiffening behaviors. Consequently, considering that the properties of the Qdot separation distribution are maintained in these calculations, these results suggests that the model provides a reasonable approximation of the influence that steric factors and strain coupling have in determining both multiple myosin stepping rates and filament affinities.

Unique Roles of Cargo Elasticity and Size in Multiple myoVa Dynamics

The ability to reproduce experimental trends for multiple myoVa state distributions, transition rates, velocities, and run lengths suggests that this model provides a reasonable framework to explore how the structural and elastic properties of a complex or cargo will impact multiple myosin behaviors. New calculations were performed, where the scaffold elastic spring constants κ_complex were varied within their compliant/intermediate extension regime, allowing the role of complex elasticity on multiple myoVa behaviors to be explored (Fig. 3). The motor separation distance/scaffold extension distance where the complexes stiffen due to strain was varied separately.

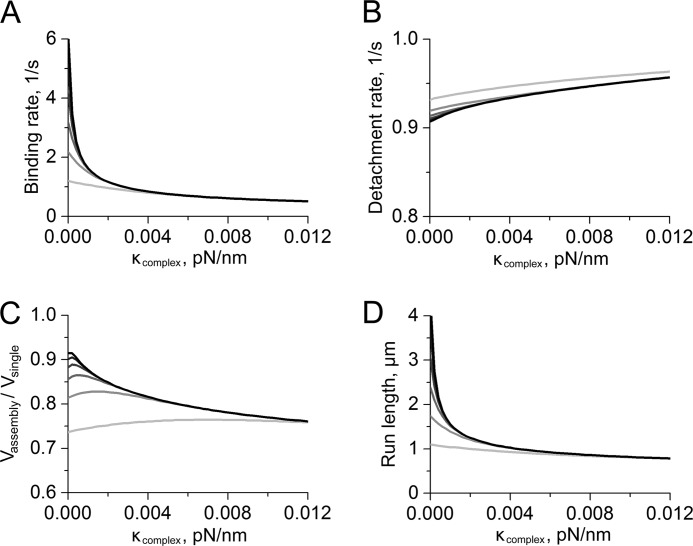
FIGURE 3.

Predicted dependences of two-myoVa transport parameters on the strength and distance-dependent properties of elastic coupling between motors. The grayscale in all four plots indicates the extension distance at which κ_complex was assumed to increase to a value of 0.1 pN/nm due to the strain-induced stiffening of the complexes as described under “Results.” This distance was varied from 100 nm (light gray) to 350 nm (black) in increments of 50 nm. A, calculations of the average motor-filament binding rate, 〈k_on[1→2]〉. B, the average transition rate describing the partial detachment of a complex from the filament, 〈k_off[2→1]〉. C, ratios of the average complex velocities (V_assembly) to single myoVa velocity (V_single). D, calculations of average two-myoVa run lengths.

As reported for multiple kinesins (17), calculated myoVa filament binding rates 〈k_on[1→2]〉 decrease rapidly with increasing κ_complex, whereas the partial complex detachment rate, 〈k_off[2→1]〉 increases (Fig. 3, A and B). Strain coupling due to the stretching of elastic linkages within the complex lowers cargo run lengths by reducing motor filament affinities. Multiple myoVa velocities also are predicted generally to decrease with increasing κ_complex, which also reduces two-motor run lengths (Fig. 3, C and D). Velocity is not found to decrease for multiple kinesins experimentally or theoretically. Our survey of model parameters suggest that the dependence of two-myoVa velocities on κ_complex is largely derived from the large step size and relatively low stalling force of a single myoVa motor, and the corresponding sensitivity of myoVa stepping rates to the forces developed between the motors when their linkages are stretched. For example, average velocities of elastically coupled myoVa motors are predicted to be sensitive to the effective length of the single myosin power stroke, which according to the formalism developed by Fisher and Kolomeisky (30), is parameterized by the formula, θ × d_step = 0.3 × 36 nm = 10.8 nm in our model (supplemental Fig. S5), where θ is a dimensionless factor that approximates the position of the transition state along the myosin stepping pathway relative to the ground state. Assuming a constant value for κ_complex, average two-myoVa velocities decrease with increasing θ. Here, complexes composed of motors possessing a large power stroke move with low velocities because this distance determines how far they must stretch for their leading motor to step forward, and hence, the amount of work that this motor must perform to complete its stepping transition. This behavior also depends on the probability that a two-motor complex will move with two filament-bound motors and is therefore sensitive to parameters that influence motor-filament affinities (supplemental Fig. S5).

A striking result of the above calculations is that two-myoVa binding rates, average velocities, and run lengths are predicted to be very sensitive to the extension distance at which the complexes are assumed to exhibit strain-induce stiffening. Average 〈k_on[1→2]〉 binding rates, two-myoVa velocities, and run lengths all decrease appreciably as this distance decreases from 350 to 100 nm (Fig. 3 and Fig. 4). Moreover, these effects occur even if the complexes are assumed to be infinitely compliant at intermediate extension distances (i.e. κ_complex = 0), indicating that the strain-induced stiffening dominates much of the multiple myosin behaviors observed in our experiments. For this reason, we attribute the deviations between our model predictions of average velocities of complexes assembled using the 8-nm scaffolds to the simple approximation of the present model of the strain-induced stiffening of these scaffolds. Improving the present model predictions will likely require more explicit knowledge and treatment of this behavior at large extension distances.

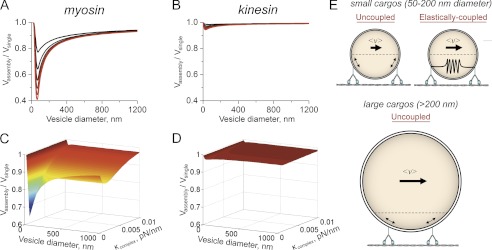
FIGURE 4.

Comparison of cargo velocities driven by two myosin and two kinesin motors. A and B, ratio of the average two-myoVa (A) and two-kinesin velocities (B) (V_assembly) to a single motor velocity (V_single) plotted as a function of the diameter of a vesicular cargo. Curves shown on both plots were calculated for complexes with the same physical characteristics, but where the unloaded, microscopic motor filament binding rate (k_on⁰) was varied from 0.025 1/s (black curve) to 0.15 1/s (red curve) in increments of 0.025 1/s. C and D, three-dimensional plots of the velocities ratio from A and B as function of vesicle diameter and over a range of values for κ_complex at intermediate extension distances. E, schematic depicting the dependence of two-myoV velocity on cargo size. The dashed line on the cargo denotes the region on the cargo surface where both motors can bind without introducing cargo deformations. Local elastic coupling between the motors, which also modulates cargo velocity when cargos are small, is also depicted by the spring connecting the motors.

Interestingly, the above analyses also suggest that velocities of cargo transport driven by two myoVa motors will depend on the cargo size. This is true even if their elastic coupling is negligible at intermediate extension distances as would be the case if the motors were anchored to a vesicular cargo possessing a fluid membrane. Calculations displaying this dependence are shown in Fig. 4. The distance at which strain-induced stiffening occurred (i.e. the distances where κ_complex switched from 0 to 0.1 pN/nm) was assumed to correspond to the maximum distance motors can be separated on a spherical cargo, while remaining bound to the filament without introducing cargo deformations. With these assumptions, average two-myoVa velocities are minimized at a cargo diameter of ∼60–75 nm (Fig. 4A). Motor stepping rates are reduced by the strain associated with cargo deformations when the two motors are separated by a distance exceeding 55–70 nm. Consequently, the narrow range of separation distances where strain is negligible dictates that a high proportion of motor stepping events will be affected by intermotor strain. Below this cargo size, two-myoVa velocities increase toward the single myoVa velocity because strain decreases motor-filament binding rates and thus reduces the probability that a cargo will be transported by two motors. Cargo velocities also increase as cargo sizes become larger because the range of separation distances where strain is negligible also increases. Finally, we note that the introduction of other forms of intermotor coupling can alter these dependences. For example, weak, local elastic coupling between motors is generally predicted to reduce the sensitivity of two-myoVa velocities to cargo size because these interactions decrease motor filament affinities (Fig. 4, C and E). Nevertheless, cargo velocities are still reduced compared with single-myosin velocities over a broad range of cargo elasticities and sizes. In contrast, the velocities of cargos that are transported by two kinesin motors are largely indistinguishable from single kinesin velocities in nearly all cases (Fig. 4, B and D).

DISCUSSION

The dynamic behaviors of motor complexes containing two elastically coupled myoVa motors were examined using Qdot motor labeling and tracking procedures that facilitate direct analyses of the relative motions of each motor within a complex as well as the rate that they transition between different motor-bound configurations via motor filament binding and detachment. These experiments provide a foundation to parameterize transition rate models of multiple motor dynamics that account for the influence of elastic coupling on cargo transport by multiple motors in the absence of an applied load. Overall, the present experimental and theoretical analyses both show that elastic coupling tends to reduce multiple myosin run lengths and velocities. In contrast, analogous coupling is primarily found to influence cargo filament affinities when cargo transport is driven by multiple kinesins. This distinction largely derives from the large step size and small stall force of a single myoVa motor. These properties result in sensitivities of motor stepping rates to strain that are comparable with the dependence of motor filament binding and detachment rates on the development of intermotor tension. As a result, multiple myoVa motors exhibit much more rich and complex dependences of multiple velocities and run lengths on the structural and mechanical properties of the cargo, particularly when compared with multiple kinesins. Interestingly, our prior analyses suggest that this behavior will also allow multiple myosins to cooperate more productively than multiple kinesins in the presence of an applied load, especially when load varies spatially and temporally (19). Although this behavior, as well as the precise nature of elastic coupling between motors on endogenous cargos requires additional experimental analyses, the ability to label and monitor the motions of individual motors in these assays and the corresponding computational analyses will constitute useful tools for these studies.