Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2012 Jul 18;32(29):9824–9830. doi: 10.1523/JNEUROSCI.0207-12.2012

A Retinal Source of Spatial Contrast Gain Control

Benjamin Scholl 1, Kenneth W Latimer 1, Nicholas J Priebe 1,✉
PMCID: PMC3432019  NIHMSID: NIHMS395452  PMID: 22815497

Abstract

Sensory cortex is able to encode a broad range of stimulus features despite a great variation in signal strength. In cat primary visual cortex (V1), for example, neurons are able to extract stimulus features like orientation or spatial configuration over a wide range of stimulus contrasts. The contrast-invariant spatial tuning found in V1 neuron responses has been modeled as a gain control mechanism, but at which stage of the visual pathway it emerges has remained unclear. Here we describe our findings that contrast-invariant spatial tuning occurs not only in the responses of lateral geniculate nucleus (LGN) relay cells but also in their afferent retinal input. Our evidence suggests that a similar contrast-invariant mechanism is found throughout the stages of the early visual pathway, and that the contrast-invariant spatial selectivity is evident in both retinal ganglion cell and LGN cell responses.

Introduction

Natural stimuli are composed of a wide range of stimulus features, which can vary greatly in signal strength. To extract these features properly, sensory systems employ methods to detect and respond selectively to stimulus features even while there are changes in signal strength and signal background. A primary method to address this problem is to apply gain mechanisms that acclimate signal strength without modifying the relevant signal features.

In V1, where stimulus strength is defined by contrast, neurons maintain invariant selectivity to specific visual features (e.g., orientation, spatial phase) under widely varying contrast conditions (Sclar and Freeman, 1982; Li and Creutzfeldt, 1984; Albrecht and Geisler, 1991; Finn et al., 2007). For low-contrast (weak) signals the spiking responses of V1 neurons are rapidly amplified, but for higher-contrast (strong) signals, responses are compressed, effectively creating a dynamic range across different contrasts (Dean, 1981; Tolhurst et al., 1981; Albrecht and Hamilton, 1982).

A number of phenomenological models have been developed to describe such invariant tuning in V1 (Hamos et al., 1987; Albrecht and Geisler, 1991; Heeger, 1992; Carandini et al., 1997). For the contrast gain control model, outputs of a linear filter are scaled by a contrast-dependent function involving either an intrinsic mechanism (Albrecht and Geisler, 1991) or divisive normalization (Heeger, 1992; Carandini et al., 1998). Although contrast gain control models accurately represent cortical contrast invariance and provide concise explanations for many cortical responses, they do not provide visibility into the location of the first emergence of invariance in the visual processing pathway.

Indeed, the origin of cortical contrast invariance has remained a mystery. It is possible that subcortical afferents from the LGN relay cells to V1 or retinal inputs to the LGN (Dubin and Cleland, 1977; Shapley and Enroth-Cugell, 1984; Hamos et al., 1987; Baccus and Meister, 2002; Gollisch and Meister, 2008) could drive or contribute to the observed cortical invariance. Both LGN relay cells and retinal ganglion cell (RGCs) show a reduction in response gain with increasing contrast of an optimal stimulus (Shapley and Victor, 1978, 1979; Shapley and Enroth-Cugell, 1984; Troy et al., 1993; Bonin et al., 2006).

To determine whether cortical contrast invariance for spatial phase arises in subcortical visual processing stages, we made extracellular recordings in vivo from the LGN to measure the spiking modulation of responses to optimal and nonoptimal contrast-reversing gratings. A key element of cortical contrast invariance is that response saturation is governed by stimulus contrast for both optimal and nonoptimal stimulus conditions. We found that, as for V1 simple cells, LGN relay cells exhibit response saturation that is governed by the same contrast for optimal or nonoptimal stimuli. Further, we also recorded s-potentials, which reflect single RGC inputs to LGN cells, and found that s-potentials show response saturation at the same contrast for all stimuli. Therefore the appropriate signals that underlie cortical contrast invariance for spatial phase emerge as early as the retina in the visual pathway.

Materials and Methods

Physiology.

Single-unit extracellular recordings were made from V1 and LGN neurons in anesthetized, paralyzed male and female cats (2–4 kg). Anesthesia was induced with ketamine (5–15 mg/kg) and acepromazine (0.7 mg/kg), followed by intravenous administration of a mixture of propofol and sufentanil (Yu and Ferster, 2010). After surgery the animal was placed in a stereotactic frame for the duration of the experiment. Recording stability was increased by suspending the thoracic vertebrae from the stereotactic frame and performing a pneumothoracotomy. Eye drift was minimized with intravenous infusion of vecuronium bromide. Anesthesia was maintained during the course of the experiment with continuous infusion of propofol and sufentanil. Body temperature, EKG, EEG, CO2, blood pressure, and autonomic signs were continuously monitored. The nictitating membrane was retracted using phenylephrine hydrochloride and the pupils were dilated using topical atropine. Contact lenses were inserted to protect the corneas. Supplementary lenses were selected by direct ophthalmoscopy to focus the display screen onto the retina. Extracellular electrodes (1–2 MΩ, Microprobe; 2–6 MΩ, FHC) were advanced either into V1 (area 17, ∼2 mm lateral of midline) or the LGN (6 mm anterior and 9 mm lateral, Horsley-Clarke coordinates) with a motorized drive (Sutter Instrument Company). After the electrode was in place, warm agarose solution (3–4% in normal saline) was placed over the craniotomy to protect the surface of the cortex and reduce pulsations. V1 recordings were limited to simple cells, which are known to receive direct LGN input. LGN recording were made from both X-cells and Y-cells. To determine cell type we first measured spatial frequency tuning using drifting gratings. We then presented contrast-reversing gratings at a spatial frequency higher than the spatial frequency determined to be the cutoff in response to drifting gratings.

Neurons with a frequency doubling response were labeled Y-cells, and those without were labeled X-cells.

All procedures were approved by the Animal Care and Use Committee of the University of Texas at Austin.

Visual stimulation and records.

Visual stimuli were generated by a Macintosh computer (Apple) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) for Matlab (Mathworks) and presented on a Sony video monitor placed 50 cm from the animal's eyes. The video monitor had a noninterlaced refresh rate of 100 Hz and a spatial resolution of 1024 × 768 pixels, which subtended 40 cm horizontally and 30 cm vertically. The video monitor had a mean luminance of 50 cd/cm2. Grating stimuli were presented for 1.5 s, preceded and followed by 250 ms blank (mean luminance) periods. We initially characterized stimulus orientation, spatial frequency, spatial location, and size best evoking a response. In V1 we chose the preferred eye and in the LGN the eye chosen depended on whether we recorded in layer A or A1. Both drifting sinusoidal gratings and counterphase flickering gratings at different spatial phases were presented at different contrast levels (2–90%). In V1 and LGN, both small (radius 1–2 degrees) and large (radius 4–12 degrees) gratings were used. Raw voltage trace and spike times identified online were sampled at 16–25 kHz during recordings. V1, LGN, and s-potential spike times were converted to spike rate by cycle-averaging responses at the stimulus temporal frequency for each contrast and spatial phase. The Fourier transform was used to measure the modulation at the temporal frequency of the visual stimulus (F1). F1 responses for each stimulus condition were used in subsequent analysis and model fitting.

Extracting s-potentials.

To extract the times of the s-potentials, we began by first constructing a template of the s-potential waveform by examining a 1.25 ms window before each LGN relay cell spike. S-potential waveforms were evident in that window, but the timing of the s-potentials was different for each LGN cell spike. To identify s-potential times preceding LGN spikes, a Gaussian mixture model (GMM) was used to determine the portion of the raw trace attributable to the s-potential, similar to Bayesian spike sorting methods using GMMs (Lewicki, 1998). The GMM assumed each voltage trace segment was composed of three components summed together: the s-potential waveform, a constant LGN cell waveform, and Gaussian noise with constant variance. Because s-potentials could appear at different temporal positions relative to an LGN spike, we formed a prior distribution (discrete) of s-potential temporal positions that was Gaussian-shaped with a SD of 0.0625 ms and had a maximum shift of 0.5 ms from mean position. Priors enforcing sparseness and smoothness were added over s-potential and LGN waveforms to regularize the estimates (to avoid overfitting the data). Under this model we obtained maximum a posteriori (MAP) estimates for s-potential waveforms in each recording. A brief mathematical description of our likelihood model and posterior is given as:

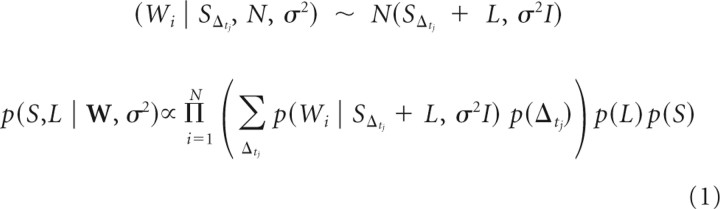graphic file with name zns02912-2196-m01.jpg

where W is the collection of all windows from the voltage trace, Wi is an individual voltage trace, L is an LGN spike waveform, S is an s-potential waveform, SΔtj is an s-potential waveform shifted in time by Δt, and N is the normal distribution.

Once the template s-potential waveform was recovered, we examined the entire voltage record to determine all s-potential spike times. A moving window was applied to the entire voltage trace and, at each time point, compared with the template s-potential waveform. We computed a likelihood value of each window being generated by a multivariate Gaussian distribution with mean equal to the estimated s-potential waveform and constant, temporally uncorrelated variance. A threshold was applied to the likelihood to identify s-potentials. Thresholds were chosen individually for each recording to match differences in noise conditions. The threshold was initially set to be 2 SDs above the mean of the likelihood values at all the times. These values were then tuned to enforce a conservative estimate of s-potential counts. A strict 1 ms refractory period was enforced after each threshold was crossed, which counted as an identified s-potential event. Before a known LGN spike occurred, the threshold was lowered to represent a prior on the s-potential probability, but the final output did not assume an s-potential occurred before all LGN spikes.

Results

Where does contrast gain control first emerge along the visual pathway to form invariant spatial tuning? Contrast saturation in response to drifting gratings is exhibited in RGCs, LGN relay cells and V1 simple and complex cells (Dean, 1981; Tolhurst et al., 1981; Albrecht and Hamilton, 1982; Shapley and Enroth-Cugell, 1984; Cheng et al., 1995). It is unclear, however, whether the contrast saturation at subcortical stages also exhibits spatial invariance: that is, saturation occurring at a single stimulus contrast, independent from the spatial position of the visual stimulus. To determine at which visual processing station this spatial invariance first emerges, we measured contrast saturation of neurons in the LGN and RGCs with contrast-reversing gratings while systematically changing the spatial phase of the grating.

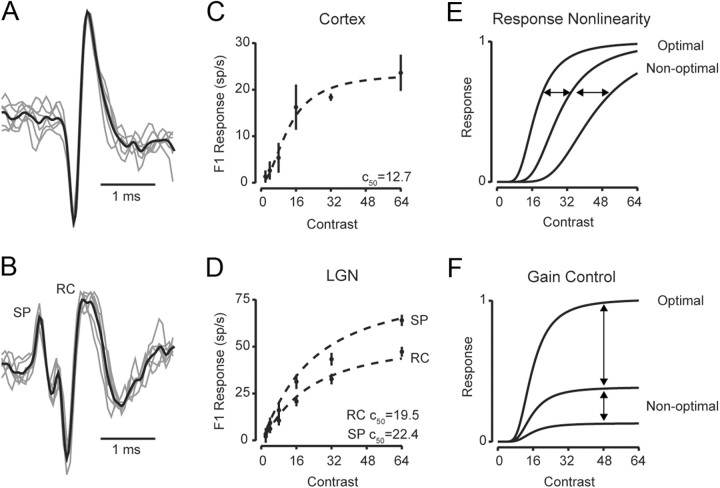
We initially characterized contrast saturation properties of individual V1 simple cells and LGN neurons using single-unit extracellular recordings (Fig. 1A,B). In each recording we presented contrast-reversing gratings of preferred spatial phase, spatial frequency, and temporal frequency while stimulus strength was varied by changing contrast. In V1, orientation of drifting gratings stimuli was also optimized. Both V1 neurons and LGN relay cells exhibited response saturation with increasing contrast for the modulation component (F1) of their responses (Fig. 1C,D). To quantify the degree of response saturation at high contrasts, responses were fit with the Naka-Rushton/Michaelis-Menten equation (Naka and Rushton, 1966; Baylor and Hodgkin, 1973):

graphic file with name zns02912-2196-m02.jpg

where α is a gain factor, c50 is the semisaturation constant and m is the output nonlinearity exponent. Neurons in both V1 and LGN showed typical contrast response functions as stimulus strength increased, with semisaturation contrast values (C50) for V1 neurons lower than that of LGN relay cells (C50V1 = 14.5 ± 12.6 SD and C50LGN = 19.4 ± 4.9 SD) (Fig. 1C,D) (Sclar et al., 1990; Finn et al., 2007).

Figure 1.

Figure 1.

Open in a new tab

Contrast response curves along the visual pathway. A, Example extracellular traces from a simple cell in V1. B, Example extracellular traces from an LGN relay cell (marked RC) and the s-potential (marked SP) that preceded the LGN relay cell action potential. (C, D) Contrast response functions are plotted based on the F1 amplitude from the cortical simple cell (C) and the s-potential and LGN relay cells (D). Dashed lines indicate fits using Equation 1. Two different models could account for response saturation: (E) In the response nonlinearity model, saturation occurs at the same response amplitude whether the stimulus is optimal or not. Instead the C50 systematically changes with different spatial stimuli; F, In the gain control model, saturation occurs at the same contrast for different stimuli. Instead the maximum response depends on whether the stimulus is optimal.

In some LGN recordings, a small waveform often preceded relay cell action potentials. These s-potential waveforms are a consequence of RGC action potentials that provide input to the recorded LGN relay cell (Fig. 1B), and thus represent the RGC input to the LGN. To extract accurately the s-potentials, we first identified the s-potential waveforms preceding relay cell action potentials and then used this waveform model to identify s-potentials throughout the complete raw extracellular trace for that recorded cell (see Materials and Methods). From extracted s-potentials, we fit a contrast response function using Equation 1 (Fig. 1D), which also exhibited saturation with increasing contrast for F1 responses across cells (C50SP = 19.7 ± 4.4 SD).

Although our records indicate that contrast saturation is exhibited along the visual pathway from retina to LGN to V1, these records do not distinguish between mechanisms that may underlie saturation. It may be the case that response saturation at high contrast is due to an inability of the neuron to elicit a larger number of action potentials because of intrinsic mechanisms (“response saturation” model). In this model, the neuron's input is linearly related to stimulus contrast, and the contrast saturation is due to an output nonlinearity. Importantly, if response saturation were due to such an intrinsic mechanism then presenting a stimulus with different spatial configurations—thereby eliciting weaker responses—should have different saturation profiles (Fig. 1E). An alternative explanation for response saturation is that the neuron's input itself passed through a saturating nonlinearity, which does not depend on the stimulus configuration (“gain control” model). An important prediction from this model is that the spatial configuration of the stimulus should not affect the contrast at which response saturation occurs (Fig. 1F). Previous work in V1 has demonstrated that spiking response saturation occurs at the same contrast for different spatial stimuli, supporting a gain control model for cortical responses (Albrecht and Geisler, 1991; Heeger, 1992; Carandini et al., 1997).

To determine whether the response saturation or gain control model applies to contrast saturation at each stage of visual processing, we measured contrast response functions for V1 simple cells (n = 11) while varying the spatial phase of stationary sinusoidal contrast-reversing gratings. At high contrasts, some spatial phases elicited strong responses (Fig. 2A, 135 degrees), while others elicited weak responses (Fig. 2A, 225 degrees). The spiking selectivity of cortical neurons did not change with contrast, but instead low-contrast responses are scaled versions of high-contrast responses, indicative of contrast-invariant spatial tuning. For further examination of this scaling, contrast response functions were plotted for each stimulus spatial phase (Fig. 2B), and the C50 at each spatial phase was extracted from Naka-Rushton/Michaelis-Menton fits. While semisaturation constants varied little (mean C50 = 12.7 ± 5.4 SD), the contrast governing saturation did not systematically depend on whether the stimulus evoked strong or weak responses (r2 = 0.054). The contrast-invariant spatial tuning in our V1 recordings are thus consistent with a contrast gain control model, instead of the response saturation model which predicts that saturation would depend on absolute response, not contrast.

Figure 2.

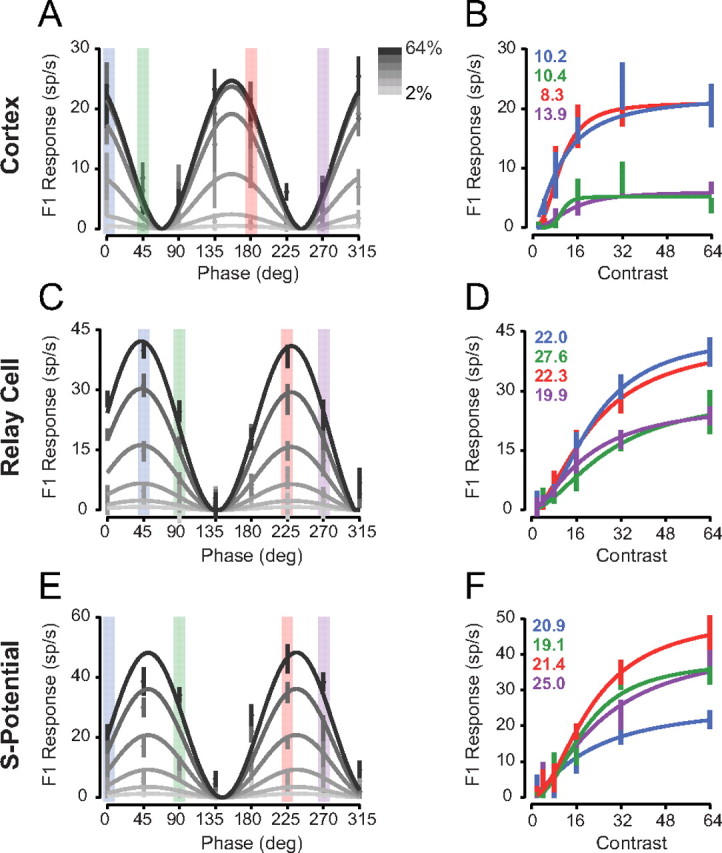
Figure 2.

Open in a new tab

Contrast response curves for different spatial phases. A, Example V1 neurons spiking F1 responses to contrast-reversing gratings of different spatial phases and contrasts are plotted relative to the stimulus spatial phase. Solid lines indicate the fits of the contrast gain control model. B, The same data from A, plotted as a function of contrast for each spatial phase. Solid lines indicate separate fits to each spatial phase using Equation 1, and the C50 for each spatial phase is indicated. C, D, Same format as A, B for an LGN relay cell. E, F, Same format as A, B for a retinal s-potential.

Contrast-reversing gratings produced responses in LGN relay cells (n = 36) resembling those in V1 simple cells. Stimulus spatial phase substantially varied overall response amplitude (Fig. 2C), but individual contrast saturation curves across stimulus spatial phases were similar (Fig. 2D) (mean C50 = 23.0 ± 3.3 SD). A similar pattern also emerged in isolated s-potentials from innervating retinal action potentials in LGN relay cell recordings (n = 12). RGC responses varied in amplitude relative to spatial phase and invariantly scaled with contrast (Fig. 2E,F). Analogous to V1 and LGN cell responses, RGC semisaturation constants from Naka-Rushton/Michaelis-Menten fits varied little with stimulus spatial phase (mean C50 = 21.6 ± 2.5 SD) and contrasts governing saturation were uncorrelated with response strength (r2 = 0.085). This pattern of responses suggests that a stimulus-invariant contrast gain control mechanism operates across multiple visual processing stages including V1, the LGN, and the retinal output.

To compare directly the gain control model and response nonlinearity model in describing spiking responses to contrast-reversing gratings, we performed a least-squares fit using each model (Fig. 3). We defined the gain control model using the following equation (Albrecht and Geisler, 1991):

graphic file with name zns02912-2196-m03.jpg

In the gain control model a linear input (h) is scaled by a gain control factor and passed through a threshold nonlinearity (Fig. 4B). The gain control factor is dependent on stimulus contrast, a semisaturation constant, and an exponent. In agreement with previous cortical studies (Albrecht and Geisler, 1991) we find that this gain control model accurately predicts our recorded measurements from V1 neurons (r2 = 0.91, Fig. 3A). We also fit the data to a response nonlinearity model using the following equation:

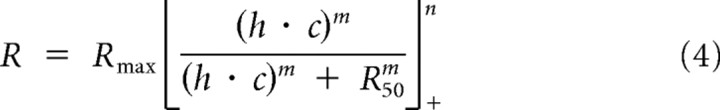graphic file with name zns02912-2196-m04.jpg

In this model, a linear input (h) is scaled by contrast and then passed through a final nonlinearity (Fig. 4A). The final nonlinearity is composed of an exponent, half-maximum response constant, and threshold rectification. Compared with the gain control model, the response nonlinearity model fails to reproduce key aspects of our recorded cortical neuron responses (Fig. 3B). In particular, this model predicts that saturation depends on the overall response to the stimulus; however, our recorded responses saturate at similar contrasts despite differences in response amplitude at each spatial phase. Consequently the response nonlinearity model consistently overestimated cortical responses (r2 = 0.71). In V1, it is clear that a contrast-dependent gain control model, invariant to stimulus spatial phase, best describes responses to contrast-reversing gratings (Albrecht and Geisler, 1991).

Figure 3.

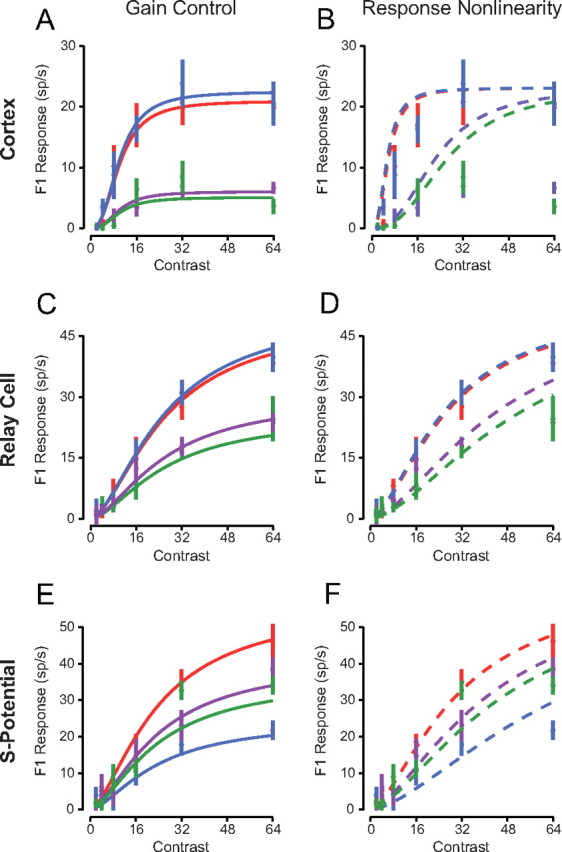
Figure 3.

Open in a new tab

Comparison of the gain control and response nonlinearity models. A, Contrast response curves were fit to functions with gain-control model fits for the example V1 neuron in Figure 2. B, The contrast responses were fit with the response-nonlinearity model. C, D, Same as A, B for an LGN relay cell. E, F, Same as A, B for the s-potential recording.

Figure 4.

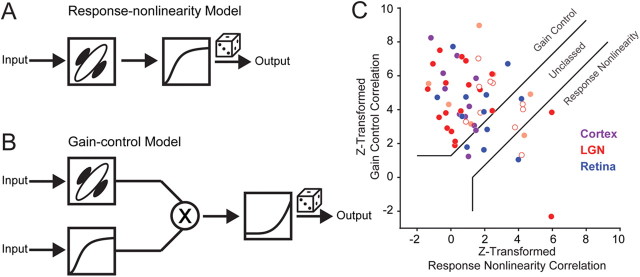
Figure 4.

Open in a new tab

Models describing contrast saturation in the visual pathway and correlation analysis. A, Response-nonlinearity model has a single final nonlinearity that depends on stimulus strength and scales contrast saturation rate (as in Fig. 1E). B, Gain control model has an independent mechanism invariant of stimulus strength and scales peak response amplitude with stimulus strength (as in Fig. 1F). C, Scatterplot of Fisher z-transformations of partial correlations between the actual responses and those predicted from the gain control model (ordinate) and from the response nonlinearity model (abscissa). Each point indicates a different cortical cell (purple), LGN relay cell (red: open Y, closed X, lightly shaded, not X/Y classified) and RGC s-potentials (blue). Following Movshon et al. (1986) and Smith et al. (2005), solid lines indicate basis for classification.

We then compared the ability of these two models to capture response saturation of LGN relay cells and innervating RGC action potentials, as described by s-potentials (Fig. 3C–F). For both LGN relay cells and RGCs, the contrast gain control model provided better fits than the response nonlinearity model for the same reason as in cortical neuron records: the rate of saturation is spatially invariant and response saturation strongly depends on contrast. A gain control model predicted recorded LGN relay cell and RGC responses (r2 = 0.91 and r2 = 0.89 respectively), while the response nonlinearity model overestimated responses, especially for high-contrast stimuli (r2 = 0.84 and r2 = 0.86, respectively). The similarity in r-squared values for these models is because of the shared correlation between models, since both models have the same linear input determining phase selectivity. To quantify accurately the differences we used a correlation analysis that removes shared correlation and classifies neurons as gain control, response nonlinearity, or unclassed (Fig. 4C) (Movshon et al., 1986). Correlations were computed using the pairs of actual and predicted responses from each model for all stimuli. The equations for partial correlation were:

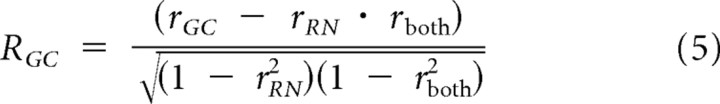graphic file with name zns02912-2196-m05.jpg
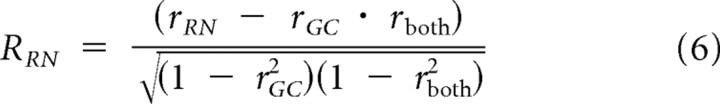graphic file with name zns02912-2196-m06.jpg

where RGC and RRN are the partial correlations, rGC and rRN are the correlations between the gain control and response nonlinearity model predictions with measured responses, and rboth is the correlation between predicted responses from each model. The z-transform of RGC was then plotted as function of the z-transform of RRN for all recordings, showing that a gain control model best describes measured F1 responses in V1 simple cells, LGN relay cells, and RGCs (Fig. 4C).

In all three stages of the early visual pathway, most of our recordings were classified as gain control (Cortex: 82%, LGN: 72%, s-potential: 58%), while few were classified as response nonlinearity (Cortex: 0%, LGN: 11%, s-potential: 8%) (Fig. 4C). Almost all records have a positive gain control correlation (RGC mean = 0.55 ± 0.21 SD, Fig. 4C). Some cells were unclassed, which may be a result of similar predictions from the response nonlinearity and gain control models. For example, if cells do not saturate significantly, the response nonlinearity and gain control models make similar predictions. We found no differences, however, in C50 values between LGN relay cells classified as gain control and those unclassed (Welch's t test, p > 0.2). In addition, while we had records from both LGN X and Y cells, there were no differences in classification between these two cell types (ANOVA, p > 0.4, Fig. 4C).

We did uncover a striking similarity between the classification of s-potential and LGN relay cell pairs: 83% of the pairs had matched classifications. The remaining cells had partial correlation values that closely straddled the classification line between gain control and unclassed. This similarity is perhaps unsurprising because individual LGN relay cells in the cat are known to be innervated by only one or very few RGC inputs (Cleland et al., 1971; Hamos et al., 1987) and s-potential efficacy is reported as >50% (Cheng et al., 1995; Sincich et al., 2007). Because of the strength of this synaptic connection, resemblance of LGN spiking responses to spikes from presynaptic RGC counterparts would be expected.

Since stimulus size was optimized for each recording in the LGN, and this may or may not reflect size preference in V1, we asked whether a gain control model best described LGN relay cell and RGC F1 responses to larger stimuli. From additional LGN recordings (n = 19) using large stimuli (4–12 degree diameter) we found that the majority of the records were still classified as gain control (LGN: 63%, s-potential: 60%), and that only few were classified as response nonlinearity (LGN: 22%, s-potential: 0%). A comparison of classification for large and optimal size stimuli in individual recordings did reveal that a minority of neurons switched between the unclassed and gain control model, but the direction of this switch was not consistent.

An alternative formulation of the gain control model suggested by Albrecht and Geisler (1991) (Eq. 3) is based on a linear-nonlinear (LN) cascade model. This model separates the components of gain control (normalization) and rectification nonlinearity. To determine whether a gain control model based on the LN cascade model also fit our records relative to the response nonlinearity model, we substituted the model suggested by Albrecht and Geisler (1991) (Eq. 3) with a LN formulation based on Carandini et al. (1997):

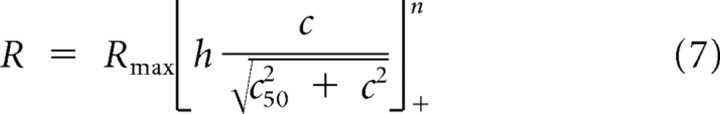graphic file with name zns02912-2196-m07.jpg

where h is the linear response, c50 is the semisaturation constant, and n is the response rectification nonlinearity. Using the partial correlation analysis above resulted in a similar distribution of neurons classified as gain control (Cortex: 72%, LGN: 56%, s-potential: 58%), and a minority classified as response nonlinearity (Cortex: 0%, LGN: 14%, s-potential: 25%). The precise formulation of the gain control model, therefore, does not seem to alter our finding that response saturation occurs early in the visual pathway in a manner that depends on stimulus contrast, and not on response saturation. The gain control model captured the response saturation for majority of neurons, while the response nonlinearity model was able to capture response saturation for only a minority of neurons. This demonstrates that aspects of cortical contrast gain control such as spatial invariance are observed at early precortical stages in the visual pathway.

Discussion

A remarkable feature of cortical neuronal responses is the ability to preserve selectivity even in the face of large changes in signal strength. Despite differences in stimulus contrast, V1 neurons are able to maintain invariant selectivity for stimulus features such as spatial phase or orientation. Yet the underlying mechanisms and visual processing stage at which such invariance first emerges have remained unknown. To identify where spatial phase invariance first emerges, we measured F1 responses of LGN relay cells and innervating RGCs while measuring contrast-response functions to contrast-reversing stationary gratings for which these neurons are strongly tuned. We found that invariance to these grating stimuli is evident in all central visual responses we measured: tuning for the contrast-reversing gratings scaled with contrast, maintaining invariance despite large changes in contrast across retina, LGN and cortex. Although the observed stimulus invariance could arise independently and duplicatively from mechanisms acting separately at each visual processing stage, the simplest explanation is that the spatial invariance observed in LGN relay cells and V1 neurons is inherited from their feedforward ganglion cell inputs, demonstrating that spatial invariance for contrast-reversing gratings originates in the retina.

Our records are not the first demonstration of spatial invariance in LGN relay cells. Using contrast reversing gratings similar to those used here, Shapely and Victor (1978) showed that temporal frequency tuning is invariant to spatial phase, despite a scaling in overall response amplitude. Temporal frequency tuning does, however, depend on contrast, shifting systematically to lower frequencies as contrast is reduced (Shapley and Victor, 1978, Sclar, 1987).

A number of different intrinsic and synaptic mechanisms could be the source of retinal spatial contrast gain control (Baccus and Meister, 2002; Gollisch and Meister, 2008, 2010). In RGCs, intrinsic sodium, potassium and other leak conductances are altered by fluctuations in stimulus luminance or membrane potential (Kim and Rieke, 2003; Weick and Demb, 2011). Further, those intrinsic conductances responsible for the nonlinear transformation of membrane potential into action potentials (spike threshold) are also attenuated by changes in contrast (Zaghloul et al., 2005). Alongside intrinsic mechanisms, synaptic mechanisms also may contribute to spatial contrast gain control, as the bipolar cells that provide input to RGCs adapt to local contrast. This adaptation of the bipolar cell response gain leads to systematic changes in the transfer function between stimulus luminance and the RGC output (Manookin and Demb, 2006; Beaudoin et al., 2007, 2008). Thus, both synaptic and intrinsic conductances in the retina potentially play roles in generating the contrast-invariant spatial phase tuning observed in our records.

Historically, the observation of contrast saturation in V1 neurons led to the development of two different phenomenological models for its generation. In one model—the response nonlinearity model—saturation with stimulus contrast is attributed to a nonlinear saturation of response after the stimulus has passed through its selectivity filter (Fig. 4A). While this model accounts for response saturation to a single, preferred stimulus, it does not account for the invariance of LGN relay cell saturation. As shown in our recorded s-potentials, LGN relay cell responses and cortical cell responses, contrast saturation occurs at the same contrast, independent of whether a stimulus excites a neuron weakly or strongly. The response saturation model, however, links saturation to response amplitude, contrary to the observed saturation that is independent of the ability to evoke responses, and thus provides relatively poor fits to the data. The second model—the gain control model—is able to account for observed contrast saturation because it inserts a nonlinearity associated with contrast at the input stage, independent of the ability of the stimulus to pass through a neuron's selectivity filter (Fig. 4B). Our observations that contrast saturation occurs at the same contrast for stimuli that weakly or strongly excite neurons are thus consistent with a gain control mechanism that acts very early in the visual pathway.

Despite our observation that contrast response curves saturate at the same contrast for all visual stimuli at each visual processing station, we did observe a significant difference in the response saturation at each visual processing station. The semisaturation contrast was systematically shifted to lower contrasts along the visual pathway. These differences in contrast saturation indicate that additional contrast-dependent mechanisms may exist such as short-term synaptic depression or inhibition to enhance the initial gain control mechanism provided by retinal mechanisms.

We find invariance for contrast-reversing gratings at each processing stage we examined, but it is important to emphasize that all stimulus feature invariance observed along the visual pathway cannot be ascribed to retinal mechanisms. For example, contrast-invariant orientation tuning emerges in V1 and cannot be accounted for by the mean firing rate of the feed forward LGN relay cells, as they are not selective for stimulus orientation (Hubel and Wiesel, 1961; Skottun et al., 1987; Troyer et al., 1998). Instead, contrast-invariant orientation tuning emerges within V1—the site at which orientation selectivity also first emerges—and is therefore due to mechanisms within V1 (Hubel and Wiesel, 1961; Finn et al., 2007). Because different aspects of response selectivity emerge as information advances through the visual system, gain control mechanisms should exist at each processing station (Sclar et al., 1990; Simoncelli and Heeger, 1998). Our observation for contrast-reversing gratings thus indicates that the retina can account for stimulus invariance for changes in spatial phase, but leave open a role for additional gain control mechanisms acting at later stages along the visual pathway as different aspects of the visual scene are processed.

Footnotes

This work was supported by grants from the National Institutes of Health (EY-019288) and The Pew Charitable Trusts. We are grateful to Jessica Hanover and Bill Geisler for helpful discussions.

References

  1. Albrecht DG, Geisler WS. Motion selectivity and the contrast-response function of simple cells in the visual cortex. Vis Neurosci. 1991;7:531–546. doi: 10.1017/s0952523800010336. [DOI] [PubMed] [Google Scholar]
  2. Albrecht DG, Hamilton DB. Striate cortex of monkey and cat: contrast response function. J Neurophysiol. 1982;48:217–237. doi: 10.1152/jn.1982.48.1.217. [DOI] [PubMed] [Google Scholar]
  3. Baccus SA, Meister M. Fast and slow contrast adaptation in retinal circuitry. Neuron. 2002;36:909–919. doi: 10.1016/s0896-6273(02)01050-4. [DOI] [PubMed] [Google Scholar]
  4. Baylor DA, Hodgkin AL. Detection and resolution of visual stimuli by turtle photoreceptors. J Physiol. 1973;234:163–198. doi: 10.1113/jphysiol.1973.sp010340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beaudoin DL, Borghuis BG, Demb JB. Cellular basis for contrast gain control over the receptive field center of mammalian retinal ganglion cells. J Neurosci. 2007;27:2636–2645. doi: 10.1523/JNEUROSCI.4610-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beaudoin DL, Manookin MB, Demb JB. Distinct expression of contrast gain control in parallel synaptic pathways converging on a retinal ganglion cell. J Physiol. 2008;586:5487–5502. doi: 10.1113/jphysiol.2008.156224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bonin V, Mante V, Carandini M. The statistical computation underlying contrast gain control. J Neurosci. 2006;26:6346–6353. doi: 10.1523/JNEUROSCI.0284-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
  9. Carandini M, Heeger DJ, Movshon JA. Linearity and normalization in simple cells of the macaque primary visual cortex. J Neurosci. 1997;17:8621–8644. doi: 10.1523/JNEUROSCI.17-21-08621.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Carandini M, Heeger DJ, Movshon JA. Cerebral Cortex. New York: Plenum; 1998. Linearity and gain control in V1 simple cells. [Google Scholar]
  11. Cheng H, Chino YM, Smith EL, 3rd, Hamamoto J, Yoshida K. Transfer characteristics of lateral geniculate nucleus X neurons in the cat: effects of spatial frequency and contrast. J Neurophysiol. 1995;74:2548–2557. doi: 10.1152/jn.1995.74.6.2548. [DOI] [PubMed] [Google Scholar]
  12. Cleland BG, Dubin MW, Levick WR. Sustained and transient neurones in the cat's retina and lateral geniculate nucleus. J Physiol. 1971;217:473–496. doi: 10.1113/jphysiol.1971.sp009581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dean AF. The relationship between response amplitude and contrast for cat striate cortical neurons. J Physiol. 1981;318:413–427. doi: 10.1113/jphysiol.1981.sp013875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dubin MW, Cleland BG. Organization of visual inputs to interneurons of lateral geniculate nucleus of the cat. J Neurophysiol. 1977;40:410–427. doi: 10.1152/jn.1977.40.2.410. [DOI] [PubMed] [Google Scholar]
  15. Finn IM, Priebe NJ, Ferster D. The emergence of contrast-invariant orientation tuning in simple cells of cat visual cortex. Neuron. 2007;54:137–152. doi: 10.1016/j.neuron.2007.02.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gollisch T, Meister M. Rapid neural coding in the retina with relative spike latencies. Science. 2008;319:1108–1111. doi: 10.1126/science.1149639. [DOI] [PubMed] [Google Scholar]
  17. Gollisch T, Meister M. Eye smarter than scientists believed: neural computations in circuits of the retina. Neuron. 2010;65:150–164. doi: 10.1016/j.neuron.2009.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamos JE, Van Horn SC, Raczkowski D, Sherman SM. Synaptic circuits involving an individual retinogeniculate axon in the cat. J Comp Neurol. 1987;259:165–192. doi: 10.1002/cne.902590202. [DOI] [PubMed] [Google Scholar]
  19. Heeger DJ. Normalization of cell responses in cat striate cortex. Vis Neurosci. 1992;9:181–197. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
  20. Hubel DH, Wiesel TN. Integrative action in the cat's lateral geniculate body. J Physiol. 1961;155:385–398. doi: 10.1113/jphysiol.1961.sp006635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kim KJ, Rieke F. Temporal contrast adaptation in the input and output signals of salamander retinal ganglion cells. J Neurosci. 2001;21:287–299. doi: 10.1523/JNEUROSCI.21-01-00287.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kim KJ, Rieke F. Slow Na+ inactivation and variance adaptation in salamander retinal ganglion cells. J Neurosci. 2003;23:1506–1516. doi: 10.1523/JNEUROSCI.23-04-01506.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lewicki MS. A review of methods for spike sorting: the detection and classification of neural action potentials. Network. 1998;9:R53–R78. [PubMed] [Google Scholar]
  24. Li CY, Creutzfeldt O. The representation of contrast and other stimulus parameters by single neurons in area 17 of the cat. Pflugers Arch. 1984;401:304–314. doi: 10.1007/BF00582601. [DOI] [PubMed] [Google Scholar]
  25. Manookin MB, Demb JB. Presynaptic mechanism for slow contrast adaptation in mammalian retinal ganglion cells. Neuron. 2006;50:453–464. doi: 10.1016/j.neuron.2006.03.039. [DOI] [PubMed] [Google Scholar]
  26. Movshon JA, Adelson EH, Gizzi MS, Newsome WT. The analysis of moving visual patterns. Exp Brain Res Supplementum. 1986;11:117–151. [Google Scholar]
  27. Naka KI, Rushton WA. S-potentials from colour units in the retina of fish (Cyprinidae) J Physiol. 1966;185:536–555. doi: 10.1113/jphysiol.1966.sp008001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
  29. Sclar G. Expression of “retinal” contrast gain control by neurons of the cat's lateral geniculate nucleus. Exp Brain Res. 1987;46:589–596. doi: 10.1007/BF00270692. [DOI] [PubMed] [Google Scholar]
  30. Sclar G, Freeman RD. Orientation selectivity in the cat's striate cortex is invariant with stimulus contrast. Exp Brain Res. 1982;46:457–461. doi: 10.1007/BF00238641. [DOI] [PubMed] [Google Scholar]
  31. Sclar G, Maunsell JH, Lennie P. Coding of image contrast in central visual pathways of the macaque monkey. Vision Res. 1990;30:1–10. doi: 10.1016/0042-6989(90)90123-3. [DOI] [PubMed] [Google Scholar]
  32. Shapley RM, Victor JD. The effect of contrast on the transfer properties of cat retinal ganglion cells. J Physiol. 1978;285:275–298. doi: 10.1113/jphysiol.1978.sp012571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shapley R, Victor JD. The contrast gain control of the cat retina. Vision Res. 1979;19:431–434. doi: 10.1016/0042-6989(79)90109-3. [DOI] [PubMed] [Google Scholar]
  34. Shapley RM, Enroth-Cugell C. Visual adaptation and retinal gain controls. Prog Retinal Res. 1984;3:263–346. [Google Scholar]
  35. Simoncelli EP, Heeger DJ. A model of neuronal responses in visual area MT. Vision Res. 1998;38:743–761. doi: 10.1016/s0042-6989(97)00183-1. [DOI] [PubMed] [Google Scholar]
  36. Sincich LC, Adams DL, Economides JR, Horton JC. Transmission of spike trains at the retinogeniculate synapse. J Neurosci. 2007;27:2683–2692. doi: 10.1523/JNEUROSCI.5077-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Skottun BC, Bradley A, Sclar G, Ohzawa I, Freeman RD. The effects of contrast on visual orientation and spatial frequency discrimination: a comparison of single cells and behavior. J Neurophysiol. 1987;57:773–786. doi: 10.1152/jn.1987.57.3.773. [DOI] [PubMed] [Google Scholar]
  38. Smirnakis SM, Berry MJ, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997;386:69–73. doi: 10.1038/386069a0. [DOI] [PubMed] [Google Scholar]
  39. Smith MA, Majaj NJ, Movshon JA. Dynamics of motion signaling by neurons in macaque area MT. Nat Neurosci. 2005;8:220–228. doi: 10.1038/nn1382. [DOI] [PubMed] [Google Scholar]
  40. Tolhurst DJ, Movshon JA, Thompson ID. The dependence of response amplitude and variance of cat visual cortical neurones on stimulus contrast. Exp Brain Res. 1981;41:414–419. doi: 10.1007/BF00238900. [DOI] [PubMed] [Google Scholar]
  41. Troy JB, Oh JK, Enroth-Cugell C. Effect of ambient illumination on the spatial properties of the center and surround of Y-cell receptive fields. Vis Neurosci. 1993;10:753–764. doi: 10.1017/s0952523800005447. [DOI] [PubMed] [Google Scholar]
  42. Troyer TW, Krukowski AE, Priebe NJ, Miller KD. Contrast-invariant orientation tuning in cat visual cortex: thalamocortical input tuning and correlation-based intracortical connectivity. J Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Weick M, Demb JB. Delayed-rectifier K channels contribute to contrast adaptation in mammalian retinal ganglion cells. Neuron. 2011;71:166–179. doi: 10.1016/j.neuron.2011.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Yu J, Ferster D. Membrane potential synchrony in primary visual cortex during sensory stimulation. Neuron. 2010;68:1187–1201. doi: 10.1016/j.neuron.2010.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zaghloul KA, Boahen K, Demb JB. Contrast adaptation in subthreshold and spiking responses of mammalian Y-type retinal ganglion cells. J Neurosci. 2005;25:860–868. doi: 10.1523/JNEUROSCI.2782-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES