Improving the Correction of Eddy Current-Induced Distortion in Diffusion-Weighted Images by Excluding Signals from the Cerebral Spinal Fluid

Abstract

Iterative Cross-Correlation (ICC) is the most popularly used schema for correcting eddy current (EC)-induced distortion in diffusion-weighted imaging data, however, it cannot process data acquired at high b-values. We analyzed the error sources and affecting factors in parameter estimation, and propose an efficient algorithm by expanding the ICC framework with a number of techniques: (1) Pattern recognition for excluding brain ventricles; (2) ICC with the extracted ventricle for parameter initialization; (3) Gradient-based Entropy Correlation Coefficient (GECC) for optimal and finer registration. Experiments demonstrated that our method is robust with high accuracy and error tolerance, and outperforms other ICC-family algorithms and popular approaches currently in use.

1. Introduction

Diffusion Tensor Imaging (DTI) is a powerful imaging technique for the non-invasive characterization of the microstructure of normal and pathological tissues. DTI data, however, are vulnerable to geometric distortion caused by eddy current (EC). DTI data typically are acquired using echo-planar imaging (EPI) pulse sequences. Consequently, rapid switches between the strong gradients of diffusion-sensitizing magnetic fields inevitably create residual gradients that produce EC-induced distortion. Often the bandwidth of the phase-encoding direction is routinely much narrower than the other two (readout-encoding and frequency-encoding) directions, making the phase-encoding direction of the diffusion-weighted (DW) image more sensitive to contamination of EC-induced distortions caused by the DW gradient. Furthermore, because the amplitude and direction of the diffusion gradients determine the magnitude of the EC-induced distortion, DW imaging (DWI) data acquired along different directions of gradient contain different distortion. Misregistration among DWI data along differing gradient directions will produce errors in the reconstruction of the diffusion tensors in virtually every voxel of an image, and subsequently in the derived measurements. These include the apparent diffusion coefficient (ADC)[1], fractional anisotropy (FA)[2] or ellipsoidal area ratio (EAR)[3], and the procedure of fiber tracking. Therefore, EC-induced distortions must be corrected in all DW images before a diffusion tensor is reconstructed. Many algorithms have been developed for correcting EC-induced distortions, and can be classified into three categories. The first category are those algorithms that rely on improving MRI pulse sequences, including those compensating ECs by changing the shape of the gradient amplitude envelope [4] and those designing special pulse sequences [5–7]. For example, the bipolar gradient imaging schema [6] minimized EC-induced distortion by using pairs of bipolar gradients, which requires a prolonged diffusion-weighted time and thus results in an obvious signal attenuation due to transverse relaxation. Most investigators, however, do not have easy access to the proprietary computer codes required to program pulse sequences.

The second category of algorithms for correcting EC-induced distortions generally operates on DWI data in k-space [8–10]. The processing and computations involved in the k-space correction algorithms, however, are often complex. For example, one representative work [10] proposed first measuring the phase evolution caused by EC fields along a set of reference DW gradient directions that are parallel to the coordinate axes, using these measurements to estimate the true phase evolution along particular spatial directions other than those that are parallel to the coordinate axes, and then using those estimates to remove EC-induced distortions from the k-space data. The third category refers to post-processing methods that usually coregister the DW images to a reference image. In most cases, the reference image is one set of the baseline images that is in theory acquired without the application of a DW gradient and is therefore considered to be free of EC-induced distortions by DW gradients. The methods in this third category are appealing because they are generally flexible in permitting the correction of imaging data off-line.

Among these various post-processing methods, the Iterative Cross-Correlation (ICC) algorithm [11], is one of the most popularly adopted. It estimates EC-induced distortion in DW images by cross-correlating the DWI data with the reference images along the phase-encoding direction. Unfortunately, ICC is known to correct accurately only DWI data that are acquired at b-values lower than 300s/mm² [12]. This is because DW signals deriving from the regions of cerebrospinal fluid (CSF) within the images, when measured at higher b-values, are much weaker than those measured in the reference images, thereby undermining the accuracy of the cross-correlation of those DW images with the reference [11]. A number of remedies have been proposed to address this limitation of the ICC algorithm [12–15], such as using a fluid attenuated inversion recovery (FLAIR) sequence to suppress signals from CSF [13] or acquiring an additional set of images using gradients of opposite polarity to estimate the EC-induced distortion present in the original dataset [15]. These remedies, however, generally require either the acquisition of additional imaging data or the manipulation of specific pulse sequences, thereby significantly increasing the already lengthy scan time. Moreover, the need to acquire additional imaging data means that these revised ICC methods no longer involve only post-processing procedures that can be at the convenience of the investigator off-line.

Because the primary determinant of the errors in estimating distortion using the ICC algorithm derives from the difference in image contrast between the reference and DW images in the regions containing CSF, excluding the signal of the CSF when estimating distortion should immediately and dramatically improve the performance of an ICC-based algorithm for correcting EC-induced distortion in DWI data. Compared with the currently available methods for suppressing signals from CSF [13], this purely postprocessing approach would not require extra pulse sequence or imaging data.

We therefore propose to improve the ICC algorithm by excluding the CSF signal from the distortion estimation. We first segment the brain and coarsely identify the regions of CSF (including both cortical and ventricular CSF) in a binary mask that excludes the CSF regions. This mask is then used within the conventional ICC algorithm to estimate the initial parameters of distortion. As the segmentation step may not have accurately outlined the regions of CSF, we then use Mutual Information (MI) instead of cross-correlation in the cost function to refine the estimation of distortion for coregistering the reference with the DW images. We use MI because it has been shown to be a robust and accurate measure of similarity for registration of multimodal images in many studies [16–19]. With this measure, we use a 3-paramter affine transformation and an algorithm called Limited memory Broyden Fletcher Goldfarb Shanno with bound constraint (L-BFGS-B) to find the optimal parameters for correcting distortion (see the Method section)[20]. L-BFGS-B algorithm can perform optimization without computing the Hessian matrix, which is known to be difficult to obtain in numerical calculation [20].

2. Preliminary

Iterative Cross-Correlation

The ICC model estimates distortion parameters by calculating the cross-correlation between the DW and reference images along each corresponding column of their reconstructed images at a higher resolution. The distortion is characterized by three parameters, M, T and S within the plane of an image slice (for convenience we use the notation that the image lies in the XY plane, with X, Y, and Z being the frequency-, phase-, and slice-encoding directions, respectively). M represents the uniform scaling that the residual gradient produces in the phase-encoding direction Y; T represents the uniform translation that the residual gradient in the slice-encoding direction Z produces along Y; and S represents shear deformation that the residual gradient in the frequency-encoding direction X produces parallel to Y. As mentioned earlier, EC-induced distortion is routinely more severe along the Y direction than in the other two directions, and the distortion along the other two directions can be neglected. We therefore just consider correcting distortion along the Y direction. In the process of evaluating the EC-induced distortions in a slice-wise manner, the displaced locations Y′ of the voxels in each column X of the distorted image can thus be defined as follows:

$$Y^{\prime }=MY+T+SX=MY+T^{\prime }(X)+\epsilon$$ (1)

where ε is noise; and T′ (x) is the distance of translation along Y, which depends linearly on X. The MTS (i.e., magnification, translation and shear) parameters, thus can be estimated by maximizing the cross-correlation between corresponding columns of the reference and DW images [11].

Mutual Information

MI is based on the concept of entropy, which describes dispersion in the distribution of gray scale values in an image. Maes [21] proposed the use of the entropy correlation coefficient (ECC) (Equation (2)). The ECC is less sensitive to slight changes of overlap between the images being coregistered:

$$\mathit{ECC}(R,D)=\frac{2·I(R,D)}{H(R)+H(D)}$$ (2)

where H(R) and H(D) are the Shannon marginal entropies of two images R and D, respectively; I(R,D)=H(R)+H(D)−H(R,D); and H(R,D) is their Shannon joint entropy, which indicates the dispersion of the joint probability distribution calculated by all the overlapping portions of the images R and D. The original Shannon entropy calculation did depend on image intensity, but did not depend on the pixel location in the images that provides information of spatial characteristics, a feature that is always critical to the success of image registration. Having realized this important fact, other investigators then proposed to add into the MI calculation a measure that characterizes the intensity gradients at corresponding points of the images [22]. Inspired by this approach, we propose in the present work to combine gradients information with ECC and thus define the (GECC), as follows:

$$\begin{array}{l}\mathit{GECC}(R,D)=G(R,D)\mathit{ECC}(R,D)\\ G(R,D)=\sum _{(x,x^{\prime })\in R\cap D}(w({\alpha }_{x,x^{\prime }}(\sigma ))min(\mid \nabla x(\sigma )\mid ,\mid \nabla x^{\prime }(\sigma )\mid ))\\ {\alpha }_{x.x^{\prime }}(\sigma )=\mathit{ar}cos\frac{\nabla x(\sigma )·\nabla x^{\prime }(\sigma )}{\mid \nabla x(\sigma )\mid \mid \nabla x^{\prime }(\sigma )\mid }\\ w(\alpha )=\frac{cos(2\alpha )+1}{2}\end{array}$$ (3)

where G (R, D) is gradient information computed for each point x in R and its corresponding point x′ in D. ∇x(σ) and ∇x′ (σ) denote the gradient vectors of R and D at points x and x′ with a Gaussian kernel of scale σ respectively. |·| denotes the calculation of magnitude. α_x,x′ (σ) is the angle between the two gradient vectors. w is a weighting function that emphasizes both very small angles (around zero) and angles that are approximately equal to π[22]. Note in Equation (3) that multiplying the weighting function and minimum of the gradient magnitudes favors the strong gradient occurred in both images, where either the two gradient vectors are parallel, or the two magnitudes are significant, or both are true. Summation of these products for all points in R and D thus provides general information on the interaction of gradient in the two images, which will be multiplied to the original ECC.

In general, MI works best when the histogram of two images shows highly clustered voxel intensities. Voxel values in the CSF regions are dramatically different in the raw data acquired at differing b-values, thereby containing large variations. This variation consequently significantly disperses the voxel clusters in the joint histograms used in MI. Therefore, identifying and then excluding CSF regions or assigning the CSF regions with a unified intensity value will help to optimize the coregistration of DWI data to the reference data using MI.

Because improper initialization will definitely cause excessive number of iterations in an optimization procedure, which increases the opportunity of generating local extrema [23], properly initializing the parameters to MI in our procedure is deemed crucial for accurately and effectively estimating the EC-induced distortion. This is particularly important when MI registration is applied to the low-resolution multimodal images. Moreover, such proper initialization of the registration parameters is expected to effectively narrow down the scopes for searching the true values in the registration at finer resolutions in the late stages, so that it will help to further accelerate the optimization procedure [24]. Our method contains such an initialization process (the next section).

3. Materials and Methods

The Method

We first used BET (Brain Extraction Tool, FSL4.0, http://fsl.fmrib.ox.ac.uk/fsl/bet) to extract the brain from extra-cerebral tissue. We then used FAST (FMRIB’s Automated Segmentation Tool, FSL4.0, http://fsl.fmrib.ox.ac.uk/fsl/fast) to segment the brain. We then use a pattern recognition tool developed in-house using active contour [25] to identify the ventricles in the brain and thus formed a brain mask that excluded the background and CSF signals.

We then applied the ICC algorithm to the masked images that excluded the CSF signals to obtain an approximate estimation of the distortion parameters MTS. (We call the procedure up to this step an ICC-mask algorithm.) Based on these masked images, we next conducted a finer estimation of the distortion parameters using MI within a small range of the initial values. (For future reference, we name the procedure of coregistration combining MI with the CSF mask without taking advantage of the step of parameter initialization a MI-mask algorithm.) The 3-paramter affine registration based on MI was thus optimal for the EC-induced distortion. We calculated GECC between two corresponding images as a cost function to estimate suitable values of MTS within the finer range. The values yielding the highest GECC were selected to confirm the optimal MTS corresponding to the distorted image D. The L-BFGS-B algorithm was used to identify the highest GECC within the search space. For convenience, our approach, including all of the above-mentioned steps (i.e., ICC-mask for initializing the searching of parameters and then MI starting from the initialized parameters using the CSF mask), will be referred to as “our method” (in short, ICC-mask plus MI-mask).

In addition, it is worth noticing that artifacts due to the interpolation of voxel intensity during the procedure of imaging registration and warping may introduce additional bias that may have a non-negligible impact on the accuracy of estimating the distortion parameters. Such interpolation-induced artifacts occurring in the MI function may thus seriously impair the accuracy of registration [26]. We therefore used an approximate Hanning-windowed Sine function to correct the artifacts caused by interpolation of image intensities [27], and to moderate the sharp changes that MI can introduce into the dispersion of the joint histogram distribution. The joint dynamic profiles of entropies were consequently smoothed and local extrema in the procedure of iterative searching tended to disappear.

In summary, our method consists of following steps (Fig. 1):

Figure 1.

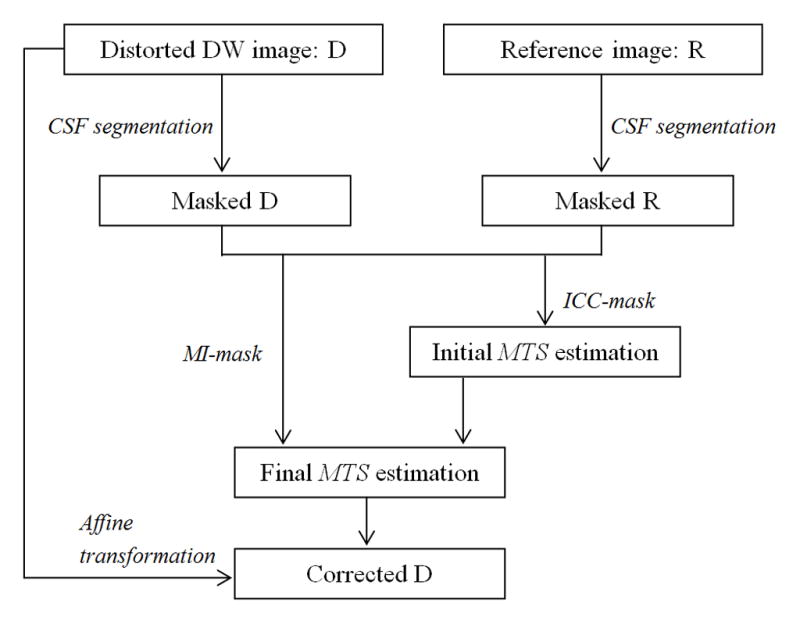
The flow chart of our proposed method for correction of eddy-current induced distortion.

1. Generation of two binary masks M_r and M_d for the reference image R and the distorted image D respectively, in which value 0 masks the CSF in the brain region and background outside of the brain;

2. Generation of the masked images R and D for the subsequent estimation;

3. Application of the ICC algorithm to the masked images R and D for an initial estimation of the parameters MTS. The ICC algorithm searches the scaling factor M₀ within the range of 0.85–1.15 (uniform scale, as suggested elsewhere [11]) at an incremental step of 0.005; the translation factor T₀ and shear factor S₀ are estimated by linear regression fitting on the cross-correlation values that the ICC algorithm has estimated for each column [11].

4. Application of the 3-parameter affine registration based on GECC to the masked images R and D for more accurate estimations of the parameters MTS in the finer searching space (M: M₀±0.1; T:T₀± 2; S₀: S±0.2). Because MI is suitable for registration of imaging data with different contrast, such as the reference baseline data and the DWI data in our case, we use ICC to estimate the initializing values for finer registration to be conducted using MI.

Simulations and Experiments

To examine the effectiveness of our proposed method for distortion correction, we conducted four experiments using three types of data: simulated, real human data and hybrid human data. The first two were simulations that used simulated data and the other two used human data.

In the first simulation experiment, we demonstrate the performance of our method using simulated datasets. We simulated a reference image A and one set of images B containing EC-induced distortions. Both images were created in Matlab 2008a (The Mathworks, Inc., MA, USA) and were of dimension 256×256. We first generated an image A₀ that mimicked the contrast of a typical T2-weighted image containing an annulus-like structure. For simplicity, we used only the inner circular region to simulate, in combination, both the cortical and ventricular CSF. The intensities within the inner ring were higher than those within the body of the annulus. We superimposed onto this image a small amount of Rician noise (standard deviation σ =10) to obtain image A. We then generated an image similar to A₀ that had a reversed contrast in the inner circle and in the body of the annulus. We superimposed onto the image more severe Rician noise (standard deviation σ = 40) to simulate the situation in the real world that the DW image always suffers heavier noise than do the reference ones; and we then distorted the image with parameters MTS within the range {M (0.85,1.15), T (−2, 2), S (−0.2, 0.2)}, to obtain the set of distorted images B (Fig. 2) (Note: the parameters MTS denote transformations in the direction from the distorted to the reference image space). We simulated a total of 200 sets of images A and B with MTS values evenly distributed within the above-mentioned scopes.

Figure 2.

A typical example of the simulated datasets for the first Experiment. (a) Reference image A, which is the simulated baseline image; (b) A typical instance of image B, which is distorted with noise added, simulating the conventional diffusion-weighted image that contains eddy-current induced distortion.

We then qualitatively evaluated the performance of our algorithm by extracting the boundary of the reference image A and superimposing it onto both the uncorrected and corrected images B. To assess functions of two components, the CSF mask and the MI calculation, we also directly compared the performance of our method (MI-mask after parameter initialization using ICC-mask) with those of the following methods: ICC, ICC-mask, ICC-MI (ICC algorithm for initialized parameters and MI algorithm without using the CSF mask), ICC-mask-MI (ICC-mask algorithm and MI algorithm, using parameters initialized by ICC-mask but without using the CSF mask in the MI step). Methods were compared by checking the estimated MTS parameters against the parameters that we used in preparing the simulated data. We also tested both the MI and MI-mask algorithms that did not take advantage of initial parameters, and found that the results contained large errors and are not included here. The estimation accuracy of each of the parameters was indexed by the mean error ε̄ and corresponding standard variance σ_ε as follows:

$$\begin{array}{l}\overline{\epsilon }=\frac{1}{N}\sum _{t=1}^N\frac{|P_i-P_0|}{\left|P_0\right|},\\ {\sigma }_{\epsilon }=\frac{1}{N}\sqrt{\sum _{t=1}^N{(\frac{|P_i-P_0|}{\left|P_0\right|}-\overline{\epsilon })}^2}\end{array}$$ (4)

where P_i is the estimated parameter in each simulation; P₀ is the actual parameter that we used in each simulation; and N is the number of repeated simulations.

In addition, we calculated the voxel-wise mean Euclidian distance (MED) of image intensity between the undistorted DW data (reference) and the corrected DW images to highlight the difference between each correction and the ground truth. We repeated this process for all 200 simulated datasets.

The second simulation assessed the robustness of our algorithm, examining how the accuracy of segmenting the CSF affected the performance of our method. We assumed that removal of any portion of the CSF would improve the accuracy of the ICC algorithm. Due to inherent imperfections in segmentation algorithms, we sought to assess whether our method could tolerate error in excluding signal from the complete region of CSF. We thus randomly deformed the true CSF mask of the simulated distorted image within a range that led to 20%–100% overlap between the deformed masks and the true mask (mismatch percentage ≤ 80%). The overlap percentage is defined as:

$$\mathit{overlap}=\frac{\sum v_d\cap v_{\mathit{ori}}}{\sum v_d\cup v_{\mathit{ori}}}\times 100\%$$ (5)

where the v_ori and v_d and are the CSF parts in the original mask and deformed mask, respectively. We then compared the corrected results using ICC-mask, ICC-mask-MI and our algorithm quantitatively by checking the MEDs of the image intensity. This experiment was also repeated 200 times. The correlation between MED and degree of overlap generally reflects the impact of the accuracy of CSF masks on the accuracy of estimating the parameters for distortion correction.

In the third experiment, we used 10 datasets from healthy human participants to assess the effectiveness of our method in practice. We evaluated the performance of our method qualitatively by superimposing the extracted contour of the reference baseline data onto the corrected DWI and FA data for visually checking the morphological agreement, and quantitatively by checking the percentage of ill-conditioned tensors in the reconstructed DTI data. Because tensors are by definition to be positive definite and artifacts due to various reasons including EC-induced distortion will damage the feature, this percentage is a terminal index for evaluating the quality of the DWI. These comparisons were conducted for results generated using the conventional ICC algorithm, the FDT (FMRIB Diffusion Tool, http://www.fmrib.ox.ac.uk/fsl/fdt/), and our method for EC distortion correction. The EC distortion correction in FDT, short for FDT algorithm, is a popular image-based multimodal registration method that can correct both EC-induced distortion and bulk subject motion in DWI data using MI-based affine registration. Because the comparison was purely for checking the performance of EC-induced distortion, we used data that were acquired with no or negligible motion for comparability of the results across these methods.

In the fourth experiment, we further accessed the effectiveness of our algorithm using synthesized hybrid human datasets, which were artificially imposed more severe distortion to real-world adult human data by randomly altering M, T, and S parameters in a prespecified range {M (0.85,1.15), T (−2,2), S (−0.2, 0.2)}. We did so because the DWI data acquired from the scanners commercially available today have already been corrected for EC-induced distortion, leaving limited space for testing our method and comparing it with other tools (also see Discussion section). That is, although we would have liked to compare the performance of methods on real-world data we instead had to impose simulated distortion. We compared corrected results using our method with the conventional ICC and the FDT algorithms qualitatively. The contours of the brains extracted from the FA maps of the DWI images corrected by these methods were compared visually against the reference data. In addition, a quantitative comparison based on the ill-conditioned tensors in the reconstructed DTI data was also performed for the DWI data produced by the different correction algorithms.

Imaging Protocol

The DWI images of each of the 10 participant were acquired with their written consent on a GE 3.0 Tesla MR scanner (General Electric, Milwaukee, Wisconsin) using a single-shot spin-echo echo planar imaging (SE-EPI) pulse sequence with diffusion gradients at b=1000 s/mm² applied along 15 non-collinear spatial directions in addition to 3 baseline images acquired without applying a diffusion gradient. (This DTI sequence employed bipolar gradients for diffusion.) Slice thickness was 2.5 mm with no gap, and about 60 axial slices were acquired to cover the entire brain, at an in-plane interpolated resolution of 0.9375 mm. Echo time (TE) was minimal at about 80 ms; repetition time (TR) = 15700 ms; field of view (FOV) =240mm × 240mm, matrix =132×128, number of excitation (NEX) = 2. The final images were machine-interpolated to an in-plane resolution of 256×256. Total DWI scanning time was 9 minutes 57 seconds. Slices were orientated parallel to the anterior commissure-posterior commissure (AC-PC) plane.

4. Results

In the first simulation experiment, our method demonstrated a significant improvement over the ICC, the ICC-mask, ICC-MI, and ICC-mask-MI algorithms in estimating the distortion parameters (Fig. 3). The contour of the reference image perfectly matched the contour of the distortion corrected image generated from our method whereas there were clear disagreements with the distortion corrected image using the other methods. This was most pronounced with the ICC method. The individual MTS values also support this impression (Table 1), which shows that the values of MTS calculated by the other algorithms (especially the ICC algorithm) deviated significantly from the known values. The MTS estimation which resulted from the ICC algorithm had a large divergence from the ground truth and was also inconsistent with large variations. Results using the ICC-mask, ICC-MI, and ICC-mask-MI algorithms were not stable in estimating T and S, whereas our method demonstrated consistently small errors and deviations (Table 1). The MED values between the reference and the corrected DW images generated using our method were between 0 and 15. This contrasted with the MED values of 15–37 between the reference and the ICC corrected images, 5–21 between the reference and the ICC-mask corrected images, 11–35 between the reference and the ICC-MI corrected images, and 9–21 between the reference and the ICC-mask-MI corrected images. These performance comparisons (Fig. 3, and Table 1) demonstrate that removal of the CSF signal can significantly improve the accuracy of the estimation of M and that combining the use of a CSF mask and MI can make the evaluation of T and S more accurate.

Figure 3.

A comparison of the performance of distortion correction using various methods based on the simulated data. The boundary of the reference image was extracted and superimposed onto the corrected images. (a) The distorted image B as shown in Fig.2b; (b) The corrected result by the standard ICC; (c) The result by ICC-mask; (d) The result by ICC-MI; (e) The result by ICC-mask-MI; and (f) The corrected result by our method. The result using our method achieved the best agreement between the extracted contour of the reference image and the corrected DWI data.

Table 1.

Quantitative comparisons of the performance of the standard ICC, the ICC-mask, the ICC-MI, the ICC-mask-MI, and our algorithm. The mean error and corresponding standard variance error of the estimated MTS parameters were calculated, respectively. The mean Euclidian distance (MED) values of image intensity based on the 200 images simulated with varying values of MTS are also shown in the table. The standard ICC performed the worst and the most unstable, whereas the algorithms combining with the CSF mask or MI obviously improved performance. The mean error and standard variance error of the estimated parameters in our algorithm were the smallest, indicating that our method performed the best. The errors of MTS were calculated separately using Equation (4), with arbitrary unit (a.u.).

	M error	T error	S error	MED
ICC	0.0394±0.1224	1.6717±3.8361	0.3185±0.9641	31.14±4.2628
ICC-mask	0.0021±0.0008	0.1523±0.1765	0.0453±0.1695	13.97±1.9945
ICC-MI	0.0044±0.0022	0.2746±0.6153	0.0511±0.1197	15.34±1.9554
ICC-mask-MI	0.0026±0.0015	0.1520±0.3324	0.0377±0.1156	15.00±1.3831
Our Method	0.0016±0.0004	0.0843±0.1177	0.0115±0.0221	12.29±1.0716

In the second simulation experiment, the accuracy of ICC was dramatically improved when the CSF mask was incorporated: the MED of the ICC-mask approach decreased from 35 when no CSF was used to approximately 16 (the MED of using the ICC algorithm alone was not shown because it was a straight line and far from the others), indicating the great benefit that the CSF mask offers (Fig. 4). This confirmed our hypothesis that any exclusion of CSF would help improve the performance of ICC. The experiment also demonstrated the benefit of the combined ICC-mask and MI approach, as its MED ranged around 16 in comparison to the MED of ICC-mask, which was 16–26 (Fig. 4). Our method performed the best (MED ranged narrowly from 13–16) using MI-mask with parameters initialized by the ICC-mask algorithm. Moreover, in contrast to the ICC-mask algorithm, our method was much less sensitive to the error contained in the binary CSF mask. However, increased accuracy in the CSF mask did lead to a decrease in estimation errors of the parameters. Although the performance of ICC-mask-MI was relatively consistent when the mask mismatch varied, our method overall outperformed the ICC-mask-MI method because the MED of our method was consistently lower (Fig. 4). This is especially true for overlap >50%.

Figure 4.

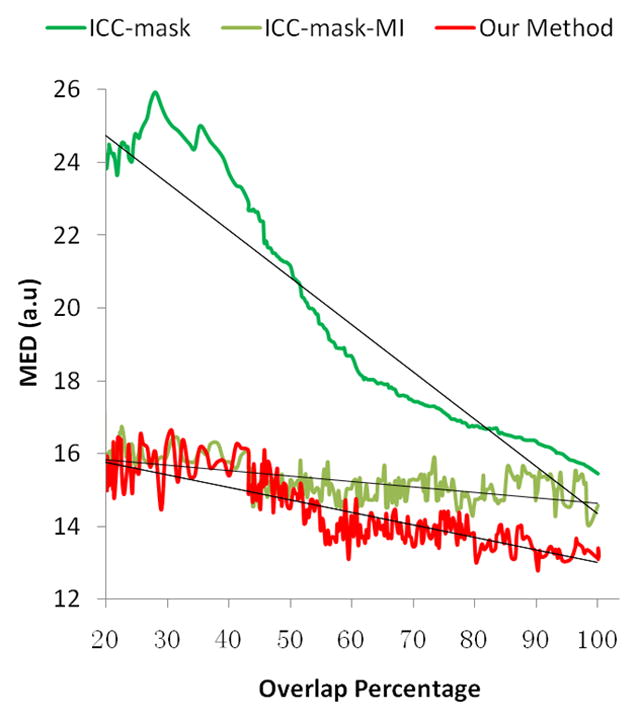
Quantitative comparisons of the performance of the ICC-mask, ICC-mask-MI and our algorithm with varying degrees of inaccuracy in segmentation of the CSF. MED is the mean Euclidian distance of image intensity with arbitrary unit (a.u.), which is calculated based on 200 images simulated with distortion parameters MTS = (1.1, 1.5, 0.15). The dark lines illustrate the linear trend of the performance of ICC-mask, ICC-mask-MI, and our method respectively. Obviously, the accuracy of the CSF mask has a great impact on the performance of the ICC-mask algorithm (the dark green curve). Combining ICC-mask with MI (the light green curve) greatly improves the overall performance, whereas our method (the red curve) can further improve the performance in estimating the parameters for correcting the EC-induced distortion. This results in errors consistently lower than the ICC-mask-MI approach (the light green line). This experiment demonstrates that identifying and then excluding CSF is important, both in the ICC and MI algorithms, and properly initializing the parameters is helpful to achieve higher accuracy in performing distortion correction.

In the third experiment, which used human data, the superimposed contour of the baseline image again demonstrated that using our algorithm was much better than using the ICC algorithm and also better than the FDT algorithms, especially in lower boundaries of the brain. Comparing the FA maps generated from DWI data with and without correction (Fig. 5), we can see that using our method provided much clearer details and structures, largely because it more accurately coregistered DWI data acquired along differing directions of the DW gradients, thereby improving the accuracy of tensor estimation. The fuzzy boundary surrounding the brain in the FA map generated using DWI data corrected with our method was much thinner than the boundaries in the uncorrected data and those corrected using the ICC or FDT algorithm (Fig. 5). Note the human data were acquired using bipolar gradients, and thus the major portion of EC-induced distortion was already removed in the obtained imaging data. This indicates that distortion correction of the data using our algorithm was more accurate than it was using the competitors’.

Figure 5.

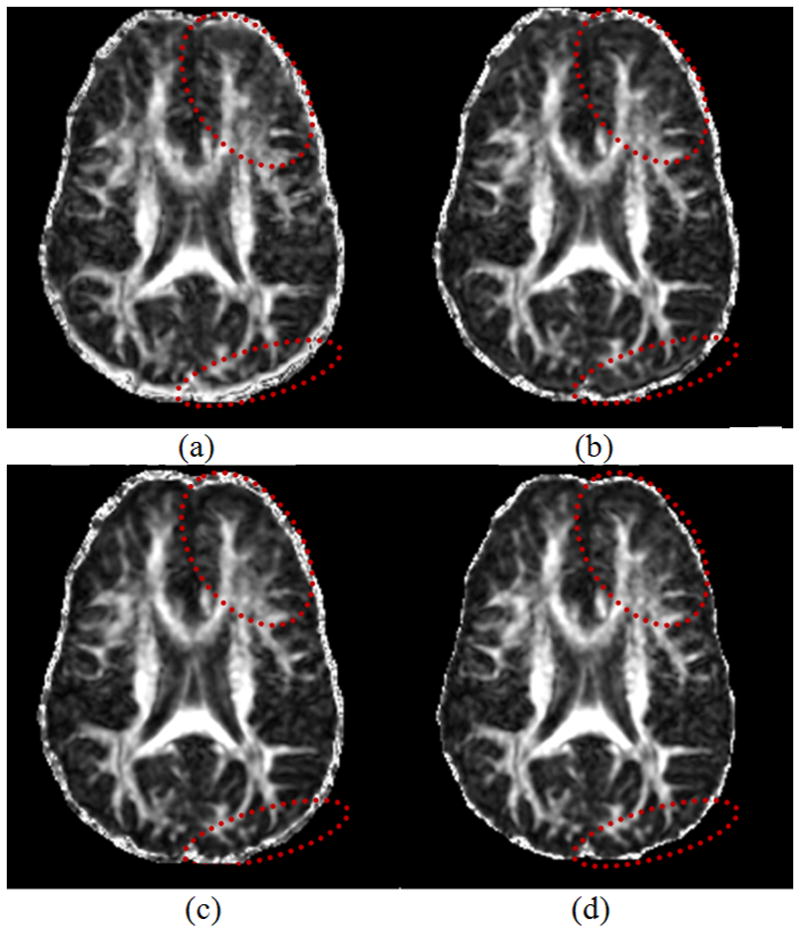
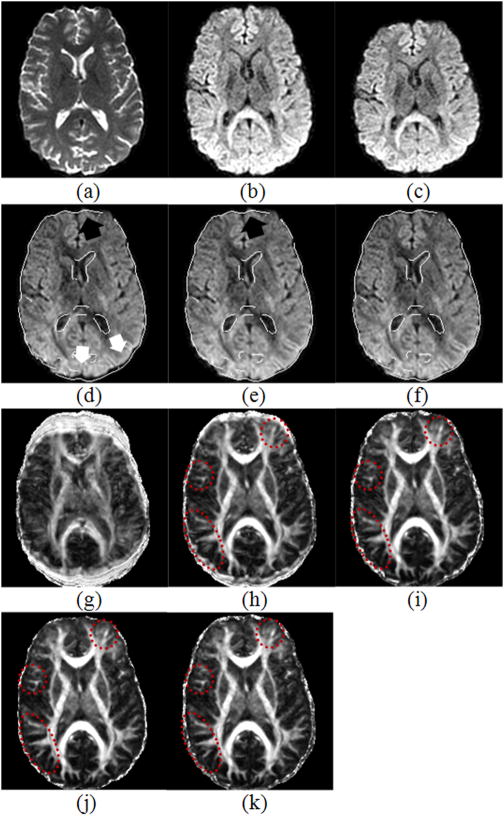
A comparison of Fraction Anisotropy (FA) maps generated from the DW images corrected using the ICC, FDT, and our method. (a) Uncorrected image; (b) Image corrected by ICC; (c) Image corrected by FDT; (d) Image corrected by our method. Note particularly the regions indicated by the ellipses where our method generated the clearest structures, implying that our method best corrected the distortion so that all DWI were well coregistered. Moreover, the fuzzy boundary around the brain is thinner in (d) than in (a), (b) and (c), indicating once again that our method more accurately coregistered the DWI data.

Quantitative evaluation of the percentage of ill-conditioned tensors (Table 2) showed that all three methods reduced the number of non-positive definite tensors, indicating that all three approaches did improve the distorted DWI data to some extent. This improvement varied according to method: 5.56% for ICC, 13.58% for FDT, and 39.51% for our method, once again, showing that the performance of our method was superior to the other two methods. Finally, a comparison of the overlapped areas based on the extracted contour of the reference data that was superimposed onto the corrected images revealed that our algorithm generated the best morphological match between the corrected images and the reference image (ICC: 95.49%, FDT: 96.83%, and our algorithm: 97.72%), suggesting that our method not only effectively corrected DWI data volumetrically, but also morphologically with high accuracy. The MED analysis, the comparisons of ill-tensor percentages and overlap areas based on the 10 real datasets thus unanimously suggested that our method outperformed its competitors.

Table 2.

A comparison of the percentages of ill-conditioned tensors reconstructed from DWI data corrected for EC-induced distortions using the different algorithms in the third experiment. “Improvement” is the reduction compared with the number of ill-tensors in the uncorrected DWI data. Our algorithm yielded the fewest ill-conditioned tensors and greatest improvement.

	Not Corrected	ICC	FDT	Our Method
Ill-conditioned	1.62%	1.53%	1.40%	0.98%
Improvement	-	5.56%	13.58%	39.51%

The fourth experiment, using the hybrid human datasets, corroborated the first and third experiments and buttressed the case that our method is superior to the ICC and FDT. Our method improved on the competitors both morphometrically, with nearly perfect registration (Fig. 6), and volumetrically, with the greatest improvement in achieving the smallest percentage of ill-conditioned tensors that was calculated based on all the brain voxels in the image (Table 3).

Figure 6.

A comparison between different approaches using the hybrid human datasets based on the corrected DWI data and their corresponding Fractional Anisotropy (FA) maps. The boundary of the reference image was extracted and superimposed onto the corrected images. (a) The reference baseline image; (b) The original raw DW image directly downloaded from our MR scanner; (c) An artificially distorted DW image to be corrected; (d) Image corrected using ICC; (e) Image corrected using FDT; (f) Image corrected using our method; (g) The FA map corresponding to the distorted data in (c); (h) The FA map corresponding to the ICC-corrected data in (d); (i) The FA map corresponding to the FDT-corrected data in (e); (j) The FA map corresponding to the data corrected by our method in (f); (k) The FA map corresponding to the original reference (undistorted) dataset in (b). Note particularly the regions at the tip of the arrows, where mismatches between the image and the contour were apparent in the images corrected by ICC (gaps at the tip of the white arrows) and FDT (image went beyond the contour at the tip of the black arrow). Such mismatches are not present in the image corrected by our method. Comparing the circled regions illustrates the clarity difference between the corrected results using different approaches. In this comparison, our method appears to perform the best.

Table 3.

A comparison of the percentages of ill-conditioned tensors reconstructed from the hybrid DWI data corrected for EC-induced distortions using the different algorithms in the fourth experiment. “Improvement” is the reduction compared with the number of ill-tensors in the uncorrected hybrid DWI data. Raw DWI refers to the data before superimposing the artificial distortions. Our method performed more efficiently than did the other algorithms.

	Hybrid	ICC	FDT	Our Method	Raw DWI
Ill-conditioned	4.13%	0.74%	0.68%	0.47%	0.37%
Improvement	-	82.08%	83.54%	88.62%	-

5. Discussion

We have presented a novel algorithm for effectively correcting EC-induced distortions in DWI data acquired using SE-EPI sequences. This model employs a number of techniques as detailed in the text from different fields to improve the performance of the ICC-family of algorithms for correcting distortions. The experiments with DWI data acquired at high b-values (1000 s/mm² in our case) have shown that this method not only has overcome the major limitation of the ICC-family algorithms, i.e. the inability to treat distortions in DWI data acquired at b-values larger than 300 s/mm² [12], but it also has vastly outperformed the ICC and FDT methods that are popularly used in practice today for correcting EC-induced distortions.

Compared with other MI-based correction methods [17, 19], our MI-based registration algorithm for EC-induced distortions in DWI data has two distinct features: First, our algorithm identifies the regions of the CSF and then excludes the signals from CSF to initialize the estimation procedure for improve the accuracy of MI registration. Second, this algorithm uses the CSF mask to help further improve the accuracy of MI registration. In addition, our MI registration algorithm also adopts L-BFGS-B for searching optimized solution and a Hanning-windowed Sine function for correcting the artifacts caused by interpolation of image intensities. Last but not least, our method is purely a postprocssing approach, which is independent from manipulating pulse sequences or the k-space and therefore is relatively easier for average users.

Segmentation of the CSF is a key to the success of the accurate estimation of parameters for distortion correction. As shown by the tests using simulations and real human data which adopts the ICC algorithm to correct distortion, with or without the CSF mask, using the mask can significantly improve the accuracy in estimating the distortion. Using the CSF mask also helps improve the accuracy of MI registration, because the CSF mask merges the small clusters of varying intensities in the CSF regions to the cluster of background, thereby enhancing this uniformly valued cluster which is large and consequently benefits MI registration [24]. Moreover, we have shown that the identification of the CSF regions does not have to be ideal. That is, our method is robust, regardless of whether the CSF portion is relatively under or over identified. Although the performance of ICC-mask-MI is relatively consistent when the mask mismatch varied, our method has demonstrated a consistently lower MED compared with the ICC-mask-MI method (Fig. 4). Because of this high fault tolerance, our method does not require the segmentation of CSF to be performed separately and repeatedly for the baseline reference and the DWI data, even though they usually are originally mismatched slightly. Using our method therefore will not impose an overhead of manual work for carefully segmenting and excluding the CSF regions. Instead, it will be widely applicable and robust when using any available segmentation technique.

MI is a good approach for coregistering imaging data with differing contrast. However, good initialization of the parameters is necessary for accurate MI registration. In the first simulation experiment, we also tested estimation of the parameters for correcting distortions by registration procedures using purely the MI methods without first initializing the parameters with good confidence (i.e. using the MI and MI-mask algorithms). The results demonstrated that an appropriate initialization of the distortion parameters is critically important to the final success of correcting the EC-induced distortion. This is because DWI data are usually noisy with low resolution but contain only mild distortion, which can be diminished only by specially crafted approaches designed with extra care. In our method, we used ICC-mask algorithm as a good method for parameter initialization before performing MI registration. This initialization method is easy to implemented and time-efficient. We found from our experiments that the ICC-mask algorithm is an appropriate way for initializing the parameters from the outset.

We showed that our algorithm yielded marked improvements in the correction of EC-induced distortion using simulated data. The improvement for human data directly acquired from the MR scanner was less significant because commercially acquired scanners correct most of the distortion, leaving comparatively less room for our algorithm or any other algorithm to improve it. For example, the DTI pulse sequence on our scanner uses bipolar gradients, resulting in DWI data with only slight residual of EC-induced distortion. Nevertheless, residual distortion was detected and corrected by our algorithm better than by the competing algorithms. Whereas the simulations were designed for the purpose of quantitatively showing that our algorithm performs effectively for DWI data, the fourth experiment, parallel to the simulation tests, was designed to show this for human data. We synthesized hybrid human datasets by artificially imposing more severe distortion on human data with randomly adopting M, T, and S parameters in a prespecified range. Again, in this case, our algorithm outperformed the others (Fig. 6 & Table 3).

EC-induced distortion is not simply a geometrical distortion. Instead, it is a consequence of the narrow bandwidths used in EPI and residues of the strong diffusion-sensitizing gradients required for DTI. It affects every voxel of the image but not merely those at the edge of the brain. Thus commonly-used morphological methods for recovering the shape of the brain using only its morphological boundary are not suitable for correcting EC-induced distortions, because boundary-based techniques consider only the geometry information of the boundary voxels and interpolate this information across the entire imaging volume. Such correction has little to do with the intrinsic physical process that generated the distortion. In addition, interpolation of the DWI measurements during correction also needs to be carefully considered [26]. A valid algorithm for correcting DWI distortion must consider the intensity information from every voxel in the image as part of a volumetric texture for calculation. This requires a complicated model for voxel transformation to correct EC-induced distortion. Our method corrects in this way, and we have shown that our method is able to volumetrically and morphologically correct the data with high accuracy (Figs. 5 & 6, Table 2 & 3).

Because the acquisition of a DWI dataset is usually lengthy, the data thus acquired may sometimes inevitably contain motion artifacts. Several available approaches therefore have considered correcting motion together with EC-induced distortions [18, 28, 29]. However, we would prefer to separate the two issues, because the essential physics models for subject motion and EC-induced distortion are completely different, and the impact of subject motion on the change of DWI measurement is unknown. Arbitrarily modifying the value of voxels to compensate for motion artifacts may introduce unpredictable bias to the correction of EC-induced distortion. Moreover, EC-induced correction is usually performed within the plane of image slices, whereas motion can occur along any spatial dimension. Even if the motion in 3D could be perfectly recovered, compensating the DWI measurements thereafter in the recovered voxels would be an independent problem, because DWI measurements are associated with gradients that are specific to particular spatial orientations. Considering these difficulties, previous work [18, 28, 29] trying to combine motion correction and distortion correction has made the simplified assumption that motion occurs only between the acquisitions of consecutive DWI volumes. Unfortunately, such an assumption is too strong and not generally true in practice. Even worse, in such models motion artifacts occurring in limited slices could be spatially propagated and transferred to neighboring image slices due to motion correction in 3D prior to or along with distortion correction, thereby severely compromising the dataset. In certain extreme cases of using such models, motion correction occurs when we test a dataset that contains absolutely no motion but has relatively significant distortions. We believe the ignorance and improper modeling of the interaction between the motion and distortion is the main reason in such cases. We therefore chose to tackle only the issue of distortion correction in this paper.

Finally, because EC-induced distortion intrinsically relates to the spatial orientation and strength of the diffusion gradients, our future efforts will aim to characterize this relationship and develop a systematic correction for it to further improve the accuracy and validity of our correction algorithms. Also, developing a more realistic model that accounts for the motion in EC-induced correction is crucial and this requires a strategy for properly adjusting the associated gradient to each voxel that is to be corrected for motion and then for distortion.

Abbreviations

ADC

Apparent Diffusion Coefficient

BET

Brain Extraction Tool

CSF

Cerebral Spinal Fluid

DTI

Diffusion Tensor Image

DW

Diffusion Weighted

DWI

Diffusion Weighted Imaging

EAR

Ellipsoidal Area Ratio

EC

Eddy Current

ECC

Entropy Correlation Coefficient

MTS

Magnification, Translation and Shear (distortion parameters)

FA

Fractional Anisotropy

FAST

FMRIB’s Automated Segmentation Tool

FDT

FMRIB Diffusion Toolbox

FLAIR

Fluid Attenuated Inversion Recovery

GECC

Gradient-based Entropy Correlation Coefficient

ICC

Iterative Cross-Correlation

L-BFGS-B

Limited memory Broyden Fletcher Goldfarb Shanno with bound constraint

MI

Mutual Information

SE-EPI

Spin Echo Echo-Planar Imaging

Biographies

Wei Liu finished her bachelor study in Physics Department of East China Normal University in 2005 and then continued to the doctoral study. She studied in Psychiatry Department of Columbia University as a visiting student, during 2008 to 2011. Her research interest focuses on post-processing of diffusion tensor images and related analysis.

Xiaozheng Liu is a Ph.D. candidate in the Department of Physics, East China Normal University. He was a visiting student in Psychiatry Department of Columbia University from 2009 to 2011. His research interest includes post-processing of diffusion tensor images and medical image processing.

Guang Yang received his Ph.D. from Department of Physics, East China Normal University. Now he is an associate professor in Shanghai Key Laboratory of Magnetic Resonance, East China Normal University. His research interest includes MRI image processing and experiments simulation.

Zhenyu Zhou was a postdoctoral research fellow in Psychiatry Department of Columbia University from 2008 to 2011. His research interest focuses on the areas of image and signal processing of fMRI and diffusion tensor images.

Gengying Li is a professor of Shanghai Key Laboratory of Magnetic Resonance of East China Normal University. His main research interest focuses on the MRI techniques, specially on MRI instrumentation.

Yongdi Zhou obtained his Ph.D. in neuroscience from University of California, Los Angeles, now is a professor and the dean of the School of Psychology, East China Normal University. His research interest focuses on the cognitive neuroscience, neurophysiology.

Marc Dubin earned his Ph.D. in Neurobiology and an M.D. from the University of Rochester School of Medicine. He is currently an assistant professor at Cornell University Department of Psychiatry. His research interest includes cognitive neuroscience, neurophysiology, and neuroimaging of depression.

Ravi Bansal is an associate professor in the Department of Psychiatry, Columbia University. He specializes in magnetic resonance image processing and analysis.

Bradley. S. Peterson is a Suzanne Crosby Murphy Professor of Psychiatry and the Director of MRI Unit in the Department of Psychiatry, Columbia University. His research interest focuses on neuroimaging and brain disorders.

Dongrong Xu obtained his Ph.D. in Computer Science from Zhejiang University, now is an associate professor at Columbia University College of Surgeon and Surgery and a senior research scientist at New York State Psychiatric Institute. His research interest includes biomedical image processing and analysis and virtual reality technology in brain function research, and scientific visualization.