Identification of Pulmonary Fissures Using a Piecewise Plane Fitting Algorithm

Abstract

We describe an automated computerized scheme to identify pulmonary fissures depicted in chest computed tomography (CT) examinations from a novel perspective. Whereas CT images can be regarded as a cloud of points, the underlying idea is to search for surface-like structures in the three dimensional (3D) Euclidean space by using an efficient plane fitting algorithm. The proposed plane fitting operation is performed in a number of small spherical lung sub-volumes to detect small planar patches. Using a simple clustering criterion based on their spatial coherence and surface area, the identified planar patches, assumed to represent fissures, are classified into different types of fissures, namely left oblique, right oblique and right horizontal fissures. The performance of the developed scheme was assessed by comparing with a manually created “reference standard” and the results obtained by a previously developed approach on a dataset of 30 lung CT examinations. The experiments show that the average discrepancy is around 1.0 mm in comparison with the reference standard, while the corresponding maximum discrepancy is 20.5 mm. In addition, 94% of the fissure voxels identified by the computerized scheme are within 3 mm of the fissures in the reference standard. As compared to a previously developed approach, we also found that the newly developed scheme had a smaller discrepancy with the standard reference. In efficiency, it takes approximately 8 minutes to identify the fissures in a chest CT examination on a typical PC. The developed scheme demonstrates a reasonable performance in terms of accuracy, robustness, and computational efficiency.

I. INTRODUCTION

Pulmonary fissures typically divide the human lung into five primary lobes (three in the right lung and two in the left lung), and each individual lobe acts as a relatively independent functional unit. For example, Matsuo et al. [1] observed that the pulmonary function was affected significantly by the normal lobar volume (NLV) of the lower lobes. Knowledge of the characteristics of pulmonary fissures may be useful in the detection, classification, and assessment of different lung diseases. For example, incompleteness of pulmonary fissures is often considered in surgical planning and its existence may advance the spread of specific diseases (e.g., pneumonia) [2,3]. Moreover, pulmonary fissures and their configuration could also be used for precise localization of lesions, in particular in terms of the possible involvement of different lobes [4–6]. Hence, accurate identification of pulmonary fissures is considered clinically important. Unfortunately, the large number of images in a CT examination makes it mentally challenging and time-consuming for experts to manually delineate pulmonary fissures in a slice-by-slice manner. At the same time, their frequently fuzzy appearance makes fissure segmentation from other lung regions, computationally, a challenging task.

A number of computerized schemes have been developed to identify pulmonary fissures. Most of these start with an initial detection procedure followed by some type of further refinement steps. The initial detection step typically aims to discard non-fissure regions while retaining as many fissure regions as possible. In implementation, this step is often achieved by identifying either points of interest (POI) or regions of interest (ROI). To identify POIs, Pu et al. [7] used a simple thresholding operation; Wiemker et al. [8] used Hessian-matrix and structure-tensor based filters; Rikxoort et al. [9–10] used a pattern recognition procedure based on a training dataset and a “supervised” filter. In contrast, ROIs are usually identified by taking advantage of the 3D distance from “fissure to blood vessel” [11–12], or other airway trees related anatomical information [13–14]. The refinement procedure is primarily designed to accurately define lines or surfaces. Two-dimensional (2D) line detection methods include a curve-growing strategy [15–16], Vanderbrug linear feature detection [17], edge detection [14], and Gaussian and mean curvature analyses [18]. Unlike these methods, Zhang et al. [20–22] presented a method for automatic segmentation of oblique fissures using an atlas-based initialization procedure followed by a two-step graph searching procedure to delineate the fissures. As 3D surface representation is generally more robust in depicting pulmonary fissures than 2D lines, methods to detect 3D surfaces as a way of identifying pulmonary fissures were recently developed. For example, Ukil et al. [13] used a “ridgeness” measure followed by a 3D graph search [19] to find the optimal surface within the ROI. Pu et al. [7] used a computational geometry based approach, including the marching cubes algorithm (MCA), Laplacian smoothing, and extended Gaussian image (EGI), to achieve high detection sensitivity of fissure plane patches and to eliminate other non-fissure related patches. Rikxoort et al. [9–10] and Ross et al. [23] used second-order information to group points into plates. Kuhnigk et al. [12] used an interactive 3D watershed algorithm. Unlike fissures depicted on a single 2D slice that may be too thick for accurate line detection or line-like structures that could be interrupted by the presence of disease, image noise or image artifacts, surfaces do not have these types of problems. However, the existing 3D surface identification approaches may have some limitations. For example, the 3D graph search algorithm [19] depended on the robust segmentation of vascular tree; the algorithms based on the second-order information [9–10] may be sensitive to image noises or artifacts.

In this study, we proposed an analytical plane fitting algorithm to automatically identify pulmonary fissures depicted in CT examinations. Here, CT images are treated as a cloud of points and the lung volume is subdivided into spherical volumes. Potential partial fissure regions (if any) within each spherical volume are detected by locating the structure that appears as a planar structure in the specific volume from the perspective of surface (plane) fitting. A detailed description of the proposed scheme and the test results when applied to 30 chest CT examinations follow.

II. METHODS

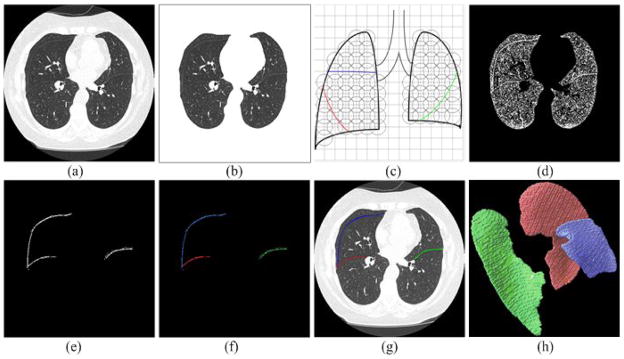
Given the fuzzy appearance of pulmonary fissures on CT examinations, humans can still visualize fissures primarily because of image contrast representing tissue density differences (albeit low) between the fissures and surrounding parenchyma. The motivation of this work is to exploit this characteristic. Whereas pulmonary fissures are 3D freeform surfaces that can be approximated using a number of small plane patches, we propose to divide the lung into small spherical volumes (with overlap) and develop a novel robust and efficient analytical approach to fit a plane (if any) within each sphere. In implementation, given a chest CT examinations (Fig. 1(a)), the proposed fissure detection scheme consists of five basic steps as shown in Fig. 1: (1) lung volume segmentation, (2) lung volume partition or subdivision, (3) filtering using a median filter, (4) fissure patch detection using an analytical plane fitting algorithm, and (5) classification of different fissure types. The filtering step simply makes use of the image contrast characteristic and the plane fitting process makes use of the voxel density characteristic. Since the proposed analytical plane fitting algorithm is a key component of this scheme, we describe it separately in this section.

Fig. 1.

Basic steps of the pulmonary fissure segmentation scheme: (a) a chest CT examination, (b) the segmented lung volume of (a), (c) the subdivision of the segmented lung volume, (d) application of a point filtering, (e) fissure detection after application of the analytical plane fitting algorithm, (f) the clustered types of fissures, (g) identified fissures displayed as overlay, and (h) the 3D surface model of the detected fissures in (g).

A. The Analytical Plane Fitting Algorithm

A.1 Objective Function Selection

A plane in 3D Euclidean space has three degrees of freedom and is determined uniquely by three parameters. A plane F can be defined as F = {p|p ∈ R³, f(p) = 0} where:

$$f(p)=cos(\alpha )sin(\theta )x+sin(\alpha )sin(\theta )y+cos(\theta )z-\rho$$ (1)

where (α, θ, ρ) are the three parameters defining the plane F.

Given N points p_i = (x_i, y_i, z_i), i = 1,…, N, in a Euclidean 3D space, our aim is to find a plane F that minimizes the following objective function:

$$E(\alpha ,\beta ,\rho )=\sum _{i=1}^{N}D{(p_i,F)}^2,$$ (2)

where D(p_i, F) is the distance between point p_i and plane F. It is not difficult to infer from Eq. (2) that the distance function D(p_i, F) plays a pivotal role in the minimization. We note that for reasons explained in detail in Section B, in this study, the scattered points p_i are voxels in CT images and located within a predefined spherical region (sub-volume). This constraint does not affect the generality of the algorithm, because a “bounding sphere” could always be found for a given cluster of points in space. A straightforward solution of Eq. (2) can be derived using a conventional least square method, where D(p_i, F) =|f(p_i)|. However, despite its efficiency, results of the least square method could be easily affected by outliers (Fig. 2(a)–(b)). Therefore, we chose to use the distance function D defined in Eq. (3) that is able to provide a relatively accurate solution in the presence of outliers [24][25]:

$$D{(p_i,F)}^2=\{\begin{array}{lll}f{(p_i)}^2\hfill & if\hfill & f{(p_i)}^2<u^2\hfill \\ u^2\hfill & if\hfill & f{(p_i)}^2\ge u^2\hfill \end{array},$$ (3)

where u is a scalar. In this study, u is tightly related to fissure thickness and it can be set to approximate half of the depicted fissure thickness (e.g., 1.5 mm). Here, we can reformulate Eq. (2) as

Fig. 2.

Illustration of the plane fitting algorithm.(a)–(b) show the fitted lines in a two-dimensional point set. The lines in green represent the results obtained by the least square fitting method, and the lines in red represents the results obtained by the proposed density fitting method. (c) shows a 3D point cloud in a spherical volume that is extracted from an actual chest CT examination. (d) visualizes the point cloud in (c) using the inner product of the points vectors and the normal vector (i.e., Eq. (7)). (e) shows the fitted plane (in red) using the developed method. (f) shows the function ε(α, θ) corresponding to the 3D point cloud in (c).

$$E^{\prime }={Nu}^2-E$$ (4)

Substituting Eq. (2) and Eq. (3) into Eq. (4), the plane fitting is now transformed from minimizing E(α, β, ρ) (i.e., Eq. (2)) into maximizing E′(α, β, ρ) (i.e., Eq. (5)) by finding a set of optimal parameters (i.e., (α, θ, ρ)):

$$\begin{array}{l}{E}^{\prime }(\alpha ,\theta ,\rho )={Nu}^2-E(\alpha ,\theta ,\rho )\\ =\sum _{i=1}^N(u^2-D{(p_i,F)}^2)\\ =\sum _{f{(p_i)}^2<u^2}(u^2-f{(p_i)}^2)+\sum _{f{(p_i)}^2\ge u^2}(u^2-u^2)\\ =\sum _{f{(p_i)}^2<u^2}(u^2-f{(p_i)}^2)\end{array}$$ (5)

It can be seen from Eq. (5) that only the points whose distances to the plane F are smaller than u affect the objective function E′. As the density of the points in space is used to detect fissure planes (if any) in a small spherical sub-volume, we propose to divide function E′ in Eq. (5) by the corresponding cross-sectional area S of a plane F(α, θ, ρ) and thereby the density-based plane fitting becomes a problem of finding optimal parameters (α, θ, ρ) by maximizing Eq. (6):

$$\epsilon (\alpha ,\theta ,\rho )=\frac{E^{\prime }(\alpha ,\theta ,\rho )}{S(\alpha ,\theta ,\rho )}=\frac{{\displaystyle \sum _{f{(p_i)}^2<u^2}}{w}_i(u^2-f{(p_i)}^2)}{\pi (r^2-f{(o)}^2)}$$ (6)

where S(α, θ, ρ) = π(r² − f(o)²) is the cross-sectional area of the plane F(α, θ, ρ) with respect to the sphere, and o and r denote the center and the radius of the sphere, respectively. The motivation of dividing E′ (α, θ, ρ) by S is to assure that the objective function ε is independent of the cross-section area and therefore is only determined by the point density near the plane.

Whereas the objective function (Eq. 6) is not convex, one cannot simply use a gradient descent method to optimize the parameters. Although an exhaustive brute-force search could be used as a solution, the computational complexity is extremely high. For a grid system (α, θ, ρ) with a size of N_α × N_θ × N_ρ, the computational complexity in time is O(N_α × N_θ × N_ρ × N) and this is unacceptable in practice. Hence, an efficient optimization algorithm is desirable. In the following, we propose to reduce the computational complexity to O(N_{(α, θ)} × N) without sacrificing accuracy and robustness, thereby making the algorithm practical for the fissure identification task.

A.2 Optimization of Parameter ρ Using an Integration-Based Approach

Assuming α and θ are fixed, let n = (cos(α) sin(θ), sin(α) sin(θ), cos(θ)) denote the norm of a plane F and

$$q_i=p_i·n=cos(\alpha )sin(\theta )x_i+sin(\alpha )sin(\theta )y_i+cos(\theta )z_i$$ (7)

where · represents inner product. By substituting Eqs. (1) and (7) into Eq. (6), ε(α, θ, ρ) can be rewritten as:

$$\epsilon (\rho \mid \alpha ,\theta )=\frac{{\displaystyle \sum _{f{(p_i)}^2<u^2}}(u^2-f{(p_i)}^2)}{\pi (r^2-f{(o)}^2)}=\frac{{\displaystyle \sum _{{(q_i-\rho )}^2<u^2}}(u^2-{(q_i-\rho )}^2)}{\pi (r^2-{(n·o-\rho )}^2)}=\frac{{\displaystyle \sum _{\rho -u<q_i<\rho +u}}(u^2-{q_i}^2+2\rho q_i-{\rho }^2)}{\pi (r^2-{(n·o-\rho )}^2)}$$ (8)

Given a variable m and a unit vector n, when m = min q_i, we have max q_i ≤ m + 2r because points p_i are inside a spherical volume with radius of r. Let:

$$\begin{array}{l}{a}_j=\sum _{m+(j-1)\lambda \le q_i<m+j\lambda }-{q_i}^2,\\ b_j=\sum _{m+(j-1)\lambda \le q_i<m+j\lambda }2q_i,\\ c_j=\sum _{m+(j-1)\lambda \le q_i<m+j\lambda }-1,\end{array}$$ (9)

where j = 1,2,…, N_ρ, N_ρ = 2r/λ, and λ is the grid interval of a discretized ρ. In this study, λ is set at a small value (e.g., λ = 0.1 mm. Whereas the CT image resolution is typically larger than 0.5 mm, this grid interval is relatively very small and sufficient for our specific application). Let A, B, C be the integrations of a, b, and c as in Eq. (10):

$$\begin{array}{l}{A}_j=\sum _{k\le j}{a}_k=A_{j-1}+a_j,\\ B_j=\sum _{k\le j}{b}_k=B_{j-1}+b_j,\\ C_j=\sum _{k\le j}{c}_k=C_{j-1}+c_j,\end{array}$$ (10)

Now the objective function (Eq. 8) at each ρ (= m+jλ) is computed as:

$$\epsilon (\rho \mid \alpha ,\theta )=\frac{(A_k-A_l)+\rho (B_k-B_l)+({\rho }^2-u^2)(C_k-C_l)}{\pi (r^2-{(n·o-\rho )}^2)},$$ (11)

where l = (ρ − m − u)/λ and k = (ρ − m + u)/λ. Here, ρ − m and u are integral multiples of λ; hence, both l and k are integers. Using integration we now have an optimal ρ for each (α, θ) pair with a reduced computational complexity in time from O(N × N_ρ) to O(N + N_ρ).

A.3 Optimization of (α, θ) Using a Multi-scaling or a Coarse-to-Fine Strategy

Let ε(α, θ) denote $\underset{\rho }{max}\epsilon (\rho \mid \alpha ,\theta )$, an optimal parameter pair (α_opt, θ_opt ) can be found by solving:

$$({\alpha }_{\mathit{opt}},{\theta }_{\mathit{opt}})=arg\underset{0\le \alpha ,\theta <\pi }{max}\epsilon (\alpha ,\theta ).$$ (12)

The objective function ε(α, θ) is not convex with respect to (α, θ). Whereas the regularized distance function in Eq.(3) is continuous, ε(α, θ) is continuous and hence the function values over the region (Ω) near the optimal (α_opt, θ_opt ) is similarly greater than the values over other regions (as illustrated in Fig. 2(f)). Taking advantage of this characteristic, we use a coarse-to-fine strategy in order to efficiently search for optimal (α, θ) pairs. We first search in (α, θ) space with a relatively coarse error δ (i.e., search interval of α and θ) for a near optimal pair (α_c, θ_c) in terms of Eq. (12). Thereafter, we search for the final optimal parameter pair (α_opt, θ_opt ) in the sub-space defined by ([α_c − 0.5δ, α_c + 0.5δ] and [θ_c − 0.5δ, θ_c + 0.5δ]) with a smaller predefined error δ_refine (e.g. δ_refine = 0.01). For pulmonary fissure identification, δ = 0.1 is sufficient for the initial search in order to avoid being trapped in local minima. For the example in Fig. 2(f), where the spherical sub-volume with a cloud of points is extracted from an actual chest CT examination, the region Ω near the optimal (α_opt, θ_opt) is larger than a circle with a radius of 0.3, i.e., $\mathrm{\Omega }\supseteq \{(\alpha ,\theta )\mid \sqrt{{(\alpha -{\alpha }_{\mathit{opt}})}^2+{(\theta -{\theta }_{\mathit{opt}})}^2}\le 0.3\}$. Fig. 2(f) shows the objective function ε(α, θ) corresponding to the three-dimensional point cloud in Fig. 2(c), where $\epsilon (\alpha ,\theta )=\underset{\rho }{max}\epsilon (\rho \mid \alpha ,\theta )$. Using the coarse-to-fine strategy, search times for (α, θ) will be reduced from $\frac{{\pi }^2}{{\delta }_{\mathit{refine}}^2}$ to $\frac{{\pi }^2}{{\delta }^2}+\frac{{\delta }^2}{{\delta }_{\mathit{refine}}^2}$. For example, for δ = 0.1 and δ_refine = 0.01, the actual search time of (α, θ) is reduced from 10⁵ to 10³ approximately.

To increase the efficiency given a desired level of accuracy, it is preferable to have the candidate normal vectors n = (cos(α) sin(θ), sin(α) sin(θ), cos(θ)) corresponding to (α, θ) homogenized (i.e., uniformly sampled) on half a unit spherical surface. Otherwise, there could be a number of similar directions repeatedly searched when θ is small (e.g. for θ=0, n = (0,0,1) would be the same even if α is set at different values). In this study, we simply assign θ = 0: δ: π and α = 0: δ/sin(θ): π to generate the (α, θ) pairs and the normal vectors n, respectively, and the search times for optimal (α, θ) pairs will be further reduced from $\frac{{\pi }^2}{{\delta }^2}+\frac{{\delta }^2}{{\delta }_{\mathit{refine}}^2}$ to $\frac{2\pi }{{\delta }^2}+\frac{{\delta }^2}{{\delta }_{\mathit{refine}}^2}$.

To demonstrate the robust and generic characteristics of this fitting algorithm, we applied it to some 2D and 3D cloud of points in Fig. 2. For the 2D examples (Fig 2(a)–(b)), the lines in green represent the results obtained by the least square fitting method, and the lines in red represents the results obtained by the proposed density fitting method. It can be seen that the proposed fitting scheme is able to accurately identify the lines in spite of the presence of a large number of outliers, while the least square fitting method is sensitive to the presence of outliers.

B. Pulmonary Fissure Identification

B.1 Lung Segmentation

Lung volume segmentation (Fig. 1(b)) enables limiting the search space during fissure detection, thereby improving computational efficiency and eliminating the possibility of erroneous (false positive) fissure detections outside the actual lung regions [27–28]. In this study, we use an automated lung segmentation approach proposed in [26], namely Adaptive Border Marching Algorithm (ABMA), to segment the lung volume depicted on CT images. As a geometric technique, this algorithm is able to obtain a “smooth” lung boundary with high computational efficiency by “bridging” regional concave regions of lung boundaries in a progressive marching manner. A detailed description of the scheme along with experimental results can be found in [26].

B.2. Volume Subdivision

In this study, an axis-aligned bounding box (AABB) is used to establish a volumetric grid system for each CT examination, where each cell (sub-volume) is empirically set at a size of 5×5×5 mm³. Centered at each vertex of the grid system, a sphere with a radius r is used as a sub-volume (Fig. 1(c)). As pulmonary fissures typically have relatively low curvature within a small region, r is empirically set at a value of 10 mm in this study. Such a small sub-volume will assure that the contained fissures appear approximately as a planar patch. We use spheres rather than cubic boxes in this study, as spheres are rotation invariant and the cross-sectional area of a sphere along any direction can be computed efficiently. Given a grid interval of 5 mm, the distance of any point K to the nearest vertex O is smaller than $\sqrt{3+5^2}/2\text{mm}$ in the 3D Euclidean space.

B.3. Point Filtering

To narrow the search space for pulmonary fissures, we filter the segmented lung volume in a two-stage manner (Fig. 1(d)). First, as the intensity or voxel value (I(p)) of pulmonary fissures typically varies from −900 HU (Hounsfield Unit) to −300 HU, voxels with intensity values outside this range are labeled as non-fissure voxels and removed. Second, as there are rarely large vessels near fissures and the majority of fissure regions have intensity levels higher than their surrounding regions (voxels), voxels with intensity values smaller than the median intensity in a local region are removed as well. The size of the local region of interest is defined as a spherical volume described in Section B.2.

B.4. Fissure Detection through Fitting of a Plane within a Candidate Sphere

Given a sphere with a center o(x₀, y₀, z₀) and a radius r of 10 mm and the remaining candidate points ${\{p_i\}}_{i=1}^N$ inside the sphere (Fig. 2(c)) after the filtering operations, we fit an optimal plane F parameterized by (α, θ, ρ) using the objective function in Eq. (6). As intensity values of voxels representing pulmonary fissures could vary significantly in different examinations and in different regions within the same examination, we consider the density distribution alone for plane fitting. To increase the robustness in identifying fissures representing planes (if any) within each sphere, we only considered a plane F(α, θ, ρ) with a distance less than 5 mm to the center of the sphere (o), i.e., d = |f(o)|≤ 5 mm, where f(o) is defined in Eq. (2). This will assure that the cross-sectional area of F in regards to the spherical volume π(r² − d²) is larger than π(10² − 5²) ≈ 236 mm². Since the distance of any point (K) to the nearest grid vertex is less than 5 mm, there exists a sphere (centered at the nearest vertex) with a distance from its center to the point of interest (K) which is less than 5 mm. Therefore, all points on a candidate fissure are ultimately considered during the fitting process. Given an optimal plane F_j(α_j, θ_j, ρ_j ) identified in the jth spherical volume, if the energy function ε(α_j, θ_j, ρ_j) (refer to Eq. 6) is greater than a predetermined threshold T, the identified circular cross-section (plane) will be considered (assumed to be) a part of the fissure. In this study, we use an adaptive threshold T (e.g., T = 0.6max_jε(α_j, θ_j, ρ_j)). Applying the density-based fitting algorithm to all spherical sub-volumes will result in the identification of pulmonary fissures (Fig. 3). Because only the remaining voxels after the point filtering operation that are closed to the fitted planes are treated as fissure points, the identified (output) fissures are smooth in appearance.

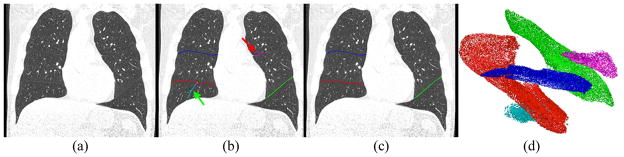
Fig. 3.

Fissure detection and classification results: (a) a CT examination, (b) the detected, sorted, and classified fissures (overlay with different colors), and (c) the final fissure segmentation and classification (overlay) after the removal of non-fissure regions as indicated by the arrow in (b), where the voxels in green, red and blue indicate the left oblique, right oblique and right horizontal fissures, respectively. (d) visualizes the detected fissure voxels and their classification in 3D space.

B.5. Fissure Cluster

In this study, we automatically cluster the detected fissure plane patches and classify these into the different fissure types. Let n_j denote the normal vector and K_j = o_j+(ρ_j − n_j · o_j)n_j represent the center of the (circular) cross-section with respect to the jth spherical volume, given two fissure patches F_i and F_j identified in two neighboring spherical volumes, they belong to the same cluster (i.e. F_i ~ F_j ) if either of the following conditions is met: (1) F_i is a 26-connected neighbor of F_j and |n_i · n _j|>e₁ and |(K_i−K_j) · n_i| + |(K_i−K_j) · n_j| < e₂; (2) ∃k, s.t., F_i ~ F_k and F_j ~ F_k.

Given two plane patches F_i and F_j detected in neighboring spherical volumes, the parameter e₁ is used to control the curvature or “allowable” angle between F_i and F_j, and the parameter e₂ is used to control the continuity between the distance between F_i and F_j. Here, e₁ is set at a value of 0.98 and similarly e₂ is set at a value of 2.0 mm. The clustered regions are then ranked in a decreasing order of the number of fissure sections contained in each cluster. In the left lung, the first cluster is assumed to represent the left oblique fissure (in green) and in the right lung, the first and the second clusters are assumed to represent the right oblique fissure (in red) and the right horizontal fissure (in blue), respectively (Fig. 3). All other clusters (in cyan or pink) are then removed/marked as non-fissure regions. The voxels located within the thin round plane are labeled as fissures.

C. Performance Assessment

We assess the performance of the proposed fissure detection algorithm from two perspectives. First, we compare the results obtained using the method described here with a manually created reference standard consisting of 30 CT examinations. Second, we compare the performance of the developed scheme with a previously one (we term it as “C-Method” in this study) described in [7] by applying them to the same dataset. Distance from a point p to a point set A is computed via

$$d(p,A)=\underset{q\in A}{min}d(p,q),$$ (13)

where d(p, q) denote the 3D Euclidean distance between points p and q. Given two sets of points A and B, corresponding to the fissures detected by either a computerized scheme or a human expert, we used a cumulative error distance distribution (CEDD) [7] as a summary measure of the discrepancy between two paired fissure detection results (i.e., the two point sets). The CEDD is computed as the cumulative percentage of the shortest distance between the point sets while each point is considered for this purpose. This measure not only indicates the fraction of fissures obtained by different methods that lies within a specific error, but also provides an assessment of how far the points are in one dataset from another [26]. Root mean squares (RMS), mean, and maximum distances of each case between compared methods [13] are computed as well. We note that none of the examinations in the test dataset are used for model development or parameter selection.

III. EXPERIMENTS AND RESULTS

A. The CT Dataset

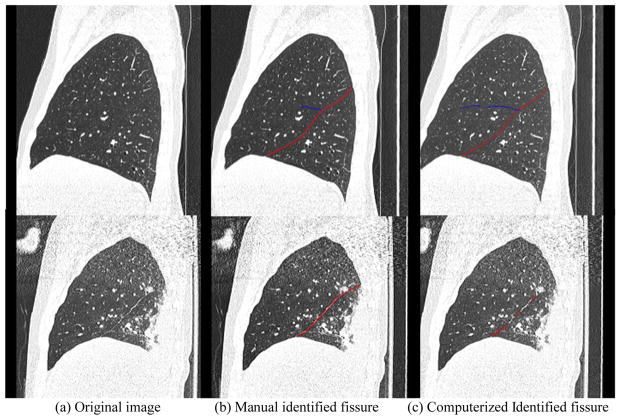
When creating the reference standard, we collected 30 lung CT examinations specifically from a chronic obstructive pulmonary disease (COPD) dataset available at the University of Pittsburgh Medical Center (UPMC). The collected cases covered a healthy dataset and five different types of lung diseases, i.e., emphysema, interstitial lung disease (ILD), pulmonary embolism (PE), pneumonia, and cystic fibrosis. For each category, five cases are selected. These examinations were reconstructed using the GE Healthcare “lung” reconstruction kernel. The section thickness ranged from 0.50 mm to 1.25 mm, and in-plane pixel size from 0.55 mm to 0.78 mm. With the aid of a computational tool developed by our group, a trained human image analyst manually traced the fissured depicted of these CT examinations and marked them using freehand sketches on the 2D sagittal views in a slice-by-slice manner because the sagittal view gives a relatively more straightforward representation of the types of different fissures as compared with other views (i.e., axial and coronal views). We note here that the transversal and coronal views are also provided for the image analyst when tracing the fissures on the sagittal view. Different types of fissures were marked separately. Only visible major and minor fissures in the CT examinations are marked (e.g. Fig. 8(b)), while accessory fissures are ignored.

Fig. 8.

Two examples with large discrepancies between the results obtained by the proposed computerized scheme and the reference standard. The left column shows the original CT images, the middle column shows the fissures in overlay in the reference standard, and the right column shows the fissures in overlay identified by the computerized scheme in this study. The top row shows a CT examination where portion of the right horizontal fissure voxels is invisible but identified by the fitting scheme; the “F to G” discrepancy is 26.3 mm. The bottom row shows a CT examination with the presence of pneumonia where the potions of the fissures were missed by the fitting scheme; the “G to F” discrepancy is 35.6 mm.

B. Experimental Results

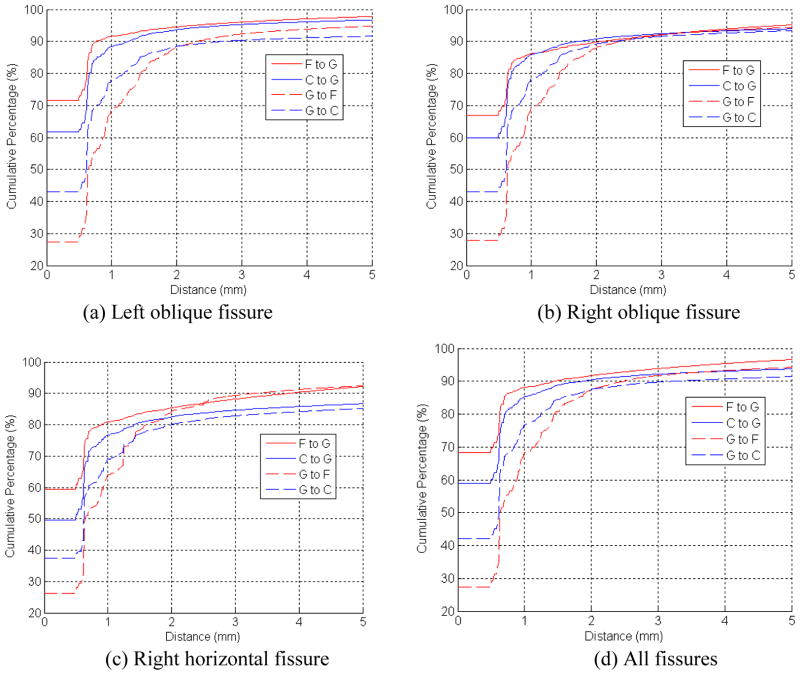
The cumulative error distance distribution (CEDD) between results obtained by the proposed fitting scheme (“F”)/the C-Method (“C”) [7] and the reference standard (“G”) is shown in Fig. 4. The “F to G” distance provides an assessment of the “false positive” identification. The “false positive” refers the voxels that were detected by the scheme as pulmonary fissures but were not marked by the image analyst as fissures. On average, 94% of the fissure voxels identified by the fitting scheme have a distance less than 3 mm to the reference standard. The “G to F” distance provides an assessment of the “false negative” identification. The “false negative” refers the voxels that were marked by the image analyst but not detected by the scheme as fissures. On average, 92% of the fissure voxels in the reference standard (“G”) have a distance less than 3 mm to those identified by the developed computerized scheme (“F”) in this study. We note that the classification algorithm failed to classify the three fissures correctly depicted on three of the 30 cases, because some accessory fissures are larger than the right minor fissures. In these cases, we manually select the clusters those represent left major fissures, right major fissures and right minor fissures for quantitative assessment purpose.

Fig. 4.

The cumulative error distance distribution (CEDD) between the proposed fitting scheme/the C-Method [7] and the manually created reference standard. (F: the developed scheme, C: the C-Method [7], G: the reference standard)

When comparing the proposed fitting scheme (“F”) with the C-Method (“C”), we can see that “F” constantly has smaller “false positive” than “C”. Though “C” has smaller “false negative” than “F” when only voxels with distance smaller than 2mm are considered, “F” has smaller “false negative” than “C” if more voxels are involved. In particular, the discrepancies for different types of pulmonary fissures between the results obtained by the computerized scheme/the C-Method [7] and the reference standard are also presented in Fig. 4(a–c). The average and standard deviation of root mean squares (RMS), mean, and maximum of the discrepancies between the reference standard and the results obtained by the computerized scheme and a previously scheme in [7] are summarized in Table I and II. When comparing the proposed scheme (“F”) with the gold standard (“G”), it can be seen that the left oblique fissures have obviously smaller discrepancy (error) than the right oblique fissure, and the right horizontal fissures have the largest discrepancy (error). When comparing the proposed scheme (“F”) with the C-Method (“C”) described in [7], we can see that the proposed scheme has smaller discrepancy with the standard reference than the previous scheme. A comparison between the results after application of the proposed fitting scheme to the normal and diseased examinations is given in Table III. It can be seen that the proposed fitting scheme has larger discrepancy (error) from/to the gold standard for the diseased examinations. Finally, an example in Fig. 5 is used to visually demonstrate the performance of the newly developed algorithm in fissure detection.

Table I.

Average (± standard deviation) of RMS, mean, and maximum discrepancy (error) in Euclidean distance between the results obtained by the newly developed scheme/the C-Method [7] and the manually generated “reference standard” on 30 CT examinations. (F: the developed scheme, C: the C-Method [7], G: the reference standard)

Fissure type	RMS (mm)		Mean (mm)		Max (mm)
	F to G	C to G	F to G	C to G	F to G	C to G
left oblique fissure	1.5 ± 1.0	1.9 ± 1.3	0.7 ± 0.6	0.8 ± 0.8	11.5 ± 4.3	14.5 ± 7.0
right oblique fissure	2.7 ± 3.5	2.5 ± 1.8	1.3 ± 2.2	11 ± 2.0	16.1 ± 7.8	16.9 ± 6.8
right horizontal fissure	3.6 ± 4.3	5.4 ± 7.2	2.5 ± 3.3	2.9 ± 3.5	16.2 ± 7.4	20.3 ± 9.5
all fissures	2.5 ± 3.3	3.3 ± 3.7	1.0 ± 1.2	1.5 ± 2.4	20.5 ± 8.4	24.0 ± 9.2

Table II.

Average (± standard deviation) of RMS, mean, and maximum discrepancy (error) in Euclidean distance between the manually generated reference standard and the results obtained by the newly developed scheme as well as the C-Method [7]) on 30 CT examinations. (F: the developed scheme, C: the C-Method, G: the reference standard)

Fissure type	RMS (mm)		Mean (mm)		Max (mm)
	G to F	G to C	G to F	G to C	G to F	G to C
left oblique fissure	2.7 ± 2.4	5.2 ± 5.7	1.6 ± 1.2	3.5 ± 3.4	19.1 ± 8.2	20.3 ± 8.5
right oblique fissure	3.5 ± 4.1	3.9 ± 4.0	2.1 ± 2.2	2.8 ± 2.1	20.1 ± 8.1	22.9 ± 9.2
right horizontal fissure	3.4 ± 4.2	6.8 ± 6.6	2.2 ± 2.5	4.3 ± 3.9	18.1 ± 8.6	22.8 ± 9.3
all fissures	3.1 ± 3.5	5.0 ± 5.2	1.9 ± 1.7	3.4 ± 3.2	23.6 ± 10.1	29.6 ± 11.1

Table III.

Average (± standard deviation) of mean discrepancy (error) in the Euclidean distance between the manually generated reference standard and the results after the application of the developed scheme to the collected normal and diseased CT examinations. (F: the developed scheme, G: the reference standard)

Fissure type	F to G (mm)		G to F (mm)
	Normal	Diseased	Normal	Diseased
left oblique fissure	0.5 ± 0.1	0.7 ± 0.7	1.2 ± 0.2	1.8 ± 1.3
right oblique fissure	0.8 ± 0.1	1.4 ± 2.4	1.0 ± 0.2	2.3 ± 2.5
right horizontal fissure	0.9 ± 0.6	2.8 ± 3.7	1.2 ± 0.4	2.4 ± 2.7
all fissures	0.7 ± 0.2	1.1 ± 1.2	1.1 ± 0.2	2.1 ± 1.8

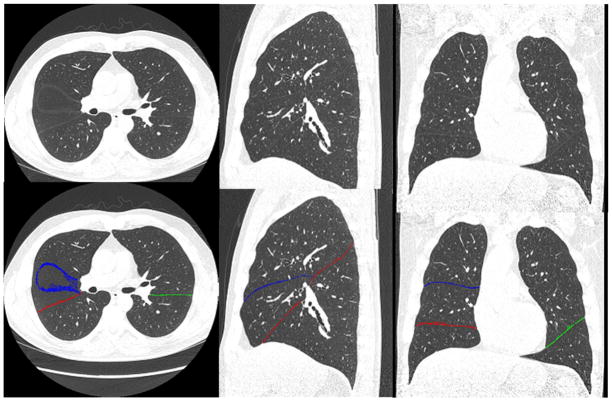
Fig. 5.

An example demonstrating the performance of the newly developed scheme for identifying pulmonary fissures depicted in a relatively normal examination. The top row shows the original CT images, and the bottom row shows the identified fissures in overlay. The left, middle, and right columns show the axial, the sagittal, and the coronal views, respectively.

V. DISCUSSION

We developed a fully automated fissure identification scheme that was based on a novel piecewise plane fitting algorithm and assessed its performance by comparing the identified results with those in a reference standard. Totally, 30 chest CT examinations are used for the evaluation purpose. Both pulmonary fissures and body fat appear as surface-like regions. However, in technique, identifying pulmonary fissures depicted on CT images are different from isolating body fat from CT or MRI images [37–38], because of their distinct appearances on images. For example, (a) the appearance of pulmonary fissures is very fuzzy on CT images as compared with surrounding structures and their densities range from −900 HU ~ −300 HU, while the body fat has a relatively high density ranging from −190 HU to −30 HU [37] and their contrast with surrounding structures are relatively high; (b) pulmonary fissures are very thin tissues with a thickness of only 2mm – 3mm, while the body fat are much thicker. Given these differences, it is actually more challenging to accurately identify pulmonary fissures depicted on CT images. Similar to the computational geometry method (C-Method) described in [7], the underlying idea of this scheme is to detect small plane patches as well. However, these two schemes are completely different in methodology and implementation. The C-Method used Laplacian smoothing and EGI algorithm for plane detection, where the lung structures were modeled as a geometric surface. In contrast, the method in this paper is based on a fitting operation, where the images are treated as a cloud of points. The plane fitting algorithm has a number of distinctive characteristics or merits. First, this algorithm is generic in nature and can be applied to detect lines/planes from a cloud of points (e.g., the examples shown in Fig. 2). As a freeform surface can be approximated by a set of small planes, the algorithm can be used to detect a 3D surface as well, such as the fissure identification in this study, without any changes in methodology. Second, the developed scheme is reasonably accurate. As the comparison experiments showed that this scheme had a smaller discrepancy with the “reference standard” than the C-Method. Approximately 94% of the detected fissure voxels have a distance less than 3 mm to those in the reference standard. The reason that we selected 3 mm as an error threshold during the evaluation is due to the fact that the thickness of pulmonary fissures typically ranges from 2 ~ 3 mm [32]. The amount of the detected fissures that are within 3 mm in regard to the “reference standard” may give us a perception of the performance of the scheme in fissure detection by describing the distances between two clusters of points (fissure voxels). Also, our approach is able to detect more pulmonary fissures than the C-Method described in [7]. Third, in terms of robustness, as demonstrated in Fig. 2, the developed scheme is generally insensitive to the presence of the outliers. When we applied the method to the 30 lung CT examinations, the task was executed in a batch mode without any interruption and all the parameters were fixed. The insensitivity to the outliers is important when attempting to identify fissures depicted in CT examinations with relatively severe disease, as shown in Fig. 6 and Fig. 7. We note that the C-Method failed to detect the fissures depicted on the examination in Figure 7. Fourth, in terms of computational efficiency, the computational complexity of the fitting algorithm in time is reduced from O(N_α × N_θ × N_ρ × N) to O(N_{(α, θ)} × N). Detecting fissures in a typical chest CT examination takes only approximately 8 minutes, while the C-Method takes approximately 20 minutes and the method developed by Rikxoort et al. [29] takes approximately 90 minutes for similar examinations. Because the lung volume is subdivided into a set of spherical sub-volumes and the same procedure can be applied repeatedly, the computational efficiency of this algorithm can be further improved by using parallel programming on multiple core systems or GPU. Fifth, in terms of simplicity, the underlying idea and the implementation of this scheme are quite simple in that analytical plane fitting algorithm within small sub-volumes of lung regions lead to the identification of fissures.

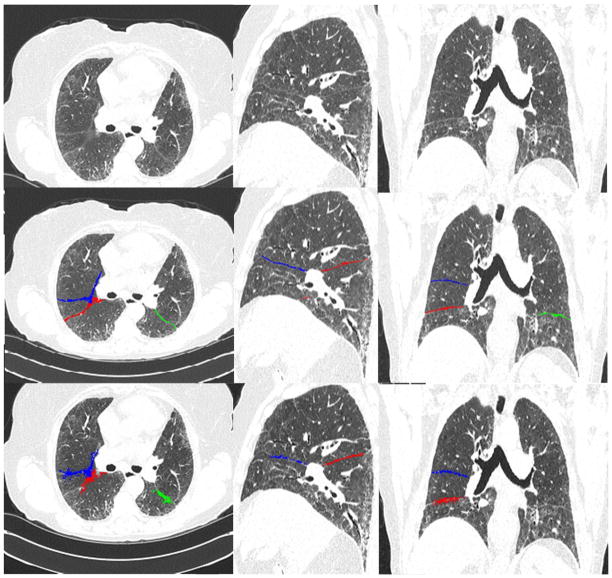
Fig. 6.

An example demonstrating the performance of the newly developed scheme, in comparison with the C-Method [7], for identifying pulmonary fissures depicted in a diseased examination with ILD (Interstitial Lung Disease). The top row shows the original CT images, the middle row shows the fissures identified by the proposed scheme, and the bottom row shows the fissures identified by the C-Method [7]. The left, middle, and right columns show the axial, the sagittal, and the coronal views, respectively.

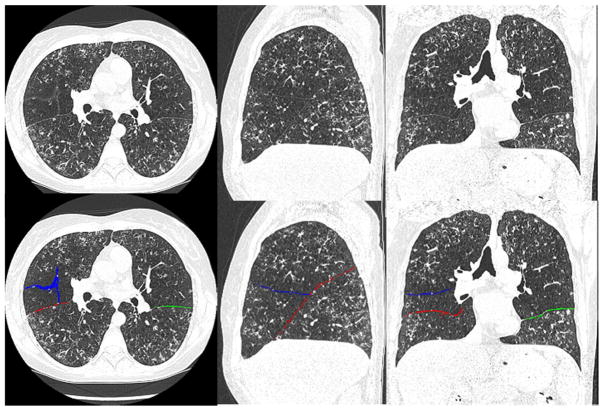
Fig. 7.

An example showing the detected pulmonary fissures by the proposed scheme in an abnormal examination with severe bronchiectasis (cystic fibrosis). The top row shows the original CT images, and the bottom row shows the identified fissures in overlay. The left, middle, and right columns show the axial, the sagittal, and the coronal views, respectively.

When comparing the results obtained by the developed scheme with a reference standard, our experiments (i.e., Fig. 4, Table I and Table II) show the following phenomena. First, the cumulative percentage of the “F to G” is consistently and obviously larger than that of the cumulative percentage of the “G to F” if the discrepancy is less than 0.5 mm. When the discrepancy is less than 3.0 mm, the difference in the cumulative percentage of the “G to F” and the “F to G” is shrunk significantly. This phenomenon implies that the manually marked fissures have somewhat perturbations. We admit that this is true because perturbations are unavoidable during manual tracing process. As a result, the “reference standard” is not perfect. Second, the left oblique fissures have obviously smaller discrepancy (error) than the right oblique fissure and the right horizontal fissures have the largest discrepancy (error). The reason is obvious when considering the relatively high fuzzy appearance of the right horizontal fissures (right minor fissures). The same observation has been reported in Pu et al.’s study [30]. In particular, we notice that the maximum discrepancy from the computerized scheme to the reference standard (“F to G”) is approximately 20 mm and from the reference standard to the computerized scheme (“G to F”) is approximately 24 mm. The large “F to G” discrepancy may be caused by the identification of invisible fissures by the fitting scheme (e.g., the example in the top row of Fig. 8), while the large “G to F” discrepancy is typically caused by the fact that the computerized scheme may fail to detect some fissures in diseased cases (e.g., the example in the bottom row of Fig. 8).

This scheme involved the determination of a few parameters. We adopted a conservative approach to determine the values of these parameters by leveraging their underlying physical background instead of using any training dataset. For example, in the fissure clustering procedure, we set the value e₁ as 0.98, which corresponds to an angle of around 10 degree. This small angle is sufficient for the smoothness between two planar patches. Similar for the parameter e₂, an error of 2 mm is sufficient for the continuity of two neighboring planar patches when considering that the fissure thickness is typically around 2 ~ 3 mm [32]. During our development, we do not choose the parameters based on the images we experienced. For quantitative regional lung CT analyses, it is often desirable to have individual lobes identified. However, the existence of incomplete fissures, which may be caused by the fissure identification scheme or other reasons (e.g., anatomy or imaging resolution) [2–3,33–36], makes it impossible to directly obtain pulmonary lobes using the detected fissures. A post-processing is typical required to estimate the incomplete regions of pulmonary fissures. Some discussions about these issues and the potential solutions can be found in [7, 30].

In spite of the above mentioned strengths, the described approach has several limitations. First, our approach failed to detect some fissures that might make the fissure discontinued in space. An examples in Fig. 8 (bottom row) shows that the fitting scheme fails to detect some portions of the fissures due to relatively high intensities (>−300 HU) in the missed regions. This is caused by the fact that pulmonary fissures are assumed in this study to have an intensity ranging from −900 HU to −300 HU (Section II.B.3) in order to narrow the search space. As a result, the fissures with high intensities are filtered out. In order to improve the performance of the developed scheme, a more adaptive approach in identifying the potential pulmonary fissure candidates may be needed. Second, in theory, the developed scheme may not result in an accurate result around the intersection of the major and minor fissures in the right lung. However, because only points (voxels) that are very close to the associated planes affect the energy function, and meanwhile the neighboring sub-volumes (spheres) have relatively large overlaps, the scheme will deliver a relatively accurate result. Third, the classification strategy based on a simple size criterion may not be robust enough for some examinations depicting diseases. The classification algorithm fails to classify the three fissures correctly on three of the 30 cases and we manually classify the three cases for the comparison. An example of misclassification is shown in Fig. 9. This stems from the fact that some specific diseases may result in segmenting relatively large surfaces that could actually be larger in terms of area than that of the minor fissure. Currently, we are investigating how to leverage lung anatomical knowledge (e.g., a lung atlas) to improve performance in this regard by discarding falsely detected regions (surfaces). Finally, like many previous approaches [13, 29], evaluating the performance of the fissure identification scheme is often difficult due to the lack of the “ground truth.” In this study, we used a manually generated “reference standard” to relatively assess the performance of this scheme. We admit that the manually created “reference standard” is associated with some errors due to the unavoidable perturbation during the manual tracing process. However, the comparison between the results obtained by the scheme and the “reference standard” provides a relative straightforward conception in regard to the accuracy of the developed scheme.

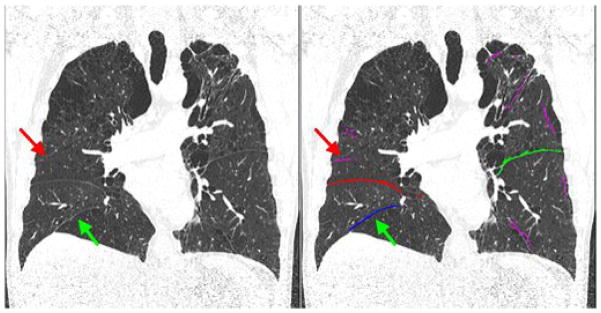
Fig. 9.

An example showing a miss-classification of pulmonary fissures. The regions in pink indicate the discarded fissures. Red arrow indicates the true right horizontal fissure and green arrow indicates the cluster that was falsely recognized as the right horizontal fissure.

VI. CONCLUSION

We described a fully automated pulmonary fissure detection and classification approach by taking advantage of the contrast of pulmonary fissures on CT images. This approach uses a unique strategy to convert a complex freeform surface identification problem into a plane fitting task. An efficient and robust plane fitting algorithm was developed for this purpose and it is designed primarily to identify a plane in a point cloud in the 3D Euclidean space. Our comparison experiments with a manually created reference standard and a previous approach [7] demonstrate that this newly developed scheme can achieve a reasonable performance in accuracy, robustness, and efficiency.