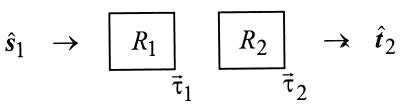PMD fundamentals: Polarization mode dispersion in optical fibers

Abstract

This paper reviews the fundamental concepts and basic theory of polarization mode dispersion (PMD) in optical fibers. It introduces a unified notation and methodology to link the various views and concepts in Jones space and Stokes space. The discussion includes the relation between Jones vectors and Stokes vectors, rotation matrices, the definition and representation of PMD vectors, the laws of infinitesimal rotation, and the rules for PMD vector concatenation.

1. Introduction

In the more than 15 years since the introduction of the early concepts (1, 2), the fundamentals of polarization mode dispersion (PMD) in optical fibers have become an important body of knowledge basic for the design of high-capacity optical communication systems. PMD effects are linear electromagnetic propagation phenomena occurring in so-called “single-mode” fibers. Despite their name, these fibers support two modes of propagation distinguished by their polarization. Because of optical birefringence in the fiber, the two modes travel with different group velocities, and the random change of this birefringence along the fiber length results in random coupling between the modes. With current practical transmission technology the resulting PMD phenomena lead to pulse distortion and system impairments that limit the transmission capacity of the fiber. Excellent reviews are available (3, 4), covering the practical aspects and applications of PMD concepts to fiber transmission systems and the effects of PMD on nonlinear fiber transmission (5). In this review we aim to complement these surveys and to collect and synthesize the fundamental concepts and theory of PMD, interweaving and linking the principal laws and key formulas that appear scattered in various places in the literature. We will explore the connection between frequency-domain and time-domain analyses and the isomorphic relation between the three-dimensional (3-D) view using real-valued 3-D Stokes vectors and the two-dimensional (2-D) view using complex-valued 2-D Jones vectors. Isomorphic pairings of operators such as these have been widely used elsewhere in physics such as in mechanics (6), in quantum mechanics (7), and even in the unification of quantum theory and general relativity (8). We borrow this methodology for our purposes.

As a preparation, we will first examine the description of polarization of light in the 3-D space of Stokes vectors (Stokes space) and the 2-D space of Jones vectors (Jones space, defined by the transverse coordinates x and y in the laboratory). Pauli spin matrices and spin vectors are the key to connect these two spaces and will be discussed in Appendix A, together with the necessary spin vector algebra. Because propagation through the fiber rotates the Stokes vectors of the light, we devote the following section to the rotation matrices in both Stokes and Jones space—i.e., the Lie groups SU(2) and SO(3) (9). Next, we examine the PMD vectors and principal states of polarization (PSPs) used to describe light propagation in randomly birefringent fibers and the associated differential group delay (DGD). We do this for a variety of representations and establish their connections. Several laws of infinitesimal rotation have been very valuable for visualizing PMD effects in Stokes space. Their connection to PMD vectors will be discussed. Finally, we review the various rules for PMD vector concatenation valuable for analyzing PMD of concatenated pieces of fiber. These rules appear in sum, integral, and differential form.

2. Notation

The unified view to which we aspire requires a unified notation. We attempt to keep our notation simple and transparent while linking to the notation already established as much as possible. The following is an abbreviated listing of our notation:

x, y, z: fiber coordinates; z is the direction of propagation; x and y are the transverse coordinates—i.e., those of Jones space.

e^{j(ω₀t−βz)}: continuous wave traveling in the z direction; j is the imaginary unit, ω₀ the angular carrier frequency, t time, and β the propagation constant.

E, Ẽ: electric field vectors; Ẽ(ω) is the Fourier transform of the complex transverse (x, y) electric field vector E(t) and has a complex amplitude e such that

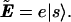2.1

The vector of the real electric field is Re(Ee^jω₀t).

ω: deviation from the angular carrier frequency ω₀ of the light. The optical frequency is (ω₀ + ω).

|s〉: 2-D complex Jones (column) ket vector, |s〉 = (_sy^s_x). The bra 〈s| indicates the corresponding complex conjugate row vector—i.e., 〈s| = (s^*_x, s^*_y). The bra–ket notation is used to distinguish Jones vectors from Stokes vectors. Our Jones vectors are all of unit magnitude—i.e., 〈s|s〉 = s^*_xs_x + s^*_ys_y = 1.

ŝ: 3-D Stokes vector of unit length indicating the polarization of the field, and corresponding to |s〉. The component of ŝ are the Stokes parameters.

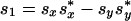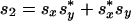2.2

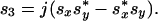By this definition, s₃ = 1 for right-circular polarized light (s_y = js_x) conforming with the traditional optics definition (10). However, left-circular definitions are also used in the literature (11). We always use the same letter symbols for corresponding Jones and Stokes vectors. Note that a common phase shift of both components of |s〉 does not change ŝ.

I: 2×2 or 3×3 identity matrix. The distinction should be clear from context.

T: 2×2 unitary transmission matrix in Jones space. Relates output to input via

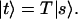2.3

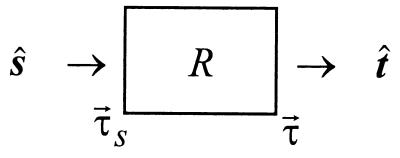
We use the symbols s and t when necessary for clarity to designate respective input and output quantities, as illustrated in Scheme S1.

Scheme 1.

Block diagram of optical fiber under test.

U: 2×2 Jones matrix, with det(U) = 1. Related to T by

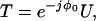2.4

where φ₀ is the common phase.

R: 3×3 rotation matrix in Stokes space isomorphic to U. Relates output to input via

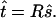2.5

σ₁, σ₂, σ₃: 2×2 Pauli spin matrices, for our purposes defined as

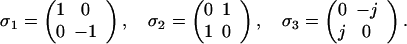2.6

σ⃗: Pauli spin vector in Stokes space, σ⃗ = (σ₁, σ₂, σ₃).

β⃗⋅σ⃗: 2×2 matrix in Jones space, β⃗⋅σ⃗ = β₁σ₁ + β₂σ₂ + β₃σ₃.

β⃗: 3-D birefringence vector in Stokes space describing local fiber properties.

τ⃗: our output PMD vector in Stokes space. Its length τ is the DGD, and its direction is that of the Stokes vector of the slow principal state. In a commonly used notation introduced by Poole (2, 3), the output PMD vector is labeled Ω⃗; its length, also the DGD, is labeled Δτ. The two PMD vectors τ⃗ and Ω⃗ are related by inversion through the s₃ axis, for reasons discussed in Appendix B in the supplemental data at www.pnas.org.

p̂, q̂, r̂: unit Stokes vectors; p̂ and q̂ are sometimes used to describe the polarization of the slow and fast principal states, respectively, while r̂ is used for a rotation axis.

Subscript ω: indicates differentiation—i.e., ds/dω = s_ω.

3. Jones and Stokes Vectors

This preparatory section deals with the representation of polarization in Jones and Stokes spaces and the connection between the two. Throughout this paper we assume that there is no fiber nonlinearity and no polarization-dependent loss, and that the usual loss term of the fiber has been factored out so that we can deal with unitary transmission matrices, T and U, and 3-D rotation matrices, R,

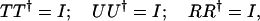3.1

where the dagger denotes the Hermitian conjugate. Note that R has real elements, hence R^† is simply the transpose of R. The input and output field components Ẽ_s(ω) and Ẽ_t(ω) at frequency ω are related by

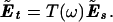3.2

After dropping the field magnitudes and using the unit Jones vectors (12) to describe the state of polarization this becomes

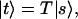3.3

where |s〉 and |t〉 include phase and polarization information.

The Pauli spin matrices allow us to write the components s_i of the Stokes vector corresponding to |s〉 in the compact form (11)

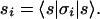3.4

With the spin vector σ⃗ (9, 13) the Stokes vector is, simply,

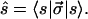3.5

In the following we discuss several useful connections between the Jones and Stokes vectors, particularly the projection operator, dot products, and vector superpositions.

As a preparation, recall that the scalar product of two Jones vectors |p〉 and |q〉 is

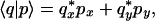3.6

and that their dyadic operator is

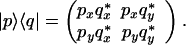3.7

From Eqs. 3.6 and 3.7 one can see that

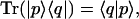3.8

where Tr stands for the trace operator.

Projection Operator.

As shown in Appendix A, any complex 2×2 matrix can be expanded in terms of the unit matrix I and the three spin matrices (7, 11). For Hermitian matrices, the coefficients are real. We will have several occasions to use this technique, perhaps the most useful being an examination of the projector |s〉〈s| of a Jones vector |s〉. The result of such an expansion is the surprisingly simple relation

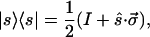3.9

where ŝ is the Stokes vector corresponding to |s〉 and where we use Eqs. A.8, A.9, and 3.8 in the form Tr(σ_i|s〉〈s|) = 〈s|σ_i|s〉 = s_i. After multiplication with |s〉, Eq. 3.9 becomes

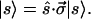3.10

Eq. 3.10 shows another important connection between Jones and Stokes vectors: the Jones vector |s〉 is an eigenvector of ŝ⋅σ⃗ with unit eigenvalue.

Dot Products.

An immediate application of the projector rule 3.9 is the establishment of a connection between the dot (scalar) products of two Jones vectors |p〉 and |q〉 and of their associated Stokes vectors p̂ and q̂. We use 3.9 with s = p and multiply by |q〉 from the right and 〈q| from the left, obtaining

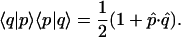3.11

A well-known special case of this connection is a pair of orthogonal Jones vectors with 〈q|p〉 = 0. Their Stokes vectors are antiparallel—i.e., q̂ = −p̂. In the following we will label such pairs of orthogonal Jones vectors, with antiparallel Stokes vectors, as |p〉 and |p₋〉, for example. Any such pair forms a complete orthogonal set in Jones space, since we have

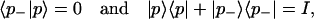3.12

where the second (completeness) relation follows from 3.9.

Let us now look at a pair of input Jones vectors |p_s〉, |q_s〉 and the transmitted vectors |p_t〉, |q_t〉 at the fiber output. They are related by Eq. 3.3. Using Eqs. 3.1 and 3.3, it is easy to show that the input and output dot products are preserved—i.e.,

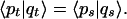3.13

When 3.13 is inserted in 3.11, we see that the magnitude of Stokes dot products is also preserved on transmission: i.e., transmission through the fiber is represented by a rotation of the Stokes vectors. This rotation property is, of course, a direct consequence of the orthogonality 3.1 of the matrix R.

Vector Superposition.

Here we consider a Jones vector |s〉 represented as a superposition

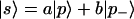3.14

of any two orthogonal vectors |p〉 and |p₋〉. How is this superposition mirrored in Stokes space? For the complex constants a and b, using Eqs. 3.12 and 3.14, we have

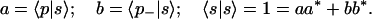3.15

The Stokes vectors of |s〉, |p〉, and |p₋〉, are ŝ, p̂, and −p̂. Inserting 3.14 into 3.5, one gets

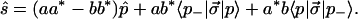3.16

Combining the eigenvector relation 3.10 and the spin vector relation A.3, we find that 〈p₋|σ⃗|p〉 = 〈p₋|σ⃗(p̂⋅σ⃗)|p〉 = jp̂ × 〈p₋|σ⃗|p〉 can be expressed by two real-valued Stokes vectors p̂₂ and p̂₃ in the form 〈p₋|σ⃗|p〉 = p̂₂ + jp̂₃, where p̂, p̂₂, and p̂₃ are a right-handed orthogonal set in Stokes space. Thus Eq. 3.16 becomes

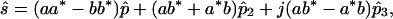3.17

representing a 3-D superposition in Stokes space. Note the similarity to Eq. 2.2: The two Jones vectors corresponding to polarization along the x and y axes form just such an orthogonal pair. In general, the vector p̂ defines an axis on the Poincaré sphere. Jones vectors with equal power split aa*/bb* between |p〉 and |p₋〉 appear on a circle perpendicular to this axis. The phase difference between the superposition coefficients a and b determines the azimuth on that circle.

4. Rotational Matrix Expressions

We have noted above that the change of the polarization of light on transmission through a fiber can be described as the rotation of its Stokes vector. There are matrix forms that highlight these rotational properties—i.e. the rotation axis r̂ and the rotation angle ϕ. These matrices are basic for an understanding of PMD fundamentals, and they have been used for the measurement of PMD vectors in the laboratory (14). We devote this section to a discussion of several expressions for such matrices in both Jones and Stokes space. First we establish a general connection between the matrices U and R of the two spaces, corresponding to the special unitary and special orthogonal Lie groups SU(2) and SO(3) (9).

Connection Between U and R.

To derive this connection we use Eqs. 2.3, 2.4, 2.5, and 3.5 to write two expressions for the output Stokes vector t̂

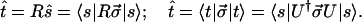4.1

Since both expressions are valid for any input state |s〉, we can extract from Eq. 4.1 the equation

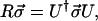4.2

which is the desired connection between the matrix R of Stokes space and the Jones matrix U. Note that, even though det(U) = 1, Eq. 4.2 does not determine the algebraic sign of U, which causes some difficulty in the determination of U from experimental results. The direct parallel of this sign uncertainty is the double-valued spinor representation of SO(3) in quantum mechanics (9).

Rotational Forms of the Jones Matrix.

An input Stokes vector ŝ that is collinear with the rotation axis r̂ of R will not be rotated upon transmission through the fiber. The Jones vectors corresponding to r̂ and −r̂ are |r〉 and |r₋〉, which must therefore be the eigenvectors of the corresponding U. Since |r〉 and |r₋〉 constitute a complete orthogonal set of Jones vectors, we can express U in the form U = λ₁|r〉〈r| + λ₂|r₋〉〈r₋|, where λ₁ and λ₂ are its eigenvalues. Since UU^† = I and det(U) = 1, the eigenvalues of U must be of unit magnitude and their product must be unity. Thus, we can write the Jones matrix U in the rotational form

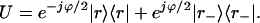4.3

Using Eq. 3.9, with r replacing s, we can express Eq. 4.3 in the alternate form

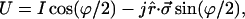4.4

where ϕ is the rotation angle in Stokes space, as we shall see below. This U also has the concise form

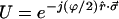4.5

(see Eq. A.12). To get from 4.5 to 4.4 entails the power series expansion of the exponential in 4.5 followed by the use of (r̂⋅σ⃗)² = I to reduce the result to 4.4. Recall that |r〉 and |r₋〉 are the eigenstates of r̂⋅σ⃗, with eigenvalues 1 and −1. Warning: the reader should not confuse the eigenstates discussed here with the principal states of PMD to be discussed in the next section. Eigenstates of U have the same polarization at input and output. Only for very special cases, such as phase plates, are these eigenstates the same as the principal states.

Rotational Forms in Stokes Space.

Here we use the relation 4.2 to convert the rotational form 4.4 of the Jones matrix U into the isomorphic form for the matrix R in Stokes space. We insert 4.4 into the right-hand side of 4.2 and obtain

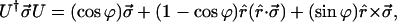4.6

having made use of the spin vector rules A.3, A.4, A.7, and A.13 to simplify the resulting expressions. Comparison of 4.6 with 4.2 yields the rotational form of R

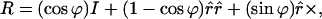4.7

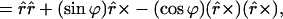where the 3-D dyadic r̂r̂ is the projection operator and r̂× is the crossproduct operator

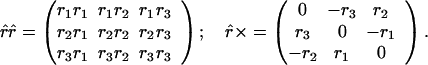4.8

One can see from 4.7 that for any Stokes vector ŝ, Rŝ represents a right-handed rotation of ŝ through an angle ϕ about the direction r̂. The Muller Matrix method for measuring PMD vectors uses this form for extracting rotation axis and angle from measured data for R (14).

The elegant compact expression for U given in Eq. 4.5 has an isomorphic counterpart in Stokes space (15) in

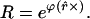4.9

Here the argument of the exponential is a 3×3 matrix operator. To prove the equivalence of this form with 4.7 one uses the power series expansion of the exponential, and the identities

4.10

to collect the terms appearing in this expansion.

Elementary Rotations.

Elementary rotations (6) in Stokes space are those that rotate the Stokes vectors around the 1, 2, and 3 axes of the Poincaré sphere. The matrices describing those are special cases of 4.4 and 4.7. We call them U₁, U₂, U₃ and R₁, R₂, R₃. In 4.4, r̂⋅σ⃗ reduces to σ_i, yielding

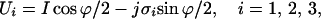4.11

while in 4.7 only r_i = 1 is different from zero. The elements of U_i and R_i are listed in Table 1.

Table 1.

Elementary rotations

Note that U₁ and R₁ describe the rotation caused by a birefringent phase plate with the slow principal axis aligned with the x-axis in Jones space. U₂ and R₂ correspond to a phase plate set at 45° angle in Jones space. U₃ and R₃ describe a rotation by ϕ/2 around the z-axis.

5. PMD Vectors

PMD phenomena in optical fibers typically used for communications occur because of the presence of birefringence in the fiber. This birefringence changes randomly along the fiber length (3, 4). It stems from asymmetries in the fiber stress and geometry, such as elliptical cross sections, microbends, or microtwists. Often such a fiber is visualized or modeled as a sequence of random birefringent sections whose birefringence axes and magnitude change randomly with z (along the fiber). There are different manifestations of PMD depending on the view taken. In the frequency domain view one sees, for a fixed input polarization, a change with frequency ω of the output polarization. In the time domain one observes a mean time delay of a pulse traversing the fiber which is a function of the polarization of the input pulse. The two phenomena are intimately connected.

There exist special orthogonal pairs of polarization at the input and the output of the fiber called the PSPs. Light launched in a PSP does not change polarization at the output to first order in ω. These PSPs have group delays, τ_g, which are the maximum and minimum mean time delays of the time domain view. The difference between these two delays is called the DGD. Typical mean values of the DGD are 1 to 50 ps for a 500-km long fiber, depending on fiber type. The PMD vector τ⃗ describes both the PSPs and the DGD in the fiber. It is a Stokes vector pointing in the direction of the slow PSP with a length equal to the DGD.

Some insight into the PMD problem can be had simply by contemplating a piece of polarization-maintaining fiber. Its PSPs are the polarizations along the principal axes of birefringence of the fiber. In this case the two axes can be treated separately, and in general have different phase shifts φ and different group delays dφ/dω. One can see that the different values of φ(ω) will also produce changes in the output state of polarization as a function of frequency unless the input is launched in one of the PSPs. It may seem surprising that PSPs occur in a fiber exhibiting random birefringence as a function of z. However, they do, as discovered by Poole and Wagner (2). The DGD grows roughly as the square root of the length of fiber, as is characteristic of a random walk problem. This section is devoted to the discussion of the PMD vectors.

We will discuss four mathematical expressions for the PMD vector, one based on Jones matrix eigenanalysis, one on σ-expansion, one on time domain moments, and one on Müller matrices. These expressions correspond to four different yet closely related views of PMD and form the basis for different experimental approaches, such as time-domain and frequency-domain PMD measurements.

Jones Matrix Eigenvector Analysis.

The analysis of Poole and Wagner (2) is based on the Jones matrix U and the frequency-domain view, identifying the group delay of a narrow-band pulse propagating through the fiber with the frequency derivative of the phase of the field. As is the case for polarization-maintaining fiber, they found two output polarization states t̂ that do not change to first order in frequency. These states have different group delays, and also exhibit the maximum and minimum mean time delays for narrow-band pulses of arbitrary input polarization. Note that our PMD vector τ⃗ is defined for right-circular Stokes space, while the widely used PMD vector Ω⃗ of Poole et al. (2, 3) is defined for left-circular Stokes space. The connection between τ⃗ and Ω⃗ is detailed in Appendix B in the supplemental data at www.pnas.org. We have chosen the symbol τ⃗ as appropriate for a quantity with the dimension of time.

According to Eqs. 2.3 and 3.3 we have a transmission equation

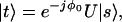5.1

relating the input and output Jones vectors |s〉 and |t〉. As pulses are described by wave packets with a finite frequency band, we need to consider the frequency dependence of |t〉. We assume fixed input polarization and phase—i.e., |s〉_ω = 0 (hence ŝ_ω = 0), as is appropriate for a simple pulse entering the fiber at time zero. By differentiating 5.1 and eliminating |s〉, we obtain for the change of the output Jones vector

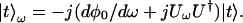5.2

Eq. 5.2 tells us that for most input polarizations, the output polarization will change with frequency in first order. The frequency derivative of the common phase φ₀ identifies a mean group delay τ₀ common to all polarizations

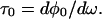5.3

Poole et al. (2, 3), in effect, noted that if |t〉 is either of the two orthogonal eigenstates of the operator jU_ωU^†, then t̂_ω = 0, and so |t〉_ω should be expressible in the form

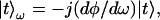5.4

where φ is the phase of |t〉. We show below that the operator jU_ωU^† is Hermitian and that its trace is zero. Thus its eigenvalues are real and add to zero. We designate them τ/2 and −τ/2. Comparing 5.2 with 5.4, identifying dφ/dω in 5.4 with a group delay τ_g, and using 5.3, we get the two values of group delay

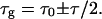5.5

The eigenstate of jU_ωU^† associated with the larger value of group delay we designate |p〉, so that the orthogonal eigenstate having the smaller value of group delay becomes |p₋〉. The slow PSP, |p〉, thus satisfies the Jones matrix eigenvector equation

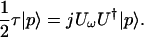5.6

According to 5.5 the DGD is τ. Since the determinant of a Hermitian matrix is the product of its eigenvalues, we have det(jU_ωU^†) = −τ²/4. From this, noting that det(U) = 1, we can extract an expression for τ, namely

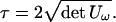5.7

The PMD vector τ⃗ is the Stokes vector of |p〉 multiplied with the DGD

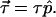5.8

Pauli Spin Matrix Expansion.

We now pause to examine the operator jU_ωU^†. Differentiation of the unitary condition 3.1 yields the relation

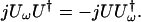5.9

Since the Hermitian conjugate of the product of two operators is the product of the Hermitian conjugates of the individual operators taken in the opposite order, we see that the matrix product jU_ωU^† is Hermitian. We also have det(U) = 1. Consider the expansion

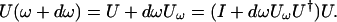5.10

Since the determinant of the product of two matrices is the product of their determinants, and det(U) = 1, one can see that det(U(ω + dω)) = 1 also only if the trace of U_ωU^† is zero. This is the argument necessary to arrive at 5.5. Given these properties of jU_ωU^†, and its eigenvalues ±τ/2, it follows that it can be written in the form

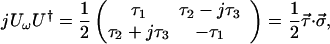5.11

where the last expression is in the spin vector form. To show that 5.11 and 5.8 identify the same vector τ⃗, we substitute 5.11 into the eigenvalue equation 5.6, yielding

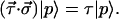5.12

In view of 3.10, we observe that τ⃗ = τp̂, as in 5.8, is the solution of 5.12. The σ-expansion of the Jones matrix product of 5.11 is, thus, a very practical tool, because it yields the PMD Stokes vector components as the coefficients of the expansion.

In Section 4 we derived the spin vector expansion of a Jones matrix U in terms of the rotational variables r̂ and ϕ. By substituting 4.4 into 5.11 we can gain an expression for τ⃗ in terms of these variables and their frequency derivatives. The result, using the spin vector rules A.5 and A.6 to reduce the intermediate factors, and the identity r̂_ω⋅r̂ = 0, is

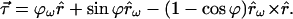5.13

When U is given in the Caley/Klein form

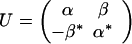5.14

we obtain the DGD from 5.7 as (2)

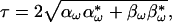5.15

and for the components τ_i

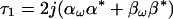5.16

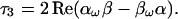Input and Output PMD Vectors.

The above discussion has focused on expressions for the PMD vector at the fiber output. There are practical cases where the corresponding PMD vector at the input is needed. This can be obtained by a simple transformation. We distinguish input and output quantities by the subscripts s and t (see Fig. 1). The relation between the PSPs |p_s〉 and |p_t〉 is governed by 3.3, which transforms the Jones vectors of the PSPs in the form

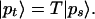5.17

Matrices M_s operating on vectors at the input transform to output matrix operators M_t = TM_sT^†. Applying this transformation to the matrix τ⃗⋅σ⃗ gives

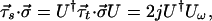5.18

where we have used 5.11 and T = e^−jφ₀U. Thus, the components of the input PMD vector τ⃗_s are the coefficients of the σ-expansion of the matrix product U^†U_ω. As the PMD vectors are Stokes vectors they are transformed by the Müller rotation matrix R isomorphic to U (see Eq. 4.2) as

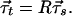5.19

Moments and Mean Signal Delay.

Moments are widely used to characterize pulse transmission, and they have also been applied to PMD phenomena (15–18). Here we describe their use for determining and defining PMD vectors. One should note that moments are very appropriate for the description of signal delays in systems involving two (or more) modes of propagation such as those involving PMD effects, whereas concepts such as group velocity and group delay have a strict definition for an individual mode only. The PMD phenomenon can split an input pulse into two or more pulses at the fiber output, leading to polarization-dependent pulse shapes. To maintain our awareness of this complexity we use the word “signal” for the output rather than “pulse.”

To prepare for the discussion of moments we represent a signal at fiber position z by the complex field vector E(z, t) in the time domain and by its Fourier transform Ẽ(z, ω) in the frequency domain. The tilde distinguishes between them.

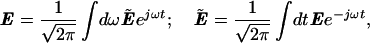5.20

where all integrals extend from −∞ to +∞. Let the fields be normalized so that the energy in the pulse is

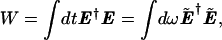5.21

where the right equation is Parseval's theorem.

The mean time t_g(z) at which a signal passes location z is defined by its center of gravity or first moment W₁

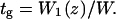5.22

Using the convolution theorem, the first moment can be written in either the time domain or the frequency domain

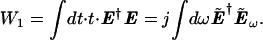5.23

We now use the transmission and Jones matrices to express the output field Ẽ_t in terms of the input Ẽ_s, Ẽ_t = T Ẽ_s, and use the derivatives,

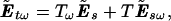5.24

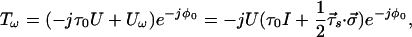5.25

to substitute in 5.22 and 5.23. Defining the mean signal delay τ_g as the difference between the mean arrival times at output (t) and input (s), one gets

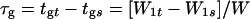5.26

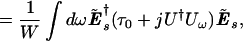where τ₀ = dφ₀/dω as before. Substituting the σ-expansion 5.18 for jU^†U_ω = ½τ⃗_s⋅σ⃗, the mean signal delay can be written in the form

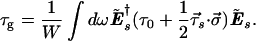5.27

We proceed by representing the input field Ẽ_s by its complex amplitude e, its unit Jones vector |s〉, and the corresponding Stokes vector ŝ (see Eq. 3.5),

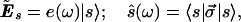5.28

where the signal energy becomes W = ∫dωe*e. Inserting this above, we obtain (15, 18) for the mean signal delay

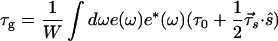5.29

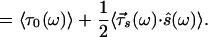where τ⃗_s is the input PMD vector as before. This expresses τ_g as the spectral mean (denoted by the 〈 〉 bracket) of the spectral density e*e weighing τ₀(ω) and the dot product between input PMD vector τ⃗_s(ω) and the input Stokes vector. This expression for the mean signal delay is valid for any input pulse shape and spectral variation of its polarization.

Specializing to frequency-independent input polarization ŝ and a narrow pulse spectrum such that τ₀ and τ⃗_s can be regarded constant over the signal band, 5.29 simplifies to (16)

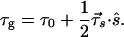5.30

This agrees with 5.5, which was derived for the special case of input polarizations aligned with the PSPs. Eq. 5.30 gives the mean signal delay for any input polarization. Inputs at the PSPs are seen to lead to the maximum and minimum delays τ_g. In fact, the mean signal delay τ_g can be simply interpreted as the power-weighted average of the two PSP delays. To see this, consider the representation of the input polarization as the superposition 3.14, |s〉 = a|p〉 + b|p₋〉, of the PSPs. These delays are (τ₀ ± τ/2) and the power-weighted average delay is

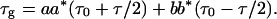5.31

We can now use the dot-product rule 3.11 to show the equivalence of 5.31 and 5.30. The simple form of 5.30 allows a determination of the PMD vector τ⃗_s in the time domain (19).

The higher moments W_n = ∫dt tⁿE^†E can be used to determine further detail on the properties of transmitted pulses. The second moment

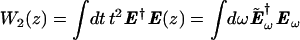5.32

provides information about rms pulse spreading. Proceeding along similar lines as above and the substitution of 5.24, we obtain

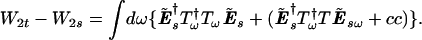5.33

From 5.25 it follows that

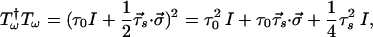5.34

where we have used spin-vector rule A.8. To simplify 5.33 further we use 5.28, assume frequency-independent input polarization |s〉, and characterize the complex input amplitude e(ω) by its real amplitude a(ω) and phase δ(ω)

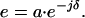5.35

The result is

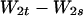5.36

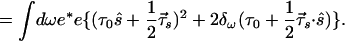For the special case of δ_ω = 0, this form agrees with the result of Karlsson (15). This special case assumes freedom from frequency chirp in the optical pulse and a symmetric pulse shape, or, more precisely, that E*(−t) = E(t).

Müller Matrix Expression for τ⃗.

A fourth way of determining the PMD vector uses Stokes space and the Müller (rotation) matrix R isomorphic to U. The background for this will be given in Section 6. For completeness we show the result here. It is

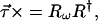5.37

where × denotes the cross-product operator as in 4.8.

This method relies on the determination of the rotation matrix R and its derivative in the frequency domain.

6. Laws of Infinitesimal Rotation

The laws of rotation assume a particularly simple form when the rotations are infinitesimally small—e.g., for a small change in fiber length or frequency. These are well known in mechanics (6) and are widely used in the related phenomena of PMD, coupled modes of propagation, and two-waveguide systems (3, 20–24). Here these laws allow simple geometrical interpretations in Stokes space (on the Poincaré sphere). We shall discuss infinitesimal laws for the birefringence vector, the PMD vector, and the dynamical PMD equation.

Birefringence Vector.

Consider the change of the polarization |s〉(z) of light at fiber location z due to a small length addition dz of fiber. This change is influenced by the fiber's local birefringence characterized by its effective relative dielectric tensor ɛ(z)—i.e., a cross-sectional average of the fiber characteristics for the fiber mode of interest. The change is governed by the wave equation for a spectral component of the effective transverse field vector Ẽ(z) of the mode,

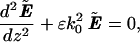6.1

where k₀ = 2π/λ₀ is the propagation constant of free space, and λ₀ is the free-space wavelength. To proceed, we use a σ-expansion of the ɛ-tensor of the form

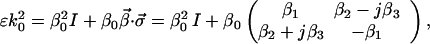6.2

where β₀ is the common propagation constant. The coefficients β_i of the expansion are the components of the local birefringence vector β⃗(z) in Stokes space. This vector has the character of a propagation constant and has been a useful tool in describing birefringence in PMD phenomena (3, 22, 25) (see Appendix B in supplemental data at www.pnas.org for the connection of β⃗ to the vector W⃗ used in part of the literature). In addition to this expansion we use an adiabatic approximation assuming that the polarization, |s〉(z), and ɛ(z) all vary slowly with z, and by setting

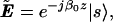6.3

where |s〉 includes a slowly varying phase. We continue by inserting 6.2 and 6.3 into 6.1. We drop the d²|s〉/dz² term in accordance with the adiabatic assumption and find the adiabatic wave equation for the Jones vector |s〉(z),

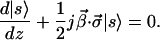6.4

The right-hand side of 6.2 shows the form of the fiber's dielectric tensor as expressed by the components β_i of the birefringence vector β⃗. It is apparent that optical activity (circular birefringence) is included in this description. For the special case of linear birefringence aligned with the fiber's x-axis we have β₂ = β₃ = 0 and β₁ = Δnk₀, where Δn is the differential refractive index. The corresponding ordinary and extraordinary indices are

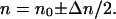6.5

There is a close relationship between the birefringence vector β⃗ and the concept of a local normal mode used in the theory of optical waveguides for the analysis of guides whose characteristics change with length z, such as our ɛ(z). At a given location z₀, the local normal modes are defined as the modes of a uniform guide with the characteristics of location z₀—i.e., a guide with uniform ɛ(z) = ɛ(z₀) in our case. Inserting this assumption into 6.1, we obtain the field of the two local normal modes Ẽ(z) = e^−jβ_Mz|s_M〉 whose polarization |s_M〉 does not change along the length. Because of 3.10 we know that |s_M〉 must be an eigenvector of β⃗⋅σ⃗. The polarization of the local normal modes is, thus, described by the Stokes vectors ±β⃗. The propagation constant β_M of the modes depends on their polarization in the form

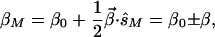6.6

assuming that β₀ ≫ β.

We now return to the case of interest where β⃗(z) changes along the fiber length z. To describe the change of polarization with z we differentiate the Stokes vector ŝ = 〈s|σ⃗|s〉 and obtain

6.7

Finally, we combine 6.4 and 6.7, use the spin vector rules A.6, A.7, and A.13, and obtain the law of infinitesimal rotation for birefringence

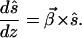6.8

Integration of 6.8 yields a formal expression for the Müller matrix R of the fiber as in 2.5.

PMD Vector τ⃗.

Here we consider the change of polarization at the fiber output due to a small change in frequency ω. The polarization at the input is held constant. We start with Eq. 5.2 written as

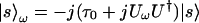6.9

for the change of the output polarization |s〉_ω, where the subscript ω indicates differentiation. The differential of the corresponding Stokes vector is

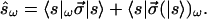6.10

Finally, we combine 6.9 and 6.10, using the σ-expansion 5.11 for the product U_ωU^†, apply spin vector rule A.6, A.7, and obtain the law of infinitesimal rotation

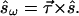6.11

The geometrical interpretation of this simple law is a rotation of the output Stokes vector on the Poincaré sphere as ω changes. The rotation axis is the PSP p̂ and the rotation rate is the DGD τ.

The infinitesimal rotation law 6.11 allows us to express the PMD vector in terms of the rotation (Müller) matrix R that relates the input and output Stokes vectors ŝ(0) and ŝ(z) by ŝ(z) = Rŝ(0). We differentiate this relation [while keeping the input ŝ(0) fixed] and obtain

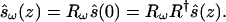6.12

Comparison of 6.11 and 6.12 yields the operator relationship

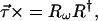6.13

which we have already listed in 5.37.

The Dynamical PMD Equation.

The dynamical PMD equation results from a combination of the infinitesimal rotation laws for PMD and birefringence (22). It is the basis for the statistical theory of PMD (23). Poole's derivation starts by differentiation of 6.8 with respect to ω and of 6.11 with respect to z. The results are combined by eliminating ∂²ŝ/∂z∂ω, and simplified by the relation a⃗×(b⃗×c⃗) = b⃗(a⃗⋅c⃗) − c⃗(a⃗⋅b⃗), yielding

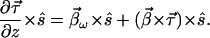6.14

As this is valid for any ŝ, we can extract the included equation

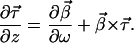6.15

This is the dynamical PMD equation describing the evolution of the PMD vector with distance. In the next section we shall see that it is intimately connected to the powerful PMD concatenation rules.

7. PMD Vector Concatenation Rules

The PMD vector concatenation rules (13, 16, 22, 23, 26) are a powerful set of simple tools that allow the determination of the PMD vector of an assembly of concatenated fiber sections when the PMD vectors of the individual sections are known. Among their uses is the analysis of the evolution of the PMD vector with fiber length (26), statistical PMD modeling (23), PMD simulation, and the design of multisection PMD compensators. They appear in a variety of related forms, including the sum, differential, and integral formulations for both the first-order and second-order PMD vectors. As a preparation for the discussion of these formulations, we shall first review the relations between the output and input PMD vectors of a single fiber section.

Transformation of PMD Vectors.

Consider a fiber section with rotation matrix R and input and output Stokes vectors ŝ and t̂ as shown in Scheme S2. The corresponding PMD vectors at input and output are τ⃗_s and τ⃗. They are related by

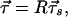7.1

as discussed earlier (5.19). The expression for the output vector τ⃗ in terms of R was already given in 6.13; it is

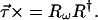7.2

As cross-product operators transform like matrices from output to input we obtain the expression for the input PMD vector as

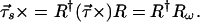7.3

When higher-order PMD effects are considered, τ⃗ is usually called the “first-order” PMD vector, its frequency derivative τ⃗_ω is the “second-order” PMD vector, the second derivative τ⃗_ωω is the “third-order” PMD vector, etc. The input/output transformation for the second-order PMD vectors τ⃗_sω and τ⃗_ω is derived by differentiating 7.1 and substituting 7.2, giving

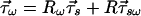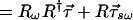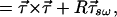with the result

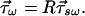7.4

This shows that the input and output second-order PMD vectors transform the same way as the first-order vectors of the section. For the third-order PMD vectors one gets the somewhat more complicated relationship

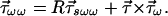7.5

Scheme 2.

PMD of Two Concatenated Sections.

Here, we consider two concatenated fiber sections with rotation matrices R₁ and R₂ as shown in Scheme S3. The output PMD vectors of each of the individual sections are τ⃗₁ and τ⃗₂.

Scheme 3.

Our goal is to determine the output PMD vector of the combined assembly. The rotation matrix R of the two-section assembly is the matrix product

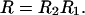7.6

Combining this with 7.2, we find for the PMD vector τ⃗ of the assembly that

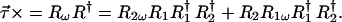7.7

Now we recall that R₁R₁^† = I, apply 7.2 for the individual sections as well as a transformation of matrix operators as in 5.18

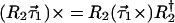7.8

to simplify 7.7 into the form

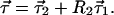7.9

This is the basic concatenation rule. It can be generalized to multiple sections as well as differentially small sections. It can also be transformed to the input of the fiber, or, for that matter to any desired fiber cross section. The rule is very similar to that for impedances of a transmission line: to get the PMD vector of an assembly, transform the PMD vectors of each individual section to a common reference cross section and take the sum of all those vectors.

The concatenation rule for the second-order PMD vector τ⃗_ω follows from 7.9 by differentiation and substitutions similar to those above. One obtains

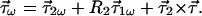7.10

The Differential Concatenation Rule.

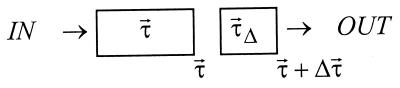
Here, we apply the two-section concatenation rule to a long piece of fiber with output PMD vector τ⃗ and a differentially small fiber addition of length Δz as shown in Scheme S4.

Scheme 4.

We want to answer the question: How does τ⃗(z) change due to the differential addition of length Δz? The answer to this question is already provided by the dynamical PMD equation 6.15. Our discussion will show that the latter is identical to the differential form of the concatenation rule. It will establish a link between this rule and the laws of infinitesimal rotation treated in Section 6. For this purpose we need to determine the rotation matrix R_Δ and the PMD vector τ⃗_Δ of the differential addition Δz. We use the local birefringence vector β⃗ of the addition and the law of infinitesimal rotation (6.8) and get for the change Δŝ of the Stokes vector ŝ entering the element

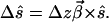7.11

In terms of R_Δ, the output Stokes vector ŝ + Δŝ can be expressed as

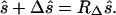7.12

Comparison of 7.11 and 7.12 yields the desired expression for the rotation matrix of the differential addition

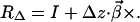7.13

To obtain its PMD vector τ⃗_Δ we differentiate 7.13, apply 7.2, and drop terms of second order in Δz with the result

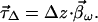7.14

The PMD concatenation rule 7.9 for the addition of the differential fiber element is

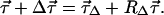7.15

Now we can insert 7.13 and 7.14, divide by Δz, and get

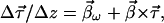7.16

which is the dynamical PMD equation 6.15 on transition to infinitesimal Δz.

The differential concatenation rule for the second-order PMD vector is obtained along similar lines or by differentiation of 7.16. It is

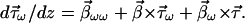7.17

Concatenation Rules for Many Sections.

Consider now a fiber consisting of m individual sections, which is sketched in Scheme S5.

Scheme 5.

The rotation matrices R_n and the output PMD vectors τ⃗_n of each section are considered known. The PMD vectors τ⃗ and τ⃗_ω of the combined assembly can be determined by repeated application of the two-section rules 7.9 and 7.10. The resulting expressions simplify if we define the rotation matrix of the last m − n + 1 sections as

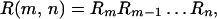7.18

where R(m, m) = R_m and R(m, m + 1) = I, and the output PMD vector of the first n sections as τ⃗(n).

Using these definitions, the sum rules for the first- and second-order PMD vectors of the assembly are

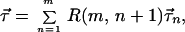7.19

and

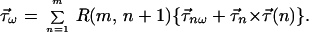7.20

Integral Form of the Concatenation Rule.

The above sums turn into integrals when one makes the transition to infinitesimal sections of length dz and uses the birefringence vector β⃗(z) to express the PMD vector τ⃗(z) of an infinitesimal section

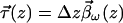7.21

as in 7.14. For a fiber of length L, we express the rotation from z to L as R(L, z) corresponding to 7.18 and get the integral formulations of the output PMD vectors at L as

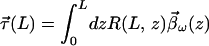7.22

and

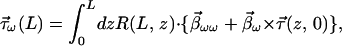7.23

where τ⃗(z, 0) is the PMD vector for the piece of the fiber extending from 0 to z.

Abbreviations

PMD

polarization mode dispersion

3-D and 2-D

three- and two-dimensional

PSP

principal state of polarization

DGD

differential group delay

Pauli Spin Matrices and Spin Vectors

In this section we give a brief review of the properties of the Pauli spin matrices defined in Section 2 and of some key formulas for the spin vectors σ⃗ which will be used in the main body of the paper (9). The spin vector notation provides a convenient way of dealing with the complex 2×2 matrices that occur in the Jones matrix analysis of lightwave transmission. In addition it simplifies the connection between the complex 2-D Jones vectors and their corresponding real 3-D Stokes vectors. The spin matrices are Hermitian and unitary—i.e.,

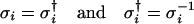A.1

and have zero trace, Tr σ_i = 0. They obey the well-known multiplication rules

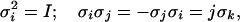A.2

where the indices (i, j, k) can be any cyclic permutation of (1, 2, 3). The spin vector notation consists of treating the three spin matrices of Jones space as the three components of a vector in Stokes space. For example, the dot product a⃗⋅σ⃗ = a₁σ₁ + a₂σ₂ + a₃σ₃ is a 2×2 matrix in Jones space. Thus, the spin vector σ⃗ contains elements of both spaces, and is useful in examining their connection. By using rule A.2, any function of the σ matrices that can be expanded in a power series can be reduced to an expression linear in the σ matrices and the unit matrix I. Useful examples of such reductions, expressed in spin vector notation, are

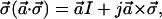A.3

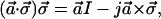A.4

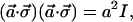A.5

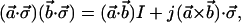A.6

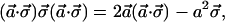A.7

where I is the 2×2 unit matrix and a⃗ and b⃗ are any vectors in Stokes space, and a is the length of the vector a⃗. Although limited space does not permit us to write out the detailed derivations for the above, note that A.4 is the complex conjugate of A.3 and that A.5 is a special case of A.6. Note also that a⃗⋅σ⃗ does not commute with b⃗⋅σ⃗ unless a⃗×b⃗ = 0.

In general, any 2×2 matrix M may be expanded in the form

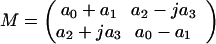A.8

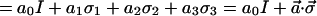with coefficients a_i given by

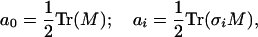A.9

where to show A.9 we use A.2 along with Tr(I) = 2 and Tr(σ_i) = 0. In A.8 we have used the spin vector σ⃗ to write the expansion in compact notation. An illustrative example of A.8 is

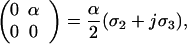A.10

which is intended to demonstrate its universality. Note that the right-hand sides of A.3 through A.7 are matrices of the form of A.8.

If M is Hermitian (M^† = M), then the a coefficients in the expansion A.8 are real. If M is unitary (M^† = M⁻¹), then it can be expressed in the form

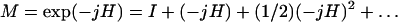A.11

where H is a 2×2 Hermitian matrix, and the right-hand side is the usual power series expansion of the exponent function (12). If we express the matrix H of A.11 in the form A.8 with real coefficients, we get for the unitary matrix

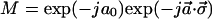A.12

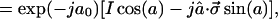where aâ = a⃗. In A.12 the first form results because the unit matrix I commutes with the others, and the last form results from expanding exp(−ja⃗⋅σ⃗) in a power series and using A.5 to reduce the result to a form linear in I and the Pauli matrices. It is easy to show directly that if M has the form A.12, then M^†M = I. Note that if the trace of any matrix M is zero, then the coefficient of I must be zero. Also, it is not difficult to show from A.12 that if a unitary matrix M, such as U in the text, satisfies det(M) = 1, then the coefficient exp(−ja₀) is restricted to the values 1 or −1.

A great practical value of the spin vector notation is that σ⃗ can be converted into any Stokes vector (ŝ) by forming a quadratic form as in 3.5. This simplicity carries to more complex expressions such as in

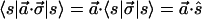A.13

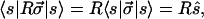where R is a 3×3 matrix. In the sense of A.13 it is often appropriate to regard σ⃗ as an arbitrary vector in Stokes space. For example, in the text we often use the fact that if a⃗⋅σ⃗ = b⃗⋅σ⃗, it follows that a⃗ = b⃗. This result also follows from A.8 and A.9, since the vector components a_i can be recovered from the dot product a⃗⋅σ⃗.