Structural informatics, modeling and design with an open-source Molecular Software Library (MSL)

Abstract

We present the Molecular Software Library (MSL), a C++ library for molecular modeling. MSL is a set of tools that supports a large variety of algorithms for the design, modeling and analysis of macromolecules. Among the main features supported by the library are methods for applying geometric transformations and alignments, the implementation of a rich set of energy functions, side chain optimization, backbone manipulation, calculation of Solvent Accessible Surface Area (SASA) and other tools. MSL has a number of unique features, such as the ability of storing alternative atomic coordinates (for modeling) and multiple amino acid identities at the same backbone position (for design). It has a straightforward mechanism for extending its energy functions and can work with any type of molecules. While the code base is large, MSL was created with ease of developing in mind. It allows the rapid implementation of simple tasks while fully supporting the creation of complex applications. Some of the potentialities of the software are demonstrated here with examples that show how to program complex and essential modeling tasks with few lines of code. MSL is an ongoing and evolving project, with new features and improvements being introduced regularly, but it is mature and suitable for production and has been used in numerous protein modeling and design projects. MSL is open source software, freely downloadable at http://msl-libraries.org. We propose it as a common platform for the development of new molecular algorithms, and to promote the distribution, sharing and reutilization of computational methods.

Introduction

Over the past decades computational biology has been contributing more and more frequently to the understanding o f macromolecular structure and the mechanisms of biological function. While the number of high resolution protein structures in the Protein Data Bank (PDB) is steadily growing, the experimental methods currently available for structural determination do not nearly approach the level of throughput that would be necessary to characterize the universe of known protein sequences [1]. This generates high interest in reliable and affordable protein modeling methods, as ways for investigating the function of proteins and predicting their interactions and specificity. Computational methods can take advantage of today's large structural database and essentially expand it. Homology based methods have now reached excellent levels of performance in predicting the structure of many proteins when one of their close relative has been experimentally determined [2,3]. Comparative structural analysis can be used to identify common themes and key interactions in sets of related proteins. The structural database can also be disassembled into fragments, and these fragments form the basis for ab initio structural prediction methods and provide templates for filling in the missing elements in experimental structural models [4]. Molecular modeling can today work directly in combination with experimental structural methods such as NMR to help building accurate structural models from incomplete or reduced dataset [5]. Modeling is also becoming a fundamental tool for assisting experimental design, ration al mutagenesis and protein engineering. It also provide an invaluable framework for interpreting experimental data. Such approach has greatly helped to improve our knowledge of proteins that are intrinsically difficult to study with the traditional structural methods, such as, for example, the integral membrane proteins [6–8]. Finally, molecular modeling methods allow today to create proteins de novo. Protein design has become an important tool for investigating the fundamental principles that govern stability, specificity and function in proteins and can be applied to the creation of new reagents and probes [4,9–11].

With the continued increase in power and decrease in cost of high-throughput computing, computational biology is likely to continue to grow and become even more integrated with the experimental disciplines. To fully support this trend and promote the use of the existing methods and the creation of new powerful algorithms, it is important to spread the availability of molecular modeling libraries, providing the community with tools that are fully featured, powerful, easy to use and, ideally, free to distribute and modify. Here we present MSL, an open-source C++ library that fulfills these criteria and supports the creation of efficient methods for structural analysis, prediction and design of macromolecules. MSL is not a single program but a set of objects that facilitate the rapid development of code for molecular modeling. The object oriented library is targeted toward researchers who need to develop simple or sophisticated modeling and analysis programs. The main objectives of MSL are to allow the implementation of simple tasks with maximum ease (e.g. measuring a distance or translating a molecule) while fully supporting the creation of complex and computationally intensive applications (such as protein modeling and design). This objective has been achieved by developing efficient code. The design of an intuitive APIs and the maximization of the modularity of the objects has allowed to keep the code base simple and easily expandable, agnostic to the type of molecule and thus suitable to work with proteins, nucleic acids or any other small or large molecules. For these reasons MSL is ideal for supporting the implementation of a large variety of structural analysis, modeling and design algorithms that appear in the growing computational biology literature. The adoption of a common platform for the implementation of computational methods would greatly benefit the scientific community as a whole. It would to help avoid fragmentation and promote the distribution of the methods and their integration. The open source model allows the continued development of the code, higher scrutiny and quality control, and deeper understanding of the methods. This model has been successfully adopted by other scientific projects (for example the bioinformatics toolsets BioPerl [12] and BioPython [13]).

The development of the MSL libraries has been active over the past four years and a growing list of algorithms has already been implemented, with more features and enhancement to come. The platform has been successfully applied to numerous areas of biological computing, including modeling [14,15] and de novo design of membrane proteins [16], modeling large conformational changes in viral fusion proteins [17], designing a switchable kemp eliminase enzyme [18], studying distributions of salt bridging interactions [19], the development of an empirical membrane insertion potential [20], the development of new conformer libraries [21] and other ongoing projects. In this article we highlight a number of unique and powerful capabilities of MSL, using several key worked examples to provide the reader with a basic understanding of the MSL object structure. For example, we illustrate how to access molecular objects, apply geometric transformations, model a protein, make mutations, apply a rotamer library, calculate energies and do side chain optimization. Further, we illustrate a side chain conformation prediction program that is distributed with the library and present its performance statistics against a large set of proteins structures. A comprehensive set of tutorials and helpful documentation is currently being assembled on the MSL website (http://www.msl-libraries.org) where MSL is also freely available for download.

Molecular objects in MSL

Molecular representation: flat-array versus hierarchical structure

At the very core of any molecular modeling software is the representation of the molecule. A simple level of representation may be sufficient for a number of tasks. For example, a program that translates a molecule only requires access to the atoms' coordinates. In such case a “flat-array” of individual atoms can be rapidly created and is memory efficient. This representation would allow a quick iteration over atoms to apply the transformation. Other tasks may benefit from a more complex representation. For example, a program for computing backbone dihedral (φ/ψ) angles of a position needs to access the C and N atoms of the preceding and following amino acids. The identification of the relevant atoms becomes more rapid if the macromolecule is stored as a “hierarchical” representation, in which the atoms are subdivided by residue, and the residues are ordered into a representation of the chain. Because of these conflicting needs, MSL implements both flat-array and structured hierarchical approaches and lets the programmer decide what is most efficient and appropriate for a given task.

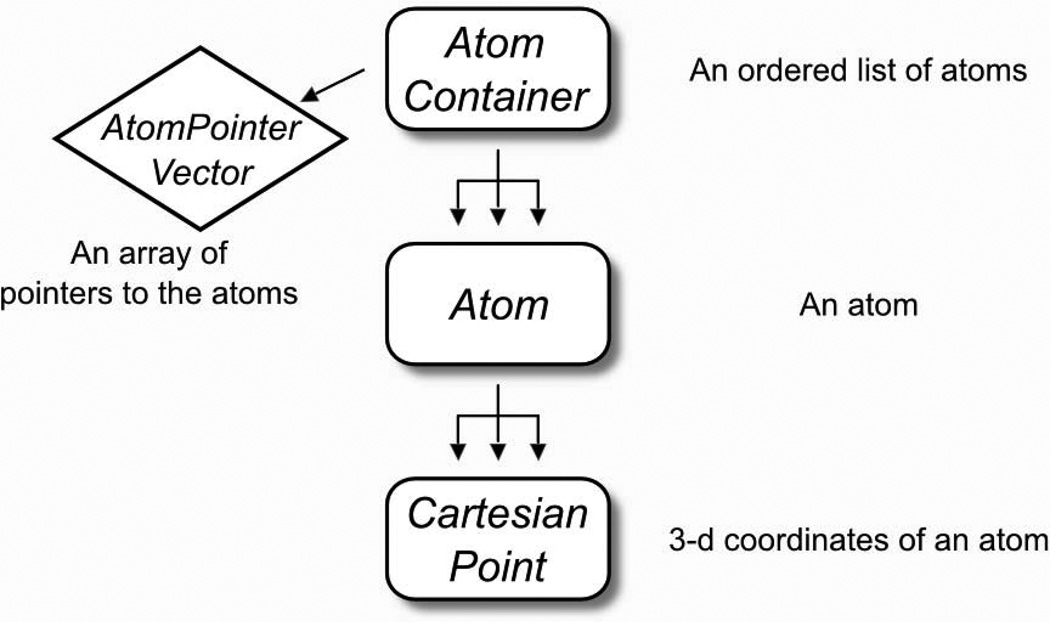
The flat-array representation – called AtomContainer – is schematically explained in Fig. 1. The AtomContainer acts as an array of Atom objects that can be iterated over using an integer index. Each Atom holds all of its relevant information (such as atom name, element, atom type, coordinates and bonded information). Inside the Atom, the coordinates are held by a CartesianPoint, which handles all the geometric functions. The AtomContainer has functions for inserting and removing atoms, checking their existence by a string “id” (chain id + residue number + atom name, i.e. “A,37,CA”), and has functions for reading and writing PDB coordinate files [22].

Fig. 1. The “flat-array” molecular container: the AtomContainer.

The AtomContainer is the lightweight molecular container included in MSL. Internally it contains an array of Atom pointers (as an AtomPointerVector), and it is ideal for tasks that require iteration among atoms. Each Atom contains one or more coordinates in the form of CartesianPoints.

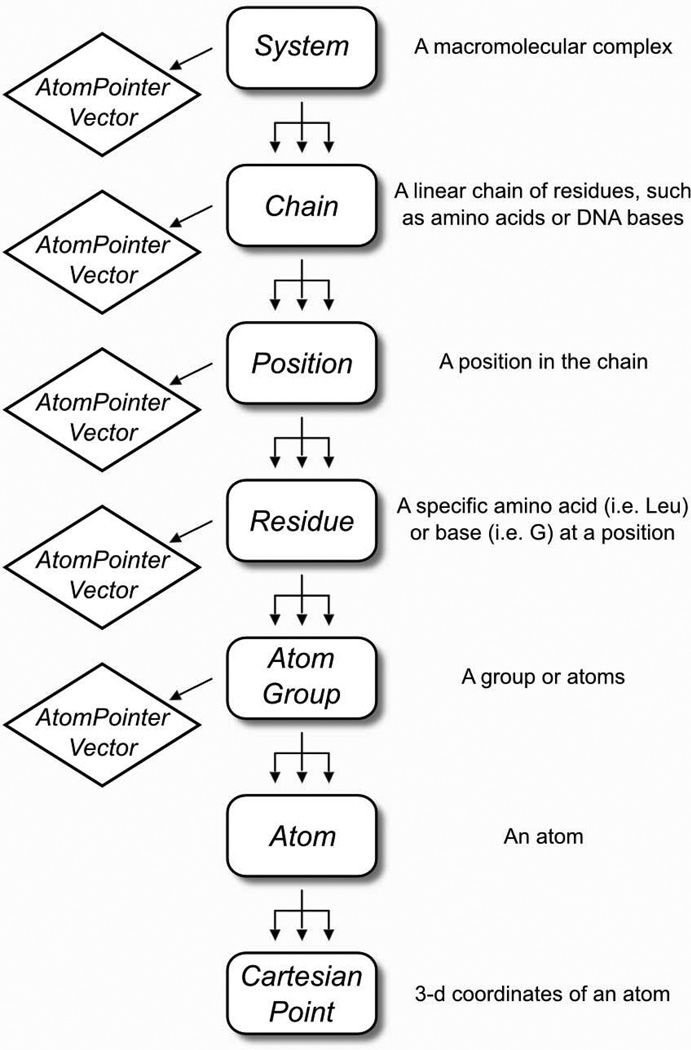
The hierarchical representation in MSL has seven nested levels, as illustrated in Fig. 2. The System is the top-level object that contains the entire macromolecular complex, and is divided into Chain objects. Chains are divided into Position objects. Within the Position there is one (and sometime more) Residue objects, corresponding to the specific amino acid types in a protein, for example Leu or Val. The distinction between a Position and a Residue enables easy implementation of mutation and protein design algorithms, where the position along the protein chain remains constant, but the amino acid types within the Position are allowed to change. The Residue can be divided into any number of AtomGroup objects, which contains the Atom objects. This subdivision allows for electrostatic groups or other subdivisions atoms, such as backbone or side chain atoms.

Fig. 2. The “hierarchical” molecular containers: the System and its subdivisions.

MSL has several levels of molecular representation, from the System to the Atom, described in the figure. Note the distinction between a Position (designated with a number) and the Residue (a specific amino acid type, such as “Leu”, “Ile”). A Position can have multiple residues (only one being active at any give time) which is useful for introducing mutations and protein engineering. The Atom objects are generated within the AtomGroup, but every container builds an array of pointers to the atoms (an AtomPointerVector) that belong to their branch. These atom pointers can be requested with a getAtomPointers() call and passed to external objects for processing.

Printing out molecular objects

MSL is created with ease of programming in mind. An example of this philosophy is MSL facilitates the printing of information contained within molecular objects, which is also extremely convenient for debugging. The following example shows how to print atoms and higher molecular containers through the << operator.

1  #include "AtomContainer.h"
2  #include "System.h"
3
4  using namespace MSL; // use the necessary namespaces (it will be dropped
5  using namespace std; // in the following examples)
6
7  int main() {
8     AtomContainer molAtoms; // the flat-array container
9     molAtoms.readPdb("input.pdb");
10
11    Atom & a = molAtoms[0]; // get an atom by reference
12    cout << "Printing an Atom" << endl;
10    cout << a << endl;
11
12    cout << "rinting an AtomContainer" << endl;
13    cout << molAtoms << endl;
14
15    System sys; // the hierarchical container
16    sys.readPdb("input.pdb");
17
18    cout << "Printing a System" << endl;
19    cout << sys << endl;
20
21 }

The Atom prints its atom name, residue name, residue number, chain id and the coordinates. As explained later, atoms can store more than one set of coordinates, called alternative conformations in MSL. The current conformation and total number of conformations is printed in parenthesis.

Printing an Atom
N   ALA   1  A [    2.143    1.328    0.000] (conf  1/ 1) +

The AtomContainer prints a list of all its atoms.

Printing an AtomContainer
N   ALA   1  A [    2.143     1.328    0.000] (conf  1/ 1) +
CA  ALA   1  A [    1.539     0.000    0.000] (conf  1/ 1) +
CB  ALA   1  A [    2.095    −0.791    1.207] (conf  1/ 1) +
C   ALA   1  A [    0.000     0.000    0.000] (conf  1/ 1) +
…

The System prints its sequence, where each chain identifier starts the line followed by the three letter amino acid codes of its sequence. The residue numbers are included in curly brackets for the first and last residue, or when the order breaks in the primary sequence numbering.

Printing a System
A: {1}ALA ILE VAL TYR SER LYS ARG LEU {9}ALA

Iterating through chains, positions and atoms

All containers, even those in MSL's hierarchical representation, can operate on atoms as ordered lists. The AtomContainer, System, Chain, Position and Residue all contain a list of their atoms (stored internally as an AtomPointerVector object, which is an array class derived through inheritance from the Standard Template Library [23] vector class). The individual atoms can be accessed using the square bracket operator ([ ]). The next example shows how to iterate and print all atoms in a System.

1  #include "System.h"
2
3  int main() {
4     System sys;
5     sys.readPdb("input.pdb");
6
7     for (uint i=0; i<sys.atomSize(); i++) {
8        cout << sys[i] << endl; // print the i-th atom using the [] operator
9     }
10 }

The hierarchical architecture of the System allows also iterate through positions and chains using the appropriate get function.

…
1  …
2
3  for (uint i=0; i<sys.positionSize(); i++){
4     cout << sys.getPosition(i) << endl; // print the i-th position
5  }
6  for (uint i=0; i<sys.chainSize(); i++){
7     cout << sys.getChain(i) << endl; // print the i-th chain
8  }
9 }

Accessing atoms by id and measuring distance and angles

A powerful alternative mechanism to access an atom is through a comma-separated string identifier formed by the chain id, residue number and atom name (i.e. “A,37,CA”). This can be done intuitively using a square bracket operator ([“A,37,CA”]). The following example demonstrates how to access atoms with both the numeric index and string id operators. It also shows how to calculate geometric relationships between atoms (using the Atom's functions distance, angle and dihedral).

1  #include "AtomContainer.h"
2
3  int main() {
4     AtomContainer molAtoms;
5     molAtoms.readPdb("input.pdb");
6
7     // Using the operator[string _id] (format "chain,residue number,atom name")
8     double distance = molAtoms["A,37,CD1"].distance("B,45,ND1");
9
10    // Using the operator[int _index]
11    double angle = molAtoms[7].angle(molAtoms[8], molAtoms[9]);
12
13    // measure the phi angle at position A 23
14   double phi = molAtoms["A,22,C"].dihedral(molAtoms["A,23,N"], molAtoms["A,23,CA"],
molAtoms["A,23,C"]);
15    return 0;
16 }

For brevity and simplicity the examples illustrated here often omit recommended error checking code. In the above example it would be safe to check for the existence of the atoms with the atomSize and atomExists functions before applying the measurements:

1  if (molAtoms.atomSize() >= 10) {
2     double dihe = molAtoms[7].dihedral(molAtoms[8], molAtoms[8], molAtoms[9]);
3  }
4
5  if (molAtoms.atomExists("A,37,CD1") && molAtoms.atomExists("A,37,ND1")) {
6     double d = molAtoms("A,37,CD1").distance(molAtoms("A,37,ND1"));
7  }

Communication between objects with the AtomPointerVector

The molecular objects store all their atoms internally as an array of atom pointers, the previously mentioned AtomPointerVector. The memory is allocated (and deleted) by the molecular object that created the atoms. All atom pointers of a molecular object can be obtained with the getAtomPointers() function.

1  #include "AtomContainer.h"
2
3  int main() {
4     AtomContainer molAtoms;
5     molAtoms.readPdb("input.pdb");
6
7     // get the internal array of atom pointers of the container
8     AtomPointerVector pAtoms = molAtoms.getAtomPointers();
9
10    for (uint i=0; i<pAtoms.size(); i++) {
11       cout << *(pAtoms[i]) << endl; // derefernce the pointer and print the atom
12    }
13    return 0;
14 }

The AtomPointerVector serves a fundamental purpose in MSL as the intermediary of the communication between objects that perform operation on atoms. The next section exemplifies this work-flow.

Rigid body transformations of a protein structure

The Transforms object is the primary tool used in MSL to operate geometric transformations. It communicates with the AtomContainer through an AtomPointerVector. As shown in the example, just five lines of code are sufficient for reading a PDB coordinate file, applying a translation and writing the new coordinates to a second PDB file. The reading and writing of the coordinate files is accomplished by the readPdb and writePdb functions of the AtomContainer.

1  #include "AtomContainer.h"
2  #include "Transforms.h"
3
4  int main() {
5     AtomContainer molAtoms;
6     molAtoms.readPdb("input.pdb");
7
8     Transforms tr;
9     tr.translate(molAtoms.getAtomPointers(), CartesianPoint(3.7, 4.5, −2.1));
10
11    molAtoms.writePdb("translated.pdb");
12    return 0;
13 }

Atom selections

The AtomPointerVector is also a mediator in another important function: the selection of subsets of atoms. The AtomSelection object takes an AtomPointerVector and a selection string (i.e. “name CA”) to create subsets of atoms based on boolean logic. The resulting selection is returned as another AtomPointerVector. The syntax adopted is similar to that of PyMOL, a widely used molecular visualization program [24]. In the following example a selection is used to rotate only the atoms belonging to chain A. The communication between AtomContainer, AtomSelection and Transforms through the AtomPointerVector is made explicit.

1  #include "AtomContainer.h"
2  #include "Transforms.h"
3  #include "AtomSelection.h"
4
5  int main() {
6      AtomContainer molAtoms;
7      molAtoms.readPdb("input.pdb");
8
9      AtomPointerVector pAtoms = molAtoms.getAtomPointers();
10
11     AtomSelection sel(pAtoms); // initialize the AtomSelection
12     AtomPointerVector pSelAtoms = sel.select("chain A"); // select chain A
13
14     CartesianPoint Zaxis(0.0, 0.0, 1.0); // the axis of rotation
15
16     Transforms tr;
17     tr.rotate(pSelAtoms, 90.0, Zaxis); // rotate by 90 degrees around the Z axis
18
19     molAtoms.writePdb("rotated.pdb");
20     return 0;
21 }

The example above shows a simple selection string but the logic can be complex. For example “name CA+C+N+O and chain B and resi 1–100” will select the backbone atoms of the first 100 residues of chain B. A label can be added at the beginning of the selection string (“bb_chB, name CA+C+O+N and chain B”). The label itself can then be used as part of the logic in a subsequent selection, as seen in line 17.

1  #include "AtomContainer.h"
2  #include "AtomSelection.h"
3
4  int main() {
5     AtomContainer molAtoms;
6     molAtoms.readPdb("input.pdb");
7
8     // create a selection object passing all atom pointers
9     AtomSelection sel(molAtoms.getAtomPointers());
10
11    // create a selection for all CA atoms called "allCAs" and print its size
12    AtomPointerVector pSelAtoms = sel.select("allCAs, name CA");
13    cout << "The selection allCAs contains " << pSelAtoms.size() << " atoms" << endl;
14
15    // selections can be operated with complex logic
16    AtomPointerVector pSelAtoms2 = sel.select("bb_chB, name CA+C+O+N and chain B"); // all backbone
atoms of chain B
17    AtomPointerVector pSelAtoms3 = sel.select("res9B_bb, bb_chB and resi 9"); // a selection name can
be used as part of the logic (here selecting the backbone atoms of residue 9 on chain B
18  }

Molecular modeling in MSL

Altering the conformation of the molecule

MSL offers a number of methods for remodeling a protein. The coordinates of an atoms can be set with the setCoor function.

1  Atom a;
2  a.setCoor(3.564, −2.143, 6.543);

The conformation of a protein can also be changed by rotating around bonds, changing the bond angles, and varying the bond distances. In other words, conformations can be set using a system of “internal” coordinates (bonds, angles and dihedrals). The Transforms object offer functions that can be used to model a protein (setBondDistance, setBondAngle and setDihedral). The next example shows how to alter the conformation of the backbone (φ/ψ angles).

1  #include "AtomContainer.h"
2  #include "AtomSelection.h"
3
4  int main() {
5       AtomContainer molAtoms;
6       molAtoms.readPdb("input.pdb");
7
8       // before changing the conformation we need to know what atoms are bonded to each other
9       AtomBondBuilder abb;
10      abb.buildConnections(molAtoms.getAtomPointer());
11
13      // lets change the phi/psi of residue A 37
12      Transforms tr;
13      tr.setDihedral(molAtoms("A,36,C"),molAtoms("A,37,N"),
14             molAtoms("A,37,CA"),molAtoms("A,37,C"), −62.0);
15      tr.setDihedral(molAtoms("A,37,N"),molAtoms("A,37,CA"),
16             molAtoms("A,37,C"),molAtoms("A,38,N"), −41.9);
17  }

Because in most cases the intent is to move two parts of the protein relative to each other, and not simply one atom, it is necessary to have the atom connectivity information. This was done in lines 9–10 by passing the atoms to AtomBondBuilder, an object that creates the bond information based on the atomic distances. The connectivity information is used to update the coordinates of the atoms that are downstream of the dihedral angle (any atom between the last dihedral atom and the end of the chain). This means that a set_dihedral invocation takes all the coordinates of the atoms downstream and multiplies them by the appropriate transformation matrix.

The strategy illustrated above is straightforward to implement for small changes (i.e. edit a side chain dihedral angle). For larger conformational changes, the procedure is inefficient because most of the coordinates would be recalculated multiple times. A more economic alternative is to edit a table that stores all internal coordinates, and use it to rebuild the molecule in the new conformation one atom at the time – a concept borrowed from the molecular forcefield and dynamics package CHARMM [25]. MSL implements an object for internal coordinate editing called the ConformationEditor.

1  #include "System.h"
2  #include "PDBTopologyBuilder.h"
3  #include "ConformationEditor.h"
4
5  int main() {
6
7     // create an empty System and build the IC table with the PDBTopologyBuilder
8     System sys;
9     PDBTopologyBuilder PTB(sys, "pdb_topology.inp");
10    PTB.buildSystemFromPDB("input.pdb");
11
12    // Create a Conformation Editor and read the file with the definitions of angles such
13    // as phi, psi, and conformations such as "a-helix"
14    ConformationEditor CE(sys);
15    CE.readDefinitionFile("PDB_defi.inp");
16
17    // Edit the rotamer of LEU A 37 to have chi1=62.3 and chi2=175.4
18    CE.editIC("A,37", "N,CA,CB,CG", 62.3); // using atom names
19    CE.editIC("A,37", "chi2", 175.4); // using a predefined label chi2="CA,CB,CG,CD1"
20
21    // set the backbone of A 37 in beta conformation
22    CE.editIC("A,37", "phi", −99.8);
23    CE.editIC("A,37", "psi", 122.2);
24
25    // you can even set entire stretches in helical conformation
26    CE.editIC("A,20–A,30", "a-helix"); // a-helix defines phi, psi and even the bond angles
27
28    // when done with all edits, the changes are applied at once to the protein conformation
29    CE.applyConformation();
30
31    sys.writePdb("edited.pdb");
32  }

Storing multiple conformations and switch between them

An extremely useful feature of MSL is the ability of storing multiple coordinates for each atom. This is done internally within the Atom by representing the coordinates as an array of CartesianPoint objects. Only one of the coordinates is active at any given time. This information is stored by a pointer, and the active coordinates can be readily switched by readdressing it. This feature allows for storing different conformations of parts or the entirety of a macromolecule. The following example demonstrates how to switch between sets of coordinates at the level of an Atom.

1  #include "AtomContainer.h"
2
3  int main() {
4     AtomContainer molAtoms;
5     molAtoms.readPdb("input.pdb");
6
7     // add two alt conformation to the first atom, A,1,N
8     molAtoms[0].addAltConformation(4.214, −6.573,  2.123);
9     molAtoms[0].addAltConformation(4.743,  3.123, −1.986);
10
11    cout << "The atom has " << molAtoms[0].getNumberOfAltConformations() << " conformations" << endl;
12    cout << "The active conformation's index is " << molAtoms[0].getActiveConformation() << endl;
13    cout << molAtoms[0] << endl; // print the atom
14    molAtoms[0].setActiveConformation(2);
15    cout << "The active conformation is now " << molAtoms[0].getActiveConformation() << endl;
16    cout << molAtoms[0] << endl;
17    return 0;
18 }

Output (note the change of conformation number with the the brackets):

The atom has 3 conformations
The active conformation's index is 0
N    ALA    1  A [     3.756     −6.987      2.456] (conf 1/  3) +
The active conformation's index is now 2
N    ALA    1  A [     4.743      3.123     −1.986] (conf 3/  3) +

Using a rotamer library

The multiple coordinates provide a mechanism for storying alternate conformations of side chains (or rotamers). The rotamers can be loaded on the molecule using the SystemRotamerLoader object, which reads a rotamer library file (line 13). The setActiveRotamer function of the System (line 18) can switch between rotamers by changing the active coordinates of all side chain atoms at once.

1  #include "System.h"
2  #include "PDBTopologyBuilder.h"
3  #include “SystemRotamerLoader.h”
4
5  int main() {
6
7     // create an empty System
8     System sys;
9     sys.readPdb("input.pdb");
10
11    // Use the SystemRotamerLoader to load 10 rotamers on LEU A 37. The
12    // rotamers are built and stored as alternative atom conformations
13    SystemRotamerLoader rotLoader(sys, "rotlib.txt");
14    rotLoader.loadRotamers("A,37", "LEU", 10);
15
16    // cycle to set the LEU at position A 37 in all possible rotamers
17    for (int i=0; i<sys.getTotalNumberOfRotamers("A,37"); i++) {
18       sys.setActiveRotamer(“A,37”, i);
19       // do something…
20    }
21 }

The rotamer library is stored in a text file with the format of the Energy Based conformer library [21], which is distributed with MSL. Support for other formats could be easily implemented. The following example shows the format of a rotamer library file, which includes the residue name (RESI), the the mobile atoms (MOBI), the definition of the degrees of freedom (DEFI) and the first three rotamers of Dunbrack's backbone independent library [26] for Leu (CONF).

1  RESI LEU
2  MOBI CB   CG   CD1   CD2
3  DEFI N    CA   CB    CG
4  DEFI CA   CB   CG    CD1
5  CONF   58.7   80.7
6  CONF   71.8  164.6
7  CONF   58.2  −73.6
8  …

The file format can also include variable bond angles and bond lengths (DEFI records with two and three atoms respectively), which is necessary for the support of a conformer library [21,27,28].

Temporarily storing coordinates using named buffers

In addition to the alternative coordinates mechanism, MSL supports a second distinct mechanism for storing multiple coordinates which is essentially a “clipboard” that enables a programmer to save the coordinates – even sets of multiple alternative coordinates – in association with a string label. The label can be used later to restore the saved coordinates, replacing the current coordinates. This is useful, for example, for saving an initial state to return to after a number of moves, or to restore a state if a move happen to be rejected. The next example shows how different sets of coordinates can be saved and reapplied.

1  #include "AtomContainer.h"
2  #include "Transforms.h"
3
4  int main() {
5     AtomContainer molAtoms;
6     molAtoms.readPdb("input.pdb");
7     molAtoms.saveCoor("original"); // save the original coordinates to a buffer
8
9     // move the atoms somewhere else and save the new coordinates to another buffer
10    Transforms tr;
11    tr.translate(molAtoms.getAtomPointers(), CartesianPoint(3.7, 4.5, −2.1));
12    molAtoms.saveCoor("translated"); // save the new coordinates
13
14    molAtoms.applySavedCoor("original"); // restore the original coordinates
15    molAtoms.applySavedCoor("translated"); // restore the translated coordiantes
16
17    molAtoms.clearSavedCoor(); // this gets rid of all saved coordinates
17    return 0;
18 }

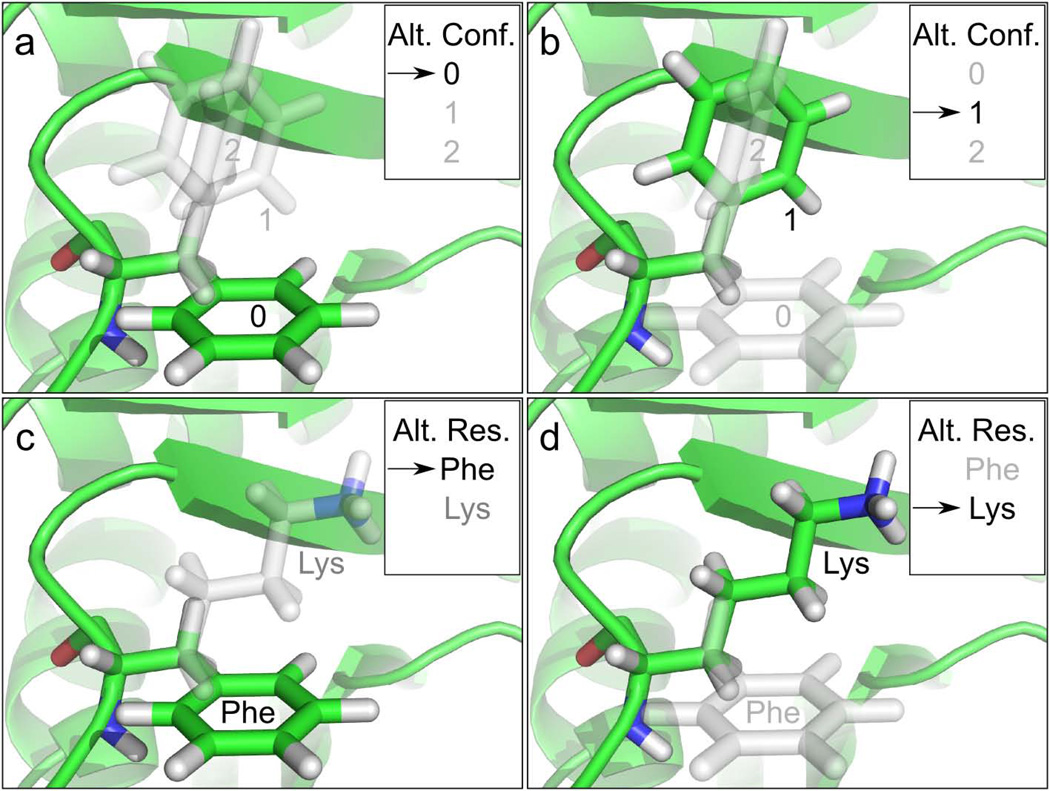
Making mutations: alternative amino acid types at the same position

MSL supports protein engineering applications and thus allows easy substitutions of amino acid types at a position. Analogously to how an Atom can store and switch between alternative coordinates, a Position can store and switch between multiple Residue objects, each corresponding to a different amino acid type (see Figure 3). Each amino acid type can have multiple rotamers (as shown above), therefore a System can simultaneously contain the entire universe of side chain conformations and sequence combinations that is a the base of a protein design problem. In the following simple example we show how to switch amino acid identity after reading a PDB file. The example below uses the PDBTopologyBuilder to obtain the new amino acid type from a topology file (in this case, Lys). Lys and Phe co-exist at position 37 – only one of them being active at any given time – and line 24 shows how to switch back to the original amino acid type.

1  #include "System.h"
2  #include "PDBTopologyBuilder.h"
3  #include “SystemRotamerLoader.h”
4
5  int main() {
6
7     // create an empty System and read a PDB with the PDBTopologyBuilder
8     System sys;
9     sys.readPdb(“input.pdb”);
10
11    // use the PDBTopologyBuilder to add LYS to the system at position A 37.
12    PDBTopologyBuilder PTB(sys, "top_pdb.inp"); // read a topology file
13    PTB.addIdentity("A,37", "LYS"); // add the LYS
14    sys.setIdentity("A,37", "LYS"); // make LYS the active identity
15
16    // The LYS was in a default orientation. Let's load the first rotamer
17    // from a rotamer library (no promise it won't clash)
18    SystemRotamerLoader rotLoader(sys, "rotlib.txt");
19    rotLoader.loadRotamers("A,37", "LYS", 1);
20
21    sys.writePdb("mutated_to_LYS.pdb");
22
23    // let's revert to the original PHE and write another PDB
24    sys.setIdentity("A,37", "PHE");
25    sys.writePdb("original.pdb");
26 }

Fig. 3. Multiple alternative coordinates and multiple alternative identities.

A unique and distinctive feature of MSL is the ability of storing multiple alternative coordinates in an Atom, and multiple alternative amino acid identities in a Position. Panels a and b illustrate a case in which a Phe side chain has three alternative conformations, one of which active (green), two inactive (gray). The internal redirection of a pointer switches the active conformation of the side chain's atoms from 0 to 1, changing rotamer. Panels c and d show a case in which a Position contains two alternative residues or amino acid identities. The redirection of a pointer switches the active amino acid identity from Phe to Lys. These two features – multiple coordinates and multiple identities – can be combined, and a Position can load multiple amino acid types in multiple conformations, a feature that greatly eases the development of protein design code.

Energy calculations in MSL

Energy functions

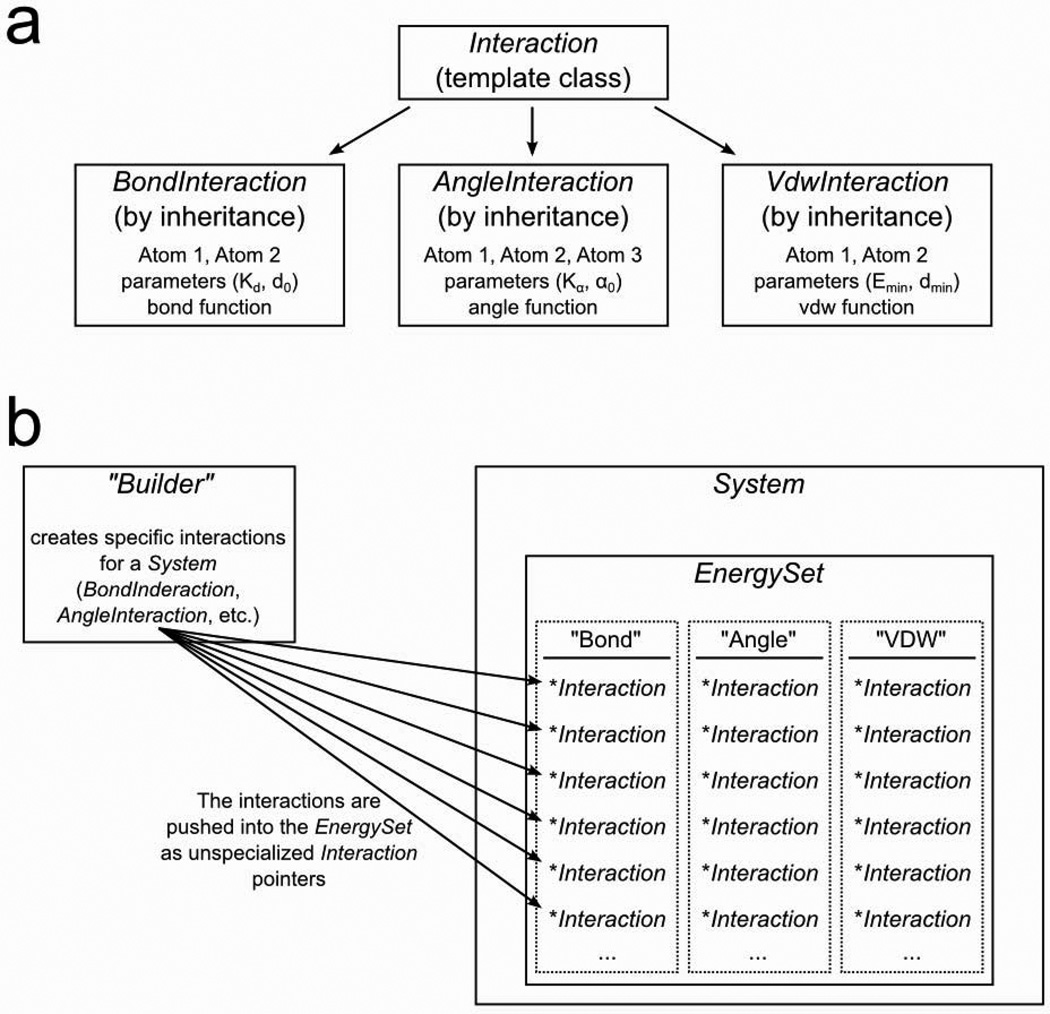
MSL supports a number of energy functions. The code base is designed to provide flexibility in calculating energies, and to be easily expanded to include new functions. The energetics in MSL are calculated by an object called the EnergySet. As illustrated in Fig. 4, the EnergySet contains an internal hash (stl::map) of all possible energy terms (such as covalent bond energy or van der Waals energy). Each hash element contains an array (stl::vector) of pointers to Interaction objects. Each Interaction represents for example a bond or a van der Waals interaction between two specific atoms. The Interaction contains all that is necessary to calculate the energy: the pointers to the atoms involved, the parameters (i.e. for bond energy a spring constant and an equilibrium distance), and a mathematical function to calculate the energy. To calculate the total energy of a System, all interactions of each type are summed. It is also possible to calculate the interaction energies of specific subsets of atoms by using selections.

Fig. 4. Energetics in MSL: Interaction objects and the EnergySet.

MSL is designed to allow easy addition of new energy functions (or terms). a. Energy terms inherit a generic Interaction class. The specialized interaction class (Bond,Angle,VDW) contains pointers to the relevant atoms, all needed parameters and the mathematical formula. b. The energy calculations in MSL are performed by the EnergySet, which resides inside the System. The EnergySet stores the interactions in a bi-dimensional container. The first dimension is a hash (stl::map) in which a string is associated with each specific energy term (i.e. “Bond”, “Angle”, etc). Inside the hash is an array (std::vector) of all the Interactions pertinent to a specific term. To obtain the total energy of the System, the EnergySet iterates the 2D structure, summing up the energy of each individual interaction. The EnergySet is filled with interactions using a Builder.

In the next example, we demonstrate the support for the CHARMM basic force field (vdw, coulomb, bond, angle, urey-bradley, dihedral, improper terms). In order to compute energetics with the CHARMM forcefield, the System must be created using the CharmmSystemBuilder. The CharmmSystemBuilder reads the information necessary to build the molecule and populate the EnergySet from standard CHARMM topology and parameter files (line 9). In the example, the coordinates are read from a PDB file (note: the residue and atom names must be in CHARMM format, which is similar to the PDB convention but differs in the naming scheme of some atoms).

1  #include "System.h"
2  #include "CharmmSystemBuilder .h"
3  #include "AtomSelection.h"
4
5  int main() {
6
7     System sys;
8     // build the system with standard CHARMM 22 topoliogy and parameters
9     CharmmSystemBuilder CSB(sys, "top_all22_prot.inp", "par_all22_prot.inp");
10    CSB.buildSystemFromPDB("input.pdb"); // note, the PDB must follow CHARMM atom names
11
12    // verify that all atoms have been assigned coordinates, using an AtomSelection
13    AtomSelection sel(sys.getAtomPointers());
14    sel.select("noCoordinates, HASCOOR 0"); // selects all atoms without coordinates
15    if (sel.selectionSize("noCoordinates") != 0) {
16       cerr << "Missing some coordinates! Exit" << endl;
17       exit(1); // in case of error, quit
18    }
19
20    // calculate the energies and print a summary
21    sys.calcEnergy();
22    cout << sys.getEnergySummary();
23
24 }

MSL can print a summary (line 22) that details the total energy of each terms and the number of interactions.

================ ====================== ===============
Interaction Type Energy                 Interactions
================ ====================== ===============
CHARMM_ANGL                   15.788323           236
CHARMM_BOND                    9.362135           131
CHARMM_DIHE                   25.590364           331
CHARMM_ELEC                  −55.028815          8279
CHARMM_IMPR                    0.009295            21
CHARMM_U-BR                    1.840063           120
CHARMM_VDW                   −16.147911          8279
================ ====================== ===============
Total                        −18.586546         17397
================ ====================== ===============

Subsets of energy terms can be turned off if desired. The following two lines would limit the calculations to the vdW term.

1    sys.getEnergySet()->setAllTermsInactive(); // set all inactive
2    sys.getEnergySet()->setTermActive("CHARMM_VDW"); // turn on VDW

The next example shows how to mutate a protein and then find the minimum energy among a set of 10 possible rotamers at that position. Instead of the total energy, in this case we use selections to calculate the interaction energy between Lys A 37 and the rest of the protein. The two selections labels (created at lines 22–23) are passed to the calcEnergy function to calculate the interaction energy of the subsets of atoms (line 29).

1  #include "System.h"
2  #include "CharmmSystemBuilder.h"
3  #include "SystemRotamerLoader.h"
4  #include "AtomSelection.h"
5
6  int main() {
7
8     System sys;
9     CharmmSystemBuilder CSB(sys, "top_all22_prot.inp", "par_all22_prot.inp");
10    CSB.buildSystemFromPDB("input.pdb"); // note, the PDB must follow CHARMM atom names
11
12    // add LYS at position A 37
13    CSB.addIdentity("A,37", "LYS"); // add the LYS
14    sys.setActiveIdentity("A,37", "LYS"); // set LYS as the active identity
15
16    // Load 10 rotamers on LYS
17    SystemRotamerLoader rotLoader(sys, "rotlib.txt");
18    rotLoader.loadRotamers("A,37", "LYS", 10);
19
20    // create two selections for calculating interaction energies
21    AtomSelection sel(sys.getAtomPointers());
22    sel.select("LYS_A_37, chain A and resi 37"); // LYS_A_37 is a label for the residue
23    sel.select("allProt, all"); // allProt is a label for all atoms
24
25    // find the rotamer of LYS A 37 with the lowest energy
26    uint minRot = 0; double minE = 0;
27    for (uint i=0; i<10; i++) {
28       sys.setActiveRotamer("A,37", i); // set the LYS in the i-th rotamer
29       double E = sys.calcEnergy("LYS_A_37", "allProt"); // interaction
30       if (i == 0 || E < minE) {
31          minRot = i; minE = E;
32       }
33    }
34    cout << "The lowest energy state is rotamer index # " << minRot << endl;
35 }

MSL implements the CHARMM force field, including the required 1–4 electrostatic rescaling (e14fac), fixed and distance-dependent dielectric constants, and distance cutoffs, with a switching function to bring the energies smoothly to zero. The energies calculated in MSL reproduce those obtained with CHARMM [25], as tested. In addition, MSL implements Lazaridis' EFF1 implicit solvation models [29] (the membrane solvation model IMM1 [30] is currently under development), a hydrogen bond term derived from SCWRL 4 [31], the EZ membrane insertion potential [20], knowledge-based potentials, such as DFIRE [32] and a single-body “baseline” term (a value associated with a single atom in a residue, useful in protein design). Weights can also be added to rescale the energy of each individual terms, if needed.

Adding new energy functions to MSL

MSL is geared toward the development of new methods, and it supports the creation and integration of new energy functions. To create a new energy function a programmer needs to code a new type of Interaction, which contains all that is needed – the pointers to the relevant atoms and the necessary parameters – to calculate an energy. The specialized interactions are derived using inheritance from a virtual Interaction class. The specialized interaction objects are added to the EnergySet as generic Interaction pointers, and thus the EnergySet is blind to the specific nature of the interaction, and does not need to be modified every time a new type of energy is added. To add a new term to the EnergySet an external object called a “builder” (such as the CharmmSystemBuilder or the HydrogenBondBuilder) is required. The builder is the object that is responsible for the creation of all the individual interactions that are pertinent for a given System. This particular strategy support the introduction any new type of interaction without having to modify the core of MSL energetics (the System and the EnergySet).

Algorithms and tools in MSL

Side chain optimization

MSL supports a number of algorithms for the optimization of side chain conformation that can be applied to protein modeling, docking or protein design tasks. The SideChainOptimizatonManager is the object in charge of this specific task. The SideChainOptimizatonManager receives a System which already contains positions that have either multiple rotamers and/or multiple identities (known as variable positions). The object separates the interactions of the EnergySet into “fixed” (involving atoms that are in invariable positions), “self” (involving atoms from a single variable position) and “pairwise” (involving atoms from two variable positions). From these, it can reconstruct the total energy of any state. In the example below the system contains four variable positions (line 22) and the energy of the state defined by rotamers 3, 7, 0 and 5 is calculated.

1  #include "System.h"
2  #include "CharmmSystemBuilder.h"
3  #include "SideChainOptimizationManager.h"
4
5  int main() {
6     System sys;
7     CharmmSystemBuilder CSB(sys, "top_all22_prot.inp", "par_all22_prot.inp");
8     CSB.buildSystemFromPDB("input.pdb"); // note, the PDB must follow CHARMM atom names
9
10    // Add 10 rotamers to 4 positions
11    SystemRotamerLoader rotLoaded(sys, "rotlib.txt");
12    rotLoader.loadRotamers("A,21", "ILE", 10);
13    rotLoader.loadRotamers("A,23", "LEU", 10);
14    rotLoader.loadRotamers("A,43", "ASN", 10);
15    rotLoader.loadRotamers("A,62", "MET", 10);
16
17    SideChainOptimizationManager SCOM(&sys); // pass the system as a pointer
18    SCOM.calculateEnergies(); // this function pre-calculates all interactions
19
20    // get the energy of a state (A21: 4th rotamer, A23 8th rot., etc)
21    vector<uint> state(4, 0);
22    state[0] = 3; state[1] = 7; state[2] = 0; state[3] = 5;
23    double E = SCOM.getStateEnergy(state);
24
25    // print a summary of the state
26    cout << SCOM.getSummary(state) << endl;
27 }

The state is the index of the desired rotamer at each position. If there are multiple identities at one Position, the state would range to include the sum of all the rotamers for each identity. For example, if a Position has two identities (Leu and Ile) with 10 rotamers each, the state could be any number from 0–19 where 0–9 corresponds to the 10 Leu rotamers and 10–19 corresponds to the 10 Ile rotamers.

The SideChainOptimizationManager supports a number of side chain optimization algorithms that search for the global energy minimum in side chain conformational space. The current implementation includes Dead End Elimination (DEE) [33] (Goldstein single and pair), simulated annealing Monte Carlo (MC), MC over Self Consistent Mean Field (SCMF) [34], Quench [35] and a linear programming formulation [36] (note, at the time of writing Quench and LinearProgramming are present as a stand alone implementation but they are currently being folded into the SideChainOptimizationManager). The algorithms can be run individually or in sequence. The next example shows how to run DEE followed by SCMF/MC search.

1  int main() {
2     // …
3     // Create System and add rotamers and alternate identities as in
4     // lines 1–15 of the previous example
5
6     SideChainOptimizationManager SCOM(sys);
7     SCOM.calculateEnergies();
8     SCOM.setRunDEE(true); // run Dead End Elimination with default configuration
8     SCOM.setRunSCMFBiasedMC(true); // run SCMF/MC on the rotamers that have not been eliminated
9     SCOM.runOptimizer();
10
11     vector<uint> bestState = SCOM.getMCfinalState(); // the result of the optimization
12
13     cout << SCOM.getSummary(bestState); //print the energy summary
14
15     sys.setActiveRotamers(bestState); // set the system in the final state
16     sys.writePdb("best.pdb"); // write the structure out
17 }

Some of the above algorithms require per-computation of all pairwise energies between all rotamers at the variable positions (for example DEE), while other are amenable to computation of the energies as they are needed (for example, MC). The SideChainOptimizationManager supports both options.

Energy Minimization

MSL can improve the energy of a structure by relaxing it to the nearest local minimum, a procedure called energy minimization. MSL takes advantages of the multidimensional minimization procedures included in the GNU Scientific Library (GSL) [37]. For those energy terms that have been implemented with their cartesian partial derivatives (such as all CHARMM force field terms), MSL can minimize using faster algorithms such as Steepest Descent and the Broyden-Fletcher-Goldfarb-Shanno (BFGS), a quasi-newton method. When gradient information is not available, minimization can be performed using a Simplex Minimizer. The GSLMinimizer can perform constrained as well as unconstrained energy minimization. Performing minimization in MSL is extremely simple:

1  #include "GSLMinimizer.h"
2  #include "CharmmSystemBuilder.h"
3
4  int main(){
5     // Read input.pdb and build a system
6     System sys;
7     CharmmSystemBuilder CSB(sys, "top_all22_prot.inp", "par_all22_prot.inp");
9     CSB.buildSystemFromPDB("input.pdb")) {
10
12     GSLMinimizer min(sys); // Initialize the minimizer
13
14     // OPTIONS: One can change the default algorithm
15     // min.setMinimizeAlgorithm(GSLMinimizer::BFGS);
16
17     // One can also fix certain atoms with a selection string
18     // min.setFixedAtoms("name N+C+CA+O+HN"); // fix the backbone
19
20     // Optionally, one can perform constrained minimization
21     // min.setContrainForce(10.0); // all atoms with a 10 kcal/(mol*Å2) force constant
22     // min.setContrainForce(10.0, "name N+C+CA+O+HN"); // only the backbone
23
24     // Perform the minimization
25     sys.printEnergySummary(); // Print the energy summary before the minimization
27     min.minimize();
25     sys.printEnergySummary(); // Print the energy summary after
32
33     sys.writePdb("output.pdb");
34 }

Sequence Regular Expressions

A common feature in software scripting languages is regular expressions, which can describe complex string patterns. A very simple example of using regular expressions to match multiple strings is the regular expression string “[hc]at”, which matches both “hat” and “cat”. Regular expressions have been used in many bioinformatic algorithms, for instance to match complicated protein sequence motifs [38].

A useful analysis task is to find pieces of protein structure that correspond to an interesting and/or functional sequence motif. For example, a common folding motif in membrane proteins is three amino acids of any type bracketed by two glycines (the GxxxG motif [39,40]). It may be interesting to find all 5 amino acid fragments in a database membrane protein structures that fit the GxxxG motif. The following example shows how MSL can accomplish this task by utilizing MSL objects built using BOOST functionalities.

First a membrane protein structure file is read in. A single chain is extracted from the System (line 4). A regular expression object and search string are then created (line 10). Next, the GxxxG pattern of “G.{3}G” is searched against the Chain object (line 13). A list of matching residue ranges is returned in “matchingResidueIndicies”. Lastly, each match is printed out.

1  System sys;
2  sys.readPdb("MembraneProtein.pdb");
3
4  Chain &chA = sys.getChain("A");
5
6  // Regular Expression Object
7  RegEx re;
8
9  // Find 2 glycines with 3 residues of any type in between
10 string regex = "G.{3}G";
11
12 // Now do a sequence search and return the min,max indices within the Chain object
13 vector<pair<int,int> > matchingResidueIndices = re.getResidueRanges(ch,regex);
14
15 // Loop over each match.
16 for (uint m = 0; m < matchingResidueIndices.size();m++){
17
18    // Loop over each residue for this match
19    int match = 1;
20    for (uint r = matchingResidueIndices[m].first; r <= matchingResidueIndices[m].second;r++){
21
22      // Get the residue
23      Residue &res = ch.getResidue(r);
24
25      // ‥ print out matched residues …
26      cout << "MATCH("<< match <<"): RESIDUE: "<<res.toString()<<endl;
27   }
28 }

Modeling backbone motion

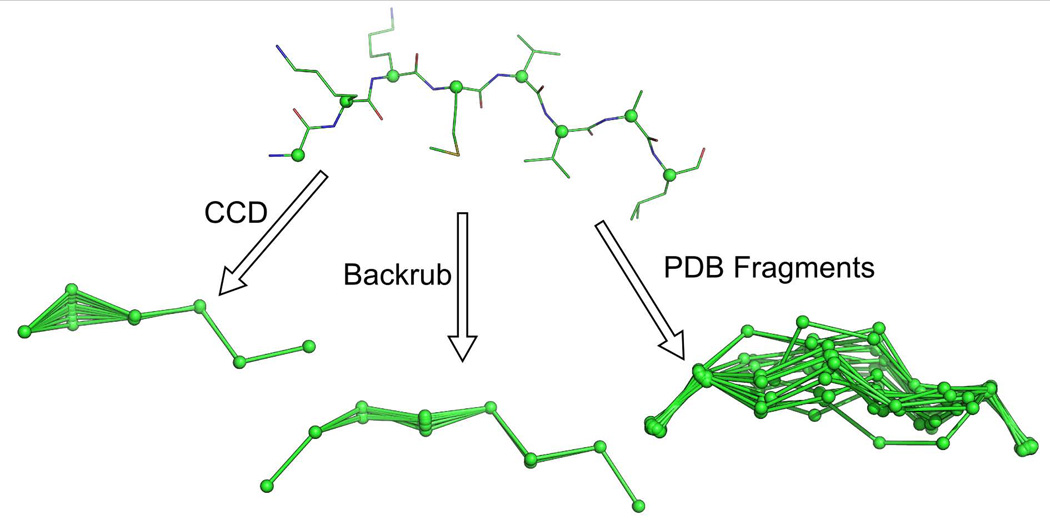
Integrating backbone motion into protein design algorithms has become a major push in the field [41]. In MSL, we have implemented three algorithms for modeling backbone motion between fixed Cα positions: Cyclic Coordinate Descent (CCD) [42], Backrub [43] and PDB Fragment insertion [44] (Figure 5). These algorithms can also be utilized to insert new pieces of protein structure between two fixed Cα positions. These algorithms are Cα based but all atoms versions can be implemented. The CCD algorithm sets the backbone conformation of a single residue to a random value, breaking the polymer chain. A set of dihedral rotations around the preceding Cα – Cα virtual bonds are discovered that both close the broken chain and produce a new conformation for the peptide. The Backrub algorithm works in steps that take three consecutive amino acids and rotates around their Cα – Cα virtual bonds to produce new backbone conformations. The PDB Fragment method searches a structural database for stretches of amino acids that fit the geometry of the first and last two residues, but the residues in between are unique conformations. The next examples demonstrate these algorithms.

1  #include “CCD.h”
2      …
3      // Read C-alpha only pdb file into a System object
4      System sys;
5      sys.readPdb(“caOnly.pdb”);
6
7      CCD sampleCCD; // CCD algorithm object
8
9      // Do local sampling inside CCD object
10      sampleCCD.localSample(sys.getAtomPointers(),10,10); // 10 models, max 10 degrees
11
12      System newSys(sampleCCD.getAtomPointers()); // Get System object with alternative conformations
13
14      newSys.writePdb("ccdEnsemble.pdb",true); // Write out all the models NMR-style

Fig. 5. Backbone motions implemented in MSL.

The internal C-alpha atoms of an eight residue peptide were sampled using three different algorithms implemented in MSL. The Cyclic Coordinate Descent (CCD) algorithm breaks the peptide chain, then discovers a set of rotations which can close the loop (this algorithm holds the first and last C-alpha atom fixed and are not shown in the figure). The Backrub algorithm was developed to recapitulate the backbone movements found in high resolution crystal structures and uses rotations around virtual C-alpha-C-alpha bonds. The PDB fragment method searches across a structural database and finds all fragments with the same geometry as found between the first two and last two residues of the original eight residue peptide.

Next we show how one can use the Backrub algorithm:

1      // Read pdb file into a System object
2      System sys;
3      sys.readPdb(“example.pdb”);
4
5      // A BackRub object
6      BackRub br;
7
8      // Do local sampling inside BackRub object
9      br.localSample(sys.getChain(0),1,7,10); // Start residue, end residue and number of samples
10
11     System newSys(br.getAtomPointers()); // Get System object with alternative conformations
12
13     newSys.writePdb("brEnsemble.pdb",true); // Write out all the models NMR-style

Next we show how one can use the PDB Fragment insertion algorithm. While the previous two examples use transformation operations to move the backbone atoms, this algorithm searches across a database of structures to find a suitable fragment that closes the gap between two positions (called “stem” residues). For a demonstration on how to create a database of structures we refer to the tutorial section on the MSL website.

1      // Read pdb file into a System object
2      System sys;
3      sys.readPdb(“example.pdb”);
4
5      vector<string> stems; //Stems are kept fixed, search for segment in-between
6      stems.push_back("A,1");
7      stems.push_back("A,2");
8      stems.push_back("A,7");
9      stems.push_back("A,8");
10
11     PDBFragments fragDB("./tables/fragdb100.mac.db"); // Set the name of the binary structure
database
12     fragDB.loadFragmentDatabase(); // Load the fragment database
13
14     // Do local sampling inside PDBFragment object
15     int numMatchingFrags = fragDB.searchForMatchingFragments(sys,stems);
16
17     if (numMatchingFrags > 0){
18            System newSys(fragDB.getAtomPointers());
19            newSys.writePdb("pdbEnsemble.pdb",true);
20     }

Other useful modeling tools and procedures

Filling in missing backbone coordinates (BBQ)

In the following example, we illustrate a geometric algorithm implemented in MSL. The Backbone Building from Quadrilaterals (BBQ) algorithm, developed by Gront et al [45]. BBQ allows for the insertion of all backbone atoms into a structure when a Cα only trace is available, as in the CCD and PDB Fragment insertion methods.

1  #include "BBQTable.h"
2  #include "System.h"
3
4  int main() {
5     System sys;
6     // Read in a pdb file that only includes C-alpha atoms.
7     sys.readPdb("caOnly.pdb");
8     BBQTable bbq("bbq_table.dat");
9
10    // Now fill in the missing backbone atoms for each chain
11    for(int chainNum = 0; chainNum < sys.chainSize(); ++chainNum) {
12       bbq.fillInMissingBBAtoms(sys.getChain(chainNum));
13    }
14
15    // Write out a pdb with all of the backbone atoms.
16    // Note: Due to the way the BBQ algorithm works, no backbone
17    // atoms will be generated for the first and last residues in a chain.
18    sys.writePdb("output.pdb");
19 }

Molecular alignments

A second example of a geometric algorithm is molecular alignment. MSL can be used to align two molecules and compute a RMSD. Alignments are based on quaternion math, supported by the Transforms object. The following example demonstrates the alignment of two homologous proteins based on their CA atoms.

1  #include "AtomContainer.h"
2  #include "Transforms.h"
3  #include "AtomSelection.h"
3
4  int main() {
5     AtomContainer mol1;
6     mol1.readPdb("input1.pdb"); // read the first molecule
7     AtomContainer mol2;
8     mol2.readPdb("input2.pdb"); // read the second molecule
9
10    AtomSelection sel1(mol1.getAtomPointers());
11    AtomPointerVector CA1 = sel1.select("name CA"); // get the CAs of molecule 1
12
13    AtomSelection sel2(mol2.getAtomPointers());
14    AtomPointerVector CA2 = sel2.select("name CA"); // get the CAs of molecule 2
15
16    if (CA1.size() != CA2.size()) {
17       cerr << "ERROR: the number of CA atoms needs to be identical!" << endl;
18       exit(1);
19    }
20    cout << "The RMSD before the alignment is " << CA1.rmsd(CA2) << endl;
21
22    Transforms tr;
23    // move the entire molecule 2 based on the CA1/CA2 alignment
24    tr.rmsdAlingment(CA2, CA1, mol2.getAtomPointers());
25
26    cout << "The RMSD after the alignment is “ << CA1.rmsd(CA2) << endl;
27
28    mol2.writePdb("input2_aligned.pdb");
29    return 0;
30 }

Solvent Accessible Surface Area

The calculation of a Solvent Accessible Surface Area (SASA) is an important molecular feature that is used for analysis and modeling purposes. The SasaCalculator can use default element-based radii or atom-specific radii if provided (such as the CHARMM atomic radii, for example, when the molecule is setup with the CharmmSystemBuilder).

1  #include "AtomContainer.h"
2  #include "SasaCalculator.h"
3
4  int main() {
5     AtomContainer molAtoms;
6     molAtoms.readPdb("input.pdb");
7
8     SasaCalculator SC(molAtoms.getAtomPointers());
9     SC.calcSasa();
10    SC.printSasaTable(); // print a table of SASA by atom
11    SC.printResidueSasaTable(); // print a table of SASA by residues
12    return 0;
13 }

Example of applications distributed with MSL: side chain structure prediction and backbone motions

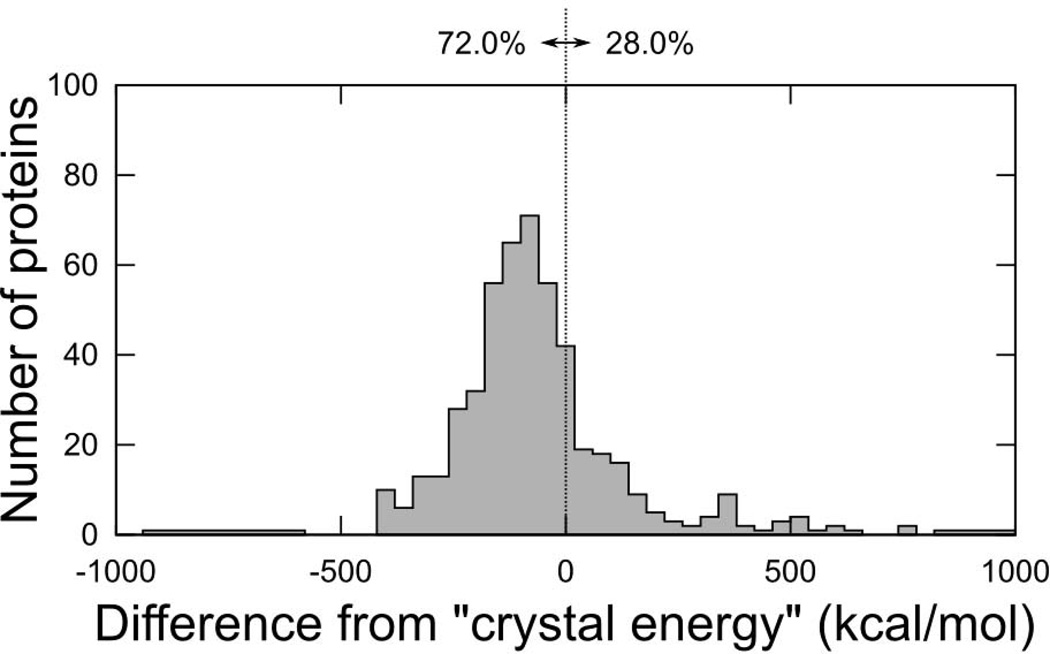
MSL is primarily a library of tools developed for allowing the implementation of new molecular modeling methods. However, a number of programs are also distributed in the source repository and more will likely be contributed in the future. In the following section we briefly demonstrate the performance of two of such programs, because of their general utility, and because their source could be used to see many of the features previously described “in action” and as a template to create new applications. The program repackSideChains is a simple side chain conformation prediction program. It takes a PDB file, strips out all existing side chains (if they are present), and predicts their conformation using side chain optimization. Under the hood, the program utilizes a series of side chain optimization algorithms previously described. Run with default options, it starts by performing DEE [33] followed by a round of SCMF [34] on the rotamers that were not eliminated, and finally a Monte Carlo search starting from the most probable SCFM rotamers (the choice of algorithms is configurable by command line arguments). We applied the program to 560 proteins backbones obtained from the structural database. The side chains were placed using a set of energy functions that included CHARMM22 bonded terms and van der Waals function, and the hydrogen bond function from SCWRL4 [31], using the Energy-Based library [21] at the 85% level (1,231 conformers). The program recovered the crystallographic side chain conformation of nearly 80% of all buried side chain (max 25% SASA, χ1+χ2 recovery, with a tolerance threshold of 40°), ranging from about 55% (Ser) to 90% (Phe, Tyr and Val). The total hydrogen bond recovery in the same set of calculations is 60% (all side chains). Fig. 6 shows the distribution of the final energy of the repacked proteins compared to the energy of a the minimized crystal structures, which is a reasonable reference. The program produces structures that are lower than the energy of the minimized crystal structure in 72% of the cases. The average time for performing side chain minimization was around 1 minute for a 100 amino acid protein, and 5–8 minutes for a 300 amino acid protein. It should be noted that the program could also be adjusted to use different combination of energy function or rotamer/conformer libraries. The different terms of the energy functions can also be relatively weighted as desired.

Fig. 6. Performance of the Energy-Based library in total protein repacks.

Final energy after optimization of all side chains in 560 proteins, for the Energy-Based library. For easier comparison energies are plotted after subtracting the energy of the minimized crystal structure (“crystal energy”). The dashed line separates the proteins that score better than the crystal energy (percentages indicated), a convenient reference under the assumption that in most cases it represents a good target for an optimization.

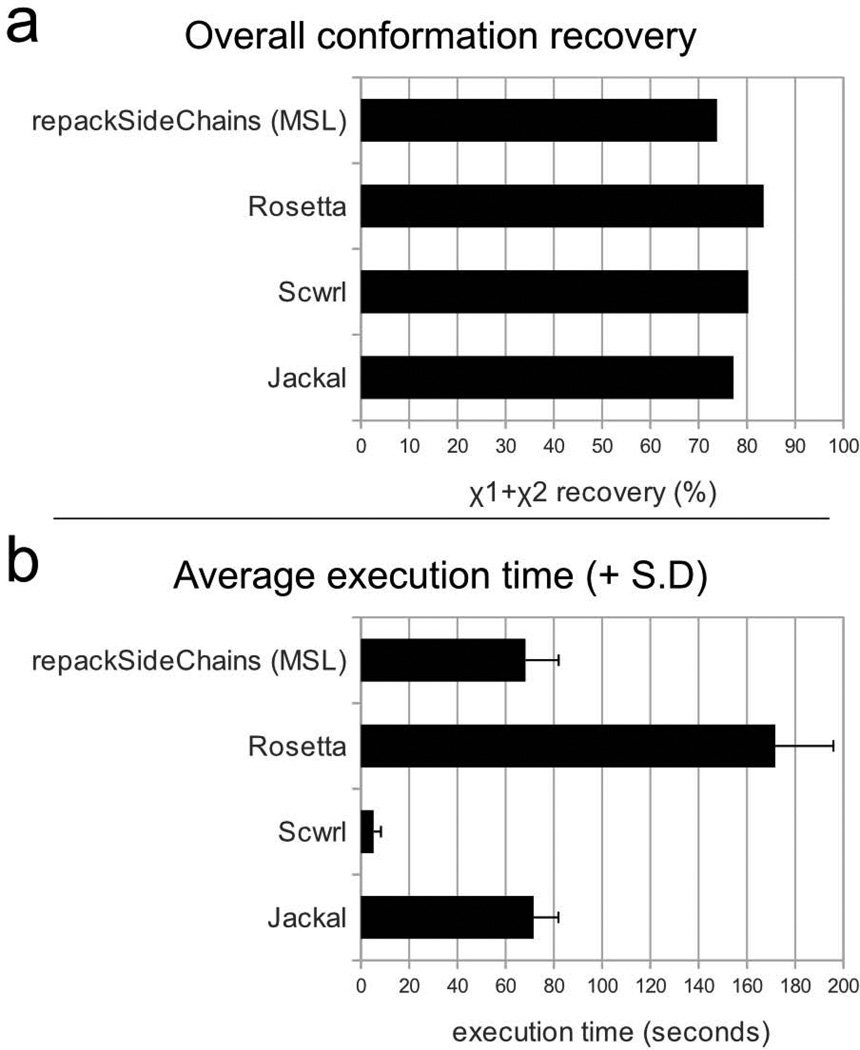
The side chain prediction application repackSideChains offers an opportunity to compare the performance of some of MSL's capabilities against other modeling software. Side chain conformation predictions were performed in parallel on a set of 34 medium size proteins (up to 250 amino acids) with repackSideChains and three commonly used side chain prediction programs, Rosetta [46], SCWRL [31] and Jackal [28], and the resulting χ angle recoveries and average execution times are shown in Fig. 8. The levels of recovery are similar among the four programs, with Rosetta having an edge above the other programs. In term of execution time, SCWRL is a clear winner, while the time of the three other programs is comparable. It should be remarked here that MSL's repackSideChains is a relatively simple program that has not been extensively optimized to maximize side chain recovery. The program is provided as a utility and as an example for creating programs that incorporate similar functionalities. Nevertheless, its performance is in line with the average in terms of speed and is close in terms of recovery to the other benchmarks.

Fig. 8. Comparison of the performance of MSL's repackSideChains with other side chain prediction programs.

a) Side chain recovery performance. The figure plots the overall χ1+χ2 recovery of all side chains in a set of 34 proteins of size up to 250 amino acids. Only the buried side chains were considered (max 25% SASA). A side chain was considered “recovered” correctly if both χ1 and χ2 were predicted with a tolerance threshold of ±20%. b) Execution time. The histogram shows the average execution time of the 33 side chain prediction runs with the four programs. The error bar represents the standard deviation. Rosetta is the program with the best overall recovery in the test, while SCWRL is the fastest one. The performance of MSL program repackSideChains is in line with the other programs with respect to speed, and close to the benchmarks in terms of recovery. It should be noted that repackSideChains is distributed as a utility and example program and it has not been extensively refined for maximum performance. Detailed information on the χ1, χ1+χ2, χ1+χ2 χ3 and χ1+χ2 χ3+χ4 recovery of each amino acid type is presented in the supplementary information.

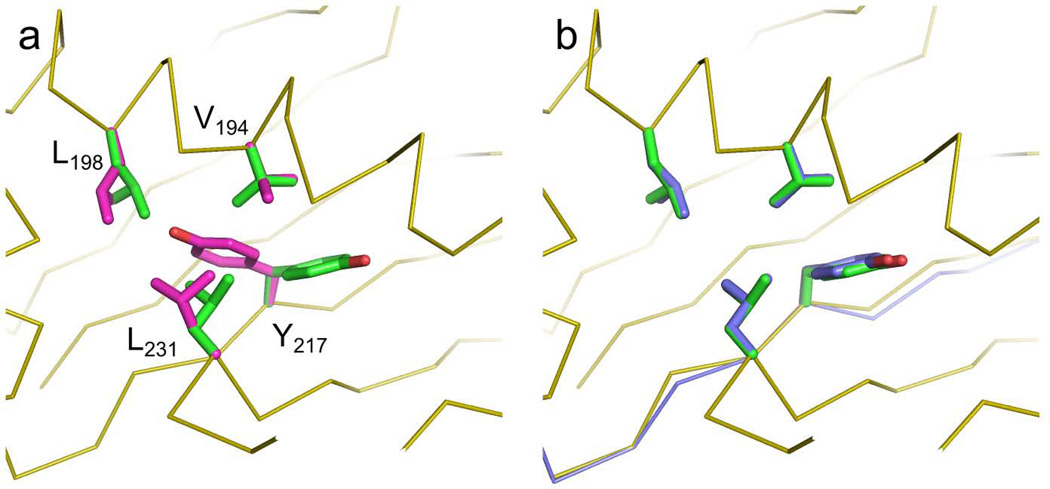
The availability of a variety of modeling algorithms in MSL enables the solution of complex problems. Here, we demonstrate the utility of one of the flexible backbone algorithms presented above (the Backrub algorithm [43]). We selected one of the structures in which core amino acids were not predicted correctly by repackSideChains (Fig. 7a, PDB code 1YN3). The static backbone structure has been implicated as a primary source of error in side chain repacking, and thus prediction can be ameliorated by exploration of near-native models [47]. We applied the program backrubPdb to generate an ensemble of near-native protein structures of 1YN3. Each of these near-native models were subjected to side chain optimization through repackSideChains and the results were analyzed. A slight (<0.5Å) backbone shift resulted in a structure that was lower in energy than the fixed-backbone model and had correctly placed side chains, as illustrated in Fig. 7b. The generation of an ensemble of backbones takes only few seconds. The repackSideChains and backrubPdb are separate standalone programs, however, it would be straight forward to include both backbone flexibility and side chain repacking capabilities into a single program. Tutorials on how to run the two programs are available on the MSL web site.

Fig. 7. Enhanced performance of rotamer recovery using flexible backbone modeling.

In panel A, the original backbone is shown in orange ribbons. The side chain conformations in the crystal structure of 1YN3 are shown in green. Side chain prediction with the repackSideChains program produced the conformations of four core residues displayed in magenta. In the model, the χ1 of Y₂₁₇ assumes a g− conformation instead of the g+ conformation that is observed in the crystal structure. Concurrently there is also a rearrangement of other three nearby positions to non-native rotamers. After the backbone has been locally relaxed with the Backrub algorithm (panel B, in blue) the lowest energy model recovers the native conformation.

Version control

MSL is currently in an advanced beta state and rapidly evolving. The library is used for production work, but new features are being implemented on a regular basis. The API of most core objects is stable, although it can be occasionally revised. The codebase is kept under version control on the open source repository SourceForge (http://mslib.svn.sourceforge.net). New versions are tagged with 4-level number identifiers. At the time of writing, the current version is 0.22.2.10. The first number is the version number, currently zero as the software is considered in beta. The second number is incremented with every update that significantly affects the API. The third version number is for significant changes that do not affect the API or do so only in a minor way (such as the addition of a new object). The last number is for small changes and bug fixes. All old versions are available for download from the “tags” subdirectory on the repository. By tagging MSL versions, users can put exact source code versions in publications allowing for reproduction of the result. The entire development history of MSL since the source was opened in 2009 is commented in the file src/release.h. The other function of the release.h file is to define a global variable “MSLVERSION”, which is set to the current version number. This variable enables the programmer to encode a mechanism for tracking what specific MSL version was used to compile a program. In the following example, when the −v argument is provided the programs returns the MSL version.

1  #include "release.h"
2
3  int main(int argc, char *argv[]) {
4     if (argc > 1 and argv[1] == "−v”) {
5        // the program was called with the −v option: print the MSL version number
6        cout << "Program compiled with MSL version " << MSLVERSION << endl;
7     }
8     // rest of the code here
9     return 0;
10 }

Conclusion

MSL is a large, fully featured code base that includes over 130 objects and more than 100,000 lines of code. We have discussed a number of simple examples that demonstrate how to perform complex operations with just a few lines of code. MSL supports some unique features, such as multiple atom coordinates and multiple residue identities, a number of energy functions that are readily expandable, and other tools and algorithms that will enable rapid implementation of a large variety of molecular modeling procedures. Other MSL features that have not been presented here include coiled-coil generation, symmetric protein design, synthetic fusions of two proteins, both PyMOL integration and PyMOL script generation, integration with the statistical package R [48] for producing high quality plots and use of its statistical procedures. MSL is less specialized and more comprehensive than other open source packages that have been designed with a specific task in mind (for example, the EGAD package [49]). Because it is modular, expandable, and largely agnostic to file formats, it can be applied to any variety of analysis and modeling problems and macromolecular types, including nucleic acids, sugars, or small molecules.

In our opinion the most important feature of the software library is not any of the numerous methods that are currently implemented, but the fact that it merges all these capabilities together in a single platform. Most of the methods in MSL are already individually present in other programs. However, because they are integrated into a single package, they can be easily adopted by others, improved on and mixed to create new functionalities. Therefore any new method contributed to the MSL code base will be immediately be available not only to end users but also to the entire community of developers to build on it. We call for other interested developers to join the open source project.