Maladaptive “Gambling” by Pigeons

Abstract

When humans buy a lottery ticket or gamble at a casino they are engaging in an activity that on average leads to a loss of money. Although animals are purported to engage in optimal foraging behavior, similar sub-optimal behavior can be found in pigeons, They show a preference for an alternative that is associated with a low probability of reinforcement (e.g., one that is followed by a red hue on 20% of the trials and then reinforcement or by a green hue on 80% of the trials and then the absence of reinforcement) over an alternative that is associated with a higher probability of reinforcement (e.g., blue or yellow each of which is followed by reinforcement 50% of the time). This effect appears to result from the strong conditioned reinforcement associated with the stimulus that is always followed by reinforcement. Surprisingly, although it is experienced four times as much, the stimulus that is never followed by reinforcement does not appear to result in significant conditioned inhibition (perhaps due to the absence of observing behavior). Similarly, human gamblers tend to overvalue wins and undervalue losses. Thus, this animal model may provide a useful analog to human gambling behavior, one that is free from the influence of human culture, language, social reinforcement, and other experiential biases that may influence human gambling behavior.

Maladaptive gambling by humans can be defined as making a decision to choose a low probability but high payoff alternative over a high probability, low payoff alternative (not gambling), such that the net expected return is less than what one has wagered. That is, choices that over the long term are very likely to result in losing more than winning. Such gambles are typical of casino games such as slot machines, roulette, and black-jack, and are especially true of lotteries. Several popular explanations have been given for what appears to be maladaptive behavior. One view is that people often are unaware of the odds of winning and if they are, they have a difficult time interpreting the meaning of those odds. For example, the value that humans give to 1:100, 1:1000, and 1:1,000,000 are relatively similar, yet the odds of their payoff are quite different. This could be considered the result of inadequate experience. A second account has to do with the fact that in most public gambling, when someone wins, it is more salient than when someone loses (bells ring and lights flash at casinos when someone wins big and big winners of lotteries are often mentioned on the news). This is sometimes referred to as an example of the availability heuristic (Tversky & Kahneman, 1974). A third possibility is that humans are social animals and there is additional social reinforcement that often accompanies winning (e.g., at casinos). Finally, people who engage in gambling behavior often describe the activity as enjoyable independent of wins and losses. Presumably, the life these people lead is not sufficiently interesting and gambling makes it more attractive.

Recently, a more analytic approach to human decision making has been suggested that may help separate more basic behavioral processes from the above mechanisms (Evans, 2003; Klaczynski, 2005). It has been proposed that human decision making depends on two different sources of input, primary and secondary processes. Primary processes are those governed by relatively simple associative learning processes, often existing without awareness (Klaczynski, 2005) and often taking the form of a “gut” level reaction, an emotion, or an impulse (e.g., Haidt, 2001; Loewenstein, Weber, Hsee, & Welch, 2001; Slovic, Finucane, Peters, & MacGregor, 2007). Secondary processes comprise what we normally think of as thought processes, the conscious effort to weigh options, consider possibilities, and attempt to resolve dilemmas. They consist of what humans are aware of, but they are relatively limited in capacity (Dijksterhuis, 2004; Evans, 2003) because humans are limited in the number of factors that they consciously can take into account.

According to this theory, the evaluation of risk can result from either primary or secondary decision processes. Primary processes are always in play but secondary processes can be recruited when the time to make a decision is not constrained and when decisions can be based on relatively few sources of information (Dijksterhuis, 2004; Greene, Morelli, Lowenberg, Nystrom, & Cohen, 2008). Also it is often the case that secondary processes are retrospective and come into play after the decision is made. That is, after decisions are made using primary processes, individuals may consider the reasons for having made those decisions (sometimes referred to as rationalization, Smith & Mackie, 2007). This leads to a curious phenomenon. One may believe that a decision was made rationally (based on secondary processes) for the purpose of justifying how it was made, when in fact it was made largely under the control of primary processes. Thus, it may be that many of the processes that govern human decision making are of the primary type. If this analysis is correct, one may be able to study such decision making processes more directly in animals because their decisions are also likely to be largely under the control of primary decision processes.

However, examination of the behavioral ecology literature suggests that one should not find evidence of maladaptive gambling in nonhuman animals (choice of an alternative that provides less reward) as long as they are given adequate experience with the alternatives. According to optimal foraging theory, animals should be less susceptible to the attraction of a poor gamble because their survival is likely to be at stake (Stephens & Krebs, 1986). That is, animals should make optimal choices because evolution should have favored the survival of animals that do (MacArthur & Pianka, 1966). Given appropriate experience, nonhuman animals are presumed to be sensitive to the relative amounts of food obtained from different alternatives or patches (see Fantino & Abarca, 1985).

1. Animal models of human gambling

Thus, it is reasonable to ask if nonhuman animals show choice behavior analogous to the suboptimal behavior shown by humans when humans purchase a lottery ticket or engage in casino gambling. One task that has been modified for use with animals (rats) is the Iowa Gambling Task (Rivalan, Ahmed, Dellu-Hagedorn, 2009; Zeeb, Robbins, & Winstanley, 2009). In the Zeeb et al. study, rats chose among four options that varied among them in the probability of reinforcement (0.4 to 0.9), amount of reinforcement (1–4 pellets), probability of a punishment timeout following a trial (0.1 to 0.6), and the duration of the timeout (5 s to 40 s). Using this task, Zeeb et al. found that the rats chose adaptively, maximizing food pellets earned per unit time. Interestingly, the rats continued to choose optimally when the duration of the timeout was equated over conditions (the duration of the timeout appeared to have little effect on the rats choice) but they failed to choose optimally when the probability of the time out was equated (the probability of the timeout and thus the probability of reinforcement enhanced the value of the large reinforcer even though the longer timeout meant that it occurred less often per unit time). Under those conditions, they undervalued the negative effects of the long time outs and instead were attracted to the larger magnitude of reinforcement, and by so doing they received only half of the maximium number of pellets per unit time.

Rivalan et al. (2009) also gave rats a choice between an alternative that provided a small amount of food on some trials and a short penalty on other trials and an alternative that provided a larger amount of food but a very long penalty on other trials. However, because of the long penalties, the alternative associated with the larger amount of food actually resulted in only 20% as much food per unit time. Although a majority of the rats performed optimally and chose the alternative that provided a small amount of food and the short penalty, a substantial number of the rats preferred the alternative that provided a larger amount of food and the longer penalty. These results suggest that some rats may be relatively insensitive to the duration of the penalty and thus perform sub-optimally in terms of food per unit time.

Research that we have conducted with pigeons using a simpler task that may be more analogous to human gambling suggests that they, like humans, may be susceptible to maladaptive choices. The origins of this research go back to a line of research that assessed the degree to which animals would work for information, independently of differential reinforcement. That is, research that was conducted to ask if animals would choose to obtain a signal for reinforcement or a signal for its absence even when those signals had no effect on the probability of reinforcement associated with those choices.

2. Information or conditioned reinforcement?

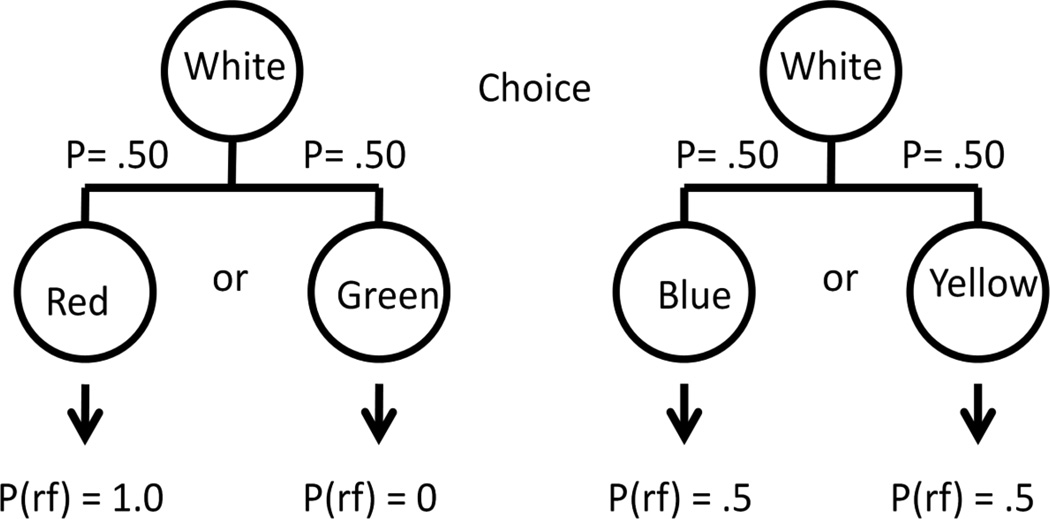
We (and others) have shown, in fact, that when the probability of reinforcement is equated, pigeons prefer to obtain stimuli that signal reinforcement or its absence over stimuli that ambiguously signal reinforcement (Dinsmoor, 1983; Roper, & Zentall, 1999). In Roper and Zentall’s procedure, on half of the trials, choice of one alternative resulted in the presentation of a stimulus that reliably predicted reinforcement and on the other half of the trials resulted in the presentation of a stimulus that reliably predicted the absence of reinforcement. Technically, these stimuli should be referred to as a conditioned excitatory and conditioned inhibitory stimulus, respectively, if responding is not required to the signal for reinforcement, but in the present article I will refer to them as discriminative stimuli because pigeons generally peck at stimuli that predict reinforcement whether they are required to or not and they refrain from pecking at stimuli that predict the absence of reinforcement. Thus, choice of the first alternative was associated with 50% reinforcement (see the left side of Figure 1). Choice of the other alternative resulted in the presentation of one of two stimuli each of which was followed by reinforcement 50% of the time (see the right side of Figure 1).

Figure 1.

Design of experiment by Roper and Zentall (1999). Pigeons chose between two alternatives. Choice of one alternative was followed by either a stimulus (red) that was always followed by reinforcement or a different stimulus (green) that was never followed by reinforcement. Choice of the other alternative was followed by either of two stimuli (blue or yellow) both of which were followed by reinforcement 50% of the time. Spatial location and colors were counterbalanced.

Roper and Zentall (1999) found that the pigeons showed a strong preference for the first alternative, the one that was followed by presentation of discriminative stimuli. This result has sometimes been taken as evidence that animals prefer information over its absence. According to information theory (Shannon & Weaver, 1949) maximal information (uncertainty reduction) should occur when there is the largest discrepancy between the information available prior to the choice and the information provided following the choice. Specifically, prior to the choice, the delivery of reinforcement was most uncertain (50%). Thus, the appearance of the discriminative stimulus provided the greatest reduction in uncertainty (either 100% or 0% reinforcement).

To test this theory, Roper and Zentall manipulated the overall probability of reinforcement (while holding equal the probability of reinforcement associated with both alternatives). Consistent with information theory, when the overall probability of reinforcement associated with both alternatives was high, 87.5%, although there was still a preference for the alternative that that was followed by discriminative stimuli, the preference was a much weaker; reinforcement was expected on most trials and it was obtained. However, inconsistent with information theory, when the overall probability of reinforcement was low (when the probability of the appearance of the stimulus that predicted reinforcement was only 12.5% and the probability of reinforcement associated with the other alternative was also 12.5%) the preference for stimuli that predicted reinforcement (or its absence) was even stronger than it was when the overall probability of reinforcement was 50%. According to information theory the preference also should have been weaker because reinforcement should not have been expected and generally was not obtained. Similar results have been reported by others (see Fantino, 1977).

Roper and Zentall (1999) suggested that positive contrast between the expected reinforcement and the obtained reinforcement provided a better account of their results than information theory. When the probability of expected reinforcement was low and it was obtained, contrast would have been large (a change from 12.5% to 100%) whereas when expected reinforcement was high and it was obtained, contrast would have been small (a change from 87.5% to 100%).

Roper and Zentall also found that in the absence of differential reinforcement, pigeons are willing to work harder (peck more times and thus accept an increase in delay to reinforcement) to receive stimuli predictive of reinforcement and its absence. Thus, pigeons preferred the alternative that provided discriminative stimuli even when there was some additional cost in delay to obtaining them.

3. A pigeon model of human gambling

The question of more recent interest to us was would pigeons be willing to forgo food to obtain discriminative stimuli (stimuli predictive of reinforcement and its absence). There is reason to believe that they would. Earlier research had found that under the right conditions, some pigeons preferred an alternative associated with 50% reinforcement that produced discriminative stimuli (half of the time a stimulus that reliably predicted reinforcement, half of the time a different stimulus that reliably predicted the absence of reinforcement) over an alternative that always predicted reinforcement (Belke & Spetch, 1994; Fantino, Dunn, & Meck, 1979; Mazur, 1996; Spetch, Belke, Barnet, Dunn, & Pierce, 1990; Spetch, Mondloch, Belke, & Dunn, 1994). Apparently, under these conditions, when given a choice between 50% reinforcement and 100% reinforcement, some pigeons behaved “irrationally” and chose the 50% reinforcement option, although others did not.

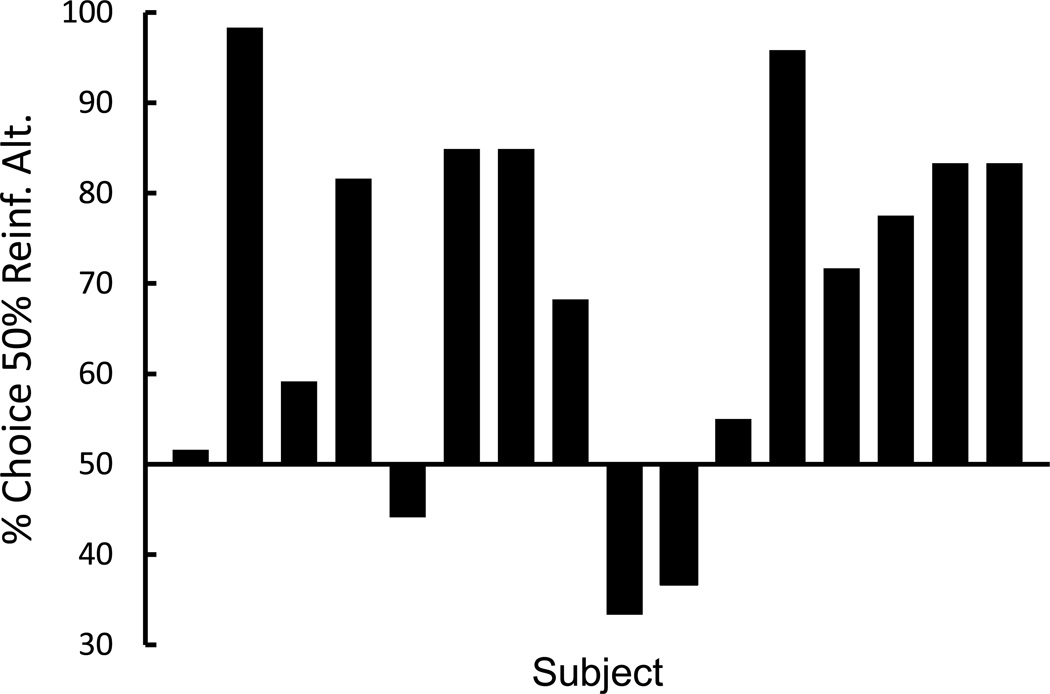
We proposed that if we reduced the difference in the probability of reinforcement between the two alternatives, we might find more consistent results. In our design (Gipson, Alessandri, Miller, & Zentall, 2009) we pitted 50% reinforcement with discriminative stimuli against 75% reinforcement with nondiscriminative stimuli (see the design in Figure 2). These pigeons were given a choice between two white lights, one on the left the other on the right. A single peck to one light resulted in the presentation of one of two colored lights (S1 or S2) for 30 s. If it had been S1, it was always followed by reinforcement. If it had been S2, it was never followed by reinforcement. Thus, choice of that alternative resulted in the appearance of a discriminative stimulus and the overall probability of reinforcement was 0.50. A single peck to the other white light resulted in the presentation of one of two different colored lights (S3 or S4) for 30 s and in either case it was followed by reinforcement with a probability of 0.75. Thus, choice of the second alternative resulted in a higher probability of reinforcement than choice of the first alternative. To ensure that the pigeons had adequate experience with the contingencies of reinforcement associated with the two alternatives, in each training session the pigeons received 24 forced trials with each alternative, as well as 12 choice trials. Thus, they received 12 forced trials with each discriminative and nondiscriminative terminal link stimulus. In support of our hypothesis we found a reliable “maladaptive” preference of 69% for the alternative associated with 50% reinforcement (see Figure 3)

Figure 2.

Design of experiment by Gipson et al. (2009). Pigeons chose between two alternatives. Choice of one alternative was followed by either a stimulus (red) that was always followed by reinforcement on half of the trials or a different stimulus (green) that was never followed by reinforcement on the remaining trials. Choice of the other alternative was followed by either of two stimuli (blue or yellow) both of which were followed by reinforcement 75% of the time. Spatial location and colors were counterbalanced.

Figure 3.

Results of Gipson et al. (2009). Most of the pigeons (13 of 16) showed a preference for discriminative stimuli and a probability of 50% reinforcement over nondiscriminative stimuli and a probability of 75% reinforcement.

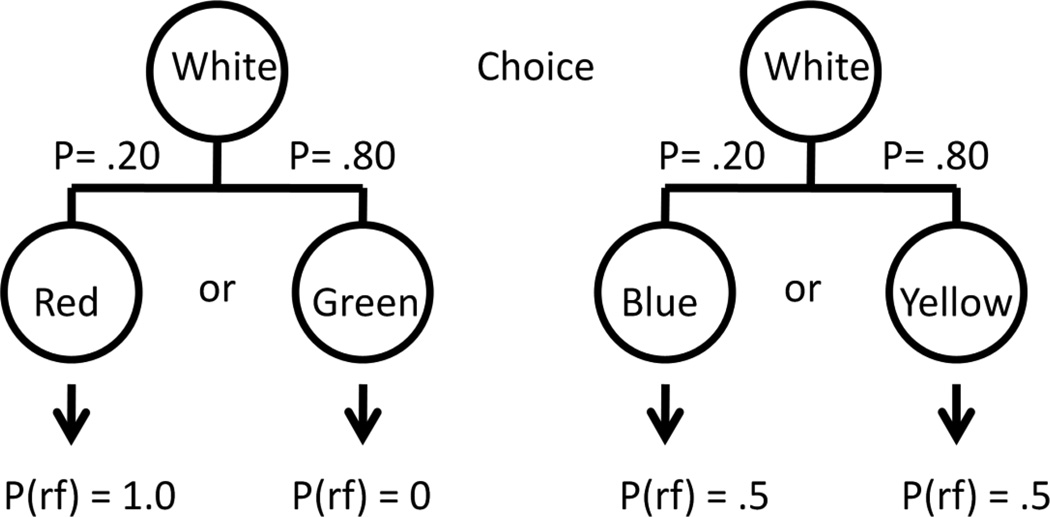
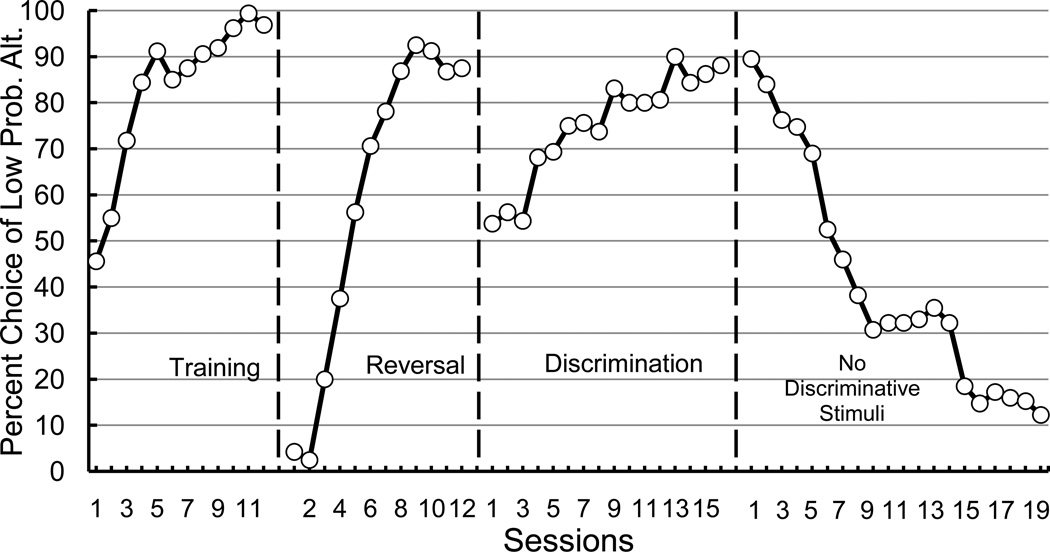
In a follow up study, we found that if we reduced the probability of reinforcement associated with the discriminative stimulus alternative, we could obtain an even larger preference for that alternative (Stagner & Zentall, 2010). Specifically, the probability of reinforcement associated with the discriminative stimulus alternative was only 0.20 (the stimulus that reliably predicted reinforcement occurred on only 20% of the trials), whereas the probability of reinforcement associated with the nondiscriminative stimulus alternative was 0.50 (2.5 times the probability reinforcement associated with the discriminative stimulus alternative, see Figure 4). Under these conditions, the pigeons showed an even stronger preference (97%) for the discriminative stimulus alternative. Acquisition of this preference is shown in the left panel of Figure 5. In Phase 2 of that experiment, the contigencies associated with the two alternatives were reversed and the pigeons quckly reversed their preferences (see the left middle panel of Figure 5). In Phases 1 and 2 of that experiment, the two alternatives associated with the different contingencies were signaled by spatial locations. In Phase 3, shapes that varied in their spatial location from trial to trial became the signals for the alternatives associated with the different contingencies and once again, the pigeons quickly learned to choose the stimulus that was followed by the discriminative stimuli and the lower overall probability of reinforcement (see the middle right panel of Figure 5). Finally, to determine the role of the discriminative stimuli in the preference for the alternative associated with the lower overall probability of reinforcement, the probability of reinforcement associated with those two stimuli was equated at 0.20. That is, the stimulus that was presented on 20% of the trials and was originally associated with 100% reinforcement was reduced to 20% reinforcement and the the stimulus that was presented on 80% of the trials and was originally associated with 0% reinforcement was increased to 20% reinforcement. This change left the overall probability of reinforcement associated with the two alternatives as they were in the earlier phases of the experiment, however, now the pigeons showed a strong preference for the alternative associated with the higher probability of reinforcement (see the right panel of Figure 5). Thus, it was the discriminative stimuli that signaled reinforcement and its absence that were responsible for the pigeons’ sub-optimal choice.

Figure 4.

Design of experiment by Stagner and Zentall (2010). Pigeons chose between two alternatives. Choice of one alternative was followed by either a stimulus (red) on 20% of the trials that was always followed by reinforcement or a different stimulus (green) on 80% of the trials that was never followed by reinforcement. Choice of the other alternative was followed by either of two stimuli (blue or yellow) each of which was followed by reinforcement 50% of the time. Spatial location and colors were counterbalanced.

Figure 5.

Results of Stagner and Zentall (2010). Left panel: Acquisition of the preference for discriminative stimuli with a probability of 20% reinforcement over nondiscriminative stimuli with a probability of 50% reinforcement. Middle left panel: Acquisition of the preference for discriminative stimuli with a probability of 20% reinforcement over nondiscriminative stimuli with a probability of 50% reinforcement when the contingencies associated with the spatial choice were reversed. Middle right panel: Acquisition of the preference for discriminative stimuli with a probability of 20% reinforcement over nondiscriminative stimuli with a probability of 50% reinforcement when the alternatives were signaled with shape stimuli. Right panel: Acquisition of the preference for nondiscriminative stimuli with a probability of 50% reinforcement over nondiscriminative stimuli with a probability of 20% reinforcement.

An alternative means of assessing the degree of preference for one alternative over another is to ask what reduction in delay to reinforcement associated with the less preferred alternative would be needed to make the subject indifferent between the two alternatives. For example, there is good evidence that a reduction in the delay of reinforcement can substitute for a smaller magnitude of reinforcement, a procedure often used in self control experiments (Mazur, 1987).

In an unpublished experiment (Zentall & Stagner, unpublished data) we trained pigeons using the Stagner and Zentall (2010) procedure (20% reinforcement with discriminative stimuli vs. 50% reinforcement with nondiscriminative stimuli) using a fixed 10 s terminal link (the colored stimulus that followed each initial link was presented, response independent, for a fixed 10 s). Following training, using a modification of Mazur’s (1996) procedure, the duration of the terminal link following choice of the alternative associated with a higher probability of reinforcement and the nondiscriminative stimuli was gradually decreased from 10 s to 0 s and then gradually increased until it returned to 10 s. When the choice data from descending and ascending procedures were averaged, we found that the pigeons were indifferent between the two alternatives when the delay to reinforcement associated with choice of the nondiscriminative stimuli was between 2 and 4 s compared with a 10 s delay to reinforcement associated with choice of the discriminative stimulus alternative. Thus, one way to describe the preference for the discriminative stimuli over the nondiscriminative stimuli would be to say that for these pigeons, the discriminative stimuli were worth about three times the delay of reinforcement together with 40% of the total amount of reinforcement.

4. A better pigeon model of human gambling behavior

Although the results of experiments by Gipson et al. (2009) and Stagner and Zentall (2010) clearly demonstrated maladaptive choice behavior by pigeons, when humans gamble, the alternatives generally involve different magnitudes of reinforcement (typically money) rather than different probabilities of reinforcement. Thus, one may purchase a lottery ticket for $1 in hope of winning a large amount of money. It is possible that the effect we have been observing with the manipulation of probability of reinforcement occurs because the pigeons are avoiding an alternative that results in stimuli associated with an uncertain outcome (0.75 probability of reinforcement in Gipson et al., 2009, and 0.50 probability of reinforcement in Stagner & Zentall 2010). If the effect that we have been studying with pigeons is a good analog of human gambling behavior, it should be possible to find a similar effect by manipulating the magnitude of reinforcement, rather than the probability of reinforcement, and removing the uncertainty of the outcome associated with the nondiscriminative stimuli.

Zentall and Stagner (in press) gave pigeons a choice between two alternatives. Choice of one alternative on 20% of the trials produced a stimulus that always predicted the delivery of 10 pellets of food and on the remaining 80% of the trials, produced a stimulus that always predicted the delivery of 0 pellets. Thus, this alternative was associated with an average of 2 pellets per trial (see design in Figure 6). Choice of the other alternative always produced one of two stimuli each of which always predicted the delivery of 3 pellets. Thus, the second alternative was associated with a consistent 3 pellets per trial. Once again, if pigeons are sensitive to the amount of food they obtain over time, they should select the 3-pellet option. However, contrary to this prediction, the pigeons showed a strong, 87%, preference for the variable 2-pellet alternative over the fixed 3-pellet alternative.

Figure 6.

Pigeons chose between two alternatives. Choice of one alternative was followed by either a stimulus (red) on 20% of the trials that was always followed by 10 pellets of reinforcement or a different stimulus (green) on 80% of the trials that was never followed by reinforcement. Choice of the other alternative was followed by either of two stimuli (blue or yellow) both of which always were followed by 3 pellets of reinforcement. Spatial location and colors were counterbalanced.

To ensure that this preference did not result simply from the pigeons’ preference for variable reinforcement over fixed reinforcement, we repeated the experiment and made the discriminative stimuli nondiscriminative. That is, choice of the alternative that provided an average of 2 pellets per trial now produced one of two stimuli, each of which was associated with a 0.20 probability of providing 10 pellets. The alternative that provided a consistent 3 pellets per trial continued to do so. Under these conditions, the pigeons quickly learned to behave “rationally.” That is, they showed an 80% preference for the alternative associated with 3 pellets per trial. Thus, it was not the variability of reinforcement associated with the 20% reinforcement alternative that was responsible for the preference for that alternative but the discriminative stimuli that followed that choice.

5. Mechanism responsible for sub-optimal choice by pigeons

Why do pigeons prefer discriminative stimuli associated with an overall lower probability of reinforcement over nondiscriminative stimuli associated with a higher probability of reinforcement? Dinsmoor (1983) argued that conditioned reinforcement together with reinforced observing behavior was responsible. Any stimulus that predicts reinforcement with a high probability (in this case 100%) will become a conditioned reinforcer and will elicit observing behavior. Although it is clear that such a stimulus should be preferred over a stimulus that predicts reinforcement only 50% of the time (Stagner & Zentall, 2010) or even 75% of the time (Gipson et al., 2009) the question that remains is why the stimulus that was never associated with reinforcement (the S−) showed little evidence of developing conditioned inhibition, especially given that in the Stagner and Zentall study, the S− was presented four times as often as the stimulus that was always followed by reinforcement (see Figure 4).

If the S− failed to become a conditioned inhibitor it could have been because, on a given trial, once it was identified as the S− it is possible that the pigeon turned away from it, thus reducing its inhibitory effect (i.e., it maintained little observing behavior; see Dinsmoor, 1985). Consistent with this possibility, the pigeons in Gipson et al., 2009, Stagner and Zentall (2010), and Zentall and Stagner (in press) rarely pecked at the S−, whereas in each of those experiments they pecked at all of the stimuli that were followed by reinforcement. Interestingly, however, Dinsmoor found that when pigeons were presented with an S− and they were able to turn it off (but turning it off did not change the schedule of reinforcement that was in effect), they did so. Thus, the S− stimulus did appear to have some inhibitory properties.

One could test the hypothesis that the S− failed to become a conditioned inhibitor because of a reduction in observing behavior to the S− stimulus by using a diffuse stimulus such as a houselight as the S− stimulus. If the failure to observe or remain in the presence of the Sstimulus was responsible for the preference for the alternative providing less reinforcement, pigeons that were exposed to a diffuse stimulus that signaled the absence of reinforcement should develop more inhibition to the S− and thus, should show a preference for the alternative associated with the higher probability of reinforcement. We have very recently conducted such a study and found that most of the pigeons continued to prefer the discriminative stimulus alternative associated with an overall lower probability of reinforcement (Stagner & Zentall, unpublished data).

An alternative approach to studying the role of the relative absence of conditioned inhibition in the preference for the alternative associated with the lower probability of reinforcement would be to attempt to actually measure its inhibitory properties. Several procedures have been suggested to assess conditioned inhibition (Hearst, Besley, & Farthing, 1970). One of these involves the presentation of a compound consisting of a known conditioned reinforcer (S+), together with the presumed conditioned inhibitor. Evidence for conditioned inhibition is found when responding to the S+ decreases when the S− is presented in compound with the S+. To devise such a test with the Stagner and Zentall (2010) design (20% vs. 50% reinforcement) one would have to use a shape S− rather than the colored S− used by Stagner and Zentall. Then, assuming that after training the pigeons show a preference for the discriminative stimuli over the nondiscriminative stimuli, one would present a compound of the S+ and S− and compare responding to it to responding to the S+ by itself. To ensure that a reduction in responding to the compound cannot be attributed to the presentation of a novel stimulus (the S+/S− compound) one should also compare S+/S− compound responding to an alternative novel compound consisting of the S+ together with another known conditioned reinforcer (e.g., a shape stimulus trained as one of the stimuli followed by 50% reinforcement associated with the other alternative). If choice of the alternative associated with presentation of discriminative stimuli resulted from the absence of conditioned inhibition to the S−, one should see little decrement in responding to the S+/S− compound, relative to responding to the control compound.

If little conditioned inhibition to the S− is responsible for the sub-optimal choice behavior shown by pigeons, one might be able find further evidence for reduced inhibition in individual differences in the magnitude of the preference. That is, one could ask if the degree of preference for the alternative associated with presentation of discriminative stimuli would predict the decrement in responding to the S+/S− compound. If choice of the alternative associated with presentation of discriminative stimuli resulted from the absence of conditioned inhibition to the S−, one should find a negative correlation between the degree of preference for the discriminative stimuli and the decrement in responding to the S+/S− compound.

Interestingly, a theory based on the absence of conditioned inhibition to losses also has been proposed to account for human gambling behavior. Breen and Zuckerman (1999) reported that humans who gamble regularly have been found to attend more to their wins and less to their considerably more frequent losses than occasional gamblers.

A second account of the preference for 20% reinforcement over 50% reinforcement is that choice of the 50% reinforcement alternative but not the 20% reinforcement alternative results in a considerable amount of nonreinforced responding. Choice of the 20% reinforcement alternative results in very little nonreinforced pecking because pecking to the S+ is always reinforced, whereas there is generally very little pecking to the S−. On the other hand, on half of the trials involving the 50% reinforcement alternative there is nonreinforced pecking. Although this hypothesis provides a reasonable account of the data from Gipson et al. (2009) and Stagner and Zentall (2010) it has more difficulty accounting for the data from Zentall and Stagner (in press) because reinforcement followed all choices of the alternative associated with the nondiscriminative stimuli. However, those data too could be explained in terms of the cost of pecking per unit of food (G. Madden, personal communication, December 15, 2010). If one assumes that pecking is somewhat aversive and that the pigeons peck almost as much at stimuli that predict 3 pellets of food as those that predict 10 pellets of food, the cost per pellet of pecking for 3 pellets of food would be greater than the cost per pellet of pecking for 10 pellets of food.

Although the assumption that pecking is somewhat aversive seems quite reasonable, in fact, pecking is typically confounded with delay of reinforcement. That is, pigeons will prefer less pecking over more pecking if less pecking gets them reinforcement faster. But what if the time to reinforcement is held constant? Delay reduction theory (Fantino & Abarca, 1983) is based on the notion that delay to reinforcement rather than pecking (or effort) determines preference. In support of delay reduction theory, we have recently found that in the absence of differential delay to reinforcement, pigeons do not necessarily prefer not pecking over pecking (Singer, Berry, & Zentall, 2007). When pigeons were given a choice between pecking and refraining from pecking and the time to reinforcement was carefully controlled, most pigeons were indifferent between the two schedules, and of the pigeons that did show a preference, it was not always a preference to refrain from pecking. Thus, nonreinforced responding (or responding leading to a lower magnitude of reinforcement) to terminal link stimuli is not likely responsible for the choice of the initial link leading to the lower probability of reinforcement.

6. The evolutionary basis for sub-optimal choice

A behavioral ecologist might argue that pigeons show maladaptive choice behavior in these experiments only because the laboratory conditions under which they are trained are artificial. They might argue that such conditions would not occur in nature and thus, animals would not be expected to have evolved the ability to detect the differential probabilities of reinforcement under such conditions. In fact, it may be that natural conditions would tend to favor such behavior. For example, one could imagine that in nature, choice of a low probability but high payoff alternative might increase the probability of encountering the high payoff outcome (e.g., by bring the animal closer to a patch that contains a greater density of the high payoff). Thus, although in the laboratory, choice of the alternative that provides discriminative stimuli does not yield the best outcome, one could argue that in nature, it more than likely would. This analysis of (or speculation about) the origins of maladaptive gambling behavior may provide an insight into why it is that humans and other animals perform sub-optimally under these conditions. If so, it leaves unanswered the question of why humans and other animals do not learn that such behavior is maladaptive. After all, the forced trials guarantee extended experience with the contingencies of reinforcement associated with the two alternatives and in our research (as well as with habitual gamblers) there is no indication that the preference for the lower probability of reinforcement associated with the discriminative stimuli declines with additional experience with the contingencies of reinforcement.

Although the laboratory conditions under which we have found maladaptive choice behavior in pigeons may not mirror the conditions found in nature, they may be quite similar to the conditions under which humans show monetary gambling. One difference between the human and pigeon tasks is that the pigeons are confronted with a two alternative forced choice, whereas humans generally are presented with a go/no-go decision (to gamble to refrain from gambling). But this difference makes it ever more surprising that humans choose to gamble because the option to abstain from gambling generally is not only associated with larger magnitude of reinforcement (because the expected return from gambling typically is less than 1.0) but choosing to gamble generally incurs an additional cost in delay to reinforcement (to gamble one has to buy a lottery ticket and wait for the drawing or travel to a casino).

7. Conclusion

The demonstration that pigeons show maladaptive gambling behavior under conditions similar to those under which humans gamble suggests that gambling behavior may be a basic psychological process that can be studied more easily with an animal model because it reduces the likelihood that social, experiential, and other uniquely human biases will interact with the basic behavioral processes presumed to underlie this paradoxical behavior. Furthermore, to the extent that pigeons show sub-optimal choice behavior under conditions that mimic human gambling behavior, an animal model may be useful in studying variables that contribute to (or discourage) habitual gambling behavior by humans.

Research Highlights.

• Pigeons choose sub-optimally when choice results in discriminative stimuli

• They prefer 20% reinforcement with discriminative stimuli over 50% without

• They prefer a 20% prob. of getting 10 pellets over a 100% prob. of 3 pellets

• This behavior provides a model of human gambling behavior