Dynamics of Attentional Selection under Conflict: Toward a Rational Bayesian Account

Abstract

The brain exhibits remarkable facility in exerting attentional control in most circumstances, but it also suffers apparent limitations in others. Our goal is to construct a rational account for why attentional control appears sub-optimal under conditions of conflict, and what it implies about the underlying computational principles. The formal framework we employ is based on Bayesian probability theory, which provides a convenient language for delineating the rationale and dynamics of attentional selection. We illustrate these issues using the Eriksen flanker task, a classical paradigm that explores the effects of competing sensory inputs on response tendencies. We show how two distinctly formulated models, based on compatibility bias and spatial uncertainty principles, can account for the behavioral data. We also suggest novel experiments that may differentiate these models. In addition, we elaborate a simplified model that approximates optimal computation, and may map more directly onto the underlying neural machinery. This approximate model uses conflict monitoring, putatively mediated by the anterior cingulate cortex, as proxy for compatibility representation. We also consider how this conflict information might be disseminated and used to control processing.

Our sensory systems are constantly bombarded by a rich stream of sensory inputs. Selectively filtering these inputs and maintaining useful interpretations for them are important computational tasks faced by the brain. It has traditionally been thought that these tasks suffer from the consequences of limited neuronal resources at perceptual, decisional, and motor levels, thus necessitating the selective enhancement of processing of some sources of information over others (B. A. Eriksen & Eriksen, 1974). More recently, formal modeling based on Bayesian probability theory has suggested that differential processing is computationally desirable, in addition to any resource limitation considerations (Dayan & Zemel, 1999; Dayan & Yu, 2002).

Bayesian probability theory is a powerful and increasingly prevalent ideal observer framework for understanding differential processing. For example, it has been applied at a trial-by-trial level to offer a quantitatively precise formulation for how different sources of noisy information should be combined to inform an observer’s internal model about the external world. For instance, several studies in recent years have shown that human subjects combine differentially reliable sensory inputs from different modalities in a computationally optimal way (Jacobs, 1999; Ernst & Banks, 2002; Battaglia, Jacobs, & Aslin, 2003; Dayan, Kakade, & Montague, 2000). More recently, it has been shown that human subjects, in certain reward learning (Behrens, Woolrich, Walton, & Rushworth, 2007) and motor adaptation (Körding, Tenenbaum, & Shadmehr, 2007) tasks, are also close to optimal when combining immediate inputs with differentially reliable past observations.

In addition to such trial-by-trial integration, there has also been much interest as to how the brain incrementally processes sensory inputs on a much finer, sub-second time-scale (Ganz, 1975; C. W. Eriksen & Schultz, 1979). It is known that for simple decision-making tasks in which subjects must decide which of two sources is responsible for generating a continual stream of noisy inputs, the optimal solution, which minimizes a trade-off between accuracy and delay (Wald & Wolfowitz, 1948), is to integrate evidence for each of the two hypotheses up to a fixed evidence threshold, and choose the corresponding hypothesis. Under similar experimental conditions, it appears that human and animal subjects accumulate sensory inputs and make perceptual decisions in a manner close to this optimal strategy (Laming, 1968; Luce, 1986; Ratcliff & Rouder, 1998; Bogacz et al., 2006). Moreover, when monkeys use eye movements to indicate their perception of motion direction, neurons in the posterior parietal cortex, known to be engaged in the preparation of eye movements, appear to integrate sensory evidence over time with dynamics similar to that prescribed to the evidence integrator by the optimal algorithm (Gold & Shadlen, 2002).

Building on these two lines of successful work, we examine here the within-trial temporal dynamics of attentional selection (Yu & Dayan, 2005a). When there are multiple, possibly conflicting stimuli present in the visual scene, attentional selection is necessary to filter out the irrelevant inputs and produce the appropriate percept and response. We are interested in the computational principles underlying the attentional selection process that controls the relative processing of the individual stimuli and which eventually resolves the conflict. A classical paradigm known as the Eriksen flanker task, in which subjects are asked to identify a central target stimulus flanked by either compatible or incompatible flanker stimuli, has yielded behavioral data suggesting certain idiosyncratic characteristics of this selection process (B. A. Eriksen & Eriksen, 1974). To summarize the data, the interference from incompatible flankers is especially strong shortly after stimulus onset, so as to produce responses below chance, and then it is gradually overcome as accuracy asymptotes at a high level (Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988). We use a Bayesian optimality framework to show that concomitant with the processing of the identity of the individual stimuli in the Eriksen task, there should be secondary processing of compatibility across stimuli, and that it is the dynamic interaction between the two processes that give rise to the specific temporal pattern of flanker interference found in the Eriksen task.

In the next section, we review the relevant experimental data from the Eriksen task, and motivate two distinct hypotheses, what we term the compatibility bias and spatial uncertainty models, to account for the data. Subsequently, we introduce the Bayesian framework, and demonstrate how the two hypotheses can be implemented concretely using a shared Bayesian architecture but with subtly different model assumptions. We then present analytical and numerical results showing that optimal processing in either model, under the constraints of their respective assumptions, leads to the empirically observed below-chance accuracy level for short reaction-time incompatible trials. We also use the two models to capture additional behavioral data on variations of the Eriksen task, as well as using the two models to make distinct predictions in novel experiments. Finally, we propose an approximation to the optimal strategy. This is motivated by the computational complexity of the optimal Bayesian computations, and prior work suggesting the existence of neural mechanisms responsible for the monitoring of processing conflicts, which may serve as a useful proxy for the optimal computations concerning compatibility.

Review of Eriksen Data

In the Eriksen task (B. A. Eriksen & Eriksen, 1974), subjects are asked to discriminate a target stimulus (e.g. whether it is the letter S or H) flanked by distractors on either side. The flankers can either be compatible with the central target stimulus (e.g. HHHHH) or incompatible (e.g. SSHSS), and subjects are explicitly instructed to base their discrimination exclusively on the central stimulus. Despite the instructions, subjects appear incapable of completely ignoring the flankers. They exhibit what is known as the compatibility effect: they are slower and less accurate on incompatible trials than compatible trials (B. A. Eriksen & Eriksen, 1974). Here, we focus on a variant of the original task which has provided hints about the nature of the dynamic modulation of sensorimotor processing by selective attention (Gratton et al., 1988; Servan-Schreiber, Bruno, Carter, & Cohen, 1998).

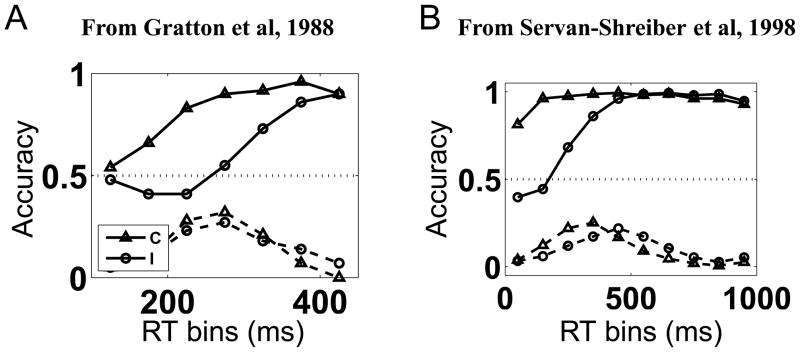
In this variation (which is sometimes called the ‘deadlined’ Eriksen task), subjects are explicitly encouraged to produce more trials with short reaction times (RTs) than they would normally emit, and a curve showing accuracy as a function of RT (called a conditional accuracy curve) is plotted (see Figure 1). This shows that the effect of the flankers is neither uniform, nor even monotonic over time. Rather, interference from the flankers appears to have an impact that is maximal shortly after stimulus presentation, but diminishes with time. Strikingly, for responses made within a couple hundred ms after stimulus presentation, subjects perform at worse than chance level for incompatible trials (i.e., their responses are primarily driven by the flankers instead of the target). This produces a characteristic “dip” below chance level (.5) in the conditional accuracy curve.

Figure 1.

Accuracy vs. RT in the Eriksen task. In both (A) and (B), the solid lines denote the empirical probabilities of making a correct response as a function of binned reaction times; the dashed lines denote the empirical distribution over RT bins. Triangle: compatible. Circle: incompatible. The dotted line denotes chance performance for comparison. (A) Data adapted from (Gratton et al, 1988); reaction times gauged by electromyographic activities (EMG). (B) Data adapted from (Servan-Schreiber, Bruno, Carter, & Cohen, 1998); RT measured by button presses. The details of the data sets differ, but several qualitative commonalities stand out: (i) incompatible trials are less accurate and slower than compatible ones, (ii) for short-RT bins on incompatible trials only, accuracy “dips” below chance before rising gradually.

Figure 1 shows two examples of this phenomenon, using data obtained from two independent implementations of the deadlined Eriksen task (Gratton et al., 1988; Servan-Schreiber et al., 1998). While the specific details of the distribution of reaction times, and the precise trade-off between accuracy and reaction time, differ between the two studies, the dip in performance on short-RT incompatible trials is prominent in both. A previous neural network model has provided a mechanistic account of this phenomenon (Cohen, Servan-Schreiber, & McClelland, 1992), and has been used to address a wide variety of other behavioral phenomena observed in the Eriksen Task (Servan-Schreiber et al., 1998). However, while this earlier work illustrates how these behavioral phenomena might arise from neural mechanisms, it did not set out to explain why these mechanisms should operate as they do. Here, we seek the normative principles underlying them.

One possible explanation is that subjects assume that spatially proximate visual stimuli/patches are featurally similar, and express this in a bias for compatibility. This could arise through evolutionary adaptation or developmental learning, on the basis of the strong spatial regularities that exist in natural scenes (Baddeley, 1997; Atick, 1992). Indeed, many visual illusions such as the perceptual filling-in effect (Ramachandran & Gregory, 1991) appear to depend on a strong tendency to assume spatial continuity of visual objects in the scene. This may explain why flanker stimuli influence processing at the start of a trial, before their incompatibility is recognized and attention can be preferentially allocated to the central target. That is, verbal task instructions (to attend and respond to the central target) may fail to overcome strong prior expectations, until evidence from the stimulus itself accumulates to override the effect of these prior expectations.

Another potential explanation is associated with crowding (Intriligator & Cavanagh, 2001). That is, the cortical neurons that process complex features such as the letters used in the Eriksen task have relatively large receptive fields, and so a stimulus at one point will evoke responses in a population of neurons whose receptive fields are centered at varying distance from that point. This “cross-talk” leads to uncertainty about the spatial location of the different stimuli, at least early on during processing, thus allowing the flankers an incorrect influence over discrimination in the incompatible condition. Another way to look at this is associated with the binding problem. It has been observed under different conditions that when a visual display is presented for a short amount of time (e.g. 200 ms), subjects sometimes correctly perceive the identity of objects in the display, but err as to their relative locations; and they can even make mistakes in binding the featural and spatial properties of an object (Treisman & Schmidt, 1982). This implies that spatial and featural properties are two related but distinct dimensions of stimulus attributes, and that both need active processing and integration.

Here, we use a normative Bayesian approach to formalize these intuitive concepts and examine their implications for the computations underlying behavior and neural processing. This is an extended form of an ideal observer, in which the characteristics of the problem are precisely formulated in a generative model, and the statistical inverse of this generative model, which is known as a recognition model specifies the ideal way to act. The performance of the ideal observer is an upper bound on how well any possible system, artificial or natural, could perform the task, under the same constraints. We consider an extended ideal observer, for which the inputs to the inference process (which may suffer from spatial “smearing”) are considered to be a part of the generative model.

More concretely, the generative model describes the task for inference, specifying everything from the experimental design to the noisy neural inputs. Here, the generative model demands two major sets of assumptions: those about the statistics of the task, and those about how the physical stimuli give rise to the noisy neural inputs. The former class is given by the external environment, the latter is a function of the properties and limitations of the biological hardware (e.g. receptor sensitivity and neuronal spiking mechanisms). The recognition model, which is the inverse of this generative model, specifies the optimal inferential algorithm. It determines how the noisy inputs should be utilized to compute the best action or output; different assumptions about the generative model lead to different a recognition model, and so a different requirement on downstream neurons if they are to make appropriate inferences about the external events and properties generated the inputs. The excellent performance of animals in a wide variety of visual tasks suggests that the brain is good at implementing near-optimal inference for various generative models. Under the assumption of (near-) optimality, we can therefore ‘reverse-engineer’ the design principles and limitations underlying neural processing, by comparing subjects’ performance with that of different Bayes-optimal inference algorithms.

A Bayesian View of the Eriksen Task

We first introduce a basic generative model that captures the general features of the Eriksen task. We then elaborate the basic structure with two sets of modifications, which respectively implement the compatibility bias and spatial uncertainty hypotheses. Later we will also analyze their respective inference models. Both the generative and inference models are built out of probabilistic quantities and relationships, which capture the stochasticities and uncertainties inherent to the generative process. We simplify the model schematics wherever possible, in order to make the key points with the least amount of clutter.

Generative Model

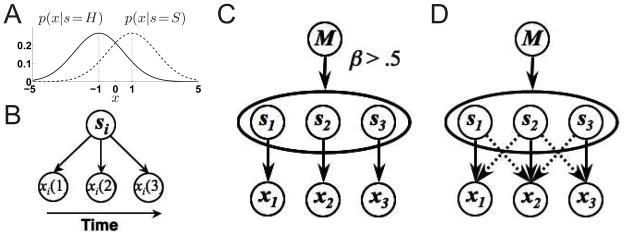
For each trial, we model the visual stimulus as being made up of an array of three stimuli, s₁, s₂, and s₃, for “left”, “center”, and “right”, respectively. On each trial, each s_i can be either H or S. As is the case with most implementations of the Eriksen task, we assume that the flankers are identical (s₁ = s₃), and that they can be the same (compatible) or different (incompatible) from the target (s₂). We use the variable M to denote the trial compatibility: M =C for compatible, M =I for incompatible. The prior probability of a trial being compatible (P(M =C)) or incompatible (P(M =I)), before seeing any inputs, should reflect the true probability of the two trial types (typically .5 for both types). Finally, for a given trial type (C or I), there are two equally likely stimulus settings: SSS and HHH for M =C, SHS and HSH for M =I.

Given the three stimuli on each trial, a noisy pattern of visual inputs is generated. For simplicity, we assume that there are three populations of neurons whose activities, x_t ≜ [x₁(t), x₂(t), x₃(t)], are respectively driven by the three stimuli, s = s₁, s₂, s₃, in a Gaussian fashion:

$$p(\mathbf{x}\mid \mathbf{s})=p(x_1\mid s_1)p(x_2\mid s_2)p(x_3\mid s_3)=\mathcal{N}(\mu (s_1),{\sigma }^2)\mathcal{N}(\mu (s_2),{\sigma }^2)\mathcal{N}(\mu (s_3),{\sigma }^2).$$ (1)

(μ, σ²) denotes a Gaussian probability distribution with mean μ and variance σ². We assume, for now, that each x_i is drawn from a Gaussian distribution centered at −1 if s_i = H, and +1 if s_i = S (see Figure 2A).

Figure 2.

Generative model for the Eriksen task. (A) When s_i = H, each x_i(t) is drawn from a normal distribution centered at −1; for s_i = S, the samples are drawn from a similar distribution centered at 1. Thus, a single sample confers partial and noisy information about the underlying stimulus. (B) Within a trial, a fixed setting of s_i gives rise to iid samples of x_i(t) over time. (C) In the compatibility bias model, the prior probability over compatible is greater than chance: β > .5. Each x_i depends only responds to one stimulus s_i and not to the others. (D) Spatial uncertainty model: p(x_i(t)|s) depends not only on s_i but also the neighboring stimuli.

We also assume that, on a time scale significantly shorter than the typical reaction time, successive observations x₁, x₂, …, x_t, … are generated from the stimuli s in an independent and identical (iid) fashion (see Figure 2B):

$$p({\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_t\mid \mathbf{s})=p({\mathbf{x}}_1\mid \mathbf{s})p({\mathbf{x}}_2\mid \mathbf{s})\dots p({\mathbf{x}}_t).$$ (2)

This captures the assumption that more and more sensory information enters the visual system over time, and this growing information can be used to make increasingly more accurate perceptual discriminations.

To implement the compatibility bias hypothesis, we simply let the prior probability for M =C be greater than the true chance value. That is, we let β ≜ P(M =C) > .5, as shown in Figure 2C. To implement the spatial uncertainty hypothesis, we let each x_i depend on not only its most preferred stimulus, but also partially on its neighbors (see Figure 2D). So for instance, x₂ may depend on s₁ and s₃ in addition to s₂. Mathematically, we write this as:

$$\begin{array}{l}{x}_1(t)~\mathcal{N}(a_1{\mu }_1+a_2{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)\\ x_2(t)~\mathcal{N}(a_1{\mu }_2+a_2{\mu }_1+a_2{\mu }_3,{\sigma }_1^2+2{\sigma }_2^2)\\ x_3(t)~\mathcal{N}(a_1{\mu }_3+a_2{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)\end{array}$$

where a₁ and σ₁ are the “signal” and “noise” due to the primary stimulus, and a₂ and σ₂ are due to a neighboring stimulus. As with the compatibility bias model, we assume that μ_i = −1 if s_i = H, and μ_i = +1 if s_i = S. We could combine the two hypotheses by making β >.5 and a₂ and σ₂ non-zero, which would produce even greater interference effects; but in order to understand the independent effects of these two manipulations, we assume uniform prior (β =.5, also known as agnostic prior) in the spatial uncertainty model, and allow no spatial overlap (a₂ = σ₂ =0) in the compatibility bias model.

Inference Model

Given a stream of inputs x₁, x₂, …, the ideal observer’s belief about the identity of the target s₂ and compatibility M at time t, captured by the probability distribution P(s₂, M |x₁, …, x_t) is a function of his belief at the previous time point P(s₂, M|x₁, …, x_t−1) and the latest input x_t. Bayes’ Rule spells this out explicitly:

$$P(s_2,M\mid {\mathbf{X}}_t)=\frac{p({\mathbf{x}}_t\mid s_2,M)P(s_2,M\mid {\mathbf{X}}_{t-1})}{{\sum }_{s_2^{\prime },M^{\prime }}p({\mathbf{x}}_t\mid s_2^{\prime },M^{\prime })P(s_2^{\prime },M^{\prime }\mid {\mathbf{X}}_{t-1})}$$ (3)

where X_t ≜ [x₁, …, x_t] is shorthand for all the inputs observed up until time t. This joint distribution, a function of time, is known as the posterior distribution (from Latin a posteriori, meaning after having observed the new data vector x_t). This distribution encapsulates all the information that can be gleaned from the past inputs X_t. This iterative process is initialized by any prior assumptions about the relative prevalence of compatible (M =C) and incompatible (M =I), as well as the possible stimulus configurations under these two trial types.

P(s₂, M |x₀) = P (s₂, M) = .5β for M =C and .5(1 − β) for M =I. .5 here indicates that there is equal prior probability of s₂ being H and S.

In order to make a perceptual decision based on this evolving trajectory of posterior probability, we compute the total (known as marginal) probability of s₂ being H, by summing over our uncertainty over compatibility (M =C or M =I):

$$P(s_2=H\mid {\mathbf{X}}_t)=P(s_2=H,M=C\mid {\mathbf{X}}_t)+P(s_2=H,M=I\mid {\mathbf{X}}_t)$$ (4)

Because probabilities have to sum up to 1, the marginal probability of s₂ = S is just 1 − P(s₂ = H|X_t). We then compare each of these two marginal probabilities against against a decision threshold q, and report the target is H if P(s₂ = H|X_t) > q, report S if P(s₂ = S|X_t) > q, or continue observing otherwise. This policy is a variant of the sequential probability ratio test (SPRT) (Wald, 1947), which is known to optimize any combination of speed-accuracy trade-off (by varying the threshold) for 2-alternative forced choice (2AFC) tasks (Wald & Wolfowitz, 1948; Liu & Blostein, 1992). Performance of humans and other animals in 2AFC tasks seems broadly consistent with the SPRT (Ratcliff & Smith, 2004), and there is some evidence that competing neural populations subserving decision-making may implement a strategy close to the SPRT (Schall & Thompson, 1999; Gold & Shadlen, 2002), or its continuous analog (Bogacz et al., 2006).

In order to encourage a sufficient number of short reaction time trials, subjects are warned whenever their responses exceed a deadline (Gratton et al., 1988; Servan-Schreiber et al., 1998). Related work in stochastic control theory suggests that if the cost of detection delay dramatically increases (to be more than the cost of making an error) beyond a deadline, then the optimal policy is a pair of symmetrically decaying thresholds toward .5 from above and below (Frazier & Yu, 2008), rather than a fixed threshold (as in SPRT and DDM). Intuitively, if the deadline is imminent, it is better to make a decision with low confidence instead of waiting until the deadline. Even when the deadline not imminent, but known to be occurring soon, there is little incentive for continuing information-collection if a few more data points are not expected to push our belief drastically toward one of the other hypothesis. For simplicity, we approximate this optimal but more elaborate policy by assuming that the deadline induces a small probability γ of making premature responses at time 0, before any observation is made.

Results

Compatibility Bias

Even though the Eriksen task only asks the subjects to report target identity, and not compatibility, that information is nevertheless present. Using our Bayesian formulation, which at any given time provides a joint belief state over target identity s₂ and trial compatibility M, we demonstrate that the secondary processing of compatibility is critical for producing the observed flanker interference effects. Intuitively, compatibility matters because if the stimuli are perceived to be compatible, then flanker inputs should be integrated cooperatively with the target inputs in order to reach more accurate decisions faster; conversely, if the stimuli are perceived to be incompatible, then flanker inputs should be integrated competitively. Consequently, the observer’s prior belief about the relative prevalence of compatible trials, β, has a drastic effect on the inference about the target s₂.

As shown in Figure 3, when there is a prior bias toward compatible (β >.5), the system is primed to integrate the inputs cooperatively from the outset, causing incompatible flankers to have an incorrect influence on the inference about s₂. With sufficient passage of time, the evidence for incompatibility can eventually overwhelm the prior and induce correct competitive integration of flankers. This correction, however, can only impact trials in which the system has not already reached the decision threshold (typically for the incorrect response), driven by the initially incorrect integration strategy. Consequently, incompatible trials that terminate early tend to be driven by the flankers and result in incorrect decisions, and those that terminate late tend to be more accurate. In the Appendix A, we show that flankers have no influence when the prior probability distribution is uniform (β =.5), but that a biased prior (β >.5) leads to incorrect processing of the flankers after one or a few data samples – though this effect can be eventually overcome if the observation process is not terminated.

Figure 3.

Compatibility Bias Model. This implements the Bayesian inference model with a prior biased toward compatible trials (P(M =C) > .5). This implies that the compatible pathway is more activated than the incompatible one at the onset of the trial. Thus, flankers have incorrect influence on the processing about the central stimulus on a trial that is actually incompatible. With time, enough bottom-up sensory evidence can accumulate to overwhelm the biased prior and lead the system to correctly deduce that the stimuli are in fact incompatible, and therefore allow the inputs to be integrated competitively as they should be. However, this would only happen if the decisional threshold q has not already been crossed and the trial terminated. Consequently, on short response-time trials, the incorrect processing of the flankers makes the discrimination worse than chance, whereas on the long response-time trial, the accuracy level rises significantly.

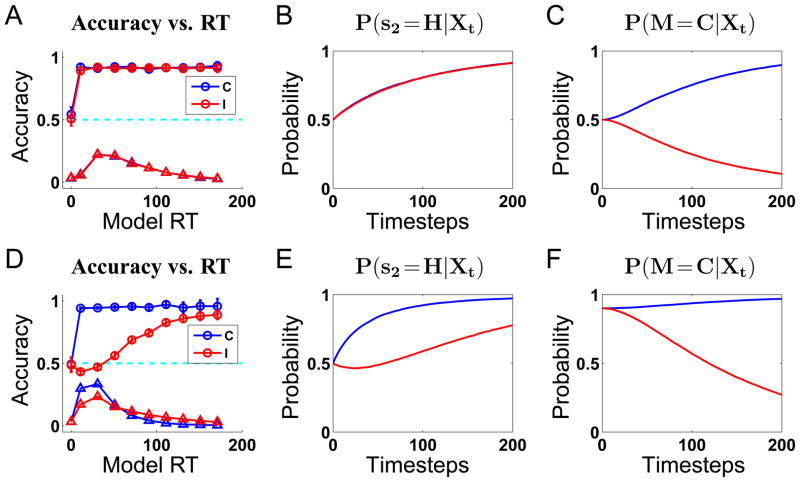
Elsewhere (Liu, Yu, & Holmes, 2008), we have shown that the compatibility bias model can be expected to produce a “dip” in the marginal posterior after one sample (P(s₂|X₁)) under rather loose constraints on the model parameter: β > 3/4 (or more generally, for n flankers, β > (n + 1)/2n). Presumably a dip in the posterior underlies any dip in the decision accuracy for short-RT trials. This makes the intuitively appealing predictions that the behavioral dip should be more prominent when β is large, or when the number of flankers is large. To demonstrate the effect of the compatibility prior more concrete, we simulate the model for an unbiased prior β =.5 (see Figure 4A), and a biased one β =.9 (see Figure 4D). The other parameters are σ =9 (input noise level), γ =.03 (probability for premature response), q =.9.

Figure 4.

Inferential performance for the compatibility bias model, with equal priors β =.5 (A,B,C), and biased priors β =.9 (D,E,F). (A) For equal priors, accuracy as a function of RT (○), and the RT distributions (△), are identical between compatible (blue) and incompatible (black) trials. Data averaged over 10000 trials and binned into 10 equally spaced bins for each of compatible and incompatible conditions, error bars are SEM. (B) The mean trajectories of the marginal posterior P(s₂ = H|X_t) (correct answer) for the compatible (blue) and incompatible (black) conditions are identical. (C) The marginal posterior P(M =C|X_t) (compatible) rises from 0.5 toward 1 for compatible stimuli (blue), and falls toward 0 for incompatible (black), at an identical rate. (D) For biased priors, accuracy level is close to 1 in the compatible condition, except for the premature responses, which are at chance. In the incompatible condition, accuracy is below chance level for short react times, and rises toward 1 for trials with longer RT. The distribution of RT is broader and delayed for the incompatible condition compared the compatible condition. (E) The mean trajectories of the marginal posterior P(s₂ = H|X_t) (correct answer) for the compatible condition rises steadily from 0.5 toward 1, while that for the incompatible condition first “dips” below 0.5, before climbing back up toward 1 as time passes. (F) The marginal posterior P(M =C|X_t) rises from β toward 1 for compatible trials, and falls toward 0 for the incompatible condition.

In the equal prior case, the conditional accuracy curve is identical for compatible and incompatible trials, clearly in contrast to the behavioral data of Figure 1. But for the biased prior case, the model produces the “dip” for incompatible trials, as well as longer and broader distribution of RT for incompatible, relative to compatible, trials. A more precise way to quantify the influence of the prior on perceptual dynamics is shown in Figure 4B and Figure 4E. The evolution of the mean trajectory of the posterior probability of s₂ = H (the correct answer) over time for compatible and incompatible conditions are identical for equal priors, but significantly different for biased priors. In the latter, compatible trials benefit slightly (limited by a ceiling effect) from the biased prior, because the flanker stimuli are correctly and efficiently integrated from the start (compare Figure 4E to Figure 4B). However, incompatible trials are greatly disadvantaged by the bias, as the posterior first dips toward the wrong answer, s₂ = S, before slowly rising toward s₂ = H. On average, given an equal number of compatible and incompatible trials, this disadvantage significantly overwhelms the slight benefit accrued in the compatible condition, as is apparent by comparing Figure 4A and Figure 4D.

Also shown in Figure 4C and Figure 4F, the marginal posterior probability for M =C tends toward 1 for compatible trials, and falls toward 0 for incompatible trials. Under the equal prior assumption, the two traces diverge symmetrically from .5 toward 0 and 1; under the biased prior assumption, the two begin near 1, and it takes the incompatible trace quite some time to reach its asymptotic value close to 0.

Spatial Uncertainty

To understand the influence of spatial uncertainty on the decision making process, consider an extreme case in which each of the sensory input x_i is driven equally by all of the stimuli. Then nothing distinguishes the stimuli spatially. Based on such inputs, the answer to whether the central stimulus is H or S would be driven by a majority vote based on the noisy inputs, and the flankers would have undue influence given their superior number compared to the single target. Now suppose this spatial uncertainty can be resolved gradually over time, then the problem evolves from taking a majority vote based on a “bag of letters” to giving a precise answer in the context of the specific spatial arrangement of the stimuli.

Because of the dependence of the x_k on the neighboring stimuli s_j, j ≠ k, and because of the larger number of parameters, a full analysis of the spatial uncertainty model is more challenging than for the compatibility bias model. Elsewhere (Liu et al., 2008), we show that under certain approximating assumptions, the key to the “dip” is that the ratio of the means, a₁/a₂, must be within a certain range bounded by functions of the noise variances σ₁ and σ₂. Intuitively, when a₁/a₂ is too large, then there is little spatial uncertainty; when a₁/a₂ is too small, then the inputs lose their spatial specificity.

To illustrate properties of the spatial uncertainty model, we use the following simulation parameters: a₁ =1.7, a₂ = .3, σ₁ =6, σ₂ =3.5, β =.5, γ =.03, q =.9. As with the biased prior model, the spatial uncertainty model can also produce the accuracy “dip” for short reaction-time trials unique to the incompatible condition (Figure 5A), accompanied by a similar underlying dip in the posterior probabilities (Figure 5B). The model also captures the basic flanker effects of delaying the reaction times and broadening their distribution in the incompatible condition, as was seen in the experimental data of Figure 1.

Figure 5.

Inferential performance for the spatial uncertainty model. (A) Accuracy level is close to 1 for all RT’s in the compatible condition (blue). In the incompatible condition (black), accuracy is below chance level for short react times, and rises toward 1 for trials with longer RT. The distribution of RT (triangle) is broader and delayed for the incompatible condition (black) compared to compatible (blue). Data averaged over 10000 trials and binned into 8 equally spaced bins for each of compatible and incompatible conditions, error bars are SEM. (B) The mean trajectory of the marginal posterior probability of s₂ = H (the correct answer) for the compatible condition (blue) rises steadily from 0.5 toward 1, while that for the incompatible condition (black) first “dips” below 0.5, before climbing back up toward 1 as time passes. (C) The marginal posterior for M =C diverges from .5 toward 1 and 0 for compatible (blue) and incompatible (black) trials, respectively.

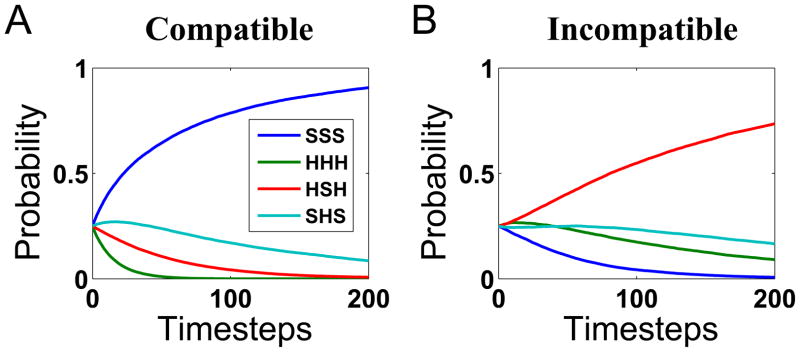
In Figure 6, we see more precisely the impact of the spatial “smearing”: the incompatible array SHS has strong rival explanations in not only SSS, a natural competitor, but also HSH, a strong competitor created by the spatial overlap. Because both of these rival explanations favor reporting s₂ = S, at short reaction times, accuracy can be below chance.

Figure 6.

Mean trajectories of posterior probabilities for the spatial uncertainty model. (A) Given the stimulus array HHH (s₂ = H, M =C), the posterior probability for HHH rises toward 1 over time, as the posterior probability for all the alternative explanations fall toward 0. (B) Given the stimulus array SHS (s₂ = H, M =I), the posterior probability for SHS beats out the rest with time. However, the rise is less steep, and the combined influence of the second and third mostly likely candidates (SSS and HSH, the latter due to the spatial “smearing” in the inputs) at the start of the trial are sufficient to result in the posterior probability for s₂ = H to dip below .5 in Figure 5.

Additional Results

Despite the conceptual simplicity of our Bayesian models, as well as the small number of parameters, they are actually quite powerful. To illustrate this power, we consider how the models perform in capturing behavioral data from other variations of the Eriksen task.

Sequential effects

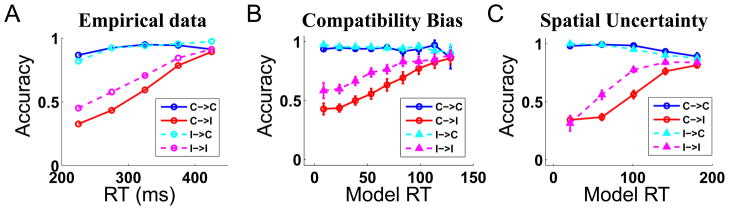
We have shown, through the compatibility bias model, that any prior bias subjects bring into the task can have a drastic influence on target discrimination. However, it is reasonable to suspect that, with sufficient exposure to a particular frequency of compatibility trials, the subjects may modify their internal (implicit) prior about compatibility to be closer to the true value, if not actually matching it exactly. If subjects are adjusting their internal priors on a trial-to-trial basis, then we should expect their performance to differ following a compatible versus incompatible trial. This has indeed been observed in the Eriksen task (Gratton, Coles, & Donchin, 1992). As shown in Figure 7A, the differential performance between compatible and incompatible trials, including the presence of the dip, was attenuated following an incompatible trials relative compatible trials. Allowing our Bayesian models also to adjust the compatible prior after each trial, we show that the compatibility bias model (Figure 7B) and the spatial uncertainty model (Figure 7C) exhibit sequential effects similar to experimental data. The expanded models incorporate one additional parameter each, which is the assumed probability that the frequency of compatible trials is allowed to change from trial to trial. For the compatibility model, the simulation results are obtained by assuming this parameter to be .3; for the spatial uncertainty model, this parameter is .7. However, the qualitative features of the results are not especially sensitive to the choice of this parameter (data not shown; expanded discussion in a separate manuscript under preparation).

Figure 7.

Sequential effects in behavioral data and model predictions. (A) Data adapted from (Gratton et al, 1992). The difference in accuracy for compatible and incompatible trials diminish following an incompatible trial, compared to a compatible one. The “dip” is also attenuated for the incompatible curve (magenta compared to red), although the accuracy level is not much changed for the compatible curve (cyan similar to blue). In the legend, C → I means compatible trial followed by incompatible, analogously for the others. (B) Similar pattern of “behavior” for the compatibility bias model. (C) Similar pattern of “behavior” for the spatial uncertainty model.

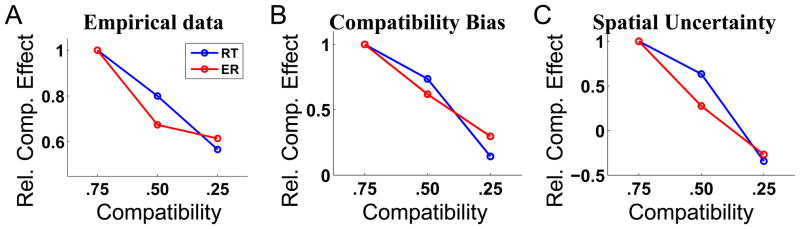
Compatibility manipulation

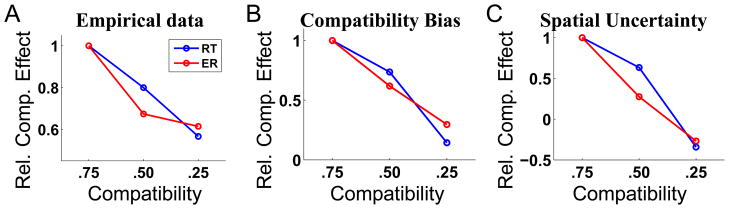
Since prior assumptions about compatibility play such an important role, manipulations of the relative frequency of compatible and incompatible trials should modify the compatibility effect (difference in RT or error rate, ER, between incompatible and compatible conditions) correspondingly: higher frequency of compatible trials should enhance the effect, while lower frequency should decrease the effect. This was demonstrated by an experiment (Gratton et al., 1992) that had separate sessions in which compatibility frequency was .75, .5, and .25, respectively. Figure 8A shows how the compatibility effect, measured in both RT and ER, decline as the experimental frequency of compatibility decreases. The RT data (blue) are normalized to the compatibility effect (in ms) for the .75 condition; the ER data (red) are similarly normalized against the .75 condition. As shown in Figure 8B and C, the compatibility bias model and the spatial uncertainty model can both produce this effect – here, we allow the model to adjust its internal estimate of compatibility on a trial-to-trial basis, exactly as in the previous simulation of sequential effects.

Figure 8.

Effects of manipulating block compatibility on behavioral data and model predictions. (A) Data adapted from (Gratton et al, 1992). When experimental frequency of compatibility trials decreased, the compatibility effect (incompatible - compatible) measured both in terms of RT (blue) and ER (red) also decreased. Using a similar mechanism for adjusting perceived compatibility on a trial-to-trial basis as in Figure 7, both (B) the compatibility bias model, and (C) the spatial uncertainty model, can produce qualitative features of the empirically observed pattern of behavior. For all three sub-plots, the data are divisively normalized by the compatibility effect for the .75 condition, see text for more details.

Spatial separation

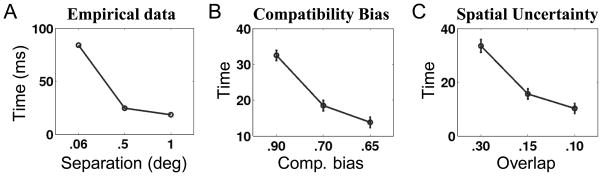
Another set of interesting data comes from a study in which the spatial separation between the flankers and the target was manipulated (B. A. Eriksen & Eriksen, 1974). The finding, as one might expect, was that the compatibility effect (for RT) decreased as the spatial separation increased (Figure 9A). For the spatial uncertainty model, it is fairly straight-forward to imagine how the spatial separation can be implemented (by decreasing the overlap between stimulus responses, parameterized by a₂), and what its consequences would be (decreasing compatibility effect). Figure 9C shows the simulation results, which qualitatively match the experimental data. It is less obvious how this can be accommodated by the compatibility bias model. One possibility is that the bias is not a single value (β), but rather a whole function that depends on the distance d between the target and flankers (i.e. β(d)). Figure 9B shows that this extended compatibility model (assuming β(.06)=.9, β(.5)=.7, β(1)=.65) can also qualitatively capture te experimental data on spatial separation.

Figure 9.

Effects of spatial separation on behavioral data and model predictions. (A) Data adapted from (Eriksen and Eriksen, 1974). When spatial separation between flankers and target increased (measured in degrees of visual angle), the compatibility effect in RT decreased. (B) For the compatibility bias model, a similar pattern of effects can be obtained if we assume that the prior bias for compatibility is not a fixed quantity, but rather a function of distance (see text for details). (C) The spatial uncertainty model can also capture the effects if we assume that the receptive fields overlap diminishes with separation (see text for details).

Novel Predictions: Compatibility Detection

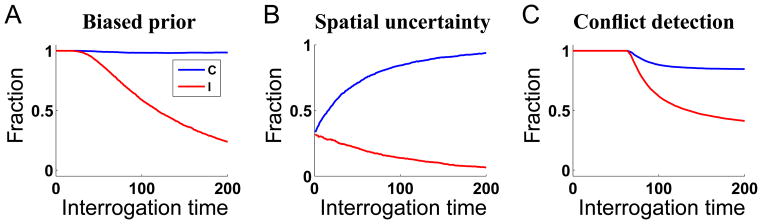
It is reassuring that both the compatibility bias model and the spatial uncertainty model can account for the compatibility effect and the dip, and, with slight modifications, account for a range of additional results. But which one is right? For this, we need a set of novel experimental predictions, on which the two models actually make different predictions. One such experiment is to query the subjects about stimulus compatibility explicitly. If the main objective of the task is still to report stimulus identity, but the subjects are queried about compatibility occasionally after they have reported identity, then the compatibility bias model predicts a bias for reporting “compatible” on short-RT incompatible trials if the prior is biased (Figure 10A), and no response bias if the prior is uniform (Figure 10B). Somewhat surprisingly, the spatial uncertainty model also predicts a “compatible” bias at short RT. The reason, as illustrated in Figure 10C, is a selection bias for noisy inputs that chance to concur on early-crossing trials (Figure 10D). In contrast, the conflict monitoring model predicts that while there is a “compatible” bias in both compatible and incompatible trials, they both bias toward “incompatible” for long-RT trials (Figure 10E) – this is due to the close coupling between compatibility and identity inference in this model (Figure 10F).

Figure 10.

Incidental compatibility discrimination. (A) For the compatibility bias model, biased prior results a in high fraction of compatible at all RT’s for compatible trials, as well as for short-RT incompatible trials, but this bias drops off sigmoidally toward 0 (correct answer) for increasingly longer RT incompatible trials. (B) Under equal priors, both compatible and incompatible trials start at probability .5 for very short RT trials, and then diverge symmetrically toward 1 and 0, respectively, as RT lengthens. (C) The pattern of compatibility responses in the spatial uncertainty model is very similar to (A), except that premature responses before stimulus onset are at chance. (D) The mean trace of the posterior probability of M being compatible for early-RT trials (RT < 40; blue) in the compatible condition is biased toward 1 early on, while that for late-RT trials (RT > 100; black) descend smoothly from .5 toward 0. (E) In the conflict detection model, compatibility detection is very similar between compatible (blue) and incompatible (black) trials. (F) The red and blue lines are RT distributions for compatible trials, in which the conflict measure does or does not exceed the conflict threshold, respectively. Magenta and cyan are the same distributions for truly incompatible trials. In both cases, trials that terminate before 95 timesteps tend not to exceed the conflict threshold, while those that terminate after do.

In a subtly, but critically, different variant, we can also explicitly interrogate the subjects about stimulus compatibility for fixed-duration stimuli (with no reference to the target stimulus identity), then both the compatibility bias and conflict monitoring models predict a bias for reporting compatible for short-RT incompatible trials (Figure 11A;B). In contrast, the spatial uncertainty model predicts a small but significant bias for reporting incompatible at short RT’s for both truly compatible and incompatible stimuli (Figure 11C). A more detailed discussion of this compatible bias can be found in Appendix B.

Figure 11.

Interrogative compatibility discrimination. For the compatibility bias and spatial uncertainty models, we assume that the subject reports “compatible” at interrogation time t if its posterior probability, P(M =C|X_t), exceeds .5 (and “incompatible” otherwise); for the conflict detection model, we assume the subject reports “compatible” at the interrogation time if the conflict threshold has not been exceeded, and “incompatible” otherwise. Both the compatibility bias (A) and conflict detection (C) models predict that there should be a strong bias at short interrogation times to report “compatible” for both truly compatible and incompatible trials, but that subjects increasingly report “incompatible” for longer viewing times in truly incompatible trials. (B) The spatial uncertainty model makes the very different different prediction that there should be a bias to report “incompatible” at short interrogation times for both truly compatible and incompatible stimuli, and that this bias fades for longer viewing times.

Neural Implementation and Conflict Monitoring

A growing body of work posits that neuronal activities may encode probabilistic information about the sensory world (Zemel, Dayan, & Pouget, 1998; Anderson, 1995; Rao, 2004; Sahani & Dayan, 2003; Weiss & J, 2002; Gold & Shadlen, 2002; Deneve, 2005; Ma, Beck, Latham, & Pouget, 2006; Yu, 2007), given the noisy, stochastic nature of sensory stimulation and neuronal processing. For the Eriksen task, Eq. 3 spells out the key probabilistic quantities that need to be kept track of over the course of a trial, as well as the way in which they need to be combined in order to correctly infer the properties of the stimulus of interest (s₂ in this case).

One potential neuronal implementation of these computations is directly suggested by the schematic diagrams in Figure 3. The first, “input” layer relays the bottom-up sensory information about the identity of the individual stimuli. The second, “hidden” layer computes the relative probability of all possible configurations of the stimulus array. The third, “output” layer integrates the information from the hidden layer and reports on the overall probability of the target stimulus being H or S. The computations and connectivity required are directly derivable from Eq. 3. The first term in the numerator of the computation of the joint posterior in Eq. 3 can be thought of as representing the bottom-up inputs. The second term represents self-excitation from the previous time-step. The final output is obtained by dividing by the sum of the un-normalized quantities, reminiscent of the divisive normalization commonly supposed to occur during visual processing (e.g. Carandini & Heeger, 1994,Yu02b) and in neural computations more generally (e.g. Schwartz & Simoncelli, 2001; O’Reilly & Munakata, 2000).

For the specific case of the Eriksen task, this neural representation seems possible. However, the Eriksen task is a relatively simple and constrained problem compared to the general class of perceptual discrimination problems faced by the brain. For instance, there can be many stimuli (n) in a visual scene, and each one of them can take on one of a large number (k) of possible configurations. Exact Bayesian inference requires the system to simultaneously entertain all possible interpretations of the visual display, and compute the relative probability of all possible (kⁿ) stimulus configurations. As the stimulus display becomes even moderately complex, this leads to a combinatorial explosion that would quickly exceed the representational capacity that the brain can devote to processing any given display. Thus, explicit implementation of the Bayesian optimal computations seems impractical for the general case. However, there may be approximations to these computations that are not subject to a combinatorial explosion as stimulus size increases, and that can be practically implemented by neural mechanisms. We consider one such possibility in the section that follows.

Conflict monitoring

Nature may have endowed the brain with an approximate solution that avoids the complexity. There is a growing body of empirical and theoretical work suggesting that the monitoring of conflict is a critical component of flexible cognitive control (Carter et al., 1998; M. M. Botvinick, Braver, Carter, Barch, & Cohen, 2001; Yeung, Botvinick, & Cohen, 2004). Conflict is typically thought of as the co-activation of competing or incompatible representations, and such conflicts recruit cognitive control mechanisms to select one alternative from the competing ones. Dorsal ACC has consistently been associated with processing conflict in a variety of tasks, including the Eriksen task (M. M. Botvinick, Cohen, & Carter, 2002; Yeung et al., 2004). In particular, the ACC appears to be more activated during an incompatible trial than a compatible one. The brain might use conflict monitoring as a proxy for compatibility inference, in an approximation to Bayes-optimal computations in the Eriksen task. The system could start with the assumption that stimuli are compatible (similar to the compatibility bias model described above), but also monitor the conflict level as inputs stream in. When excessive conflict is detected, the default assumption (that the stimuli are compatible) is revised, and the systems alters its subsequent integration strategy.

We formalize the neurally inspired approximate inference strategy by simplifying the inference algorithm. Although the inputs x₁, x₂, x₃ are still generated by the generative model of the compatibility bias model, the simpler inference model we employ will not longer represent compatibility explicitly. That is, we assume by default that the observations are generated by a compatible stimulus array (i.e. HHH versus SSS). The iterative Bayesian update rule simplifies to:

$$P(s_2=H\mid {\mathbf{X}}_t)=\frac{p(x_1(t)\mid s_1=H)p(x_2(t)\mid s_2=H)p(x_3(t)\mid s_3=H)P(s_2=H\mid {\mathbf{X}}_{t-1})}{{\sum }_{s=H,S}p(x_1(t)\mid s_1=s)p(x_2(t)\mid s_2=s)p(x_3(t)\mid s_3=s)P(s_2=s\mid {\mathbf{X}}_{t-1})}$$ (5)

The posterior probably of S is simply P(s₂ = S|X_t) = 1 − P (s₂ = H|X_t), and they are both initialized as P(s₂ = H) = P (s₂ = S) = .5, since H and S are equally prevalent. Compared to Eq. 3, the approximate posterior computation in Eq. 5 is significantly simpler. But while the inference algorithm no longer explicitly represents compatibility, it is still possible to recover useful information about compatibility from the simplified posteriors. Under the cooperative integration strategy detailed above, we expect that compatible flankers would cooperate with the target to provide relatively strong evidence for s₂ being either S or H per time step; whereas incompatible stimuli would conflict with each other and provide weaker overall evidence for s₂ either way. Thus, if we monitor a measure of how strongly the inputs favor one or the other hypothesis (the degree of conflict), then we could get an idea for trial compatibility as well.

One candidate for quantifying conflict is the cumulative entropy of the posterior distribution:

$$H_t=H_{t-1}-P(s_2=H\mid {\mathbf{X}}_t)logP(s_2=H\mid {\mathbf{X}}_t)-P(s_2=S\mid {\mathbf{X}}_t)logP(s_2=S\mid {\mathbf{X}}_t)$$ (6)

The entropy function attains its maximum at P(s₂ = H|X_t)= P (s₂ = S|X_t)= .5, when the inputs are likely in conflict with each other. It is minimal at P(s₂ = H|X_t)=0 or 1, when the inputs are likely in agreement with each other. Over time, the cumulative value of this function can be expected to rise more quickly for the incompatible condition than the compatible one. Thus, this measure could provide a proxy for inferring the compatibility of the stimulus array.

Another possibility is more closely related to instantiations of conflict proposed in previous models of conflict monitoring (e.g. M. M. Botvinick et al., 2001; Yeung et al., 2004): that is, equating conflict with the cumulative product of the posterior probabilities:

$$E_t=E_{t-1}+P(s_2=H\mid {\mathbf{X}}_t)P(s_2=S\mid {\mathbf{X}}_t)$$ (7)

The product, like the entropy, also attains its maximum when the two alternatives are equally probable at .5, and minimum when one or the other has probability 1. Figure 12A shows that both of these measures distinguish between compatible and incompatible conditions. In fact, their average traces evolve remarkably similar on the normalized scale in Figure 12A. Therefore, we use the second quantity E_t as the conflict measure, as the implementation of multiplication, compared to computing the entropy, is simpler and closer to the conflict measure used in previous models that have addressed both behavioral and neuroscientific findings (M. M. Botvinick et al., 2001; Yeung et al., 2004). We suggest that dorsal ACC may be the neural substrate for computing this conflict measure, and the predicted differential response to compatible and incompatible stimuli (Figure 12A) is consistent with the experimental observation of ACC response in the Eriksen task (M. Botvinick, Nystrom, Fissel, Carter, & Cohen, 1999).

Figure 12.

Conflict monitoring scheme as an approximation for compatibility bias. (A) Both the cumulative entropy measure of Eq. 6 and the product measure of Eq. 7 can distinguish between the compatible and incompatible trials. For each measure, the two traces are averaged over 5000 trials and divisively normalized by the maximum of the incompatible trace. (B) Short-RT incompatible trials alone have accuracy below chance. Reaction time for incompatible trials are longer on average and also more broadly distributed. (C) The “dip” in the posterior probabilities in the incompatible condition underlies the “dip” observed in behavior.

In this model, a cooperative integration strategy, appropriate for a compatible array, is assumed until the conflict measure exceeds some threshold, after which the competitive scheme, appropriate for an incompatible array, is assumed and the posterior computation changes to:

$$P(s_2\mid {\mathbf{X}}_t)\propto p(x_2(t)\mid s_2)P(s_2\mid {\mathbf{X}}_{t-1}).$$ (8)

For the simulations, we used .5 for the conflict threshold on the normalized scale of Figure 12A (15 on the un-normalized scale); performance is not very sensitive for a range of values of this threshold (details omitted). Consistent with our previous suggestion that the noradrenergic system mediates the detection of unexpected events that requires a change in processing strategy (Dayan & Yu, 2006), we propose here that norepinephrine may also be involved in the detection of unusual conflict levels that necessitate a change in the integration strategy of sensory inputs.

Note that we use only the central stimulus here, and ignore the flanker stimuli. Better performance could be achieved if we used the full expression in Eq. 3 and summed P(s₂ = H, M|X_t) and P(s₂ = S, M|X_t), since flankers provide useful information as long as they are integrated correctly (although as discussed above, Eq. 10 suggests that the flankers gradually become irrelevant over time, even in exact inference). As we are concerned with biological implementation, there are more reasons to believe that the visual system can control integration strategy by broadening or restricting the “spotlight” of spatial attention (Greenwood & Parasuraman, 1999), than by dynamically adjusting to arbitrarily complex patterns of stimulus processing.

Against this background of conflict monitoring and integration strategy control, we use the same decision rule as before: whenever P(s₂|X_t) exceeds the threshold q =.9 for either setting (s₂ = H or S), the corresponding perceptual decision is reported and the observation process is terminated.

Figure 12B shows that this approximate algorithm captures the main experimental findings as before. The parameters used to generate the noisy inputs are the same as those used in the simulation of the compatibility bias model; only the inference algorithm is different. The results are similar to those obtained in the compatibility bias model (Figure 4). This was expected, since this model is similar to taking the compatibility bias to an extreme value of 1 (though not identical). The main difference, as shown in Figure 12C, is that the rise in posterior probability for s₂ = H (correct answer) is slower for both compatible and incompatible trials than in the compatibility bias model, revealing the computational inefficiency induced by the approximation scheme.

Discussion

In this article, we presented a Bayesian analysis of performance in the Eriksen task. This analysis compares two possible explanations for the key behavioral data observed in this task, one involving compatibility bias, and the other spatial uncertainty. The compatibility bias model suggests that the task involves spatial arrangements that are atypical under a prior appropriate for normal scenes. The spatial uncertainty model emphasizes the spatial extent of visual receptive fields. We presented analytical and numerical results showing that both of these models can account for the basic compatibility effect, as well as the accuracy dip below chance for short-RT incompatible trials. We also showed how these models may be slightly modified to account for a range of additional factors that modify the compatibility effect, such as trial-to-trial adjustment, blocks of different compatible trial frequency, and spatial separation between target and flankers. In addition, we suggest a way of differentiating the two models using the novel experimental manipulation of asking subjects to report compatibility explicitly.

Due to the representational and computational complexity of Bayesian inference in general, we do not expect the brain to implement exact Bayesian computations in their full complexity. We therefore also considered a biologically motivated approximation to the compatibility model. This approximation relies on conflict monitoring as a proxy for the explicit processing of stimulus compatibility. We suggest it may be implemented in the anterior cingulate cortex, which has been shown previously to be preferentially activated by incompatible stimuli (compared to compatible), and which has been suggested to play a key role in cognitive control (Carter et al., 1998; M. M. Botvinick et al., 2001; Yeung et al., 2004). Our work represents a first example of a model explicitly using conflict monitoring for within trial adjustment of attentional control.

Upon detection of excessive conflict, the ACC needs to engage appropriate alterations across a wide swath of sensory, associative, and motor processing areas. Previously, we have suggested that the neuromodulator norepinephrine mediates the detection of unexpected events in the world, and engages appropriate adjustments in processing strategy (Dayan & Yu, 2006). Diffusely projecting neurons in the locus coeruleus, the source of cortical norepinephrine, show robust responses to novel stimuli, introduction of reward pairings, and extinction or reversal of these contingencies (Sara & Segal, 1991; Sara, Vankov, & Hervé, 1994; Vankov, Hervé-Minvielle, & Sara, 1995; Aston-Jones, Rajkowski, & Kubiak, 1997). Norepinephrine is also known to modulate the P300 component of ERP (Pineda, Westerfield, Kronenberg, & Kubrin, 1997; Missonnier, Ragot, Derouesné, Guez, & Renault, 1999; Turetsky & Fein, 2002), which has been associated with the processing of various types of violation of expectations: “surprise” (Verleger, Jaskowski, & Wauschkuhn, 1994), “novelty” (Donchin, Ritter, & McCallum, 1978), and “odd-ball” detection (Pineda et al., 1997). Given that locus coeruleus and anterior cingulate cortex have strong reciprocal connections, and moreover locus coeruleus projects diffusely to all cortical areas, the norepinephrine system seems ideally placed to play this signaling role.

Our work is related to a previous neural network model of the Eriksen task (Cohen et al., 1992; Servan-Schreiber et al., 1998). Through the interaction among input, attention, and output layers, this model was able to reproduce the main characteristics in the behavioral data cited here as well as a range of other effects. Under our normative framework, it is appropriate to ask about the relationship between this previous model and an algorithmic rendition of one of the Bayesian recognition models or their approximations. The earlier model is actually a close relative of the approximate conflict monitoring scheme proposed here, with influence over central discrimination from units representing the flankers being gradually suppressed over time. However, in the conflict model, the suppression is driven by the level of conflict, which reflects the probability that the stimulus array is incompatible. In the neural network model, the temporal dynamics of this suppression arose strictly from an interaction between activity in the input and attention layers.

This work is also related to our earlier work examining the representation and learning of statistical contingencies on a trial-to-trial basis (Yu & Dayan, 2005b). Based on a Bayesian optimality argument, and a large body of pharmacological, physiological, and behavioral data, it was proposed that the neuromodulators acetylcholine and norepinephrine carry specific uncertainty information and play a critical role in the statistical learning of the cue-target relationship. This is analogous to the learning about the relative frequency of compatible in the Eriksen task. In the current work, we assumed that for the most part that the subjects have already learned a stable representation of the generative parameters for the task. While we briefly touched upon the issue of trial-to-trial adjustments of compatibility prior in the sequential effects simulations, we did not fully integrate this with our earlier work on neuromodulatory control over statistical learning. One direction of our future work is to integrate these ideas more explicitly.

While we demonstrated in this work how our model accounts for a core set of experimental data on the Eriksen task, we leave for future work a rich set of additional findings such as the dissociable and additive effects of conflict at both sensory and response levels (B. A. Eriksen & Eriksen, 1974), and the effect of grouping due to color or contour (Baylis & Driver, 1992). Since we modeled the response as directly reflecting the sensory evidence accumulation process, without any intervening noise or delay, our models cannot accommodate sensory conflict in the absence of response conflict, nor vice versa. Likewise, our model would have to be extended to include a representation of color, contour, and object, in order to capture grouping effects.

It is worth noting that while the generative models for the compatibility bias and spatial uncertainty models were presented as rather distinct models, there is a formal relationship in the statistical assumptions underlying the computations. In some sense, overlapping receptive fields is a way to implement a spatial smoothness prior. It is reminiscent of a Gaussian process (Williams & Rasmussen, 1996), in which spatial smoothness is enforced through assumptions about localized spatial correlations underlying the noisy observations. Given the brain’s limited representational and computational capacity, it is optimal if its statistical assumptions are matched to the statistical regularities in the natural sensory environment. The key difference between the two models is really the representational level of “confusion” between the relevant and irrelevant stimuli/features. In the compatibility bias model, it is more cognitive in nature, possibly represented in the prefrontal cortex, and is accessible to explicit queries about compatibility. In the spatial uncertainty model, this confusion is implemented at a low-level, possibly in the visual cortex itself, and is inaccessible to explicit queries about compatibility. It should also be noted that the two explanations of compatibility bias and spatial uncertainty may be simultaneously applicable. The idiosyncratic behavior elicited in subjects for the Eriksen task may be due to both the spatial receptive field overlap in the visual cortex, and a compatibility bias implemented in higher-level control regions such as parietal or frontal areas.

The concepts developed in this work may shed light on a wider class of selective attention tasks. There are two main computational principles that have general significance. One is that attentional selection consists of dynamic interaction between top-down information, such as rules of selection, and bottom-up sensory inputs, which are noisy and imprecise at any given instant. For instance, in the Eriksen task, whether the flankers should exert a cooperative or competitive influence depends on whether the stimulus array is perceived to be compatible or incompatible. Another key concept is that when there are multiple, potentially conflicting stimuli within a visual scene, the simultaneous processing of the relationship among these stimuli is critical for the selective favoring of certain stimuli over others. The interaction between global processing associated with the structure of the stimulus array (e.g. compatibility in the Eriksen task), with local processing of individual stimulus features (e.g. S or H), together give rise to the particular temporal pattern of distractor interference seen in this class of selective attention experiments.

An obvious application of this general theory is the Stroop task, in which subjects are required to name the physical color of a word stimulus whose meaning may be either compatible or incompatible with the color. The Bayesian framework presented here can easily be extended to the Stroop case, in which the distractor inputs are not displaced spatially but modally. The compatibility bias model would then implement the prior bias that the stimulus properties across different dimensions of a single object (e.g. semantic and physical color) tend to be compatible or correlated. The spatial uncertainty model, more aptly the “modal” uncertainty model, would capture the idea that neurons responsive to color and semantics are corrupted by each other at the input level (Herd, Banich, & O’Reilly, 2006).

More broadly, most existing attentional models focus on mechanisms that explain the phenomenology of human performance at the behavioral level (e.g., how competition is resolved), sometimes constrained by specific information about underlying neural mechanisms (e.g. Reynolds, Chelazzi, & Desimone, 1999; McAdams & Maunsell, 2000) or more general principles of neural computation (e.g. Mozer & Behrmann, 1990; Cohen, Romero, Servan-Schreiber, & Farah, 1993). Building on a recent surge of Bayesian models of attention (Dayan & Zemel, 1999; Dayan et al., 2000; Yu & Dayan, 2005a) elucidating how the formal information processing demands of a selection task can themselves be directly responsible for behavior, we demonstrate here the applicability to task involving perceptual or response conflict, as well as potential neural mechanisms that implement the necessary computations.

Appendix A

Flanker Influence as a Function of Compatibility Prior

We first state and prove a proposition that shows formally the irrelevance of flankers when the compatibility prior is uniform (P(M =C)=P(M =I)=.5). We then show how a biased prior β > .5 leads to incorrect processing of the flankers after one or a few data samples, but that this effect can be overcome if the observation process continues indefinitely.

Proposition

Given the generative model specified in the text, including a uniform prior over compatibility (β =.5), the cumulative posterior probability over the central stimulus s₂ is independent of the flankers, such that P(s₂|X_t) only depends on the t samples of x₂ and not on x₁ or x₃.

Proof

For conciseness, we first introduce the notation: $g_{j,k}^t\triangleq p(x_k(1),\dots ,x_k(t)\mid s_k=j)$, where k ∈ {1, 2, 3}, j ∈ {H, S}. Given the generative model, we have the following

$$\begin{array}{l}p(s_2=H,{\mathbf{X}}_t)=p(s_2=H,M=C,{\mathbf{X}}_t)+p(s_2=H,M=I,{\mathbf{X}}_t)\\ =P(s_2=H,M=C)p({\mathbf{X}}_t\mid s_2=H,M=C)+P(s_2=H,M=I)p({\mathbf{X}}_t\mid s_2=H,M=I)\\ =.5\beta g_{H,1}^t{g}_{H,2}^t{g}_{H,3}^t+.5(1-\beta )g_{S,1}^t{g}_{H,2}^t{g}_{S,3}^t\end{array}$$

Similarly, we have $p(s_2=S,{\mathbf{X}}_t)=.5(1-\beta )g_{H,1}^t{g}_{S,2}^t{g}_{H,3}^t+.5\beta g_{S,1}^t{g}_{S,2}^t{g}_{S,3}^t$. Thus,

$$\begin{array}{l}P(s_2=H\mid {\mathbf{X}}_t)=\frac{p(s_2=H,{\mathbf{X}}_t)}{p(s_2=H,{\mathbf{X}}_t)+p(s_2=S,{\mathbf{X}}_t)}\\ =\frac{g_{H,2}^t(\frac{1-\beta }{\beta }\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}+1)}{g_{H,2}^t(\frac{1-\beta }{\beta }\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}+1)+g_{S,2}^t(\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}+\frac{1-\beta }{\beta })}\end{array}$$ (9)

It follows that when $\beta =(1-\beta )=.5,P(s_2=H\mid {\mathbf{X}}_t)=g_{H,2}^t/(g_{H,2}^t+g_{S,2}^t)$, which does not depend on s₁ or s₃; P(s₂ = S|X_t) = 1 − P(s₂ = H|X_t) is also independent of s₁ and s₃.

From Eq. 9, we also get some insight into the implications of a biased prior. In the limit as β → 1, the posterior after a few samples (small t), $P(s_2=H\mid {\mathbf{X}}_t)\to 1/(1+\frac{g_{S,2}^t}{g_{H,2}^t}\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t})$. Let us consider the incompatible case, s₂ = H, s₁ = s₃ = S: if the dependence of x_i on s_i are similar for i ∈ {1, 2, 3}, then the ratio inside the denominator would be greater than 1, and the posterior would be smaller than 0.5; the converse is true for s₂ = S, s₁ = s₃ = H. In general, this “dip” in the posterior toward the “wrong” direction for small t is present whenever there are at least two flankers (but not if there is only one).

When t → ∞, then regardless of the value of β, as long as it is not degenerate (0 or 1), $\frac{1-\beta }{\beta }\frac{g_{H,2}^t}{g_{S,2}^t}\to \infty$, and $\frac{1-\beta }{\beta }\frac{g_{S,k}^t}{g_{H,k}^t}\to \infty$, for k ∈ {1, 3}. We therefore have the following limit:

$$P(s_2=H\mid {\mathbf{X}}_t)\to \frac{g_{H,2}^t\frac{1-\beta }{\beta }\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}}{g_{H,2}^t\frac{1-\beta }{\beta }\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}+g_{S,2}^t\frac{g_{S,1}^t{g}_{S,3}^t}{g_{H,1}^t{g}_{H,3}^t}}=\frac{g_{H,2}^t\frac{1-\beta }{\beta }}{g_{H,2}^t\frac{1-\beta }{\beta }+g_{S,2}^t}=\frac{\frac{g_{H,2}^t}{g_{S,2}^t}\frac{1-\beta }{\beta }}{\frac{g_{H,2}^t}{g_{S,2}^t}\frac{1-\beta }{\beta }+1}$$ (10)

which is a quantity independent of the flankers, and itself goes toward 1. This implies that if the sensory observation process were to go on indefinitely, then the effects of the flankers and the prior compatibility bias would both disappear over time on an incompatible trial, leading to near-perfect discrimination.

Appendix B

“Incompatible” Bias for short RT Predicted by Spatial Uncertainty Model

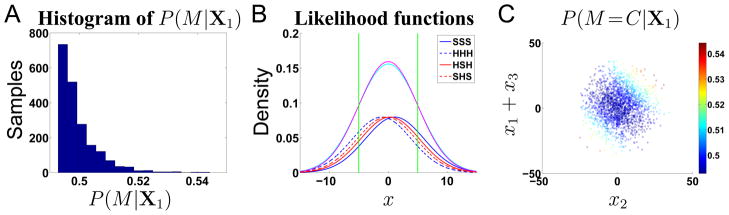
Figure B1 illustrates the explanation behind the apparent bias to report “incompatible” on short-RT interrogation trials in the spatial uncertainty model (Figure 11B). Figure B1A shows a histogram of the value of P(M =C|X₁) for 2000 trials. Although the mean of this distribution is .50, it is highly skewed, such that the majority of trials (67.5%) weakly favor “incompatible” (P(M =C|X₁) < .5), and a minority favor “compatible” (P(M =C|X₁) > .5). This skewed distribution and the consequent “incompatible” bias arises from the spatial smearing, as shown in Figure B1B. Due to the overlapping receptive fields, the pair of likelihood functions for compatible stimuli (blue solid and dashed lines) are spaced farther apart than the pair of (red solid and dashed lines) likelihood functions for incompatible ones. Consequently, the total evidence for incompatible (magenta), which sums up the red functions, is higher than that for compatible (cyan), which sums up the blue functions, in the middle portion, and lower on the two outer regions. The two green vertical lines demarcate the boundaries. When the observations are actually generated from one of the compatible stimulus conditions, notice that the majority of the mass fall into the region bounded by the green lines. Figure B1B is a schematic illustration of these ideas, and uses parameters that facilitates their visualization, rather than reflecting the actual parameters used in the simulations. Moreover, in the actual computations, the likelihood functions of the three p(x_i|s) need to be combined multiplicatively (if uniform prior over M is assumed), before they can be added to form the marginal posterior over M.

Figure B1.

Incompatibility bias in the spatial uncertainty model under interrogation. (A) The histogram for P(M =C|X₁) obtained from 2000 simulated trials is centered at .5 but highly skewed. The majority of trials (67.5%) weakly favor “incompatible” (P(M =C|X₁) < .5), and a minority favor “compatible” (P(M =C|X₁) > .5). (B) The red lines are the likelihood functions for x for the two incompatible stimuli types, and the blue lines are for the two compatible stimuli. Cyan and magenta are the sum of the compatible and incompatible likelihood functions, respectively. Most of the mass from any one of the four individual likelihood functions falls into the region bounded by the green lines, where the marginal posterior probability for incompatible is higher than compatible. (C) The marginal posterior P(M|X₁) favors incompatible (dark blue) for most of the samples, which are actually drawn from M =C (and s₂ = H).

Figure B1C shows the cause behind the incompatible bias in a slightly different way. It shows a scatter plot of samples of x₂ (horizontal axis), and x₁+x₃ (vertical axis), drawn from the distribution p(x|s₂ = H, M = I) (parameters same as in Figure 5). The color-scale corresponds to the posterior probability for compatible, P(M =C|X₁), for each of these samples. Note that the vast majority of samples fall around values for x₂ and x₁+x₃ that are close to 0, where the probability for compatible is below .5. Only a small fraction of the samples fall outside this broad, diagonal blue band, where the posterior probability for compatible is greater than .5.