A mixed-model approach for genome-wide association studies of correlated traits in structured populations

Abstract

Genome-wide association studies (GWAS) are a standard approach for studying the genetics of natural variation. A major concern in GWAS is the need to account for the complicated dependence-structure of the data both between loci as well as between individuals. Mixed models have emerged as a general and flexible approach for correcting for population structure in GWAS. Here we extend this linear mixed model approach to carry out GWAS of correlated phenotypes, deriving a fully parameterized multi-trait mixed model (MTMM) that considers both the within-trait and between-trait variance components simultaneously for multiple traits. We apply this to human cohort data for correlated blood lipid traits from the Northern Finland Birth Cohort 1966, and demonstrate greatly increased power to detect pleiotropic loci that affect more than one blood lipid trait. We also apply this to an Arabidopsis dataset for flowering measurements in two different locations, identifying loci whose effect depends on the environment.

Introduction

Most GWAS to date have been conducted using the simplest possible statistical model: a single-locus test of association between a binary SNP genotype and a single phenotype. Given that most traits of interest are multifactorial, this clearly amounts to model misspecification, and the resulting danger of biased results whenever there is non-independence (linkage disequilibrium) between causal loci (for example due to population structure) is well known^1,2,3. Much less attention has been devoted to the fact that phenotypes may also be correlated. Whenever multiple measurements are taken from individuals, the resulting phenotypes will be correlated because of pleiotropy, which is of direct interest, as well as shared environment and linkage disequilibrium, which are usually confounding factors. Taking these correlations into account is important not only because of the importance of understanding pleiotropy, but also because we may expect increased power compared to marginal analyses. Intuitively, correlated traits amount to a form of replication. The importance of correlated phenotypes becomes even clearer when we consider measurements across environments. The canonical example here is an agricultural field experiment using inbred lines, a setting in which no one would consider analyzing phenotypes from different environments independently of each other, because the whole point of the study is to separate genetic from environmental effects and identify genotype-environment interactions. In human genetics, disentangling genetic and environmental effect is also of obvious interest, although much more challenging as the environment usually cannot be experimentally manipulated⁴.

There is a long history of multi-trait models in quantitative genetics^5,6,7,8,9, but these methods have rarely been applied to GWAS. In this paper we demonstrate how a standard linear mixed model from animal breeding¹⁰ may be used to model correlated traits while at the same time correcting for dependence among loci (e.g., due to population structure). As designs like cohort studies become more prevalent, the need for modeling correlated traits as well as population structure will grow^2,11,12, and the same is true for the increasing number of non-human GWAS ^{13,14,15,16,17}.

The mixed model, which handles population structure by estimating the phenotypic covariance that is due to genetic relatedness, or kinship, between individuals, has previously been shown to perform well in GWAS^{2,13,18,19,20,21,22}. Here we extend this approach to handle correlated phenotypes by deriving a fully parameterized multi-trait mixed model (MTMM) that considers both the within-trait and between-trait variance components simultaneously for multiple traits (Online Methods), and implementing it for GWAS. The idea is not new^{23,24,25,26,27}, but it has never been applied for association mapping on a genome-wide scale. Alternative approaches for GWAS in multiple traits exist, but they generally fail to control for population structure^28,29, and often are not applicable to genome-wide data.

We validate our approach using extensive simulations based on available SNP data from A. thaliana³⁰, demonstrating that our model increases power to detect associations while controlling the false discovery rate. We then demonstrate its usefulness by considering correlated blood lipid traits from the Northern Finland Birth Cohort 1966 (NFBC1966)³¹, and environmental plasticity in an A. thaliana data set that contains flowering measurements for two simulated growth seasons in two different locations³². Finally, we discuss its utility, not only in terms of increasing power to detect associations, but also in terms of understanding the basic genetic architecture of the phenotypes.

RESULTS

Simulations

Pairs of correlated phenotypes were simulated by adding phenotypic effects to genome-wide SNP data from A. thaliana³⁰. A single randomly selected SNP was set to account for up to 2% of the phenotypic variance, but with the possibility of different effects in each of the two phenotypes (see below). In addition, 10,000 SNPs were given much smaller effects to simulate the genetic background. A randomly chosen fraction of these background SNPs was shared between the two phenotypes, allowing for variation in the degree of phenotypic correlation (Supplementary Fig. 1, Online Methods).

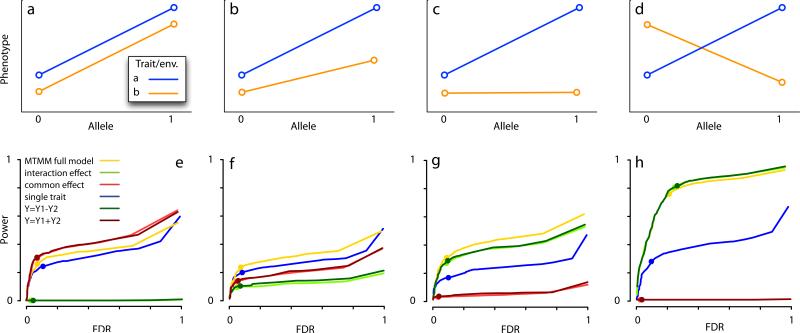
We compared our ability to identify the focal locus using MTMM and marginal, single-trait analyses (using the smallest p-value from the latter to ensure a fair comparison). Three different tests were used: a full test that compares the full model, including the effect of the marker genotype and its interaction, with a model that includes neither; an interaction effect test that compares the full model to one that does not include interaction, and finally; a common effect test that compares a model with a marker genotype to one without (see Online Methods for details). As expected, the results depended strongly on the effect of the focal polymorphism (Fig. 1). When it had the same effect in both phenotypes (i.e., positive pleiotropy or a common effect across environments; see Fig. 1a), MTMM performed slightly better than the single trait mixed model (MM) regardless of whether we tested for full model fit, or just for a common effect (Fig. 1e). The reason for this is the increased power that results from analyzing the traits together. Testing for an interaction effect alone is pointless as no interaction exist.

Figure 1.

Simulation results. (a–d) illustrate the scenarios simulated: (a) positive pleiotropy, alt. common effect across environments; (b) positive pleiotropy, alt. common effect across environments, with size of effect differing between traits/environments; (c) effect only on one trait, alt. only in one environment; (d) negative pleiotropy, alt. opposite effect across environments. (e) shows the estimated relationship between power and false discovery rate (FDR) using six different statistical tests (see text and Online Methods) for the scenario described in (a). (f) shows the estimated relationship between power and false discovery rate (FDR) for the scenario described in (b). (g) shows the estimated relationship between power and false discovery rate (FDR) for the scenario described in (c). (h) shows the estimated relationship between power and false discovery rate (FDR) for the scenario described in (d). Dots on curves denote nominal Bonferroni-corrected 5% significance thresholds. Note that both power and FDR are calculated with respect to the single focal locus, only.

When the effect of the polymorphism is slightly weaker in one trait/environment (Fig. 1b), testing for a full model fit using MTMM again outperforms single-trait analyses (Fig. 1f). Testing only for a common or interaction effect using MTMM is also less effective. Although an interaction effect now exists, it is too weak to be detected. However, as the strength of the interaction effect increases (Figs. 1c,d), it becomes possible to detect directly, and the relative advantage of using MTMM increases dramatically (Figs. 1g–h).

An alternative to carrying out two marginal single-trait analyses might be to combine the phenotypes, e.g., by fitting the traits principal components or their sum or difference. We tested the latter and as might be expected, this approach works very well when the focal SNP has exactly the same (or the opposite, when using the difference) effect on the phenotype (Fig. 1a,d). However, if the effect of the SNPs differs between the two traits, MTMM outperforms these approaches (Fig. 1b–c).

It should be noted that, because the background SNPs are correlated due to population structure, simple single-locus tests of association are strongly biased towards false positives, just like in the original data¹⁴. The mixed model effectively removes this bias, regardless of whether we analyze one phenotype at a time using a single trait MM or both simultaneously using MTMM (Supplementary Fig. 2). However, analyzing these data with methods that do not take population structure into account is clearly not a realistic option (Supplementary Fig. 3).

In addition to the model just described, we simulated an oligogenic scenario in which each phenotype was determined by 20 loci, each of which could, with equal probability: affect that phenotype only; affect both phenotypes in the same way, or; affect both phenotypes but in opposite ways. The behavior of each locus was chosen independently, and the resulting distribution of correlations between the phenotypes was thus centered around zero (Supplementary Fig. 4), which is very different from the positively correlated phenotypes generated under the first simulation scenario (Supplementary Fig. 1). MTMM is intended for correlated phenotypes, and is expected to perform less well when phenotypes are weakly correlated. The oligogenic simulation results supported this intuition. For weakly correlated pairs of phenotypes, single-trait analysis often outperformed MTMM (especially for detecting SNPs with effect in one phenotype only), however, for more strongly correlated phenotypes, the results agreed with those presented above in that MTMM always outperformed marginal analyses (Supplementary Fig. 5). Note that the correlation does not have to be positive: for negatively correlated phenotypes, MTMM has relatively higher power to detect SNPs with the same effect in both phenotypes, whereas for positively correlated phenotypes, it performs best for SNPs that have opposing effects (note that it may sometimes make sense to simply change the direction of correlation by negating one of the phenotypes when analyzing real data).

As noted in the introduction, an advantage of MTMM is that it can be used for correlated phenotypes regardless of whether the phenotypes represent different measurements (and the correlations are due to pleiotropy), or the same trait measured in different environments (cf. Fig. 1a–d). However, the simulations above assume that the phenotypic correlations are solely due to genetics, not environment, and this is only likely to be true for studies involving inbred lines in controlled environments. Certainly correlations between pleiotropic traits will reflect environment as well as genotype. To verify that MTMM is able to separate these effects, we simulated another 5,000 pairs of correlated traits using the 10,000locus model, but now with correlations reflecting environmental as well as genetic covariance (see Online Methods). Both the environmental and genetic correlations were well estimated (Supplementary Fig. 6), although it should be noted that the residuals of the genetic and environmental correlation estimates are negatively correlated (Supplementary Fig. 6d). The accuracy of these estimates does affect the performance of GWAS, but the effect appears to be relatively minor (Supplementary Fig. 7).

Pleiotropy in human data

To illustrate the utility of MTMM for traits that are correlated because they are part of the same biological system, we reanalyzed data from the Northern Finland Birth Cohort 1966 (NFBC1966)³¹ (see Online Methods for details). We focused on measurements of four blood metabolites that are strongly involved in cardiovascular heart disease³³, namely triglycerol (TG), low-density lipoprotein (LDL), high-density lipoprotein (HDL), and C-reactive protein (CRP). These metabolites are significantly correlated, and MTMM analysis indicates that the correlations are caused by genetics as well as environment (Table 1), supporting the notion that these traits are mechanistically related and/or have linked causal loci. For HDL/CRP and TG/CRP the correlations of the genetic effects are in the opposite direction of the environmental correlations. However, in these cases, the genetic correlations are not significantly different from zero, and it is likely that the phenotypic correlations driven primarily by the shared environment.

Table 1.

MTMM estimates of correlation and heritability in the NFBC 1966 data

		Genetic			Environmental
	Phenotypicα	corr.	SE	pval	corr.	SE	pval	Heritabilityβ
HDL/TG	-0.37	-0.42	0.14	0.024	-0.36	0.06	1:58 × 10-8	0.38/0.18
HDL/LDL	-0.13	-0.19	0.11	0.085	-0.09	0.08	0.26	0.39/0.45
HDL/CRP	-0.19	0.24	0.23	0.25	-0.34	0.06	1:50 × 10-7	0.39/0.14
TG/LDL	0.32	0.31	0.14	0.062	0.35	0.06	9:64 × 10-7	0.19/0.44
TG/CRP	0.21	-0.50	0.39	0.115	0.34	0.05	3:19 × 10-9	0.18/0.13
LDL/CRP	0.09	0.08	0.19	0.65	0.10	0.06	0.12	0.45/0.13

^αDirect estimates of the Pearson correlation are identical to the precision given.

^βThe SE of all heritability estimates is between 0.05 and 0.06. Single-trait estimates are: 0.38 (HDL), 0.18 (TG), 0.45 (LDL) and 0.13 (CRP).

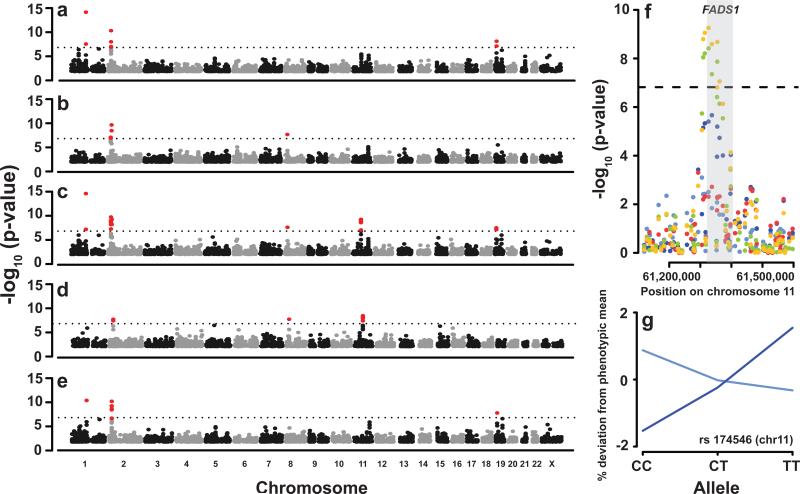
In terms of associations, the results from the joint analysis of TG and LDL suffice to illustrate how two of our main predictions were borne out. First, almost all SNPs that were found to be significantly associated in the marginal analysis of either LDL or TG were also significant in the joint analysis (Table 2). However, MTMM arguably provides greater insight into the nature of the associations, as it reveals interaction effects. Second, MTMM finds associations that the marginal analyses do not. In particular, for positively correlated phenotypes such as TG and LDL, we expect MTMM to have much greater power to detect polymorphism whose effects differ greatly between the phenotypes. A nice example of this is the FADS1-FADS2 locus, which was not significant in either marginal analysis, but becomes highly significant using MTMM thanks to a very strong interaction effect (Table 2 and Fig. 2). These genes are excellent candidates, and were mentioned in the previous analysis of the NFBC1996 data³¹. Strikingly, they were also identified in a massive meta-analysis involving more than 100,000 individuals³⁴, which furthermore reported opposite effects on TG and LDL, in agreement with the strong interaction effect we observe (Fig. 2g) using a sample of only 5,000 individuals.

Table 2.

SNPs detected in the analysis of LDL and TG using a genome-wide significance of 0.05

		MTMM(p-valueα)			EMMAX(p-valueα)
SNP	Position	full test	interaction	common	LDL	TG
CELSR2 region, chromosome 1
rs611917	109616775	6.42 × 10-8	3.19 × 10-3	7.72 × 10-7	1.80 × 10-8	0.46
rs646776	109620053	2.48 × 10-15	1.42 × 10-6	3.28 × 10-11	3.92 × 10-15	0.77
APOB region, chromosome 2
rs10198175	20997364	6.32 × 10-7	0.02	1.33 × 10-6	9.48 × 10-8	0.29
rs3923037	21011755	6.39 × 10-9	0.13	2.64 × 10-9	2.72 × 10-7	7.17 × 10-7
rs6728178	21047434	9.57 × 10-10	0.11	4.37 × 10-10	7.95 × 10-8	1.81 × 10-7
rs6754295	21059688	1.31 × 10-9	0.14	4.97 × 10-10	7.10 × 10-8	4.12 × 10-7
rs676210	21085029	2.43 × 10-9	0.04	2.56 × 10-9	7.23 × 10-7	9.21 × 10-8
rs693	21085700	1.80 × 10-10	0.19	5.00 × 10-11	2.84 × 10-11	2.79 × 10-3
rs673548	21091049	1.63 × 10-9	0.04	1.85 × 10-9	5.97 × 10-7	6.43 × 10-8
rs1429974	21154275	4.85 × 10-7	0.02	1.06 × 10-6	7.69 × 10-8	0.24
rs754524	21165046	5.30 × 10-8	0.02	1.39 × 10-7	7.83 × 10-9	0.17
rs754523	21165196	4.51 × 10-7	0.02	1.01 × 10-6	7.15 × 10-8	0.24
GCKR region, chromosome 2
rs1260326	27584444	5.33 × 10-10	2.10 × 10-8	7.73 × 10-3	0.21	1.87 × 10-10
rs780094	27594741	5.98 × 10-9	4.22 × 10-8	0.01	0.44	3.15 × 10-9
LPL region, chromosome 8
rs10096633	19875201	2.42 × 10-8	2.04 × 10-8	0.06	0.97	1.93 × 10-8
FADS1 region, chromosome 11
rs174537	61309256	1.60 × 10-9	9.02 × 10-9	0.01	6.82 × 10-6	3.81 × 10-3
rs102275	61314379	8.79 × 10-10	6.20 × 10-9	4.86 × 10-3	4.13 × 10-6	3.82 × 10-3
rs174546	61326406	5.52 × 10-10	3.83 × 10-9	4.88 × 10-3	3.69 × 10-6	3.12 × 10-3
rs174556	61337211	2.56 × 10-9	4.43 × 10-8	1.93 × 10-3	2.03 × 10-6	0.01
rs1535	61354548	2.08 × 10-9	1.35 × 10-8	0.01	6.04 × 10-6	4.96 × 10-3
rs2072114	61361791	8.77 × 10-8	7.31 × 10-7	4.77 × 10-3	1.59 × 10-5	0.03
LDLR region, chromosome 19
rs11668477	11056030	3.16 × 10-8	0.15	1.18 × 10-8	3.89 × 10-9	0.02
rs2228671	11071912	7.20 × 10-8	5.30 × 10-4	4.87 × 10-6	4.47 × 10-8	0.96

^αP-values below the Bonferroni-corrected 5% cut-off of 1.5 × 10^-7 are highlighted in red.

Figure 2.

GWAS of LDL and TG. (a–b) Manhattan plots for the marginal, single-trait analyses of LDL(a) and TG(b), respectively. (c–e) Manhattan plots for the joint MTMM analyses: (c) full model; (d) interaction effect, and; (e) common effect. The dashed horizontal line denotes the 5%Bonferroni adjusted genome-wide significance level. (f) Closeup of the FADS1-FADS2 region on chromosome 11. The points for the single-trait analyses are shown in light (TG) and dark blue (LDL), while the point for MTMM are shown in orange (full test), light green (interaction effect), and red (common effect). The gray shading denotes the FADS1 gene region. (g) Estimated phenotypic effect of the rs174546 SNP in light (TG) and dark blue (LDL).

The other five trait combinations gave similar results (Supplementary Tables 1-5). Almost all SNPs that were identified using single-trait analysis were also detected using MTMM, either due to a strong common or strong interaction effect. In addition, MTMM also detected two more regions that were not identified using marginal analyses. First, the gene PPP1R3B was identified due to strong common effects in the joint analyses of HDL and CRP, and HDL and TG. These pairs of phenotypes are negatively correlated (Table 1), so we expect MTMM to have increased power to detect common effects. The association with PPP1R3B was not found in previous analyses of these data³¹, but was reported (and confirmed) in the much larger meta-analysis of blood lipids³⁴. Second, the TOM40-APOE region was identified in the joint analysis of TG and CRP, this time due to an interaction effect (TG and CRP are positively correlated). Albeit not quite significant, this association was noted in the previous analysis of these data³¹, and was also found in the meta-analysis³⁴.

G × E in A. thaliana data

The other natural application for MTMM is when phenotypes are correlated because they represent the same trait measured in different environments. In such a setting, we are often directly interested in finding genes that are involved in the differential response to the environment, i.e., genotype-by-environment (G × E) interactions. We tested this application using a data set from A. thaliana in which flowering time was measured (for a global collection of naturally occurring inbred lines) in environmental control chambers for two simulated seasons (“Spring” and “Summer”) and two simulated locations (“Spain” and “Sweden”)³². Flowering time varies in a clinal manner, and is generally thought to be important in local adaptation. It is thus both natural and interesting to try identifying genes that are responsible for the differential flowering response to different environments³².

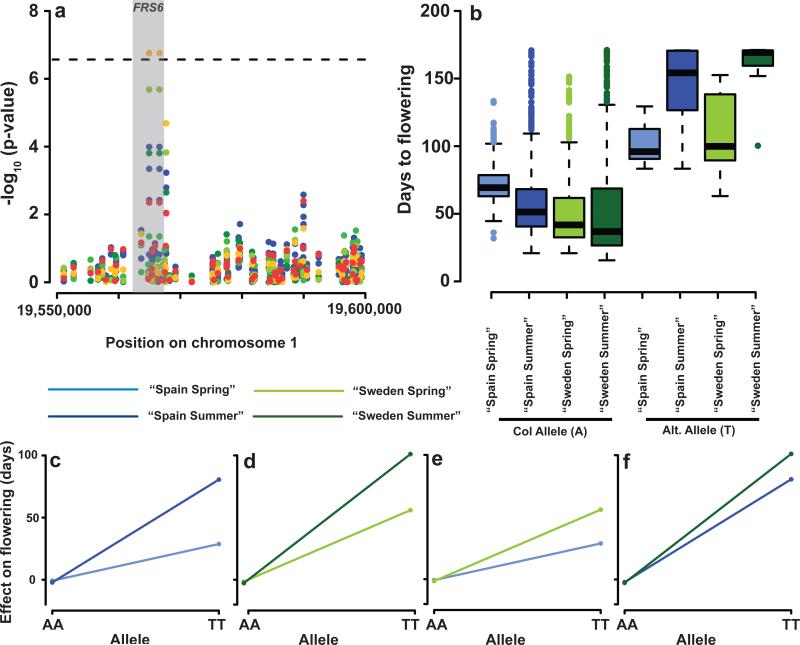
We analyzed the A. thaliana data using a full 2 × 2 factorial model, i.e., in addition to estimating the effect of genotype, season, and location, we have two pairwise interaction terms (see Online Methods and Supplementary Note). The results are summarized in Figure 3 (for details, see Supplementary Figures 8-9 and Supplementary Tables 6-7). Perhaps surprisingly, we found very few interaction effects. Out of a total of 41 significant SNP associations, only three appeared to be due to interactions. A rare allele (MAF = 4 % ) on chromosome 5 was identified as a significant genotype-by-season effect, but it does not correspond to any obvious candidate (Supplementary Fig. 10). A more convincing example was provided by the two tightly linked and perfectly correlated SNPs on chromosome 1. These were identified by comparing the full model to one without interaction terms, although the interaction with the simulated season seems to be strongest (Fig. 4). The minor allele (MAF = 3 %) is associated with delayed flowering (Fig. 4b), but the effects depends strongly on the season, and is much more pronounced in the (simulated) summer. Interestingly, both SNPs are in the coding region of the gene FRS6, which is known to be involved in the phyA-mediated response to far-red light³⁵. T-DNA knockout lines of this locus have an early-flowering phenotype, the magnitude of which depends on day length (one of the factors that vary between the simulated seasons).

Figure 3.

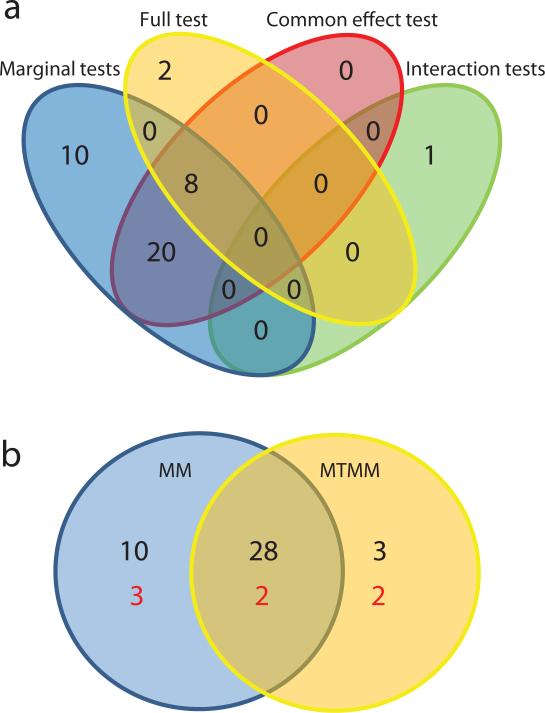
Venn diagrams summarizing the GWAS of A. thaliana flowering data³². (a) Classification of the 41 significant SNPs according to the test(s) in which they were significant. (b) Classification of the 41 SNPs (black) and corresponding gene regions (red) according to whether they were found using marginal (MM) or joint (MTMM) analysis.

Figure 4.

Summary of FRS6 results. (a) Closeup of a 50kb region on chromosome 1 showing significant G _ E associations. The gene FRS6 is highlighted in gray. The results for the four marginal analysis (using a single trait MM) are shown in blue, while the MTMM results are shown in orange (full test), light green (three-way interaction), green (genotype by location), dark green (genotype by season), and red (common effects).(b) Phenotypic distribution as a function of experimental condition and genotype. (c–f) Plots contrasting the allelic effect in different comparisons: (c) the effect of the season in ‘Spain’; (d) the effect of the season in ‘Sweden’; (e) the effect of the location in ‘Spring’; (f) the effect of the location in ‘Summer’. The effect depends strongly on the season within each location (c–d) and less strongly on location with season (e–f).

Of the remaining 38 SNPs, 28 we found by both marginal and joint analysis (as common effects), and 10 were found only by marginal analysis. While our simulations would seem to suggest that MTMM should always have higher power than marginal test, even for detecting common or unique effects, this is clearly not always the case. The phenotypes analyzed here are extremely highly correlated as well as heritable (all coefficients typically well above 0.9; see Supplementary Table 6). In such cases, the advantage of increasing the sample size through joint analysis does not necessarily outweigh the cost of a more complex model with more degrees of freedom.

DISCUSSION

We have shown how the classical mixed model from breeding may be used for GWAS of correlated phenotypes in structured populations, often providing greater statistical power than marginal analyses. However, we emphasize that our approach is much more than an ad hoc method for increasing power. The model we use effectively dates back to Fisher³⁶, and can be derived from basic genetic principles under the assumption that heritable phenotypic variation is due to very large numbers of genes of very small effect (Online Methods). Assuming that this is a reasonable approximation (and it seems to be, for a growing number of traits), we can disentangle genetic correlations from environmental correlations, whenever these uncorrelated. This allows us to address fundamental questions about the nature of variation. When applied to traits that may be biologically related the resulting variance component estimates allow us to assess the level of pleiotropy without estimating effects of individual loci. Using data from different human blood lipids, we demonstrated how the phenotype covariance can be decomposed into genetic and environmental terms, suggesting that most of these traits are indeed correlated due to shared genetics (i.e., they are pleiotropic or due to causal sites in linkage disequilibrium). A similar approach was recently used by Price et al.³⁷ to assess the heritability of RNA expression levels within and across human cell tissues.

Irrespective of this, we also demonstrated increased power, detecting several interesting loci affecting human blood lipid level that were not significant in the single trait analysis, but that have all been replicated in GWAS studies using much larger sample sizes. This finding alone strongly argues for routine application of our method to correlated phenotypes.

As an example of how the method can be used to detect environmental interactions, we applied our method to an A. thaliana flowering time dataset, where the plants had been phenotyped under four different environmental conditions (in a classical 2times2 factorial design). These phenotypes are highly correlated as well as highly heritable, and the estimated variance components suggest that there is in fact very little difference between the environments at the genetic level (Supplementary Table 6). Hence, it is arguably not surprising that we detected little in terms of interaction effects. While it is of course possible that we simply do not have the power to detect interactions, it is notable that analogous studies in maize have also failed to detect large G × E interaction effects³⁸. The result from A. thaliana and maize are strikingly different from what has been reported for mouse³⁹, yeast⁴⁰, and even humans⁴, but the reason for these differences are far from clear given the dramatically different study designs.

Full factorial designs with replicated genotypes are of course not possible in most organisms; however, we note that MTMM does not require this. Indeed, a mixed-model approach has previously been proposed for estimating G × E variance components in humans²⁵ (using a special case of our model in which heritabilities are assumed to be equal across environments; see Online Methods). Either approach is directly applicable to human data.

Although we have focused on relatively simple pairwise correlations in this paper, it is easy to model more than two phenotypes using MTMM. Conceptually we believe that extending this to larger multi-trait experiments should allow for greater benefits in estimating error terms and elucidating functional relationships between suites of traits. However for such complex models, the computational complexity grows fast and the results become increasingly difficult to interpret compared to sequential two-trait analyses.

This is a well-known problem in statistics and quantitative genetics, but MTMM has the additional caveat that it assumes that the increasingly complex covariance structure, which is estimated in the absence of fixed effects, remains constant as these are added. Various intermediate approaches are possible, e.g. variance components might be estimated using a full model once, followed by GWAS using sub-models: more work in this area is clearly desirable.

Finally, when the phenotypes are not correlated, or if the correlation is not due to genetics (something that can be deduced from the variance component estimates), a single trait mixed model will generally have greater power to detect causal loci that are phenotype-specific.

When, precisely, this will be the case is hard to predict, however, we suggest using the MTMM approach as a complement to rather than replacement for marginal GWAS. The advantages are clear: it allows the detection of both interactions and pleiotropic loci in a rigorous statistical framework, while simultaneously accounting for population structure.

URLs

MTMM has been implemented in a set of R scripts (MTMM) for carrying out GWAS. They rely on the software ASREML⁴¹ for the estimation of the variance components. The scripts can be obtained at https://cynin.gmi.oeaw.ac.at/home/resources/MTMM.

ONLINE METHODS

Theory

Multiple traits mixed model

Following Henderson¹⁰ we can write the mixed model for the phenotypes of n individuals as

$$\mathbf{y}=X\beta +\mathbf{g}+\mathbf{e},$$ (1)

where y is a vector of the n phenotype values. In this notation, the trait mean is included, together with other fixed effects, in the design matrix X. The β are the effect sizes of the fixed effects, $\mathbf{g}\sim N(0,{\sigma }_g^{2}K)$ is a random effect, and $\mathbf{e}\sim N(0,{\sigma }_e^{2}I)$. It follows that the covariance matrix for the trait values, y, is

$$\text{var}\left(\mathbf{y}\right)={\sigma }_g^{2}K+{\sigma }_e^{2}I,$$ (2)

Where K is a n×n kinship or relatedness matrix. If we consider two traits, y₁,y₂ measured on the same set of individuals, then under the mixed model for the k ’th phenotype follows the partitions of the variance accordingly, i.e., $\text{var}\left({\mathbf{y}}_k\right)={\sigma }_{gk}^{2}K+{\sigma }_{ek}^{2}I$. However, for the covariance matrix between the two phenotypes it is not obvious what the appropriate model is. Henderson⁴² suggests the following covariance model:

$$\text{cov}({\mathbf{y}}_1,{\mathbf{y}}_2)={\sigma }_{g1}{\sigma }_{g2}{\rho }_{g}K+{\sigma }_{e1}{\sigma }_{e2}{\rho }_{e}I,$$ (3)

where ρ_g captures the genetic correlation between two phenotypes and the term ρ_e captures the correlation caused by shared environment and other non-genetic sources of correlations. We can generalize this for phenotypes which have been measured for different sets of individuals (see Supplementary Note).

Estimating the variance parameters

The estimation procedure for the variance components is described in the Supplementary Note.

Application to GWAS

Similar to EMMAX² or P3D²⁰ we estimate the covariance matrix only once to re-estimate a scalar in front of it for every marker. This fixes five degrees of freedom out of six in total (maximum number of variance components for two traits. For a pair of traits (the i ’th and j ’th traits), the proposed approximation effectively assumes that the three variance ratios (σ_gi/σ_ei,σ_gj/σ_ej and σ_gi/σ_gj) and the two correlations ρ_gij and ρ_eij are fixed with and without the marker in the model.

With multiple traits we can search for causal loci with common effects (across all traits) as well as trait specific loci or loci with opposite effects in different traits. Depending on what we are interested in, a GLS F-test can be constructed to compare two models. For two traits we can write the single marker model as follows:

$$\mathbf{y}=\left[\begin{array}{c}\hfill {\mathbf{y}}_1\hfill \\ \hfill {\mathbf{y}}_2\hfill \end{array}\right]={\mathbf{s}}_1{\mu }_1+{\mathbf{s}}_2{\mu }_2+\mathbf{x}\beta +(\mathbf{x}\times {\mathbf{s}}_1)\alpha +\upsilon ,$$ (4)

where x is the marker and s_i is a vector with 1 for all values belonging to the i’th trait and 0 otherwise. The ψ ~ N(0,cov(y)) is a random variable capturing both the error and genetic random effects. Depending on what kind of loci we are interested in, we propose three different F-tests tests:

• The full model tested against a null model where β = 0 and α = 0. This identifies both loci with common and differing effects in one model, but suffers in power from the extra degree of freedom.

• To identify common genetic effects we propose to test the genetic model (α = 0) against a null model where β = 0 and α = 0.

• Finally, to identify differing genetic effects between the traits we propose to test the full model against a null model where α = 0.

As both the interaction test and the common effect test are sensitive to scaling of the phenotype values, we propose to normalize them either by the total variance, or the genetic variance (as obtained in the marginal trait analysis). To minimize multiple-testing problems, one could, for example, carry out GWAS using the full model and use the other tests in post hoc analysis of significant loci.

Extending this model for arbitrary number of traits is straight-forward (one example for the analysis of four traits is described in the Supplementary Note). However, when there are more than two traits in the model, the number of possible tests grows quickly. An interesting special case is when there are several environmental variables in a factorial study design, in which case each environmental variable can be included in the model instead of the term ${\sum }_{i=1}^t{\mathbf{s}}_i{\mu }_i$, and their interactions with the genotype could replace the term $\mathbf{x}\left({\sum }_{i=1}^t{\mathbf{s}}_i\alpha \right)$. This can result in a simpler and a more tractable model than if all possible combinations of environments were treated as independent.

Genotype-environment interactions

Given two measured phenotype vectors, y₁and y₂,Yang et al.²⁵ include a G × E random effect in a mixed model as follows:

$$\mathbf{y}=\left[\begin{array}{c}\hfill {\mathbf{y}}_1\hfill \\ \hfill {\mathbf{y}}_2\hfill \end{array}\right]=X\beta +u_G+u_{G\times E}+\mathbf{e},$$ (5)

where u_G,u_G×E are random effects and have covariance matrices

$$\text{cov}\left(\left[\begin{array}{c}\hfill {\mathbf{y}}_1\hfill \\ \hfill {\mathbf{y}}_2\hfill \end{array}\right]\right)=\text{cov}\left(u_G\right)+\text{cov}\left(u_{G\times E}\right)+\text{cov}\left(\mathbf{e}\right)={\sigma }_G^2\left[\begin{array}{cc}\hfill K_{11}\hfill & \hfill K_{21}\hfill \\ \hfill K_{12}\hfill & \hfill K_{22}\hfill \end{array}\right]+{\sigma }_{G\times E}^2\left[\begin{array}{cc}\hfill K_{11}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill K_{22}\hfill \end{array}\right]+I.$$ (6)

Compared to the model proposed in equation (4), this model implicitly assumes two things: that there are no environmental correlations; and that the heritabilities are the same in each environment, i.e., $h_1^2=h_2^2$. As the individuals are different in each environment, the first assumption is appropriate. However, the second assumption is not guaranteed to hold in general, and we therefore propose relaxing it.

Simulations

10,000-locus model

We simulated 2,000 pairs of correlated phenotypes using a model under which the phenotypes consisted of one randomly chosen SNP with a “large” (additive) effect, accounting for up to 2% of the total phenotypic variance, and 10,000 randomly chosen SNPs with small additive effects. The effects sizes were drawn from a normal distribution and scaled to fix the trait heritability to 0.95. To ensure variation in trait correlations, all trait pairs shared a random fraction of the 10,000 causal loci, with the fraction drawn from a uniform distribution. The four phenotypic models were distinguished by different effect-correlations at the major locus (Fig. 1).

In addition, we simulated 5,000 pairs of correlated traits with environmental correlations. We fixed the heritability to 0.5 and allowed the genetic correlation to vary from -1 to 1. Additionally, we added a shared environmental term to the model, mimicking scenarios for both negative and positive environmental correlation.

20-locus model

We also simulated 1,000 pairs of correlated phenotypes using a 20-locus model. Each phenotype was determined by 20 loci, using a multinomial distribution, we randomly assigned to three categories with equal probabilities: i) SNPs with same effect in both phenotypes; ii) SNPs with opposite effect in the two phenotypes, and; iii) SNPs with effect in one trait only. The SNPs had additive effects drawn from an exponential distribution. Finally, the effect sizes were scaled to fix the heritabilities to 0.95. To obtain a single p-value for two traits the smaller of the two p-values for each SNP from the marginal mixed model analysis was retained.

Power calculations

For the calculation of the power and FDR, any significant SNP within 50 kb of a (or the) causal SNP was classified as a true positive; otherwise it was a false positive. The results are almost independent of the window size used (Supplementary Fig. 11). More important is the effect of the causal SNP(s). The nearly two-fold increase of power observed at a FDR of 0.1 in Figure 1 depends on the effect size of the simulated SNP (Supplementary Fig. 12). Throughout this paper, we used the single-analysis Bonferroni-corrected 5% significance threshold.

Human data

We used the 1966 North-Finland Birth Cohort (NFBC1966) which consist of phenotypic and genotypic data for 5,402 individuals³¹. Using the exact same dataset as was used in², after their filtering the dataset consisted of 5,326 individuals and 331,475 SNPs. To expedite the mapping, the unknown genotypes (< 1% in the dataset) were imputed by replacing missing values with the average genotypic value. Neither the marginal MM analysis nor the MTMM tests show evidence of population structure confounding (Supplementary Fig. 13).

Analysis of A. thaliana data

The genotype data for A. thaliana consisted of 1,307 individuals genotyped at 214,051 SNPs using a custom Affymetrix SNP chip³⁰. The phenotypes used were measurements of flowering time for 459 accessions³². Flowering time was measured in plants grown in four different environments, a factorial setting with two simulated seasons (“Spring” and “Summer”) and two simulated locations (“Spain” and “Sweden”). Analyzing the four phenotype vectors together we can derive five different F-tests (see Supplementary Note). Neither of these tests shows evidence of confounding due to population structure (Supplementary Fig. 14).