Realistic enzymology for post-translational modification: zero-order ultrasensitivity revisited

Abstract

Unlimited ultrasensitivity in a kinase/phosphatase “futile cycle” has been a paradigmatic example of collective behaviour in multi-enzyme systems. However, its analysis has relied on the Michaelis-Menten reaction mechanism, which remains widely used despite a century of new knowledge. Modifying and demodifying enzymes accomplish different biochemical tasks; the donor that contributes the modifying group is often ignored without the impact of this time-scale separation being taken into account; and new forms of reversible modification are now known. We exploit new algebraic methods of steady-state analysis to reconcile the analysis of multi-enzyme systems with single-enzyme biochemistry using zero-order ultrasensitivity as an example. We identify the property of “strong irreversibility”, in which product re-binding is disallowed. We show that unlimited ultrasensitivity is preserved for a class of complex, strongly-irreversible reaction mechanisms and determine the corresponding saturation conditions. We show further that unlimited ultrasensitivity arises from a singularity in a novel “invariant” that summarises the algebraic relationship between modified and unmodified substrate. We find that this singularity also underlies knife-edge behaviour in allocation of substrate between modification states, which has implications for the coherence of futile cycles within an integrated tissue. When the enzymes are irreversible, but not strongly so, the singularity disappears in the form found here and unlimited ultrasensitivity may no longer be preserved. The methods introduced here are widely applicable to other reversible modification systems.

1. Introduction

Zero-order ultrasensitivity first emerged as a property of a so-called “futile cycle”, in which a substrate exists in two states, unphosphorylated or phosphorylated, inter-converted by a forward-modifying kinase and a reverse-demodifying phosphatase (Figure B.1A). Mathematical analysis shows that, under conditions of enzyme saturation, in which the enzymes operate in the zero-order regime, the steady-state proportion of modified substrate exhibits unlimited ultrasensitivity to changes in enzyme concentrations, [10]. That is, the dose-response resembles a Hill function, whose Hill coefficient can be made arbitrarily large by increasing the saturation of the enzymes by the substrate. Zero-order ultrasensitivity has been found in vitro in the control of metabolic enzymes, [16, 20]. The extent to which ultrasensitivity is unlimited remains unclear as does its significance in vivo, as we review in the Discussion, but this motif remains widely influential as a paradigm of how novel functionality emerges through collective behaviour in multi-enzyme systems, [4, 11, 17, 21, 26, 34].

Figure B.1. Time-scale separations and enzyme mechanisms.

(A) A schematic of a GK loop with phosphorylation as the modification showing substrate in unmodified form, S₀, and modified form, S₁, with forward and reverse enzymes in green. The donor (ATP) and its hydrolysis products (ADP, Pi), shown in blue, are assumed to be buffered to fluctuations in demand by the metabolic processes that replenish ATP. A similar scheme would hold for other reversible, small-molecule modification (methylation, acetylation, ADP-ribosylation, etc) but not for ubiquitin-like modifications, which require a cascade of enzymes. (B) Examples of reaction mechanisms built up from the three basic reactions in (5), with those for the forward enzyme, E, on the left and those for the reverse enzyme, F, on the right. The reverse enzyme has a dead-end, or unproductive, intermediate complex, Y₆, which is reversibly formed. The top row shows two reversible mechanisms, in which the relevant product can be re-converted back to substrate. The other two rows illustrate ways in which these reversible mechanisms can become irreversible (middle row) or strongly irreversible (bottom row), with the corresponding irreversible reactions highlighted in magenta.

We stress that there is nothing futile about a futile cycle. Unlike metabolic enzymes that frequently operate reversibly close to thermodynamic equilibrium, [27], modification and demodification enzymes are able to maintain substrate states far from equilibrium through dissipative mechanisms, either largely unmodified (“off”) or largely modified (“on”). Such energy expenditure is essential for cellular information processing and decision making, [25]. To avoid further suggestions of futility, we refer from now on to the “GK loop”, in honour of Goldbeter and Koshland, who built upon the earlier work of Chock and Stadtman, [29].

While ultrasensitivity had been found previously in biological systems, most notably in allosteric proteins, [23], the unlimited ultrasensitivity in the GK loop is a striking feature. Other forms of ultrasensitivity are limited by intrinsic properties, such as the number of binding sites, rather than by expression levels, which can be regulated on a physiological time scale. The GK loop exhibits regulatable ultrasensitivity, whose unlimited extent suggests flexibility for cellular information processing. We focus particularly on understanding how this unlimited ultrasensitivity arises. In practice, substrate concentrations cannot be increased indefinitely, so the unlimited extent of the ultrasensitivity cannot be utilised in any given system. However, there is an important difference between knowing that a system has a maximum Hill coefficient of 10 versus an unlimited Hill coefficient. Experimental measurements that gave a Hill coefficient of 11 would be implausible in the former case but not in the latter. We also examine another aspect of the GK loop, which is the allocation of substrate between modification states, where we find analogous behaviour to zero-order ultrasensitivity. The extent of these behaviours and how they are determined by the enzyme mechanisms are central to understanding how the GK loop behaves in experimental contexts.

Nearly all analyses of the GK loop have assumed a Michaelis-Menten reaction mechanism for both kinase and phosphatase: a single intermediate enzyme-substrate complex is reversibly formed, which then irreversibly breaks down to release enzyme and product,

$$E+S\underset{b}{\overset{a}{\rightleftharpoons }}Y\stackrel{c}{\to }E+P.$$ (1)

Here, a, b, c ∈ ℝ_>0 are the positive rate constants for mass-action kinetics. This mechanism was put forward in 1913 for the enzyme invertase, [22], and remains surprisingly popular, despite a great deal of new knowledge, [1, 3, 30, 9]. Enzymes may have multiple intermediates and the forward and reverse enzymes have distinct mechanisms, as they accomplish distinct biochemical functions. In particular, the forward enzyme has two substrates, the one not usually mentioned being the donor for the modification (ATP, in the case of phosphorylation). While it may be reasonable to assume that donor molecules can be ignored dynamically, they can still give rise to more intermediates than in (1) because of the order of substrate binding. There is a surprising lack of discussion of such issues in the current literature and one purpose of the present paper is to begin reconciling the modern analysis of multi-enzyme systems with classical single-enzyme biochemistry.

Phosphorylation is only one of several forms of reversible modification that are now known. Others include, for instance, methylation, acetylation, palmitoylation, ADP-ribosylation and ubiquitin-like modifications, [35, 25], which may have distinct enzyme mechanisms. Our analysis applies to many of these. While post-translational modification of protein substrates has been particularly studied in the context of ultrasensitivity, our analysis is not restricted to these and substrates may be small molecules or even reversibly methylated DNA.

We exploit new methods of algebraic steady-state analysis, developed in our laboratory, that are particularly relevant for reversible modification, [12, 31, 32]. The methods introduced in [31] enable the highly nonlinear reaction network of modification and demodification, with realistic enzyme mechanisms, to be treated as if it is linear, at steady state. This enables calculations to be undertaken that were previously intractable. Biochemical rate constants are treated as undetermined symbols, whose numerical values do not need to be known in advance, thereby avoiding issues of parameter estimation and model identification and permitting mathematical analysis instead of numerical simulation. These methods are widely applicable to more complex systems of reversible modification.

2. Results

2.1. Enzymology of modification and demodification

We discuss the enzymology of reversible modification in general and specialise to the case of the GK loop in subsequent sections. Reversible modifications may be subdivided into two classes: those using small-molecule modifications, such as phosphorylation, methylation, acetylation, ADP-ribosylation etc, and those using ubiquitin-like modifications, such as ubiquitin itself as well as SUMO, NEDD, etc, [35]. The biochemistry is fundamentally different in each class, [25]. For small-molecule modification, the donor molecules are synthesised through intermediary metabolism. In the case of phosphorylation, for instance, the phosphoryl-donor, ATP, is the central energy currency of the cell, and in the case of methylation, the methyl-donor is SAM (S-adenosine methionine), a byproduct of folate biosynthesis. In contrast, for ubiquitin-like modifications, the donor molecules are polypeptides synthesised by gene transcription. Furthermore, small-molecule modification and demodification are usually catalysed by single enzymes, while ubiquitin-like modification requires a cascade of several enzymes. For reasons explained below, the current analysis has to be restricted to modifications in the first class.

We make two time-scale separation assumptions that provide the basis for the mathematical analysis that follows. There is limited experimental evidence for either assumption. This does not necessarily mean that the assumptions are invalid but, rather, that they have not yet been tested experimentally. These assumptions are habitually taken for granted in analysing reversible modification systems, although they are not always made explicit. In the absence of relevant data, it is best to think of them as convenient initial hypotheses that enable analysis and to focus on the conclusions that can be drawn from them.

As a dissipative process, reversible modification is driven by the excess in concentration of the donor over its hydrolysis products. We make the first basic assumption that the relevant metabolic processes are able to maintain the donor and its hydrolysis products at constant concentration, despite fluctuations in demand for the donor (Figure B.1A). This amounts to an assumption about time-scales: the metabolic processes are assumed to operate sufficiently fast with respect to the time scale on which demand changes. There is evidence for such buffering in phosphorylation, where it may seem reasonable because ATP is used for so many different cellular processes, but little is known about the extent of buffering for other reversible modifications. SAM, for instance, is also used for DNA methylation, which could dominate methylation demand at times of DNA synthesis.

Since the donor and its hydrolysis products are buffered, they no longer have to be treated as dynamical variables and their effects can be absorbed into the rate constants. For instance, if an intermediate enzyme-substrate complex, Y₁, binds ATP to form a ternary complex, Y₂, the corresponding reaction can now be summarised

$$Y_1\stackrel{k}{\to }{Y}_2.$$ (2)

Here, the rate constant k includes an implicit contribution from ATP, k = k′[ATP], where k′ is the actual rate constant for the underlying two-substrate reaction,

$$Y_1+\mathit{ATP}\stackrel{k^{\prime }}{\to }{Y}_2,$$

and [AT P ] is the buffered, constant concentration of the donor.

There is, however, the further problem of the order in which substrates bind to form the ternary complex. This can either be random or follow a compulsory order. If ATP binds second, the conversion reaction in (2) can be used after substrate binding,

$$S+E\to Y_1\to Y_2.$$ (3)

However, if ATP binds first, it reversibly creates a new enzyme form,

$$E+\mathit{ATP}\underset{k_{-}}{\overset{k_{+}}{\rightleftharpoons }}E-\mathit{ATP}.$$

We make the second time-scale assumption that binding of donor molecules to enzymes is sufficiently fast that it can be considered to be independently at equilibrium. In this case, [E-ATP] = k_A[ATP][E], where k_A = k₊/k₋ is the association constant for the equilibrium. Formation of the ternary complex in the reaction

$$S+E-\mathit{ATP}\stackrel{k_1}{\to }{Y}_2$$

can now be rewritten

$$S+E\stackrel{k_2}{\to }{Y}_2$$ (4)

where k₂ = k₁k_A[AT P ]. With a compulsory-order mechanism, either (3) or (4) can be used, depending on the order. With a random-order mechanism, both (3) and (4) are needed.

Enzyme mechanisms may have multiple intermediates for reasons other than donor binding. For instance, tyrosine phosphatases use a substituted enzyme mechanism in which the phosphate group is transiently attached to a cysteine residue before being hydrolysed, [3], while protein kinases may also go through multiple stages of catalytic transformation, [1]. Intermediates can be identified by the transient, stopped-flow techniques introduced by Britton Chance, [5], who was the first to characterise an intermediate complex and to measure the individual rate constants, a, b and c, in mechanisms like (1). For a modern treatment and several examples, see [2].

With the time-scale assumptions introduced above, a class of enzyme mechanisms can be constructed from the following three basic reactions: creation of an intermediate complex from a substrate form (ie: a modification state) and free enzyme; break-up of an intermediate complex to yield a substrate form and free enzyme; and conversion of one intermediate to another,

$$E+S_i\to Y_j,Y_j\to E+S_i,Y_j\to Y_k.$$ (5)

Here, S_i, S_j denote substrate forms. In the case of the GK-loop, there are only two, the unmodified form, S₀, and the modified form, S₁, but the ideas can be applied more generally to substrates with many modification states, [31].

There are two significant restrictions in (5). First, only one enzyme can participate in a mechanism. This rules out ubiquitin-like modifications, which rely on a cascade of enzymes. It may be possible to bring such cascades within the scope of this analysis, and this is work in progress, but this paper is focussed on small-molecule modifications that can be accommodated by the basic reactions in (5). Second, the scheme in (5) does not allow for two-substrate, double-displacement (substituted enzyme) mechanisms, such as ping-pong mechanisms, [6]. This is relevant only to forward enzymes, which have two substrates. Protein kinases that act on serine, threonine and tyrosine residues typically follow single-displacement mechanisms, [1]. Double-displacement mechanisms for reverse enzymes, which have only a single substrate (ignoring, as is customary, the ever present H₂O), are accommodated by (5).

The scope of (5) can be summarised as follows. First, it allows for currently-known protein kinases, [1], and phospho-protein phosphatases, [3]. This includes the histidine-aspartate two-component systems found in eubacteria, plants and fungi, which use a phospho-transfer mechanism in which ATP binds first in a compulsory order, [30]. Second, it may cover other forms of reversible small-molecule modification (methylation, acetylation, etc) but much less is known about the corresponding enzymatic mechanisms. Third, it does not cover some non-protein kinases, such as nucleoside diphosphate kinase, which use a two-substrate double-displacement mechanism, [6]. Such enzymes are usually involved in biosynthesis (flux) rather than signalling (information), for which substrate concentration may be less significant.

The reaction scheme in (5) could be generalised by explicitly including modifiers and allowing substrate to bind to modifier-bound intermediates and not just to free enzyme. This would allow for double-displacement mechanisms. However, the algebraic details are considerably more complicated and we restrict attention in the present paper to the reaction scheme in (5), with the limitations just noted.

Enzyme mechanisms are allowed to be made up from any “sensible” combination of the basic reactions in (5), no matter how complex. Some examples are shown in Figure B.1B. The forward enzyme, E, has a bi-bi mechanism with random order substrate binding and random-order product release. The reverse enzyme, F, has a uni-uni mechanism with two main intermediates, along with an unproductive, “dead-end” complex. A sensible mechanism is, informally, one that does not prejudice the formation of a steady state. For instance, there should be no irreversible formation of a dead-end complex, since that would act as a sink from which substrate could never be recovered. The dead-end complex in the examples in Figure B.1B is always reversibly formed.

The formal definition of “sensible” requires some new concepts that are introduced next. The technical detail can be found in [31] but it is helpful to introduce them in a broader context that has emerged in subsequent work, [12], and which will be used again in analysing the GK loop itself.

2.2. The linear framework

We consider a labelled, directed graph, G, with vertices, 1, · · ·, n, edges, $i\stackrel{k}{\to }j$, and no self-loops, i ↛ i. The vertices represent components (ie: chemical entities) in a biochemical system. A dynamics is defined on these components by treating each edge as if it were a chemical reaction under mass-action kinetics, with the label as rate constant. For the moment, the labels are symbolic positive real numbers, k ∈ ℝ_>0. Since each edge has a unique source, each reaction is first-order and the dynamics is therefore linear. If x_i denotes the amount (or concentration) of matter at vertex i, then the dynamics can be described by the matrix equation

$$\frac{dx}{dt}=\mathcal{L}(G).x$$ (6)

where x ∈ ℝⁿ and 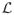(G) is called the Laplacian matrix of G. Our interest is in steady states of the dynamics, where dx/dt = 0, or, equivalently, x ∈ ker 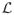(G). (For more background; see [12].)

A key observation is that if G is strongly connected then dim ker 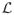(G) = 1, [31, Lemma 1]. No matter how the dynamics is initiated, with arbitrary amounts of matter at each vertex, once a steady state is reached (and some steady state is always reached), only one degree of freedom is left: if x_i is known for some i then x_j is fixed for all j ≠ i. This remarkable rigidity is the essence of the method used here.

The Matrix-Tree Theorem (MTT), [31, 33], provides a formula for calculating x_j in terms of x_i (Appendix). The MTT shows that, at steady state, x_j/x_i is a rational expression in the labels. That is, x_j/x_i is a ratio of two polynomials, each of which is a sum of products of labels.

So far, this discussion has been entirely linear. Nonlinearity is introduced through the labels. In applying the linear framework to a biochemical network, the labels are allowed to be complex algebraic expressions involving rate constants of actual reactions or concentrations of actual chemical species. For instance, k = (a₁[X₁]+a₂[X₂])a₃[X₃] is a legitimate label, where a₁, a₂, a₃ are rate constants and X₁, X₂, X₃ are species. The one essential restriction is that if a species X appears in a label, it cannot correspond to a component in the graph. This is the “uncoupling condition”. In an application, not all the species in the actual network may be components in the graph; those that are not in the graph are allowed to appear in the labels. The framework can be applied when a labelling can be found that satisfies the uncoupling condition such that the steady states of the linear Laplacian dynamics in (6) coincide with the steady states of the nonlinear dynamics of the actual network. It is important to note that this coincidence does not have to extend from the steady states to the transient dynamics. If it did, the system would be linear. All that is required is that the steady states of the two systems coincide. Dynamical nonlinearity with simple rate constants can thereby be traded for dynamical linearity with complex labels, at steady state. Such a trade-off is highly beneficial, as it allows complete calculation of the steady states of the nonlinear system.

As an illustration, we construct the graph for the reversible forward mechanism in Figure B.1B, as shown in Figure B.2A. The details are similar for any enzyme mechanism. The vertices of this graph are the intermediate complexes and the free enzyme. The edges are derived from the reactions. For substrate-binding reactions, which correspond to the edges outgoing from vertex E, the labels are compound expressions of the form k_*[S_*]. For all other reactions, the labels are simple rate constants, k_*. Since the substrates S_* are not components in the graph, the uncoupling condition is satisfied. It is shown in [31] that, with this labelling, the steady states of the linear Laplacian dynamics in (6) coincide with the steady states of the intermediate complexes and the free enzyme in the full nonlinear dynamics. It is not difficult to check this for the particular reaction mechanism in Figure B.1B but it holds in generality, no matter how complex the reaction mechanism, as long as it is based on (5), [31].

Figure B.2. Hierarchical application of the linear framework.

(A) The reversible mechanism for the forward enzyme E is shown together with the corresponding labelled, directed graph on the intermediates, Y₁, · · ·, Y₄, and the free enzyme, E. Reactions between intermediates, such as edges k₇ and k₈, or release of enzyme from an intermediate, such as edges k₂ and k₄, become edges in the graph, with the rate constant as the label. Substrate-binding to form an intermediate becomes an edge from E to that intermediate, with the substrate concentration becoming part of the label, as highlighted in blue. (B) Labelled, directed graph on the substrate forms. The labels are complex algebraic expressions derived hierarchically from the graphs for the underlying reaction mechanisms, as explained in the text. Note that both graphs are strongly connected.

A reaction mechanism is “sensible” when its graph is strongly connected. In this case, the MTT can be applied to calculate the steady state concentrations of the enzyme forms. Since intermediate complexes usually release enzyme eventually, strong connectivity is a natural condition. The exception might be a dead-end complex, as mentioned above, but as long as this is reversibly formed, strong connectivity is preserved.

Enzymologists are familiar with this construction in the guise of the King-Altman procedure, [6, 15], which is equivalent to the Matrix-Tree Theorem, [31]. It is, however, more productive to see it as one application of the linear framework just described, which has far wider applications than to enzyme mechanisms, [12], including the analysis of multi-enzyme reversible modification systems, as explained below.

2.3. Steady-state analysis of the enzyme mechanisms

To explain the analysis of enzyme mechanisms, it may be helpful to see how it works for the simple case of the Michaelis-Menten mechanism in (1). In this case, the graph is

which is sufficiently simple that its steady state can be calculated without appealing to the MTT, to give

$$[Y]=\frac{[S][E]}{K_M},$$ (7)

where [−] denotes steady-state concentration and K_M = (b + c)/a is the classical Michaelis-Menten constant. Formula (7) is the basic algebraic relationship that underlies the Michaelis-Menten rate formula, [6].

If the enzyme mechanism is built up from the reactions in (5) and the corresponding strongly-connected, labelled, directed graph is constructed, then the MTT yields similar steady-state formulas (Appendix). This works irrespective of the complexity of the reaction mechanism. For instance, for the reversible reaction mechanisms in Figure B.1B, the steady state concentrations of the intermediates are given by

$$[Y_i]=\{\begin{array}{ll}\frac{[S_0][E]}{K_{i,0}^E}+\frac{[S_1][E]}{K_{i,1}^E}\hfill & \text{for}1\le i\le 4\hfill \\ \frac{[S_0][F]}{K_{i,0}^F}+\frac{[S_1][F]}{K_{i,1}^F}\hfill & \text{for}5\le i\le 7\hfill \end{array}$$ (8)

The $K_{\ast ,\ast }^{\ast }$ in (8) are “generalised Michaelis-Menten constants” (gMMC) that relate each intermediate to the substrates and products in the reaction mechanism (Appendix). Since both S₀ and S₁ can contribute to the intermediates, two gMMCs are needed, one for each substrate form. (Irreversibility leads to simplifications, as discussed in the next sections.) The gMMCs are rational expressions in the underlying rate constants, like K_M = (b + c)/a for (7), but they can become a good deal more complicated. If the graph of the reaction mechanism has n vertices, then the polynomials in $K_{\ast ,\ast }^{\ast }$ have degree n − 1 (Appendix).

Depending on the reaction mechanism, it is possible that one or the other substrate form may not contribute to an intermediate. In this case, the corresponding term in (8) will be absent and there is no associated gMMC. However, it is helpful to indicate this by taking the gMMC to be infinite, $K_{\ast ,\ast }^{\ast }=\infty$, which has the effect of killing the term. This is merely a shorthand for saying that the term does not appear in (8); gMMCs, when they exist, are always finite, positive quantities, $K_{\ast ,\ast }^{\ast }\in {\mathbb{R}}_{>0}$.

In writing formulas like (8), we shall refer to the particular examples of reaction mechanisms in Figure B.1B. However, it should be understood that the formulas hold in general for any sensible reaction mechanisms made up from the reactions in (5). The examples in Figure B.1B allow the concepts to be made clear without having to introduce the more abstract notations of [31].

2.4. Steady-state analysis of the GK loop

Knowing the steady-state concentrations of the intermediates, the contributions of each enzyme in the GK loop can be calculated. There are two pathways to form S₁ from S₀. The direct pathway is through the forward enzyme E, which has two ways to do this, using intermediate Y₃, with rate constant k₉, and using intermediate Y₄, with rate constant k₁₃. From (8), the total rate of S₁ formation (by which we mean d[S₁]/dt) through this direct pathway is

$$\left(\frac{k_9}{K_{3,0}^E}+\frac{k_{13}}{K_{4,0}^E}\right)[S_0][E].$$

Only the gMMCs for S₀ are relevant for the production of S₁ from S₀. The second pathway is through the reverse enzyme F, operating in reverse. Y₅ is the only intermediate that yields S₁, which it does with rate constant k₁₆, so the rate of S₁ formation through this reverse pathway is

$$\left(\frac{k_{16}}{K_{5,0}^F}\right)[S_0][F].$$

As previously, only the gMMC for S₀ is relevant. The total rate for forming S₁ from S₀ is then the sum over these two pathways, which may be summarised as

$$(c_0^E[E]+c_0^F[F])[S_0].$$ (9)

Here, $c_{\ast }^{\ast }$ is a “total generalised catalytic efficiency” (tgCE), [31, 6], given by

$$c_0^E=\frac{k_9}{K_{3,0}^E}+\frac{k_{13}}{K_{4,0}^E}\text{and}{c}_0^F=\frac{k_{16}}{K_{5,0}^F}.$$ (10)

Catalytic efficiencies are well known to enzymologists as the ratio of the catalytic rate constant to the Michaelis-Menten constant, [6]. For our purposes, a similar generalised quantity may be calculated for any intermediate that releases product and the tgCE is then the sum over all intermediates that can yield the relevant substrate form, as in the formulas above. It is important to note, when dealing with realistic mechanisms, that product release and catalysis may not occur in the same step, unlike (1). Although we continue to use the phrase “catalytic efficiency”, what is relevant here is product release, which may, or may not, also correspond to catalysis. Just like gMMCs, tgCEs are rational expressions in the underlying rate constants. The steady-state rate of formation of S₀ from S₁ can now be calculated in a similar way to be

$$(c_1^F[F]+c_1^E[E])[S_1],$$ (11)

where the tgCEs can be read off from the reaction mechanism as

$$c_1^F=\frac{k_{21}}{K_{7,1}^F}\text{and}{c}_1^E=\frac{k_4}{K_{1,1}^E}+\frac{k_2}{K_{2,1}^E}.$$ (12)

A striking aspect of the formulas in (9) and (11) is that they are linear in the substrate forms. It is as if the formation of S₁ from S₀ takes place linearly with rate constant $c_0^E[E]+c_0^F[F]$ while the formation of S₀ from S₁ has rate constant $c_1^F[F]+c_1^E[E]$. This is a general feature of any reaction mechanism and it is precisely what is required to exploit the linear framework once again. We can construct a new labelled, directed graph in which the vertices are the substrate forms, S₀ and S₁ and there is an edge between them whenever some enzyme is able to convert the source vertex to the target vertex (Figure B.2B). Note that more than one enzyme may contribute to an edge. Each edge acquires a label coming from formulas like (9) and (11). Because the enzymes are not components of the graph of substrate forms, that graph also satisfies the uncoupling condition. Furthermore, it is shown in [31] that, with this labelling, the steady states of the linear, Laplacian dynamics in (6) correspond to the steady states of the full nonlinear biochemistry of the substrate forms under the relevant reaction mechanisms. Finally, the substrate graph in Figure B.2B is evidently strongly connected. These assertions hold in complete generality for reversible modification systems with multiple types of modifications, multiple sites and multiple modifying and demodifying enzymes, no matter how complex the reaction mechanisms, [31]. We exploit this here for the special case of the GK loop, which has only two substrate forms but potentially many components in total because of the realistic biochemistry.

2.5. Irreversibility yields an invariant

The strategy for analysing the GK loop is to focus on the two substrate forms and to eliminate as many of the other components as possible. There are three general properties that provide a systematic way to do this. First, the system is at steady state, implying that the flux from S₀ to S₁ is balanced by the return flux from S₁ to S₀. Second, the enzymes are neither synthesised nor degraded and are hence conserved over time. Third, the substrate is neither synthesised nor degraded and is hence also conserved over time. In this and the next section, we exploit the first two properties, and then bring in the third. In this section, we use the reversible mechanisms for E and F in Figure B.1B as running examples.

Because the graph on the substrate forms recapitulates the steady state of the full system, as outlined above, it follows from Figure B.2 that, at steady state,

$$\frac{[S_1]}{[S_0]}=\frac{c_0^E[E]+c_0^F[F]}{c_1^F[F]+c_1^E[E]}.$$ (13)

Since the forward enzyme E is conserved, it follows that

$$E_{\mathit{tot}}=[E]+[Y_1]+\cdots +[Y_4],$$ (14)

where E_tot is the total amount of enzyme in the system. Although this is constant during the dynamics, it is determined by the initial conditions and subject to change between experiments, unlike the rate constants. Using (8), this can be rewritten as,

$$E_{\mathit{tot}}=\left(1+\left(\frac{1}{K_{1,0}^E}+\cdots +\frac{1}{K_{4,0}^E}\right)[S_0]+\left(\frac{1}{K_{1,1}^E}+\cdots +\frac{1}{K_{4,1}^E}\right)[S_1]\right)[E].$$ (15)

It is then natural to introduce a total gMMC (tgMMC) for each substrate form, so that (15) can be summarised as

$$E_{\mathit{tot}}=\left(1+\frac{[S_0]}{K_0^E}+\frac{[S_1]}{K_1^E}\right)[E],$$ (16)

where the tgMMC resembles the harmonic mean of the individual gMMCs for all the intermediates,

$$K_{\ast }^E={\left(\frac{1}{K_{1,\ast }^E}+\cdots +\frac{1}{K_{4,\ast }^E}\right)}^{-1}.$$ (17)

Similar formulas hold for the reverse enzyme, F,

$$F_{\mathit{tot}}=\left(1+\frac{[S_1]}{K_1^F}+\frac{[S_0]}{K_0^F}\right)[F],\text{where}{K}_{\ast }^F={\left(\frac{1}{K_{5,\ast }^F}+\cdots +\frac{1}{K_{7,\ast }^F}\right)}^{-1}.$$

We can now divide E_tot by F_tot to arrive at the equation

$$\frac{E_{\mathit{tot}}}{F_{\mathit{tot}}}=\left(\frac{1+[S_0]/K_0^E+[S_1]/K_1^E}{1+[S_1]/K_1^F+[S_0]/K_0^F}\right)\left(\frac{[E]}{[F]}\right).$$ (18)

Equations (13) and (18) involve only the two substrate forms, S₀ and S₁, and the two free enzymes, E and F. The intermediates have been eliminated, courtesy of (8). The next step is to eliminate the enzymes. Equation (18) is expressed in terms of the single variable [E]/[F ] rather than the two variables [E] and [F ] separately. Equation (13) can be brought into a similar form, which allows [E]/[F ] to be eliminated. This can be done in generality but we will focus in the present paper on a special case that is motivated by the following definition.

A reaction mechanism is said to be irreversible if there is no route by which the product can be re-converted back to substrate. There may be many ways in which this can be achieved (Figure B.1B). In any irreversible mechanism for the forward enzyme E, if Y_i is an intermediate that can yield the substrate S₀, then $K_{i,1}^E=\infty$ (Appendix). This is plausible: in an irreversible mechanism there is no way for S₁ to contribute to an intermediate that can yield S₀. In particular, $K_{1,1}^E=K_{2,1}^E=\infty$ and so it follows from (12) that $c_1^E=0$. However, S₁ can still contribute to other intermediates, so the tgMMC, $K_1^E$, which appears in (18), is not necessarily ∞. Similar results hold if the reverse enzyme is irreversible, with $c_0^F=0$. If both mechanisms are irreversible, then equation (13) simplifies to

$$\frac{[S_1]}{[S_0]}=\left(\frac{c_0^E}{c_1^F}\right)\left(\frac{[E]}{[F]}\right).$$ (19)

It is now easy to eliminate [E]/[F ] between equations (18) and (19) to get

$$\frac{c_0^E{E}_{\mathit{tot}}}{c_1^F{F}_{\mathit{tot}}}=\left(\frac{1+[S_0]/K_0^E+[S_1]/K_1^E}{1+[S_1]/K_1^F+[S_0]/K_0^F}\right)\left(\frac{[S_1]}{[S_0]}\right),$$

which may be rearranged by cross-multiplication to give

$$t(c_0^E/c_1^F)(1+[S_1]/K_1^F+[S_0]/K_0^F)[S_0]=(1+[S_0]/K_0^E+[S_1]/K_1^E)[S_1].$$ (20)

Here, we have introduced t = E_tot/F_tot for the ratio of the enzyme totals. This quantity is the input variable to the GK loop, through changes in the availability of the enzymes. Formula (20) is a polynomial equation in [S₀] and [S₁] that holds in any steady state. It summarises the algebraic relationship between the two key variables, [S₀] and [S₁]. It is an example of an “invariant”.

An invariant is a polynomial equation between specified dynamical variables, here [S₀] and [S₁], that holds in any steady state in which all the variables are strictly positive, [14, 18]. In the definition of this concept used previously, the coefficients of the equation were required to be rational expressions in the underlying rate constants, like $1/K_1^F$. However, (20) is different in also containing as a coefficient the quantity t, which is not determined by the rate constants but, rather, by the initial conditions. Without such a coefficient, such a concise relationship between [S₀] and [S₁] as in (20) would not exist. This suggests that relaxing the definition of an invariant to allow for conserved quantities, such as E_tot and F_tot, as well as rate constants, is an useful generalisation.

The invariant in (20) has terms in both [S₀]² and [S₁]², so [S₀] can be expressed in terms of [S₁] (or vice versa) by using the well-known formula for the roots of a quadratic equation. However, the resulting expression is not straightforward to analyse because the input variable t appears in several places. We turn, instead, to a further simplification, which brings (20) into a form whose behaviour becomes transparent. The implications of (20) are reviewed further in the Discussion.

2.6. Strong irreversibility leads to a singularity at s = 1

A reaction mechanism is said to be “strongly irreversible” if the product does not rebind after release. For the forward mechanism in Figure B.1B, this requires that S₁ does not bind to E to form either Y₃ or Y₄. In particular, a strongly irreversible mechanism is always irreversible but, as is evident from Figure B.1B, there are irreversible mechanisms that are not strongly irreversible.

There is no distinction between irreversibility and strong irreversibility for the Michaelis-Menten reaction scheme in (1). It only becomes significant for realistic enzyme mechanisms.

For any strongly irreversible mechanism for the enzyme E, $K_{i,1}^E=\infty$ for all intermediates Y_i (Appendix). Again, this is plausible, as there is no way for S₁ to form part of any intermediate. In consequence, the tgMMC, $K_1^E$, has no finite contributions in (17) and so $K_1^E=\infty$. If the reverse enzyme is also strongly irreversible, then, similarly, $K_0^F=\infty$. In this case, the invariant in (20) simplifies to yield

$$t(c_0^E/c_1^F)(1+[S_1]/K_1^F)[S_0]=(1+[S_0]/K_0^E)[S_1].$$ (21)

Although this polynomial equation is still quadratic, the terms in [S₀]² and [S₁]² are now no longer present. [S₀] and [S₁] can now be re-scaled to make them nondimensional by introducing the new variables,

$$x_0=[S_0]/K_0^E,x_1=[S_1]/K_1^F.$$ (22)

Formula (21) can then be rewritten as

$$s(1+x_1)x_0=(1+x_0)x_1.$$ (23)

Here, we have introduced a new input variable, s, where

$$s=t\gamma \mu ,\gamma =\left(\frac{c_0^E}{c_1^F}\right),\mu =\left(\frac{K_0^E}{K_1^F}\right).$$ (24)

The quantities γ and μ are rational expressions in the rate constants. The re-scaling to give s in place of t simplifies the analysis below. It follows that

$$x_0=\frac{x_1}{s+(s-1)x_1}.$$ (25)

From this point, it will be helpful to think of x₀ and x₁ as variables. We will write down equations in these variables, whose solutions will give the steady-state concentrations, [S₀] and [S₁], through (22).

It is immediately apparent from (25) that something special happens when s = 1, or, equivalently, when t = 1/(γμ). In this case, x₀ = x₁ and there is no limitation on either variable. However, if s < 1, then the graph of (25) has a vertical asymptote at s/(1 − s) and x₁ is limited so that

$$x_1<\frac{s}{1-s}.$$ (26)

If x₁ were to exceed this bound then, according to (25), x₀ would be negative, leading to a contradiction. Conversely, if s > 1, then the graph of (25) is a rectangular hyperbola with a horizontal asymptote at height 1/(s − 1) and x₀ is limited so that

$$x_0<\frac{1}{s-1}.$$ (27)

It follows that the only case in which both x₁ and x₀ can reach unlimited values is when s = 1. This is summarised in Figure B.3A, which shows the different shapes of the graph of (25) depending on whether s is less than, equal to or greater than 1.

Figure B.3. The singularity at s = 1.

(A) Graphs of (25) are shown for three values of s (thick, magenta curves), as indicated. The light, black lines show the vertical asymptote to the s = 0.9 graph at x₁ = s/(1 − s) and the horizontal asymptote to the s = 1.1 graph at x₀ = 1/(s − 1). (B) The segment cut off the diagonal by the graph of (25) is shown as a thick cyan line, for the indicated values of s and s + Δ, with Δ = 0.05. When this interval lies below (left, top) or above (left, bottom) s = 1, these segments are bounded, no matter how far the diagonal is from the origin. When the interval straddles s = 1 (right, centre), the segments can be made as large as one pleases by moving the diagonal sufficiently far from the origin. Because of the asymptotes in A, the segment length is an increasing proportion of the diagonal, leading to the scaling in (28).

The change in behaviour that takes place at s = 1 is a “singularity”. This term usually describes some form of discontinuity, such as a sudden jump in values. Consider the (x₁, x₀) plane with a diagonal, defined by the line x₀ = a − x₁ between the points (0, a) and (a, 0). Only positive values of a are relevant here. The significance of this geometry will become apparent in the next section. Now take two values of s that are close together, say s and s + Δ, and consider the line segment on the diagonal that is cut off by the graph of (25) at these values of s. These segments are shown as thick cyan lines in Figure B.3B. Let l_a(s, s + Δ) be the length of the segment. We want to know how this scales with increasing a. If the interval (s, s + Δ) lies on one or the other side of 1, so that s < s + Δ < 1 or 1 < s < s + Δ, then l_a(s, s + Δ) remains bounded, no matter how large a becomes. Indeed, the segment length can never be larger than the segment of the diagonal cut off by the asymptotes of (25) at the corresponding values of s. It follows that,

$$\frac{l_a(s,s+\mathrm{\Delta })}{a}\to 0\text{as}a\to \infty .$$

However, if the interval between the s-values contains 1, so that s < 1 < s + Δ, then l_a(s, s + Δ) becomes unbounded by taking a to be sufficiently large (Figure B.3B). Furthermore, if we consider the complement of the segment on the diagonal, which falls into two disconnected pieces, each piece is individually bounded as a gets large for a similar reason as above: their lengths can never be larger than the segments of the diagonal cut off by the asymptote of (25) and the coordinate axis parallel to it. It follows that,

$$\frac{l_a(s,s+\mathrm{\Delta })}{a}\to 1\text{as}a\to \infty .$$ (28)

The discontinuity expressed by these different scalings is the singularity from which unlimited ultrasensitivity emerges. To see this, it is necessary to bring in the last general property of the GK loop, which is the conservation of substrate.

2.7. Substrate conservation yields a cubic equation

Since substrate is neither synthesised nor degraded, a conservation law holds for the total substrate,

$$S_{\mathit{tot}}=[S_0]+[S_1]+\underset{\text{forward}}{\underbrace{[Y_1]+\cdots +[Y_4]}}+\underset{\text{reverse}}{\underbrace{[Y_5]+\cdots +[Y_7]}},$$ (29)

where S_tot is determined by the initial conditions. The contribution of the intermediates to this sum can be determined as follows. If E is strongly irreversible, so that $K_1^E=\infty$, formula (16) may be rewritten as

$$E_{\mathit{tot}}=(1+x_0)[E],$$ (30)

from which we see, from the conservation of total enzyme in (14), that

$$[Y_1]+\cdots +[Y_4]=E_{\mathit{tot}}-[E]=x_0[E].$$

It also follows from (30) that [E] = E_tot/(1 + x₀), so that

$$[Y_1]+\cdots +[Y_4]=\frac{x_0{E}_{\mathit{tot}}}{1+x_0}.$$

By a similar argument for the reverse intermediates when F is strongly irreversible, we find that

$$[Y_5]+\cdots +[Y_7]=\frac{x_1{F}_{\mathit{tot}}}{1+x_1}.$$

However, the invariant for strong irreversibility in (23) tells us that

$$\frac{x_0}{1+x_0}=\left(\frac{1}{s}\right)\frac{x_1}{1+x_1},$$

where we recall from (24) that s = γμ(E_tot/F_tot). Hence, the total contribution from the intermediates is

$$[Y_1]+\cdots +[Y_7]=\frac{x_1}{1+x_1}\left(1+\frac{1}{\gamma \mu }\right)F_{\mathit{tot}}.$$

The expression depends only on [S₁] (ie: x₁) or, equivalently, by using (23), only on S₀ (ie: x₀). Strong irreversibility of both enzymes is essential for this simplification. If the enzymes are irreversible, but not strongly so, then the contribution of the intermediates becomes more complicated, with both [S₀] and [S₁] playing a role.

The substrate conservation equation in (29) can now be reformulated as

$$S_{\mathit{tot}}=K_0^E{x}_0+K_1^F{x}_1+\frac{x_1}{1+x_1}\left(1+\frac{1}{\gamma \mu }\right)F_{\mathit{tot}}$$

and this can be normalised and written entirely in terms of x₁ by using (25),

$$\frac{S_{\mathit{tot}}}{K_1^F}=\frac{x_1}{s+(s-1)x_1}\mu +x_1+\frac{x_1}{1+x_1}\left(1+\frac{1}{\gamma \mu }\right)\left(\frac{F_{\mathit{tot}}}{K_1^F}\right).$$ (31)

By cross multiplication, formula (31) yields an invariant, which is a cubic polynomial equation in x₁. By solving this to obtain [S₁], all the other variables can be determined: [S₀] comes from (25); [E] and [F ] come from (30) and its equivalent for F; and the intermediates come from (8). When both enzymes are strongly irreversible, which could still result in an an arbitrary number of components, the GK loop can be reduced to the solution of a single cubic equation.

Goldbeter and Koshland derived a cubic polynomial equation for the GK loop assuming the classical Michaelis-Menten reaction mechanism and taking the intermediate complexes into account, [10]. Our results show that, provided the enzymes are strongly irreversible, the same reduction is possible no matter how complex the reaction mechanisms. Feliu et al have pointed out that a reduction to a single equation is also possible for a cascade of GK loops, in which the kinase for one layer is the substrate for the previous, provided the classical Michaelis-Menten reaction mechanism is assumed for all layers, [8]. In this case, the degree of the polynomial equation increases with the length of the cascade. Our results suggest that the reduction to a single equation is also feasible for cascades with realistic enzyme mechanisms.

Goldbeter and Koshland showed unlimited ultrasensitivity by numerical solution of the cubic polynomial equation, for chosen values of the various constants. However, the structure of (31) lends itself to a geometric approach, which brings additional insights.

2.8. Geometric solution of the cubic equation

The solution of equation (31) may be found as follows. Some terminology is helpful, which is italicised when introduced below and illustrated in Figure B.4A. Consider, as above, the (x₁, x₀) plane. We plot three curves in this plane; the first two will be static, while the third will be moved in a certain way to find the solution. The first curve is the “diagonal” given by the graph of

Figure B.4. Geometric solution of the cubic equation.

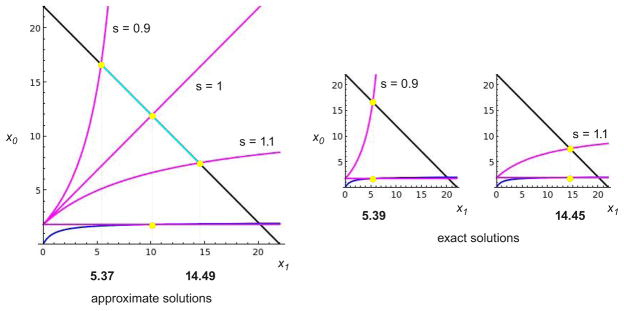
(A) Illustration of the three curves—the diagonal (black), the intermediate curve (blue) and the substrate curve (magenta)—and their key intersection points (yellow dots) in the box, as described in the text. The substrate curve, shown here with s < 1, and its associated horizontal substrate axis can be moved vertically up and down by the slider to change the position of the upper and lower points. (B) The x₁ solution is found by moving the slider until the upper and lower points lie on the same vertical line, at which point equation (31) is satisfied, as explained in the text. Since the substrate curve gives the value of x₀ corresponding to x₁, its value may also be read-off by observing from (32) that the diagonal has slope −1. Similarly, the remaining segment on the horizontal axis that extends to the intersection with the diagonal is equal to the value of the intermediate curve and gives the total amount of the intermediate complexes. The inset shows the x₁ solution for a different disposition of the curves, in which substrate is no longer in excess over enzymes. Note that the value m shown in A, determined by the intersection of the diagonal and the intermediate curve, is always an upper limit for the x₁ solution.

$$x_0=\frac{S_{\mathit{tot}}}{K_1^F}-x_1.$$ (32)

The diagonal sets the scale. All calculations take place in the square “box” determined by the intersections of the diagonal with the axes. The second curve is the “intermediate curve”, given by the graph of the last term in (31),

$$x_0=\frac{x_1}{1+x_1}\left(1+\frac{1}{\gamma \mu }\right)\left(\frac{F_{\mathit{tot}}}{K_1^F}\right).$$ (33)

This is a rectangular hyperbola with a horizontal asymptote whose height is determined by the terms in brackets. The third curve is the “substrate curve”, given by the graph of the first term in (31),

$$x_0=\frac{x_1}{s+(s-1)x_1}\mu ,$$

which can have the same shapes as in Figure B.3A for different values of s. The example in Figure B.4A has s < 1. The substrate graph should be thought of as if its origin is a moveable “slider” whose position on the vertical x₀ axis can be altered. The slider takes a horizontal “substrate axis” along with the substrate curve. The slider is restricted to move so that the substrate curve intersects the diagonal in the “upper point”, while the substrate axis intersects the intermediate curve in the “lower point” (Figure B.4A).

With this preparation, the solution to equation (31) is found by moving the slider until the upper and lower points lie on the same vertical line (Figure B.4B). For that value of x₁, the height of the box, which is $S_{\mathit{tot}}/K_1^F$, is made up of three segments whose lengths are, reading from bottom to top, the value of the intermediate curve, the value of the substrate curve and x₁ itself. This is exactly equation (31), so that the value of x₁ must be a solution of it. The corresponding value of x₀ and of the total amount of intermediate complexes can also be read off, as shown in Figure B.4B.

An immediate consequence of this construction is that there is always a unique solution for x₁ and hence for all the other components in the system, as explained in the previous section. In particular, realistic enzyme mechanisms do not give rise to multiple steady states, at least when the enzymes are strongly irreversible. (When the enzymes follow the standard Michaelis-Menten mechanism in (1), it is known that multiple steady states require more than one modification site, [19, 32].) These results hold irrespective of the complexity of the reaction mechanisms and of the values of the rate constants. It would be impossible to infer such general results by numerical integration of the underlying differential equations, illustrating one of the advantages of the symbolic and geometric methods used here.

The unlimited ultrasensitivity can be seen to emerge through the following argument. We require that when s = 1, the solution of (31) is at a point where the intermediate curve is in saturation. We first determine this saturation condition and then explain how the ultrasensitivity arises. Suppose that x₁ = x_* is in the saturation regime of the intermediate curve. By construction, the value of the intermediate curve in (33) will be very close to its asymptotic value, while, since s = 1, the value of the substrate curve will be just x_*μ. Moreover, since s = 1, t = 1/(γμ), so that the substrate-conservation equation in (31) can be approximated as

$$\frac{S_{\mathit{tot}}}{K_1^F}=x_{\ast }\mu +x_{\ast }+(1+t)\left(\frac{F_{\mathit{tot}}}{K_1^F}\right).$$

Rearranging this gives the value of x_*,

$$x_{\ast }=\frac{1}{(1+\mu )K_1^F}(S_{\mathit{tot}}-(1+t)F_{\mathit{tot}}).$$

Since $\mu =K_0^E/K_1^F$ and t = E_tot/F_tot this can be further simplified to give

$$x_{\ast }=\frac{1}{K_0^E+K_1^F}(S_{\mathit{tot}}-(E_{\mathit{tot}}+F_{\mathit{tot}})).$$

It follows from (33) that the half-saturation value of the intermediate curve occurs at x₁ = 1. Hence, for x₁ to be in the saturation regime, it is necessary that x_* ≫ 1, or, equivalently, that

$$S_{\mathit{tot}}\gg E_{\mathit{tot}}+F_{\mathit{tot}}+K_0^E+K_1^F.$$ (34)

Formula (34) falls out easily from the geometric argument used here but would be hard to obtain by numerical methods.

The unlimited ultrasensitivity arises as follows. If the x₁ solution for s = 1 lies in the saturation regime for the intermediate curve, then a small change in the position of the slider causes a large change in the position of the lower point. Because of this, if s is changed from slightly below s = 1 to slightly above, then the x₁ coordinate of the upper point will still be a good approximation to the x₁ solution (Figure B.5). If s < 1, the slider has to be moved down to find the correct solution, so the upper point will give an under-estimate, while if s > 1 the slider has to be moved up to find the correct solution and the upper point will give an over-estimate. The discrepancy between the approximate and the exact solutions can be improved as much as required by increasing the degree of saturation. It follows that the change in the x₁ solution as s goes from slightly below to slightly above 1 is determined, to a good approximation, by the length of the segment on the diagonal between the substrate curves, highlighted in cyan in Figure B.5. As we saw in Figure B.3B, this length can be increased beyond any limit by increasing the distance of the diagonal from the origin or, equivalently, by increasing S_tot in accordance with the saturation condition in (34). Such a change only affects the diagonal. Since it increases the total amount of substrate in the system, it is important to know not only that x₁ increases but also that it does so as a proportion of total substrate. This follows from the scaling established in (28). The saturating value of the proportion is no longer 1 because the intermediate complexes are also present and these can play a significant role in limiting the proportion outside the saturating regime. Indeed, if m is the x₁ coordinate of the intersection of the diagonal with the intermediate curve, then it can be seen from Figure B.4 that x₁ < m for all values of s.

Figure B.5. Unlimited ultrasensitivity in the saturated regime.

The system is shown for the indicated values of s, with the x₁ solution for s = 1 in the saturation regime of the intermediate curve (x₁ = 10.09, compared to the half-saturation value of x₁ = 1). The constants are S_tot = 22, F_tot = 1, $K_0^E=K_1^F=1$ (in arbitrary units), so that μ = 1, and γ = 1, with E_tot allowed to vary to change the value of s according to (24). When s = 0.9 or s = 1.1, the x₁ coordinates of the upper points are good approximations to the exact solutions shown on the right. The change in x₁ as s goes through 1 is therefore determined, up to a constant factor, by the line segment highlighted in cyan, whose length can be made arbitrarily large (Figure B.3B) by increasing the amount of substrate. The length of this segment becomes an increasing proportion of the diagonal, as established by the scaling in (28).

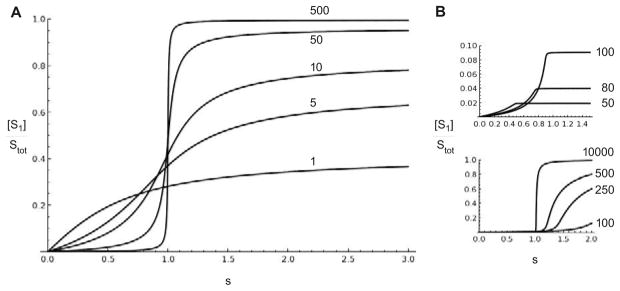
For chosen values of the constants, equation (31) can be numerically solved to show how the proportion of [S₁] varies with s (Figure B.6A). The ultrasensitivity in response steadily increases with increasing substrate, from a graded response when $S_{\mathit{tot}}=K_1^F$, through increasingly sigmoidal responses, to an abrupt switch-like response when $S_{\mathit{tot}}=500K_1^F$, with a corresponding increase in the proportion at saturation, as expected from the argument above.

Figure B.6. Dose-response of the GK loop for varying levels of substrate.

(A) The amount of [S₁] as a proportion of total substrate, S_tot, is plotted against s = γμ(E_tot/F_tot). The levels of $S_{\mathit{tot}}/K_1^F$ are indicated next to the corresponding plots. The other constants are the same as in Figure B.5. (B) The same plots with E_tot = 0.01 (top) and E_tot = 100 (bottom), with the other constants as in Figure B.5. Since F_tot = 1, μ = 0.01 in the top plot and μ = 100 in the bottom plot, compared to μ = 1 in A. Note the different horizontal and vertical scales in the two plots. Unlike the plot in A, there is marked asymmetry in the shape of the curve before and after the point of inflection, corresponding to different “operating regimes”, [11], but unlimited ultrasensitivity remains confined to s = 1.

Ultrasensitivity can arise at values of s other than 1, particularly when there is a discrepancy between the enzymes, with $K_0^E\ne K_1^F$ (so that μ ≠ 1). However, unlimited ultrasensitivity is confined to s = 1. The cases μ < 1 and μ > 1 are illustrated in Figure B.6B and show asymmetric behaviour in the ultrasensitive region, which moves closer to s = 1 as S_tot increases. These distinct shapes of dose-response correspond to the “operating regimes” identified by Gomez-Uribe et al, using the classical Michaelis-Menten reaction scheme and the total quasi-steady state approximation, [11]. In the strongly irreversible case, similar distinctions appear to hold with realistic enzyme mechanisms.

2.9. Knife-edge behaviour in substrate allocation

Ultrasensitivity is found in the response of substrate forms to changes in enzyme totals, while keeping total substrate fixed (Figure B.6). It is also instructive to see how substrate forms change with total substrate, while keeping enzyme totals fixed. Both substrate forms, S₀ and S₁ increase steadily with increasing total substrate but show two distinct behaviours (Figure B.7). If s < 1 then increasing amounts of substrate are allocated preferentially to S₀, which grows without limit, while S₁ remains below an upper bound (Figure B.7A). Conversely, if s > 1 then increasing amounts of substrate are allocated preferentially to S₁, which grows without limit, while S₀ remains below an upper bound (Figure B.7B). The asymptotic upper bounds are given by (26) and (27), respectively, and depend only on s.

Figure B.7. Knife-edge behaviour in substrate allocation.

Steady-state concentration of unmodified substrate, S₀, (blue) and modified substrate, S₁, (magenta) are plotted against total substrate, S_tot. The constants are $K_0^E=10,K_1^F=5$, so that μ = 2, and γ = 0.5, so that γμ = 1. (A) The ratio of enzyme levels, t = E_tot/F_tot, is taken to be 0.9, so that t < (γμ)⁻¹. [S₀] increases without limit with increasing total substrate, while [S₁] remains bounded above. The horizontal asymptote (black) is given by (26). (B) t = 2, so that t > (γμ)⁻¹. [S₁] increases without limit, while [S₀] remains bounded above. The horizontal asymptote (black) is given by (27).

The change between s < 1 and s > 1 can be seen more clearly by considering each substrate form as a proportion of total substrate. If, at steady state, u₀ = [S₀]/S_tot and u₁ = [S₁]/S_tot, then, in the limit as S_tot → ∞,

$$(u_0,u_1)\to \{\begin{array}{ll}(1,0)\hfill & \text{if}s<1\hfill \\ (0,1)\hfill & \text{if}s>1\hfill \end{array}$$

This is another manifestation of the fundamental singularity underlying the GK loop. In addition to zero-order ultrasensitivity, the balance between steady-state substrate accumulation in S₀ or S₁ is set on a knife edge at s = 1.

The quantity s = tγμ depends partly on the underlying rate constants, through γ and μ, as described in (24), and partly on the balance of the enzyme totals, through t = E_tot/F_tot. The levels of these enzymes can be subject to fluctuations over time, as well as to variation between cells, [28]. In contrast, enzymatic rate constants are expected to be identical over time and between cells. Hence, in the context of an integrated tissue, it is possible that t < (γμ)⁻¹ at a particular time in a particular cell, while t > (γμ)⁻¹ at another time or in another cell. This could lead to incoherent changes between the two distinct steady-state responses in Figure B.7 and a loss of integrated behaviour across a tissue.

A potential solution to this problem is to ensure that the concentration levels of the two enzymes are kept in a fixed relative stoichiometry, so that t becomes constant. The enzymes could, for instance, be tightly co-regulated or forced to form a complex. Then, at all times and in all cells, either the behaviour in Figure B.7A or the behaviour in Figure B.7B would take place, depending only on the rate constants. The resulting upper bounds in (27) and (26) would be robust to fluctuations in the levels of both substrate and enzymes.

An alternative possibility is suggested by an unusual regulatory mechanism in mammalian glucose metabolism, [7]. The conversion of glucose to pyruvate during glycolysis goes through a step in which fructose-6-phosphate (F6P) is converted to fructose-1,6-bisphosphate by the enzyme 6-phosphofructo-1-kinase (PFK-1). The reverse conversion of pyruvate to glucose during gluconeogenesis, which takes place particularly in the liver, is catalysed by fructose-1,6-bisphosphatase (FBPase-1). These two separately catalysed reactions are believed to be key rate-limiting steps in glucose metabolism, [27]. However, F6P is also converted to fructose-2,6-bisphosphate (F2,6BP), which is a terminal metabolite that appears not to be consumed by any other metabolic process. Instead, it acts as an allosteric regulator: it is a potent activator of PFK-1 and an inhibitor of FBPase-1. The concentration of F2,6BP therefore plays a key role in regulating flux through glycolysis and gluconeogenesis. The conversion between F6P and F2,6BP would be a GK loop of the type studied here, except that the forward and reverse enzymes are linked on the same bifunctional protein, 6-phosphofructo-2-kinase/fructose-2,6-bisphosphatase (PFK-2/FBPase-2). Bifunctionality may be considered an extreme type of complex formation. It provides a certain way to ensure that E_tot = F_tot and t = 1. We suggest, therefore, that the bifunctionality of PFK-2/FBPase-2 protects tissues such as the liver from the loss of integrated behaviour described above and ensures robustness of glycolytic/gluconeogenic regulation to fluctuations in the levels of metabolic substrates and enzymes. This suggestion is explored in detail in a separate paper, [7].

Bifunctionality in modification and demodification is not uncommon and studies in bacteria have suggested that it can give rise to some form of robust concentration control at steady state (see [7] for references). It has not been previously appreciated that two strongly irreversible, monofunctional enzymes in a GK loop are poised on a knife edge in respect of substrate allocation (Figure B.7). Bifunctionality may be required, not just for robust control concentration, but as a means to avoid this singularity.

3. Conclusions

The Goldbeter-Koshland loop has been a paradigm for the emergence of novel functionality from collective behaviour. While many ultrasensitive mechanisms are known, such as allosteric proteins or gene regulatory systems, a unique feature of the GK loop is that its ultrasensitivity is regulatable by changing the saturation level of the enzymes. For other mechanisms, in contrast, ultrasensitivity is limited by structural features, such as the number of binding sites, which may be altered on an evolutionary time scale but not so readily on a physiological time scale. The unlimited ultrasensitivity of the GK loop suggests considerable flexibility for cellular information processing and it has been widely studied from different perspectives, [4, 11, 17, 21, 26, 34].

However, its biological relevance has been hard to assess. Ultrasensitivity has been confirmed in vitro for phosphorylation/dephosphorylation of E coli isocitrate dehydrogenase, [16], and mammalian glycogen phosphorylase, [20]. At concentrations that are realistic in vivo, the experimentally measured ultrasensitivities have effective Hill coefficients of around 2 and 2.3, respectively. In comparison, the Hill coefficient of hemoglobin for oxygen binding is around 2.9. The issue here is that substrate concentrations are often on a par with enzyme concentrations, so that enzyme saturation may be limited. However, localisation into a multi-protein complex, as achieved through scaffold proteins, can increase local concentrations substantially so that zero-order effects become more pronounced, [34], and this sensitivity can be further amplified through additional mechanisms. Higher Hill coefficients, of around 9, have been experimentally measured in such systems, [17]. Experimental evidence also suggests that zero-order ultrasensitivity may play a key role in setting sharp boundaries during embryonic patterning, [21].

The relative simplicity of the GK loop makes it a good starting point for analysing realistic enzymology. It is somewhat surprising that the Michaelis-Menten reaction mechanism continues to be so widely used in systems biology. Michaelis and Menten cleverly designed their experimental setting so that they measured initial rates of product formation with negligible product present, [13]. Strong irreversibility could be reasonably assumed in their context, allowing them to simplify the resulting mechanism. No such justification can be provided for more recent usage of their mechanism. It is becoming increasingly important to reconcile systems biology with modern enzymology. The analysis presented here shows how this might be done but is only a starting point.

Our methods illustrate how the linear framework, that was introduced in [31] and extended in [12], can deal with arbitrarily complex reaction mechanisms. The framework provides, first, a systematic method to undertake the steady-state elimination of intermediate complexes. Second, the generalised constants emerging from this analysis can be used to rewrite the reversible modification system as linear at steady state (Figure B.2B). This linearity holds in generality for reversible modification systems with multiple substrates, multiple types of modification, multiple sites, multiple modifying and demodifying enzymes and arbitrarily complex reaction mechanisms based on (5). It follows that a very wide range of reversible modification systems can be analysed at steady state by symbolic, algebraic methods, avoiding numerical simulation and the attendant challenges of parameter identification. In fact, the linear framework underpins many examples of time-scale separation in biology, with applications in such diverse areas as enzyme allostery, G-protein coupled receptors, ligand-gated ion channels and gene regulation in bacteria and eukaryotes, [12]. The present paper provides an opportunity to introduce these ideas in the context of one of the simplest multi-enzyme systems.

It is already known that reversibility of the mechanisms compromises ultrasensitivity, [24]. What emerges from the present analysis is that reaction mechanisms can be irreversible in different ways and this can make a difference to their behaviour. This issue does not arise for the classical Michaelis-Menten mechanism, which can be irreversible in only one way, and its significance only becomes apparent when realistic mechanisms are considered. We find that if both enzyme mechanisms are strongly irreversible, then unlimited ultrasensitivity is preserved. Furthermore, the unlimited ultrasensitivity arises from a singularity in the algebraic invariant in (20) that summarises the relationship between the substrate forms. The singularity also underlies the knife-edge response to substrate allocation in Figure B.7. This raises an interesting question as to the coherence of a GK loop over time and from cell to cell within a tissue. As we have suggested, the need to impose such coherence may account for the bifunctionality of PFK-2/FBPase-2 in mammalian glucose metabolism, [7].

When the enzymes are irreversible (by which we also mean not strongly irreversible) the analysis becomes more difficult, in part because the invariant in (20) is more complicated than that in (21). However, one important observation can be made immediately: the mutually exclusive limitation on [S₀] and [S₁] no longer holds. If [S₁] increases without bound, then [S₀] cannot be limited, and conversely. To see this, divide both sides of the invariant in (20) by [S₁]² and let [S₁] → ∞, while keeping [S₀] bounded. The left hand side goes to zero while the right hand side goes to $1/K_1^E$, which can only be zero if E is strongly irreversible. Similarly, if [S₀] increases without bound while [S₁] is limited, it is necessary that F is strongly irreversible. There is no longer a singularity of the form shown in Figure B.3.

The irreversible case is therefore strikingly different from the strongly irreversible case and we speculate that unlimited ultrasensitivity may no longer hold for the former. Although a mathematical treatment of this has not yet emerged, we believe that the foundation laid here will provide the basis for it. It would be of particular interest to know how much ultrasensitivity is available and, if it is no longer unlimited, as we speculate, then what the limits are and what features of the reaction mechanisms determine these limits. It would also be very interesting to know what happens to the knife edge behaviour in Figure B.7 when strong irreversibility is no longer assumed. These are challenging open problems whose solution would give us a better appreciation for the impact of reaction mechanisms on multi-enzyme systems.

Appendix A. Appendix

The formulas in the paper were found by direct algebraic manipulation, as described in the main text. Figures B.3 to B.6 were plotted in Mathematica (Wolfram Research Inc). The calculations of the $K_{\ast ,\ast }^{\ast }$ for the irreversible and strongly irreversible cases was done by the method of [31]. We review this method and then explain the calculations.

As mentioned in §2.2, the Laplacian dynamics of a strongly-connected, labelled, directed graph has a unique steady state, up to a scalar multiple: dim ker 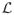(G) = 1. The Matrix-Tree Theorem (MTT), [31, 33], provides an algorithm for calculating a basis element, ρ ∈ ker 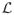(G): ρ_i is obtained by enumerating the spanning trees rooted at vertex i, taking the product of the labels on the edges of each tree and adding up the products over all the trees. A spanning tree rooted at i is a sub-graph that includes every vertex (spanning), that has no cycles when edge directions are ignored (tree) and for which only vertex i has no outgoing edges (rooted). Spanning trees are fundamental concepts in graph theory.

Note that the expression for ρ_i obtained from the MTT is a sum of positive terms. Had the linear system 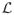(G).x = 0 been solved by determinants, the result would have been an alternating sum of positive and negative terms. The value of the MTT, and the graph theory on which it is based, is that it takes care of all the cancellations.

Suppose given a reaction mechanism for the forward enzyme E satisfying the conditions introduced in the paper and let G be the corresponding labelled, directed graph on the intermediate complexes and E (Figure B.2A). An identical argument works for the reverse enzyme F. Suppose that Y_i corresponds to vertex i for 1 ≤ i ≤ n − 1 and that E corresponds to vertex n. From the construction of G, outlined in the first section of the Results, the only edges carrying an algebraic expression of the form k_*[S_*] are those outgoing from vertex n (highlighted in Figure B.2A). All other edges have only a rate constant as label. It then follows from the MTT that

$${\rho }_i=\{\begin{array}{ll}{\alpha }_i[S_0]+{\beta }_i[S_1]\hfill & \text{for}0\le i\le n-1\hfill \\ \gamma \hfill & \text{for}i=n,\hfill \end{array}$$ (A.1)

where α_i, β_i and γ are polynomials in the rate constants. While γ ≠ 0, it is possible that either α_i = 0 or β_i = 0, depending on the reaction mechanism. Since the steady state is unique up to a scalar multiple, we must have [Y_i] = λρ_i and [E] = λρ_n, for some λ ∈ ℝ. Hence,

$$[Y_i]=\left(\frac{{\rho }_i}{{\rho }_n}\right)[E],$$

which, together with (A.1), gives equation (8) in the paper. The corresponding gMMCs are given by

$$K_{i,0}^E=\frac{\gamma }{{\alpha }_i},K_{i,1}^E=\frac{\gamma }{{\beta }_i},$$

provided α_i and β_i are non-zero. The gMMCs are rational expressions in the rate constants. Since each spanning tree has n − 1 edges, the polynomials in these expressions have degree n − 1.

If the reaction mechanism is irreversible and Y_j is an intermediate that can release S₀, then no spanning tree rooted at j can have an edge with label k_*[S₁]. If one of them did, that would imply a chemical pathway through which S₁ could yield S₀, which would contradict irreversibility. Hence, β_j = 0 in (A.1) and the corresponding gMMC does not exist. Accordingly, $K_{j,1}^E=\infty$, as claimed.

If the reaction mechanism is strongly irreversible, then G has no edges labelled k_*[S₁], since there is no rebinding of S₁. Hence, β_i = 0 for all i and $K_{i,1}^E=\infty$ for all i, as claimed.