Prediction of Therapy Tumor-Absorbed Dose Estimates in I-131 Radioimmunotherapy Using Tracer Data Via a Mixed-Model Fit to Time Activity

Abstract

Background

For individualized treatment planning in radioimmunotherapy (RIT), correlations must be established between tracer-predicted and therapy-delivered absorbed doses. The focus of this work was to investigate this correlation for tumors.

Methods

The study analyzed 57 tumors in 19 follicular lymphoma patients treated with I-131 tositumomab and imaged with SPECT/CT multiple times after tracer and therapy administrations. Instead of the typical least-squares fit to a single tumor's measured time-activity data, estimation was accomplished via a biexponential mixed model in which the curves from multiple subjects were jointly estimated. The tumor-absorbed dose estimates were determined by patient-specific Monte Carlo calculation.

Results

The mixed model gave realistic tumor time-activity fits that showed the expected uptake and clearance phases even with noisy data or missing time points. Correlation between tracer and therapy tumor-residence times (r=0.98; p<0.0001) and correlation between tracer-predicted and therapy-delivered mean tumor-absorbed doses (r=0.86; p<0.0001) were very high. The predicted and delivered absorbed doses were within±25% (or within±75 cGy) for 80% of tumors.

Conclusions

The mixed-model approach is feasible for fitting tumor time-activity data in RIT treatment planning when individual least-squares fitting is not possible due to inadequate sampling points. The good correlation between predicted and delivered tumor doses demonstrates the potential of using a pretherapy tracer study for tumor dosimetry-based treatment planning in RIT.

Introduction

Therapy with internal emitters has shown much promise in the treatment of cancer. Some of the best response rates in radionuclide therapy have been achieved with I-131-labeled radioimmunotherapy (RIT) of non-Hodgkin's lymphoma, which is considered a relatively radiosensitive malignancy.^1,2 There is, however, much room to improve the efficacy of the treatment with dosimetry-based treatment planning, especially in the refractory (previously treated with chemotherapy) group of patients where the reported overall response rates range from 54% to 71%. Currently, in external beam therapy, treatment planning with a precise calculation of the tumor-absorbed dose is mandatory before treatment. In radionuclide therapy, including I-131 RIT, such calculations are not part of the treatment protocol. In the most widely used protocol for I-131 tositumomab RIT, the therapeutic activity to be administered is calculated based on delivering 65–75 cGy to the whole body, determined from a pretherapy diagnostic (tracer) administration.² Instead of this conservative approach, there has been much recent interest in potentially tailoring treatment plans on a patient-by-patient basis to deliver an effective therapeutic dose to the tumor while avoiding critical organ (usually bone marrow) toxicity. To make advances toward this goal, correlations must be established between the absorbed dose and the outcome as well as between absorbed doses predicted by the tracer study and those delivered by the therapy. The focus of the present study was on the latter correlation, specifically in tumor. Correlations for normal organs, including bone marrow, will be investigated in the future. Tumor dose–response correlations also of much importance for dosimetry-based treatment planning were the focus of a separate publication.³

In internal emitter therapy, the pharmacokinetics of the injected radiolabeled drug typically varies from patient to patient because of their unique physiological characteristics. There has been a common practice to use a tracer quantity of the radiolabeled drug-injected pretherapy to predict the kinetics of the therapy administration, usually for the whole body or a dose-limiting organ. In pharmacokinetic analyses, cumulative exposure is estimated by the area under the time–activity curve (AUC). Methods to estimate the AUC include the trapezoidal method and more commonly, integration of a fitted smooth function such as a monoexponential or biexponential. Monoexponential curves are frequently used and are most appropriate for the whole body, in which uptake is instantaneous. A monoexponential, although commonly used, is less appropriate for individual tumors where uptake is not instantaneous and where biexponential curves are more appropriate to model the uptake and clearance of the radiopharmaceutical. Whatever functional form is chosen, added efficiency may be gained through the use of mixed models. An important advantage to a mixed-model approach is that it allows for borrowing of strength across subjects. Such an approach results in separate fitted time-activity curves for each tumor, but assumes that the parameters (from the many tumors) defining these curves follow a particular distribution, thus increasing the statistical efficiency. The utility of mixed models is well established in population pharmacokinetic modeling,⁴ which is based on the same class of nonlinear mixed-effect models utilized in this article.

Studies on the validity of using a tracer study to predict therapy kinetics and therapy-delivered doses are limited, especially for tumors. The best correlation in I-131 RIT was reported in a study of 7 NHL patients where radiation-absorbed doses for whole body, organs, and tumor from tracer and therapy administrations were within 14% of one another.⁵ On the other hand, a review article has summarized a considerable variation between dose estimates predicted from post-tracer imaging compared to those obtained from post-therapy imaging of the same patient.⁶ These limited previous studies were carried out using two-dimensional (2D) planar-imaging methods, which can be suboptimal due to the inability to accurately correct for interference from activity in overlying and underlying tissues. Quantitative three-dimensional (3D) SPECT imaging provides major advantages over 2D planar methods of activity quantification and the potential for improved dosimetric accuracy.^7,8 When iterative methods, such as ordered subset expectation maximization (OSEM), are used for SPECT reconstruction, compensation for physical limitations can be accurately modeled in the reconstruction process.⁹ Previously, we carried out a limited investigation of the tracer–therapy correlation for tumors based on SPECT data, by comparing the therapy to the tracer SPECT uptake ratio (normalized by the injected activity) at a single time point.¹⁰ The uptake ratio ranged from 0.71 to 1.82. This study however was limited to 7 patients and due to the lack of SPECT data at multiple time points did not allow for comparison of tracer and therapy residence times or predicted and delivered radiation-absorbed doses. In addition, this past study was carried out at a time when integrated systems were not clinically available; hence, SPECT-to-CT misregistration could have been a significant source of error.

Here, we examine the tracer–therapy correlation in 19 NHL patients who were imaged by SPECT/CT at multiple points after the tracer and therapy administration of I-131 tositumomab. Much emphasis was placed on accurate activity quantification, including corrections for high count-rate effects such as deadtime and pulse pileup, volumes of interest defined on CT at multiple time points to account for tumor regression/deformation, SPECT reconstruction with corrections for image-degrading effects, and a mixed-model fit to tumor time-activity data. Cumulated activities were combined with absorbed dose rates from Monte Carlo radiation transport to obtain patient specific mean tumor-absorbed dose estimates. The goal of the study was to determine the correlation between tracer and therapy residence times and the correlation between tracer-predicted and therapy-delivered mean tumor-absorbed doses to demonstrate the potential for treatment planning in I-131 RIT based on estimates from a pretherapy diagnostic study.

Methods

Patients

Patients were recruited from those undergoing I-131 tositumomab for the treatment of relapsed or refractory (previously treated with chemotherapy) follicular/low-grade or transformed B-cell lymphoma at the University of Michigan. The clinical treatment protocol has been described¹ and involves planar gamma camera measurements after the tracer administration (185 MBq) from which the amount of radioactivity necessary to deliver 65–75 cGy to the whole body is determined for each patient. The therapy is administered 8 days after the tracer. For the present research study, this protocol was unchanged, but the patients gave their separate written informed consent for the SPECT/CT imaging that was not the part of the treatment protocol. This imaging received separate University of Michigan Internal Review Board approval. Data are presented here for 19 patients (12 men, 7 women; age range, 33–81 years; median age, 53 years). The administered therapy activity ranged from 2.15 to 5.68 GBq (58–153 mCi).

SPECT/CT imaging

The imaging protocol on the Siemens Symbia TruePoint SPECT/CT system has been described previously.¹¹ The SPECT camera field of view (FOV) was 39 cm in the axial direction; hence, only a part of the body was imaged, focusing on the region with the largest tumor. In most patients, multiple (up to 7) tumors were imaged. After the tracer administration, patients were imaged three times, on day 0, 2, and 6, and after the therapy administration three times, on day 2, 5, and 7–9. The earliest post-therapy-imaging point was at 2 days because of concerns about radiation safety and high camera deadtime. At each time point, the tumor outlines were defined on CT, plane by plane, by a nuclear medicine specialist with radiology CT training. These volumes of interest from each time point were used when determining tumor time-activity curves and the mean tumor-absorbed dose, thus accounting for any changes in the tumor volume. This is especially important with malignant lymphomas, which can be highly sensitive to radiation and can have dramatic tumor regression within days of the treatment.^11,12

SPECT activity quantification including corrections for high count-rate imaging

In the present study, the I-131 activity administered for therapy was 10–30 times higher than that administered for the tracer study. During patient imaging, the count rate in the photopeak window at the earliest post-therapy imaging time point (2 days post-therapy) was up to 18,000 counts per second. Therefore, it is important to correct the therapy-imaging data for high count-rate effects such as camera deadtime and pulse pileup. Deadtime correction by the decaying source method, which is based on the departure of the observed count rate from the known exponential decay of a source, has been described previously.¹³ For the present SPECT/CT system, deadtime measurements with an I-131-filled phantom imaged on multiple days confirmed the validity of a paralyzable deadtime model. The measured deadtime constant was 2.5 μs, which was used to correct all post-therapy SPECT projection data before reconstruction. SPECT reconstruction was carried out using 35 iterations (6 subsets) of a previously implemented 3D OSEM algorithm.¹⁴ All reconstructions included detector response compensation, CT-based attenuation correction, and triple-energy window (TEW)-based scatter correction.

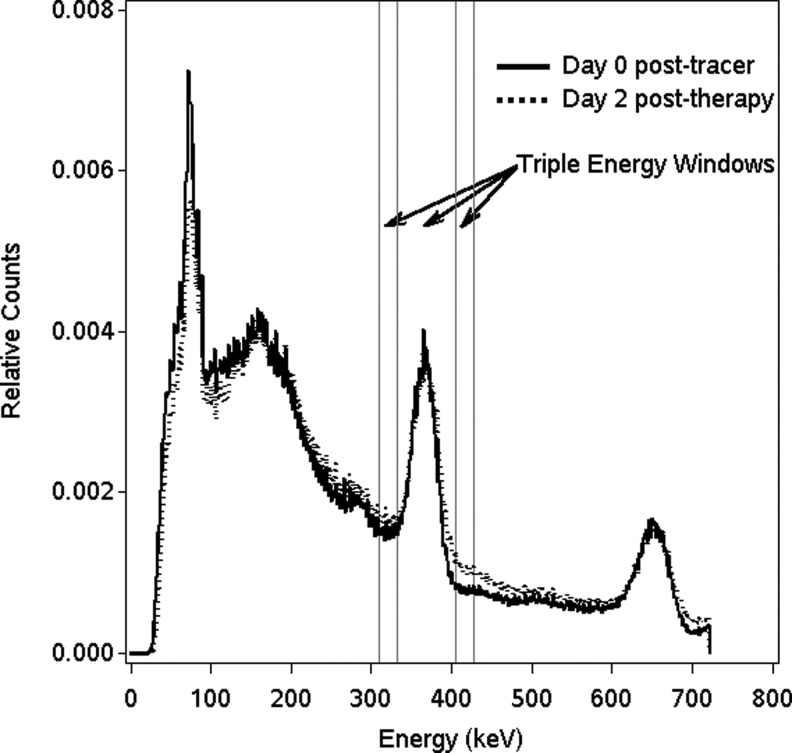
It was necessary to use a count rate-dependent calibration factor to convert reconstructed counts to activity. This was because of the observed change in the I-131 energy spectra at high count rates, which was attributed to pulse pileup effects. Figure 1 compares I-131 energy spectra measured during patient imaging at the first post-tracer time point with that measured at the first post-therapy time point. Because of pulse pileup during therapy imaging, the relative counts in the higher-energy-scatter window increases, which leads to an overestimation of scatter by the TEW method and hence an underestimation of the scatter-corrected main window counts. This change in the I-131 energy spectrum and its association to pulse pileup have been noted previously,¹⁵ and are particularly relevant to our study comparing results from tracer and therapy imaging. In the present study, to account for this effect, the calibration experiment with a known-activity hot-sphere phantom was carried out at three different count rates (as the initial activity of 20 mCi decayed over 1 month). The phantom count rates at the three measurement points were 21, 9, and 2 kcps with the higher rates typical of post-therapy imaging and the lower rate typical of post-tracer imaging of the present patients. The corresponding calibration factors were 1.46, 1.55, and 1.61 kcps/mCi. To account for partial-volume effects, recovery coefficients (RCs) were applied to tumors of volume <100 mL. The experiment to determine RCs was carried out using a phantom with multiple hot spheres in the range 4–100 mL with known amounts of I-131. The RC was defined as the ratio of SPECT-measured activity to true activity and ranged from 58% to 99%. Based on the patient's CT-defined tumor volumes, tumor activities were adjusted using the RC-versus-volume relationship.

FIG. 1.

Comparison of I-131 energy spectra measured during post-tracer imaging and post-therapy imaging of a typical patient (spectra were normalized to the same total counts).

Fitting of time activity: the mixed-model approach

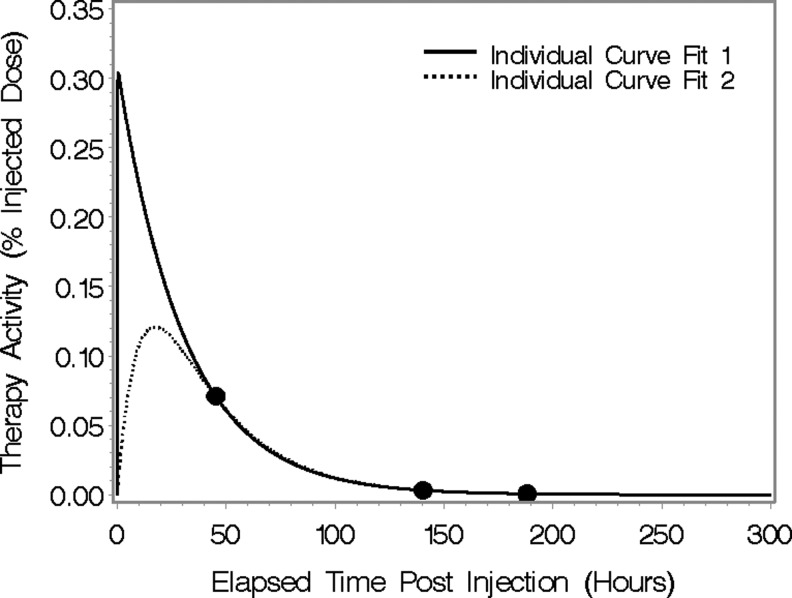
One of the difficulties with the conventional approach of fitting a single tumor's curve individually is that we would like to fit a biexponential curve (three parameters), but we have only 3 data points. Partly as a result, there are often many different combinations of parameters that fit the data well, as demonstrated in Figure 2 for a typical patient. In addition, the parameter estimates are sensitive to noise in the data and not identifiable if 1 of the 3 timepoints is missing. These different sets of parameters will also result in different AUC values. In the case of the mixed model, we obtain a unique set of parameter estimates and thus a unique estimate of AUC. Note that % injected dose in Figure 2 and throughout the article refers to the percentage activity normalized by the administered activity (without correcting for I-131 physical decay). In this section, we describe how a statistical mixed model, fit to all tumors from all subjects simultaneously, may be used to estimate cumulated activity and residence times. Mixed models refer to models containing both fixed and random effects and are widely used in a variety of applications 4, 26. The estimates of the random effects in these models are referred to as empirical Bayes. A key feature of these estimates is that they tend to shrink or penalize unlikely values. Practically, this means, for example, that if data from a tumor show an increasing activity during the clearance phase due to noise, the fitted curve from the model will still retain the standard exponential decay shape over this time interval. We discuss some of the issues involved and illustrate some of the benefits of a mixed-model approach to estimation over individual tumor curve fitting. The mixed model may be conveniently specified in two stages. The first stage specifies the functional form of the time–activity curves, whereas the second specifies the probability distribution of the individual parameter values across the population of tumors.

FIG. 2.

An illustration of the difficulty of using individual curve fits using functional forms with as many parameters as data points.

Stage 1: We assume that each tumor's time–activity curve may be specified by a biexponential curve. Specifically, we assume that the time–activity curve for tumor j of subject i is given by

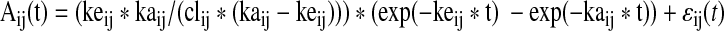(1)

where A_ij(t) is the measured activity at time t expressed as percentage of injected dose; ɛ_ij(t) is a normally distributed error term with mean 0 and a variance proportional to the mean of A_ij(t). In this parameterization, cl is typically referred to as a clearance parameter, or more empirically as a parameter that scales the curves up or down. Parameters ke and ka are typically referred to as the elimination and absorption rate constants, respectively. They control the shape of the curve, specifically how quickly it rises and falls. At this stage, the model is much like what might be assumed before doing a least-squares fit to a single tumor's data to obtain estimates.

Stage 2: In the mixed-model approach, we further assume that the ke_ij, ka_ij, and cl_ij are, on the log scale, random observations from normal distributions:

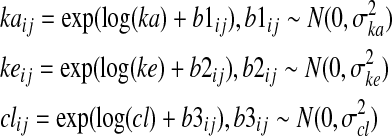(2)

Thus, ka, ke, and cl, are the median parameter values (across all tumors in the population), and b1_ij, b2_ij and b3_ij are tumor-specific deviations from the population median values. Equations (1) and (2) specify likelihood for the observed data. In population PK modeling, the parameters ka, ke, and cl and variance parameters σ_ka, σ_ke, and σ_cl are of primary interest. Our goal, however, was a tumor level prediction, and thus in the estimation of ke_ij, ka_ij, and cl_ij, that is, we were interested in the estimated time-activity curve for each individual tumor.

The model described here is part of a class of models typically referred to as nonlinear mixed-effect models. Standard maximum likelihood methods may be used to fit these models and obtain empirical Bayes estimates of the random effects ke_ij, ka_ij, and cl_ij. Details of estimation are given in Davidian and Giltinan.⁴ Estimates of AUC may be obtained as the analytical integral of A_ij(t) by plugging in empirical Bayes parameter estimates. The software package SAS V9.2 was used for model fitting.

In the present application, because the last imaging time point was typically about 145 hours postadministration for tracer and 190 hours postadministration for therapy, in computing AUC, we chose to integrate to 300 hours rather than to infinity. As discussed later, results from integration to 300 hours or infinity were very similar for all but 1 patient. Since one of our primary goals here was to assess the ability of tracer data to predict the therapy-delivered mean tumor-absorbed dose, we fit completely separate mixed models to tracer and therapy data. Our estimates of the correlation are thus not positively biased as could occur if we used a combined model.

Tumor dosimetry

The traditional approach to tumor dosimetry in internal emitter therapy has been based on the unit-density sphere model, which assumes that tumors are isolated unit-density spheres with a uniform activity distribution. The absorbed dose is then determined using published values of absorbed fraction as a function of sphere mass^16,17 or using the OLINDA/EXM code, where the sphere model has been implemented.¹⁸ This simplistic model does not account for any crossdose to the tumor from activity in other organs. Because of the limitations of this model, alternative approaches to tumor dosimetry using dose-point kernel or Monte Carlo-based methods have been used in some recent internal emitter therapy studies.^19,20 In the present study, we used SPECT/CT-imaging data coupled with the Dose-Planning Method (DPM) Monte Carlo algorithm²¹ to carryout patient-specific estimation of the mean radiation-absorbed dose to tumor. The calculation also provided 3D dose distributions and results of the 3D dose measures, including dose response, were reported in a previous publication³ and are not the focus of the present work.

The estimation of the mean tumor-absorbed dose using DPM has been described previously¹¹ and is summarized here. Because significant tumor shrinkage was observed over the imaging period (6 days post-tracer and 8 days post-therapy), the calculation of absorbed dose using DPM was split over multiple time periods (3 periods for tracer and 3 for therapy) to account for this shrinkage. Within each time period, the tumor size was assumed to be constant, but varied between periods according to the CT-defined volume. The input to DPM for each calculation was the SPECT image and CT-derived density map from a particular imaging time point, whereas the output was the absorbed dose-rate map. For each time period, the mean tumor dose rate was determined by summing voxel values of the DPM dose-rate map that were within the CT-defined tumor outline. For each time period, the residence time was determined by integrating the fitted time-activity curve over that time period. For tracer and again for therapy, tumor-absorbed doses for each time period (determined from the residence times and dose rates corresponding to that period) were summed to obtain the total mean tumor-absorbed dose. The therapy-delivered absorbed dose to the tumor was calculated based on data from the three post-therapy imaging points. The tracer-predicted absorbed dose to the tumor was calculated by scaling the results based on data from the three post-tracer imaging points by the ratio of therapy to tracer-administered activity.

Results

Table 1 gives population parameter estimates from the mixed model for tracer and therapy. The ka, ke, and cl values can be interpreted as parameter values for an average tumor. Specifically, from (2), it can be seen that the median of the ka_ij values is ka, since the b1_ij values have median 0. Similarly, the median of the ke_ij values is ke, and the median of the cl_ij values is cl. It appears that therapy estimates for ke and ka are somewhat larger and smaller, respectively, than tracer estimates, potentially implying a differently shaped curve. Our focus, however, is on individual tumor estimates, as discussed below and shown, for example, in Figures 3 and 4.

Table 1.

Mixed-Model Population Parameter Estimates

Parameter	Tracer estimate (standard error)	Therapy estimate (standard error)
ka (hours−1)	0.067 (0.011)	0.085 (0.014)
ke (hours−1)	0.778 (0.094)	1.209 (0.145)
cl (hours−1)	0.010 (0.001)	0.015 (0.001)
σka (hours−1)	1.693 (0.314)	1.682 (0.312)
σke (hours−1)	0.664 (0.157)	3.549 (0.481)
σcl (hours−1)	0.153 (0.045)	0.121 (0.030)

FIG. 3.

(A) A mixed-model fit to noisy tumor time-activity data and the least-squares fit to the individual data points. (B) A mixed-model fit to a tumor's therapy time-activity data with only a single activity value and the corresponding curve for tracer.

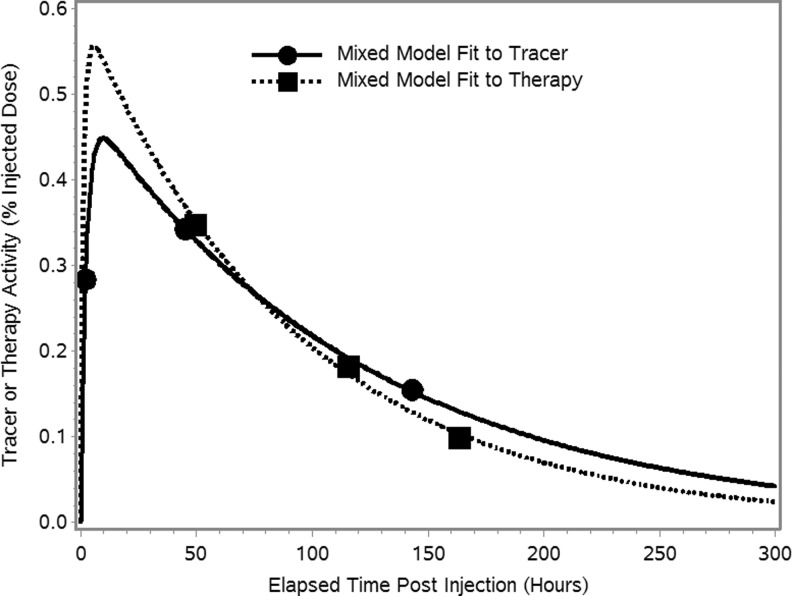
FIG. 4.

Time-activity curves for a typical tumor with biexponential function fits using a separate mixed model for tracer and therapy.

Fitted time-activity curves

Whole body

For all subjects, the whole-body time-activity data were well fit by individual least-squares fitting using a monoexponential function (R²>0.95 in all cases). Note that whole body here refers to the body section within the SPECT FOV. For all 19 patients, the mean and range of tracer and therapy whole-body residence times are given in Table 2.

Table 2.

Mean and Range (in Parenthesis) of Residence Times and Absorbed Dose

	Tracer study	Therapy study	Pearson's correlation	Slopea
Whole body (within field-of-view) residence time (hour)	32.0 (18.0–47.4)	32.1 (20.8–46.7)	0.95	0.983 (0.943,1.023)
Tumor residence time (hour)	0.31 (0.008–2.56)	0.27 (0.007–2.72)	0.98	0.993 (0.950, 1.035)
Tumor absorbed doseb (cGy)	293.6 (87.4–547.6)	319.5 (97.7–688.8)	0.86	1.043 (0.974, 1.112)

Also shown are correlation and slope estimates from linear regression models of tracer and therapy results.

^aFrom a regression model accounting for within subject correlation and with intercept fixed at zero for the tumor results.

^bPredicted value (tracer) and delivered value (therapy).

Tumor

Visual inspection of the biexponential time–activity curves fitted with the mixed model showed close agreement with the observed activity measurements. To quantify this, we calculated the differences (fitted value–observed), expressed as % injected dose. These values ranged from −0.0305 to 0.3550, with a median value of 0.0004 for tracer, and from −0.0706 to 0.0544, with a median value of −0.0002 for therapy. For tracer and therapy, 80% of differences were within±0.007 and 0.004, respectively.

The time-activity data of Figure 3 illustrate some of the benefits of a mixed-model approach to estimation over individual tumor curve fitting. One of the principle benefits is when the measured data for an individual patient are inconsistent, due to noise, for example (noise due to poor counting statistics is not a concern during post-therapy imaging, but can be significant during post-tracer imaging especially at the latter time points). For example, in the patient data of Figure 3A, the activity at the tracer-imaging time point 3 is higher than the value at the time point 2. A fit to just the 3 data points (black line) suggests unrealistically slow clearance, whereas the mixed-model estimate produces a curve of the expected shape. The individual curve is a biexponential function with extreme parameter values that do, nevertheless, optimize the least-squares criteria. Based on the results for other tumors, we believe that the mixed model yields a more realistic fitted curve (i.e., a curve with a shape exhibiting the expected uptake and clearance phases).

Another benefit of the mixed-model approach is the ability to obtain a realistic fit when there are missing data. In the present study, although patients were scheduled to be imaged three times post-tracer and three times post-therapy, a few subjects (3 out of 19) could not complete all the imaging studies as scheduled. In the case shown in Figure 3B, the patient completed the tracer imaging, but was imaged only one time after the therapy administration. The mixed-model fit to this single post-therapy data point was realistic with the expected uptake and clearance phases closely matching the mixed-model fit to the multiple tracer data points. The similarity, which is what one expects based on physiology being unperturbed by the level of the administered activity, gives us confidence in the use of the mixed model in this case.

Note that the examples shown in Figure 3 with inconsistent or missing data were exceptions, and in most cases, the measured time-activity data behaved as expected and were complete with results available for all 3 time points. A typical tumor time-activity curve with the mixed-model fit for tracer and therapy are shown in Figure 4. For all tumors, the tracer and therapy residence times are compared in Table 2.

We compared estimated residence times if fitted curves were integrated to infinity or were integrated to 300 hours. In all but one tumor, the results were within 5% of one another. In the one exception, the activity clearance from the tumor was unusually slow, and in this case, the residence time when integrating to infinity was 53% higher than the value from integrating to 300 hours. We also compared estimated residence times obtained from the mixed-model biexponential fit to those from simple least-squares monoexponential fits to individual tumors. For tracer, the ratios of the latter to the former ranged from 74% to 117%. For therapy, the same ratios ranged from 68% to 141%. For several tumors, the estimated value of ke was negative, implying increasing activity over time. We thus imposed the boundary constraint ke>0 on the estimation procedure. For these tumors with curves like that depicted in Figure 3A, the estimated residence time from the least-squares monoexponential fits would have been infinite if we had integrated to infinity rather than 300 hours. In contrast, the mixed model provided finite and reasonable estimates when integrating to infinity.

Correlation between tracer and therapy

Whole-body residence times

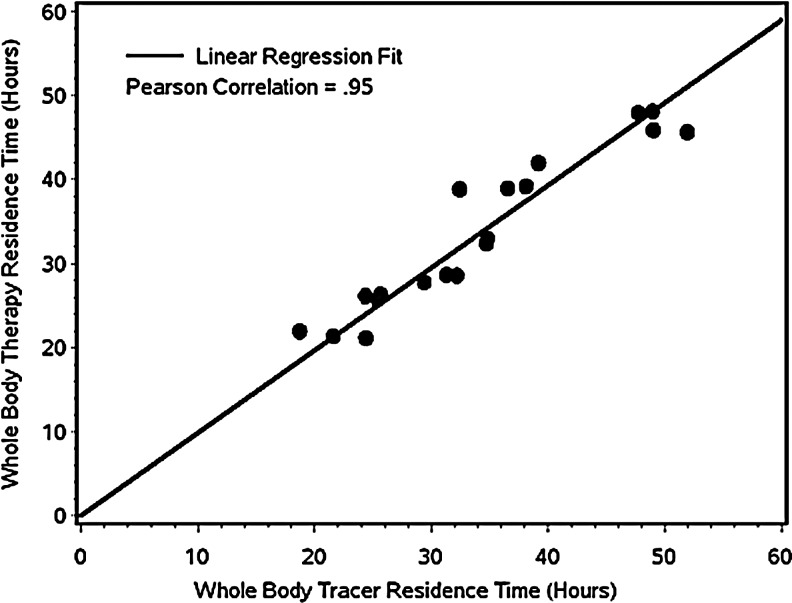
For whole body, the correlation between the tracer and therapy residence times of Table 2 are plotted in Figure 5. The correlation was excellent and statistically significant (r=0.95; p<0.0001), whereas the slope and intercept were very close to unity and zero, respectively. Since the scatter about the line is small, and the intercept and slope are what one would ideally expect, this result gives us confidence in the corrections (deadtime and pulse pileup) that were made to account for the high count rates during post-therapy imaging.

FIG. 5.

Plot of the therapy whole-body residence time versus the tracer whole-body residence time. The line of identity is not drawn, as it overlaps with the regression line.

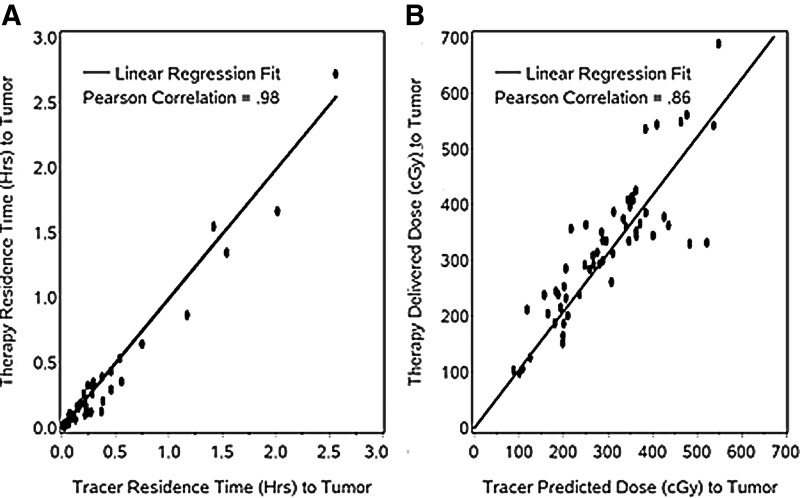
Tumor residence times

The correlation between tracer and therapy tumor residence times of Table 2 is plotted in Figure 6A. The correlation was excellent and statistically significant (Pearson's r=0.98; p<0.0001). We performed a linear regression (with intercept set=0) using tracer residence time to predict therapy residence time and tested whether the slope was equal to 1. It is generally assumed that this is the case, and our analysis confirmed this. The estimated slopes are very close to 1 and the 95% CIs bracket 1 (Table 2). We also calculated the differences between tracer and therapy, expressed as a percentage of the tracer value. These differences ranged from −67% to 103% and were within±41% for 80% of the tumors. When expressed in absolute hours, the differences ranged from −0.35 to 0.16 hours and were within±0.1 hours for 80% of the tumors.

FIG. 6.

Therapy-observed values versus tracer-predicted values at the tumor level for (A) residence time and (B) absorbed dose. Therapy and tracer values are estimated via separate mixed models. The linear regression-fitted line has an intercept set to zero. The line of identity is not drawn, as it overlaps with the regression line.

Tumor-absorbed dose

Ultimately for treatment planning, we are interested in absorbed dose rather than residence times. The correlation between the tumor-absorbed dose delivered by the therapy administration and the value predicted from the tracer (Table 2) is plotted in Figure 6B. This correlation (Pearson's r=0.86; p<0.0001), while still high, is lower than the correlation between tracer and therapy residence times. The estimated slopes with 95% CIs from a regression analysis are in Table 2. As above, we calculated the differences between tracer and therapy, expressed as a percentage of the tracer value. These differences ranged from −36% to 80% and were within±25% for 80% of the tumors. When expressed in absolute cGy, the differences ranged from −189 to 152 cGy and were within±75 cGy for 80% of the tumors. Some scatter about the fitted line is visible in Figure 6B. Possible explanations include inaccuracies in tumor definition, methods to quantify observed activity, and dose or sparsity of sampling time points.

Discussion

The tracer–therapy correlation in I-131 RIT was investigated using SPECT/CT-imaging data for 57 tumors in 19 lymphoma patients with a mixed-model fit to tumor time-activity. To our knowledge, this is the first application of statistical mixed models in internal emitter dosimetry, although this class of methods has found extensive application elsewhere in pharmacokinetics. The potential for using such a model in a radionuclide dose assessment was discussed in a recent review article.²²

Post-therapy imaging data were corrected for high count-rate effects, including camera deadtime and pulse pileup. SPECT quantification included 3D OSEM reconstruction and CT-based tumor outlines at each time point. For whole body (within FOV), excellent agreement was demonstrated between the tracer and therapy whole-body residence times (r=0.98; p<0.0001) with individual least-squares fitting using a monoexponential function.

Previously, in tumor dosimetry studies related to I-131-labeled antibodies, least-squares fitting of multiexponentials has been used when 5–7 time points were available, typically from planar imaging, whereas monoexponentials have been used when fewer time points were available.^5,19,23,24 Monoexponential fitting is inadequate to model the noninstantaneous uptake and clearance in tumor, but obtaining the necessary number of imaging time points for multiexponential fitting can be clinically unfeasible, especially in the case of SPECT/CT imaging. In the present study, use of a mixed-model approach to estimation of tumor time-activity curves allowed for biexponential fits, even though SPECT/CT-based activity measurement was available only at 3 time points and removed the dependence on starting values that are characteristic of the least-squares individual curve fits. Patient results demonstrated some of the benefits of a mixed-model approach to estimation over individual tumor curve fitting. The mixed-model approach yielded more efficient estimates and meaningful estimates even with noisy data or missing time points. Then, there was good agreement between the tracer and therapy tumor residence times (r=0.95; p<0.0001). The mixed-model biexponential fitting was also compared with simple least-squares monoexponential fitting to individual tumors. The tumor residence time determined from a monoexponential individual fit sometimes varied substantially from that obtained via the mixed-model biexponential fit with the ratio of the former to latter ranging from 68% to 141%.

If the conventional approach of estimating the absorbed dose based on baseline tumor mass and the unit-density sphere model was used here, the correlation between tracer-predicted and therapy-delivered mean tumor-absorbed doses would be the same as the correlation between tracer and therapy residence times. This is because the absorbed fraction for tracer and therapy will be the same if a constant mass is assumed, and the absorbed dose will vary linearly with the residence time. However, in the present work, we carried out a patient-specific Monte Carlo dosimetry accounting for CT-measured changes in the tumor volume during the imaging time period. In this case, the correlation between tracer-predicted and therapy-delivered mean tumor-absorbed dose can be different than the correlation for the residence time. Our correlation for absorbed dose was lower than the correlation between tracer and therapy residence time, but was still high (Pearson's r=0.86; p<0.0001).

In our mixed model described here, we have not explicitly modeled correlation between tumor responses within a subject. Although we have demonstrated excellent predictive ability with the present model, it is possible that this would further improve prediction, and will be investigated in the future. Accounting for both sources of correlation requires fitting multilevel (tumor and subject) random-effect nonlinear models, something not presently accommodated by most statistical software packages. One option is to take a Bayesian approach and fit the model via Markov Chain Monte Carlo (MCMC) methods.²⁵

Tracer-predicted and therapy-delivered absorbed doses differed by <25% for 80% of the tumors in the present analysis. While this is highly promising, clinical implementation of tumor dosimetry-based treatment planning in I-131 tositumomab RIT will require establishment of the tracer–therapy agreement for bone marrow and normal organs as well. We plan to evaluate these relationships in the future. In addition, robust correlations between dose and response must be established. Although this is yet to be achieved in I-131 tositumomab RIT of non-Hodgkin's lymphoma, promising dose–response results were previously reported using SPECT/CT-imaging-based dosimetry methods and radiobiological modeling.³

Conclusions

This study combined state-of-the-art quantitative SPECT/CT imaging, a mixed-model fit to tumor time-activity and patient-specific Monte Carlo-based dosimetry to evaluate the correlation between residence times and tumor-absorbed dose estimates from tracer and therapy studies. The strong correlation between predicted and delivered tumor-absorbed doses shown here demonstrates the potential for RIT treatment planning to deliver tailored therapeutic absorbed doses to tumors.

Acknowledgments

This work was supported by the grant 2R01 EB001994 awarded by the National Institute of Health, United States Department of Health and Human Services.

Disclosure Statement

Dr. Kaminski receives research support from GlaxoSmithKline and royalties from Bexxar. All other authors have no conflict of interest.