Abstract
This paper describes a method based on magnetic levitation (MagLev) that is capable of indirectly measuring the binding of unlabeled ligands to unlabeled protein. We demonstrate this method by measuring the affinity of unlabeled bovine carbonic anhydrase (BCA) for a variety of ligands (most of which are benzene sulfonamide derivatives). This method utilizes porous gel beads that are functionalized with a common aryl sulfonamide ligand. The beads are incubated with BCA and allowed to reach an equilibrium state in which the majority of the immobilized ligands are bound to BCA. Since the beads are less dense than the protein, protein binding to the bead increases the overall density of the bead. This change in density can be monitored using MagLev. Transferring the beads to a solution containing no protein creates a situation where net protein efflux from the bead is thermodynamically favorable. The rate at which protein leaves the bead for the solution can be calculated from the rate at which the levitation height of the bead changes. If another small molecule ligand of BCA is dissolved in the solution, the rate of protein efflux is accelerated significantly. This paper develops a reaction-diffusion (RD) model to explain both this observation, and the physical-organic chemistry that underlies it. Using this model, we calculate the dissociation constants of several unlabeled ligands from BCA, using plots of levitation height versus time. Notably, although this method requires no electricity, and only a single piece of inexpensive equipment, it can measure accurately the binding of unlabeled proteins to small molecules over a wide range of dissociation constants (Kd’s within the range of ~ 10 nM to 100 µM are measured easily). Assays performed using this method generally can be completed within a relatively short time period (20 minutes – 2 hours). A deficiency of this system is that it is not, in its present form, applicable to proteins with molecular weight greater than approximately 65 kDa.
INTRODUCTION
Methods that assay the concentration of small molecules in biological samples are broadly used as diagnostic tools, and in biomedical testing (e.g. glucose, vitamins, hormones such as progesterone and testosterone, and other metabolites such as urea and homocysteine).1 Since the concentrations of these small molecules are often more variable over time than those of diagnostic markers such as proteins, methods that can rapidly assay the concentrations of small molecules in point-of-care settings have the potential to be broadly useful. We have described magnetic levitation (MagLev) of a diamagnetic analyte in a paramagnetic fluid as a new technique for analysis.2,3 Bioanalysis provides a number of interesting opportunities for MagLev. We are especially attracted by the fact that this method does not require electricity or expensive instrumentation, and is thus suitable for use in developing countries and in point of care applications. Our previous iteration of this methodology3 has a number of attractive characteristics relative to other bioanalytical techniques, but suffers from three major disadvantages: (i) It is only applicable to ligands that can be covalently immobilized on a bead. (ii) It suffers from relatively slow kinetics; the assays typically require from hours to days to reach completion. (iii) It can only be applied to small or moderately sized proteins (MW < ~65 kDa), using the beads described previously.
This article describes a method based on MagLev for measuring the binding of bovine carbonic anhydrase (BCA; E.C. 4.2.1.1) to ligands in solution, by competition with a standard ligand immobilized on a bead. Using this method, we can assay protein-ligand binding in ~20 minutes. This interval is a significant improvement over the previous system, in which assays require from ~3 hours to days.3 This method uses diamagnetic gel beads that are labeled covalently with ligands for a protein of interest (in our case, immobilized aryl sulfonamides, which bind to BCA4) that also binds to a small molecule of interest. In an initial step, we incubate these beads with the protein and allow the protein to diffuse into the bead and bind to the immobilized ligands (the slow step). We then suspend these beads in a paramagnetic solution composed of a chelate of Gd(III) in buffer, placed between two NdFeB magnets (50 × 50 × 25 mm) oriented with like poles facing each other, 45 mm apart.2,3 With this configuration of magnets, the bead levitates at a position that depends linearly on its density. Since the protein has a higher density than the bead, release of protein from the bead decreases its density, and thus causes an increase in the height at which it levitates. Adding a low molecular weight ligand (which diffuses rapidly into the bead) to the solution releases the protein, and allows it to diffuse from the bead into the buffer at a rate that is dependent on the affinity of the protein for the ligand, and on the concentration of the ligand in solution.
This paper describes the physical-organic underpinnings of a method that is capable of establishing both concentrations of small molecule ligands, and their affinities for a protein of interest. The method is inexpensive – it requires only a single piece of equipment that holds two NdFeB magnets (~$5 – 20 each) at a defined distance. The method has a number of additional practical advantages: (i) It can be sensitive and quantitative: differences in the structure or concentration of the small molecule ligand result in predictable changes in the observable (rate of change of levitation height). (ii) It is label-free: neither the protein nor the small molecules need to be functionalized. (iii) It is rapid: single assays can easily be performed within an hour and often within 10–15 minutes. One limitation of this approach is that it requires at least one known ligand that can be covalently attached to the diamagnetic bead. A second, with the commercial beads we are using, is that it is restricted to proteins with low or intermediate molecular weights (MW < ~65 kDa). In this paper, for a variety of reasons we describe in detail below, we use bovine carbonic anhydrase (BCA) as a model protein (MWBCA ~ 29 kDa). Even with this relatively small protein, the method requires a long pre-equilibration step of BCA with the gel-bound ligands. This step can, however, be performed well in advance of the assay, and it does not impose a significant damper on the utility of our system for many applications.
EXPERIMENTAL DESIGN
Design of the device, and choice of the paramagnetic fluid, solid-support (resin), and model protein-ligand system
We have described the MagLev device used for these studies.2c,d,3 It consists of two commercial NdFeB magnets positioned with like poles facing towards each other. In this configuration of magnets, Eqn. 1 describes the vertical position of the levitating bead (h), and indicates that the position correlates linearly with the density of the bead (ρbead). In this equation, ρbead and ρm, (both kg·m−3) and χbead and χm (both unitless) are the densities and the magnetic susceptibilities of the bead and the paramagnetic medium, respectively; g is the acceleration due to gravity (9.8 m·s−2), μ0 is the magnetic permeability of free space (4π × 10−7 N·A−2), d is the distance between the magnets (0.045 m), and B0 is the magnitude of the magnetic field at the surface of the magnets (T, typically ~ 0.38 T).
| (1) |
As with our previous study,3 we used buffered aqueous solutions of disodium gadolinium (III) diethylenetriaminepentaacetic acid (2Na+·Gd(DTPA)2−) as the medium for levitation. Unless specified otherwise, all MagLev measurements were performed in a solution of 300-mM Gd(DTPA) dissolved in 6-mM phosphate buffer and adjusted to pH 7.4 using sodium hydroxide (referred to throughout this text as the “standard levitation buffer”). This composition provided a buffer with an approximate match in density to that of the PEGA beads (ρm = 1.099 g·mL−1, ρPEGA ≈ 1.07 g·cm−3), and the chosen concentration of gadolinium(III) provided a useful compromise between sensitivity and dynamic range of detection by MagLev (|χbead – χm| ≅ χm = 8.4 × 10−5; dynamic range ~ 1.056 – 1.143 g·mL−1). The viscosity of the standard levitation buffer was determined by measuring the rate of descent of a nylon sphere through this buffer (see Supporting Information); this buffer has a viscosity (μ = 0.006 Pa·s) that is approximately six times the viscosity of water. We used a ruler with a millimeter scale to measure the distance from the bottom magnet to a levitating bead (i.e., the levitation height of the bead). Using a digital camera outfitted with a macro lens, we could measure this distance with an uncertainty of ±0.1 mm.
Building on our previous research,3 we used bovine carbonic anhydrase (BCA) and aryl sulfonamides to generate a reaction-diffusion model that describes the basic biophysical chemistry of our system. We use this system for several reasons, including the fact that: (i) BCA is inexpensive and commercially available. (ii) Numerous inhibitors of BCA are known; many are commercially available, and have well-characterized binding constants.4 (iii) BCA is a small protein (~ 30 kDa) and will diffuse in and out of the PEGA beads used in this study. (iv) BCA has an exceptionally stable tertiary structure, and is not adversely affected by the levitation media. (v) There is extensive background on the use of carbonic anhydrase in physical organic studies of protein binding. In particular, values of Kd, kon, and koff, are known for a number of ligands.4
We used poly[acryloylated O,O’-bis(2-aminopropyl) polyethylene glycol] (PEGA) beads for this study (300–500 µm diameter in water).5 This commercially available resin has several advantageous properties, including: (i) PEGA beads present amine functionality (0.2 mmol·g−1); this functional group allows for straightforward chemical functionalization. (ii) The beads resist non-specific adsorption of proteins. (iii) The density of PEGA beads (ρPEGA ≈ 1.07 g·cm−3) is significantly different from the density of the protein (ρprotein ≈ 1.3–1.5 g·cm−3).6 This difference in density is required if binding of protein to the bead is to cause a usefully quantifiable change in the overall density of the bead. The main disadvantage of these commercial PEGA beads is that their small pores (as a cross-linked acrylamide gel) slow the mass transport of proteins into and through the interior of the bead, and excludes proteins with molecular weight greater than ~ 40–70 kDa.7
Unmodified PEGA beads are also difficult to visualize during levitation because their refractive index is close to that of the solution. To improve the visibility of these beads, we functionalized a small portion of the amines on them with dyes (e.g., by reaction with the isothiocyanates of rhodamine, malachite green, and 7-dimethylamino-4-methylcoumarin). These modifications make the beads easily visible under ambient or UV light.
Model for quantifying the amount of protein bound per bead with MagLev
We previously developed a model that quantifies the relationship between the amount of protein bound per PEGA bead, and the observed change in levitation height using MagLev.3 Under our standard levitation conditions, a 1-mM decrease in the concentration of protein within a bead will result in a 8.6-mm increase in levitation height.
Model describing the dissociation of protein from ligand-functionalized gel bead in the presence of a second, soluble ligand
The method reported in this paper utilizes gel beads that are covalently functionalized with a ligand that binds to a protein of interest. Since there is a difference in density between the protein and the gel beads, the association or dissociation of a protein molecule from the gel bead causes the bead to change in density. Using MagLev, we can observe this change in density in real time; these observations allow us to estimate the kinetics of protein diffusion and protein-ligand association/dissociation.
Before each experiment, we soak the gel beads in a solution of the protein. We use a relatively large volume of protein solution, such that there is > 100 times more protein than on-bead ligand. The equilibrium position of this system is described by Eqn. 2, where P is the protein within the bead, *L is the ligand immobilized on the bead, *PL is the immobilized protein-ligand complex, and the dissociation constant is defined by the ratio of the off and on rates, (throughout this text, * is used to indicate a species immobilized on the gel).
| (2) |
After equilibration, and before each experiment (t = 0), the concentration of free protein within the bead, [P]0, is defined by the partition coefficient of the protein from the solution to the interior of the bead, Kbead/sol (Eqn. 3), where [Psol] is the concentration of protein in the soaking solution.
| (3) |
In addition, the concentration of the immobilized protein-ligand complex, [*PL]0, is defined by Eqn. 4, where [*L]T is the total concentration of immobilized ligand within the bead (both bound and unbound to protein). We use concentrations of protein and immobilized ligand that ensure this equilibrium reaction is shifted almost entirely to the side of the immobilized protein-ligand complex ([*PL/[*L] ~ .30).
| (4) |
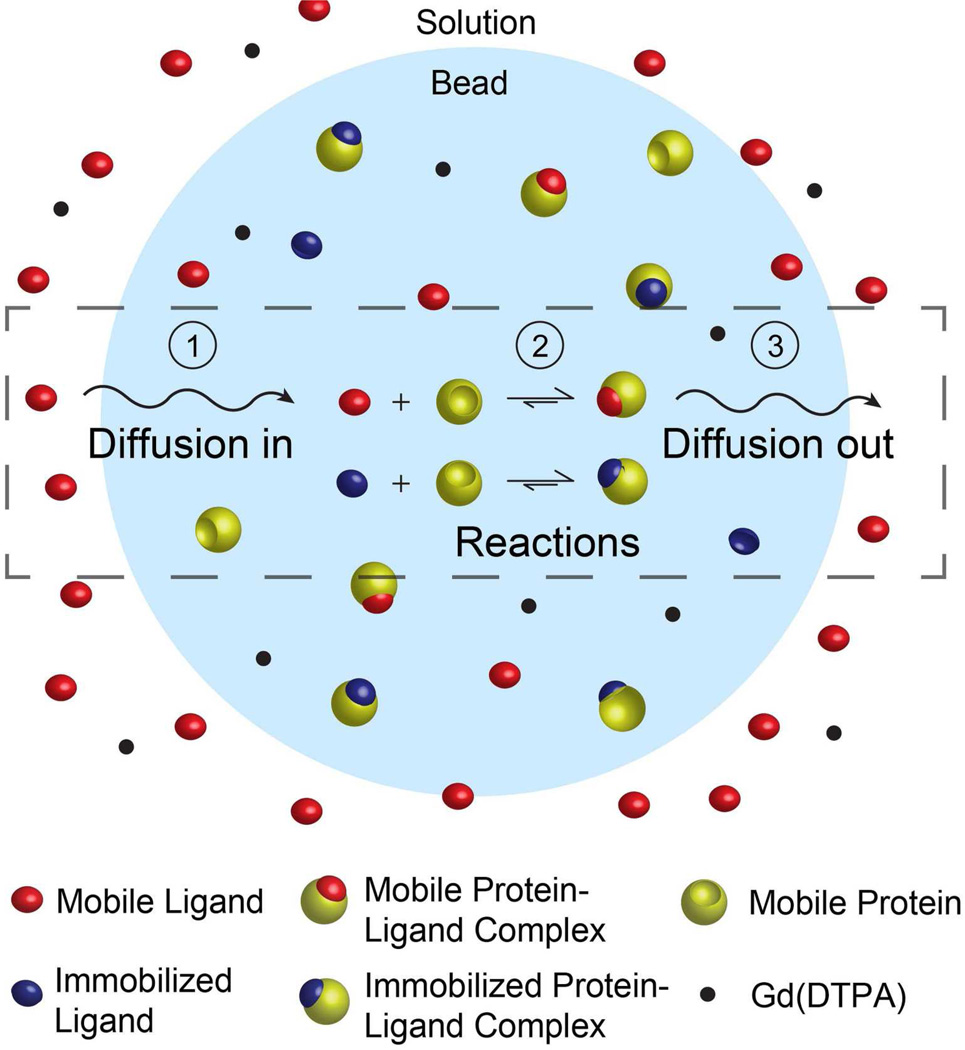
Transferring a gel bead that has been soaked in a solution of protein to a solution containing free, soluble ligands, LS, initiates a reaction-diffusion process (Figure 1). The entire RD process involves four steps (Figure 1): (i) Diffusion of free ligands, LS, from the solution into the bead. (ii) Dissociation of the protein from the immobilized ligands, according to Eqn. 1. (iii) Reaction of the soluble ligands with the unbound protein in the bead forming the mobile protein-ligand complex, PLS, according to the equilibrium reaction described in Eqn 5. (iv) Diffusion of the unbound protein, P, and mobile protein-ligand complex, PLS, from the bead to the solution.
| (5) |
Figure 1.
Reaction-diffusion model describing the dissociation of protein from ligands immobilized on a gel support, and subsequent diffusion of the protein from the inside of the bead to the solution in the presence of a second, mobile ligand. The RD process consists of four distinct steps: (i) diffusion of the mobile ligands from the solution to the interior of the bead, (ii) unbinding/binding of protein to the ligand immobilized on the bead, (iii) unbinding/binding of protein to the mobile ligand, and (iv) diffusion of the unbound protein and mobile protein-ligand complex from the bead to the solution.
Throughout these RD processes, there are five principal components: (i) the ligand immobilized on the bead, *L, (ii) the mobile ligand, LS, (iii) the unbound protein within the bead, P, (iv) the protein-ligand complex formed by protein binding to the immobilized ligands, *PL, and (v) the protein-ligand complex formed by protein binding to the mobile ligands, PLS.
A decrease in the total concentration of protein within the bead, including *PL, P, and PLS, causes a decrease in the density of the bead, which can be observed using MagLev. The total concentration of protein within the bead decreases when a protein molecule or protein-ligand complex diffuses from the interior of the bead to the surrounding solution. We have determined experimentally that the relationship between the total amount of protein within the bead, nprotein, and the change in levitation height, Δh (Δh·Vbead·(nprotein)−1 = −8.6 mm/mM, where Vbead is the volume of the bead.3
The dynamics of this process can be described mathematically by a system of reaction-diffusion equations (Eqns. 6a–e).
| (6a) |
| (6b) |
| (6c) |
| (6d) |
| (6e) |
In these equations, t is time, [*L]T is the total concentration of immobilized ligands in the bead, DP (m2/s) is the diffusion coefficient of both the unbound protein and the mobile protein-ligand complex, and DL (m2/s) is the diffusion coefficient of the mobile ligand.
In this formulation of the RD process, we assume that the diffusion coefficients of the protein and the protein-ligand complex are equal, and that all diffusion coefficients are constant both spatially and temporally. We also assume that there are no external mass-transport limitations (i.e. there are no concentration gradients of protein, protein-ligand complex, or ligand outside of the bead).
At the beginning of each experiment (t = 0), the beads contain the immobilized protein-ligand complex at concentration [*PL]0 (Eqn. 4). At t > 0, the beads are added to an aqueous levitation buffer containing a soluble ligand. The exterior of the bead is, therefore, subjected to boundary condition: [LS] = [LS]sol, where [LS]sol is the concentration of ligands in the solution.
We solve this system of RD equations numerically using the finite-difference method in spherical coordinates, implemented in C++. The numerical solution yields the concentration profile in the bead for all reacting species with respect to time. The total amount of protein in the bead, nprotein, can be obtained by integrating the three species P, PLS and *PL spatially across the bead.
In analogy to our experiments, we used the following parameters for our calculations: (i) The total concentration of ligands within the bead, [*L]T, is 3.2 mM. (ii) We assume that at the beginning of each experiment all of these ligands are occupied with protein (e.g. [*PL]0 = 3.2 mM). (iii) The radius of the beads, R, is 170 µm. (iv) The diffusion coefficient of the soluble ligand, DL, is on the order of 10−10 m2/s.8
In practice, at the start of each experiment, gel beads are transferred from a solution of protein, dissolved in the standard levitation buffer, to a microcuvette containing the ligand of interest dissolved in the same buffer. The microcuvette is then placed within the MagLev device. The beads require ~5 minutes to approach the levitation height that describes their density (the viscosity of the levitation solution is ~6 times the viscosity of pure water, see supporting information): beginning from near the top of the cuvette, the beads sink toward the bottom of the solution before beginning to move upward due to the decreasing density of the bead as protein diffuses out of the beads (for a description of the relationship between viscosity of the levitation solution, the diameter of an object, and the time it takes that object to reach its equilibrium levitation height, see reference 2c). For data analysis, we therefore discard the first five minutes of each experiment.
Analytically, the optimal conditions for the assay can be defined by considering the ratio of PLS and *PL in the presence of both the soluble and immobilized ligands. When the concentrations of these two species are similar ([PLS]/[*PL] ~ 1), the binding equilibria (Eqns. 2, 5) have a large effect on the overall rate of protein efflux.
We developed Eqn. 7 to guide us in defining the optimal range of concentrations of LS to be used for each assay.
| (7a) |
| (7b) |
This equation is derived from the hypothesis that the ratio [PLS]/[*PL] can be determined analytically by considering the two competing binding reactions (Eqns. 2, 5), and ignoring any effects of diffusion. Initially, the bead contains the immobilized protein-ligand complex at concentration [*PL]0; the system is then subjected to a concentration of the mobile ligand ~ equal to [LS]sol (DL >> DP). Given these conditions, we solve for the resulting equilibrium position of the reaction system, and extract the ratio of the mobile and immobilized protein ligand complexes at the imaginary time point δ (Eqn. 7, ).
When [PLS]/[*PL] > 5 or [PLS]/[*PL] < 1/5, the MagLev-based detection system may provide unreliable results, since, under these conditions, competition of the two ligands for binding to protein has a reduced effect on the overall rate of the RD process (vide infra). For each experiment in this study, we therefore tune [L]sol such that the calculated concentration ratio ([PLS]/[*PL])δ lies within the optimal range (1/5 to 5). A practical value for [LS]sol can be found by setting Eqn. 7a to unity and solving for [LS]sol.
We calculate the dissociation constant of the mobile protein-ligand complex by fitting plots of change in levitation height versus time to our RD model. For reasons described previously we omit the first five minutes of data from the fitting process.
The optimal conditions for determination of the Kd of the mobile protein-ligand complex lie within the range of two extreme conditions: (i) When the gel beads are subjected to a high concentration of a soluble ligand with high affinity for the target protein, the equilibrium reactions between the protein, the immobilized ligand, and the soluble ligand are shifted towards formation of the mobile protein-ligand complex, PLS, and away from the immobilized protein-ligand complex, *PL (i.e., ([PLS]/[*PL])δ >> 1). Under these conditions, the rate of protein efflux from the bead to the solution depends mainly upon the diffusion coefficient of the mobile protein-ligand complex, and not on any aspect of protein-ligand binding. (ii) On the other hand, when the beads are subjected to a low concentration of a soluble ligand with low affinity for the target protein, negligible amounts of PLS are formed (i.e., ([PLS]/[*PL])δ << 1) and the soluble ligands virtually do not participate in the RD process. Under these conditions, the RD process is limited by the dissociation of *PL and the slow diffusion of P (Eqn. 2).
We used extreme conditions (i) to measure experimentally the diffusion coefficient of the mobile protein-ligand complex within the bead (DP ~ 5 × 10−12 m2/s), and conditions (ii) to measure the dissociation constant of the immobilized protein-ligand complex, . (vide infra). Importantly, the diffusion of the ligands, DL ~ 10−10 m2/s, is much faster than the diffusion of either unbound protein or mobile protein-ligand within the beads; as a consequence, the diffusion of the ligands has a negligible effect on the overall rate of the RD process.
Overall, this method uses data collected from a kinetic process (a plot of levitation height vs. time) to extract information about a constant, the dissociation constant Kd, related to thermodynamic equilibrium. This approach is possible under conditions where the rates of protein-ligand binding and dissociation are much faster than the rate of diffusion of the protein. These conditions provide a situation where the RD process is limited by both the slow diffusion of the mobile protein-ligand complex, PLS, in the bead and also by the shift in the protein-ligand binding reactions that produce more PLS. In fact, under conditions where the rate of diffusion is faster than the rates of the binding (i.e., ([PLS]/[*PL])δ >> 1, Eqn. 7), the rate of the RD process contains insufficient information to determine the strength of protein-ligand binding.
RESULTS AND DISCUSSION
In this section, we examine the potential of MagLev as a tool for characterizing the strength of protein-ligand interactions. Unless specified otherwise, all MagLev measurements were performed in a solution of 300 mM Gd(DTPA), and 0.05% polysorbate 20, dissolved in 10 mM phosphate buffer and adjusted to pH 7.4 using sodium hydroxide. This composition provided a buffer with an approximate match in density to that of the PEGA beads. This concentration of gadolinium(III) was chosen to provide a useful compromise between sensitivity and dynamic range of detection by MagLev. The non-denaturing surfactant, polysorbate 20, was added to reduce non-specific binding of proteins to the PEGA beads, and to prevent the beads from adhering to the cuvette.
Protein slowly binds to ligands that are immobilized within gel beads
In a previous report, we verified that protein absorbs to PEGA beads only when those beads are functionalized with a small molecule ligand that binds specifically to that protein.3 Building on that work, we develop the method reported in this paper using a well-characterized system of protein and ligands: bovine carbonic anhydrase (BCA) and derivatives of benzenesulfonamide. Using standard coupling chemistry, we immobilized 4-carboxybenzene sulfonamide (1) on Rhodamine-dyed PEGA beads using standard coupling chemistry (Eqn. 8).
| (8) |
We incubated the beads, functionalized with sulfonamide 1, in a solution of 450 µM BCA dissolved in the standard levitation solution (~200 beads in 0.3 mL). Before incubation, the beads levitate at 37 ± 0.5 mm in the standard levitation buffer. After incubation for one week, the beads levitate at 11 ± 1.0 mm; longer incubation times did not result in additional changes to the equilibrium levitation height of the beads. This equilibrium levitation height is defined by the density of the beads. Protein binding to the beads increases their density. The majority of protein within the beads is bound to the immobilized ligands. The concentration of the protein-ligand complex within the bead, at equilibrium, is defined by the Kd of the protein-ligand complex. We, therefore, initially performed an experiment to calculate this dissociation constant, as outlined below.
MagLev can be used to determine the diffusion coefficient of the protein within the gel, and the dissociation constant of the immobilized protein-ligand complex
Before we could utilize this system for calculating the dissociation constants of protein-ligand complexes, it was first necessary to calculate the diffusion coefficient of the protein, DP. In order to use our RD model to extract a value for DP, we transferred sixteen beads, functionalized with sulfonamide 1, from the solution of BCA, to a fresh solution of levitation media containing a high concentration (0.1 M) of trifluoromethane sulfonamide contained within a microcuvette. This small molecule is known to bind tightly to BCA (Kd ~ 2 – 13 nM).4 Under these conditions, the combination of the high concentration and low dissociation constant of the soluble ligand ensures the reactions between the protein, the immobilized ligand, and the soluble ligand are shifted strongly towards formation of the mobile protein-ligand complex, PLS (Eqn. 7). The rate of protein efflux from the bead to the solution is, therefore, only limited by the diffusion of the mobile protein-ligand complex out of the bead. Figure 2A shows the change in levitation height of these beads (Δh, in millimeters) versus time (t, in minutes). We calculated the diffusion coefficient of the protein, DP, by fitting these data to our model of the RD process (Eqn. 6). The best fit, using DP = 5 × 10−12 m2/s, provides a value for the diffusion coefficient that is similar to previously reported values estimated by ultracentrifugation (~ 1 × 10−12 m2·s−1).9
Figure 2.
Monitoring the dissociation of BCA from 4-carboxybenzene sulfonamide labeled PEGA beads with MagLev. We incubated PEGA beads in a solution of 450 &M BCA dissolved in the standard levitation buffer for one week. A) We removed sixteen of these beads and suspended them in a 100 mM solution of trifluoromethane sulfonamide dissolved in the standard levitation buffer. We extracted the diffusion coefficient of the protein-ligand complex (DP ~ 5 × 10–12 m2/s), by fitting the resulting plot of the levitation height of these beads versus time to our RD model. B) We removed fourteen beads, rinsed them, and suspended them in the standard levitation buffer. We fit a plot of the average levitation height of these beads versus time was fit to our RD model, and used this fit to extract a value for the dissociation constant of the immobilized protein-ligand complex . In both plots, error bars show the standard deviation in the levitation heights of the beads used in a single experiment (N = 14–16).
In order to determine the dissociation constant, , of the immobilized protein-ligand complex, we measured the rate of dissociation of protein from these beads in the absence of an additional soluble ligand. Under these conditions, the protein-ligand complex, *PL is in equilibrium with unbound protein and immobilized ligands. The unbound protein is free to diffuse out of the bead, which in turn allows more *PL to dissociate. We transferred fourteen beads, functionalized with sulfonamide 1, from the solution of BCA, to a fresh solution of levitation media. We monitored the levitation height of these beads over time and fit these data to our RD model (Figure 2B). The comparison of the experimental results and the model we developed, using , demonstrates good agreement.
MagLev provides a rapid and reliable method of determining the dissociation constants of protein-ligand complexes
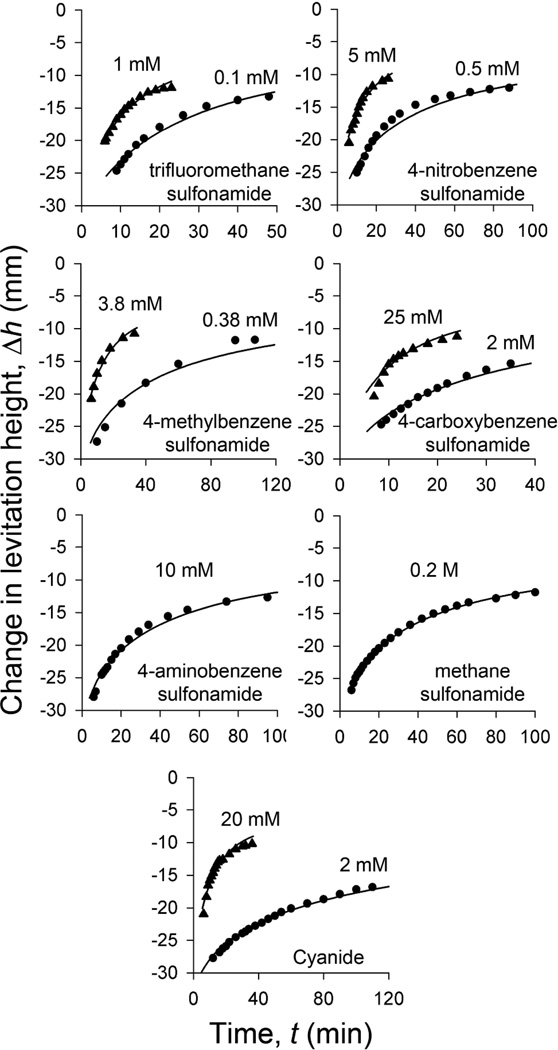
After establishing the relevant parameters for the process, we set out to utilize our model of reaction-diffusion to extract the affinities of various mobile ligands, LS, for the target protein (see Eqn. 5). We investigated seven different ligands with a range Kd’s for BCA over nearly five orders of magnitude; Figure 3 illustrates the data, and their fit to our RD model. We selected the optimal concentration of each ligand using Eqn. 7. The values for Kd, extracted using the RD model, are in close agreement with those reported in previous studies (Table 1).
Figure 3.
Dissociation of BCA from PEGA beads labeled with 4-carboxybenzene sulfonamide in the presence of seven soluble ligands, measured using MagLev. To measure these data, we first incubated PEGA beads in a solution of 450 µM BCA for one week. We then removed a batch of these beads (10 – 15 beads), rinsed them, and suspended them in a microcuvette containing the standard levitation buffer in which we had dissolved one of seven known ligands of BCA (the concentration of ligand is indicated on the graphs). We placed this microcuvette into our MagLev device and measured the change in levitation height over time (after allowing five minutes for the beads to reach their equilibrium levitation height). We used this data to calculate values for the association constant of each ligand with BCA by fitting these data to our RD model.
Table 1.
Measured and literature data for the binding of carbonic anhydrase to seven sulfonamides.
| Entry | Ligand Kd | Kdobs (nM)a | Kd or Ki (nM)b |
|---|---|---|---|
| 1 | trifluoromethane sulfonamide | 14 | 2 – 13 |
| 2 | 4-nitrobenzene sulfonamide | 95 | 65 |
| 3 | 4-methylbenzene sulfonamide | 290 | 84 |
| 4 | 4-carboxybenzene sulfonamide | 440 | 270 |
| 5 | cyanidec | 1,200 | 2,600 |
| 6 | 4-aminobenzene sulfonamide | 18,000 | 3,000 – 23,000 |
| 7 | methane sulfonamide | 69,000 | 70,000 – 320,000 |
CONCLUSION
This study establishes the physical-organic basis for a method based on magnetic levitation that is capable of detecting the binding of unlabeled protein to unlabeled ligands using no spectroscopy and minimal equipment. In the first step of this method, the protein of interest is allowed to bind to a small molecule ligand immobilized on a gel bead. In a second step, the gel bead is transferred to a paramagnetic solution and the rate at which the protein diffuses out of the gel bead into solution is calculated by monitoring the change in the density of the bead using MagLev. This rate is slowed by rebinding to additional immobilized ligand and accelerated in the presence of a second ligand dissolved in solution. In order to understand better the physical-organic chemistry underlying these processes, we developed a model of these reaction-diffusion processes that allows us to correlate quantitatively the rate of protein efflux from the gel bead with the affinity and concentration of the ligand in solution.
This study builds on our previous work in this area; this work demonstrated that MagLev is capable of detecting the binding of protein to gel-bound ligands.3 The method reported herein has two distinct advantages over our previous approach: (i) It can be used to quantify the affinity of an unlabeled protein for an unlabeled ligand. Our previously reported system is limited to ligands that can be chemically immobilized on a gel bead. (ii) Assays with the method reported in this paper typically require less than one hour. In contrast, with our previous system, each assay required many hours, or even several days to complete. (iii) The method reported in this paper can be used to measure the binding of ligands with a wide range of affinities for a target protein. In this paper, we measure dissociation constants over the range of ~ 10-nM to 100-µM. In theory, ligands with even higher and lower affinity can also be measured, although, in the latter case, the ligands must have high solubility in the levitation buffer.
With PEGA beads, this method still suffers the disadvantage that it is only applicable to relatively small proteins (MW < ~65 kDa). We believe that this problem will be resolved through the design and synthesis of beads with larger effective pore sizes and appropriate densities (ρ ≤ 1.1 g/cm3). Given that this method requires no electricity and minimal equipment, and is easy to use, it may be particularly useful in situations where portability and low cost are a high priority.
Supplementary Material
ACKNOWLEDGMENTS
This work was partially supported by the Bill & Melinda Gates Foundation (no. 51308), the Wyss Institute of Biologically Inspired Engineering, the U.S. Department of Energy (no. DE-SC0000989, funding used to support mathematical analysis of reaction-diffusion systems), and a postdoctoral fellowship from the NIH (NDS).
REFERENCES
- 1.Venn RF. Principles and Practice of Bioanalysis. London, UK: Taylor & Francis; 2000. [Google Scholar]; (b) Walker JM, Rapley R, editors. Molecular Biomethods Handbook. Totowa, NJ: Humana Press; 2008. [Google Scholar]
- 2.(a) Winkleman A, Perez-Castillejos R, Gudiksen KL, Phillips ST, Prentiss M, Whitesides GM. Anal. Chem. 2007;79:6542. doi: 10.1021/ac070500b. [DOI] [PubMed] [Google Scholar]; (b) Mirica KA, Phillips ST, Shevkoplyas SS, Whitesides GM. J. Am. Chem. Soc. 2008;130:17678. doi: 10.1021/ja8074727. [DOI] [PubMed] [Google Scholar]; (c) Mirica KA, Shevkoplyas SS, Phillips ST, Gupta M, Whitesides GM. J. Am. Chem. Soc. 2009;131:10049. doi: 10.1021/ja900920s. [DOI] [PubMed] [Google Scholar]; (d) Mirica KA, Phillips ST, Mace CR, Whitesides GM. J. Agric. Food Chem. 2010;58:6565. doi: 10.1021/jf100377n. [DOI] [PubMed] [Google Scholar]; (e) Mirica KA, Ilievski F, Ellerbee AK, Shevkoplyas SS, Whitesides GM. Adv. Mater. 2011;23:4134. doi: 10.1002/adma.201101917. [DOI] [PubMed] [Google Scholar]
- 3.Shapiro ND, Mirica KA, Soh S, Mace CR, Taran O, Shevkoplyas SS, Phillips ST, Whitesides GM. J. Am. Chem. Soc. 2012;134:5637. doi: 10.1021/ja211788e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Krishnamurthy VM, Kaufman GK, Urbach AR, Gitlin I, Gudiksen KL, Weibel DB, Whitesides GM. Chem. Rev. 2008;108:946. doi: 10.1021/cr050262p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.(a) Auzanneau F-I, Meldal M, Bock K. J. Pept. Sci. 1995;1:31. doi: 10.1002/psc.310010106. [DOI] [PubMed] [Google Scholar]; (b) Renil M, Ferreras M, Delaisse JM, Foged NT, Meldal M. J. Pept. Sci. 1998;4:195. doi: 10.1002/(SICI)1099-1387(199805)4:3%3C195::AID-PSC141%3E3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 6.(a) Chick H, Martin CJ. Biochem. J. 1913;7:92. doi: 10.1042/bj0070092. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Quillin ML, Matthews BW. Acta Cryst. 2000;56:791. doi: 10.1107/s090744490000679x. [DOI] [PubMed] [Google Scholar]; (c) Fischer H, Polikarpov I, Craievich AF. Protein Sci. 2004;13:2825. doi: 10.1110/ps.04688204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.(a) Kress J, Zanaletti R, Amour A, Ladlow M, Frey JG, Bradley M. Chem. Eur. J. 2002;8:3769. doi: 10.1002/1521-3765(20020816)8:16<3769::AID-CHEM3769>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]; (b) Auzanneau F-I, Meldal M, Bock K. J. Pept. Sci. 1995;1:31. doi: 10.1002/psc.310010106. [DOI] [PubMed] [Google Scholar]
- 8.(a) Brown W, Chitumbo K. J. Chem. Soc., Faraday Trans. 1975;71:12–21. [Google Scholar]; (b) Pickup S, Blum FD, Ford WT, Periyasamy M. J. Am. Chem. Soc. 1986;108:3987–3990. [Google Scholar]; (c) Oyaas J, Storro I, Svendsen H, Levine DW. Biotechnol. Bioeng. 1995;47:492–500. doi: 10.1002/bit.260470411. [DOI] [PubMed] [Google Scholar]
- 9.Creighton TE. Proteins: Structures and Molecular Properties. 2nd edn. New York, NY: W.H. Freeman and Company; 1993. p. 266. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.