The α-Helix to β-Sheet Transition in Stretched and Compressed Hydrated Fibrin Clots

Abstract

Fibrin is a protein polymer that forms the viscoelastic scaffold of blood clots and thrombi. Despite the critical importance of fibrin deformability for outcomes of bleeding and thrombosis, the structural origins of the clot’s elasticity and plasticity remain largely unknown. However, there is substantial evidence that unfolding of fibrin is an important part of the mechanism. We used Fourier transform infrared spectroscopy to reveal force-induced changes in the secondary structure of hydrated fibrin clots made of human blood plasma in vitro. When extended or compressed, fibrin showed a shift of absorbance intensity mainly in the amide I band (1600–1700 cm⁻¹) as well as in the amide II and III bands, indicating an increase of the β-sheets and a corresponding reduction of the α-helices. The structural conversions correlated directly with the strain or pressure and were partially reversible at the conditions applied. The additional absorbance observed at 1612–1624 cm⁻¹ was characteristic of the nascent interchain β-sheets, consistent with protein aggregation and fiber bundling during clot deformation observed using scanning electron microscopy. We conclude that under extension and/or compression an α-helix to β-sheet conversion of the coiled-coils occurs in the fibrin clot as a part of forced protein unfolding.

Introduction

Fibrin is an insoluble protein polymer that forms in the blood at sites of vascular injury. Together with platelets, fibrin builds a plug that stops bleeding. Fibrin also provides the scaffold for pathological obstructive thrombi that block blood vessels, seize blood flow, and cause myocardial infarction and ischemic stroke (1).

Fibrin is formed from its soluble precursor, fibrinogen, at the final stage of blood clotting. Fibrinogen is a 340-kDa blood plasma protein 45 nm in length and 2–3 nm in diameter, consisting of three pairs of polypeptide chains, designated Aα, Bβ, and γ, linked by 29 S-S bonds. Two distal and one central globular parts of fibrinogen are connected by two 17-nm-long triple (and partially quadruple) α-helical coiled-coils comprising 25% of amino acid residues of the whole molecule and 34% of its structured portion visualized using x-ray crystallography (2) (Fig. 1 A, inset). Fibrin formation is initiated by the cleavage of the small fibrinopeptides A and B from the N-termini of the Aα and Bβ chains, respectively, converting fibrinogen to fibrin monomer, which maintains major structural features of fibrinogen, including the coiled-coils. Monomers then self-assemble, resulting in a three-dimensional filamentous network. The fibrin clot is finally stabilized by intermolecular covalent cross-linking by a plasma transglutaminase, Factor XIIIa, rendering the clot more resilient and resistant to enzymatic cleavage (1,3).

Figure 1.

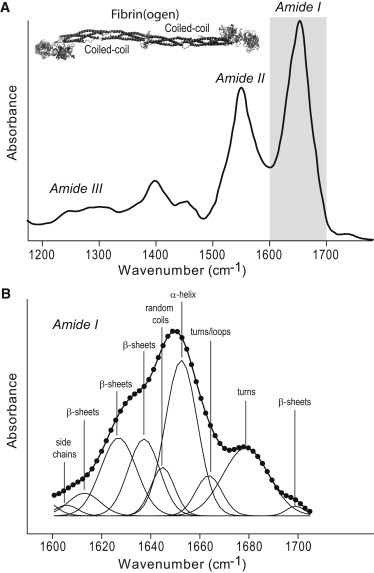
(A) Representative FTIR spectrum of a hydrated fibrin clot and the crystallographic structure of human fibrin(ogen) (2) (inset). (B) Deconvolution of resolution-enhanced amide I band and assignment to the secondary structure elements.

Because in vivo clots are formed in flowing blood or in the dynamic wound environment, the mechanical and rheological properties of fibrin are necessary for their function. The structural changes underlying deformation of a fibrin clot occur at different spatial scales, including molecular unfolding (4), which remains unclear despite recent insights (5). Based on the existence of two relatively long and coaxially aligned coiled-coils in rod-like fibrin(ogen), it has been hypothesized that the α-helix to β-strand conversion of the coiled-coils accompanies molecular extension of fibrin (6). By means of Congo red staining to detect the β-structures, which is commonly used to identify stacks of β-sheets in amyloid proteins, we revealed the formation of congophilic material, presumably new β-sheets, in stretched fibrin fibers (7), but the specificity of this method is not fully justified. The only direct experimental observation for an α-β transformation in fibrin is the low-resolution wide-angle x-ray scattering of squeezed fibrin films published back in 1943 (8), providing dubious evidence for the transition from α-helix to β-sheet upon fibrin stretching. Obviously, this quite important structural mechanism of fibrin nanomechanics needs to be probed using modern high-resolution methodologies for various types and degrees of deformation in physiologically relevant settings.

This work has been aimed at the role of secondary structure changes during deformations of fibrin polymers. In addition to tension, which has been used to study mechanical properties of fibrin, we applied pressure to watch molecular transitions in fibrin clots in response to compression, which is physiologically as relevant in relation to fibrin as extension and could occur under the pressure of arterial blood flow. Here, we present experimental data showing that both extension and compression of a hydrated fibrin clot are accompanied by changes in the α-helical coiled-coils, namely the transition of α-helix to β-sheet, determined using Fourier transform infrared (FTIR) spectroscopy.

Materials and Methods

Formation of fibrin clots

To form fibrin clots, 9 volumes of human citrated blood plasma (Blood Transfusion Center, Kazan, Russia) were mixed with 1 volume of 0.25M CaCl₂ in 5-ml plastic syringes. The clots were formed for 1–2 h at room temperature followed by thorough washing in 20 mM Tris-HCl/150 mM NaCl, pH 7.4, until the absorbance of the washing buffer at 280 nm reached zero. During formation the clots were naturally cross-linked by Factor XIIIa (Fig. S1 in the Supporting Material) because Factor XIII normally present in plasma is activated by thrombin, making their properties relevant to fibrin networks formed in vivo. The clots were kept in buffer before use and were continuously irrigated during measurements to prevent drying.

FTIR spectroscopy

Among a number of current techniques to study secondary structure of proteins, FTIR spectroscopy has been widely used for structural characterization of many polypeptides and proteins, including fibrinogen (9–13), fibrin (14,15), and fibrinogen fragments (14); however, it has never been applied to study structural dynamics of fibrin clots upon deformation.

The clots before and after deformation were analyzed in a TENSOR 27 FTIR spectrometer (Bruker Optik GmbH, Ettlingen, Germany). For inducing strain, a clot sample was clamped in a custom-built stretching device (Fig. S2) and elongated manually at a speed of ∼20 mm/min up to fourfold before it ruptured. The strained clot was positioned on the PIKE MIRacle attenuated total reflectance (ATR) device (Ge crystal, single-bounce beam path, 45° incident angle) and spectra were measured while in the stretched state. To account for potential partial light polarization on the ATR device and its interaction with the elongated anisotropic clots (16), we performed control measurements of the same stretched fibrin clots in two perpendicular orientations relative to the ATR prism without observing any difference in the FTIR spectra. To study effects of compression, a clot sample was pressed directly over a 2-mm detecting spot of the ATR crystal (Fig. S3). The pressure varied up to 300 bar but, because it was not precisely controlled, the degree of compression was roughly designated relatively small (10–50 bar), intermediate (100–150 bar), or large (200–250 bar). Spectra were recorded with 4.0 cm⁻¹ resolution and corrected for the water vapor and the buffer. For each measurement 128 scans were averaged. An unperturbed fibrin clot has a pronounced amide I band (1600–1700 cm⁻¹) as well as amide II and III bands with lower absorption intensity (Fig. 1 A). Multiple measurements were performed on freshly prepared fibrin clots, including 58 unperturbed, 39 stretched, and 33 compressed samples, each at different degrees of deformation.

Deconvolution of amide I

Quantitative analysis of the amide I band contour was done using curve fitting, second derivative, and Fourier self-deconvolution methods (17,18). Spectra were processed using Bruker OPUS software. After subtraction of the buffer and water vapor absorbencies, the resulting spectra were smoothed by a 7–13-point Savitsky-Golay function, depending on the quality of the data (19). Second-derivative spectral analysis was applied to locate the position of the overlapping components of the amide I band to assign them to different secondary structure elements (17,18,20). Fourier self-deconvolution (21) provides band narrowing through multiplication of the Fourier transform by a lineshape function and an apodization function. Generally, a value of 13 cm⁻¹ for the full bandwidth at half-height and a resolution enhancement factor of 2.4 are adequate (18). Deconvolution using a too narrow full bandwidth at half-height will not separate all the widest bands, whereas a value that is too large will overemphasize the spectrum’s narrower components leading to artifacts and possible misinterpretation. We have found optimal deconvolution to be employing Lorentzian band shape, resolution enhancement factor 2, and bandwidth 13 cm⁻¹ (Bruker OPUS 6.5 software). The applied parameters resulted in a relatively moderate resolution enhancement that prevents large spectral distortions. The fractions of each component in the resolution-enhanced amide I band were estimated quantitatively by a nonlinear least-squares fitting program Fityk (22), iterating the curve-fitting process according to the specific functions. Because Fourier self-deconvolution performed with the previous parameters results in depression of the Lorentzian contribution, the Gaussian function was selected for the best fitting. The number of components and their positions on the wavenumber scale were determined using both second derivatives and difference FTIR spectra collected during deformation of the same sample. Only spectral components exhibiting reproducible positions and consistent response to the deformation were taken into account. Based on the characteristic minima and shoulders of the second derivative curves, the spectral range of 1600–1700 cm⁻¹ was decomposed in 10 bands including two small marginal bands (1604 см⁻¹ and 1592 см⁻¹) due to side-chain absorption (Fig. 1 B) (23). They were included in the deconvolution to avoid unreliable straight baseline subtraction, but were excluded from the secondary structure quantification. A proportion of each component in the amide I band was computed as a fractional area of the corresponding peak divided by the sum of the areas of the peaks belonging to the amide I band (17,18).

Assignment of the secondary structure elements

The peaks obtained by deconvolution of the amide I band can be assigned to specific types of secondary structure based on the established correlations between crystallographic structures of proteins and their FTIR spectra (17,18,20). For the assignments made in this work, we also took into account the previous FTIR spectroscopy studies of fibrin(ogen) (9,11,14,15), with results shown in Fig. 1 B, Fig. S6, and Tables S1–S8. To make quantitative characteristics of nondeformed and deformed clots fully comparable, we always fitted spectra with the same set of parameters. During the fitting and assignment only the amplitudes of components were allowed to vary freely, but the frequency and bandwidth variations were constrained to 1–2 cm⁻¹. Fitting quality was verified by calculating the differences between fitted spectra at various deformations and comparing them with the differences between the corresponding original spectra at the same deformations. Fitting was accepted only if the spectral differences and derivatives both from the original and computed spectra coincided within the noise level. Following this approach we distinguished one major peak corresponding to α-helices at 1651 ± 2 cm⁻¹ and three different types of β-structure peaking at 1614 ± 2, 1622 ± 2, and 1636 ± 2 cm⁻¹ (Fig. 1 B). The peak at 1614 cm⁻¹ partly contains absorbance from tyrosine side chain but its relative contribution is negligibly small (23). We tested the precision of our fitting and sample to sample variability by calculating a coefficient of variation for the fractions of secondary structures from FTIR spectra of 11 independent samples of nondeformed fibrin (Table S1, summarized content). The values of coefficient of variation obtained were ∼10%, very close to those obtained with the same method for fibrin spectra from various sources (15).

Scanning electron microscopy

Clots prepared for scanning electron microscopy (SEM) were thoroughly washed with 50 mM sodium cacodylate-HCl buffer, pH 7.4, to remove excess salt and fixed overnight in 2% glutaraldehyde. Stretched clots were washed and fixed by immersion into the washing buffer or fixative while being clamped in the stretching device right after they reached a certain length. Compressed clots were immersed into the fixative within 10 s after decompression. Clots were then cut into small pieces, washed in deionized water, dehydrated in a graded series of increasing ethanol concentrations (30–100%), and impregnated with hexamethyldisilazane followed by air-drying. The specimens were mounted, sputter coated with gold-palladium in a Sputter Coating Unit E5100 (Polaron Equipment, Hertfordshire, UK) at 2.2 kV and 20 mA for 1.5 min, and examined in an XL20 scanning electron microscope (FEI, Hillsboro, OR). Several fields on each clot were examined before choosing fields that were characteristic of the entire clot. Digital electron micrographs were taken at different magnifications between 2,000× and 10,000×.

Results and Discussion

Deformation-induced molecular transformations in fibrin clots

The main finding of this study is that deformations of hydrated fibrin clots, either elongation or compression, induce distinct rearrangement of the protein secondary structure reflected by characteristic changes of FTIR spectra. At the qualitative level, these changes could be described as a redistribution of absorption intensities from higher to lower wavenumbers. This shift was confirmed by peak positions of the difference spectra and second derivative spectra observed in various peptide vibration modes: amide I (decrease at 1649–1651 cm⁻¹ and increase at 1620–1630 cm⁻¹), amide II (decrease at 1540–1550 cm⁻¹ and increase at 1520–1540 cm⁻¹), and amide III (decrease at 1290–1320 cm⁻¹ and increase at 1220–1240 cm⁻¹) (Fig. 2, Fig. 3, Fig. S4, and Fig. S5). It has been shown in FTIR studies of various proteins that absorbance at the higher wavenumbers (1649–1651 cm⁻¹, 1540–1550 cm⁻¹, and 1290–1320 cm⁻¹) is predominantly due to α-helical structures, whereas the lower wavenumbers (1620–1630 cm⁻¹, 1520–1540 cm⁻¹, and 1220—1240 cm⁻¹) are largely characteristic of β-structures (17,24). Because the shift of absorbance intensity in the amide I band was the most pronounced and well defined in terms of correspondence to secondary structure elements, we used the intensity ratio at 1622/1651 cm⁻¹ to estimate the deformation-induced changes in FTIR spectra and also as a semiquantitative determination of the β-sheet/α-helix content ratio. This parameter displayed a clear dependence on the degree of deformation both for elongation (Fig. 2, inset; Fig. S6) and compression (Fig. S6), corroborating that the observed changes in FTIR spectra and corresponding secondary structure transitions from α-helices to β-sheets are inherently coupled to the force-induced deformations.

Figure 2.

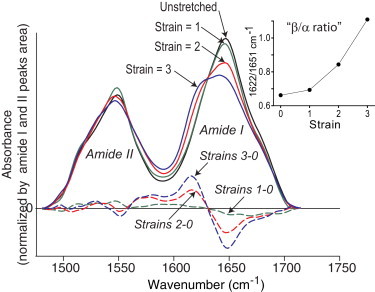
Normalized FTIR ATR spectra of unstretched plasma clot (black line) and the same clot after twofold (strain = 1, green solid line), threefold (strain = 2, red solid line), and fourfold (strain = 3, blue solid line) elongation. Corresponding difference spectra (1-0, 2-0, and 3-0) obtained by subtraction of the initial spectrum at strain = 0 are shown as the dashed lines of the corresponding color. (Inset) The absorbance intensity ratio at 1622/1651 cm⁻¹ as a function of strain. Strain is defined as stretched length/initial length-1.

Figure 3.

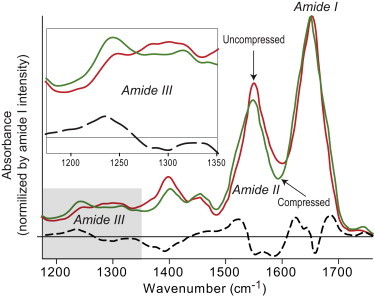
Normalized FTIR spectra of uncompressed plasma clot (red line) and the same clot after compression (green line). The difference spectrum is shown as a black dashed line. (Inset) Changes in the amide III band.

To better quantify the observed changes in FTIR spectra, we performed a determination of secondary structure elements using deconvolution of the amide I band, which is primarily governed by the stretching vibration of C=O and C–N bonds and is mainly used for secondary structure determinations (17). Curve fitting of Fourier self-deconvolved FTIR spectra with underlying band positions determined from second derivatives was performed in accordance with the procedure used earlier to analyze FTIR spectra of fibrin(ogen) (9,11,14,15,25,26) as well as other fibrillar proteins, such as α-keratin (27), silk fibroin (28), and fibronectin (29). The results of curve fitting for the secondary structure elements are shown in Fig. S6 and Tables S1–S8. On the basis of this analysis, changes in the absolute content of different secondary structure elements in response to elongation and compression of fibrin clots are summarized in Table 1.

Table 1.

Secondary structure of hydrated fibrin clots before and after stretching or compression

Types of secondary structure	Strain∗				Compression
	0	1	2	3	0	Small	Interm.	Large
α-Helices	31%	30%	25%	16%	31%	25%	19%	16%
β-Sheets	37%	40%	46%	52%	37%	44%	48%	51%
Turns, loops, random coils	32%	30%	29%	32%	32%	31%	33%	33%

^∗Strain is defined as stretched length/initial length-1.

Repeated and reproducible measurements performed on unperturbed clots show that human fibrin contains 30 ± 3% α-helices, 37 ± 4% β-sheets, and 32 ± 3% turns, loops, and random coils (M ± SD, n = 11). Notwithstanding some degree of uncertainty inherently present in deconvolution of FTIR spectra and assignment of secondary structures (17), the numbers obtained for these structures are very close to real because of at least two supporting arguments. First, the results are in good agreement with the numbers obtained from other FTIR (14,15) or Raman (30) spectroscopy studies of nondeformed fibrin, despite distinctions in the modes of measurement and analyses. Second, we confirmed our results by comparing them with the available crystallographic data, the gold standard for protein structure. Because there is no crystallographic data for the entire fibrin molecule, we validated our secondary structure analysis by comparing the FTIR spectroscopy determined α-helical content in unperturbed fibrin with the content of α-helices revealed in the x-ray crystallographic structure of human fibrinogen (PDB entry: 3GHG (2)). Taking into account some additional α-helices predicted but crystallographically unresolved in the flexible region of the fibrinogen Aα chain (31), our experimental estimation (∼30%) is quite close to the crystallographic data (27%), well within a 10% global error of secondary structure prediction based on the FTIR spectra band fitting algorithm (32).

The elongation and compression of fibrin clots was followed by a decrease of the α-helix content down to 16% upon fourfold elongation or maximal compression. Remarkably, the observed reduction in the α-helix content upon stretching or compression was approximately equal to the corresponding 14–15% increase in the fraction of β-sheets without appreciable changes in the content of turns, loops, and random structures. Similar quantitative changes in the secondary structure observed after extreme elongation and compression suggest that the clots have reached the level of deformation at which they start to become physically damaged or ruptured rather than undergo further protein unfolding. These data support the conclusion drawn from the raw spectra that both elongation and compression of fibrin clots are followed by rearrangement of the secondary structure, comprising mainly the α-helix to β-sheet transition. The strong correspondence between an increase of the β-structures and a reduction of the α-helix content suggests that secondary structure alterations upon stretching and compression occur in the coiled-coil regions of a fibrin molecule.

Taken together these results indicate that forced fibrin elongation and compression are accompanied by a significant α-β conversion under relatively high deformations. It is noteworthy that the α-β transition in response to stress has been demonstrated for a number of filamentous proteins, such as α-keratin (27,33), keratin-like intermediate filaments (34), desmin (35), and vimentin (36). Inasmuch as the occurrence of the α-β transition directly depends on the length of α-helices with a 3.8-nm threshold (37), the 17-nm-long α-helical coiled-coils in fibrin are fully compatible with this transformation.

Deformation-induced β-sheet-mediated protein aggregation in fibrin clots

The rising degree of deformation in stretched/compressed fibrin was followed by a progressively increasing shoulder in the absorbance spectra peaking at 1622–1624 cm⁻¹ (Figs. 2 and 3). The second derivative split that shoulder into two components: 1622–1624 cm⁻¹ and 1612–1618 cm⁻¹, the latter being almost absent in the unperturbed fibrin. Marked deformation was accompanied by a substantial increase of 1612–1618 cm⁻¹ at the expense of a 1651-cm⁻¹ α-helical component along with a decrease of intensity at 1637–1638 cm⁻¹ and 1622–1624 cm⁻¹ (Fig. S4 and Fig. S5). Because all three peaks in the 1612–1638 cm⁻¹ range reflect β-structures, the shift to the smaller wavenumbers suggests that there is a deformation-dependent redistribution in the types of β-structures, most likely due to emergence of newly formed intermolecular β-sheets associated with protein aggregation (38).

Deconvolution of the amide I band contour confirmed that deformation induced not only an overall quantitative increase of the β-structures, but also caused their qualitative rearrangement. Fig. 1 B, Fig. S6, and Tables S1–S8 show that there are three major types of β-structures in fibrin reflected by deconvolution components at 1612–1614, 1624–1627, and 1636–1638 cm⁻¹. These types of β-structures responded differently to extension and compression of a fibrin clot (Fig. S7). The content of the 1636–1638-cm⁻¹ type of β-structures remained almost unchanged, whereas two other fractions increased according to the degree of deformation. The fraction peaking at 1612–1614 cm⁻¹ increased two- to threefold in the maximally deformed clots, whereas the fraction peaking at 1624–1627 cm⁻¹ increased moderately by 18–35%. These data indicate that some types of β-structures remain unperturbed during fibrin deformation, whereas others are newly formed as a result of conversion from α-helices. The infrared-spectral parameters of the nascent β-structures are characteristic of the intermolecular β-sheets involved in protein aggregation (38,39).

To see what might happen to fibrin fibers under elongation and pressure, we performed SEM of stretched and compressed fibrin clots in comparison with unperturbed fibrin (Fig. 4). What can be unambiguously gleaned from the scanning electron micrographs is that both deformed clots, stretched and compressed, clearly undergo dramatic fiber bundling. The phenomenon of fiber bundling in response to elongation of a clot was demonstrated previously (4), whereas, to the best of our knowledge, this effect has never been observed before for compressed fibrin clots.

Figure 4.

SEM images of unperturbed (A), fourfold stretched (B), and strongly compressed (C) fibrin clots. Magnification bar = 10 μm. Note fiber bundling both in the stretched and compressed fibrin clots.

Essentially, the bundling of fibrin fibers observed using SEM is a microscopic manifestation of protein aggregation that occurs within and between filaments and protofibrils. This aggregation is followed by water expulsion underlying volume shrinkage of fibrin clots during deformation (4). On the basis of our results and the literature, it is quite possible that protein aggregation during extension and compression of fibrin fibers is associated with the α-β transition followed by β-sheet-mediated protein aggregation. It has been shown that aggregation of protein molecules is driven by the formation of intermolecular hydrogen bonds responsible for intermolecular β-sheet structure (40); therefore, the decrease of α-helix in favor of β-sheet aggregates have been proposed as a general mechanism of oligomerization of bovine serum albumin (41). Progressive transformation from α-helix to β-sheets in bovine serum albumin was followed by an increasing shoulder at 1620 cm⁻¹ in the FTIR spectrum attributed to the intermolecular β-sheet structure (42). With respect to protein-specific variation in the peaks of vibration spectra, this finding is similar to the changes that we observed as a deformation-dependent increase in intensity at 1612–1614 см⁻¹ and 1624–1627 cm⁻¹ (Fig. S7), which comprises formation of intermolecular β-sheets (17,38,39). Thus, the α-β transition followed by formation of an intermolecular β-sheet structure and protein aggregation could be a common mechanism underlying the different types of fibrin deformation.

Reversibility and time course of the α-β transition

To see whether the deformation-induced α-β transition is reversible or not, the clots were examined 15 min after they were released from the stretcher or decompressed while being kept in the buffer. Fig. 5 A shows that at strains 1 and 2 the relaxed fibrin clots partially restored the absorbance intensity ratio at 1622/1651 cm⁻¹, which roughly corresponds to the β-sheet/α-helix content ratio, indicating partial reversibility of the α-β transition in the experimental timescale. There was a clear inverse relationship between the degree of reversibility and the strain (inset of Fig. 5 A). It is noteworthy that the ability of stretched fibrin clots to reverse their FTIR spectra upon relaxation (assessed by the shift of intensity ratio at 1622/1651 cm⁻¹) corresponded to partial recovery of the macroscopic length of hydrated clots (correlation coefficient R = 0.75, p < 0.05). The changes in FTIR spectra induced by compression of fibrin clots were also partially reversible (Fig. 5 B). The residual 1622/1651 cm⁻¹ intensity ratio after decompression correlated well with the values observed in the same samples at the peak of compression (R = 0.85, p < 0.05) (Fig. 5 B, inset), indicating that the ability to recover (lower values of the 1622/1651 cm⁻¹ intensity ratio upon decompression) displayed an inverse relationship with the degree of compression (higher values of the 1622/1651 cm⁻¹ intensity ratio upon compression).

Figure 5.

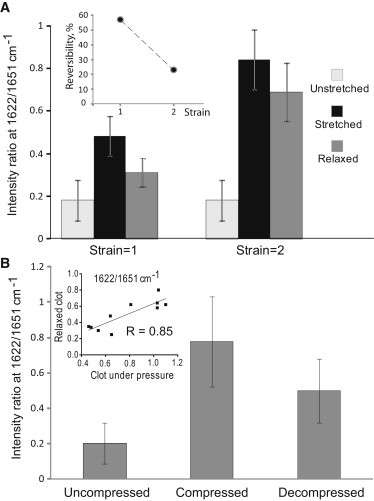
Reversibility of the deformation-induced changes in FTIR ATR spectra. (A) The average ratio of second derivative of absorbance intensities at 1622/1651 cm⁻¹ in unstretched, stretched at strains 1 (n = 9) and 2 (n = 4), and relaxed fibrin clots. (Inset) Relative reversibility of the average ratio of absorbance intensities at 1622/1651 cm⁻¹ as a function of strain. The reversibility was calculated as 100^∗(average value in the stretched state – average value after relaxation)/(average value in the stretched state – average initial value). (B) The average ratio of second derivative of absorbance intensities at 1622/1651 cm⁻¹ in uncompressed, compressed, and decompressed fibrin clots (n = 10) at various pressures. (Inset) The residual ratio of absorbance intensities at 1622/1651 cm⁻¹ in individual decompressed fibrin clots plotted against the ratio measured in the same fibrin clots at the peak of compression. Error bars represent standard deviations.

The partial macroscopic reversibility of the fibrin clots fits with the deformation-induced α-β transition in fibrin (Fig. 5); however it does not exclude other mechanisms of fibrin elasticity, such as straightening and unfolding of the αC regions (43). If we think of the α-β transition as a biphasic process with elastic and plastic components, then it would be reasonable to assume that the force-induced transition of α-helix to β-sheet is reversible, whereas subsequent intermolecular aggregation of β-structures is irreversible, making the reversibility of the entire deformation dependent on the fraction of β-sheets, which correlates directly with the degree of deformation (Table 1).

To estimate how fast and stable are the observed changes in the secondary structure, FTIR spectra of the same clots were measured over time, starting as soon as possible after considerable stretching or compression and followed by repeated measurements with ∼10-min intervals. Because of technical limitations, it took 3–10 min after clot deformation to start data acquisition and 3 min to record a spectrum at each time point. To avoid effects of drying, the clots were kept wet in the stretched or compressed state by continuously irrigating them with buffer. Three different fibrin clots were watched over time under each experimental condition. Fig. S8 shows the time course of the intensity ratio at 1622/1651 cm⁻¹ (from second derivative spectra), which was quite sensitive to alterations in the raw FTIR spectra induced by deformation of fibrin clots. The results demonstrate that the FTIR spectra remained unchanged for at least ∼1 h after deformation as the clots were kept under strain or pressure, implying that they were observed under equilibrium conditions. In other words, in our experimental settings the rate of nonequilibrium α-β transition was too fast to be followed in the real timescale. In other words, the α-β transition occurred sometime between deformation and the first measurement (within 3–10 min) and remained steady under the action of a constant force.

Effect of dehydration of fibrin clots on the FTIR spectra

Because plasma clots contain >99% liquid (2.5 g/L of fibrinogen in plasma corresponds to 0.25% protein) and deformation of fibrin clots is followed by a dramatic loss of water due to mechanical squeezing as well as expulsion during protein aggregation (4), we tested whether the observed changes in the secondary structure were induced solely or substantially by the loss of water, we studied whether mechanical dehydration per se can account for the observed changes in the secondary structure. When an unperturbed hydrated fibrin clot was dried, either partially in the air or almost completely over P₂O₅, the measurable changes in FTIR spectra had nothing to do with transition of the α-helices into β-sheets (Fig. S9). Instead, loss of loosely bound water was detected as the clot shifted from the wet to air-dried states. Much more pronounced changes occurred upon deeper drying over P₂O₅. Positive peaks on the difference trace at 1510, 1664, 1676, and 1692 cm⁻¹ suggest an increase of turns and unhydrated peptide groups. Negative peaks at 1556, 1621, and 1643 cm⁻¹ point to the breakup of some α-helices, β-sheets, and dehydration of random structures (18,20,24). The data indicate that dehydration cannot account for the observed secondary structure changes upon fibrin deformation.

Conclusions and Potential Implications

In conclusion, FTIR spectroscopy of wet washed human plasma clots allowed us to demonstrate the α-helix to β-sheet transition that occurred in coiled-coils during substantial extension and compression of fibrin gels. We showed that a decrease of α-helix was equivalent to an increase of β-structures without changes in other secondary structure elements, suggesting that the change occurred in the coiled-coils. The extent of the α-β transition was directly proportional to the degree of deformation and was a pure mechanical effect without a significant role of dehydration. The observed α-β transition both in elongation and compression was associated with β-sheet-mediated protein aggregation as revealed by fiber bundling observed in the scanning electron micrographs and characteristic changes of FTIR spectra, indicating formation of interchain β-sheets. The alterations of secondary structures were partially reversible with the degree of reversibility being inversely proportional to the strain or pressure applied. The results provide additional evidence for the α-β transition as a universal mechanism of forced unfolding of filamentous proteins with relatively high α-helical content. The data also shed light at the molecular structural origins of the elasticity and plasticity of the fibrin polymer, underlying its mechanical role in preventing bleeding and in thrombosis.

Taken together, our results provide insight into the molecular basis of fibrin clot mechanics and a general mechanism for deformability of proteins, but they also have important physiological and medical implications. First, the α-β transition may toughen fibrin at large deformations because β-sheets are more resistant to shear than α-helices (37), and clot stiffness has been known to correlate directly with the incidence of myocardial infarction and other cardiovascular diseases. Second, the ability of fibrin to undergo the α-β transition and aggregation may result in formation of tightly packed β-sheets, analogous to those of amyloid structures. Of importance, fibrin clots displayed amyloid-like features upon extension revealed by staining by Congo red (7), and accumulation of β-amyloid peptide (Aβ) makes fibrin clots more resistant to proteolytic degradation (44). There is also genetically determined fibrin(ogen)-related amyloidosis in some dysfibrinogenemias (45). Third, controlling the α-β transition could potentially lead to new strategies for elimination of thrombi by either stabilizing or destabilizing the coiled-coil, rendering clots more sensitive to treatment.