Abstract
The crowded environment of cells poses a challenge for rapid protein-protein association. Yet, it has been established that the rates of association are similar in crowded and in dilute solutions. Here we probe the pathway leading to fast association between TEM1 β-lactamase and its inhibitor protein BLIP in crowded solutions. We show that the affinity of the encounter complex, the rate of final complex formation, and the structure of the transition state are similar in crowded solutions and in buffer. The experimental results were reproduced by calculations based on the transient-complex theory for protein association. Both experiments and calculations suggest that while crowding agents decrease the diffusion constant of the associating proteins, they also induce an effective excluded-volume attraction between them. The combination of the two opposing effects thus results in nearly identical overall association rates in diluted and crowded solutions.
Introduction
Classic biochemistry employs models of ideal solutions, in which solute molecules are assumed to have no volume and their concentration is negligible, such that they do not influence the reaction under study (1). In contrast, real solutions, especially crowded ones, contain high concentrations of finite size molecules. These background molecules may interact with each other and with the molecules under study in a number of ways, including electrostatic, hydrophobic, van der Waals, and steric interactions (2).
Protein-protein association is a multistep process. It starts with a translational diffusion of the proteins, which may result in their collision. Because the interaction interfaces typically form small patches on the associating proteins, most collisions will be unproductive, and the collision complex will dissociate back to the unbound state. In some cases, rotational diffusion will enable the proteins in the collision complex to find their correct mutual orientation, and form a fruitful encounter complex. The relative separation and orientation between the subunits in this encounter complex are close to that of the final complex, but most of the short-range interactions characterizing the final, native complex are still absent (3,4). In recent years, it has become evident that encounter complexes are formed both on- and off-pathway during complex formation (5–8). Stabilizing fruitful-encounter complexes by optimizing electrostatic attraction leads to faster association, whereas stabilizing the off-pathway-encounter complexes has no influence on binding (9). The encounter complex may evolve to form the final complex through the transition state, during which short-range hydrogen bonds, hydrophobic and van der Waals interactions are formed, water molecules are excluded from the interface, and structural rearrangements may take place (3). The overall rate at which association occurs is a combination of the rates along the association pathway,
| (1) |
where k1 and k−1 are the rates of encounter-complex formation and dissociation, and k2 is the rate at which the encounter complex evolves to the final complex (4).
To estimate the effects of crowding on complex stability and rates, Minton used the scaled particle theory, first formulated by Lebowitz (10) and Gibbons (11), and showed that for spherical molecules in a solution of inert spherical background molecules, association is enhanced (Minton (12)). Around each molecule there is an excluded volume from which the centers of mass of all other molecules are excluded (13). Macromolecular association causes partial overlap of the excluded volumes, resulting in increased available volume in the solution; thus, binding events in crowded solutions are entropically favored (14). Berg (15), and later Zhou et al. (16) refined this theory by proposing that the excluded-volume effect indeed enhances association in the case where two spherical monomers form a spherical dimer. However, in the more realistic scenario, where the complex would be shaped roughly as a dumbbell, the excluded-volume effect would be much smaller and can even cause destabilization of dimerization.
The effect of crowding on the association rate depends on the nature of the reaction, namely, whether it is diffusion-limited or transition-state-limited. According to the Stokes-Einstein relation, translational diffusion scales with the inverse of solution viscosity. Accordingly, collision rates would be reduced and diffusion-limited reactions would be slower in the crowd. For transition state-limited reactions, an enhanced rate is predicted; because the transition state and the final complex are geometrically similar, an overlap of excluded volumes already occurs at the transition state, effectively lowering the free-energy barrier in crowded solutions (17). Equivalently, an attractive force may exist between the proteins when they are close in space. Asakura and Oosawa (18) and Vrij (19) proposed that macromolecules in solution induce an attractive force between colloidal particles called the “depletion interaction”.
However, it is argued that, in most cases, there is no clear division into diffusion-limited and transition-state-limited regimes, and the overall effect would be a combination of the two opposing effects, manifested as a moderate effect on the binding rate over a wide range of volume occupancies (20,21). Kim and Yethiraj (22) calculated the expected rate change with different reaction probabilities, and found that for small probabilities (as is the case for protein-protein association) crowding has no effect on the overall association rate. Indeed, measurements of heterocomplexes association in the presence of crowding agents have shown only a small influence on association rate constants (23–25).
To date, only overall binding rate constants were measured under crowding, and the question of how crowders affect the pathway of protein-protein association was left unanswered. Here, we studied the effects of crowders on the binding of TEM1-β-lactamase to its protein inhibitor BLIP. Using fluorescently labeled proteins, we determined the affinity of the encounter complex and the rate of final complex formation in the presence and absence of crowding agents. In addition, we employed double-mutant cycle analyses to compare the structure of the transition state under crowding to its structure in buffer. Finally, we show how the experimental results fit calculations using the transient-complex theory (26).
Materials and Methods
Crowding agents
20 kDa Polyethylene glycol (PEG 20) and 40 kDa dextran (dextran 40) were purchased from Sigma-Aldrich (St. Louis, MO).
Viscosity measurements
Viscosity measurements were done using a Cannon-Fenske Routine Viscometer 150/I750 (Cannon, State College, PA) at 25°C.
Protein expression and purification
TEM1 and BLIP were mutated, expressed, and purified as described in Albeck and Schreiber (27). CyTEM and YBLIP were constructed, expressed, and purified as described in Phillip et al. (28).
Determination of affinity and rate constants along the association pathway
Binding of fluorescently labeled TEM1 and BLIP was monitored under pseudo-first-order conditions at 25°C in 25 mM Tris buffer (pH 7.2) using a stopped-flow fluorescence apparatus from Applied Photophysics (Leatherhead, Surrey, UK). Measurements for the binding of TEM1 with the BLIP-D163K mutant were also made in the presence of 120 mM NaCl and in the presence of 4, 8, and 12% PEG 20 or 15% dextran 40 as crowding agents. Samples were excited at 435 nm and emission was detected using a cutoff filter of 515 nm. TEM1 was kept at low (<5 μM) concentration, while BLIP was used at higher concentrations of up to 120 μM. Observed rates of association were fitted to Eq. 2 (29),
| (2) |
where [BLIP] is the BLIP concentration and K1 = k−1/k1 is the dissociation constant of the encounter complex. In principle, Eq. 2 should include k−2, the rate of the final complex dissociating into the encounter complex, but under our experimental conditions, this contribution was negligible. At low [BLIP], Eq. 2 reduces to kobs = (k2/K1)[BLIP], with a second-order rate constant kon = k2/K1. Comparison of the latter result with Eq. 1 implies k2 << k−1.
Transition state structure modeling
Transition state structure was modeled according to the method developed by Harel et al. (8), which is briefly described in the following paragraphs. For additional details and discussion about the method, refer to the previous publication (8). Modeling the transition state structure was carried out in three steps: 1), association rate constant measurements for the wild-type and single mutant complexes; 2), determination of the residue-residue pairwise interactions in the transition state by double-mutant cycle analysis; and 3), modeling of the transition state structures by in silico structure perturbations and cutoff analysis.
Kinetic measurements
Association rate constants (kon) for unlabeled TEM1 and BLIP were measured using a stopped-flow fluorescence apparatus from Applied Photophysics. Measurements were done at 25°C in 10 mM HEPES buffer (pH 7.2) in the presence and absence of 15% dextran 40. To detect change in tryptophan fluorescence upon binding, samples were excited at 280 nm and emission was detected using a cutoff filter of 320 nm. Association rate constants were determined under both pseudo-first-order and second-order conditions, and the same values were obtained.
Double-mutant cycles
The coupling energy values (ΔΔG‡int) were used as a measure for the pairwise interactions at the transition state (8,30,31) and were calculated using
| (3) |
| (4) |
where and denote the association rate constant of the wild-type and mutated complexes respectively, X and Y represent the wild-type residues, and A represents a mutation. Double-mutant cycles for non-Ala mutations were calculated using the mutated protein as pseudo-wild-type. A negative value of ΔΔG‡int indicates an attraction between the two residues involved (X and Y), whereas a positive value indicates repulsion. The standard error of the mean was calculated based on multiple repetitions of the same measurements. The error of ΔΔG‡int was calculated from the error of the four individual ΔG‡ values. Accordingly, the standard error of the mean for ΔΔG‡int was ±0.9 kJ/mol.
Transition state structure analysis
The analysis was based on the assumption that there is a correlation between the ΔΔG‡int values and the distances between the residues in the transition state structure (31). To generate a comprehensive set of potential transition state structures, small and systematic in silico structure perturbations were performed on the final complex structure as described previously in Harel et al. (8), resulting in 2220 hypothetical structures. For each structure, the number of residue pairs that had both a ΔΔG‡int value above a certain cutoff and a distance below a certain cutoff was determined. If the number of complying pairs was above the pairs-cutoff, the occupancy score for that structure was raised. Every structure was analyzed using several sets of cutoffs, varying the ΔΔG‡int-cutoff, the distance-cutoff, and the pairs-cutoff. The ΔΔG‡int cutoffs ranged from 1.68 kJ/mol in steps of 0.84 kJ/mol up to 5.88 kJ/mol. ΔΔG‡int values were taken in their absolute value for simplicity. The distance cutoffs ranged from 6 Å to 10 Å in 1 Å steps. The pairs-cutoff was two, three, and four residue pairs. Finally, each of the 2220 structures was colored according to its occupancy score. A structure that passed a higher, more stringent filter-set was colored cooler.
Prediction of association rate constant in crowded solutions
The transient complex is an on-pathway late intermediate formed by diffusion. This intermediate should be structurally close to the transition state referred to previously in this article. According to the transient-complex theory (26), the association rate constant is calculated as
| (5) |
where k°on is the basal rate constant for reaching the transient complex by free diffusion, and the Boltzmann factor captures the effect of electrostatic interactions on the association rate. Crowding agents slow down the relative diffusion of the associating proteins but also induce an effective interaction between the associating proteins. Taking these two effects into account, the association rate constant becomes (32)
| (6) |
where is the basal rate constant with the decreased relative diffusion constant, Dc, of the associating proteins in the crowded solution, and ΔΔG∗c is the crowder-induced interaction energy of the transient complex.
The implementation of our transient-complex theory for predicting the association rate constant in a dilute solution has three components (26,33): 1), specification of the transient complex by mapping the interaction energy landscape within and around the native-complex well; 2), determination of the basal rate constant, k°on, by Brownian dynamics simulations; and 3), calculation of the electrostatic interaction energy of the transient complex by solving the Poisson-Boltzmann equation.
The ratio of the association rate constants in a crowded solution and in a dilute solution can be written as
| (7) |
To a good approximation, ΔΔG∗c can be equated to the ratio of the diffusion constant, Dc, in crowded solution to the counterpart, D, in dilute solution. For a test protein in a PEG solution, when the protein size, L, is less than the radius of gyration, Rg, of PEG, it was found that Dc/D follows the scaling law (34)
| (8) |
where ξ denotes the blob size of PEG. This is related to the PEG concentration, c, via
in which the overlap concentration c∗ is given by
where M is the molar mass of PEG and NA is Avogadro’s number. The dependence of Rg (in Å) on the molar mass (in g per mole) of PEG is given by Rg = 0.2 M0.58. For PEG 20, Rg = 62 Å and c∗ = 30 g/L. The diameters of TEM1 and BLIP are ∼34 Å. At a concentration of 100 g/L of PEG 20 (equivalent to ∼10% (w/w)), Eq. 8 predicts a sixfold decrease for the diffusion constant of these proteins. Dextran 40 at 15% is expected to yield a similar (approximately fourfold) decrease in the diffusion constant (35).
To calculate ΔΔG∗c, the crowder-induced interaction energy of the transient complex, we used our recently developed postprocessing method (36). Briefly, ΔΔG∗c was found as the difference in transfer free energy, from a dilute solution to the crowded solution, between the transient complex and the two separated proteins. The transfer free energy of a test protein was calculated by fictitiously placing the test protein into various locations inside the crowded solution. At each location, the interaction energy between the test protein and the crowders was calculated; a Boltzmann average over the various locations then yielded the transfer free energy.
To simplify the calculation of the transfer free energy, we modeled the crowder particles as spheres and the associating proteins at the atomic level. The crowder radius was chosen as 30 Å, a size that previous studies using spherical models of crowding agents suggest to be reasonable for both PEG 20 and dextran 40 (37,38). These previous studies demonstrated that modeling these crowder particles as spheres yielded physically reasonable and semiquantitative explanations of observed crowding effects. Moreover, the magnitude of crowding effects predicted by the sphere modeling is comparable to that predicted by an atomistic representation of crowders (S. Qin and H.-X. Zhou, unpublished). Here we only included excluded-volume interactions between the test protein and the crowders. For dextran as a crowder, there is experimental evidence supporting the notion that the dominant interactions are of the excluded-volume type (39–41). To further speed up the transfer free energy calculations, we compared sample results against an empirical formula (42) and found the latter to be quite accurate. Accordingly, subsequent calculations used the empirical formula.
Results
Determination of binding affinity and rate constants along the association pathway
The affinity of encounter complexes is too low (in the μM to mM range), and their kinetics too transient to be determined using equilibrium methods. One way of studying the stability of encounter complexes is by measuring the observed rate of association (kobs) at increasing protein concentration beyond the diffusion-limited regime, where kobs ceases to increase linearly with protein concentration (43). However, at protein concentrations where association becomes reaction- and not diffusion-limited, it is not feasible to rely on tryptophan fluorescence to monitor association, due to high background fluorescence.
We therefore used TEM1 β-lactamase and its inhibitor BLIP fused to the fluorescent proteins CyPet and Ypet, respectively (named CyTEM and YBLIP), to measure association rates. The interaction between CyTEM and YBLIP produces a strong FRET signal that is monitored upon excitation at 435 nm and emission at >515 nm. Due to the low direct excitation of the acceptor by the donor wavelength, we were able to use high concentrations of the BLIP-acceptor protein, while retaining very good raw signals for the association.
In the absence of previous data, we first measured the affinity of the encounter complex, K1, and the rate of conversion from encounter to final complex, k2, for the wild-type and the electrostatically optimized BLIP-D163K mutant, without crowders at two different ionic strengths. For the BLIP-D163K mutant, a replacement of an aspartate with a lysine residue produces an improved charge complementarity between the interacting proteins (44). This mutation is expected to increase the encounter-complex affinity, while having little effect on the rate of final complex formation (45). Fig. 1 shows the observed rate of association for different BLIP concentrations, fitted to Eq. 2. At low BLIP concentrations (<10 μM) the reaction is diffusion-limited, and the observed rates fit a straight line, yielding the second-order association rate constant kon.
Figure 1.
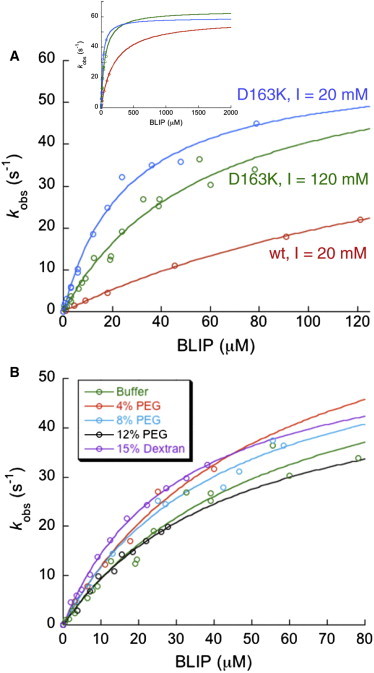
Kinetic analysis of the TEM1-BLIP association. (A) Wild-type TEM1 binding to the wild-type BLIP and to the D163K mutant at two ionic strengths. The observed rates were plotted against BLIP concentration and fitted to Eq. 2. (Inset) Extrapolated fit of the data. (B) Wild-type TEM1 binding to the BLIP D163K mutant in the presence of crowders.
At higher BLIP concentrations, the reaction becomes partially reaction-limited, and therefore a curvature is apparent. The fitted parameters are summarized in Table 1. Values of k2 were equal for the wild-type and mutant complexes, whereas K1 was eightfold lower for the BLIP-D163K mutant. Moreover, higher ionic strength (with 120 mM NaCl) destabilized the mutant encounter complex (with approximately twofold increase in K1), which is in accordance with theory and previous experimental findings (43). Under these conditions, the 95% confidence interval is 31–85 μM for K1 and 47–81 s−1 for k2. These results demonstrate that using pseudo-first-order kinetics with fluorescently labeled TEM1 and BLIP proteins is a suitable approach for measuring the effects of mutations and solution conditions on K1 and k2, and that electrostatic forces specifically stabilize the encounter complex for binding, while having no affect on k2.
Table 1.
Association kinetics of TEM1 with BLIP
| BLIP | Ionic strength (mM) | K1 = k−1/k1 (μM) | k2 (s−1) | kon = k2/K1 (M−1 s−1) |
|---|---|---|---|---|
| WT | 20 | 202 (21) | 58 (4) | 2.9 × 105 |
| D163K | 20 | 26 (3) | 59 (3) | 23 × 105 |
| D163K | 120 | 58 (13) | 64 (8) | 11 × 105 |
K1 and k2 were extracted from the fit to Eq. 2. Standard errors are in parentheses.
Effects of crowding agents on binding affinity and rate constants along the association pathway
Because the affinity of the encounter complex was higher for the electrostatically optimized mutant BLIP-D163K compared to wild-type BLIP, all further experiments were performed using this mutant. As crowders, we used 4, 8, and 12% PEG 20 as well as 15% dextran 40 solutions. The viscosities of these solutions were experimentally determined using a Cannon-Fenske Routine Viscometer at the conditions of the kinetic measurements and found to be between 3.7 and 19.4 times that of water (Table 2). To avoid potential interactions between crowders and proteins (other than the excluded-volume type), we measured the binding in the presence of 120 mM salt. In Fig. 1 B, the observed rates of association in the different solutions are plotted against the protein concentrations and fitted to Eq. 2. The shape of the curves is very similar to that observed in the absence of crowders. The fitted parameters summarized in Table 2 indicate that the different crowded solutions did not significantly affect K1, k2, or kon.
Table 2.
Association kinetics of WT TEM1 with BLIP D163K in buffer and crowded solutions
| Solution | Relative viscosity | K1 = k−1/k1 (μM) | k2 (s−1) | kon = k2/K1 (M−1 s−1) |
|---|---|---|---|---|
| Buffer | 1 | 58 (13) | 64 (8) | 11 × 105 |
| 15% dextran | 10.6 | 31 (3) | 59 (3) | 19 × 105 |
| 4% PEG | 4 | 55 (20) | 77 (19) | 14 × 105 |
| 8% PEG | 9 | 43 (10) | 63 (7) | 15 × 105 |
| 12% PEG | 19.4 | 47 (13) | 53 (10) | 11 × 105 |
Relative viscosities were measured using a Cannon-Fenske Routine Viscometer. K1 and k2 were extracted from the fit to Eq. 2. Standard errors are in parentheses.
Structural characterization of the binding transition state in crowded solution
Previously, we have characterized the binding transition state for the TEM1-BLIP system in dilute solutions (8). Here we used the same method to characterize the transition state under crowding. Because the effect of crowding agents on binding affinity and rate constants along the association pathway was similar in all solutions tested, we focused on 15% dextran 40 as a representative crowded solution. All kinetic measurements were performed using unlabeled TEM1 and BLIP proteins.
The association rate constants of a large set of single-residue mutants were used to determine the coupling energies, ΔΔG‡int, between these residues at the transition state. The mutants were divided into two sets: 1), the Ala mutant set, covering 44 pairs of residues and comprised of mutants in which Ala replaced the original residue; and 2), the Fast mutant set, covering 24 pairs of residues and composed of mutants that were previously identified as accelerating the association rate constant by replacing the negative charge on TEM1 E168, E171 or BLIP D163 to Lys (8). Then, the coupling energies were correlated to an ensemble of hypothetical transition state structures created in silico to determine the extent to which these structures support the experimental data (see Materials and Methods). The wild-type association rate constant measured in the dextran solution was 5 × 105 M−1 s−1, which is indistinguishable from its rate in buffer (4.6 × 105 M−1 s−1). Equal kon values in buffer and in dextran were also determined for many other mutant complexes (Fig. 2 A). The calculated ΔΔG‡int values of both mutant sets are shown in Fig. 2 B and in Table S1 in the Supporting Material. None of the pairs in the Ala mutant set had a significant ΔΔG‡int value, similar to the observation made previously in buffer (8). Next, we examined the Fast mutant set. Here, we identified three pairs of residues with significant ΔΔG‡int values; the interacting residues were D163K on BLIP and either E171, E168, or E104 on TEM1 (see Fig. S1 in the Supporting Material). It is worth noting that the distances between the interacting residues in the final complex are <7 Å, suggesting that the transition state resembles the final complex.
Figure 2.
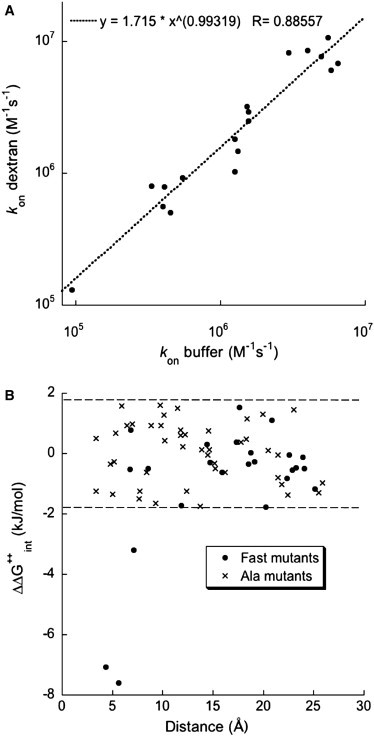
Association rate constants and interaction energies of mutant TEM1-BLIP complexes. (A) Measured association rate constants for 18 mutants in buffer are plotted against the rate constants in 15% dextran 40. (B) Calculated ΔΔG‡int values are plotted against the distance between the residues pairs in the final complex. All but three ΔΔG‡int values were within two standard errors from zero (dashed lines).
The ΔΔG‡int values were then used to model the transition state structures in the crowded solution. A quantity of 2220 potential structures was generated by rigid structure perturbation, and the generated structures were correlated with the experimental data. In Fig. 3, the plotted histograms represent the number of structures (y axis) in which the indicated number of residue pairs (x axis) passed a specific cutoff filter; here, the cutoffs were ΔΔG‡int > 1.8 kJ/mol and residue-residue distances <10 Å. The real data were plotted in comparison to data obtained from 100 random runs, where, in each hypothetical structure, each ΔΔG‡int value was arbitrarily assigned to a distance between two residues. Although there was no significant difference between the real and random data for the Ala mutant set, a very significant increase in specific interactions was observed for the Fast mutant set.
Figure 3.
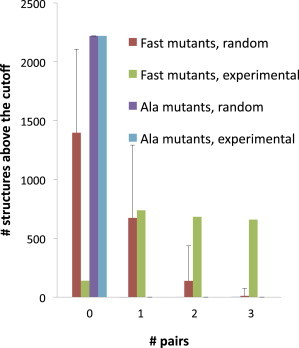
Histograms of a representative cutoff analysis. The histograms show the number of structures (y axis) in which the indicated number of residue pairs (x axis) passed the following filter: ΔΔG‡int > 1.8 kJ/mol and D (inter-residue distance) < 10 Å. The real data is displayed next to the data obtained from 100 random runs (brown and purple bars, with the associated standard deviation), where each ΔΔG‡int value was arbitrarily assigned to a distance between two residues.
To simulate the transition state structures, a range of distances, ΔΔG‡int values, and number of pairs-cutoffs was applied to each structure. The results of this analysis for the TEM1-BLIP system in dextran versus the same proteins in buffer are presented in Fig. 4 A; a structure that passed a higher, more stringent filter set is colored cooler (from red to blue). In both solutions, the transition state was mapped to the same region for the Fast mutant set, whereas for the Ala mutant set the transition state was diffusive with no apparent guidance toward final complex formation. The top-scoring structures under crowding and in buffer are very similar. Fig. 4 B shows representative top-scoring transition state structures under crowding and in buffer. In both of the transition state structures, BLIP is in the proximity of residues 145–149, 241–245, and 214–216 on TEM1, which are part of the interface in the final complex. Apparently, final docking involves desolvation and a final alignment of BLIP on TEM1.
Figure 4.
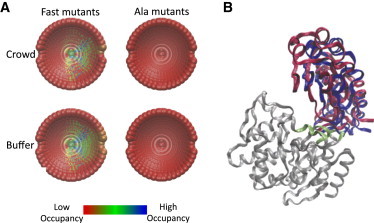
(A) Occupancy maps of the transition state for protein-protein association. Each point represents the center of mass of one of the 2220 perturbed structures. The different colors are related to the cutoff stringency; cooler colors designate a structure that passed a more stringent cutoff filter (thus, has a high occupancy at the transition state structure). The upper two are for measurements done in 15% dextran 40, while the bottom two are for measurements done previously in buffer (8). (B) Representative transition-state structures for the crowding (blue) and buffer (red) analyses. TEM1 is colored in gray with its interacting surface in green.
Computational study of the effect of crowding agents on association rate constant
To rationalize the experimental results, and to obtain more insights into the mechanisms of crowding effects on the association pathway, we computed the association rate constant using the transient-complex theory.
The crowding agents had two different effects on the association rate constant: First, they decrease the diffusion constant of the associating proteins (from D to Dc). This decrease, as measured by D/Dc, was approximately sixfold for PEG 20 at ∼10% (Fig. 5). Dextran 40 produced a similar decrease at 15%. If this were the only effect, kon would decrease by the same factor. However, the crowding agents had a second effect on the associating proteins: they induced an effective interaction between them.
Figure 5.
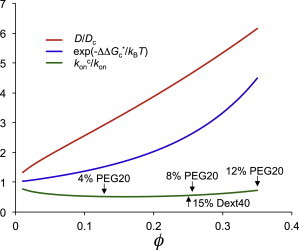
Calculated effects of crowding agents on the association rate constant. The volume fraction ϕ is calculated from the equivalent sphere (with a 30 Å radius) of PEG 20. The D/Dc curve is calculated according to Eq. 8 (assuming a diameter of 34 Å for each associating protein); the calculation of ΔΔG∗c is described in Materials and Methods (with the associating proteins represented at the atomic level). These two quantities together give kc°on/k°on according to Eq. 7, under the approximation that the pre-exponential factor kc°on/k°on is equal to Dc/D, which is the inverse of D/Dc. The identification of PEG 20 at different w/w percentages is based on the concentration of the equivalent crowder sphere. The identification of 15% dextran 40 is based on the expected fourfold value for D/Dc.
For dextran (and perhaps for PEG as well), the dominant interaction between the crowding agent and test proteins appears to be of the excluded-volume type. The crowder-induced interaction energy, ΔΔG∗c, is then negative, favoring the association process (Fig. 5). When the two effects of crowding agents are combined, a kcon/kon value of ∼0.5 is obtained, demonstrating that the crowder-induced attraction largely cancels the effect of the retarded diffusion. The deviation from the experimentally measured values of kcon/kon (Table 2) corresponds to only 1.7 kJ/mol in energetic terms, which is certainly within the limit of any theoretical model of crowding.
Discussion
In their native, cellular, environment, proteins are immersed in a dense solution of other macromolecules. Still, they are able to perform their tasks, such as interacting with other proteins, in a fast and specific manner. Polymers like PEG, dextran, and Ficoll, together with various proteins, have been used to mimic the crowded in vivo environment.
Overall association rates, as well as the first step in complex formation, were previously probed in the presence of crowding agents. It was shown that association rate constants are not much affected by high concentrations of crowders, even though the viscosity is significantly increased (23,46). According to the Stokes-Einstein theory, which was verified for our model system (47), the translational diffusion constant decreases with increasing solution viscosity. The observation that retarded diffusional encounter between the proteins does not translate into reduced rates of association has been explained by the caging effect: macromolecules in solution cage the two approaching proteins, thus increasing the probability of complex formation (48). Dissociation rate constants were also shown to be quite indifferent to the presence of crowders in solutions (46). This robustness of dissociation rates suggests that the first and rate-determining step of complex dissociation, namely the transition from final complex to encounter complex (k−2), is not affected by crowders.
In previous studies we used a systematic set of crowding agents and probed their effects on association rate constants. In this study we wished to characterize the effects of crowding on the association pathway between TEM1 and BLIP. We have determined the affinity of the encounter complex, mapped the transition state for binding, and compared the experimental results to those obtained by calculations based on the transient-complex theory. Whereas smaller molecular mass crowders slow association, the effect diminishes with increasing molecular mass (48). Indeed, Ficoll 70 kDa in a previous study (24) and PEG 20 kDa and dextran 40 kDa in this study showed no inhibitory effect on the measured kon. Banks and Fradin (49) observed anomalous diffusion of a tracer protein in dextran solutions; however, for dextran 40 kDa at the concentration used in this study, this effect was modest, and would probably have little effect on association rates under crowding.
In protein association, the initial encounter of the proteins is followed by rearrangement of the encounter complex. At high protein concentrations, the second step may become rate-limiting, leading to a hyperbolic dependence of kobs on protein concentration, as was observed for the association between Ras and Raf or RalGDS (43), and here for the association between TEM1 and BLIP. The affinity of the encounter complex (K1), as determined by plotting kobs versus protein concentration, is typically in the high micromole range. For the TEM1-BLIP system we determined a value of 200 μM for the wild-type complex, which decreased eightfold for the electrostatically optimized BLIP-D163K mutant. This measurement clearly shows that the D163K mutant, which was designed for fast association, optimizes the stability of the encounter complex while having no effect on the rate of final complex formation (k2). Similar results were obtained for the electrostatically optimized RalGDS mutants binding Ras (43). The stabilization of the encounter complex and transition state for TEM1-BLIP binding is supported by a more-specific transition state of the charged optimized mutant, as previously determined using double-mutant cycle analysis (8).
Comparing the effect of charge optimization to that of crowding shows clear differences between the two. Crowding has no major effect on kon, K1, k2, or the mapped transition state for binding. From the experimental results we also found similar structures for the transition state under crowding and in buffer (Fig. 4). Altogether, the excluded-volume effect is not realized in a lower free-energy barrier for the transition state.
The observation that crowding agents do not significantly affect the association rate constant was attained for other hetero-complexes and for other crowding agents as well (23–25). Yet, other processes, namely polymerizations and aggregations, were previously reported to be accelerated in crowded solutions (17,50). Because the effects of macromolecular crowding on the formation of oligomers are cumulative (51), it is quite reasonable that the crowder-induced interaction energy takes over the retarded diffusion in the case of high-order associations.
In our calculations we chose to model the crowding agents as hard-sphere particles to illustrate that the effective attraction is present regardless of the details of the crowder molecules. Although we could have used a more sophisticated model for the crowders by introducing more adjustable parameters, the basic conclusion would hold due to the magnitude of the effective attraction. Theoretical considerations have suggested that the excluded-volume effect also results in an increased stability of the complex (2,15). However, for heterodimeric complexes, this prediction was experimentally refuted (46). McGuffee and Elcock (52) performed detailed molecular simulations of binding within crowded environments and showed that nonspecific transient interactions with the crowded environment largely canceled the excluded-volume stabilizing effect. We are currently investigating the possibility that such interactions with the crowders indeed impair the stabilizing excluded-volume effect.
Our view on the effects of crowding on protein-protein association kinetics is summarized in Fig. 6. Crowding agents exert two opposing effects on the association rate: slowing it through retarded diffusion and accelerating it by inducing an effective attraction between the two proteins. This attraction arises from excluded-volume interactions between the proteins and the crowder molecules. Overall, the effect of crowding agents on protein-protein dimerization rate constants is close to null.
Figure 6.
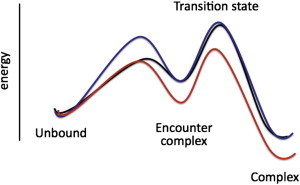
Free energy profiles illustrating the effects of crowding (blue) and increased electrostatic attraction (red) on the pathway of protein association. In both cases, k2 is not changed. However, whereas crowding is neutral toward K1 (due to slower k1 and k−1), increased electrostatic attraction (due to low salt or mutants) stabilizes the encounter complex and leads to a lower K1.
Acknowledgments
We thank Dr. Ori Cohavi for reviewing the manuscript.
This work was supported by the Israel Science Foundation (founded by the Israel Academy of Sciences and Humanities) 495/10 and by National Institutes of Health GM88187.
Supporting Material
References
- 1.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 2.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 3.Schreiber G. Kinetic studies of protein-protein interactions. Curr. Opin. Struct. Biol. 2002;12:41–47. doi: 10.1016/s0959-440x(02)00287-7. [DOI] [PubMed] [Google Scholar]
- 4.Schreiber G., Haran G., Zhou H.X. Fundamental aspects of protein-protein association kinetics. Chem. Rev. 2009;109:839–860. doi: 10.1021/cr800373w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tang C., Iwahara J., Clore G.M. Visualization of transient encounter complexes in protein-protein association. Nature. 2006;444:383–386. doi: 10.1038/nature05201. [DOI] [PubMed] [Google Scholar]
- 6.Ubbink M. The courtship of proteins: understanding the encounter complex. FEBS Lett. 2009;583:1060–1066. doi: 10.1016/j.febslet.2009.02.046. [DOI] [PubMed] [Google Scholar]
- 7.Volkov A.N., Bashir Q., Ubbink M. Shifting the equilibrium between the encounter state and the specific form of a protein complex by interfacial point mutations. J. Am. Chem. Soc. 2010;132:11487–11495. doi: 10.1021/ja100867c. [DOI] [PubMed] [Google Scholar]
- 8.Harel M., Cohen M., Schreiber G. On the dynamic nature of the transition state for protein-protein association as determined by double-mutant cycle analysis and simulation. J. Mol. Biol. 2007;371:180–196. doi: 10.1016/j.jmb.2007.05.032. [DOI] [PubMed] [Google Scholar]
- 9.Harel M., Spaar A., Schreiber G. Fruitful and futile encounters along the association reaction between proteins. Biophys. J. 2009;96:4237–4248. doi: 10.1016/j.bpj.2009.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lebowitz J.L. Scaled particle theory of fluid mixtures. J. Chem. Phys. 1965;43:774–779. [Google Scholar]
- 11.Gibbons R.M. The scaled particle theory for particles of arbitrary shape. Mol. Phys. 1969;17:81–86. [Google Scholar]
- 12.Minton A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol. Cell. Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 13.Ralston G.B. Effects of “crowding” in protein solutions. J. Chem. Educ. 1990;67:857–860. [Google Scholar]
- 14.Ellis R.J. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 2001;11:114–119. doi: 10.1016/s0959-440x(00)00172-x. [DOI] [PubMed] [Google Scholar]
- 15.Berg O.G. The influence of macromolecular crowding on thermodynamic activity: solubility and dimerization constants for spherical and dumbbell-shaped molecules in a hard-sphere mixture. Biopolymers. 1990;30:1027–1037. doi: 10.1002/bip.360301104. [DOI] [PubMed] [Google Scholar]
- 16.Zhou H.X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Minton A.P. Influence of macromolecular crowding upon the stability and state of association of proteins: predictions and observations. J. Pharm. Sci. 2005;94:1668–1675. doi: 10.1002/jps.20417. [DOI] [PubMed] [Google Scholar]
- 18.Asakura S., Oosawa F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 1954;22:1255–1256. [Google Scholar]
- 19.Vrij A. Polymers at interfaces and the interactions in colloidal dispersions. Pure Appl. Chem. 1976;48:471–483. [Google Scholar]
- 20.Zhou H.X. Protein folding and binding in confined spaces and in crowded solutions. J. Mol. Recognit. 2004;17:368–375. doi: 10.1002/jmr.711. [DOI] [PubMed] [Google Scholar]
- 21.Ando T., Skolnick J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl. Acad. Sci. USA. 2010;107:18457–18462. doi: 10.1073/pnas.1011354107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kim J.S., Yethiraj A. Effect of macromolecular crowding on reaction rates: a computational and theoretical study. Biophys. J. 2009;96:1333–1340. doi: 10.1016/j.bpj.2008.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ladurner A.G., Fersht A.R. Upper limit of the time scale for diffusion and chain collapse in chymotrypsin inhibitor 2. Nat. Struct. Biol. 1999;6:28–31. doi: 10.1038/4899. [DOI] [PubMed] [Google Scholar]
- 24.Kozer N., Schreiber G. Effect of crowding on protein-protein association rates: fundamental differences between low and high mass crowding agents. j. Mol. Biol. 2004;336:763–774. doi: 10.1016/j.jmb.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 25.Schlarb-Ridley B.G., Mi H., Bendall D.S. Implications of the effects of viscosity, macromolecular crowding, and temperature for the transient interaction between cytochrome f and plastocyanin from the cyanobacterium Phormidium laminosum. Biochemistry. 2005;44:6232–6238. doi: 10.1021/bi047322q. [DOI] [PubMed] [Google Scholar]
- 26.Alsallaq R., Zhou H.X. Electrostatic rate enhancement and transient complex of protein-protein association. Proteins. 2008;71:320–335. doi: 10.1002/prot.21679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Albeck S., Schreiber G. Biophysical characterization of the interaction of the beta-lactamase TEM-1 with its protein inhibitor BLIP. Biochemistry. 1999;38:11–21. doi: 10.1021/bi981772z. [DOI] [PubMed] [Google Scholar]
- 28.Phillip Y., Kiss V., Schreiber G. Protein-binding dynamics imaged in a living cell. Proc. Natl. Acad. Sci. USA. 2012;109:1461–1466. doi: 10.1073/pnas.1112171109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Strickland S., Palmer G., Massey V. Determination of dissociation constants and specific rate constants of enzyme-substrate (or protein-ligand) interactions from rapid reaction kinetic data. J. Biol. Chem. 1975;250:4048–4052. [PubMed] [Google Scholar]
- 30.Horovitz A. Non-additivity in protein-protein interactions. J. Mol. Biol. 1987;196:733–735. doi: 10.1016/0022-2836(87)90045-3. [DOI] [PubMed] [Google Scholar]
- 31.Schreiber G., Fersht A.R. Energetics of protein-protein interactions: analysis of the barnase-barstar interface by single mutations and double mutant cycles. J. Mol. Biol. 1995;248:478–486. doi: 10.1016/s0022-2836(95)80064-6. [DOI] [PubMed] [Google Scholar]
- 32.Zhou H.X. Rate theories for biologists. Q. Rev. Biophys. 2010;43:219–293. doi: 10.1017/S0033583510000120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qin S., Pang X., Zhou H.X. Automated prediction of protein association rate constants. Structure. 2011;19:1744–1751. doi: 10.1016/j.str.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Holyst R., Bielejewska A., Wieczorek S.A. Scaling form of viscosity at all length-scales in poly(ethylene glycol) solutions studied by fluorescence correlation spectroscopy and capillary electrophoresis. Phys. Chem. Chem. Phys. 2009;11:9025–9032. doi: 10.1039/b908386c. [DOI] [PubMed] [Google Scholar]
- 35.Goins A.B., Sanabria H., Waxham M.N. Macromolecular crowding and size effects on probe microviscosity. Biophys. J. 2008;95:5362–5373. doi: 10.1529/biophysj.108.131250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Qin S., Zhou H.X. Atomistic modeling of macromolecular crowding predicts modest increases in protein folding and binding stability. Biophys. J. 2009;97:12–19. doi: 10.1016/j.bpj.2009.03.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liu Z., Weng W., Ferrone F.A. Free energy of sickle hemoglobin polymerization: a scaled-particle treatment for use with dextran as a crowding agent. Biophys. J. 2008;94:3629–3634. doi: 10.1529/biophysj.107.117465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Batra J., Xu K., Zhou H.X. Nonadditive effects of mixed crowding on protein stability. Proteins. 2009;77:133–138. doi: 10.1002/prot.22425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sasahara K., McPhie P., Minton A.P. Effect of dextran on protein stability and conformation attributed to macromolecular crowding. J. Mol. Biol. 2003;326:1227–1237. doi: 10.1016/s0022-2836(02)01443-2. [DOI] [PubMed] [Google Scholar]
- 40.Snoussi K., Halle B. Protein self-association induced by macromolecular crowding: a quantitative analysis by magnetic relaxation dispersion. Biophys. J. 2005;88:2855–2866. doi: 10.1529/biophysj.104.055871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hatters D.M., Minton A.P., Howlett G.J. Macromolecular crowding accelerates amyloid formation by human apolipoprotein C-II. J. Biol. Chem. 2002;277:7824–7830. doi: 10.1074/jbc.M110429200. [DOI] [PubMed] [Google Scholar]
- 42.Qin S., Zhou H.X. Generalized fundamental measure theory for atomistic modeling of macromolecular crowding. Phys. Rev. E. 2010;81:031919. doi: 10.1103/PhysRevE.81.031919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kiel C., Selzer T., Herrmann C. Electrostatically optimized Ras-binding Ral guanine dissociation stimulator mutants increase the rate of association by stabilizing the encounter complex. Proc. Natl. Acad. Sci. USA. 2004;101:9223–9228. doi: 10.1073/pnas.0401160101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Selzer T., Albeck S., Schreiber G. Rational design of faster associating and tighter binding protein complexes. Nat. Struct. Biol. 2000;7:537–541. doi: 10.1038/76744. [DOI] [PubMed] [Google Scholar]
- 45.Selzer T., Schreiber G. New insights into the mechanism of protein-protein association. Proteins. 2001;45:190–198. doi: 10.1002/prot.1139. [DOI] [PubMed] [Google Scholar]
- 46.Phillip Y., Sherman E., Schreiber G. Common crowding agents have only a small effect on protein-protein interactions. Biophys. J. 2009;97:875–885. doi: 10.1016/j.bpj.2009.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kuttner Y.Y., Kozer N., Haran G. Separating the contribution of translational and rotational diffusion to protein association. J. Am. Chem. Soc. 2005;127:15138–15144. doi: 10.1021/ja053681c. [DOI] [PubMed] [Google Scholar]
- 48.Kozer N., Kuttner Y.Y., Schreiber G. Protein-protein association in polymer solutions: from dilute to semidilute to concentrated. Biophys. J. 2007;92:2139–2149. doi: 10.1529/biophysj.106.097717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Banks D.S., Fradin C. Anomalous diffusion of proteins due to molecular crowding. Biophys. J. 2005;89:2960–2971. doi: 10.1529/biophysj.104.051078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chebotareva N.A., Kurganov B.I., Livanova N.B. Biochemical effects of molecular crowding. Biochemistry (Mosc.) 2004;69:1239–1251. doi: 10.1007/s10541-005-0070-y. [DOI] [PubMed] [Google Scholar]
- 51.Batra J., Xu K., Zhou H.X. Effect of macromolecular crowding on protein binding stability: modest stabilization and significant biological consequences. Biophys. J. 2009;97:906–911. doi: 10.1016/j.bpj.2009.05.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.McGuffee S.R., Elcock A.H. Diffusion, crowding and protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


