Abstract
A methodology is presented to characterize complex protein assembly pathways by fluorescence correlation spectroscopy. We have derived the total autocorrelation function describing the behavior of mixtures of labeled and unlabeled protein under equilibrium conditions. Our modeling approach allows us to quantitatively consider the relevance of any proposed intermediate form, and Kd values can be estimated even when several oligomeric species coexist. We have tested this method on the AAA+ ATPase Rubisco activase (Rca). Rca self-association regulates the CO2 fixing activity of the enzyme Rubisco, directly affecting biomass accumulation in higher plants. However, the elucidation of its assembly pathway has remained challenging, precluding a detailed mechanistic investigation. Here, we present the first, to our knowledge, thermodynamic characterization of oligomeric states of cotton β-Rca complexed with Mg·ADP. We find that the monomer is the dominating species below 0.5 micromolar. The most plausible model supports dissociation constants of ∼4, 1, and 1 micromolar for the monomer-dimer, dimer-tetramer, and tetramer-hexamer equilibria, in line with the coexistence of four different oligomeric forms under typical assay conditions. Large aggregates become dominant above 40 micromolar, with continued assembly at even higher concentrations. We propose that under some conditions, ADP-bound Rca self-associates by forming spiral arrangements that grow along the helical axis. Other models such as the stacking of closed hexameric rings are also discussed.
Introduction
Knowledge of the oligomeric state of a protein is essential for understanding its function. It has been estimated that more than 80% of proteins in Escherichia coli are composed of two or more subunits, and among these, ∼80% are homooligomers (1,2). Oligomerization is believed to be evolutionarily advantageous, as it provides opportunities for error control and regulation (1,3). However, the oligomerization state of a protein is often difficult to determine. Although several in vitro methods such as size exclusion chromatography, analytical ultracentrifugation, and chemical cross-linking can be employed, these techniques are not always adequate to identify transient intermediates.
For some proteins, the oligomerization state can be modulated by environmental factors such as concentration, temperature, pH, phosphorylation, or ligand binding (2,3). Nucleotide binding partakes in the assembly of Rubisco activase (Rca), a chemomechanical motor protein that plays an essential role in regulating Rubisco (ribulose 1,5-bisphosphate caboxylase/oxygenase) activity in higher plants (4–7). The enzyme Rubisco catalyzes the incorporation of CO2 into simple carbohydrates (8), however, its activity is diminished by the generation of competitive inhibitors that produce dead-end complexes (9,10). In many photosynthetic organisms, the ring-forming ATPase Rca catalyzes conformational changes to reactivate Rubisco for carbon fixation (7). The activity of Rca is upregulated by high ATP and downregulated by high ADP levels, and moderate heat stress causes activity loss (4,11–13).
Rca (∼383 residues) belongs to the AAA+ superfamily, a ubiquitous group of proteins that uses ATP hydrolysis to carry out mechanical work on macromolecular substrates (14). The AAA+ module consists of the N-terminal ring-forming domain bearing the Walker A and B motifs, and a less conserved C-terminal domain positioned around the periphery of toroidal assemblies (14). Adenine nucleotides bind at the domain interfaces, with hydrolysis thought to be coupled to large-scale C-domain motions. Recently, the first x-ray models of some fragments of higher plant Rca have become available, the 1.9 Å structure of the creosote C-domain (15) and the 2.9 Å structure of the tobacco AAA+ module comprising residues 68–360 (16). However, the Rca-specific N- and C-terminal regions flanking the AAA+ domain remain structurally uncharacterized. The nucleotide-free tobacco protein crystallized in a pseudohexameric spiral, and closed-ring hexameric models were generated by fitting the coordinates into negative stain electron microscopy (EM) maps (Fig. S1 in the Supporting Material) (16). Notably, the 3.0 Å crystal structure of a bacterial Rca was recently reported in combination with EM images that depict symmetric hexameric rings in the presence of ATP and ribulose-bis-phosphate (RuBP) (17).
Rca is a member of the extended classic AAA+ clade known for the formation of closed-ring hexamers (14). Some members of this clade require nucleotides and macromolecular binding partners to generate functional oligomers (18), whereas others require nucleotides to control their interactions with partner proteins (19). Several families consist of tandem arrays of AAA+ modules that stack on top of each other (20). In this group, a well-studied example is ClpA, where hexamerization is ATP- and Mg2+-dependent (21). However, for Rca, the assembly pathway has been difficult to determine due to the high degree of size polydispersity observed in all protein preparations. Based on size-exclusion high-performance liquid chromatography (SE-HPLC), molecular mass estimates have ranged from 58 to well over 550 kDa, with strong dependence on protein concentration and other assay conditions (ATP, ATP-γ-S, Mg2+, ADP, apoform, polyethylene glycol, ionic strength, glycerol, temperature) (5,12,22). Typically, SE-HPLC elution profiles consist of broad, asymmetric bands indicative of a large number of coeluting oligomeric species, with nucleotides facilitating self-association (5). Although an intermolecular salt bridge appears to be disrupted in the tobacco Rca-R294A and R294V variants (23), ATP-dependent hexamers have been identified by mass spectrometry and EM (16,24). The allosteric regulation of Rca is of intense current interest, as subunit assembly modulates the extent of biological carbon fixation. However, due to the difficulties inherent in characterizing coexisting oligomeric species, the regulation of Rca activity remains poorly understood. To elucidate bioenergetic parameters of Rubisco reactivation, a complete thermodynamic understanding of the stepwise assembly pathway is essential.
Here, we used fluorescence fluctuation methods to examine the cotton β-Rca (nonredox) assembly process in the presence of Mg⋅ADP (adenosine diphosphate complexed with Mg2+). These techniques rely on the measurement of fluorescence intensity fluctuations in a small number of molecules contained in an optically restricted volume (25,26). In fluorescence correlation spectroscopy (FCS), temporal fluorescence fluctuations are analyzed by means of the autocorrelation function (g(τ)). Results are then interpreted in terms of the dynamics of the different processes underlying these fluctuations, such as Brownian motion (27,28). FCS has been widely used to study molecular transport in vitro and in vivo (29–33), to study chromosome dynamics (34,35), and protein oligomerization (36,37). Our results show that Rca self-associates in a stepwise fashion to higher-order forms that exceed the molecular mass of a hexamer. Assembly models are discussed in relation to experimental data.
Materials and Methods
Cloning, expression, and purification of 6His-tagged and untagged cotton β-Rca
This work was carried out on cotton β-Rca-378AC, a short-form Rca with a C-terminal Ala-Cys insert (38). A blunt-ended polymerase chain reaction product coding for β-Rca-378AC was amplified from a pET23a+ expression plasmid and cloned into a linear pET151/D-TOPO vector, which was transformed into One Shot TOP10 competent cells according to the manufacturer’s instructions (Invitrogen, Grand Island, NY). The correct insert was verified by DNA sequencing of individual transformants.
The pET151/D-TOPO vectors with correct insert were transformed into E. coli BL21∗(DE3) (Invitrogen). Single colonies were cultured overnight in 25 mL LB media plus 100 μg/mL carbenicillin, and used to inoculate 1 L LB plus 100 μg/mL carbenicillin. Growth was continued at 250 rpm and 37°C until the OD600 reached ∼0.6. The cultures were cooled to ∼25°C, 100 mg of isopropyl-β-D-thiogalactoside was added to each flask, and growth was continued at 200 rpm and 25°C. After 8 h, the cells were harvested by centrifugation and pellets frozen at −80°C. Thawed cell paste was suspended in 50 mL of 25 mM HEPES pH 8.0, 20 mM imidazole pH 8.0, 300 mM NaCl, 10% glycerol, 1 mM EDTA, 1 mM phenylmethanesulfonylfluoride, 1 mM dithiothreitol (DTT), 0.5 mM ADP, and 0.1% Triton X-100, and then disrupted by sonication. The lysate was pelleted by centrifugation, and the supernatant was passed through a 0.8 μm syringe filter and loaded onto a Ni-NTA column (Qiagen, Valencia, CA). Rca was purified using an imidazole buffer step gradient (25 mM HEPES pH 8.0, 300 mM NaCl, 1 mM DTT, and 0.5 mM ADP, plus imidazole). After washing with 50 mM and 100 mM imidazole buffer, His-tagged Rca was eluted with 25 mL of 500 mM imidazole buffer. Protein fractions were pooled, 1.2 mg of tobacco etch virus protease was added to cleave the 6His tag, and the sample was dialyzed overnight at 10°C against 1 L of 25 mM Tris pH 8.0, 300 mM NaCl, 0.1 mM ADP, 0.1 mM DTT, and 1 mM EDTA. The dialysate was reapplied to a Ni-NTA column, and tobacco etch virus-cleaved Rca was collected in the flow-through and 20 mM imidazole wash. Protein was concentrated in Centriprep concentrators (Millipore, Milford, MA) to a volume of ∼2.5 mL. Using a PD-10 column (GE Healthcare, Piscataway, NJ), the buffer was exchanged into 25 mM HEPES pH 8.0, 250 mM KCl, 5 mM MgCl2, 2 mM ADP, and 10% glycerol. Protein concentration was determined by the Bradford method, with typical yields of 3–4 mg/L cell culture. Recombinant cotton β-Rca-378AC was also expressed in E. coli without an affinity tag, and purified by classical procedures as described previously (39). All Rca preparations were flash-frozen and stored at −80°C.
Dye conjugation methodology
Cotton β-Rca-378AC was covalently labeled with the ALEXA 546 C5- maleimide fluorophore (Invitrogen, Eugene, OR) using published procedures (38). A typical reaction consisted of 236 μl of 28 μM Rca, 3 μl of 500 mM ADP, buffer stock, and 54 μl of 1.93 mM Alexa dye stock (prepared in 50 mM phosphate pH 7.2), to provide a final volume of 300 μl in 50 mM phosphate pH 7.2. Control reactions were supplemented with 50 mM DTT before the addition of Alexa. All reaction tubes were incubated overnight at 4°C. To remove excess label, 300 μl saturated ammonium sulfate was added to each tube followed by incubation for 30 min at 4°C. The pellets were collected in a microcentrifuge (12,000 rpm), suspended in 170 μl 25 mM HEPES pH 7.5, 250 mM KCl, 1 mM ADP, and 10% glycerol, and desalted by two passes through a gel filtration spin column (Sephadex G50-fine, 2 ml bed volume, 400 × g centrifugation for 2 min). 6 μl aliquots (30–60 μM Rca) were flash-frozen in 1X sample buffer and stored at −80°C. 1X sample buffer contained 25 mM HEPES pH 7.6, 250 mM KCl, 2 mM ADP, 5 mM MgCl2, and 10% glycerol.
HPLC, spectrophotometric, and mass spectrometric analysis of labeled protein
Alexa-labeled Rca samples were analyzed by reverse-phase HPLC (Waters 600 HPLC system, Waters 996 photodiode array detector) on a C18 analytical column (Vydac) using a linear water/acetonitrile gradient with 0.1% trifluoroacetic acid. Protein was monitored by optical density (O.D.) 280 nm, and Alexa by O.D. 550 nm. All protein eluted at 53 min, whereas free ALEXA eluted at 47.5 min. The protein fraction was collected and its absorbance spectrum determined (650–250 nm, UV2401-PC spectrophotometer, Shimadzu, Kyoto, Japan) using 50% acetonitrile/trifluoroacetic acid as a blank. The spectrum was used to calculate the molar Alexa/protein ratio. The concentration of Alexa was determined from the O.D. 556 nm (ε556 = 104,000 M−1cm−1) and the concentration of Rca from the O.D. 280 nm after correction for dye contributions. To this end, the O.D. 556 was multiplied by the correction factor 0.146, and the resulting value subtracted from the O.D. 280. The Rca extinction coefficient was calculated from the protein’s sequence (ε280 = 44,350 M−1cm−1). To verify the correct molecular mass of labeled protein, MALDI spectra were collected on a Voyager DE STR mass spectrometer (see the Supporting Material).
Sample preparation for fluorescence fluctuation measurements
In a typical experiment, 57 μl 2X sample buffer (50 mM HEPES pH 7.6, 500 mM KCl, 4 mM ADP, 10 mM MgCl2, and 20% glycerol) and 57 μl nanopure water were added to 6 μl labeled Rca (52 μM) to provide a 2.6 μM stock of labeled protein. A 30 μM stock of unlabeled Rca was prepared in a similar manner. All solutions were kept at 22°C while performing FCS experiments (no more than 2.5 h). For each experiment, appropriate amounts of labeled and unlabeled Rca were combined in a tube containing 1X buffer to give the desired final protein concentration. For example, to prepare a mix of 50 nM labeled and 5.0 μM unlabeled Rca, 3.8 μl of 2.6 μM labeled Rca stock were combined with 33.3 μl of 30 μM unlabeled Rca stock, and 81.5 μl each of 2X buffer and nanopure water were added (200 μl final volume). To allow for subunit equilibration, each sample was incubated for 10 min at 22°C before analysis. All experiments were performed on 50 nM labeled and 0–125 μM unlabeled Rca.
Fluorescence fluctuation experiments
FCS and photon count histogram (PCH) measurements were carried out using a custom made confocal microscope. A 532 nm CW laser (Compass 215m-10 Coherent, Santa Clara, CA) was focused ∼4 μm above the coverslip using an oil immersion objective (Olympus PlanApo 100X/1.4NA Oil). Laser power was attenuated to ∼80 μW using a neutral density filter. Emitted fluorescence was collected using the same objective and then passed through a 50 μm pinhole to reject the out-of-focus light. The signal was detected using a silicon avalanche photodiode (SPCM-AQR-14; Perkin-Elmer, Fremont, CA). A band pass filter (Omega 3RD560-620) in front of the detector was employed to further reduce the background signal. An ALV correlator card (ALV 5000/EPP, ALV-GmbH, Langen, Germany) was used to correlate the detected fluorescence signal. Typical acquisition times were on the order of 10 min. Data for PCH analysis were acquired with 10 μs resolution using a PCI-6602 acquisition card (National Instruments, Austin, TX). Samples were measured in perfusion chambers (Grace BioLabs, Bend, OR) pretreated with 0.1 mg/ml bovine serum albumin (New England BioLabs, Ipswich, MA) to minimize Rca adsorption onto the cover glass.
FCS data analysis
In FCS, fluctuations are analyzed in terms of their temporal behavior by means of the autocorrelation function, g(τ) (27,28)
| (1) |
Here, I(t) is the fluorescence intensity at time t, the angular brackets denote averaging over the data accumulation time, and δI (t) = I (t)- 〈I(t)〉 represents fluctuations from the mean (27,28). For the simplest case in which a single species diffuses freely in solution and the point spread function of the instrument is adequately described by a three-dimensional (3D) Gaussian, the autocorrelation function can be expressed in terms of the diffusion coefficient of the fluorescent molecules (D) as
| (2) |
where r0 and z0 are the radial and axial semiaxes of the Gaussian confocal volume, and 〈N〉 is the mean number of molecules in an effective observation volume Veff = (π/2)3/2 z0 (27,28). The instrument was calibrated daily by measuring the FCS decays of free TAMRA dye (D = 414 μm2s−1 (40,41), ) and/or free Alexa-546 dye (D = 341 μm2s−1 (42), ) in buffer, and fitting the experimental decays to Eq. 2 using r0 and z0 as fitting parameters. The diffusion coefficient of Rca was then determined by fitting the experimental FCS decays using the values of r0 and z0 measured on the same day.
PCH data analysis
In PCH, the same raw data used to calculate the FCS decay are converted to a count rate probability distribution by determining the relative frequency with which 0, 1…k photons are measured in a given sampling time. This experimentally determined frequency histogram is then analyzed in terms of theoretical models of the probability distribution function that describe the expected distribution of photon counts for the system (43,44). In contrast to FCS, the description of the PCH of a single species diffusing in a 3D Gaussian volume cannot be expressed analytically. However, the histogram can be calculated numerically, and it is uniquely characterized by two parameters: the mean number of molecules that occupy the observation volume, 〈N〉, and the molecular brightness defined as the average photon counts detected per diffusing particle per second, ε (43,44). ε is expected to be directly proportional to the number of labeled subunits present in the particle (monomer, dimer, etc.), which is a direct measure of the oligomerization state of the protein. The value 〈N〉 was obtained from the amplitude of the FCS decay (Eq. 2), and the experimental PCH was then analyzed using ε as the only fitting parameter.
Diffusion coefficients of monomeric and oligomeric species
To interpret FCS data, we estimated the relative diffusion coefficients of different oligomers in two different ways. In the first approach, we used a value for D measured at 50 nM Rca as the diffusion coefficient of the monomer (D1). According to the Stokes-Einstein equation, D of a spherical particle is inversely proportional to the cubic root of its volume. If all oligomers are approximately spherical with constant specific volume, Dk = D1/k1/3 for an oligomer with k subunits. The influence of molecular shape (i.e., nonspherical particles) was found to be minor in the interpretation of the experimental results (see the Supporting Material). Alternatively, the radius of gyration Rg of different oligomeric states was calculated from the coordinates of the reconstructed closed-ring hexamer of tobacco Rca (pdb ID code 3ZW6) (16) as (45)
| (3) |
The models for the monomer, dimer, trimer, and tetramer consisted of the coordinates of one, two, three, or four adjacent subunits, respectively. D was calculated from Stokes-Einstein’s equation as
| (4) |
where T is taken as 293 K, η is the solution viscosity (taken as pure water), and kB is Boltzmann’s constant. The first summand in the parenthesis takes into account that the structural models comprise 76.54% of the mass of the full-length protein, and that the physical radius of a sphere is (5/3)1/2Rg (45). The second summand represents the contribution of hydration. Here, Mw is the MW of the protein, Nav is Avogadro’s number, δwater is the density of water, and h is the mass of hydration water (typically 0.2–0.6 g water/g protein (46)). In our calculations, we arbitrarily used h = 0.4. This parameter has only a minimal effect on the calculated ratios of D and does not affect data interpretation (see the Supporting Material).
Results
We have developed PCH and FCS methods to investigate Rca assembly at pH 7.6 in the presence of 2 mM ADP and 5 mM Mg2+. To this end, we have labeled cotton β-Rca-378AC with a maleimide-functionalized Alexa 546 fluorophore by chemical modification of an engineered cysteine residue (38). In this variant, Ala-Cys was inserted after residue 378 of the 380-residue protein (38), positioning the label 20 residues downstream of the C-terminus of the AAA+ x-ray model (Fig. S1) (16). Compared to wild-type, the insertion mutant was reported to exhibit 81% of ATPase and 53% of Rubisco reactivation activity, although derivatization was shown to increase these activities to 150% and 131%, respectively (38). In line with previous reports (38), MALDI spectra were consistent with a single molecular mass of appropriate MW (see the Supporting Material). Absorbance scans collected on HPLC-purified denatured protein provided a molar ratio of 1.04 ± 0.08 (n = 4) label attached per protein chain.
Both FCS and PCH rely on the analysis of fluorescence fluctuations under equilibrium conditions. The average number of molecules present in the observation volume, 〈N〉, is required to be small for the amplitude of intensity fluctuations to be large relative to its mean, imposing an upper limit of ∼300 nM on the concentration of labeled Rca. Therefore, we performed experiments at higher Rca concentrations by mixing labeled and unlabeled protein. This strategy has been used to investigate oligomerization or aggregation in a large variety of proteins such as α-synuclein (47), tubulin (37), barstar (48), and the tumor suppressor p53 (36), and it assumes that the labeled and unlabeled subunits equilibrate producing oligomers that bear a variable number of fluorescent subunits. Although mixing greatly complicates PCH analysis, a substantial amount of information can be extracted by FCS analysis.
Rca is a monomer at concentrations below 300 nM
Experiments on labeled Rca were performed in the 50–300 nM range. At each subunit concentration, the diffusion coefficient was calculated by fitting the experimental FCS decays to Eq. 2. At 50 nM labeled Rca, a value of D50nM = 64.7 ± 3.7 μm2s−1 was obtained by fitting 10 independent experiments. At higher concentrations, the diffusion coefficients were obtained by averaging four independent determinations, and were found to be indistinguishable from D50nM within error (Fig. S2). These results suggest that the Rca oligomerization state does not change between 50 and 300 nM. In addition, the mean number of particles obtained from the inverse of the FCS amplitude (Eq. 2) scales linearly with Rca concentration as expected for monodisperse samples (Fig. S2). Self-association would decrease the particle number, resulting in a downward curvature of this plot.
The experimentally determined D50nM can be compared to the diffusion coefficient calculated from the Rg value of a single subunit. Based on the crystallographic model (16), we estimate D1 for an Rca monomer to be 59.1 μm2s−1 at 20°C (see Materials and Methods). Because the experimental value is somewhat larger than the calculated one, whereas aggregation would reduce D, these results provide further support for monomeric Rca in the 50–300 nM range. Further evidence supporting a monomer can be obtained from PCH analysis, which is based on the molecular brightness (ε) defined as the average photon count detected per particle per second. Because each Rca monomer is labeled with a single fluorophore, ε of a dimer is expected to be twice that of a monomer. Although the PCH of a single species diffusing in a 3D volume cannot be expressed analytically, the histogram can be calculated numerically in terms of the parameters 〈N〉 and ε (43). At each Rca concentration, we determined ε from a nonlinear fit of the experimental data, fixing 〈N〉 at the value obtained from the amplitude of the FCS decay (Eq. 2). To obtain the molecular brightness of individual labels, analogous experiments were performed with free dye in solution. Assuming that the fluorescence quantum yield and extinction coefficient of the dye are not affected by the protein environment, the ratio of the molecular brightness of labeled Rca (ε) and the free dye (εFD) is a measure of the oligomerization state of the protein. The ratios ε/εFD were obtained by PCH analysis of experiments on labeled Rca and on free dye from 50 to 300 nM, and are plotted in Fig. S2. Over this concentration range, the ratios remain constant within error at an average value of 0.8. The small reduction in brightness suggests that the product of the extinction coefficient and fluorescence quantum yield of the dye is diminished upon attachment to the protein. Regardless, the observed ratio is consistent with monomeric Rca, as self-association would provide a ratio greater than 1.
Rca forms oligomers in the 1–10 μM range, and large complexes at higher concentrations
To investigate Rca assembly above 300 nM concentration, we mixed labeled and unlabeled protein, and assumed that subunit equilibration will lead to a random distribution of labels over all oligomeric forms. In support of this notion, control experiments with varying incubation times (0–60 min) performed on 8 μM Rca demonstrated that the results do not depend on the time elapsed between sample preparation and data acquisition. Above ∼550 nM, the FCS decays of solutions containing 50 nM labeled and increasing amounts of unlabeled Rca show a continuous shift to longer timescales (Fig. 1 A), suggesting the formation of oligomers whose size and relative concentrations depend on total protein concentration (labeled and unlabeled). Control experiments carried out on free Alexa 546 in buffers containing up to 127 μM unlabeled Rca showed no measurable changes in the FCS decay of the dye, ruling out the possibility that the shifts observed with labeled Rca are due to changes in solution viscosity or index of refraction.
Figure 1.
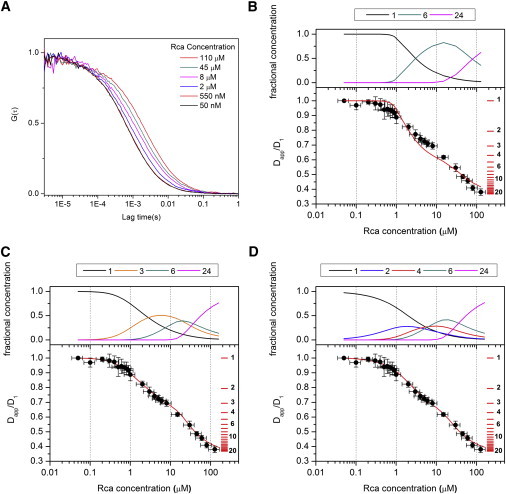
Rca assembly mechanisms. (A) Representative FCS decays obtained with 50 nM labeled and increasing concentrations of unlabeled Rca. The concentrations in the inset represent total protein (labeled and unlabeled). (B–D) Comparison of experimental results and modeling. The solid circles are experimental values of the ratio of the apparent diffusion coefficient at each concentration (Dapp) and the diffusion coefficient obtained at 50 nM (D1). The horizontal red lines are placed at values of Dapp/D1 = k−1/3 for k = 1, 2… 20, and represent the expected Dapp/D1 values for monomers, dimers, etc. The solid curves were calculated according to Model 1 (panel B), Model 2 (panel C), and Model 3 (panel D) with the Kd values from Table 1. The concentration profiles above each graph (panels B–D) represent the fractional subunit concentrations of the different oligomeric forms assumed to contribute to each model, as calculated from the total Rca concentration and the Kd values in Table 1.
Consistent with previous reports (5,12), the FCS data indicate that at subunit concentrations above 10 μM, Rca assembles to form supramolecular complexes significantly larger than hexamers. Despite the complexity of the assembly mechanism, all FCS decays can be fit with a simple one-component model (Eq. 2), such that an apparent diffusion coefficient (Dapp) can be extracted (see below). Therefore, the ratio Dapp/D1 can be calculated for each experiment regardless of the number of contributing species (Fig. 1, B–D). To provide a scale, the expected ratios Dapp/D1 = k−1/3 for k = 1…20 for the pure oligomeric forms are shown as red horizontal bars on the right side of the graphs. At 100 μM Rca, we observe a ratio of 0.38, substantially smaller than the value of 0.55 expected for k = 6, suggesting large aggregates bearing on the order of ∼24 subunits. The variations in relative diffusion coefficients that would result from nonspherical molecular shapes and different amounts of bound water cannot account for this difference (see the Supporting Material).
Rajagopalan et al. (36) used FCS to investigate the self-association of the tumor suppressor protein p53, which was known to form tetramers from dimeric intermediates. Because in this case the dissociation constants are separated by about two orders of magnitude, no more than two oligomeric forms coexist at any protein concentration. As a consequence, a graph of diffusion time versus protein concentration exhibits two clear inflection points at concentrations around the monomer/dimer and dimer/tetramer transitions, which allows the estimation of Kd values directly from this plot with minimal mathematical modeling (36). In contrast, we observe a smooth shift in the diffusion constant with concentration, indicating that Rca assembly involves a number of intermediates in a wide range of concentrations. This feature is supported by published SE-HPLC data (5,12,22,23). Therefore, the interpretation of FCS data in terms of Rca assembly requires modeling the diffusion coefficients of individual component species, and a mathematical model that describes the total autocorrelation function in terms of the contributions of all oligomeric species present at each protein concentration.
Derivation of the total autocorrelation function to describe mixed-species FCS
The autocorrelation function for a polydisperse sample containing M components of well-defined diffusion coefficient (Di) and brightness (εi) is (28)
| (5) |
where
| (6) |
is the normalized autocorrelation function for species i, r0 and z0 are the radial and axial semiaxis of the Gaussian confocal volume (see Materials and Methods), and Ni is the mean number of molecules of the ith species in the observation volume. In general, Eq. 5 will depend on the diffusion coefficients of all oligomers present in solution, and the dissociation constants of the different assembly equilibria. Despite the complexity of Eq. 5 we could fit all FCS decays with the one-component model of Eq. 2 to obtain an apparent diffusion coefficient, Dapp (see the Supporting Material for a more in-depth discussion and representative examples). This indicates that the linear combination of several one-component decays gives a total autocorrelation decay that cannot be distinguished experimentally from that obtained for a monodisperse sample. It should be noted that Dapp is not the average of individual diffusion coefficients, because each species contributes to the autocorrelation function as the square of its brightness. For instance, dimers bearing two labels contribute four times as much to G(τ) than monomers bearing one label.
In Figs. 1, B–D, experimental FCS results are represented as the ratio between Dapp obtained from the fit to Eq. 2 and the diffusion coefficient for the monomer D1 measured at 50 nM Rca. Error bars represent the standard deviation of at least four determinations. To obtain assembly models consistent with the experimental Dapp/D1 ratios, the brightness in Eq. 5 must be expressed in terms of the assembly state of the protein and the number of labeled subunits present in each oligomeric species. The brightness of each species εi is proportional to the number of fluorophores n (i.e., the number of labeled subunits present in the oligomeric particle). Assuming that the protein assembles into oligomers of k subunits, Eq. 5 can be expressed as
| (7) |
where Nk,n is the number of particles in the observation volume containing k Rca subunits and n fluorophores (0 ≤ n ≤ k), and gk(τ) is the normalized autocorrelation function defined in Eq. 6. Eq. 7 is similar to the model discussed by Yu et al. (49) to analyze the FCS decays of micelles containing a variable number of fluorophores, although in this work the authors examined only the amplitude of the decay and used a single diffusion coefficient for all micelles. Due to the mixing of labeled and unlabeled subunits, the number of fluorophores in a given oligomeric particle is a random variable distributed according to the binomial distribution. The probability that an oligomer of size k contains n labeled monomers is therefore given by
| (8) |
where f, the fraction of fluorescently labeled protein monomers, is determined by the relative concentrations of labeled (CL) and unlabeled (CU) subunits present in the mixture: f = CL/(CL + CU). The value of Nk,n is then given by pk,nNk, where Nk = is the total number of particles in the observation volume containing k subunits and any number of fluorophores. Nk can be expressed in terms of molar concentrations as CkVeffNAV, where Ck is the concentration of the oligomer of size k, Veff is the effective observation volume in liters (Veff = (π/2)3/2 r02z0) (26), and NAV is Avogadro’s number. The values of Ck, in turn, are determined by the dissociation constants of the different oligomerization equilibria and the total protein concentration (CL + CU).
The total autocorrelation function can then be expressed in terms of the concentrations of labeled and unlabeled Rca (CL, CU), the optical parameters of the setup (r0, z0), the diffusion coefficient of each oligomeric state (Dk), and the concentrations of the different oligomers in the solution (Ck).
| (9) |
We were able to estimate Dk values from the x-ray structure of tobacco Rca (see Materials and Methods). Therefore, Ck is the only unknown parameter in Eq. 9, with values depending on the Kds and total Rca concentration. Therefore, the analysis of FCS decays requires previous knowledge of the number of different oligomeric species present and the mechanism by which each one is formed. Although this information is limited for Rca, different assembly mechanisms can be tested for their consistency with experimental data (Table 1). To this end, we first assume a set of values of k to represent the types of oligomers present in equilibrium, and a mechanism for their formation. A set of Kd values is then assumed, from which the concentration of each oligomer (Ck) is calculated as a function of Rca concentration (CU + CL). Equation 9 is then used to predict the theoretical total autocorrelation function at each Rca concentration. As with the experimental data, each of the theoretical decays is fitted to Eq. 2, from which a calculated value for Dapp is obtained that describes the FCS decay of a complex mixture of species. The relative apparent diffusion coefficients Dapp/D1 expected for the assumed mechanism are plotted as a function of concentration (Fig. 1, B–D, solid lines), and compared to the experimental data. The equilibrium constants are then modified iteratively until the calculated set of Dapp/D1 values is consistent with observations within error bars.
Table 1.
Optimized dissociation constants
| Model | Equilibria | Kd values |
|---|---|---|
| 1 | 50 μM5 | |
| 103μM3 | ||
| 2 | 5 μM2 | |
| 5 μM | ||
| 35 μM3 | ||
| 3 | 3.5 μM | |
| 1 μM | ||
| 1 μM | ||
| 25 μM3 |
Dissociation constants (Kd) for each assembly step were obtained by modeling according to Eq. 9. Model 1 is judged to be inconsistent with experiment, whereas Models 2 and 3 provide good fits to the data.
Interpretation of FCS data in terms of alternative Rca assembly mechanisms
Although to date, the Rca assembly mechanism remains poorly characterized, some information on subunit stoichiometries is available. In our laboratory, we routinely observe dimeric forms by SE-HPLC (R. M. Wachter, unpublished results). Recently, hexameric forms have been observed by mass spectrometry and EM (16,17,24). In combination with the high propensity of classic AAA+ domains to hexamerize, these data provide strong support for a six-subunit intermediate state. Therefore, we analyzed the experimental FCS decays in terms of Rca self-association from monomers to hexamers to larger aggregates. Within this framework, we considered three mechanisms, Model 1 (monomer-hexamer-24 mer), Model 2 (monomer-trimer-hexamer-24 mer), and Model 3 (monomer-dimer-tetramer-hexamer-24 mer) (Table 1). In Fig.1, B–D, we show predicted and experimental Dapp/D1 values, as well as the fractional concentration kCk/ΣkkCk of each oligomer as calculated from the predicted Kd values (panels above each graph).
Using Eq. 9, our calculations predict that Model 1 would cause a sharp decrease in Dapp, as illustrated by the red curve in Fig. 1 B, which shows the predicted autocorrelation function using Kd1 = 50 μM5 and Kd2 = 103 μM3. However, the observed relative Dapp values decrease rather smoothly in the low μM range (Fig. 1 B, solid circles), suggesting the formation of intermediates. Although a reduction in Kd1 would provide a better fit to the experimental data at the very low concentration range, such an adjustment would drop the Dapp/D1 ratio to ∼0.6 around 1 μM Rca, whereas the experimental values remain high at ∼0.9. Therefore, Model 1 is judged to be inconsistent with the data.
At least one intermediate is needed to predict the more moderate decrease in diffusion coefficients observed in the low μM range. Therefore, in Model 2, we introduce a trimer as an intermediate. The best match between experimental data and modeling was obtained using Kd1 = 5 μM2, Kd2 = 5 μM, and Kd3 = 35 μM3 (Table 1 and Fig.1 C). To estimate the uncertainties in dissociation constants, we evaluated a range of Kd1 values that produce results consistent with experiment. These tests show that Kd1 values in the range of 3.5–10 μM2 provide a good fit to the data within experimental error (Fig. S9 A). The values of Kd2 and Kd3 used to generate these curves were optimized for the lowest and highest Kd1 values in this range (Kd2 = 15 μM, Kd3 = 2 μM3 for Kd1 = 3.5 μM2; Kd2 = 1.3 μM, Kd3 = 70 μM3 for Kd1 = 10 μM2). Clearly, a single trimeric intermediate is sufficient to describe the FCS results adequately.
However, based on the observation of dimers (see above), we considered an additional mechanism that proceeds through dimeric and tetrameric forms (Model 3, Fig. 1 D). For this assembly path, the best agreement with experimental data was obtained with Kd1 = 3.5 μM, Kd2 = 1 μM Kd3 = 1 μM, and Kd4 = 25 μM3 (Fig. 1 D). Because Model 3 has an additional adjustable parameter compared to Model 2, a wider range of Kd values provide a good fit, such as Kd1 values in the range of 2.0–20 μM (Fig. S9 B). The values of Kd2–Kd4 were optimized for the values of Kd1 on each extreme of the range (for Kd1 = 2 μM, Kd2 = 2 μM, Kd3 = 1 μM, and Kd4 = 20 μM3; for Kd1 = 20 μM, Kd2 = 0.03 μM, Kd3 = 2 μM, and Kd4 = 8 μM3). The concentration profiles predicted by this set of dissociation constants show more variations than the profiles obtained for Model 2 (Fig. S9 B). This is a consequence of the fact that our experimental results can be adequately described with one less species (Model 2).
Even at the highest concentrations tested, a clear plateau in Dapp/D1 is not observed, suggesting that more highly aggregated states are in equilibrium with assemblies of roughly 24 subunits. Because a precise MW determination of large aggregates is not possible, we suggest that hexameric species self-associate to form 24-subunit complexes (Fig. 2). However, it is important to stress that we cannot distinguish between 18 and 24 mers due to the uncertainty inherent in our experiments (Fig. 1, B–D, red horizontal scale bars). Additionally, we cannot rule out that larger species are formed by the continuous binding of dimers to smaller forms (Rcak + Rca2 = Rcak+2), leading to the formation of helical arrangements as observed in the Rca AAA+ crystal structure (16) (Fig. 2).
Figure 2.
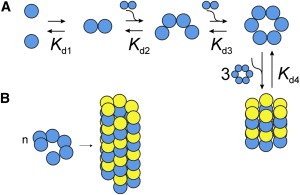
Rca assembly pathways consistent with experimental data. Schematic representation of Model 3 involving dimeric and tetrameric intermediates on the pathway of hexamer formation. Higher-order assemblies are shown as stacks of closed hexameric rings (A) or as pseudohexameric spirals (B).
Discussion
Frequently, the mechanistic enzymology of complex protein assemblies is less well understood. A detailed molecular description of subunit cooperativity requires knowledge of the stoichiometries and fractional concentrations of all component species. We have developed an FCS-based method to address this question, and have tested our methodology on the highly aggregate-prone chaperone-like protein Rca. We show that the low nanomolar to mid-micromolar range is accessible by mixing labeled and unlabeled protein, and anticipate that this method will be particularly useful for the examination of dynamic equilibria that involve fast subunit exchange. Although in higher plants, the ATPase activity of Rca regulates the level of carbon fixation, its assembly process has remained intractable for many years (5,12). The FCS experiments presented here provide a framework for the development of appropriate thermodynamic models for self-association. Our data provide clear evidence of multiple oligomeric states under equilibrium conditions. Although the FCS results appear to mimic a wealth of SE-HPLC data, chromatography cannot provide equilibrium stoichiometries for a highly dynamic system, a feature that has impeded a thorough mechanistic investigation of Rca.
In this work, we have monitored the Mg·ADP-mediated assembly process of cotton β-Rca at pH 7.6. Our PCH and FCS results show that the monomer is the dominating species at subunit concentrations below 0.5 μM, in line with EM images of amorphous particles at 0.5–1 μM tobacco Rca-R293V with Mg·ADP (16). Within the 100 μM concentration range, our data are consistent with the formation of high-MW aggregates comprising roughly 24 subunits. As the assembly process appears to be continuous, with no obvious plateau at any concentration, stoichiometries of intermediate states cannot be extracted by FCS (Fig. 1, B–D). Therefore, we use evidence from other sources to interpret the FCS results. Experimental evidence of Rca hexamers has been accumulating (16,17,24). By EM, the ATP-dependent formation of closed 6-unit rings has been observed for 0.5–1 μM tobacco Rca-R293V, whereas the crystal structure provided a spiral hexameric model (16). In general, members of the AAA+ classic clade have been crystallized in both helical and closed-ring hexameric arrays, although only toroids are considered part of the ATPase cycle. For example, the AAA+ domain of FtsH with attached protease forms a toroidal hexamer (50), whereas the absence of the protease domain leads to helical assemblies (51). The assembly pathway of the related AAA+ protein ClpA involves dimeric and tetrameric forms (21,52), providing support for Rca assembly according to Model 3. However, in contrast to Rca, the ClpA Mg·ATP-dependent pathway involves tight complexes that can be isolated, with a dimer-tetramer Kd of ∼1 nM and a tetramer-hexamer Kd below 0.17 nM (21).
Rca assembly mechanisms
We have considered three different assembly mechanisms that proceed to the ∼24-subunit stage (Table 1), and find that the formation of hexamers must occur through at least one (Model 2), or more likely, two intermediate steps (Model 3). Model 3 suggests that the rise of the hexamer is initiated at 1 μM Rca (Fig. 1 D), and dominates between 10 and 30 μM, whereas the tetramer contributes significantly between 5 and 20 μM. Higher-order assemblies (k > 6) start forming at ∼15 μM, and become dominant above 40 μM. In the high range, the data do not provide sufficient detail to warrant the modeling of forms intermediate to 6 and 24 subunits, and therefore cannot be used to distinguish between models of closed hexameric rings (Fig. 2 A) and pseudohexameric spirals (Fig. 2 B). Although some AAA+ proteins contain stacks of toroidal rings (20), the helical filament model appears particularly attractive, because it allows for the continuous assembly of extended structures by the sequential addition of dimers. The Kd values extracted for the dimer-tetramer and tetramer-hexamer equilibria are estimated to be ∼1 μM (Table 1), suggesting that the addition of a dimer to either a dimer or a tetramer is energetically equivalent. This feature supports a spiral assembly (Fig. 2 B) and provides a rational for the broad size distribution observed by SE-HPLC (5,12).
This work provides evidence that under typical kinetic assay conditions (5–20 μM Rca), as much as four different Rca species coexist (Fig. 1, B–D). Our method has opened the door to the future investigation of Rca assembly as a function of different ADP/ATP ratios, as modulated by the energy charge of the chloroplast stroma. Long term, we expect that a complete thermodynamic description of Rca assembly will aid in elucidating the mechanism of Rubisco reactivation.
Acknowledgments
This work was supported by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the U.S. Department of Energy through grants DE-FG02-09-ER16123 (to R.M.W and M.L.) and DE-FG02-08ER-20268 (to M.E.S.)
Contributor Information
Rebekka M. Wachter, Email: rwachter@asu.edu.
Marcia Levitus, Email: mlevitus@asu.edu.
Supporting Material
References
- 1.Goodsell D.S., Olson A.J. Structural symmetry and protein function. Annu. Rev. Biophys. Biomol. Struct. 2000;29:105–153. doi: 10.1146/annurev.biophys.29.1.105. [DOI] [PubMed] [Google Scholar]
- 2.Hashimoto K., Nishi H., Panchenko A.R. Caught in self-interaction: evolutionary and functional mechanisms of protein homooligomerization. Phys. Biol. 2011;8:035007. doi: 10.1088/1478-3975/8/3/035007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ali M.H., Imperiali B. Protein oligomerization: how and why. Bioorg. Med. Chem. 2005;13:5013–5020. doi: 10.1016/j.bmc.2005.05.037. [DOI] [PubMed] [Google Scholar]
- 4.Crafts-Brandner S.J., Salvucci M.E. Rubisco activase constrains the photosynthetic potential of leaves at high temperature and CO2. Proc. Natl. Acad. Sci. USA. 2000;97:13430–13435. doi: 10.1073/pnas.230451497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Portis A.R., Jr. Rubisco activase - Rubisco’s catalytic chaperone. Photosynth. Res. 2003;75:11–27. doi: 10.1023/A:1022458108678. [DOI] [PubMed] [Google Scholar]
- 6.Portis A.R.J., Jr., Li C., Salvucci M.E. Regulation of Rubisco activase and its interaction with Rubisco. J. Exp. Bot. 2008;59:1597–1604. doi: 10.1093/jxb/erm240. [DOI] [PubMed] [Google Scholar]
- 7.Wang Z.Y., Portis A.R.J. Dissociation of ribulose-1,5-bisphosphate bound to ribulose-1,5-bisphosphate carboxylase/oxygenase and its enhancement by ribulose-1,5-bisphosphate carboxylase/oxygenase activase-mediated hydrolysis of ATP. Plant Physiol. 1992;99:1348–1353. doi: 10.1104/pp.99.4.1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Spreitzer R.J., Salvucci M.E. Rubisco: structure, regulatory interactions, and possibilities for a better enzyme. Annu. Rev. Plant Biol. 2002;53:449–475. doi: 10.1146/annurev.arplant.53.100301.135233. [DOI] [PubMed] [Google Scholar]
- 9.Pearce F.G., Andrews T.J. The relationship between side reactions and slow inhibition of ribulose-bisphosphate carboxylase revealed by a loop 6 mutant of the tobacco enzyme. J. Biol. Chem. 2003;278:32526–32536. doi: 10.1074/jbc.M305493200. [DOI] [PubMed] [Google Scholar]
- 10.Andersson I. Catalysis and regulation in Rubisco. J. Exp. Bot. 2008;59:1555–1568. doi: 10.1093/jxb/ern091. [DOI] [PubMed] [Google Scholar]
- 11.Salvucci M.E., van de Loo F.J., Stecher D. Two isoforms of Rubisco activase in cotton, the products of separate genes not alternative splicing. Planta. 2003;216:736–744. doi: 10.1007/s00425-002-0923-1. [DOI] [PubMed] [Google Scholar]
- 12.Barta C., Dunkle A.M., Salvucci M.E. Structural changes associated with the acute thermal instability of Rubisco activase. Arch. Biochem. Biophys. 2010;499:17–25. doi: 10.1016/j.abb.2010.04.022. [DOI] [PubMed] [Google Scholar]
- 13.Carmo-Silva A.E., Salvucci M.E. The activity of Rubisco’s molecular chaperone, Rubisco activase, in leaf extracts. Photosynth. Res. 2011;108:143–155. doi: 10.1007/s11120-011-9667-8. [DOI] [PubMed] [Google Scholar]
- 14.Snider J., Houry W.A. AAA+ proteins: diversity in function, similarity in structure. Biochem. Soc. Trans. 2008;36:72–77. doi: 10.1042/BST0360072. [DOI] [PubMed] [Google Scholar]
- 15.Henderson J.N., Kuriata A.M., Wachter R.M. Atomic resolution x-ray structure of the substrate recognition domain of higher plant ribulose-bisphosphate carboxylase/oxygenase (Rubisco) activase. J. Biol. Chem. 2011;286:35683–35688. doi: 10.1074/jbc.C111.289595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stotz M., Mueller-Cajar O., Hayer-Hartl M. Structure of green-type Rubisco activase from tobacco. Nat. Struct. Mol. Biol. 2011;18:1366–1370. doi: 10.1038/nsmb.2171. [DOI] [PubMed] [Google Scholar]
- 17.Mueller-Cajar O., Stotz M., Hayer-Hartl M. Structure and function of the AAA+ protein CbbX, a red-type Rubisco activase. Nature. 2011;479:194–199. doi: 10.1038/nature10568. [DOI] [PubMed] [Google Scholar]
- 18.Hartman J.J., Vale R.D. Microtubule disassembly by ATP-dependent oligomerization of the AAA enzyme katanin. Science. 1999;286:782–785. doi: 10.1126/science.286.5440.782. [DOI] [PubMed] [Google Scholar]
- 19.Smith D.M., Fraga H., Goldberg A.L. ATP binds to proteasomal ATPases in pairs with distinct functional effects, implying an ordered reaction cycle. Cell. 2011;144:526–538. doi: 10.1016/j.cell.2011.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hattendorf D.A., Lindquist S.L. Cooperative kinetics of both Hsp104 ATPase domains and interdomain communication revealed by AAA sensor-1 mutants. EMBO J. 2002;21:12–21. doi: 10.1093/emboj/21.1.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kress W., Mutschler H., Weber-Ban E. Assembly pathway of an AAA+ protein: tracking ClpA and ClpAP complex formation in real time. Biochemistry. 2007;46:6183–6193. doi: 10.1021/bi602616t. [DOI] [PubMed] [Google Scholar]
- 22.Wang Z.Y., Ramage R.T., Portis A.R.J., Jr. Mg2+ and ATP or adenosine 5′-[gamma-thio]-triphosphate (ATP gamma S) enhances intrinsic fluorescence and induces aggregation which increases the activity of spinach Rubisco activase. Biochim. Biophys. Acta. 1993;1202:47–55. doi: 10.1016/0167-4838(93)90061-u. [DOI] [PubMed] [Google Scholar]
- 23.Li C., Wang D., Portis A.R.J., Jr. Identification of critical arginine residues in the functioning of Rubisco activase. Arch. Biochem. Biophys. 2006;450:176–182. doi: 10.1016/j.abb.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 24.Blayney M.J., Whitney S.M., Beck J.L. NanoESI mass spectrometry of Rubisco and Rubisco activase structures and their interactions with nucleotides and sugar phosphates. J. Am. Soc. Mass Spectrom. 2011;22:1588–1601. doi: 10.1007/s13361-011-0187-8. [DOI] [PubMed] [Google Scholar]
- 25.Jameson D.M., Ross J.A., Albanesi J.P. Fluorescence fluctuation spectroscopy: ushering in a new age of enlightenment for cellular dynamics. Biophys Rev. 2009;1:105–118. doi: 10.1007/s12551-009-0013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Müller J.D., Chen Y., Gratton E. Fluorescence correlation spectroscopy. Methods Enzymol. 2003;361:69–92. doi: 10.1016/s0076-6879(03)61006-2. [DOI] [PubMed] [Google Scholar]
- 27.Elson E.L., Magde D. Fluorescence correlation spectroscopy. 1. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 28.Thompson N.L. Fluorescence correlation spectroscopy. In: Lakowicz J.R., editor. Topics in Fluorescence Spectroscopy. Plenum Press; New York: 1991. pp. 337–355. [Google Scholar]
- 29.Boxer S.G. Molecular transport and organization in supported lipid membranes. Curr. Opin. Chem. Biol. 2000;4:704–709. doi: 10.1016/s1367-5931(00)00139-3. [DOI] [PubMed] [Google Scholar]
- 30.Kahya N., Schwille P. Fluorescence correlation studies of lipid domains in model membranes. Mol. Membr. Biol. 2006;23:29–39. doi: 10.1080/09687860500489099. (Review) [DOI] [PubMed] [Google Scholar]
- 31.Berland K.M., So P.T.C., Gratton E. Two-photon fluorescence correlation spectroscopy: method and application to the intracellular environment. Biophys. J. 1995;68:694–701. doi: 10.1016/S0006-3495(95)80230-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lukacs G.L., Haggie P., Verkman A.S. Size-dependent DNA mobility in cytoplasm and nucleus. J. Biol. Chem. 2000;275:1625–1629. doi: 10.1074/jbc.275.3.1625. [DOI] [PubMed] [Google Scholar]
- 33.Wachsmuth M., Waldeck W., Langowski J. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J. Mol. Biol. 2000;298:677–689. doi: 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
- 34.Abney J.R., Cutler B., Scalettar B.A. Chromatin dynamics in interphase nuclei and its implications for nuclear structure. J. Cell Biol. 1997;137:1459–1468. doi: 10.1083/jcb.137.7.1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hemmerich P., Weidtkamp-Peters S., Diekmann S. Dynamics of inner kinetochore assembly and maintenance in living cells. J. Cell Biol. 2008;180:1101–1114. doi: 10.1083/jcb.200710052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rajagopalan S., Huang F., Fersht A.R. Single-molecule characterization of oligomerization kinetics and equilibria of the tumor suppressor p53. Nucleic Acids Res. 2011;39:2294–2303. doi: 10.1093/nar/gkq800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Krouglova T., Vercammen J., Engelborghs Y. Correct diffusion coefficients of proteins in fluorescence correlation spectroscopy. Application to tubulin oligomers induced by Mg2+ and Paclitaxel. Biophys. J. 2004;87:2635–2646. doi: 10.1529/biophysj.104.040717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Salvucci M.E. Potential for interactions between the carboxy- and amino-termini of Rubisco activase subunits. FEBS Lett. 2004;560:205–209. doi: 10.1016/S0014-5793(04)00111-5. [DOI] [PubMed] [Google Scholar]
- 39.Barta C., Carmo-Silva A.E., Salvucci M.E. Purification of Rubisco activase from leaves or after expression in Escherichia coli. In: Carpentier R., editor. Photosynthesis Research Protocols. 2nd ed. Humana Press; New York: 2011. pp. 363–374. [DOI] [PubMed] [Google Scholar]
- 40.Gendron P.O., Avaltroni F., Wilkinson K.J. Diffusion coefficients of several rhodamine derivatives as determined by pulsed field gradient-nuclear magnetic resonance and fluorescence correlation spectroscopy. J. Fluoresc. 2008;18:1093–1101. doi: 10.1007/s10895-008-0357-7. [DOI] [PubMed] [Google Scholar]
- 41.Muller C.B., Loman A., Enderlein J. Precise measurement of diffusion by multi-color dual-focus fluorescence correlation spectroscopy. Europhys. Lett. 2008;83:46001. [Google Scholar]
- 42.Petrásek Z., Schwille P. Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy. Biophys. J. 2008;94:1437–1448. doi: 10.1529/biophysj.107.108811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chen Y., Müller J.D., Gratton E. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 1999;77:553–567. doi: 10.1016/S0006-3495(99)76912-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Perroud T.D., Huang B., Zare R.N. Photon counting histogram for one-photon excitation. ChemPhysChem. 2003;4:1121–1123. doi: 10.1002/cphc.200300824. [DOI] [PubMed] [Google Scholar]
- 45.Rubinstein M., Colby R.H. Oxford University Press; Oxford: 2003. Polymer Physics. [Google Scholar]
- 46.Squire P.G., Himmel M.E. Hydrodynamics and protein hydration. Arch. Biochem. Biophys. 1979;196:165–177. doi: 10.1016/0003-9861(79)90563-0. [DOI] [PubMed] [Google Scholar]
- 47.Nath S., Meuvis J., Engelborghs Y. Early aggregation steps in alpha-synuclein as measured by FCS and FRET: evidence for a contagious conformational change. Biophys. J. 2010;98:1302–1311. doi: 10.1016/j.bpj.2009.12.4290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sahoo B., Balaji J., Maiti S. Protein aggregation probed by two-photon fluorescence correlation spectroscopy of native tryptophan. J. Chem. Phys. 2008;129:075103. doi: 10.1063/1.2969110. [DOI] [PubMed] [Google Scholar]
- 49.Yu L.L., Tan M.Y., Wohland T. Determination of critical micelle concentrations and aggregation numbers by fluorescence correlation spectroscopy: aggregation of a lipopolysaccharide. Anal. Chim. Acta. 2006;556:216–225. doi: 10.1016/j.aca.2005.09.008. [DOI] [PubMed] [Google Scholar]
- 50.Bieniossek, C., B. Niederhauser, and U. Baumann. 2009. Apo-FtsH crystal structure. RCSB protein data bank, http://www.pdb.org. [DOI] [PMC free article] [PubMed]
- 51.Niwa H., Tsuchiya D., Morikawa K. Hexameric ring structure of the ATPase domain of the membrane-integrated metalloprotease FtsH from Thermus thermophilus HB8. Structure. 2002;10:1415–1423. doi: 10.1016/s0969-2126(02)00855-9. [DOI] [PubMed] [Google Scholar]
- 52.Veronese P.K., Stafford R.P., Lucius A.L. The Escherichia coli ClpA molecular chaperone self-assembles into tetramers. Biochemistry. 2009;48:9221–9233. doi: 10.1021/bi900935q. [DOI] [PubMed] [Google Scholar]
- 53.Perrin F. The Brownian movement of an ellipsoid. - The dielectric dispersion of ellipsoidal molecules. J. Phys. (Paris) 1934;5:497–511. [Google Scholar]
- 54.Meseth U., Wohland T., Vogel H. Resolution of fluorescence correlation measurements. Biophys. J. 1999;76:1619–1631. doi: 10.1016/S0006-3495(99)77321-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


