Abstract
We propose a 2D mechanical model of a tubular epithelium resembling the early Drosophila embryo. The model consists of a single layer of identical cells with energy associated with the tension of cell cortex. Depending on the relative tension of the apical, basal, and lateral sides of the cells, tissue thickness, and the degree of external constraint, the minimal-energy states of the epithelial cross section include circular shapes as well as a range of inward-buckled shapes. Some of the solutions are characterized by a single deep groove, which shows that an epithelium consisting of cells of identical mechanical properties can infold. This is consistent with what is seen in embryos of certain Drosophila mutants. To ensure that the infolding occurs at a predetermined section of the epithelium, we extend the model by increasing the cross-sectional area of a subset of cells, which is consistent with observations in wild-type embryos. This variation of cell parameters across the epithelium is sufficient to make it fold at a specific site. The model explores previously untested minimal conditions for tissue invagination and is devoid of specificity needed to accurately describe an in vivo situation in Drosophila.
Introduction
Epithelial folding is a common process in the development of animals. This morphological change can displace cells from within a planar sheet to a new location, thereby creating new layers of cells or organ primordia. Epithelial folding is often the first step in gastrulation, initiating the transition from a simple epithelial sphere or ovoid, called the blastula, to a more complex, multilayered embryo (1). Much effort has been made to understand both the molecular basis and the mechanical properties of tissue folding.
The role of mechanics in morphogenesis is generally appreciated (2), and it is worth asking to what extent epithelial folding can be understood purely on mechanical grounds. The earliest physical models studied were made of spring steel and wire (3), brass bars and rubber bands (4), or gelatin under varying salt and osmotic conditions (5) to reproduce the overall form of a buckling epithelium. Computer simulations have been used since the early 1980s (6) as an alternative way of exploring increasingly more elaborate models. A sheet of material may respond to forces acting upon it by random, passive bends. Depending on the properties of regions and the control of the forces, the same sheet may also form folds in a controlled and predictable manner—the situation that usually pertains in live tissues.
One feature of the cells in a biological tissue that makes a fold is that they usually differ from the neighboring cells. Differences can be based on cell-type-specific gene expression (7–9) or protein distribution (10–14), which affect the mechanical properties of cells (11,13,15,16). In line with this, all current theoretical models have investigated how a subpopulation of cells whose properties differ from those in surrounding tissues can produce a fold in the embryo. One of the first theories of tissue folding (6) showed how a local behavior of individual cells within the epithelium (e.g., a decrease of their apical surface area) is sufficient to generate a propagating contraction that drives tissue folding. Other studies have demonstrated that folding can be caused by the intrinsic properties of a defined field of cells (17,18). Finally, to attain a better match with cell shapes observed in vivo, the effects of additional active contributions of neighboring tissues have been explored (11,19–23), necessitating an increase in the complexity of the model.
The model that we propose here is developed following an alternative approach. Instead of elaborating an already detailed theory by incorporating additional and more refined behaviors of cells in the folding region and its surroundings, we are looking for the simplest physical mechanisms that may theoretically suffice to create invaginations. Whereas existing models rely on a cell-type-specific behavior of a subset of cells to generate tissue buckling, we now use a physical model to test whether the difference between cell populations seen in vivo is a necessary condition for this process. Given our reductionist perspective, a full explanation of tissue invagination in vivo is not the purpose of this study, and it should be understood that forces and mechanisms not discussed here are involved in this process.
A well-studied example of tissue folding is the formation of a furrow on the ventral midline of the fruit fly (Drosophila melanogaster) embryo during gastrulation, which initiates profound morphological changes. Before the ventral furrow forms, the Drosophila embryo is an elongated ellipsoidal one-cell-thick epithelium of ∼6000 cells coating the central yolk mass and surrounded by a shell called the vitelline membrane. During the first stage of furrow formation, cells in a band along the ventral side change their shapes and the ventral tissue folds inwards (8,24) (Fig. 1, a and b). We test our model by comparing the results to this example of tissue folding.
Figure 1.
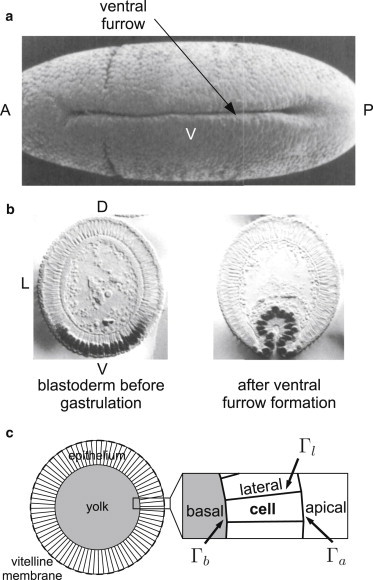
(a) Electron micrograph of the ventral side of a Drosophila embryo showing a furrow (image reproduced with permission from Sweeton et al. (24)). A, P, and V are the anterior, posterior, and ventral sides, respectively, of the embryo. (b) Fixed embryo cross sections having a circular shape (left) and invaginated (right) (images reproduced with permission from Leptin and Grunewald (8)). D, L, and V are the dorsal, lateral, and ventral sides, respectively, of the embryo. (c) The model embryo tissue cross section consists of a ring of N quadrilateral cells of area Ac enclosing a yolk of area Ay. All apical, basal, and lateral edges are characterized by line tensions , , and , respectively (arrows). The embryo is contained within a circular vitelline membrane (dashed circle).
Materials and Methods
Imaging and cell analysis
An embryo cross section was taken by using a Zeiss 780 (Peabody, MA) two-photon confocal microscope coupled to a Chameleon laser (Coherent, Santa Clara, CA) on a MRLC::GFP-tagged living embryo. This specific line has been chosen to easily localize the basal site of cells since Myo-II is basally localized in all embryo cells before the onset of gastrulation. The image was taken at 200 μm inside the embryo from the posterior pole. The cell apical region, for cell-diameter quantification, was imaged on the dorsal, dorsolateral, lateral, ventrolateral, and ventral regions of mCherry-membrane-tagged living embryos with a monolithic digital light-sheet scanning microscope. Cell analysis and quantifications were done using ImageJ (25) and Cell Profiler (26) software.
Model
We construct a 2D model representing a cross section of a tubular epithelium, whose geometry resembles the early Drosophila embryo. We assume that the cross section of the embryo captures all variable terms in the Hamiltonian based on surface energy (21,23). The N cells in the embryo cross section are represented by quadrilaterals arranged in a ring encompassing a given amount of yolk (Fig. 1 c). Both cells and the yolk are assumed incompressible (17,21) so that the area of each quadrilateral cell, Ac, is fixed (27) and identical for all cells, and the area of the polygonal shaped yolk, Ay, is also fixed (we comment on how this corresponds to Drosophila in Fig. S1 of the Supporting Material). The epithelium is surrounded by a circular shell of a variable degree of stiffness (17). The shell plays the role of the vitelline membrane in vivo and is referred to by the same name (Fig. 1 c). The energy of the system is attributed exclusively to the three types of cell sides (28). The line tensions of cell lateral, basal, and apical edges (, , and , respectively) can be modulated independently from one another. The energy of the model epithelium reads
| (1) |
where , , and are the lengths of the apical, basal, and sum of two lateral edges in cell i and the sum goes over all cells. The factor accounts for the fact that each lateral side is shared by two neighboring cells. Using the reduced apical and basal line tensions,
| (2) |
the total energy (Eq. 1) can be cast in dimensionless form:
| (3) |
where , , and are the reduced sums of all apical, basal, and lateral edge lengths, respectively. The radius of the yolk before formation of the ventral furrow, , sets the length scale of the problem. As in the study by Pouille and Farge (17), the vitelline membrane is treated as an elastic shell of resting radius rv corresponding to the circular cross section. The membrane exerts an exponentially increasing pressure on all parts of the epithelium whose distance from the center exceeds rv. For , the pressure reads
| (4) |
and for the pressure is zero. Here, controls the magnitude of the membrane pressure and is the pressure in the yolk before tissue buckling (17). The pressure of the vitelline membrane contributes an additional energy term given by , where the sum goes over all cells and is the area of the part of cell i outside the resting circular vitelline membrane of radius rv. For ri, we use the centroid of the part of the outline of cell i that reaches beyond rv.
To simulate the formation of a ventral furrow with starting morphometric properties comparable to the in vivo situation, we fix the number of cells, N, to 80 and set . Thus, the thickness of the epithelium is ∼18% of the diameter of the embryo cross section, and the total area of the yolk is ∼68% of the area of the epithelium. The only remaining dimensionless parameters of the model are the reduced apical and basal line tensions. By numerically minimizing the energy of the epithelium (Eq. 3) subject to the two area constraints and the vitelline membrane pressure, we find the equilibrium shapes. The values of α and β in the real biological system are not known, so we numerically explore the (α, β)-plane and focus on the parameter values that produce biologically relevant shapes. The model is implemented within the Surface Evolver package (29), where it can be represented and solved. Within Surface Evolver, our model cells are constructed starting from vertices connected by straight edges. The edges carry the energy specified by Eq. 3 and the enclosed area is fixed. The minimal-energy configuration is found iteratively starting from an initial shape. For any given set of parameters, we used several initial shapes to ensure that we found the minimal-energy, rather than a metastable, shape. In each step of the iteration, the net force exerted by the edges on a vertex is computed and the vertex is displaced proportional to this force. The descent is optimized by halving and doubling the (auxiliary) time step to bracket the energy minimum. Thus, each vertex slides along the direction of the steepest energy gradient toward the minimal-energy state. When the force on each vertex is zero, equilibrium is reached and the energy no longer changes.
To avoid possible metastable states and to allow the search for the minimal-energy shape, we introduced random displacement of vertices (jiggling). Jiggling randomly displaced each vertex independently with a Gaussian distribution. In our simulation, an average displacement no larger than a few percent of the mean edge length was sufficient to kick the model epithelium from a possible metastable state. Jiggling was followed by further steepest-gradient relaxation. The jiggling magnitude was gradually decreased during the simulation to allow the system to reach the minimal-energy state.
By changing the initial conditions as well as the magnitude of jiggling, we searched for the equilibrium shape at a given α and β. For all parameter values that we explored, there is always a single most pronounced energy minimum that is assumed to be the global one. At a given α and β, this minimum is reached for any starting shape that we analyzed.
Results and Discussion
Phase diagram
The diagram of stable model embryo cross sections shown in Fig. 2 a is the result of varying the reduced tensions α and β for an epithelium of N = 80 cells with cell/yolk area ratio of contained within a vitelline membrane, which generates a pressure parameterized by . Note that the shapes shown in Fig. 2 a are all drawn with the infolding facing downward, although the model itself has no specific dorsal-ventral orientation: the buckling can occur at any random angular position along the epithelium. The (α, β)-plane can be roughly partitioned into two regions. At large values of α and β, the equilibrium shapes are circular, whereas at small α or β they are buckled. The shapes lying along any upper left to lower right diagonals where α + β = const. (e.g., on the dashed line where α + β = 4.4) are very similar to one another in terms of the depth of the groove; some of these resemble the furrow cross section in real embryos (cf. Fig. 1 b). In the part of the diagram with small α and small β, the infolding is deeper, and in shapes located in the lower left corner, it reaches the opposite side of the model epithelium. Finally, shapes in the upper left, as well as the lower right, corner of Fig. 2 a are characterized by more complex contours of the epithelium. For example, the (α = 3, β = 0.6) shape (Fig. 2 c) has two symmetric creases on the basal side of the epithelium adjacent to the groove.
Figure 2.
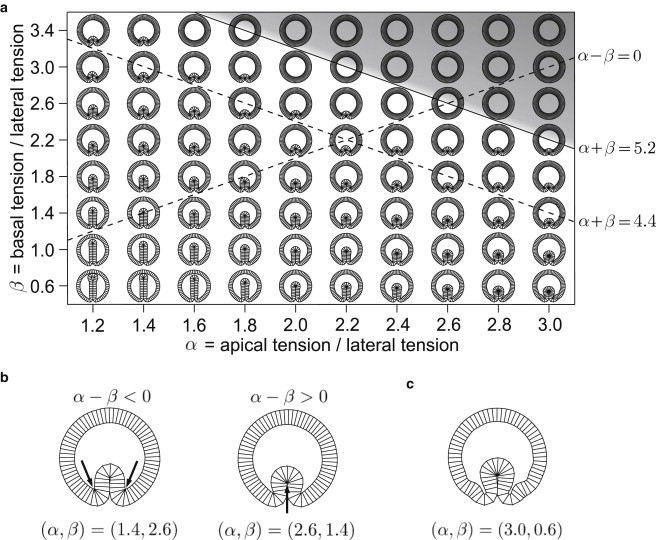
(a) Phase diagram of the model embryo cross section for N = 80, , and . The large α, large β shapes located in the shaded area are circular, whereas those at a small enough α + β show infoldings. The solid line where α + β = 5.2 separates circular shapes from the rest. The α − β = 0 dashed line connects states where apical and basal tensions are identical. Cross-sections arranged along the upper left/lower right dashed diagonal where α + β = 4.4 emphasize that the infoldings in shapes of identical α + β are of similar depth. Still, the details of their contours depend on the differential tension α − β. (b) If apical tension is larger than basal tension (α − β > 0), the infolding is more round and its tip contains more cells than in shapes with α − β < 0. Note the localized constrictions on the basal side (indicated by arrows in the shape with α = 1.4, β = 2.6) and on the apical side (arrow in shape with α = 1.6, β = 1.4). (c) The shape with α = 3.0, β = 0.6 has some aberrant structures and short-wavelength features that are a consequence of the very large differential tension α − β. In this figure and in Figs. 3–5, shapes have no specific dorsal-ventral orientation.
The mechanism producing buckled shapes can be understood by considering that the length of the epithelium midline (the line equidistant between the basal and apical sides of the epithelium) is controlled by the sum of the apical and basal tensions, α + β, which plays the role of an effective line tension of the midline. For α + β > 5.2 the minimal-energy shape is circular, thereby minimizing the length of the midline. As α + β is decreased, it becomes energetically advantageous to increase the length of the apical and basal edges at the expense of the lateral edges. The midline length is globally increased and the epithelium folds inward because it is contained within the vitelline membrane. The effective line tension α + β can be decreased by decreasing either α or β or both. A geometric explanation of the threshold value α + β > 5.2 is presented in the Appendix. This explains why shapes lying along a diagonal where α + β = const. are generally similar. However, a closer comparison of the model epithelia located in the upper left and lower right corners of Fig. 2 a shows that some features of their shapes depend on the differential tension α − β. If α − β > 0, apical constriction occurs in a larger number of cells, and the tip of the infolding in, e.g., the (α = 2.6, β = 1.4) shape consists of more cells than that in the (α = 1.4, β = 2.6) shape (Fig. 2 b). At the same time, fewer cells participate in the two bends at the edge of the infolding that consist of basally constricted cells.
The phase diagram shows a graded transformation of the circular shapes into shapes with grooves and increasingly deeper infoldings. If we consider tissue buckling as a sequence of equilibrium states, the various shapes in Fig. 2 a can be compared to the different phases of furrow formation in vivo. Many pathways leading from the starting circular state toward an infolded state are admissible. Two clear examples are the horizontal and vertical trajectories corresponding to a continuous decrease of α and β, respectively. The simplest way of decreasing either α or β is to decrease the apical or basal line tension ( and , respectively) while keeping the lateral line tension, , unchanged.
Varying conditions for buckling
Having established that the proposed model is able to generate buckled shapes, we now explore how this mechanism works when its parameters (pressure of the vitelline membrane, epithelial thickness, and number of cells in the model tissue) are varied one at a time.
We first examine the effect of the vitelline membrane by changing its stiffness, which is controlled by . Fig. 3 a shows that in the absence of the membrane (i.e., for ), the model epithelium cross sections can deviate from the circle shape. Instead, the region of the (α, β) space explored here is dominated by elliptical and biconcave shapes. For α − β > 1.5 and α − β < −1.5 (the upper left and lower right corners of the phase diagram), the cross sections are marked by tissue bending or indentations (Fig. 3 a). Thus, for small values of α − β, the vitelline membrane plays a major role in containing the tissue and making it form indentations. For large magnitude of α − β, the epithelium is buckled even in the absence of the vitelline membrane. The reason is that at large magnitude of differential tension, the length of either the apical (for α − β > 1.5) or basal sides (α − β < −1.5) is forced to shrink as much as possible, and this is realized if the epithelium buckles. Fig. 3, b and c, shows phase diagrams for increasing vitelline membrane pressure and , respectively. Within the region of the (α, β) space investigated here, the vitelline membrane is necessary to allow the formation of a single groove with no additional tissue bending or indentations (cf. Fig. 3, a–c). At the location of the groove, a gap between the apical side of cells and the vitelline membrane forms. Due to fixed cell and yolk area constraints, this is possible only if some cell vertices are pushed beyond the resting vitelline membrane radius, rv. As is increased while keeping all other parameters constant, the model epithelium is progressively constrained within the initial circular boundary defined by the vitelline membrane (Fig. 3 d). In the limit of where no cell is allowed to go beyond rv, there is no space for the gap to form, and the whole diagram is occupied by circular cross sections. In this regime, the membrane acts as a solid constraint that does not allow any deviation of the apical contour from the circle.
Figure 3.
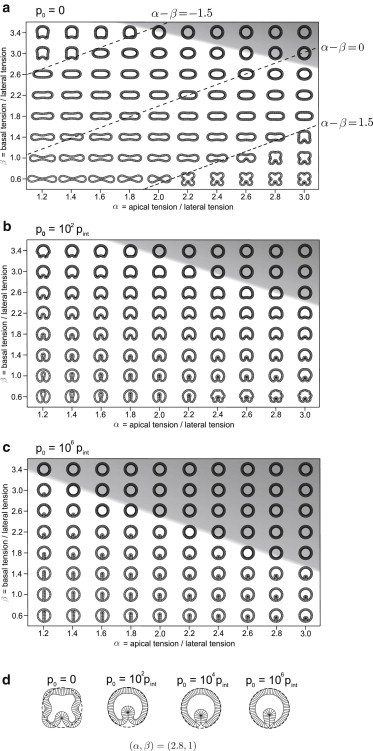
Model embryo cross sections in the (α, β)-plane for N = 80 and contained within the vitelline membrane with (a) (the three dashed lines connect shapes where α − β = −1.5, 0, and 1.5), (b), and (c). In the absence of the vitelline membrane (a), the shapes generally depart considerably from the circular contour (shaded area) unless α and β are both large. As the vitelline pressure is increased, the shapes become increasingly more circular and occupy an ever larger part of the phase diagram explored here. (d) The tendency toward circular shape with increase in pressure is also seen in the four selected shapes of identical α and β but dissimilar . The dashed circle represents the resting shape of the vitelline membrane in the circular embryo.
We next change the thickness of the epithelium by varying the cell/yolk area ratio, , while keeping the number of cells and the vitelline membrane pressure the same, as in Fig. 2 a. By decreasing from the initial value of used in Fig. 2 a, the region of the phase space where buckled shapes are stable gradually shrinks, as illustrated by the diagram shown in Fig. 4 a. Conversely, as is increased, the buckled shapes occupy an ever larger part of the phase space (see the diagram in Fig. 4 b). Two additional phase diagrams corresponding to a lower value of the vitelline membrane pressure and cell/yolk area ratios are shown in Fig. S3 and Fig. S4.
Figure 4.
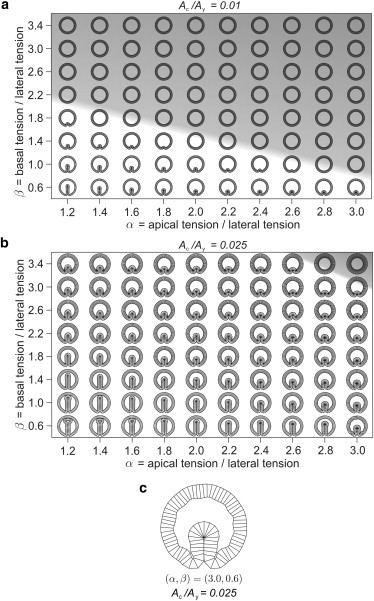
Effective thickness of the model epithelium controlled by the cell/yolk area ratio is an essential parameter of the threshold for fold formation. (a and b) In the epithelium with (a), the buckled shapes are stable in the bottom part of the phase diagram, whereas for (b), they fill almost the whole of it. N = 80 and for all shapes. The region occupied by circular shapes is shaded. (c) An enlarged shape with α = 3.0, β = 0.6, and has some aberrant structures and short-wavelength features resulting from a very large differential tension α − β. To minimize the lengths of apical sides, the main invagination is accompanied by several smaller grooves.
Finally, we study the role of the number of cells in the model. We compare the model epithelia with N = 120, 80, 40, 20, and 10 cells while keeping the total area of the epithelium NAc and all other parameters the same as in Fig. 2. As exemplified by N = 40 shapes (Fig. 5), decreasing the number of cells in the cross section causes the shapes to be less smooth. Apart from this difference, the shapes for N = 40 are very similar to those for N = 80 shown in Fig. 2. Since halving the cell number also results in a 50% reduction of the total energy associated with the lateral sides, the tensions needed to generate shapes of similar appearance also differ by a factor of ∼2. For example, the shape roughly corresponds to the shape. The N = 40 and N = 20 phase diagrams for a vitelline membrane with lead to similar conclusions (Fig. S5 and Fig. S6).
Figure 5.
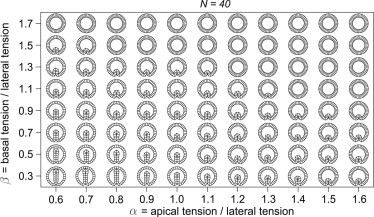
Phase diagram of model epithelia with N = 40 and (so that the total area of the epithelium, , is the same as in Fig. 2a and . The shapes shown here are quite similar to those in Fig. 2, although the number of cells is halved. To make the comparison meaningful, the apical and basal tensions need to be rescaled and a shape is to be compared to a shape.
For the various conditions in which we observed buckling, the role of the sum, α + β, as well as the role of differential tension α − β, is the same as in Fig. 2. Buckling appears only if α + β is small enough. In the case where α − β > 0, apical constriction is observed, whereas if α − β < 0, basal constriction takes place.
Comparison with ventral furrow formation in Drosophila embryo
Our numerical model suggests that tissue buckling can be generated by tuning the apical, basal, and lateral tensions of mechanically identical cells. We now compare these results to the formation of the ventral furrow in the Drosophila embryo. We are interested primarily in the overall logic of the process rather than in the precise shape of individual cells or in the detailed agreement of the infolded model shapes and the cross section of a Drosophila embryo. We thus ask which global aspects of folding are captured by the proposed model.
We first measure the compliance of the vitelline membrane in vivo and compare it to the changes in the radius of the vitelline membrane during fold formation in the model. Quantitative analysis shows that in vivo the vitelline membrane stretches only slightly, but a close inspection shows that a space filled with fluid separates the apical cell sides and the vitelline membrane (Fig. S2). During ventral furrow formation, the apical sides move toward the vitelline membrane and the space in between is reduced. What is represented as the vitelline membrane in the model is in vivo the vitelline membrane together with the interstitial fluid. In vivo measurements show that the thickness of the interstitial layer during furrow formation decreases by ∼2 μm, which amounts to ∼2% of the resting vitelline membrane radius. In our model, we take into account the changes in the area that is enclosed in the model vitelline membrane by a soft constraint that allows the area inside the model vitelline membrane to change. For the model system with vitelline membrane pressure , the radius of the membrane of the invaginated shape is ∼10% larger than the radius of the resting model vitelline membrane. For , the radius stretches by ∼2%, whereas for it stretches by ∼0.5%. The case with is thus comparable to the in vivo case.
The most striking difference between the embryo and the model epithelium is that in the former the invagination always occurs on the ventral side, whereas in the latter the furrow can form at any random angular position along the epithelium. In the Drosophila embryo, the site of invagination is determined by the developmental program of the ventral cells, which is controlled by transcription factors that are activated in these cells and determine their fate and their mechanical properties. However, situations exist in which all cells in the embryo have identical or nearly identical fates along the dorsal-ventral axis, because the fate-determining transcription factors are activated in a uniform or nearly uniform manner (30). In the extreme case, such embryos form no furrow, but in some cases, a furrow is formed on the ventral side of the embryo (8), although all cells express the ventral developmental program and therefore have similar or even identical mechanical properties. Thus, the cells around the whole circumference of these embryos undergo apical flattening (8), a process that is normally characteristic only for the ventral cells. This shows that 1), a lesser degree of cell difference than that seen in wild-type embryos is sufficient for furrow formation; and 2), more subtle asymmetries or other unknown factors may be responsible for positioning the furrow on the ventral side. We therefore tested modifications of our model that would fix the site of buckling.
As in other models (11,18–23,31), we first changed the mechanical properties by altering the force distribution in a subgroup of cells. We found that increasing apical tension or decreasing basal tension in these cells makes them more prone to invaginate. However, in line with the idea of maintaining the three types of tension identical in all cells, we sought a scenario free of specific active mechanisms. We thus looked for other possible factors that could produce a bias in our model. Specifically, we examined the differences in cell geometry in vivo.
We analyzed the cross section and surface view of six gastrulating embryos and we measured the geometry of a total of 9268 cells in different regions of the embryo before the onset of furrow formation. We found that just before the onset of gastrulation (defined as the time just before apical constriction of ventral cell surfaces or displacement of ventral nuclei toward the interior can be detected), cells in the ventral region are ∼20% longer (Fig. 6 a) and ∼10% wider (Fig. 6 b) than dorsal cells, resulting in a difference in the cross-sectional area of ∼30%. We then tested whether the site of buckling could be controlled by changing the cross-sectional area of cells in one region of the model embryonic epithelium while keeping the apical, basal, and lateral tensions the same in all cells. We found that the larger cells are more prone to invaginate. In our model epithelium with N = 80, , and , a 5% increase of the cross-sectional area of 18 cells is sufficient to position the invagination within this same set of cells (Fig. 6 c). Larger cell-area variations are needed for stiffer vitelline membranes.
Figure 6.
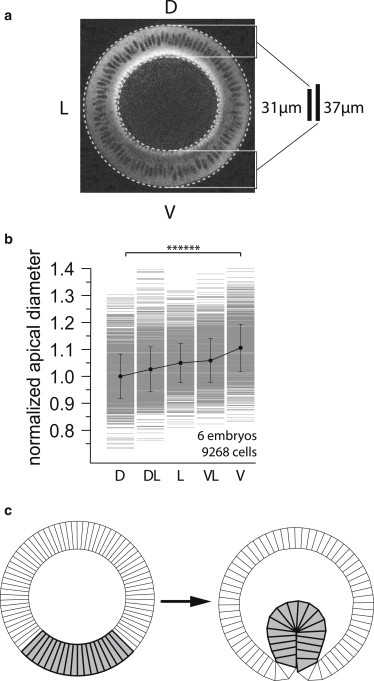
(a) Cross section of a Drosophila MRLC::GFP embryo (see Methods) just before the onset of gastrulation. Cells on the ventral region (V) are 37 μm long, whereas cells in the dorsal (D) region are 31 μm long. (b) Histogram of the apical diameter of cells positioned at the dorsal (D), dorsal-lateral (DL), lateral (L), ventral-lateral (VL), and ventral (V) sides of the embryo. Measurements are normalized to the average diameter of the dorsal cells. (c) Shape transformation of the model cross section epithelium where the area of the 18 shaded cells in the mesoderm is 30% larger than in other cells with : in the shaded cells, . The circular shape (left) is the initial, unstable state at α = 2.8 and β = 1.0, whereas the invaginated shape (right) is the energy-minimizing stable state. The other parameters read N = 80 and .
Conclusions
In summary, we show that a model 2D embryonic epithelium can produce a single deep infolding even in a situation where all cells have identical properties and no localized mechanical forces are imposed on a subset of cells. This mechanical instability is somewhat reminiscent of the buckling of an expanding surface that is laterally constrained, which has been used to account for pattern formation in plant shoots (32,33). Results from our model are consistent with experimental evidence from Drosophila embryos. Embryos in which cells along the dorsal-ventral axis have a lesser degree of difference than in the wild-type are still able to form a furrow. In the proposed model, infolding can be induced at a specific location by changing the cross-sectional area of a subgroup of cells. The measured cell-size differences in the living embryo before the onset of gastrulation exceed the threshold for furrow localization predicted by our model for the vitelline membrane pressures that we have examined. If this mode of creating and positioning an invagination were at work in vivo, it would most likely act in cooperation with other mechanisms to ensure reliability and reproducibility of the process. This model explores the minimal properties for an invaginating epithelial system, which can be further tested against the in vivo data, for instance by using laser-based ablation to measure the tension of the different sides of cells in various regions of the embryo in wild-type and mutant conditions (34,35). Our model can also predict the amount of strain imposed on each cell side. At any given α and β, the equilibrium shape of an isolated cell can be computed by minimizing Eq. 1 at fixed cell area Ac. By comparing the lengths of cell sides in the epithelium to those of an isolated cell, we can quantify the strain. The computed strain patterns shown in Fig. S7, Fig. S8, and Fig. S9 demonstrate the localization of strain in some theoretical shapes. Laser-cutting experiments could probe the strain of cell sides, which would allow further testing of the predictions of our model.
Acknowledgments
We thank G. Belušič, C.-P. Heisenberg, F. Graner, A. Jacinto, R. D. Kamien, P.-F. Lenne, A. Politi, S. Roth, S. Svetina, and A. Šiber for helpful discussions. We thank E. Stelzer and his group for the monolithic digital light-sheet scanning microscope imaging support. A.H. acknowledges the hospitality of the Department of Physics and Astronomy, University of Pennsylvania, where a part of this study was done. We thank the European Molecular Biology Laboratory (EMBL) Advanced Light Microscopy Facility (ALMF) and Carl Zeiss for continuous support of the EMBL ALMF.
This work was supported by the Slovenian Research Agency through Grant No. P1-0055, by the National Science Foundation through Grant No. DMR05-47230, by a grant from the Slovene Human Resources Development and Scholarship Fund, by EMBO founds and by the European Science Foundation (ESF) for the activity entitled Quantitative Models of Cellular and Developmental Biology. M.R. was supported by an EMBO-Marie Curie cofounded Long-Term Fellowship and is supported by a Human Frontier Science Program Long-Term Fellowship.
Appendix
The sum of the apical and basal tensions, α + β, plays the role of an effective line tension of the midline. The mechanism of the transition from the circular to the buckled shape that occurs as α + β is decreased can be understood by realizing that as the sum of the two tensions decreases, the perimeter of the epithelium midline increases at the same amount of yolk. As a result, the shape that is circular at large α + β buckles as α + β is decreased. We can approximately predict the threshold at which the transition happens by computing the perimeter of the epithelium midline and the area that it encloses as a function of the two tensions for the case without the vitelline membrane. If we assume that the cells are rectangular, with lateral sides , apical sides , basal sides , and area Ac, then the energy of a cell reads
| (5) |
so that
| (6) |
Then the optimal length of the apical side is the solution of equation
| (7) |
so that
| (8) |
The perimeter of the epithelium midline is approximately
| (9) |
and the enclosed area, Ae, approximately equals
| (10) |
In a circle with perimeter P and area A, the ratio equals 1; therefore, the transition from a circular to a buckled shape happens when
| (11) |
By inserting the parameters that we used (N = 80, Ac = 11, Ay = 600), we find that the threshold is at α + β = 5.38.
Supporting Material
References
- 1.Leptin M. Gastrulation movements: the logic and the nuts and bolts. Dev. Cell. 2005;8:305–320. doi: 10.1016/j.devcel.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 2.Lecuit T., Lenne P.F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 3.Butschli O. Sitzungsberichte Akademie Wissenschaffen; Heidelberg: 1915. Bemerkungen zur mechanischen Erklärung der Gastrulainvagination (Remarks on the mechanics explaining the invagination of the gastrula) [Google Scholar]
- 4.Lewis W.H. Mechanics of invagination. Anat. Rec. 1947;97:139–156. doi: 10.1002/ar.1090970203. [DOI] [PubMed] [Google Scholar]
- 5.Spek J. Differenzen im Quellungszustand der Plasmakolloide als eine Ursache der Gastrulainvagination, sowie der Einstülpungen und Faltungen von Zellplatten überhaupt (Differences in swelling states of plasma colloids as causes of invaginations in the gastrula, and of invaginations and foldings of cell sheets in general) Kolloidchemische Beihefte. 1918;9:259–399. [Google Scholar]
- 6.Odell G.M., Oster G., Burnside B. The mechanical basis of morphogenesis. I. Epithelial folding and invagination. Dev. Biol. 1981;85:446–462. doi: 10.1016/0012-1606(81)90276-1. [DOI] [PubMed] [Google Scholar]
- 7.Rohrschneider M.R., Nance J. Polarity and cell fate specification in the control of Caenorhabditis elegans gastrulation. Dev. Dyn. 2009;238:789–796. doi: 10.1002/dvdy.21893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Leptin M., Grunewald B. Cell shape changes during gastrulation in Drosophila. Development. 1990;110:73–84. doi: 10.1242/dev.110.1.73. [DOI] [PubMed] [Google Scholar]
- 9.Vincent A., Blankenship J.T., Wieschaus E. Integration of the head and trunk segmentation systems controls cephalic furrow formation in Drosophila. Development. 1997;124:3747–3754. doi: 10.1242/dev.124.19.3747. [DOI] [PubMed] [Google Scholar]
- 10.Dawes-Hoang R.E., Parmar K.M., Wieschaus E.F. Folded gastrulation, cell shape change and the control of myosin localization. Development. 2005;132:4165–4178. doi: 10.1242/dev.01938. [DOI] [PubMed] [Google Scholar]
- 11.Sherrard K., Robin F., Munro E. Sequential activation of apical and basolateral contractility drives ascidian endoderm invagination. Curr. Biol. 2010;20:1499–1510. doi: 10.1016/j.cub.2010.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kölsch V., Seher T., Leptin M. Control of Drosophila gastrulation by apical localization of adherens junctions and RhoGEF2. Science. 2007;315:384–386. doi: 10.1126/science.1134833. [DOI] [PubMed] [Google Scholar]
- 13.Lee J.Y., Marston D.J., Goldstein B. Wnt/Frizzled signaling controls C. elegans gastrulation by activating actomyosin contractility. Curr. Biol. 2006;16:1986–1997. doi: 10.1016/j.cub.2006.08.090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Anderson D.C., Gill J.S., Nance J. Polarization of the C. elegans embryo by RhoGAP-mediated exclusion of PAR-6 from cell contacts. Science. 2008;320:1771–1774. doi: 10.1126/science.1156063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Martin A.C., Kaschube M., Wieschaus E.F. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457:495–499. doi: 10.1038/nature07522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee J.Y., Harland R.M. Actomyosin contractility and microtubules drive apical constriction in Xenopus bottle cells. Dev. Biol. 2007;311:40–52. doi: 10.1016/j.ydbio.2007.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pouille P.A., Farge E. Hydrodynamic simulation of multicellular embryo invagination. Phys. Biol. 2008;5:015005. doi: 10.1088/1478-3975/5/1/015005. [DOI] [PubMed] [Google Scholar]
- 18.Allena R., Mouronval A.S., Aubry D. Simulation of multiple morphogenetic movements in the Drosophila embryo by a single 3D finite element model. J. Mech. Behav. Biomed. Mater. 2010;3:313–323. doi: 10.1016/j.jmbbm.2010.01.001. [DOI] [PubMed] [Google Scholar]
- 19.Clausi D.A., Brodland G.W. Mechanical evaluation of theories of neurulation using computer-simulations. Development. 1993;118:1013–1023. [Google Scholar]
- 20.Davidson L.A., Koehl M.A.R., Oster G.F. How do sea urchins invaginate? Using biomechanics to distinguish between mechanisms of primary invagination. Development. 1995;121:2005–2018. doi: 10.1242/dev.121.7.2005. [DOI] [PubMed] [Google Scholar]
- 21.Muñoz J.J., Barrett K., Miodownik M. A deformation gradient decomposition method for the analysis of the mechanics of morphogenesis. J. Biomech. 2007;40:1372–1380. doi: 10.1016/j.jbiomech.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 22.Conte V., Muñoz J.J., Miodownik M. A 3D finite element model of ventral furrow invagination in the Drosophila melanogaster embryo. J. Mech. Behav. Biomed. Mater. 2008;1:188–198. doi: 10.1016/j.jmbbm.2007.10.002. [DOI] [PubMed] [Google Scholar]
- 23.Conte V., Muñoz J.J., Miodownik M. Robust mechanisms of ventral furrow invagination require the combination of cellular shape changes. Phys. Biol. 2009;6:016010. doi: 10.1088/1478-3975/6/1/016010. [DOI] [PubMed] [Google Scholar]
- 24.Sweeton D., Parks S., Wieschaus E. Gastrulation in Drosophila: the formation of the ventral furrow and posterior midgut invaginations. Development. 1991;112:775–789. doi: 10.1242/dev.112.3.775. [DOI] [PubMed] [Google Scholar]
- 25.Rasband W.S. National Institutes of Health; Bethesda, MD: 2011. ImageJ User Guide. [Google Scholar]
- 26.Carpenter A.E., Jones T.R., Sabatini D.M. CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 2006;7:R100. doi: 10.1186/gb-2006-7-10-r100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kaschube M. Contractile forces driving embryonic development. APS March Meeting. 2011 2011. 56:P7.00001a (Abstr.) [Google Scholar]
- 28.Derganc J., Svetina S., Žekš B. Equilibrium mechanics of monolayered epithelium. J. Theor. Biol. 2009;260:333–339. doi: 10.1016/j.jtbi.2009.06.021. [DOI] [PubMed] [Google Scholar]
- 29.Brakke K. The surface evolver. Exp. Math. 1992;1:145–165. [Google Scholar]
- 30.Roth S., Stein D., Nüsslein-Volhard C. A gradient of nuclear localization of the dorsal protein determines dorsoventral pattern in the Drosophila embryo. Cell. 1989;59:1189–1202. doi: 10.1016/0092-8674(89)90774-5. [DOI] [PubMed] [Google Scholar]
- 31.Ramasubramanian A., Taber L.A. Computational modeling of morphogenesis regulated by mechanical feedback. Biomech. Model. Mechanobiol. 2008;7:77–91. doi: 10.1007/s10237-007-0077-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Green P.B., Steele C.S., Rennich S.C. Phyllotactic patterns: A biophysical mechanism for their origin. Ann. Bot. 1996;77:515–527. [Google Scholar]
- 33.Green P.B. Expression of pattern in plants: combining molecular and calculus-based biophysical paradigms. Am. J. Bot. 1999;86:1059–1076. [PubMed] [Google Scholar]
- 34.Farhadifar R., Röper J.C., Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 35.Rauzi M., Verant P., Lenne P.F. Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


