Abstract
Information processing and decision-making is based upon logic operations, which in cellular networks has been well characterized at the level of transcription. In recent years, however, both experimentalists and theorists have begun to appreciate that cellular decision-making can also be performed at the level of a single protein, giving rise to the notion of protein logic. Here we systematically explore protein logic using a well-known statistical mechanical model. As an example system, we focus on receptors that bind either one or two ligands, and their associated dimers. Notably, we find that a single heterodimer can realize any of the 16 possible logic gates, including the XOR gate, by variation of biochemical parameters. We then introduce what to our knowledge is a novel idea: that a set of receptors with fixed parameters can encode functionally unique logic gates simply by forming different dimeric combinations. An exhaustive search reveals that the simplest set of receptors (two single-ligand receptors and one double-ligand receptor) can realize several different groups of three unique gates, a result for which the parametric analysis of single receptors and dimers provides a clear interpretation. Both results underscore the surprising functional freedom readily available to cells at the single-protein level.
Introduction
Cells depend on cues from their environment to initiate behaviors, including growth, division, differentiation, and death. Based upon these environmental signals, cells must make decisions, such that the correct response is initiated. Although a particular environmental signal often elicits a particular cellular response, it is well established that signals can also act in combination (1–4). In this case, the response triggered when two signals are present can be distinct from the responses triggered by each signal alone. The cell thereby acts as a logic gate, integrating two inputs to produce a single output. For example, the AND gate produces an output if both inputs are present, but it produces no output if either a single input or no input is present. For the process of decision-making, the logic gate is the basic unit of computation, and therefore many studies have been devoted to its role within biochemical networks. Indeed, the role of logic gates within transcriptional networks has been studied in depth: systematic theoretical studies have predicted (5–8) and experimental studies have confirmed (9–12) that transcriptional networks can access all possible types of logic gate.
Recently, it has become clear that individual proteins can perform logic operations as well. Although this notion was initially suggested almost two decades ago (4), recent experiments have provided striking demonstrations. For example, performance of an AND gate by the actin regulatory protein N-WASP has been observed in vivo (3): when both of its inputs Cdc42 and PIP2 are present, they jointly unfold the active domain, leading to the activation of its target Arp2/3. Moreover, synthetic proteins based upon naturally existing proteins have been constructed and shown to perform a number of different logic operations (13,14). Although these experiments beautifully illustrate the capacity for single proteins to encode logic, they are restricted to a limited set of logic gates. It therefore remains an open question if all possible logic gates can be accessed by single proteins, in particular the more complex gates like XOR, which includes nonmonotonic behavior.
Despite the fact that transcriptional logic has been explored in depth, to our knowledge no systematic theoretical study of protein logic has been done. A recent study by Motlagh and Hilsner focused on the nonmonotonic behavior of a single protein with several allosteric subunits, providing an understanding of how the action of a ligand as an agonist or an antagonist could be switched by the presence of a second ligand (15). Beyond this nonmonotonic behavior, however, other mappings of ligand presence to protein activity were not considered. By framing the problem as one of logic computation, we here obtain a comprehensive understanding of the functional mappings available to single proteins, thereby answering the question of which logical functions are possible, and under what conditions. Moreover, we use a less complex model than that used by Motlagh and Hilser (15), and we nonetheless find rich functional behavior, including nonmonotonicity, as characterized by the XOR gate.
For several reasons, we focus on receptor proteins, although our approach is easily extended to other protein types: First, receptors can be stimulated by multiple ligands (16–19), which naturally suggests a logic gate framework, in which multiple inputs (ligand concentrations) are integrated into one output (receptor activity). Second, receptors process signals directly at the plasma membrane. It is becoming increasingly recognized that the plasma membrane is a hub of information processing, acting as a mediator between the cell and its environment, along and across which signals are stored, processed, and relayed (20). Receptors are integral to this process, as they affect decisions directly at the detection level, before further intracellular transduction leads to the ultimate cellular response. The encoding of logic by receptors thus has the potential to be low-cost, because it is achieved with a single protein, and rapid, because it occurs at the beginning of the signaling pathway. Finally, receptors often exist in the form of dimers or higher oligomers. For example, G-protein-coupled receptors (GPCR) and ErbB receptors can each form dimers consisting of receptors of the same type (homodimers) or of receptors of different types (heterodimers) (16,21,22). A dimer has the capacity to perform the same or more logic operations than each of its monomeric constituents, a fact that we demonstrate here. Moreover, as we describe here, dimerization permits function space to be explored combinatorially: a cell can potentially change which logical function is performed simply by modulating which combination of monomers actually dimerizes.
We use a statistical mechanical model to develop a predictive framework for protein logic. To begin, we numerically probe the logic gates accessible to individual receptor monomers and dimers by parameter variation, which has relevance on evolutionary timescales. We find that a single dimer can implement any of the possible logic gates with two inputs, a result that we support analytically. Next, we introduce what to our knowledge is a novel idea: that a diverse set of logic gates can be performed, not by variation of parameters, but by modulating the dimerization of a fixed set of monomers. Such modulation may be achieved at the level of transcription and translation of monomeric proteins, or via post-translational modifications that enable monomers to dimerize; as such, we argue that dimeric recombination provides a way for a cell to modulate decisions on the timescales of gene expression or cell signaling. We find that the simplest set of receptors (two single-ligand receptors and one double-ligand receptor) can realize several different groups of three unique gates and that together these groups include all possible gates. We provide clear analytic support for this result, following the previous parametric analysis of single monomers and dimers. This result shines an interesting light onto why receptors, or proteins in general, exist in the form of dimers. Both results underscore the surprisingly rich capacity for cells to encode decisions using single molecules. Finally, throughout the study, we discuss biological systems that implement these logical functions at the single-protein level.
Methods
We study receptor function by appealing to an equilibrium statistical mechanical model. Statistical mechanical models have been used quite fruitfully in the study of many molecular biology problems, including receptor activity and gene regulation (23). In the case of receptors, several models are well known. All assume that a receptor can exist in either an active (A) or an inactive (I) state, and that binding of a ligand changes the receptor bias for each state. In the Koshland-Nemethy-Filmer (KNF) model, ligand binding directly activates the receptor (24). That is, the bias is complete: a ligand-bound receptor is active, and an unbound receptor is inactive. This condition is relaxed in the Monod-Wyman-Changeux (MWC) model, in which ligand-bound receptors can be in either state, but coupled receptors switch between states in synchrony (25). Finally, in the conformational spread (CS) model (26,27), both conditions are relaxed: a ligand-bound receptor can be in either state, and coupled receptors can be in different states. Because we are interested in the minimal model that can capture the ability to perform logic gates, we adopt the MWC model; the KNF model prohibits certain logic gates by construction, whereas the CS model allows excess parametric freedom (clearly, what can be achieved by the MWC model can be achieved by the CS model). Furthermore, the MWC model has been shown to agree with experiments on receptors (28–30).
The input in our model is the pair of concentrations [S1] and [S2] of two different ligands. The output is the probability for a receptor monomer or dimer to be in its active state. We consider three monomer types and the associated dimers (Fig. 1): a monomer that binds ligand 1 (U), one that binds ligand 2 (V), and one that binds both ligands (W). In the last case, ligand binding is competitive: there is only one binding pocket, so only one ligand type can bind at a time. Noncompetitive binding, in which both ligand types can bind simultaneously, is captured by the QUV dimer (Fig. 1).
Figure 1.
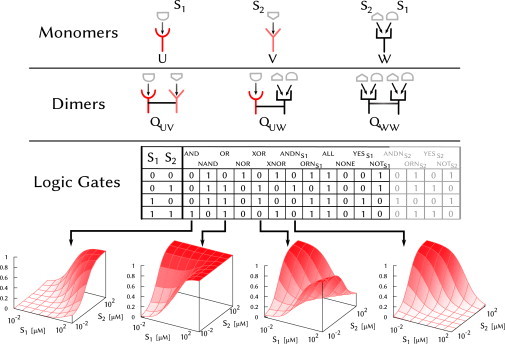
Setup. We consider receptor monomers (top row) that bind ligand 1 (U), ligand 2 (V), or both competitively (W), and their associated dimers (middle row). (Bottom row) The table defines the 16 possible two-input logic gates in terms of binary input and output; below the table, for the four functionally unique gates, we plot the continuous analogs given by the statistical mechanical model.
The probability pA for a receptor to be in the active state is computed from the partition functions, which enumerate all possible ways a receptor can be in either the active (ZA) or inactive (ZI) state:
| (1) |
The explicit forms of the partition functions under the MWC model are presented as each monomer and dimer is discussed in the Results. For intuition, we provide an example here: the partition functions for monomer W are
| (2) |
| (3) |
where the parameter is the Boltzmann factor corresponding to the energy difference E0 between the active and inactive state, and the parameters Kij are the dissociation constants of ligand i ∈ {1, 2} in activity state j ∈ {A, I}. The variables [S1] and [S2] are the ligand concentrations. In Eq. 2, the three terms correspond, respectively, to the receptor being active when no ligand is bound; when ligand 1 is bound; and when ligand 2 is bound. The same holds for Eq. 3 with the receptor being inactive.
The dependence of pA on [S1] and [S2] defines the receptor’s function (Fig. 1, bottom row). Functions are categorized based on the idealized behavior prescribed by the 16 possible two-input binary logic gates (Fig. 1). Mathematically, the function approaches binary logic when the output is either minimal (pA → 0) or maximal (pA → 1) in each of the four states, defined by each input being absent ([S1] = 0 or [S2] = 0) or present ([S1] > 0 or [S2] > 0).
Numerically, when varying parameters to assess whether a receptor can realize a particular logic gate, we use a variant of the Wright-Fisher algorithm (31,32), which models the evolution of a population. In the Wright-Fisher algorithm, evolution occurs in discrete, synchronous steps, and the population size remains constant. At each step, each member of the population produces offspring in proportion to its fitness. Then, mutations occur, and the mutated offspring comprise the population for the next step. In our case, for a given receptor, we have a population of R initial parameter points φr. Each point has fitness fr, and the total fitness for the receptor is . At each step, R new points (i.e., offspring) are drawn from the distribution pr = fr /F, which weights each point by its fitness. Each new point is then mutated by multiplying a randomly selected parameter by the factor (1 + δ), where δ is drawn uniform randomly from the range [−Δ:Δ]; we take Δ = 0.3.
We define fitness as the agreement between the real-valued output of the statistical mechanical model pA and the binary output of a specific ideal logic gate. The ideal logic gate is prescribed by the goal function G([S1],[S2]), which takes the value 0 or 1 depending on whether each input is switched off ([S1] < [S∗] or [S2] < [S∗]) or switched on ([S1] > [S∗] or [S2] > [S∗]), where we take the threshold value [S∗] = 1 μM. We compare pA and G over an N × N grid of input values, spaced logarithmically over the ranges of [S1] and [S2], which we take to be [10−2–102] μM. The fitness is thus
| (4) |
The results in this article are obtained for N = 4. Taking N = 2 leads to suboptimal results, while taking different values of N > 2 yields similar results to N = 4. Similar results are also obtained for a fitness function with N = 2 and an additional central point at [S1] = [S2] = [S∗], at which G is the average of the truth table for the gate.
The optimization parameters, as well as the bounds within which the model parameters are initialized and constrained during optimization, are given in Table S1 in the Supporting Material. The chosen bounds fall within experimentally observed ranges and are consistent with typical values used in previous modeling studies; we elaborate upon this point in detail in Section S1 in the Supporting Material.
When investigating whether multiple gates can be performed at fixed parameters by formation of the possible dimer combinations, we optimize for several logic gates at one time (see Section S1 in the Supporting Material). In practice, a given point in parameter space specifies both the dissociation constants Kij (which are intrinsic to each monomer U, V, and W, and do not change when they are recombined) and the Boltzmann factors ω0 and ωii (which are dimer-specific).
Results
First, we identify the logic gates that each receptor monomer and dimer can perform by parameter variation. Here, several derived analytic constraints support the numerical results. Then, we investigate the extent to which distinct logic gates can be formed using a set of monomers with fixed parameters by forming the possible dimer combinations. Several groups of distinct gates are possible, a finding for which the first results provide a clear interpretation.
Functions accessible by parameter variation
Fig. 2 shows the set of logic gates that each monomer and dimer can perform, as determined by numerical optimization of model parameters. The most striking feature is that one of the dimers can perform all 16 possible gates. This and the other numerical results in Fig. 2 can be understood intuitively by appealing to analytic results derived from the underlying model, which we will describe in turn for each monomer and dimer.
Figure 2.
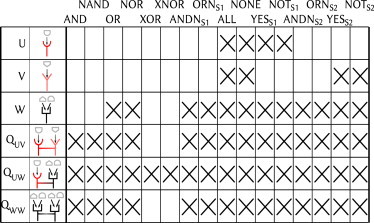
Functional versatility by parameter variation. For all monomers and dimers, we show the possible functions attainable by varying parameters. Attainability is assessed by numerical optimization and interpreted based on analytic constraints derived in the text.
Monomers
The first two monomers, receptors U and V, respond to only one input each. Therefore, they are trivially constrained to gates that depend on neither input (ALL, NONE) or on only one input (, ). Receptor W, on the other hand, allows competitive binding of both inputs, and can therefore realize several nontrivial gates.
At this point it is useful to observe that the gates exist in antagonistic pairs (a gate and its inverse), shown consecutively in Fig. 2: (AND, NAND), (OR, NOR), etc. Any receptor that can perform one member of a pair can perform the other, simply by inverting certain parameter values. Furthermore, several gates are equivalent under reversal of the two ligands (those with subscripts in Fig. 2): (, ), (, ), etc. Again, any receptor that can perform one of these can perform the other, simply by switching certain parameter values (corresponding to exchanging the effect of S1 and S2). Eliminating these redundancies, we arrive at four unique gates that respond nontrivially to both inputs:
| (5) |
We will consider only these four unique gates from this point on.
The third monomer, receptor W, whose partition functions are given in Eqs. 2 and 3, can realize two of the four unique gates: OR and . The OR gate follows straightforwardly from the situation where both ligands activate the receptor individually; their combination will then activate it as well. The gate can be formed if ligand 1 binds more strongly than ligand 2 (Kj1 ≪ Kj2), but ligand 1 only weakly biases the receptor toward the active state (KA1 ∼ KI1), whereas ligand 2 strongly biases it (KA2 ≪ KI2). In this scenario, a receptor that is inactive in the absence of both ligands (ω0 ≪ 1) will only be active in the presence of ligand 2 and not 1.
We note here that any receptor that is activated by two different ligands is a biological example of an OR gate, and many naturally occurring receptors are activated by different ligands, like the TAR receptor (19) and the EGF receptor (33). More generally, it has been shown that proteins can be synthesized with a number of specific ligand-binding sites (34); such constructs can be thought of as extensions of the OR gate to more than two inputs. Additionally, the ORN gate, the inverse of the ANDN gate, has been constructed synthetically using a single protein (see construct H2, Fig. 2 B in Dueber et al. (14)).
Receptor W cannot realize the other two unique gates, AND and XOR. Both gates require a cooperative effect when both ligands are present: in the AND gate, neither ligand activates the receptor individually, but both activate it together; in the XOR gate, each ligand activates the receptor individually, but both suppress activation together. Such cooperative effects are not possible with competitive binding. As we will see next, dimerization is required to perform these gates.
Dimers
The three monomers admit six possible dimer combinations—three homodimers and three heterodimers. The homodimers QUU and QVV respond to only one input each and are therefore trivially constrained like monomers U and V. Moreover, heterodimers QUW and QWV are equivalent upon ligand exchange and can therefore realize equivalent sets of logic gates upon parameter variation. This leaves three dimers that can realize unique sets of logic gates upon parameter variation: QUV, QUW, and QWW.
The first dimer, receptor QUV, is the simplest heterodimer: it is formed by combining monomer U, which responds only to ligand 1, and monomer V, which responds only to ligand 2. Unlike receptor W, which is limited to competitive binding, the dimeric receptor QUV has two binding pockets and therefore allows noncompetitive (i.e., cooperative) binding. Accordingly, its partition functions extend those of receptor W (Eqs. 2 and 3) to include a cooperative term,
| (6) |
| (7) |
The cooperative term contains an additional Boltzmann factor corresponding to the cooperative binding energy E12, which could originate from, e.g., a conformational change of the receptor upon binding of one ligand that opens the binding pocket for the other ligand. For example, the binding affinity of each of the inputs to the protein N-WASP is increased by a factor of ∼300 when the other input is bound (3).
Receptor QUV can realize three of the four unique gates: OR, , and AND. The OR and gates follow straightforwardly from the fact that QUV reduces to W for no cooperativity (ω12 = 0), and receptor W can realize these gates as previously discussed. The AND gate is formed when the receptor is inactive in the presence of each ligand alone but, due to the cooperative interaction, is active in the presence of both ligands together. Receptor QUV cannot realize the XOR gate: if the receptor is activated by either one of the two ligands, it must also be activated by both ligands together. The cooperative interaction enhances the effect that each ligand individually has on the activation of the receptor, but it cannot reverse it.
The intuition behind why receptor QUV can realize the AND gate can be quantified by considering the constraints that an AND gate places on the partition functions. These constraints are shown in Table 1, where and denote the maximum input values. We have recognized that a low output requires ZA ≪ ZI (see Eq. 1); therefore, the first three lines reflect that in an AND gate the output is low in the first three input conditions. Similarly, a high output requires ZA ≫ ZI, which is reflected in the last line. Receptor QUV can realize the AND gate precisely because the constraints in Table 1 can be met simultaneously. For example, taking for illustration the simplifying case of intermediate cooperativity (ω12 ≳ 0) and symmetric, saturating ligand concentrations , the equation in Table 1 reduces to
| (8) |
Indeed, we see that the AND gate requires a bias upon ligand binding that is too weak to activate the receptor individually (KI1/KA1 ≪ 1/ω0), but strong enough to activate the receptor cooperatively .
Table 1.
Constraints placed by the AND gate on the partition functions of receptor QUV, as described in the text
| [S1] | [S2] | pA | Constraint |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | ||
| 0 | 0 | ||
| 1 |
The strength of the cooperativity influences the quantitative properties of the AND gate: an increase in ω12 shifts the transition region of the gate to smaller ligand concentrations, as indeed observed in studies of the AND-like N-WASP protein (3).
In addition to N-WASP (3), the AND gate logic is observed in various other proteins. For example, in gonadotropes, the scaffold PEA-15 is activated only by the simultaneous presence of PKC and ERK (35). Similarly, the adaptor protein TIRAP functions as a coincidence detector (36), thereby only becoming activated when two inputs are present at the same time. In Vibrio harveyi, coincidence detection is also exhibited for the two quorum signals AI-1 and AI-2 (37).
The second dimer, receptor QUW, is also a heterodimer: it is formed by combining monomer U, which responds only to ligand 1, and monomer W, which responds competitively to both ligands. The partition functions for this receptor are
| (9) |
| (10) |
Here, because ligand 1 can bind to either monomer U or W, we distinguish these cases with the second subscript on K1j. There are now two cooperative terms, corresponding to the cases where monomers U and W bind, respectively, ligands 1 and 1 (ω11), or ligands 1 and 2 (ω12). Equations 9 and 10 make clear that receptor QUW reduces to receptor W (Eqs. 2 and 3) in the limit Kj1,U → ∞, and to receptor QUV (Eqs. 6 and 7) in the limit Kj1,W → ∞.
Receptor QUW can realize all four unique gates (and therefore all 16 possible gates; see Fig. 2). The OR, , and AND gates follow straightforwardly from the fact that receptor QUV, which can realize these gates, is a limiting case. The XOR gate is less trivial. Below we offer an intuitive argument for why receptor QUW can realize an XOR gate, and in Section S2 in the Supporting Material, we prove analytically that the output can be a nonmonotonic function of the two inputs for this receptor, which is required for an XOR gate.
The XOR gate is formed when each ligand individually activates the receptor by binding to monomer W. However, when both ligands are present, ligand 1 is outcompeted and thus binds to monomer U, in turn suppressing activation. It is instructive here to describe this process in more detail. Suppose that ligand 1 promotes activation when bound to W but suppresses activation when bound to U. Further, suppose that ligand 1 binds more strongly to W than to U, such that in the presence of ligand 1 alone, the receptor is active. Now suppose that ligand 2 promotes activation when bound to W. Because ligand 2 can only bind to W, in the presence of ligand 2 alone, the receptor is also active. Finally, suppose that ligand 2 interferes with ligand 1, i.e., binds more strongly to W than ligand 1 does. Then, in the presence of both ligands, ligand 2 binds to W, leaving ligand 1 to bind to U. If U suppresses activation more strongly than W promotes activation, then in the presence of both ligands, the receptor is inactive. The resulting logic is the XOR gate.
The third dimer, receptor QWW, is a homodimer: it is formed by combining two W monomers, each of which responds competitively to both ligands. The partition functions for this receptor are
| (11) |
| (12) |
Here, the factors of two account for the fact that each ligand can be bound to either of two symmetric monomers. There are now three cooperative terms, corresponding to the cases where both monomers bind ligand 1 (ω11), both bind ligand 2 (ω22), or one binds ligand 1 and the other binds ligand 2 (ω12).
Receptor QWW can realize three of the four unique gates: OR, , and AND. The OR and gates follow straightforwardly from the fact that each monomer alone can realize these gates as previously discussed. The AND gate relies on strong suppression of cooperation between monomers if they are bound to the same ligand type (i.e., ω11 → 0, ω22 → 0); this suppression prevents activation when only one ligand is present. In fact, this limit reduces Eqs. 11 and 12 to Eqs. 6 and 7 (up to factors of 2), meaning the AND gate constraint, Eq. 8, also holds here under the same conditions for which it was derived. Receptor QWW cannot realize the XOR gate: because the individual monomers are identical, no negative interference is possible, as it is for receptor QUW.
Functions accessible by recombination
In the previous section, we identified the logic gates accessible by individual receptors via variation of intrinsic biochemical parameters. In this section, we ask a separate question. We here seek the logic gates that a set of monomers can realize—at fixed parameters—simply by forming the possible dimer combinations. This question is critically related to the challenge that all cells face: to encode reliable responses using limited resources (here, a limited set of monomers) and on short timescales (here, set by gene expression and cell signaling). This question is also key to functional control at the single-protein level: if diverse logic gates can be realized by a small set of monomers, cellular function could be strongly tuned in a straightforward manner, e.g., by expressing a particular pair of monomers and not others.
The three monomers we study form four functional dimers: QUV, QUW, QWV, and QWW (the dimers QUU and QVV respond to only one input each and are neglected). This fact leads to the enticing question of whether there exist parameters at which the four dimers perform the four unique logic gates (Eq. 5). Such a finding would be highly nontrivial: all monomers are present in at least two dimers, and therefore the performance of a particular logic gate by one dimer places heavy constraints on the parameters of the other dimers.
An exhaustive search, in which we numerically optimize for each of the 4! = 24 dimer-to-logic gate mappings in turn (see Section S1 in the Supporting Material), suggests that no parameter set exists at which all four unique logic gates are performed. Moreover, replacing any subset of gates with the corresponding inverse gates and repeating gives the same result in each of the 24 = 16 cases. Interestingly, the result seems to be due to the fact that the parameters that support the XOR gate in receptor QUW (or its counterpart QWV) prohibit the AND gate in any of the other receptors. Next, we support this numerical observation with an intuitive argument.
Suppose that receptor QUW performs an XOR gate. As described in the previous section, the XOR gate requires that when ligand 1 is present alone, it activates the receptor by binding to monomer W. Because the AND gate requires the opposite behavior, namely that the receptor is inactive when ligand 1 is present alone, then the AND gate cannot be formed by any receptor in which ligand 1 only binds to W. This group includes receptors QWW and QWV, leaving only receptor QUV. Then, as also described in the previous section, the XOR gate requires that ligand 1 suppresses activation when bound to monomer U. Because the AND gate requires that the receptor is active when both ligands are present, in receptor QUV this suppression would have to be overpowered by activation via ligand 2 binding to V. However, if this were the case, the receptor would surely be active in the presence of ligand 2 alone, which is inconsistent with the behavior of an AND gate. These arguments make clear that if receptor QUW performs an XOR gate, no other receptor can perform an AND gate. The same arguments, but with the ligands exchanged, hold if receptor QWV performs the XOR gate instead of receptor QUW. Because receptors QUW and QWV are the only receptors that can perform the XOR gate, we conclude that the XOR and AND gates are not mutually accessible by recombination of monomers U, V, and W at fixed parameters.
Even though all four unique logic gates cannot be performed at fixed parameters, we do find six parameter sets at which unique groups of three logic gates are performed by three of the dimers. We denote these parameter sets as φk, for k ∈ {1, 2,…, 6}, and show the logic gates and the dimers that perform them in Fig. 3. We stress that this result is still nontrivial: two of the groups are performed by receptors QWW, QUW, and QWV, which all contain monomer W; additionally, two groups are performed by receptors QUW, QWV, and QUV, in which each monomer is represented in two of the three dimers. Due to the high degree of monomer overlap in both cases, one might have expected the three dimers to be constrained to similar functionality at fixed parameters; instead, we find that three unique logic gates can be formed. Further, Fig. 3 reveals that all four logic gates are represented among the six groups (but, as expected, never XOR and AND in the same group). Finally, the optimal solutions shown in Fig. 3 are robust to parametric perturbation: as shown in Section S3 in the Supporting Material, for all φk, most random perturbations in which each parameter changes by an average of ∼20% change the fitness of none of the three logic gates by >10%. All of these features underscore the functional versatility available to cells by dimeric recombination.
Figure 3.
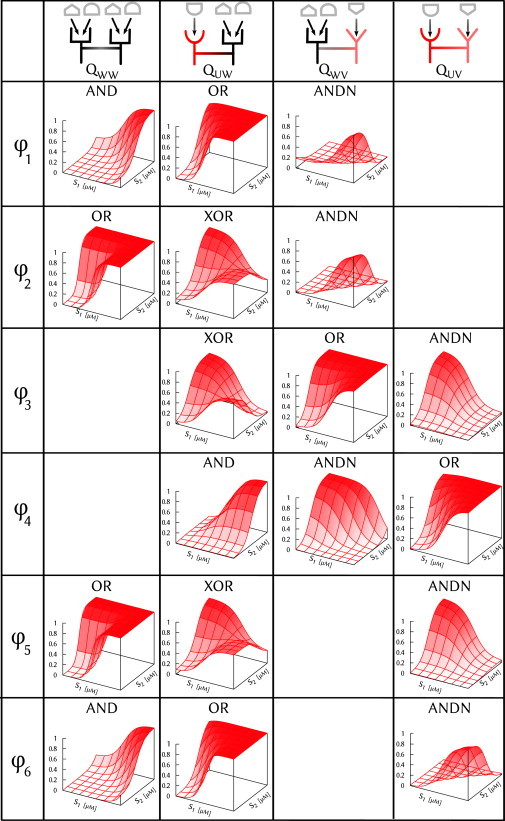
Functional versatility by recombination. Given the three monomer types, four functional units can be formed by dimerization. Six parameter sets φk are shown at which three of the four dimers perform functionally unique logic gates.
Our finding that cells can perform multiple logic gates at fixed parameters naturally raises the question of whether the gates conflict with each other, which could potentially corrupt the computation. Moreover, because we imagine that the dimers are present on the membrane in quasi-equilibrium with their monomeric constituents, we must also consider whether the gates are in conflict with the logic encoded by the monomers themselves. This latter question is straightforward to resolve. First, the monomers U and V respond to only one input each and therefore do not perform nontrivial logic gates. Second, although the monomer W can perform one of two nontrivial logic gates (OR or ANDN), the dimer QWW then also performs this gate. Any conflict between W and a dimer therefore also arises as a conflict between QWW and that dimer. We thus consider only conflict between dimers from here on.
One simple way of minimizing conflict between dimers is by selectively expressing only a particular pair of monomers and not the other monomer (Fig. 4 a). For example, at parameter set φ3 (see Fig. 3), if monomers U and V were expressed, but not W, the only dimer that could form is QUV, resulting in the unambiguous encoding of an ANDN gate. If at some later time, monomers U and W were expressed, but not V, only QUW and QWW could form; then, because QWW is not functional at φ3, the XOR gate would be encoded unambiguously. Similarly, expression of V and W but not U would encode the OR gate unambiguously. The time between these periods of selective expression would be set by gene expression and would therefore be long compared to the timescale on which the cell actually employs the logic gate to respond to the incoming signals. We observe from Fig. 3 that both parameter sets φ3 and φ4 share the property that all three gates can be encoded unambiguously by selective expression; in this sense they are optimal in terms of minimizing conflict between gates. By contrast, the other parameter sets suffer from conflict between QUW and QWW when only U and W are expressed (φ1, φ2, φ5, φ6), or between QVW and QWW when only V and W are expressed (φ1, φ2).
Figure 4.
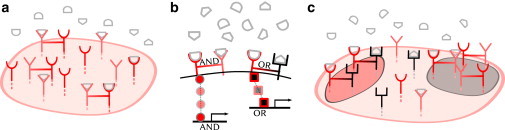
Several established mechanisms can minimize conflict between dimers’ logical functions. (a) Selective expression of only two of the three monomers allows the formation of only one functional dimer, whereas (b) specificity of the downstream component or (c) spatial segregation of membrane components allows multiple functional dimers to coexist without conflict.
Ultimately, the most general solution to the problem of dimer conflict—and indeed, one that is commonly exploited by cells—is to make the downstream response dimer-specific. Specificity can be established in several ways. The immediate downstream component can respond preferentially to one dimer and not to another, as observed for the EGF receptor family (38). The specificity could then be propagated further downstream, for example at the level of transcriptional regulation (Fig. 4 b). Alternatively, specificity can be achieved via spatial segregation of membrane components (Fig. 4 c). For example, interaction with lipid rafts is thought to separate membrane proteins into spatially distinct, nonmixed clusters, leading to added specificity in downstream computations (39,40). Either of these mechanisms would allow several types of dimers to coexist on the membrane and control, simultaneously and without conflict, distinct downstream processes according to distinct logical functions.
In the remainder of this section, we provide for parameter sets φ1 and φ2 the intuition behind how the three logic gates in Fig. 3 are performed by the corresponding receptors. In Section S4 in the Supporting Material, we provide similar intuition for parameter sets φ3, φ4, φ5, and φ6. Furthermore, in Section S4 in the Supporting Material, we argue why the groups observed in Fig. 3 (and their counterparts obtained upon ligand exchange) are the only groups of three unique logic gates that one expects to observe under this model.
Parameter set φ1 (Fig. 3, first row) corresponds to a case where each ligand only weakly promotes activation in the presence of monomer W. This feature allows receptor QWW to remain inactive when each ligand is present individually but become activated when both ligands are present together, forming the AND gate. Furthermore, ligand-bound U both promotes activation and strongly enhances the binding of ligand 2 to W. This feature allows receptor QUW to perform the OR gate: when ligand 1 is present alone, it promotes activation by binding to U; when ligand 2 is present in abundance and ligand 1 is present only in a small amount (and thus still in the off-state), the small amount of ligand 1 is nonetheless sufficient to promote activation via enhanced binding of ligand 2 to W; and when both ligands are present in abundance, the two effects combine, resulting in activation. Finally, ligand-bound V both suppresses activation and strongly enhances the binding of ligand 1 to W. This feature allows receptor QWV to perform the gate: when ligand 2 is present it suppresses activation via V, independent of ligand 1; but when ligand 1 and not (very much of) ligand 2 is present, the small amount of ligand 2 strongly enhances binding of ligand 1 to W, thus promoting activation.
Parameter set φ2 (Fig. 3, second row) corresponds to a case where ligand-bound W promotes activation. This feature is sufficient for receptor QWW to perform the OR gate. Furthermore, ligand 2 binds more strongly to V than to W, and ligand-bound V suppresses activation more strongly than ligand-bound W promotes activation. These features allow receptor QWV to perform the gate, because only in the presence of ligand 1 and not 2 will activation be promoted via W and not suppressed via V. Finally, 1), ligand 1 binds more strongly to W than to U, 2), ligand 2 binds more strongly to W than ligand 1 does, and 3), ligand-bound U suppresses activation more strongly than ligand-bound W promotes activation. These are the precise features that allow receptor QUW to perform the XOR gate, as outlined in detail in the previous section.
Discussion
We have used a statistical mechanical model to investigate the versatility of receptor function in two contexts: 1), the ability of a single receptor to access logical functions by parameter variation, and 2), the ability—at fixed parameters—or a set of receptor monomers to access logical functions by dimerizing. The first context is important on evolutionary timescales, on which mutations and environmental pressures act to change a cell’s intrinsic biochemical parameters. The second context is more critical at far shorter timescales, i.e., timescales characterizing the response of individual cells, during which gene expression and covalent modification can potentially change cellular function at the molecular level by favoring the dimerization of particular receptors over others.
In the first context, we find that a single heterodimer (receptor QUW) can realize all possible logic gates by parameter variation. Our analysis reveals that such complete functional freedom, although perhaps surprising, is in fact quite intuitive for this receptor. In particular, receptor QUW performs the most challenging function, the XOR gate, by exploiting an interference between the two ligands (i.e., when both ligands are present, one outcompetes the other for the activating binding pocket, ultimately causing suppression). Such a nonmonotonic response requires competitive binding and asymmetric activation biases, both of which are possible by heterodimerization.
In the second context, we find that the simplest combination of monomers that yields four functional dimers cannot, in fact, perform the four unique logic gates at fixed parameters—an observation we explain by arguing that the AND gate and the XOR gate are not mutually accessible. Nonetheless, numerical search reveals that several distinct groups of three unique gates are performable, a result that is nontrivial given the high degree of overlap among dimers’ parameter spaces. We offer intuitive explanations for the emergence of these groups, and further, we argue that these groups are exhaustive. The ability to perform diverse functions with a limited set of simple components is of critical importance to the question of how cells encode reliable responses with limited resources.
Although we often think of logic functions as the fundamental units of decision-making, logic operations reduce the output space to a binary variable. In principle the full input-output relation, which conveys much more information, could be used to regulate downstream responses. Indeed, the output of our statistical mechanical model is not restricted to Boolean logic, but instead provides continuous response functions. However, we argue that the most simple form of transducing information on ligands is via an input-output relation that approximates a binary response. In fact, recent experiments have shown that the information transmission capacity of a receptor is indeed ∼1 bit, which is equivalent to a binary response (41).
We have adopted a minimal model (the MWC model) to describe a minimal set of components, and we have explored the functional capabilities available under these conditions. We are further encouraged by the fact that the MWC model has been shown to agree with experiments on receptors (28–30). Nonetheless, three extensions to the model or the study itself are natural choices for further exploration. First, the conformational spread (CS) model (26,27) generalizes the MWC model, and thus it would allow for more functional freedom in logic gate construction. However, it is always a concern that generalizing one’s model can reduce the fraction of functional parameter space simply by increasing the total volume of parameter space. Second, it would be straightforward to introduce one or more additional monomers when considering recombination. For example, introducing an additional monomer that binds a single ligand might in fact admit parameter sets at which all four unique logic gates are performed, at the expense of increasing the number of individual components that the cell must produce. The impact of such a finding, however, would be reduced by the fact that more than four functional dimer combinations would be possible. Third, it would also be straightforward to consider more complex dimers (or higher oligomers), such as , in which each pocket binds both ligands competitively, but with asymmetric parameters. Of course, such increasing complexity would only be justified in the context of correspondingly detailed biological examples.
It is well established that receptors are responsive to multiple ligands. Recent experiments have indeed exploited this fact to synthetically construct proteins that perform a limited set of logic gates (42). At the same time, observations of oligomerization and protein modification on the membrane suggest that receptors can act as functional signaling units by recombination. Indeed, experiments have shown that for many receptors, such as ErbB and GPCR, monomers combine to form different dimers that have different functionality (16,21,22). We anticipate that this study will contribute to a predictive framework in which experiments like these can be interpreted and extended. The findings we report—that a single receptor can function as any logic gate and that a limited set of monomers can access diverse logic gates by dimerizing—speak to the large degree of functional control available to cells at the level of individual receptor molecules.
Acknowledgments
The authors thank Jose Alvarado for a critical reading of the manuscript.
This work is part of the research programme of the Foundation for Fundamental Research on Matter, which is financially supported by the Netherlands Organization for Fundamental Research.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Contributor Information
Wiet de Ronde, Email: deronde@amolf.nl.
Pieter Rein ten Wolde, Email: tenwolde@amolf.nl.
Andrew Mugler, Email: mugler@amolf.nl.
Supporting Material
References
- 1.Mehta P., Goyal S., Wingreen N.S. Information processing and signal integration in bacterial quorum sensing. Mol. Syst. Biol. 2009;5:325. doi: 10.1038/msb.2009.79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kaplan S., Bren A., Alon U. Diverse two-dimensional input functions control bacterial sugar genes. Mol. Cell. 2008;29:786–792. doi: 10.1016/j.molcel.2008.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Prehoda K.E., Lim W.A. How signaling proteins integrate multiple inputs: a comparison of N-WASP and Cdk2. Curr. Opin. Cell Biol. 2002;14:149–154. doi: 10.1016/s0955-0674(02)00307-1. [DOI] [PubMed] [Google Scholar]
- 4.Bray D. Protein molecules as computational elements in living cells. Nature. 1995;376:307–312. doi: 10.1038/376307a0. [DOI] [PubMed] [Google Scholar]
- 5.Hermsen R., Tans S.J., ten Wolde P.R. Transcriptional regulation by competing transcription factor modules. PLoS Comput. Biol. 2006;2:e164. doi: 10.1371/journal.pcbi.0020164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bintu L., Buchler N.E., Phillips R. Transcriptional regulation by the numbers: models. Curr. Opin. Genet. Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Istrail S., Davidson E.H. Logic functions of the genomic cis-regulatory code. Proc. Natl. Acad. Sci. USA. 2005;102:4954–4959. doi: 10.1073/pnas.0409624102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Buchler N.E., Gerland U., Hwa T. On schemes of combinatorial transcription logic. Proc. Natl. Acad. Sci. USA. 2003;100:5136–5141. doi: 10.1073/pnas.0930314100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tamsir A., Tabor J.J., Voigt C.A. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’. Nature. 2011;469:212–215. doi: 10.1038/nature09565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kramer B.P., Fischer C., Fussenegger M. BioLogic gates enable logical transcription control in mammalian cells. Biotechnol. Bioeng. 2004;87:478–484. doi: 10.1002/bit.20142. [DOI] [PubMed] [Google Scholar]
- 11.Setty Y., Mayo A.E., Alon U. Detailed map of a cis-regulatory input function. Proc. Natl. Acad. Sci. USA. 2003;100:7702–7707. doi: 10.1073/pnas.1230759100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guet C.C., Elowitz M.B., Leibler S. Combinatorial synthesis of genetic networks. Science. 2002;296:1466–1470. doi: 10.1126/science.1067407. [DOI] [PubMed] [Google Scholar]
- 13.Dueber J.E., Yeh B.J., Lim W.A. Rewiring cell signaling: the logic and plasticity of eukaryotic protein circuitry. Curr. Opin. Struct. Biol. 2004;14:690–699. doi: 10.1016/j.sbi.2004.10.004. [DOI] [PubMed] [Google Scholar]
- 14.Dueber J.E., Yeh B.J., Lim W.A. Reprogramming control of an allosteric signaling switch through modular recombination. Science. 2003;301:1904–1908. doi: 10.1126/science.1085945. [DOI] [PubMed] [Google Scholar]
- 15.Motlagh H.N., Hilser V.J. Agonism/antagonism switching in allosteric ensembles. Proc. Natl. Acad. Sci. USA. 2012;109:4134–4139. doi: 10.1073/pnas.1120519109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Citri A., Yarden Y. EGF-ERBB signaling: towards the systems level. Nat. Rev. Mol. Cell Biol. 2006;7:505–516. doi: 10.1038/nrm1962. [DOI] [PubMed] [Google Scholar]
- 17.Barton G.M., Medzhitov R. Toll-like receptors and their ligands. Curr. Top. Microbiol. Immunol. 2002;270:81–92. doi: 10.1007/978-3-642-59430-4_5. [DOI] [PubMed] [Google Scholar]
- 18.Moghal N., Sternberg P.W. Multiple positive and negative regulators of signaling by the EGF-receptor. Curr. Opin. Cell Biol. 1999;11:190–196. doi: 10.1016/s0955-0674(99)80025-8. [DOI] [PubMed] [Google Scholar]
- 19.Bray D. Signaling complexes: biophysical constraints on intracellular communication. Annu. Rev. Biophys. Biomol. Struct. 1998;27:59–75. doi: 10.1146/annurev.biophys.27.1.59. [DOI] [PubMed] [Google Scholar]
- 20.Grecco H.E., Schmick M., Bastiaens P.I.H. Signaling from the living plasma membrane. Cell. 2011;144:897–909. doi: 10.1016/j.cell.2011.01.029. [DOI] [PubMed] [Google Scholar]
- 21.Landau M., Ben-Tal N. Dynamic equilibrium between multiple active and inactive conformations explains regulation and oncogenic mutations in ErbB receptors. Biochim. Biophys. Acta. 2008;1785:12–31. doi: 10.1016/j.bbcan.2007.08.001. [DOI] [PubMed] [Google Scholar]
- 22.Minneman K.P. Heterodimerization and surface localization of G protein coupled receptors. Biochem. Pharmacol. 2007;73:1043–1050. doi: 10.1016/j.bcp.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Phillips R., Kondev J., Theriot J. 1st ed. Garland Science; New York: 2008. Physical Biology of the Cell. [Google Scholar]
- 24.Koshland D.E., Jr., Némethy G., Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 25.Monod J., Wyman J., Changeux J.-P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 26.Changeux J.-P., Thiéry J., Kittel C. On the cooperativity of biological membranes. Proc. Natl. Acad. Sci. USA. 1967;57:335–341. doi: 10.1073/pnas.57.2.335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bray D., Duke T. Conformational spread: the propagation of allosteric states in large multiprotein complexes. Annu. Rev. Biophys. Biomol. Struct. 2004;33:53–73. doi: 10.1146/annurev.biophys.33.110502.132703. [DOI] [PubMed] [Google Scholar]
- 28.Tu Y., Shimizu T.S., Berg H.C. Modeling the chemotactic response of Escherichia coli to time-varying stimuli. Proc. Natl. Acad. Sci. USA. 2008;105:14855–14860. doi: 10.1073/pnas.0807569105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hansen C.H., Sourjik V., Wingreen N.S. A dynamic-signaling-team model for chemotaxis receptors in Escherichia coli. Proc. Natl. Acad. Sci. USA. 2010;107:17170–17175. doi: 10.1073/pnas.1005017107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Skoge M.L., Endres R.G., Wingreen N.S. Receptor-receptor coupling in bacterial chemotaxis: evidence for strongly coupled clusters. Biophys. J. 2006;90:4317–4326. doi: 10.1529/biophysj.105.079905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fisher R. Clarendon Press; Oxford, NY: 1930. The Genetical Theory of Natural Selection. [Google Scholar]
- 33.Jorissen R.N., Walker F., Burgess A.W. Epidermal growth factor receptor: mechanisms of activation and signaling. Exp. Cell Res. 2003;284:31–53. doi: 10.1016/s0014-4827(02)00098-8. [DOI] [PubMed] [Google Scholar]
- 34.Looger L.L., Dwyer M.A., Hellinga H.W. Computational design of receptor and sensor proteins with novel functions. Nature. 2003;423:185–190. doi: 10.1038/nature01556. [DOI] [PubMed] [Google Scholar]
- 35.Choi S.G., Ruf-Zamojski F., Sealfon S.C. Characterization of a MAPK scaffolding protein logic gate in gonadotropes. Mol. Endocrinol. 2011;25:1027–1039. doi: 10.1210/me.2010-0387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pawson T. Dynamic control of signaling by modular adaptor proteins. Curr. Opin. Cell Biol. 2007;19:112–116. doi: 10.1016/j.ceb.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 37.Henke J.M., Bassler B.L. Bacterial social engagements. Trends Cell Biol. 2004;14:648–656. doi: 10.1016/j.tcb.2004.09.012. [DOI] [PubMed] [Google Scholar]
- 38.Sweeney C., Fambrough D., Carraway K.L., 3rd Growth factor-specific signaling pathway stimulation and gene expression mediated by ErbB receptors. J. Biol. Chem. 2001;276:22685–22698. doi: 10.1074/jbc.M100602200. [DOI] [PubMed] [Google Scholar]
- 39.Lingwood D., Simons K. Lipid rafts as a membrane-organizing principle. Science. 2010;327:46–50. doi: 10.1126/science.1174621. [DOI] [PubMed] [Google Scholar]
- 40.Kholodenko B.N., Hancock J.F., Kolch W. Signaling ballet in space and time. Nat. Rev. Mol. Cell Biol. 2010;11:414–426. doi: 10.1038/nrm2901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cheong R., Rhee A., Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science. 2011;334:354–358. doi: 10.1126/science.1204553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lim W.A. Designing customized cell signaling circuits. Nat. Rev. Mol. Cell Biol. 2010;11:393–403. doi: 10.1038/nrm2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Swem L.R., Swem D.L., Bassler B.L. Deducing receptor signaling parameters from in vivo analysis: LuxN/AI-1 quorum sensing in Vibrio harveyi. Cell. 2008;134:461–473. doi: 10.1016/j.cell.2008.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bai F., Branch R.W., Berry R.M. Conformational spread as a mechanism for cooperativity in the bacterial flagellar switch. Science. 2010;327:685–689. doi: 10.1126/science.1182105. [DOI] [PubMed] [Google Scholar]
- 45.Duke T.A., Le Novère N., Bray D. Conformational spread in a ring of proteins: a stochastic approach to allostery. J. Mol. Biol. 2001;308:541–553. doi: 10.1006/jmbi.2001.4610. [DOI] [PubMed] [Google Scholar]
- 46.Leff P., Scaramellini C., McKechnie K. A three-state receptor model of agonist action. Trends Pharmacol. Sci. 1997;18:355–362. doi: 10.1016/s0165-6147(97)01105-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


