Abstract
Numerous dyes are available or under development for probing the structural and functional properties of biological membranes. Exogenous chromophores adopt a range of orientations when bound to membranes, which have a drastic effect on their biophysical behavior. Here, we present a method that employs optical anisotropy data from three polarization-imaging techniques to establish the distribution of orientations adopted by molecules in monolayers and bilayers. The resulting probability density functions, which contain the preferred molecular tilt μ and distribution breadth γ, are more informative than an average tilt angle 〈φ〉. We describe a methodology for the extraction of anisotropy data through an image-processing technology that decreases the error in polarization measurements by about a factor of four. We use this technique to compare di-4-ANEPPS and di-8-ANEPPS, both dipolar dyes, using data from polarized 1-photon, 2-photon fluorescence and second-harmonic generation imaging. We find that di-8-ANEPPS has a lower tilt but the same distributional width. We find the distribution of tilts taken by di-4-ANEPPS in two phospholipid membrane models: giant unilamellar vesicles and water-in-oil droplet monolayers. Both models result in similar distribution functions with average tilts of 52° and 47°, respectively.
Introduction
Dyes are versatile reporters of structure and activity in biological membranes. However, the behavior of dyes bound to membranes is influenced by their orientation (1–5). The intramembrane tilt angle, φ, is the angle between the long axis of a molecule and the normal of the plane in which it resides (Fig. 1 A). In most cases, the long axis of the dye molecule can be assumed to be coincident with its transition dipole moment (TDM). Previously, studies that have quantified tilt angle have employed solid-state NMR (6–8), electron paramagnetic resonance (9,10), polarization coherent anti-Stokes Raman scattering (11), infrared dichroism (12–15), polarization anisotropy fluorescence (16–26), and second-harmonic generation (SHG) microscopy (11,27–34). Experimental data from these investigations have been complemented by computational methods for modeling molecules in membranes (8,35–38).
Figure 1.
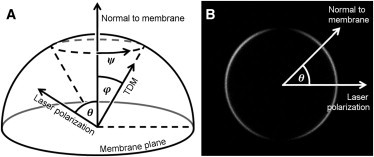
(A) Transition dipole moment (TDM) of each molecule is tilted at an angle φ from the membrane normal and an angle ψ around it. The intensity of fluorescence or SHG from the ensemble of dyes is dependent on the angle away from the laser polarization, θ. (B) Variation of SHG from di-4-ANEPPS, which varies periodically with θ around the equator of a model membrane (giant unilamellar vesicle). The shape of this curve, when fit to a model, allows extraction of trigonometric moments of the tilt distribution, Ptilt(φ). The direction of laser excitation is co-linear with the direction of signal detection and perpendicular to the plane of the image in panel B.
Further, the attachment of dyes has provided a method for investigating the tilt of membrane proteins (33). Change in tilt angle can also be used to monitor biophysical processes such as membrane potential changes. Voltage-sensitive dyes such as RH421 rely on a reorientation mechanism for their slow voltage-sensitive response as an applied electric field changes their alignment in the membrane (39,40).
The most intuitive description of molecular alignment, the expected tilt angle 〈φ〉, may be found by substituting f(φ) = φ into the general expression
| (1) |
where Ptilt(φ) is the tilt-angle probability density function (PDF) over all available orientations. Measurements of orientation-dependent phenomena typically rely on simplifications of the PDF to find 〈φ〉 but do not reach a general solution for Ptilt(φ) itself. This sheds little light on the nature of the system because identical 〈φ〉-values may arise from different PDFs, as illustrated in Fig. 2.
Figure 2.
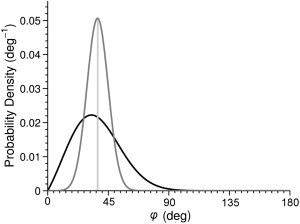
Two different probability density functions can produce identical 〈φ〉 values (vertical line). Therefore, measures of 〈φ〉 alone do not adequately describe the system. For examples, these two probability density functions differ in where the lowest energy molecular tilt (μ) lies—i.e., normal to the membrane (solid) or tilted by 37° (shaded).
We introduce two parameters, μ and γ, which, when included in the tilt PDF, allow a more complete description of the tilt distribution of any species in a biological membrane. The parameter μ describes the preferred, or lowest enthalpy, molecular state before the density of available states is considered, while γ is the range of states around μ that the dye is capable of adopting, i.e., the breadth of the distribution (see Fig. 8). Furthermore, comparison or unification of the physical techniques that extract dye orientation from experiment requires consensus on the form of the tilt PDF. By choosing a specific case, a uniaxial dye, and using a more accurate image-processing methodology, we compare the tilt PDF of a molecule in two model phospholipid membranes through the application of three methods in parallel: polarized one-photon, two-photon, and SHG imaging (Fig. 1 B).
Figure 8.
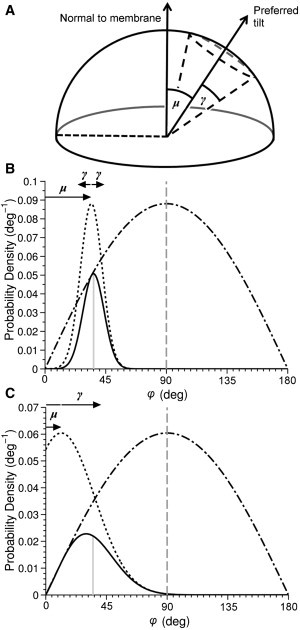
Two distinct tilt probability density functions (solid curves) showing φ (vertical solid line), and their contributing preferred tilt (dotted curves) and statistical (dot-dashed curve) terms. One PDF has a large μ and a small γ (B), whereas the other has a small μ and large γ (C). A representative cartoon (A) shows the physical interpretation of the quantities μ and γ, which may be calculated for given experimentally extracted order parameters.
Materials and Methods
Materials
Di-4-ANEPPS (3-(4-(2-(6-(dibutylamino)naphthalen-2-yl)vinyl)pyridin-1-ium-1-yl)propane-1-sulfonate) and di-8-ANEPPS (3-(4-(2-(6-(dioctylamino)naphthalen-2-yl)vinyl)pyridin-1-ium-1-yl)propane-1-sulfonate) were purchased from Biotium (Hayward, CA) and diphytanoyl phosphatidylcholine (DPhPC) was obtained as a lyophilized powder from Avanti Polar Lipids (Alabaster, AL). All other materials, including dodecane and indium-tin-oxide-coated glass slides were obtained from Sigma (St. Louis, MO).
Droplet imaging
Droplets of buffer were introduced into a bath of lipid and dye in dodecane according to the following protocol:
Phosphate-buffered saline (20 μL, 50 mM NaH2PO4, 50 mM NaCl, pH 7.0) was added to a solution of DPhPC (1.0 mg/mL) and ANNEP dye (50 μM) in dodecane (1.0 mL) in a small vial and the mixture was shaken gently. Alternatively, DPhPC (0.5 mg/mL) and ANNEP dye (50 μM) was dissolved in phosphate-buffered saline (20 μL, 50 mM NaH2PO4, 50 mM NaCl, pH 7.0) then added to dodecane (1.0 mL) in a small vial and the mixture was shaken gently. The mixture was poured into a well with a silanized borosilicate coverslip (100-μm thickness) forming the base. Droplets ∼60 μm in diameter were allowed 10 min to equilibrate and imaged by scanning multiphoton microscopy.
Giant unilamellar vesicles
Giant unilamellar vesicles (GUVs) were prepared from DPhPC in 200 mM sucrose via an electroformation method (41,42). Each dye was added to obtain a concentration of 50 μM, then the mixture was immobilized in a silica sol-gel immediately before imaging. Immobilization was performed as recently described by Esquembre et al. (43) by formation of an aqueous silica sol through hydrolysis of tetramethylorthosilicate followed by gelation with pH 7.4 buffer. Once a suitable GUV was located, SHG and two-photon fluorescence (2PF) images were obtained in transmission and epifluorescence channels, respectively.
Microscopy setup
Imaging was conducted on a custom-built microscope based around a model No. BX60M upright microscope (Olympus, Melville, NY) adapted with standard LINOS Microbench components (LINOS Photonics, L-1882, Luxembourg). The light source was a Tsunami Ti:Sapphire laser (Spectra Physics, Santa Clara, CA) producing 100-fs pulses centered at 850 nm. A LUMPlanFL N 40×0.8 NA lens (Olympus) was illuminated at the back aperture with a 90 mW beam after passing through a 1000:1 polarizing beamsplitter (Newport, Irvine, CA). After passing through an excitation filter, the two-photon epi-fluorescence was filtered with a 550–650-nm bandpass filter (FF568-Di01-25x36; Semrock, Rochester, NY) before being captured with a H7422P series photon-counting photomultiplier tube (Hamamatsu Photonics, Hamamatsu, Japan).
Use of a dichroic to filter emission may result in a polarization bias of no more than 10% and we calculate that this should influence detected light by only ±2%. SHG emission was condensed in the forward direction, passing through an excitation filter and a 422–432-nm notch filter (FF01-427/10-25; Semrock) before reaching a model No. DM0016 photon-counting photomultiplier tube (Sens-Tech, Slough, Berkshire, UK). The alignment of the emission polarizer in SHG imaging was determined using a nonlinear frequency-doubling crystal.
Laser scanning was achieved with a pair of orthogonally mounted galvanometer mirrors (VM1000+; Cambridge Technology, GSI Group, Lexington, MA). Synchronous point scanning and data collection were orchestrated through LABVIEW software (National Instruments, Austin, TX) running on a reconfigurable FPGA card (NI PCI-7830R; National Instruments).
Theory
Tilt angle from ratiometric imaging
Dipolar chromophores are uniquely suited to optical investigation through the use of one- and two-photon linear dichroism, as well as polarization-dependent SHG. For most dyes, the angle between the long molecular axis and optical transition dipole moment (TDM or dominant hyperpolarizability tensor element) is small. The fluorescence or SHG signal observed from any point in a dye-doped membrane is a function of the tilt distribution of chromophores in the membrane, Ptilt(φ), and the angle between the membrane normal and the polarization of the excitation source, θ (Fig. 1) (19,23,30,31).
In general, linear dichroism is a consequence of the photoselection rule: light absorbed by a molecule is proportional to the square of the projection of its TDM vector onto the electric field vector of the excitation field. Application of the one- and two-photon photoselection rule requires that we assume dyes have a single, well-defined TDM at the wavelength of excitation (44). We avoid effects resulting from polarization of the emission by excluding polarizers from the collection channels and choosing an experimental setup with D∞h symmetry. We ensure the highest possible polarization purity through inclusion of a 1000:1 polarizing beamsplitter as the penultimate optic before the objective, and we use a relatively low NA lens (objective NA = 0.8; see Materials and Methods) to prevent the convergence of the beam from generating significant off-axis polarization.
The direction of laser excitation is co-linear with the direction of signal detection, and the whole setup is radially symmetric with respect to this principle axis (into the page, Fig. 1 B). We choose this arrangement so that in the far field, fluorescence anisotropy does not vary with angular displacement, θ. The geometric arrangement of the TDM, in the plane perpendicular to the beam axis, means that projection of the toroidal emission onto the detector is independent of θ (44). To support this symmetry argument, we include a mathematically rigorous proof in the Supporting Material.
In the case of SHG images (where all output light is collected with condensing optics), we only consider the angular dependence of scattered second-harmonic light from dyes possessing a single dominant hyperpolarizability vector, βzzz. To satisfy these requirements, we use ANEPPS chromophores (Fig. 3 A) (45), which are dipolar molecules with a single dominant TDM and βzzz directed along the primary molecular axis (30,31). The di-4-ANEPPS and di-8-ANEPPS dyes are suitable for imaging in each of the modalities described here and have been shown to be useful voltage-sensitive plasma membrane reporters (45).
Figure 3.
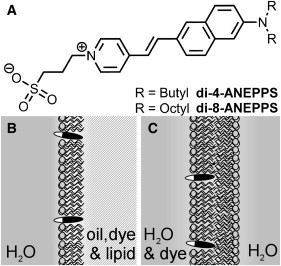
(A) Structure of di-4-ANEPPS and di-8-ANEPPS, the dyes used in this study and the membrane models used in this experiment: Phospholipid DPhPC (lipid) membranes incorporating ANEPPS dyes (solid and open lozenges) in (B) the water droplet model and (C) GUVs.
A dilute solution of chromophores ensures that dye molecules act as individual radiators or scatterers within the membrane and we assume that, in this regime, there is no effect of concentration on tilt angle.
Tilt-angle intensity functions
Absorption and subsequent fluorescence of polarized light is governed by the photoselection rule (19,44)
| (2) |
for an isolated dipolar fluorophore with its TDM oriented at an angle α to the polarization of the excitation. The relationship between the tilt of the population of chromophores and polarization of laser light can be found by starting with the molecular dipole for a uniaxial absorber,
| (3) |
and performing a series of rotations, taking into account the tilt (φ), rotation around the normal at that tilt (ψ), and the rotation relative to the laboratory frame (θ), shown in Fig. 1:
| (4) |
For a polarized electric field oscillating collinearly with the dipole,
| (5) |
photoselection may be expressed as a dot product:
| (6) |
Integration over the solid angle (ψ), rotation on its own axis (η), and the population of tilted dyes (φ) yields an expression for the angular dependence of emission for a distribution of dyes, where I0 is emission at optimum alignment:
| (7) |
After substituting and normalizing,
| (8) |
which simplifies to give an expression for the angular dependence of one-photon fluorescence:
| (9) |
Therefore, through a similar approach to that of Corry et al. (19), we find that the one-photon fluorescence (1PF) of an ensemble of dyes with a given Ptilt(φ) distribution at an angle θ from the excitation polarization depends on the expression
| (10) |
where the angular intensity function’s shape is determined by the relative contributions of the cos2θ and ½ sin2θ terms. We call the ratio of these terms the 1PF order parameter, ϑ1PF = 〈cos2φ〉/〈sin2φ〉, which in turn is a function of the tilt angle PDF (Eq. 1).
Two-photon linear dichroism depends on the square of the one-photon photoselection rule because the absorption of two photons requires two photoselection events. For two-photon excitation of a dipolar dye, we assume that absorption is dominated by a single tensor element, such that we may treat the molecule as having a single two-photon pseudo-TDM, directed along its molecular axis (23). Therefore, the two-photon selection rule (18,19,44)
| (11) |
when taking the appropriate rotations, yields the dependence of
| (12) |
integrated,
| (13) |
and, simplified, yields the expression for the angular dependence of two-photon fluorescence of
| (14) |
where the 2PF order parameters are defined ϑ2PF = 〈cos4φ〉/〈sin22φ〉 and ϑ′2PF = 〈sin4φ〉/〈sin22φ〉, and are trigonometric moments of a probability density function (see Eqs. 18B and 18C, respectively).
As with 1PF and 2PF, the angular dependence of SHG is a consequence of photoselection. For SHG, because the interaction of light with the tilted chromophores is via coherent scattering rather than absorption, the mechanism of photoselection is different. Output SHG intensity is a function of the second-order nonlinear susceptibility tensor, χ2 normal to the membrane, which is derived through the projection of molecular contributions to the hyperpolarizability onto the membrane frame (31). Because SHG is a second-order nonlinear phenomenon, we arrive at a tilt-angle-dependent expression for χ2 by performing the appropriate rotations on β, the rank 3 tensor that describes the molecule’s hyperpolarizability. We find that the induced second-harmonic dipole moment μ(0)2ω,z across the membrane has two major contributions,
| (15) |
where βz = 〈cos3φ〉Bz and βt = ½〈sin2φcosφ〉Bz are the tilt-angle-dependent hyperpolarizabilities converted from contributions in the molecular frame Bz to the membrane frame and Eω is the excitation field amplitude. Because total power radiated parallel, P||SHG, scales as the square of induced polarization, and by transforming to the laboratory frame, we arrive at the relation
| (16) |
Thus, we arrive at an expression for the angular dependence of SHG parallel to the incident field (29,30),
| (17) |
with an SHG order parameter ϑSHG = ½〈sin2φcosφ〉/〈cos3φ〉. From this collection of models, if given experimental data for how intensity, I, varies with θ, we may extract the four order parameters:
| (18A) |
| (18B) |
| (18C) |
| (18D) |
Previous studies have only extracted one of these order parameters and subsequently assumed the simplest possible distribution of tilt angles. For example, the assumption that all molecules lie at only one angle φ from the membrane normal (as in Fig. 1) results in the simplification: 〈f(φ)〉 = f(〈φ〉). Furthermore, although estimated values of 〈φ〉 may be compared between compounds, they are not particularly instructive without more information on the breadth of the distribution or the preferred tilt of the molecule (Fig. 2). More recent studies have taken tilt distribution into account—Benninger et al. (18) found 〈cos2φ〉 and 〈cos4φ〉 moments from 2PF images, but experimental imprecision left them unable to resolve a parameterized distribution function. In the study of a densely incorporated dye, Gonella et al. (34) excluded particular distributions by combining SHG imaging with grazing-incidence x-ray diffraction, but were left with a range of possible distributions due to experimental constraints.
Experimental models
The order parameters in Eq. 18, A–D, which determine the variation of I with θ, can be extracted from experimentally obtained images of membranes aligned over a range of angles relative to the excitation field. Laser scanning confocal microscopy images of spherical cell models give the signal intensity of a membrane over the full range of θ, which may then be fit to Eq. 18, A–D, to yield the relevant order parameter. We choose spherical cellular models, imaging at the equator such that the cross-sectional image is a circle or ellipse with periodically varying intensity around its circumference.
We have previously used a basic cellular model, which is constructed from droplets of water in oil encapsulated by a lipid monolayer (Fig. 3 B), providing a stable system that is easily imaged (46). Here, we show that this model provides a robust, reproducible, high-throughput method of quantifying tilt angle with the minimum of specialist equipment. The drawbacks are that the oil-water phase boundary may cause lensing effects that can divert some emitted light or distort the point-spread function required for 2PF and SHG modes. Further, oil may partition into the membrane, influencing the orientation of the embedded dye molecules.
The second model, giant unilamellar vesicles (GUVs, Fig. 3 C), is more biologically relevant but has the disadvantage of being less robust and prone to SHG fading over time as dyes undergo flip-flop (32). GUVs are more mobile and deformable than water droplets and must be immobilized or else image distortion occurs during scanning microscopy. GUVs also require a more sophisticated fabrication, have a limited lifetime, and are more difficult to produce in a quantity suitable for high-throughput imaging.
Image processing
To find the tilt-angle-dependent order parameters ϑ1PF, ϑ2PF, ϑ′2PF, and ϑSHG (Eq. 18, A–D) with a high degree of accuracy, we developed what to our knowledge is a novel image-processing methodology (Fig. 4, and see MATLAB Image Processing Software Outline in the Supporting Material). Our algorithm treats the image as a surface and fits the data to a two-dimensional function. This polar fitting approach has the advantage of taking the entire weighted radial cross-sectional circumference into account, so that all pixels in the image contribute to the fit (as opposed to user-defined region-of-interest approaches, such as taking an oval profile (1,18,25,30), which are prone to human bias and sampling error). A successful fit produces a parameterized model that may be plotted as either a two-dimensional intensity plot or three-dimensional surface (Fig. 5 D, and Fig. 6, B and D) for comparison with the original image (Fig. 6, A and C).
Figure 4.
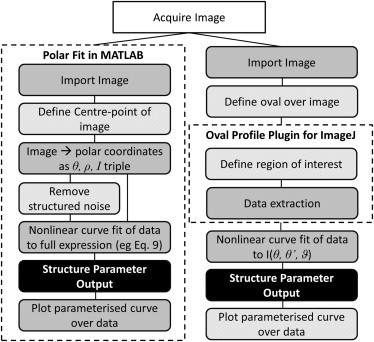
Flow chart for image processing with our polar fitting technique (left) and the oval profile technique (right), showing the reduction in the number of essential manual steps that may lead to error. Experimental steps (open), automatic steps (dark-shaded), and manual steps (light-shaded) result in the desired output (solid). (In each case, the dashed box represents the software used to process the image; steps outside of the dashed box require manual processing.)
Figure 5.
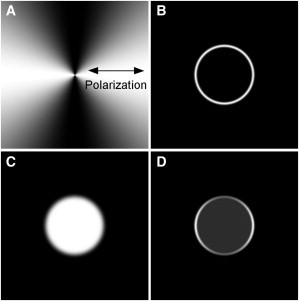
Two-dimensional (A) angular function modeled with θ′ = π/2 (relative to polarization, double-headed arrow), ϑIPF = π/2, (B) radial function modeled with ρ′ = 100 pixels, σ = 10 pixels, ε = θ″ = 0 and (C) background function modeled with σ′ = 5 pixels and ε = θ″ = 0. Their combination results in Eqs. 10 and 11 that are represented by function (D).
Figure 6.
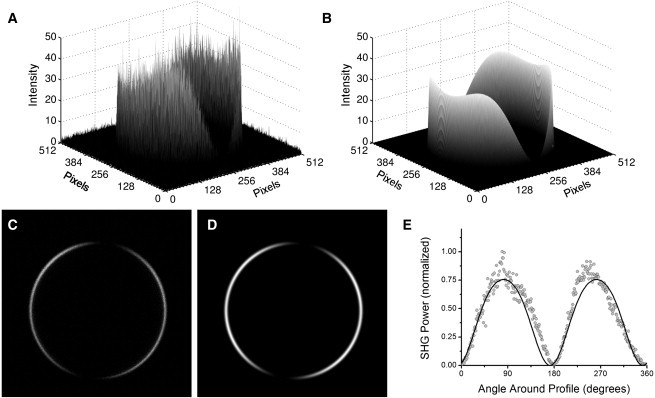
Analysis of an SHG image of di-4-ANEPPS in a monolayer of DPhPC on the surface of a water droplet in oil. The polar-fitting technique renders the SHG image as a surface (A), with signal intensity plotted on the z axis and pixel location on the x and y axis. The parameterized model (B) is also plotted for comparison. Similarly, the two-dimensional SHG image (C) is plotted alongside the two-dimensional parameterized model (D) for comparison, image dimensions: 300 × 300 μm. We also include a plot from analysis of the image by the oval profile method (E). This method considers only a subset of data points (shaded points), which do not accurately represent the image and subsequently is prone to experience more error and a poorer fit (solid line).
Images were processed by a custom-made MATLAB program (The MathWorks, Natick, MA). Once the circle center-point is either manually or semiautomatically defined, the software expresses the image in polar coordinates, whereupon each pixel is described by an angle from the excitation polarization, θ, a radius from the center of the circle, ρ, and an intensity, I. This expression of the image in polar coordinates may then be fit to Eq. 19 (Fig. 5 D),
| (19) |
where bold terms are input data and others such as a, the amplitude of the signal, are fitting parameters. I(θ,θ′,ϑ) is the angular intensity function around the circumference (see Tilt Angle from Ratiometric Imaging, above, and Fig. 5 A), which depends on θ′, the direction of polarization relative to the image frame and ϑ the characteristic order parameter of the dye in the membrane. R(ρ,ρ′,σ,ε,θ,θ″) defines the radial form, a Gaussian of breadth σ centered at a distance ρ′ from the center-point (Fig. 5 B) with eccentricity ε along a major axis θ″ from the laboratory frame. The value νn is the background or shot noise. The full expressions are presented as Eqs. S10–S12 in the Supporting Material.
Unlike SHG images, where signal is only generated from ordered regions, 1PF and 2PF images suffered from both structured and isotropic backgrounds that required the inclusion of a further modifier (besides the additional order parameter ϑ′ for 2PF images). In Eq. 20, b is a multiplier that determines the contribution of E(ρ,ρ′,σ′,ε,θ,θ″), a radial error function with breadth determined by σ′,
| (20) |
The models are parameterized using a nonlinear least-squares minimization, producing either 7 or 10 outputs, one of which is the order parameter. Reinsertion of these parameters into the model reconstructs the fit as an idealized image that may then be assessed for goodness of fit (Fig. 5 D and Fig. 6, A and B).
Results
Polar fitting versus oval profile
Our polar-fitting approach to image analysis (Fig. 6, B and C) confers a significantly greater accuracy compared to the standard oval profile approach (Fig. 6 D). We eliminate a degree of the human error involved in ellipsoid definition and use significantly more data points (by fitting the Gaussian weighted profile of the circular lineform), resulting in a fourfold improvement in the reproducibility of the fit (Table 1). Furthermore, the fitting approach is less influenced by noise overlapping the equator because we consider the image in its entirety (Fig. 7). The oval profile method relies on data points extracted from beneath a user-defined oval placed over the region of interest. Our polar-fitting manual technique requires that the user specifies only the extremities of the oval. The software uses this input to calculate the center point, and then fits an oval to the image. The semiautomated approach operates on a similar algorithm; however, the image is thresholded, then extremities of the oval are found automatically.
Table 1.
Order parameters for di-4-ANEPPS in GUVs found by three image-processing methods and the error associated with each technique for both analysis of one image and for a batch of images (n = 7)
| One image |
Twelve images |
|||
|---|---|---|---|---|
| ϑ1PF | ± Error | ϑ1PF | ± Error | |
| Oval profile | 0.729 | 0.019 (2.6%) | 0.747 | 0.078 (10.4%) |
| Polar manual | 0.715 | 0.0027 (0.4%) | 0.725 | 0.018 (2.5%) |
| Polar semiautomated | 0.716 | 0.0013 (0.2%) | 0.727 | 0.018 (2.5%) |
Figure 7.
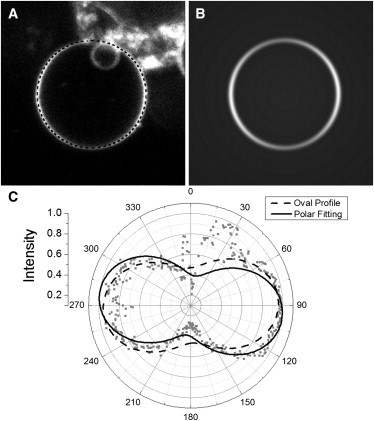
One-photon fluorescence intensity around the equator of (A) a bleb on the exterior of a cultured HeLa cell stained with di-4-ANEPPS and (B) a model image of a single bleb reconstructed from the original image after parameterization, image dimensions: 26.5 × 26.5 μm. (C). This image was processed by using two methods. In the first, the oval profile method extracts data from the delineated area (dotted line) over the bleb. Each fitting technique generates an angular intensity fit that overlays the data (shaded points). The overlap of the signal data with background fluorescence from the cell can be seen as an anomaly on the polar plot from 345° to 60°. The polar fitting (solid line) is less influenced by this anomaly than the oval profile (dashed line), resulting in a better fit.
Testing polar fitting
As a test of our protocol, inexperienced operators (n = 7) were asked to perform each of these three data extraction operations (oval profile, polar manual, and polar semiautomated) on one image. The human error from oval profiling led to a six- to ten-times greater variance when finding order parameters compared to the polar-fitting techniques. We found that in general, this difference arose from erroneous placement of the oval profile—an operation performed by eye and consequently subject to human error. Each of the inexperienced users was then asked to process a series of 12 similar images, again using each of the three processing techniques. The oval profiling approach gave order parameters with four times the experimental imprecision of our techniques, which returned order parameters with only 2.5% error (Table 1).
We demonstrate that our polar fitting approach is general and robust by processing an image superimposed with structured background noise (Fig. 7 A): blebs formed at the surface of an apoptotic cultured HeLa cell. A polar-fitting analysis of the image yields a closer fit than the oval profile method and allows reconstruction of an image of the bleb itself (Fig. 7 B). The polar fit generates a more accurate fit that is less influenced by the structured noise of the cell (Fig. 7 C).
Distributional analysis
Describing the physical system that gives rise to functional behavior and the average tilt, 〈φ〉, requires the tilt probability density function, Ptilt(φ), of molecules in the membrane. The form of Ptilt(φ) is a product of the molecule’s preferred tilt and a statistical term that describes the number of available states (Fig. 8). An amphiphilic molecule will be most stable when its lipophilic parts are embedded in the hydrocarbon core of the membrane and its hydrophilic parts are embedded in the polar region of the membrane. This tends to drive the molecule to orient normally with respect to the membrane plane (i.e., φ = 0). Our model assumes that the preferred tilt adopts a Gaussian distribution centered at a tilt μ from the normal, with a variance γ away from this tilt μ (Fig. 8). The statistical sinφ term describes the change in of density of states with φ. The normalized product is our proposed PDF,
| (21) |
where N is a complex term depending on μ and γ, which normalizes the probability density function. Given this proposed probability function, we may solve Eqs. 18, A–D, as a system of nonlinear equations for the values of μ and γ (see Fig. S10, Fig. S11, Fig. S12, and Fig. S13 in the Supporting Material). This overdetermined system may be expected to present a number of solutions; however, solving equations in pairs or the full set of four equations via a Levenberg-Marquardt minimization both provide solutions consistent with the equations plotted in μ × γ space (Fig. 9).
Figure 9.
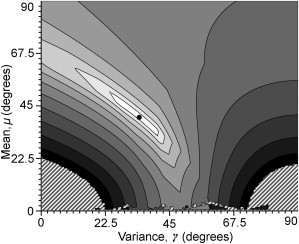
Isosurface of the normalized linear combination of solutions to Eqs. 18, A–D, for di-4-ANEPPS in GUVs. The surface is plotted on a logarithmic scale in μ × γ space: (light shading) regions of lowest error. (Hatched area) Regions of very high root-mean-square error, which have been removed from the plot for clarity. (Solid disk) Solution presented in Table 1, found by a Levenberg-Marquardt minimization algorithm. The four contributing isosurfaces may be found in Fig. S10, Fig. S11, Fig. S12, and Fig. S13 in the Supporting Material.
The combination of any two of the three microscopy modalities we employ is sufficient to estimate values of μ and γ, as demonstrated by our droplet monolayer model. In this case, 1PF images could not be obtained due to out-of-plane fluorescence, but a probability density function may still be found through the combination of SHG and 2PF (Table 2). Our solutions give values of μ and γ from which we obtain the full probability density function and then can calculate a value of 〈φ〉for comparison with literature values.
Table 2.
One-photon, two-photon, and SHG order parameters and calculated biophysical parameters, which describe the tilt-angle probability density function of di-4-ANEPPS in two-model membrane systems and di-8-ANEPPS in one
| ϑ1PF | ϑ2PF | ϑ′2PF | ϑSHG | μ | γ | 〈φ〉 | ||
|---|---|---|---|---|---|---|---|---|
| di-4-ANEPPS | Droplets | —∗ | 0.60 ± 0.033 | 0.45 ± 0.068 | 0.59 ± 0.024 | 35.8° ± 1.5° | 31.2° ± 3.6° | 47° |
| GUVs | 0.75 ± 0.056 | 0.45 ± 0.058 | 0.63 ± 0.059 | 0.44 ± 0.026 | 36.7° ± 6.6° | 38.1° ± 4.7° | 52° | |
| di-8-ANEPPS | Droplets | —∗ | 0.58 ± 0.052 | 0.23 ± 0.047 | 0.38 ± 0.040 | 21.8° ± 5.5° | 31.4° ± 3.1° | 38° |
One-photon fluorescence data cannot be obtained for the droplet model because background fluorescence is too intense.
Tilt angle of ANEPPS chromophores in membranes
Our multidimensional modeling approach yielded order parameters for ANEPPS chromophores in two-model membrane systems over three microscopy modalities (Table 2). Images of both GUVs and water droplets in oil were acquired in 1PF, 2PF, and SHG. Representative analyses are presented as Fig. S3, Fig. S4, Fig. S5, Fig. S6, Fig. S7, Fig. S8, and Fig. S9. The results, which represent the collation of a number of images (n > 6), are summarized in Table 2. After solving the order parameters for μ and γ, we can plot their probability density functions (Fig. 10), which are good descriptions of the tilt of the ANEPPS chromophores in model systems. The parameters μ and γ give a better description of the distribution of orientations than 〈φ〉; however, we calculate 〈φ〉 from μ and γ to facilitate comparison with results from other research groups. For di-4-ANEPPS, we obtain an average expectation value 〈φ〉 over the two membrane systems of 49.5° ± 2.5°.
Figure 10.
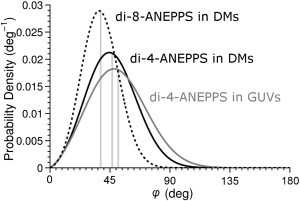
Probability density functions for di-4-ANEPPS (solid lines) and di-8-ANEPPS (dashed line) with accompanying expected tilt angles (vertical lines) for monolayers (solid) and GUVs (shaded).
A comparison with published studies of di-4-ANEPPS reveals that our values in model membranes are similar to those obtained from Langmuir-Blodgett films: 49° at a realistic bilayer pressure of 22 mN/m (28). Our outcome of 38° for the analogous di-8-ANEPPS (Table 2) agrees with both studies of black lipid membrane bilayers, in which it adopts a tilt angle of 36° ± 3° (32) and with an investigation of silicon-supported POPC bilayers, in which it tilts to 38° (48). An earlier study of similar styryl dyes (49) found that longer alkyl chains encourage tilting in membranes; however, computation by Hinner et al. (35) on slightly different compounds reached the opposite conclusion, illustrating that the factors determining tilt distribution are not fully understood. We find that the mean tilt (μ) of di-8-ANEPPS is lower than that of di-4-ANEPPS (Table 2) but that both have similar distributional variance (γ). From our values of μ and γ, we see that in both systems, di-4-ANEPPS has a preferred attitude relative to the membrane; however, the variety of positions that it can fill is larger in GUVs than in lipid monolayers. Differences in the bilayer pressure or lipid phase may account for this difference. The droplet monolayer is more likely to be swollen by its exposure to dodecane (Fig. 3, B and C), which increases lateral pressure in the membrane area and reduces the range of available states (38).
Discussion
We have demonstrated that the combined analysis of three types of optical image (1PF, 2PF, and SHG) of the same dye-containing lipid membrane provides a level of insight into the angular distribution of the dye that cannot be obtained from a single imaging technique. Appropriate treatments of fluorescence and second-harmonic generation photoselection yield a system of equations for signal strength with angular displacement from a polarized excitation. These equations may be expressed in terms of trigonometric moments of the distribution of tilts that a dipolar chromophore in a membrane may occupy.
Image analysis using the entire circular image in polar coordinates allows us to achieve a more accurate and reproducible fit than use of an oval profile. We have demonstrated the versatility and robustness of this method over a range of imaging modes and with significant background noise. The additional accuracy gained through use of this technique allows a better parameterization of Ptilt(φ), the probability density function, which describes the tilt of a population of molecules in the bilayer. The finding that tilt-angle distribution varies little between GUVs and the droplet monolayer system confirms that the droplet monolayer system is representative of a biological membrane for imaging applications. This is a valuable finding for high-throughput imaging studies because the droplet monolayer system is simpler to construct and more reliable to image (50).
Because model membranes are homogeneous on the length-scales of a multiphoton point spread function (∼1 μm), theoretical treatment of photoselection allows determination of molecular tilt. Heterogeneous cell membranes complicate this process though tilt-dependent SHG may still be observed in the presence of membrane structures such as invaginations (51). Although invaginations may obfuscate tilt-dependent fluorescence by causing deviation from the D∞h symmetry, some groups have been able to resolve fluorescence anisotropy from cellular membranes (23,29).
The ramifications of these findings extend over a range of imaging and biophysical techniques. Given the heterogeneity of cellular membranes, probing the local lipid environment is important for the study of cellular processes (3). The differences in polarity and viscosity in different regions of a cellular membrane may have a significant effect on the tilt of an exogenous dye such as di-4-ANEPPS (52). For example, understanding the orientational distribution of molecular rotors, which probe local intracellular and intramembrane viscosity, could have a large impact on how viscosity measurements are interpreted (53,54). The frustrated rotation of such probes should be a function of both their tilt and position in the membrane; a known probability density function can be inserted directly into a theoretical treatment (a singular expected tilt, 〈φ〉, cannot), the implications of which could be addressed by molecular dynamics simulations.
Further work could reveal mechanistic detail behind the electric field modulation of slow voltage-sensitive dyes, estimating the distribution of dyes before and after the application of a field. Application of potential to a membrane could affect both the mean tilt of a dye in the membrane (μ), and the range of tilts away from that position (γ). For example, a dye with a low mean tilt may have a voltage-sensitive mechanism that relies on the reduction of γ, whereas sensitivity from a dye with a high mean tilt is more likely to be a consequence of alignment of the mean dipole with the field, reducing μ. Our approach resolves these mechanisms, whereas use of a single modality would be constrained to simply monitoring the change in structure factor upon application of a field. Improving our understanding of dipolar dyes through predictable tilt behavior in membranes will lead us toward designing more effective voltage-sensitive dyes for the study of action potentials (39,40,45).
Acknowledgments
We are grateful to Dr. Pawel Swietach and Dr. Alzbeta Hulikova, Department of Physiology, Anatomy and Genetics, University of Oxford, for imaging support, and Dr. Tivadar Mach, Department of Chemistry, University of Oxford, for advice on GUV electroformation. We also thank Dr. Marina Kuimova, Department of Chemistry, Imperial College London, and Dr. William Barford, Department of Chemistry, University of Oxford, for their valuable discussions.
This work was funded by an Engineering and Physical Sciences Research Council grant. J.E.R. is funded by a Biotechnology and Biological Sciences Research Council interface studentship.
Contributor Information
James E. Reeve, Email: james.reeve@chem.ox.ac.uk.
Harry L. Anderson, Email: harry.anderson@chem.ox.ac.uk.
Supporting Material
References
- 1.Blackman S.M., Cobb C.E., Piston D.W. The orientation of eosin-5-maleimide on human erythrocyte band 3 measured by fluorescence polarization microscopy. Biophys. J. 1996;71:194–208. doi: 10.1016/S0006-3495(96)79216-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brattwall C.E.B., Lincoln P., Nordén B. Orientation and conformation of cell-penetrating peptide penetratin in phospholipid vesicle membranes determined by polarized-light spectroscopy. J. Am. Chem. Soc. 2003;125:14214–14215. doi: 10.1021/ja0366989. [DOI] [PubMed] [Google Scholar]
- 3.Janmey P.A., Kinnunen P.K.J. Biophysical properties of lipids and dynamic membranes. Trends Cell Biol. 2006;16:538–546. doi: 10.1016/j.tcb.2006.08.009. [DOI] [PubMed] [Google Scholar]
- 4.Mitra A.K., Célia H., Teyton L. Supine orientation of a murine MHC class I molecule on the membrane bilayer. Curr. Biol. 2004;14:718–724. doi: 10.1016/j.cub.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 5.Turner M.S., Sens P. Gating-by-tilt of mechanically sensitive membrane channels. Phys. Rev. Lett. 2004;93:118103. doi: 10.1103/PhysRevLett.93.118103. [DOI] [PubMed] [Google Scholar]
- 6.Cook G.A., Opella S.J. Secondary structure, dynamics, and architecture of the p7 membrane protein from hepatitis C virus by NMR spectroscopy. Biochim. Biophys. Acta. 2011;1808:1448–1453. doi: 10.1016/j.bbamem.2010.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tian F., Song Z., Cross T.A. Orientational constraints derived from hydrated powder samples by two-dimensional PISEMA. J. Magn. Reson. 1998;135:227–231. doi: 10.1006/jmre.1998.1544. [DOI] [PubMed] [Google Scholar]
- 8.Ulmschneider M.B., Sansom M.S.P., Di Nola A. Evaluating tilt angles of membrane-associated helices: comparison of computational and NMR techniques. Biophys. J. 2006;90:1650–1660. doi: 10.1529/biophysj.105.065367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fajer P.G. Determination of spin-label orientation within the myosin head. Proc. Natl. Acad. Sci. USA. 1994;91:937–941. doi: 10.1073/pnas.91.3.937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Inbaraj J.J., Laryukhin M., Lorigan G.A. Determining the helical tilt angle of a transmembrane helix in mechanically aligned lipid bilayers using EPR spectroscopy. J. Am. Chem. Soc. 2007;129:7710–7711. doi: 10.1021/ja071587l. [DOI] [PubMed] [Google Scholar]
- 11.Pfeffer C.P., Olsen B.R., Légaré F. Imaging skeletal muscle using second harmonic generation and coherent anti-Stokes Raman scattering microscopy. Biomed. Opt. Express. 2011;2:1366–1376. doi: 10.1364/BOE.2.001366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bazzi M.D., Woody R.W. Oriented secondary structure in integral membrane proteins. I. Circular dichroism and infrared spectroscopy of cytochrome oxidase in multilamellar films. Biophys. J. 1985;48:957–966. doi: 10.1016/S0006-3495(85)83859-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kukol A., Adams P.D., Arkin T.I. Experimentally based orientational refinement of membrane protein models: a structure for the Influenza A M2 H+ channel. J. Mol. Biol. 1999;286:951–962. doi: 10.1006/jmbi.1998.2512. [DOI] [PubMed] [Google Scholar]
- 14.Lundeen M., Chance B., Powers L. The transmembrane helices of beef heart cytochrome oxidase. Biophys. J. 1987;51:693–695. doi: 10.1016/S0006-3495(87)83395-7. 697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sigarev A.A., Vij J.K., Goodby J.W. Dichroic properties and the molecular tilt angle of a large-tilt angle antiferroelectric liquid crystal studied using polarized infrared spectroscopy. Ferroelectrics. 2006;343:167–175. [Google Scholar]
- 16.Badley R.A., Martin W.G., Schneider H. Dynamic behavior of fluorescent probes in lipid bilayer model membranes. Biochemistry. 1973;12:268–275. doi: 10.1021/bi00726a015. [DOI] [PubMed] [Google Scholar]
- 17.Badley R.A., Schneider H., Martin W.G. Orientation and motion of a fluorescent probe in model membranes. Biochem. Biophys. Res. Commun. 1971;45:174–183. doi: 10.1016/0006-291x(71)90066-0. [DOI] [PubMed] [Google Scholar]
- 18.Benninger R.K.P., Önfelt B., French P.M. Fluorescence imaging of two-photon linear dichroism: cholesterol depletion disrupts molecular orientation in cell membranes. Biophys. J. 2005;88:609–622. doi: 10.1529/biophysj.104.050096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Corry B., Jayatilaka D., Rigby P. Determination of the orientational distribution and orientation factor for transfer between membrane-bound fluorophores using a confocal microscope. Biophys. J. 2006;91:1032–1045. doi: 10.1529/biophysj.106.080713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fisher T.E., Marszalek P.E., Fernandez J.M. Stretching single molecules into novel conformations using the atomic force microscope. Nat. Struct. Biol. 2000;7:719–724. doi: 10.1038/78936. [DOI] [PubMed] [Google Scholar]
- 21.van der Heide U.A., Orbons B., Levine Y.K. The orientation of transition moments of dye molecules used in fluorescence studies of muscle systems. Eur. Biophys. J. 1992;21:263–272. doi: 10.1007/BF00185121. [DOI] [PubMed] [Google Scholar]
- 22.van der Heide U.A., Rem O.E., Levine Y.K. A fluorescence depolarization study of the orientational distribution of crossbridges in muscle fibers. Eur. Biophys. J. 1994;23:369–378. doi: 10.1007/BF00188661. [DOI] [PubMed] [Google Scholar]
- 23.Lazar J., Bondar A., Firestein S.J. Two-photon polarization microscopy reveals protein structure and function. Nat. Methods. 2011;8:684–690. doi: 10.1038/nmeth.1643. [DOI] [PubMed] [Google Scholar]
- 24.Livanec P.W., Huckabay H.A., Dunn R.C. Exploring the effects of sterols in model lipid membranes using single-molecule orientations. J. Phys. Chem. B. 2009;113:10240–10248. doi: 10.1021/jp903908m. [DOI] [PubMed] [Google Scholar]
- 25.Rocheleau J.V., Edidin M., Piston D.W. Intrasequence GFP in class I MHC molecules, a rigid probe for fluorescence anisotropy measurements of the membrane environment. Biophys. J. 2003;84:4078–4086. doi: 10.1016/S0006-3495(03)75133-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sund S.E., Swanson J.A., Axelrod D. Cell membrane orientation visualized by polarized total internal reflection fluorescence. Biophys. J. 1999;77:2266–2283. doi: 10.1016/S0006-3495(99)77066-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hsieh C.-L., Pu Y., Psaltis D. Second harmonic generation from nanocrystals under linearly and circularly polarized excitations. Opt. Express. 2010;18:11917–11932. doi: 10.1364/OE.18.011917. [DOI] [PubMed] [Google Scholar]
- 28.Huang J.Y., Lewis A., Loew L. Nonlinear optical properties of potential sensitive styryl dyes. Biophys. J. 1988;53:665–670. doi: 10.1016/S0006-3495(88)83147-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jiang J., Eisenthal K.B., Yuste R. Second harmonic generation in neurons: electro-optic mechanism of membrane potential sensitivity. Biophys. J. 2007;93:L26–L28. doi: 10.1529/biophysj.107.111021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Moreaux L., Pons T., Mertz J. Electro-optic response of second-harmonic generation membrane potential sensors. Opt. Lett. 2003;28:625–627. doi: 10.1364/ol.28.000625. [DOI] [PubMed] [Google Scholar]
- 31.Moreaux L., Sandre O., Mertz J. Membrane imaging by second-harmonic generation microscopy. J. Opt. Soc. Am. B. 2000;17:1685–1694. [Google Scholar]
- 32.Ries R.S., Choi H., Heath J.R. Black lipid membranes: visualizing the structure, dynamics, and substrate dependence of membranes. J. Phys. Chem. B. 2004;108:16040–16049. [Google Scholar]
- 33.Salafsky J.S. Second-harmonic generation for studying structural motion of biological molecules in real time and space. Phys. Chem. Chem. Phys. 2007;9:5704–5711. doi: 10.1039/b710505c. [DOI] [PubMed] [Google Scholar]
- 34.Gonella G., Dai H.-L., Blasie J.K. Control of the orientational order and nonlinear optical response of the “push-pull” chromophore RuPZn via specific incorporation into densely packed monolayer ensembles of an amphiphilic 4-helix bundle peptide: second harmonic generation at high chromophore densities. J. Am. Chem. Soc. 2010;132:9693–9700. doi: 10.1021/ja1010724. [DOI] [PubMed] [Google Scholar]
- 35.Hinner M.J., Marrink S.-J., de Vries A.H. Location, tilt, and binding: a molecular dynamics study of voltage-sensitive dyes in biomembranes. J. Phys. Chem. B. 2009;113:15807–15819. doi: 10.1021/jp907981y. [DOI] [PubMed] [Google Scholar]
- 36.Kyrychenko A. A molecular dynamics model of rhodamine-labeled phospholipid incorporated into a lipid bilayer. Chem. Phys. Lett. 2010;485:95–99. [Google Scholar]
- 37.Mazely T.L., Hetherington I.W.M. Second-order susceptibility tensors of partially ordered molecules on surfaces. J. Chem. Phys. 1987;86:3640–3647. [Google Scholar]
- 38.Song K.C., Livanec P.W., Im W. Orientation of fluorescent lipid analogue BODIPY-PC to probe lipid membrane properties: insights from molecular dynamics simulations. J. Phys. Chem. B. 2011;115:6157–6165. doi: 10.1021/jp109629v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Clarke R.J., Zouni A., Holzwarth J.F. Voltage sensitivity of the fluorescent probe RH421 in a model membrane system. Biophys. J. 1995;68:1406–1415. doi: 10.1016/S0006-3495(95)80313-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sugihara T., Haga H., Yamamoto S. Electric field response of second order optical nonlinearity in dye doped poled polymer. Appl. Phys. Lett. 1996;68:144–146. [Google Scholar]
- 41.Angelova M.I., Dimitrov D.S. Liposome electroformation. Faraday Discuss. Chem. Soc. 1986;81:303–311. [Google Scholar]
- 42.Mach T., Chimerel C., Fütterer C. Miniaturized planar lipid bilayer: increased stability, low electric noise and fast fluid perfusion. Anal. Bioanal. Chem. 2008;390:841–846. doi: 10.1007/s00216-007-1647-7. [DOI] [PubMed] [Google Scholar]
- 43.Esquembre R., Pinto S.N., Mateo C.R. Immobilization and characterization of giant unilamellar vesicles (GUVs) within porous silica glasses. Soft Matter. 2012;8:408–417. [Google Scholar]
- 44.Lakowicz J.R. Springer; New York: 1999. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 45.Loew L.M., Cohen L.B., Wu J.Y. A naphthyl analog of the aminostyryl pyridinium class of potentiometric membrane dyes shows consistent sensitivity in a variety of tissue, cell, and model membrane preparations. J. Membr. Biol. 1992;130:1–10. doi: 10.1007/BF00233734. [DOI] [PubMed] [Google Scholar]
- 46.Holden M.A., Needham D., Bayley H. Functional bionetworks from nanoliter water droplets. J. Am. Chem. Soc. 2007;129:8650–8655. doi: 10.1021/ja072292a. [DOI] [PubMed] [Google Scholar]
- 47.Reference deleted in proof.
- 48.Lambacher A., Fromherz P. Orientation of hemicyanine dye in lipid membrane measured by fluorescence interferometry on a silicon chip. J. Phys. Chem. B. 2000;105:343–346. [Google Scholar]
- 49.Loew L.M., Simpson L.L. Charge-shift probes of membrane potential: a probable electrochromic mechanism for p-aminostyrylpyridinium probes on a hemispherical lipid bilayer. Biophys. J. 1981;34:353–365. doi: 10.1016/S0006-3495(81)84854-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Morales-Penningston N.F., Wu J., Feigenson G.W. GUV preparation and imaging: minimizing artifacts. Biochim. Biophys. Acta. 2010;1798:1324–1332. doi: 10.1016/j.bbamem.2010.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Millard A.C., Terasaki M., Loew L.M. Second harmonic imaging of exocytosis at fertilization. Biophys. J. 2005;88:L46–L48. doi: 10.1529/biophysj.105.063768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Yeagle P.L. CRC Press; Boca Raton, FL: 2004. The Structure of Biological Membranes. [Google Scholar]
- 53.Levitt J.A., Kuimova M.K., Phillips D. Membrane-bound molecular rotors measure viscosity in live cells via fluorescence lifetime imaging. J. Phys. Chem. C. 2009;113:11634–11642. [Google Scholar]
- 54.Nipper M.E., Dakanali M., Haidekker M.A. Detection of liposome membrane viscosity perturbations with ratiometric molecular rotors. Biochimie. 2011;93:988–994. doi: 10.1016/j.biochi.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jackson J.D. Third Edition. Wiley; New York: 1998. Classical Electrodynamics. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


