Ion-Controlled Conformational Dynamics in the Outward-Open Transition from an Occluded State of LeuT

Abstract

Neurotransmitter:sodium symporter (NSS) proteins are secondary Na⁺-driven active transporters that terminate neurotransmission by substrate uptake. Despite the availability of high-resolution crystal structures of a bacterial homolog of NSSs—Leucine Transporter (LeuT)—and extensive computational and experimental structure-function studies, unanswered questions remain regarding the transport mechanisms. We used microsecond atomistic molecular-dynamics (MD) simulations and free-energy computations to reveal ion-controlled conformational dynamics of LeuT in relation to binding affinity and selectivity of the more extracellularly positioned Na⁺ binding site (Na1 site). In the course of MD simulations starting from the occluded state with bound Na⁺, but in the absence of substrate, we find a spontaneous transition of the extracellular vestibule of LeuT into an outward-open conformation. The outward opening is enhanced by the absence of Na1 and modulated by the protonation state of the Na1-associated Glu-290. Consistently, the Na⁺ affinity for the Na1 site is inversely correlated with the extent of outward-open character and is lower than in the occluded state with bound substrate; however, the Na1 site retains its selectivity for Na⁺ over K⁺ in such conformational transitions. To the best of our knowledge, our findings shed new light on the Na⁺-driven transport cycle and on the symmetry in structural rearrangements for outward- and inward-open transitions.

Introduction

Neurotransmitter:sodium symporters (NSSs), a family of secondary active transporters, terminate neurotransmission by Na⁺-driven uptake of the neurotransmitter from the synaptic cleft (1). In the transport cycle of NSSs, the transporter traverses outward-open, occluded, and inward-open conformational states in an alternating-access manner (2), and the energy stored in the Na⁺ gradient across the membrane is used in the translocation of substrate against its concentration gradient. Therefore, both the binding and dissociation of Na⁺ are critical for the conformational transitions of the transporter. Although the exact molecular mechanism of Na⁺-induced conformational dynamics is not known, Na⁺ binding has been proposed to precede substrate binding and lead to a conformational transition of the transporter toward a more outward-open conformation that facilitates the entrance of the substrate (3,4), which suggests that Na⁺ would bind favorably and selectively even in the absence of substrate.

Two Na⁺ ions are bound in the crystal structures of LeuT, a prokaryotic NSS homolog (5,6), at sites termed the Na1 site and Na2 site. The exact sequence of Na⁺ binding in the Na1 and Na2 sites is not clear, but the release of Na⁺ from the Na2 site was found to play a critical role in the transition toward an inward-open conformation, making it likely that Na⁺ binding in the Na2 site is important for establishing and maintaining the outward-open conformation (3,7,8). Indeed, both the location of the Na2 site and the role of binding and dissociation of Na2 in conformational transitions related to function (3,8) seem to be mechanistic features that are shared among transporter families with LeuT-like structural fold (9,10), even in the absence of sequence homology across the families. In contrast, the role that Na⁺ binding in the Na1 site plays in the conformational transitions in any of these transporters is less clear.

In LeuT, the Na1 site is formed by residues Ala-22 and Asn-27 of transmembrane (TM)1, Thr-254 of TM6, and Asn-286 of TM7. The Na1-bound ion is seen in the crystal structures to be in direct contact with the carboxylate group of either the cotransported substrate Leu or the inhibitor Trp bound in the primary binding site (S1 site) (5,6). In addition, Na1 is in close proximity to Glu-290 of TM7, a residue that was found to undergo a protonation/deprotonation cycle during the transport cycle (11). Na⁺ binding in the Na1 site was proposed to be essential for the stabilization of the unwound segments of TM1 and TM6, leading to the formation of the high-affinity substrate-binding pocket (6). Moreover, results from previous computational studies suggest that the presence of Na1 in the occluded state of the transporter contributes significantly to the favorable binding free energies of the bound ligands, and vice versa (12). This mutual stabilization is obviously due to the direct ionic interaction between Na1 and carboxylate group of cotransported substrate, but the observation that the interaction with substrate is critical for Na1 affinity must be considered in view of the above-mentioned favorable Na⁺ binding in the absence of substrate. Therefore, to achieve a mechanistic understanding of the transport, it is necessary to evaluate the sequence of Na⁺ and substrate binding in the Na1 and S1 sites, and to learn how Na1 affinity and binding relates to the presence of bound substrate.

In this study, we addressed some of these questions using the occluded and outward-open structures of LeuT as reference states of the transporter. Conformational rearrangements were monitored from molecular-dynamics (MD) simulations of Na⁺-bound LeuT in the absence of substrate. This Na⁺-only configuration was revealed computationally to correspond to a converged outward-open conformation suitable for substrate binding. The impact that the conformational transition from occluded to outward-open has on Na1 binding affinity and selectivity was evaluated with the use of molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) and free-energy perturbation (FEP)/MD calculations. The dynamics and energetic results regarding the transition yielded structure-based mechanistic details, and suggest the existence of a quasi-stable binding location of Na⁺ near the Na1 site.

Materials and Methods

MD simulations

Based on our established simulation protocols and the molecular system, we carried out a simulation of LeuT (PDB: 2A65) in the absence of substrate but in the presence of Na⁺ bound in Na1 and Na2, using NAMD (13) as described previously (3,14). Note that the S1 site is separated from the water phase only by the Phe-253 side chain, the fluctuation of which enables quick entry of water molecules into the cavity in the absence of substrate, without disruption of the overall integrity of the cavity. Briefly, all-atom simulations of LeuT immersed in explicit 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine lipid bilayer (POPC) were carried out with the CHARMM27-CMAP force field (15). In the isothermal-isobaric (NPT) ensemble, constant temperature (310 K) was maintained with Langevin dynamics, and 1 atm constant pressure was achieved with the hybrid Nose-Hoover Langevin piston method (16) applied to an anisotropic flexible periodic cell, with orthogonal pressure components computed independently. Particle mesh Ewald method was used to evaluate long-range electrostatic effects. A time step of 1 fs was used for the first 30 ns, and was then increased to 2 fs for the rest of the simulation. Two independent trajectories were collected. See the Supporting Material for the FEP/MD methods used in computation of ion selectivity and in alchemical transformation.

Conformational analysis

We studied the conformational changes involved in the transition between LeuT’s occluded and open extracellular-facing conformations on two 960-ns MD trajectories (MD1 and MD2). To align these trajectories, we used RMSDTT (see below).

We computed the angle between two helices (HA) using the PyMOL script AngleBetweenHelices (17). In this work, we considered the following helices of the LeuT structure: TM1a (residues 10–22), TM1b (residues 27–38), TM2a (residues 41–56), TM2b (residues 57–70), IL2 (residues 76–85), TM3a (residues 88–103), TM3b (residues 104–118), TM4 (residues 166–183), TM5 (residues 191–213), EL3a (residues 223–231), EL3b (residues 234–240), TM6a (residues 241–252), TM6b (residues 260–267), TM7 (residues 276–306), EL4a (residues 308–318), EL4b (residues 320–333), TM8 (residues 337–369), TM9 (residues 375–395), TM10a (residues 399–410), TM10b (residues 411–424), TM11a (residues 447–469), TM11b (residues 470–477), and TM12 (residues 483–513). We evaluated the Pearson correlation on smoothed data with an averaging window of 6 ns using the R program (18).

A principal component analysis (PCA) was performed with the use of Gromacs 4.0.5 on the C_α atoms of residues 5–511. The relative content of a particular PCA mode PC_i to the dynamics of the underlying trajectory is defined as ${\kappa }_i\equiv \left({\lambda }_i/{\sum }_{j=1}^{3N}{\lambda }_j\right)\ast 100\%$, where ${\lambda }_i$ is the eigenvalue of mode PC_i. The conformational difference vector between the outward-open and occluded conformations of an MD trajectory is defined as $\Delta \overrightarrow{R}\equiv {\overrightarrow{R}}_o-{\overrightarrow{R}}_c$, where ${\overrightarrow{R}}_o$ and ${\overrightarrow{R}}_c$ are the 3N-dimensional position vectors of all the Cα atoms (N) of the most outward-open and occluded conformations, respectively. These two extreme conformations are determined by the number of water molecules in the extracellular vestibule (EV) along the entire simulation trajectory, with the outward-open and occluded conformations having the maximum and minimum numbers of water, respectively. We arbitrarily define a water molecule to be in the EV if its oxygen atom is within 26 Å of the Cβ atom of Phe-259 but not within 5 Å of lipid atoms, and its z-coordinate is larger but no more than 23 Å above that of the same reference atom (the z-axis is perpendicular to the membrane and points toward the extracellular side). The normalized overlap ${\chi }_i$ between PC_i and this conformational difference vector is ${\chi }_i\equiv \left(\left|\overrightarrow{P{C}_i}·\Delta \overrightarrow{R}\right|/\left(\right|\overrightarrow{P{C}_i}|·\left|\Delta \overrightarrow{R}\right|\right))\ast 100\%$, where $\overrightarrow{P{C}_i}$ is the 3N-dimensional vector of the PC_i coordinates. The trajectory overlap ${\gamma }_i$ with the mode PC_i as a function of simulation time t is ${\gamma }_i\left(t\right)\equiv {\overrightarrow{PC}}_i·\delta \overrightarrow{R}\left(t\right)$, where $\delta \overrightarrow{R}\left(t\right)\equiv \overrightarrow{R}\left(t\right)-{\overrightarrow{R}}_{avg}$ is the 3N-dimensional vector difference between the trajectory’s instantaneous conformation $\overrightarrow{R}\left(t\right)$ of all C_α atoms and its trajectory average ${\overrightarrow{R}}_{avg}$.

Iterative root mean-square deviation fitting

We used an iterative procedure similar to that proposed by Damm and Carlson (19) to obtain a biased fitting toward the common rigid regions among all the frames in a trajectory. This superposition method relies solely on the trajectory data, without using any external information about the regions of interest. This is achieved by a succession of weighted fittings, during which the weights of the residues in the rigid regions are increased.

For an iteration i, a pairwise weighted fitting of all the selected frames (n) in the trajectory is computed, resulting in n(n − 1)/2 fits. The by-residue root mean-square deviation (RMSD) for residue j is then calculated as $RMS{D}_j=\sqrt{\sum {\left(d_{j_{p,q}}\right)}^2/\left(n\left(n-1\right)/2\right)}$, where $d_{j_{p,q}}$ is the distance between the residue j in fitted frames p and q. $RMS{D}_j$ is transformed into the new weight for residue j, $w_j$, using an exponential function $w_j=e^{-f\left[RMS{D}_j-RMS{D}_{\text{min}}\right]}$, where f is a scaling factor and $RMS{D}_{\text{min}}$ is the minimum of all by-residue RMSDs in iteration i. The new weights for all residues are then fed into the next iteration (i + 1). The first iteration has uniform weights (i.e., $w_{i=1,j}=1.0$) for all residues. For subsequent iterations (i > 1), the weights vary from residue to residue but are constant for all frames within a iteration. The iterative procedure is considered to be converged if the vector of weights, ${\stackrel{\rightharpoonup }{w}}_i$, which combines all the residue weights, deviates from ${\stackrel{\rightharpoonup }{w}}_{i-1}$ by less than a predefined Euclidean distance $\Delta w$. The iterative RMSD (iRMSD) is defined as the RMSD of two frames after weighted fitting with the converged $\stackrel{\rightharpoonup }{w}$.

For each MD trajectory in this study, we first determined the $\stackrel{\rightharpoonup }{w}$ using 800 equally distributed frames, i.e., taking a frame every 1.2 ns. The convergence criterion was chosen to be $\Delta w=0.01$, and was reached for both MD1 and MD2 after five iterations. We then used $\stackrel{\rightharpoonup }{w}$ to superimpose the frames of the trajectory taken every 0.24 ns (4000 frames in total; because the number of pairwise RMSD fits grows quadratically with the number of frames, we have to use a relatively smaller number of frames to determine the $\stackrel{\rightharpoonup }{w}$ first). As shown in Fig. S1, the iterative fitting results in higher root mean-square fluctuations (RMSFs) for the more-flexible loop regions and lower RMSFs for the more-stable TM regions than the nonbiased scheme. Thus, the iterative fitting is able to detect the residue flexibility along a trajectory in an automatic way without any prior knowledge.

The iterative fitting was implemented in the RMSDTT plug-in (20) for Visual Molecular Dynamics (VMD) (21), which uses a modified version to calculate by-residue RMSDs efficiently. The modified version of the plug-in is available from the authors.

Computation of binding enthalpies in the Na1 site

We evaluated the enthalpy of ion binding to site Na1 using an MM/PBSA approach (22) that was previously employed in studies of ion/substrate binding to the human serotonin transporter (23). In this approach, short-ranged van der Waals contributions to the binding free energy were computed with the MM force field for the interaction between the Na⁺ and the protein, using the INTE module in the CHARMM program (24). The electrostatic contribution (desolvation and complexation) to the binding free energy was obtained by solving the PB equations for each of the three states (ion only, protein only, and the ion/protein complex) using the PBEQ module in the CHARMM program, version c35b1. The PB equation was solved by using the focusing method with initial evaluation of the electrostatic potential on a coarse grid with spacing of 1.0 Å and subsequent computation with a fine grid with spacing of 0.5 Å. A set of CHARMM C27 charges were used together with atomic radii optimized for continuum electrostatics computations (25).

To evaluate the role of water molecules in the stabilization of bound cation, we performed two sets of simulations with implicit and explicit accounts for first-shell solvent molecules. For the data plotted as Protein, the receptor is the LeuT protein, including the Na⁺ bound in the Na2 site. For the data plotted as Protein+8water, the receptor additionally includes eight explicit water molecules that are the closest to the bound Na⁺ in the Na1 site. The selection of the eight explicit water molecules was updated for each frame. A dielectric constant (ε) of 2 was assigned to the receptor, and the membrane environment was modeled as a low dielectric continuum (ε = 2) with thickness of 40 Å. The choice of dielectric constant would obviously have an impact on the computations of the absolute binding free energies. However, in this work we aim to evaluate the time evolution of the binding energies rather than their absolute values.

MM/PBSA is most often used to obtain the solvation or binding free energy by averaging the computed values from an entire equilibrium trajectory. In this study, however, because the conformation of the Na1 binding site change over the timescales of our microsecond MD simulations, we report the running values (their time averages) of the binding enthalpies calculated with MM/PBSA. In this manner, we capture the fluctuations in the ion binding affinity associated with the conformational changes of the LeuT protein.

Computation of the potential of mean force for Na⁺ binding in the Na1 site

We carried out potential of mean force (PMF) calculations for Na⁺ binding to the Na1 site using the CHARMM program (24) for constructs including the substrate-bound occluded LeuT conformation, the 2A65-like frame F1, and the 3F3A-like frame F8 (see text). The reaction coordinate is the value of the Cartesian coordinate z that is perpendicular to the lipid bilayer and pointing toward the extracellular side. Harmonic biasing potentials with a force constant of 10 kcal/(mol·Å²) were applied to 109 windows using the MMFP module in CHARMM. The window size was 0.25 Å starting from −2.5 Å below the Na1 site to 24.5 Å above it (extracellular side). For each window, 1 ns of MD simulation was carried out using a timestep of 2 fs. The first 500 ps of the trajectory for each window were used to seed the initial configuration (moving the Na1 ion to the constrained position) and equilibration. The seeding procedure placed the ion in a wide range of positions within the EV and also enabled sufficient sampling along the reaction coordinate (Fig. S4). The weighted histogram method (WHAM) was then used to obtain the PMFs from the data of the last 500 ps simulations for each window (26). We computed the mean and standard error of the PMFs by blocking the data into three blocks. The reaction coordinates for the occluded state were shifted along the X axis so that the position of the center of Na1 site aligned with the 2A65-like frame F1. Each of the PMFs provides a relative free-energy profile for the system considered, with a long tail corresponding to an ion dynamics in the bulk phase. The bulk-like regions of the computed PMFs for F1, F8, and occluded LeuT display the following standard deviations (SDs): ±0.6 kcal/mol, ±0.1 kcal/mol, and ±1.0 kcal/mol, respectively. In the absence of constraints acting orthogonal to the ion escape path, the computation of absolute binding constants (K_d) for an ion is an undetermined problem (27–29), but the computed PMFs allow us to assess qualitatively the locations of quasi-stable sites along the escape pathway as well as their stability relative to the bulk region.

Results

Transition toward an outward-open conformation of LeuT

It has been suggested that the binding of Na⁺ would induce an outward-open conformation, thereby increasing access to the substrate binding site from the extracellular end (3,4,8). To determine the properties of such a Na⁺-stabilized open conformation, and to characterize the transition between the occluded and outward-open conformations, we carried out MD simulations starting from the occluded conformation (PDB: 2A65; red cartoon in Fig. 1 A) in the presence of Na⁺ in both Na1 and Na2, but without substrate bound in the S1 site. Overall, the conformational changes in two independent MD runs of 960 ns each (termed MD1 and MD2) indicate a transition from the starting occluded state to an outward-open conformation similar to that of the inhibitor-stabilized structure (PDB: 3F3A; blue cartoon in Fig. 1 A). This transition is characterized by a coordinated rearrangement surrounding the extracellular segments of TM6 and TM1 (TM6a and TM1b), especially by a prominent outward tilting of TM6a.

Figure 1.

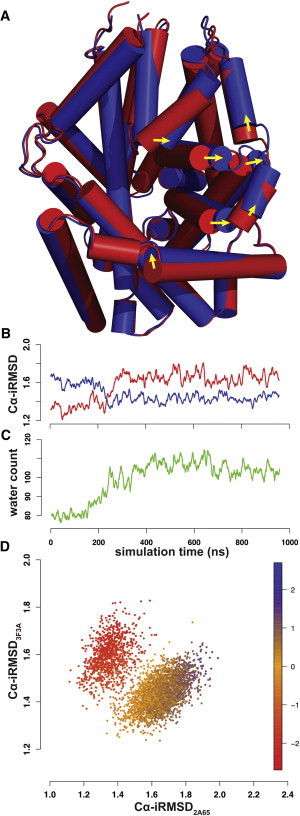
Analysis of the conformational transition in the Na⁺-only trajectory. (A) Superposition of the crystal structures of LeuT in the occluded (PDB: 2A65, red) and outward-open (PDB: 3F3A, blue) states. Major conformational rearrangements are indicated by arrows. (B) Time-dependent evolution of C_α-iRMSDs in the MD1 trajectory using both 2A65 (red) and 3F3A (blue) structures as references. (C) Time-dependent evolution of the number of water molecules in the EV along the MD1 trajectory. See Materials and Methods for the criteria used to determine that a water molecule is in the EV. The curves in panels B and C are smoothened over a 6-ns averaging window. (D) The C_α-iRMSD_2A65 is plotted against C_α-iRMSD_3F3A. Each point is color-coded by γ₁(t), the trajectory overlap with the PC1 (see Materials and Methods).

To analyze in detail the global conformational changes, we developed a new scheme of iterative fitting for the RMSD calculations (iRMSD) that can detect and attribute a relative weight according to the rigidity/flexibility of each residue position without prior specifications (see Materials and Methods). From the iRMSDs of the C_α atoms (C_α-iRMSD) with respect to the occluded and outward-open crystal structures (red and blue plots, respectively, in Fig. 1 B and Fig. S2 A), we observe similar trends of structural rearrangements in both MD1 and MD2, which bring the protein conformation closer to the 3F3A structure while deviating from the 2A65 structure. The rearrangements are accompanied by the occupation of the EV by an increasing number of water molecules (Fig. 1 C and Fig. S2 B).

To identify the intrinsic dynamic characteristics during the conformational transition, we performed a PCA on the MD1 and MD2 trajectories, and found that the first principal component (PC1) captures approximately κ₁ = 26% and 21% of the dynamics content, respectively (Table S1, Movie S1, and Movie S2). Of note, when C_α-iRMSD_2A65 is plotted against C_α-iRMSD_3F3A (Fig. 1 D and Fig. S2 C) and each data point is color-coded by the time-dependent PC1 trajectory overlap γ₁(t) (see Materials and Methods), the trajectory is separated into an occluded (upper-left) and an open (lower-right) cluster. Such a separation is more obvious in MD1, in which the transition takes >150–200 ns and is significantly slower than that observed in MD2 (Fig. 1 B and Fig. S2 A). Therefore, in the following analysis we focus on MD1, which provides more information on the transition.

In MD1, γ₁(t) has a large direct correlation with C_α-iRMSD_2A65 and an inverse correlation with C_α-iRMSD_3F3A, with Pearson correlation coefficients of 0.93 and −0.80, respectively (Fig. S3). This is in contrast to the weaker correlation between the two C_α-iRMSDs (correlation coefficient: −0.65). Thus, we chose the trajectory overlap γ₁(t) as the parameter to quantify the transition between the occluded and outward-open conformations, rather than the individual RMSD values, which are nondirectional.

Analysis of the global conformational rearrangements observed in the simulations can identify the specific structural elements that are the major contributors to the conformational transition. We identified such elements by computing along the entire trajectory the angles between helix axes of TM helix pairs (HAs), and the distances between their centers of mass (HDs). These measures were subjected to a correlation analysis with the transition parameter γ₁(t), and the top 40 HAs and HDs most correlated with PC1 were mapped on the structure (Fig. 2). Several segments near TM1b and TM6a emerge as the structural regions most prominently involved in the opening transition (Fig. 2 D, Table S2). Specifically, the changes within the TM6a-EL3-TM2a-TM1b region cause an increase in the distances of these structural elements from TM3, TM8, and TM10, whereas their distances from TM11a are decreased (Fig. 2 D). The overall trend of the transition is thus characterized by these movements in the TM6a-EL3-TM2a-TM1b region as they distance themselves from the relatively immobile group of TM3, TM8, and TM10 and enlarge the EV; the inward tilt of TM11 partially fills in the enlarged EV (Fig. 2 A).

Figure 2.

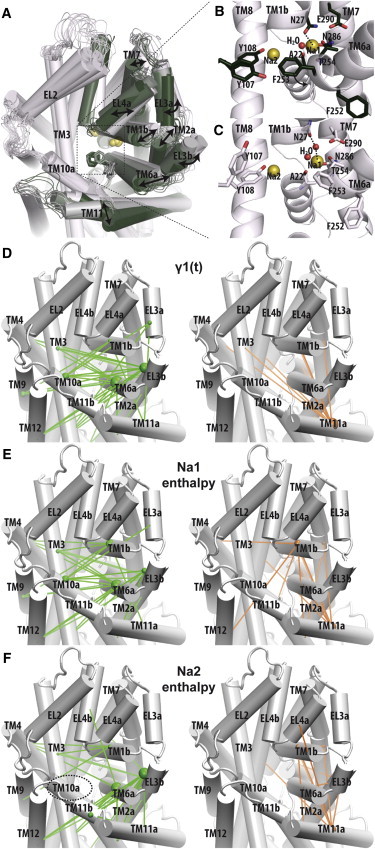
Structural elements correlated with the conformational changes along the first principal component vector (PC1). (A) The conformational transition observed in the MD1 simulation is represented as a superposition of 15 frames, selected equidistantly along the γ₁(t) of MD1, from the occluded (dark green) to the outward-open conformation (gray). The eigenvectors of PC1 of MD1 and MD2 are also visualized in Movie S1 and Movie S2, respectively. (B and C) Zoomed-in views of the region near the Na1 site in the most occluded (B) and most open (C) frames in panel A. Water molecules are represented as red beads. In panel C, nonbonded interactions between Asn-27 and Na⁺ are marked by dashed lines. (D) Distribution of the HAs and HDs that are correlated with the γ₁(t) of MD1. The top 40 HA or HD segment pairs that correlated directly (positive values, green) and inversely (negative values, orange) are mapped onto an outward-open LeuT model viewed from the extracellular side. The bars connect the centers of mass of the segment pairs; the radii of the spheres are drawn in proportion to the frequencies of the involved segments. The most frequently involved segments are EL3b and TM6a (green) and TM11 (orange). (E and F) Distributions of 40 HAs and HDs that are most correlated with the Na1 and Na2 binding enthalpies, respectively. The viewing angle, representation, and color schemes are the same as panel A. No HA or HD that is correlated with the Na2 enthalpy involves TM10a (dotted circle in F). This is a distinct difference from the correlation patterns observed for the Na1 enthalpy and γ₁(t). Correlation coefficients are given in Table S2.

We find that the large-scale transition described above is triggered by the rearrangements of the interaction network near the Na1 and S1 sites, in response to the absence of the S1 substrate. Comparing the two frames with the lowest and highest values of γ₁(t), which represent respectively the most occluded and most outward-open frames along the PC1 (Fig. 2 B and C), we observe a rearrangement of the aromatic cluster formed by residues Tyr-107 and Tyr-108 of TM3, and Phe-252 and Phe-253 of TM6, on top of the S1 site as we described previously (14). Thus, the substrate in the S1 site restrains the Phe-253 side chain in the trans rotamer through a hydrophobic-aromatic interaction, and this occludes the S1 site. However, in the absence of substrate, the Phe-253 side chain rotates away from Tyr-107 and Tyr-108, exposing the S1 site. The rearrangement induces changes of the Na1 site through the intertwined interaction networks near the S1 and Na1 sites, i.e., Phe-253 is immediately adjacent to the Na1-coordinating Thr-254, and the substrate in the S1 site interacts with the Na1 site directly. In the absence of substrate, a water molecule from the S1 site interacts with the Na1 site, as shown in both frames (Fig. 2 B and C), thereby replacing the carboxyl group of the substrate. In the outward-open frame, a second water molecule mediates the interaction of the Na⁺ with the Asn-27 that has rotated away (Fig. 2 C). In MD1, the configuration changes of Tyr-107, Tyr-108, Phe-252, and Phe-253 finish by ∼280 ns; the impact gradually propagates to the extracellular region; and the opening of the EV does not reach its full extent until after ∼400 ns (compare Fig. 4 C with Fig. 1 C).

Figure 4.

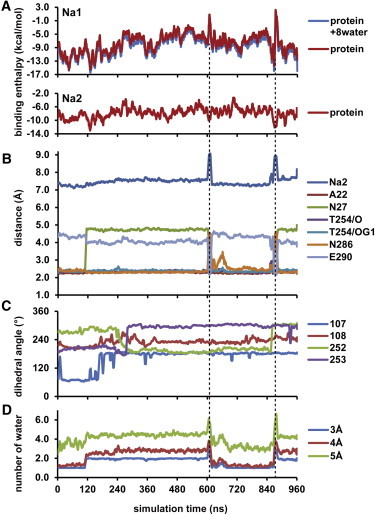
Evolution of the Na1 and Na2 binding enthalpies and the associated changes of structural elements in MD1. (A) Na⁺ binding enthalpies computed using MM/PBSA for the Na1 and Na2 sites, with a snapshot taken every 0.24 ns along the entire MD1 trajectory. Protein and Protein+8water (see text) are plotted as blue and red lines, respectively. (B) Evolution of the distances between Na1 and the indicated elements, including Na2, all of the Na1 coordinating residues, and Glu-290. (C) Evolution of the χ1 rotamers of the aromatic cluster at the extracellular gate of the S1 substrate binding site (Tyr-107, Tyr-108, Phe-252, and Phe-253 (14)). (D) Evolution of the number of waters within the indicated distances of Na1. The plots shown in all panels are moving averages of 6 ns. The zoomed-in view of panel B for the peak periods near 610 and 875 ns are shown in Fig. S5.

Calculations of Na⁺ binding to Na1 from the extracellular side lead to the identification of a nearby quasi-stable Na⁺ site

To ascertain whether Na1 maintains significant affinity for Na⁺ even in the absence of the substrate, we obtained PMF profiles for Na⁺ binding to the Na1 site starting from three states (Fig. 3 A): the most occluded (2A65-like) and outward-open (3F3A-like) Na⁺-only frames along the PC1 of MD1 (see above), and as a control, the occluded model with the bound substrate, Leu. Although the well depths on these profiles are not the exact standard state binding affinities (27–29), they enable a qualitative comparison of the binding strengths.

Figure 3.

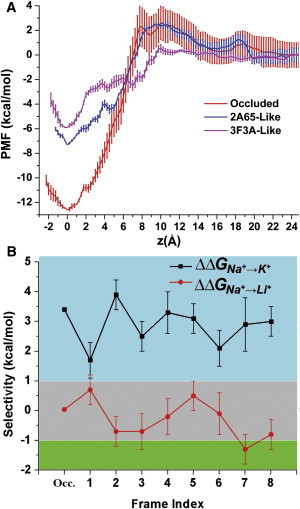
Na⁺ binding and selectivity in the Na1 site. (A) PMF profiles for Na⁺ moving from the Na1 site to the extracellular side. The profiles are shown for the occluded state with bound substrate (red), Na⁺-only 2A65-like (blue), and 3F3A-like (magenta) frames. (B) Na⁺/K⁺ and Na⁺/Li⁺ selectivity. The selectivities for the ion in the Na1 site of the occluded state of LeuT with substrate and both ions bound (occluded (Occ.) data are from Caplan et al. (7)) and eight frames (F1–F8) selected from the MD1 trajectory (see text). By definition, positive values of ΔΔG_Na⁺_→X⁺ (where X⁺ represents K⁺ or Li⁺) indicate that the conformation is selective for Na⁺ over X⁺. Thus the blue region is Na⁺ selective, the gray region corresponds to an ambiguous selectivity between Na⁺ and ion X⁺, and the green region corresponds to X⁺ selective sites. The SDs of ion selectivity are plotted as error bars.

The results for the 3F3A-like open state show that a Na⁺ ion can still bind to the Na1 site from the extracellular bulk with minor free-energy barriers, and that the Na1 site is a fairly favorable binding site with a PMF well depth of −5.9 ± 0.1 kcal/mol. However, this minimum is much shallower compared with the PMF calculated with the substrate bound in the S1 site. Thus, in the presence of Leu substrate, the minimum around the Na1 site is much deeper (−12.6 ± 1.0 kcal/mol), indicating a well-defined ion binding site. The 2A65-like Na⁺-only frame has a minimum of −7.3 ± 0.6 kcal/mol, which is ∼1.4 ± 0.6 kcal/mol deeper than the 3F3A-like Na⁺-only frame and still 5.3 ± 1.2 kcal/mol shallower than the occluded state with the bound Leu substrate. On the other hand, for an extracellular Na⁺ binding event to the Na1 site, the 2A65-like Na⁺-only frame shows a barrier of ∼2.4 kcal/mol, which is similar to that in the occluded state (∼2.6 kcal/mol). This reflects the similarity between the conformation of the transporter in the 2A65-like Na⁺-only frame and that in the occluded state with bound substrate Leu.

We note that the PMF region between −2 and +5 Å around the minima are relatively flat (with a free-energy change of <3 kcal/mol) for both Na⁺-only frames, which indicates a loose binding site and suggests the possibility that a quasi-stable binding location for Na⁺ may exist near the Na1 site. Indeed, in the trajectories of the umbrella sampling simulations (Fig. S4), the quasi-stable binding location near Na1 site and Glu-290 (defined as the Na1′ site) is very frequently visited by the Na⁺ ion. We explored this further in a set of 30 MD runs, from each of three points with high Na1 enthalpy and/or longer Na1–Na2 distance: 606.96, 878.52, and 960 ns of MD1 (see below). In each set of 10 MD runs, each run was started with a different random number seed. Of interest, in one of the trajectories restarted from 878.52 ns, the Na⁺ bound in Na1 is shifted upward and remains stable for at least 60 ns in a location ∼2 Å more extracellular than the Na1 site (Na1′ site). In this location, the Na⁺ ion is in direct interaction with the negatively charged Glu-290 while it also coordinates with the side chain of Thr-254.

Na⁺/K⁺ and Na⁺/Li⁺ ion selectivity of Na1 in the transition

To evaluate the conformational dependence of the Na1 binding selectivity along the transition, we performed ion selectivity computations using eight representative frames of the MD1 trajectory (F1–F8) as the starting configurations. These frames were selected to have equidistant and ascending values of γ₁(t) so as to cover the range along the entire trajectory. Thus, F1 and F8 (shown in Fig. 2, B and C) are the most occluded and outward-open frames along the PC1, respectively, as mentioned above.

Fig. 3 B and Table S3 show that the selectivity of Na⁺ over K⁺ in five of the eight frames (F2, F4, F5, F7, and F8) is comparable to that observed in the occluded LeuT structure with bound substrate (3.4 kcal/mol), but it is slightly reduced in F1, F3, and F6. Overall, the Na1 site in all of the selected frames remains robustly selective for Na⁺ over K⁺, showing that the Na⁺ preference of the Na1 site is preserved even in the absence of the negatively charged carboxylate group of a substrate. For the Na⁺ over Li⁺ selectivity, however, most of the eight frames indicate ambiguous selectivity at best, in similarity to the case of occluded LeuT structure with bound substrate (7). Taken together, the results indicate that the absence of substrate does not have a major impact on the selectivity of Na⁺ over K⁺ or Li⁺ in the Na1 site.

Enthalpies of Na⁺ binding to the Na1 site moderately correlate with the extent of completion of the transition toward the outward-open conformation

To characterize the changes in Na1 and Na2 affinities for Na⁺ along the transition, we applied two schemes for calculating binding enthalpy. In the first scheme, denoted as Protein, all of the water molecules were treated implicitly. In the second scheme, termed Protein+8water, eight water molecules closest to the bound Na⁺ were included explicitly and all other water molecules were treated implicitly. Although in some time spans the calculated enthalpy values are slightly lower for Protein+8water than for Protein, the two time series show very similar trends (Fig. 4 A). Therefore, we applied only the Protein scheme for the calculation of Na2 enthalpy.

Overall, along the entire MD1 trajectory, the Na1 binding enthalpy is largely in the negative range (Fig. 4 A). This is consistent with the results from the PMF calculations (Fig. 3 A) showing that even in the absence of the substrate, Na⁺ still has significant affinity for the Na1 site. In comparison, the Na2 enthalpy is entirely in the negative range and fluctuates less than the Na1 enthalpy. Of note, at ∼878 ns, there is a strong positive spike in the Na1 binding enthalpy values (ΔH = 4.3 ± 3.1 kcal/mol) for a duration of ∼10 ns. Similarly to a smaller one around 610 ns, this spike is associated with a temporary dissociation of Na⁺ from its coordinating residues, except for Thr-254 (Fig. 4 B and C and Fig. S5). The resulting upward movement of the ion produces a direct interaction with Glu-290 (Fig. 4 D).

The coordination of Asn-27 to Na1 is mostly indirect, through water molecules, and thus seems to be the weakest among all Na1 coordinating residues (Fig. 4 B). The Asn-27 side-chain rotation correlates well with the number of water molecules coordinating the Na⁺ in Na1, and also with the γ₃(t) of MD1. Of interest, in comparison with PC1, PC3 shows limited tilting of TM6a and TM1b, and TM7 and EL4a have significant rearrangements that are not obvious in PC1. These rearrangements are likely due to the weakened association between TM1b and TM7, as a result of the rotation of Asn-27 side chain away from Na1 (Fig. S3 and Movie S3). In general, an increase in partial hydration of Na1 has a disrupting effect on Na⁺ stability (compare Fig. 4 A and 4 D), but configurational changes in the second layer of residues surrounding the Na1 site can lower the enthalpy values and thus increase the affinity (e.g., among the residues in the aromatic cluster, the rotamer of Phe252 is moderately correlated with the Na1 binding enthalpy, with a Pearson coefficient of −0.61; indeed, the rotation of its χ1 rotamer back to a gauche position, as in the occluded state, is likely responsible for the decrease of enthalpy values after ∼870 ns (compare Fig. 4 A and 4 C).

To establish the relation between the Na1 and Na2 binding affinities and the conformational changes critical to the transition, we evaluated the correlation between the binding enthalpies and the conformational observables on both the global scale (γ₁(t)) and the local scale (HAs, HDs, and distances to Na1). We found γ₁(t) to be moderately correlated with Na1 enthalpy values, but significantly less correlated with Na2 enthalpy values (Pearson coefficients: 0.65 and 0.43, respectively). Similar differences were found for the local observables (Table S2 and Fig. S3). When mapped onto the structure, the 40 most correlated HAs/HDs for Na1 enthalpy (Fig. 2 E) are distributed in a pattern similar to those identified in the PC1-correlation analysis (Fig. 2 D), but the similarity is less obvious for those obtained for Na2 enthalpy (Fig. 2 F). Of interest, the extracellular segment of TM10, TM10a, which is located at the center of the EV, does not appear in any of the top 40 Na2-enthalpy-correlated HAs and HDs (dotted circle in Fig. 2 F). In contrast, five HA/HDs involving TM10a are highly correlated with both Na1 enthalpy and γ₁(t) (Table S2). Thus, the conformational changes that play a leading role in the opening transition in LeuT’s EV are more associated with changes in the Na⁺ binding affinity for the Na1 site than for the Na2 site (note that as a higher enthalpy value corresponds to lower affinity, the direct correlation between Na1 enthalpy values and γ₁(t) suggests an inverse correlation between Na1 affinity and γ₁(t); see Discussion).

Role of Na1 in the transition toward an outward-open conformation

The results described in the previous sections indicate the tendency of the transporter molecule to transition toward the outward-open conformation in the absence of substrate, and with Na⁺ bound at both Na1 and Na2 sites. To further dissect the impact of Na⁺ binding in the Na1 site on the conformation adopted by the transporter, we carried out four MD simulations in the absence of Na⁺ in Na1 (termed no-Na1). Starting from the 60 and 720 ns points of MD1 (corresponding to the relatively occluded and outward-open states in the Na⁺-only configuration; see Fig. 1), the no-Na1 configuration was simulated with either deprotonated (480 ns each from the two points) or protonated (360 ns each) Glu-290. We chose to consider the Glu-290 protonation state in our Na⁺-only simulations because the Na1 is always in close proximity to the negatively charged Glu-290, and the absence of Na1 was found to result in the protonation of Glu-290 in the inward-open conformation (11).

To evaluate the impact of various substrate, ion, and charge combinations on the global conformation from the results of these MD simulations, we measured the extent of outward-open character by the number of water molecules in the EV (i.e., more water corresponds to a more outward-open conformation). By using similar lengths of MD trajectories to calculate and compare the normalized distribution of the number of waters, we found that in the absence of Na1, the transporter protein is slightly more outward-open than in the Na⁺-only configuration with Na⁺ bound at both Na1 and Na2 sites (Fig. 5 A). The absence of Na1 results in more outward tilting of TM7 and EL4a, reminiscent of the PC3 motion of MD1 (see above, Movie S3), which is correlated with the extent of hydration near the Na1 site (Fig. S3). However, with the negative charge of Glu-290 eliminated by protonation, the transporter protein becomes less outward-open than the form with deprotonated Glu-290. This is likely due to the dehydration effect of the protonated Glu-290 on the Na1 site vicinity in the absence of bound Na⁺ (Fig. S6). We observed consistent trends from both starting points, but note that the impact of Glu-290 protonation was more obvious when the simulation was started from a more occluded state (Fig. 5 A).

Figure 5.

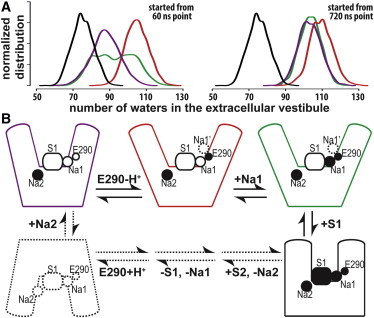
Impact of Na⁺ binding and Glu-290 protonation on the extent of the outward-open character of LeuT conformations. (A) The extents of outward-open character of various configurations are reflected by the normalized distributions of the number of water molecules in the EV. Compared with the occluded state with S1-bound substrate (black, based on a 230 ns MD trajectory described previously (3,32)), the Na⁺-only configuration (green, 60–420 and 720–960 ns periods of MD1 for the left and right panels, respectively) has ∼30 more waters in the EV, and the absence of Na1 (red, 480 ns) further opens the EV slightly. The removal of the charge of Glu-290 (purple, 360 ns) renders the EV less outward-open. Consistent trends are observed from the no-Na1 simulations started from both 60 (left) and 720 (right) ns points of MD1 (see text). The multiple peaks of the green curve in the left panel indicate that the MD1 is in a conformational transition in the 60–420 ns period. The distribution plots were generated from the water count data using a Gaussian kernel density estimate (density function in R (18)). (B) The roles of Na⁺ binding and Glu-290 protonation in the control of conformational dynamics of the transport cycle. The configurations are in the same color code as in panel A.

Discussion

The Na⁺-only MD simulations initiated from the crystallographically determined occluded state of LeuT produced a detailed mechanistic picture of global conformational rearrangement of the transporter molecule. They show that the opening of the EV is achieved in both trajectories (MD1 and MD2) by a series of structural reconfigurations near the substrate and Na1 sites, which then trigger a series of discrete but coordinated rearrangements within the TM6a-EL3-TM2a-TM1b cluster, resulting in a distancing from TM3, TM8, and TM10. The LeuT conformation resulting from these changes exhibits the main characteristics of the outward-open form of the transporter (4,14) and is similar to that stabilized by an inhibitor Trp (PDB: 3F3A). This leads to the conclusion that Na⁺ binding alone, which is shown by this study to be possible with high selectivity and significant affinity in the absence of substrate, biases the transporter toward an outward-open conformation that is ready for the binding of substrate.

While this work was being prepared, the crystal structure of the LeuT mutant Y108A (PDB: 3TT1) was released (30). This structure was determined in the absence of substrate, but with bound Na⁺ in both the Na1 and Na2 sites. It is very gratifying to report that the outward-open conformation in the crystal structure is very similar to the Na⁺-only conformation identified computationally and described here, and partially as well in an earlier documentation of the effect of Na⁺ (14). Thus, in contrast to the 3F3A outward-open structure, the 3TT1 structure in the absence of any bound ligand shows the side chain of Phe-253 in TM6 to be rotated away from Tyr-107 and Tyr-108/Phe-108 of TM3, thus exposing the S1 site, just as observed in our simulations. However, the MD simulations described here provide in addition a dynamic picture of the transition to an outward-open conformation that exhibits some subtle differences from both the 3F3A and 3TT1 structures: In those two crystal structures, TM1b tilts away from the center of the TM bundle in parallel with TM6a, whereas in the simulations, although TM1b can tilt as far as observed in the crystal structures, TM6a is more mobile than TM1b and is able to move farther away from the center of the TM bundle (Fig. 2 A). Using the F8 frame as a representative snapshot (its all-Cα RMSD values with respect to the 3F3A, 3TT1, and 2A65 structures are 1.65 Å, 1.56 Å, and 1.94 Å, respectively), a superposition on the Cα atoms of TM3 and TM8 shows that the Cα atom of Gly-242 at the extracellular tip of TM6a is positioned 3.4 Å more outward in the F8 frame than in the 3F3A structure. Of interest, in the Na⁺-only 3TT1 structure, this outward tilt is also larger than in the 3F3A structure, with a value of 1.3 Å (as a comparison reference, the difference in the position of Gly-242 between the 3F3A structure and the occluded 2A65 structure is 2.9 Å). Thus, the parallel outward tilted orientations of TM1b and TM6a revealed by the 3F3A and 3TT1 structures represent a stable configuration, but the detailed simulations reveal a dynamic relationship between these two core TMs that is not evident from the structures alone. We find that TM6a can move away from TM1b and the TM bundle in the conformational transition. In addition, the rearrangements of TM1a-TM1b and TM6a-TM6b are among the structural elements that exhibit the best correlation with the changes in the Na1 and Na2 enthalpies, respectively (Table S2). This suggests that the TM1 and TM6 conformations are tuned by the Na⁺ binding to sites positioned in the unwound regions of these TMs, arguing against rigid-body movements for TM1 and TM6 (31). However, symmetrical features as proposed by Forrest and Rudnick (31) are evident in the conformational transition, with the rearrangement of TM6a away from the bundle observed here resembling the movement of its symmetric counterpart TM1a revealed from simulation and single-molecule fluorescence resonance energy transfer measurements (3,32), and the predicted outward-tilt of TM1a is indeed observed in the recently published inward-facing structure (30).

That Na⁺ binding to the Na1 site is energetically favorable and selective (over K⁺), even in the absence of S1 substrate, is shown by our results from the PMF calculations, as well as the time series of binding enthalpies along the transition, and the free-energy simulations. These results suggest the possibility that Na⁺ binds in the Na1 site in the absence of substrate, albeit with lower affinity than in the presence of substrate. However, the ion selectivity of the Na1 site calculated along the transition between occluded and outward-open states indicates differences in this binding ability when Na⁺ is compared with K⁺ or Li⁺. Thus, for Na⁺/K⁺, the selectivity for Na⁺ is maintained along representative frames of the whole transition, which is an important finding in view of the considerable concentration of K⁺ in the physiological environment. The conservation of Na⁺/K⁺ selectivities upon removal of the ion-coordinating Leu substrate is intriguing. Previous studies (33,34) suggested that the removal of a high-field coordinating ligand, such as the charged carboxyl group substrate, from an ion binding site might lead to a reduction in the selectivities for Na⁺ over K⁺. Instead, the selectivity for Na⁺ over K⁺ in the Na1 site for many of the studied frames from the Na⁺-only trajectory is only slightly decreased. An ion coordination analysis of the FEP/MD trajectories collected for the alchemical transition of Na⁺ ↔ K⁺ bound in the Na1 site suggests that the carboxyl group of Glu-290 has a strong impact on the coordination of the bound ion and may contribute to the selectivity.

In contrast, we find for Na⁺/Li⁺ that the selectivity is rather ambiguous. This is not entirely unexpected, as Caplan et al. (7) showed that the Na⁺/Li⁺ selectivity is mostly achieved by the coupling effect between the Na1 and Na2 sites. Therefore, we conclude that the Na⁺ over K⁺ and Li⁺ selectivities of the Na1 site in the absence of the substrate remains largely the same as in the presence of the substrate.

We found that the conformational transition to outward-open is inversely correlated with the changes in Na1 binding affinity but only weakly correlated with Na2 affinity. Thus, it is likely that the Na⁺ bound at the Na2 site plays a critical role in maintaining the overall outward-open conformation in the absence of the substrate, while the presence of Na1 modulates the extent of outward-open character, with the absence of Na1 making the conformation slightly more outward-open (Fig. 5 A). Consistently, the release of Na2 (but not Na1) has been shown to be required for the conformational transition to inward-open (3,8). It is tempting to speculate that binding and release of Na⁺ in the Na1 and Na2 sites may play symmetrical roles in the outward- and inward-open transition. However, the locations of the Na1 and Na2 sites are not entirely symmetrical in the pseudo-inverted repeats, which may explain the differences in their coupling to the directional translocation of substrate.

The distinct roles that Na1 and Na2 play in the conformational transitions relevant to LeuT function are further underscored by the connection between Na⁺ binding in the Na1 site and the protonation state of Glu-290. In a previous study (11), we found that the absence of Na1 resulted in the protonation of Glu-290 in the inward-open conformation. Indeed, we find here that the removal of both the Na1-bound Na⁺ and the negative charge at Glu-290 renders the conformation less outward-open, especially when the simulation is started from a relatively more occluded state. This is consistent with the role of neutral (protonated) Glu-290 in forming the inward-open conformation. In addition, because Glu-290 is located along the potential entry route of Na⁺ toward the Na1 site (Fig. S4), the negatively charged Glu-290 is likely responsible for the broadened attraction to the Na1 site (i.e., the formation of a quasi-stable binding location near the Na1 site) and for providing part of the driving force for Na1 binding.

Our current mechanistic understanding of the sequence of (de)protonation and Na⁺ binding is summarized in Fig. 5 B. Starting from the apo inward-open state, Na⁺ binds at the Na2 site first and steers the transporter toward an outward-open conformation. The subsequent deprotonation of Glu-290 further opens up the EV and attracts Na⁺ binding at the Na1 site. The entry of the S1 substrate is facilitated by the presence of Na1, which forms a direct stabilizing interaction with the charged substrate. The combined impact of Na⁺ binding in the Na1 site and substrate binding in the S1 site induces the transporter to transition toward an occluded state. The Na2-only states (purple and red in Fig. 5 B), however, are likely only transient states in the physiological condition.