The Influence of Cell Cycle Phase on ADC in Synchronized Cells Detected Using Temporal Diffusion Spectroscopy

Abstract

The relationship between the apparent diffusion coefficient (ADC) of tissue water measured by magnetic resonance methods and the physiological status of cells is of particular relevance for better understanding and interpretation of diffusion-weighted MRI. In addition, there is considerable interest in developing diffusion-dependent imaging methods capable of providing novel information on tissue microstructure, including intracellular changes. To this end, both the conventional pulsed gradient spin echo (PGSE) methods and the oscillating gradient spin echo (OGSE) method, which probes diffusion over very short distance (<< cell size) and time scales, were employed to measured ADC of synchronized packed HL-60 cells at 7T. The results show that the PGSE method with relatively long diffusion times does not detect changes in ADC when structural variations arise during cell division. On the contrary, the OGSE method can detect and quantify major changes in intracellular organization that occur during mitosis by appropriate choice of gradient frequency. Cell structural parameters, including cell size, intracellular diffusion coefficient and surface-to-volume ratio were also obtained by fitting the OGSE data to simple analytical models. These OGSE features may be used in diffusion-weighted MRI to create parametric maps that may be useful for detecting cancer or changes caused by treatment.

INTRODUCTION

Measurements of the apparent diffusion coefficient (ADC) of water using nuclear magnetic resonance methods provide a unique approach for characterizing the micro-structure of biological tissues in vivo. Diffusion imaging is important in both clinical practice and in pre-clinical research and provides biophysical information that is correlated with the underlying pathophysiological state of tissues (1,2). However, the factors that influence ADC of tissue water remain imperfectly understood. Although cell density and cell membrane permeability may be important factors affecting ADC at long diffusion times (3,4), the values of ADC at short diffusion times may be influenced strongly by intracellular structures and their changes (5,6). Moreover, there is considerable potential value in imaging methods capable of detecting intracellular changes in tissues. Dynamic variations of major intra-cellular structures may reflect the physiological states of cells, and some of these, such as nuclear size, may be characteristic of specific diseases. For example, there is massive synthesis and rearrangement of intra-cellular macromolecules and organelles when cells undergo division, as previously reported for relaxation times (7,8). Moreover, proliferating tumors usually contain a much higher fraction of cells that are in active cell division phases, such as the S (synthesis) and M (mitosis) phases, than normal tissues, so for a full understanding of the diffusion properties of tumors it is necessary to understand how the changes that occur inside cells in different phases affect the ADC (8,9).

According to Einstein’s relation, for free diffusion in one dimension,

$$L=\sqrt{2D{t}_D}$$ [1]

where D is the self-diffusion coefficient and L is the characteristic diffusion length, the mean distance of migration of water molecules in time t_D. Thus, in free space, diffusion measurements probe distance scales that increase in direct proportion to the square root of the diffusion time, and each measurement of D via NMR methods inherently incorporates a distance and time scale over which D is evaluated. From Eq.[1], water molecules with values of D ≈ 2 µm²/ms will on average diffuse ~10 – 15 microns in times of 24 – 54 milliseconds, the typical range of diffusion times used in conventional pulsed gradient spin echo (PGSE) measurements in vivo. Because these times and distances are of the dimensions of cells or larger, and because cell membranes are not perfectly permeable, such techniques are sensitive to cell density (cellularity) and, in some tissues, to structural anisotropy. Sub-cellular structures have much shorter characteristic dimensions, so the diffusion time required for detecting the effects of intracellular structures should be considerably shorter. Conventional PGSE methods use relatively long diffusion times because of hardware limitations and the need to increase gradient strength and slew rate to achieve sufficient signal modulation with short pulses (5,10). The ADC obtained by the PGSE method then actually reflects an averaged diffusion property, in which diffusion effects are integrated over different length scales, and in cellular systems they cannot distinguish effects that are specific to sub-cellular dimensions from those at that arise at larger scales. An alternative approach for achieving short diffusion times is the oscillating gradient spin echo (OGSE) method (11), which replaces the bipolar diffusion gradients of PGSE sequences with cosine-modulated waveforms at specific frequencies. The OGSE method at moderately high frequency has the ability to probe much shorter diffusion times and intra-cellular structure (6,11), and measurements at different frequencies provides a temporal diffusion spectrum (12) that can be analyzed to reveal cellular parameters of interest (13).

Cultured cells at sufficient high cell density provide a controllable model system for simulating diffusion in tissues (5,14–17), and cells may be synchronized in different stages by various means. In the current study, water diffusion within three types of synchronized HL-60 cells was measured with both the PGSE and OGSE methods. Type I samples were synchronized to S phase with treatment of thymidine, type II were in a mixed G2/M phase with six hours recovery from type I samples. Type III were synchronized to M phase using Nocodazole (18). Cell size and cell density were controlled for all types of samples by preparing cells under the same conditions, but there was still an ADC difference between them that was apparent only at short diffusion times (high frequencies in OGSE), and which was not detectable by PGSE methods. This difference presumably arises from intracellular structural variations between the different cell phases. By fitting the OGSE temporal diffusion spectra to appropriate simple analytical models, the mean cell size, intracellular diffusion coefficient and cellular surface-to-volume ratio (S/V) were estimated. These results may assist in better understanding the relationship between ADC with different diffusion times and the physiological states of cells, which may be of more general importance for the interpretation of MR diffusion measurements.

MATERIALS AND METHODS

Diffusion Models

Temporal Diffusion Spectroscopy

In a previous study, we derived analytical expressions for the ADCs obtained by the cosine-modulated OGSE method in systems of different geometry, namely

$$\text{ADC}(f)=8{\pi }^2{\displaystyle \sum _k\frac{B_k{a}_k^2{D}_{\text{in}}^2{f}^2}{\delta {(a_k^2{D}_{\text{in}}^2+4{\pi }^2{f}^2)}^2}}\left\{\frac{(a_k^2{D}_{\text{in}}^2+4{\pi }^2{f}^2)\delta }{2a_k{D}_{\text{in}}}-1+\exp (-a_k{D}_{\text{in}}\delta )+\exp (-a_k{D}_{\text{in}}TE/2)(1-\cosh (a_k{D}_{\text{in}}\delta ))\right\},$$ [2]

where D_in is the intracellular diffusion coefficient, δ is the diffusion gradient duration, TE is the echo time and a_k, B_k are structure dependent constants and can be found in Ref. (13) for some simple geometries, including parallel planes, cylinders, spheres and spherical shells. The presence of a single homogeneous diffusion coefficient D_in in Eq.[2] assumes that all individual microscopic populations of water molecules exhibit the same RMS displacement independent of the population's location within the simple geometry or actual biological cell. This will be true (a good approximation) at long diffusion times (low frequencies) where all microscopic populations of water molecules can be expected to have explored the full space and, thus, have the same RMS displacement. However, the OGSE method with relatively high frequencies (short diffusion times) is sensitive to the influence of intracellular structures, such as nuclei (6), so Eq.[2] may fail to predict the diffusion behavior at high frequencies (see below).

Surface-to-volume ratio and effective diffusion time

It has been shown that when the diffusion time is short, using the PGSE method, the ADC of water inside a porous medium with smooth boundaries is dependent on the surface-to-volume ratio (S/V) of the pores and the diffusion time t_D (19). An extension shows such dependence holds for permeable membranes in packed erythrocytes (5). For the OGSE method, the relatively long continuous gradient waveforms violate the short gradient approximation and thus there does not exist a single equivalent diffusion time. Parsons et al. introduced the effective diffusion time Δ_eff and obtained (12)

$$\frac{\mathit{\text{ADC}}({\mathrm{\Delta }}_{\text{eff}})}{D_0}=1-\frac{4}{9\sqrt{\pi }}c\frac{S}{V}\sqrt{D_0{\mathrm{\Delta }}_{\text{eff}}}-A\frac{S}{V}{D}_0{\mathrm{\Delta }}_{\text{eff}}+O\left[{\left(D_0{\mathrm{\Delta }}_{\text{eff}}\right)}^{3/2}\right],$$ [3]

where D₀ is the free diffusion coefficient of the medium, and A and c are coefficients that vary between systems. Note that an apparent S/V can be extracted from Eq.[3] to describe the average dimension of restricting structures inside biological tissues at short diffusion times. This apparent S/V may not be directly used to measure cell size because of the influence of intracellular structures, but it still provides a valuable parameter to describe the microstructure of tissues.

For the cosine-modulated OGSE method, the effective diffusion time in free space is given by (12)

$${\mathrm{\Delta }}_{\text{eff}}=\frac{1}{4f},$$ [4]

where f is the frequency of the oscillating gradient waveform. The correction factor c in Eq.[3] is dependent on various parameters, including system geometry, gradient waveforms and the frequencies in use, and it is not easily defined analytically. Computer simulations using a finite difference method (20) were performed to obtain c numerically. For a spherical geometry and the experimental parameters used in the current work, c was found to be 0.73.

Cell preparation

HL-60 cells were cultured with RPMI 1640 medium supplemented with 10% fetal calf serum (FCS), 50 U/ml penicillin and 50 µg/ml streptomycin in a humidified 37°C incubator maintained at 5% CO₂. Cells were spread every three days by 1:10 dilution and cell density was limited to be no more than 0.8 ×10⁶ cells/ml. For each experiment, three types of samples were prepared. For type I cells, HL-60 cells were synchronized to S phase by treating log-phase cells (0.4×10⁶ cells/ml) with 50 µM thymidine for 24 hours, then fresh media containing 50 µM thymidine was added for another 24 hours. For type II (G2/M phase) cells, the arrested S phase cells were cultured for an additional 6 hours in full growth medium after removing and washing out thymidine (21). For type III cells, HL-60 cells were synchronized to M phase by treating with 100ng/ml Nocodazole for 24 hrs. All cell samples (each with a total 30×10⁶ of cells) were collected, washed with PBS, and transferred into 200 µl PCR tubes. The cells were then pelleted by centrifugation with a Bio-rad microcentrifuge at 7000rpm for 6 minutes. The supernatant medium was removed carefully by suction without disturbing the packed cell pellet. The cell pellets were directly used for NMR diffusion experiments. Data from the PGSE measurements of all cell samples of each cell type showed little variation, indicating cell size and density were relatively consistent.

Cell cycle distribution was determined by flow cytometry. Briefly, aliquots of washed cell samples used for MRI experiments were resuspended with PBS/0.1% BSA, fixed with 3x volume of cold (−20°C) absolute ethanol and kept at −20°C for at least one hour. The cells were then spun down and washed twice with PBS, and resuspended with propidium iodide (PI) staining solution (3.8mM sodium citrate, 50ug/ml PI, 0.5mg/ml RNase A in PBS), and incubated over 3 hours at 4°C before FACS analysis. Flow cytometry was performed with a FACSCalibur (BD Biosciences, Mountain View, CA), and the data were analyzed with CellQuest software (BD Biosciences). The relative cell sizes of the three types of samples were initially estimated by the light scattering of the flow cytometry, and further confirmed by direct examination under light microscope with and without staining by hematoxylin and eosin (H & E).

NMR measurements

All measurements were performed on a 7.0-T, 16-cm bore Varian DirectDrive™ spectrometer (Varian Inc. Palo Alto, CA) equipped with a Doty PFG/diffusion z-gradient coil (Doty Scientific Inc. Columbia, SC) with strength capacity up to 3500G/cm. b values ranging from 0.5 ms/µm² to 10 ms/µm² were used in the PGSE measurements. The OGSE pulse sequence was identical to the PGSE except for the substitution of two apodized cosine-modulated gradients in place of the two bipolar gradients. Details of the OGSE pulse sequence can be found in Ref (10). For direct comparison, both diffusion methods utilized TR=3s, TE=64ms, diffusion gradient duration δ=20ms and separation Δ=24ms. All ADCs were obtained only using two b values (b=0, 1 ms/µm²). The OGSE method measured frequency ranging from 50Hz to 2kHz, corresponding to gradient strength ranging from 28.0 G/cm to 1052.0 G/cm. Measurements with both positive and negative z-axis diffusion gradients were performed and the geometrical means of the two signals were obtained to calculate ADC. By this means, the cross terms between diffusion gradients and the background gradient were removed (22). The sample temperature was monitored at 18°C.

Calibration of b values

An apodized cosine-modulated gradient waveform was used to avoid the sharp rise time at the start and end of each pulse, and the corresponding b value is given by (10)

$$b=\frac{{\gamma }^2{G}^2\sigma }{4{\pi }^2{f}^2}\left(1-\frac{1}{8n}\right)$$ [5]

where γ is the gyromagnetic ratio, G gradient strength and n number of oscillations in each gradient waveform. At very high frequencies and amplitudes, the gradient calibration is less reliable and from experience may bias the estimates of ADC by ≈ 5%. This would not affect the relative percentage ADC difference between samples, but could affect the fitted structural parameters. To correct for this potential artifact, a doped water phantom (5mM CuSO₄) was measured with the same sequence and the effective b values at high frequencies were calculated based on the assumption of a constant ADC for water without restrictions. All ADCs from cells were then corrected using these effective b values.

RESULTS

Cell Synchronization and Viability

For six samples, type I shows an average 70.5±2.6% (mean±SD) cells arrested in S phase, type II 48.7±2.0% in G2/M phase and type III 87.3±4.9% in M phase including polyploids. After 2 hours of NMR experiments, cell viability showed no noticeable change, with more than 99% of cells still viable based on a trypan blue exclusion assay.

Comparison of PGSE and OGSE Measurements

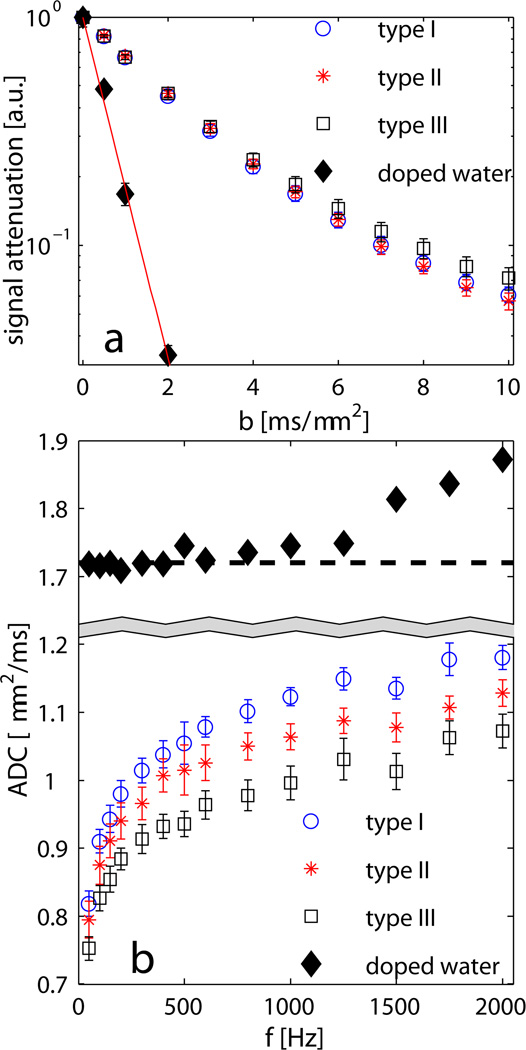
Diffusion signals obtained by PGSE measurements from a doped water phantom (5mM CuSO₄) as a function of b values are shown in Fig.1a and the corresponding ADC was calculated as 1.72±0.03µm. The ADCs of the three types of samples were compared. The averaged ADCs of the type I and type II samples obtained by the PGSE method were not significantly different (0.42±0.01 and 0.42±0.02µm²/ms, and the Wilcoxon rank-sum test gives p=0.70), while type III samples had a slightly smaller ADC (0.39±0.02µm²/ms and p=0.20 compared to type I). Moreover, Fig.1a shows the signal attenuation curves of the type I and II samples cannot be differentiated from each other (p>0.3 for each b value) even with b values up to 10 ms/µm², while the signal attenuation from type III was distinguishable (p<0.05 given by the Wilcoxon rank-sum test) for b > 4 ms/µm². The ADCs of a doped water phantom at different frequencies obtained using the OGSE method are shown in Fig.1b. When f>1kHz, the ADCs of the doped water phantom are overestimated because of the less reliable gradient calibration. Corrected using real b values at different frequencies, ADCs of three types of samples were obtained using the OGSE method and showed significantly difference (>5%) for type I and II, and >10% difference for type I and III, especially at relatively higher frequencies (>500Hz, see Fig.1b). The Wilcoxon rank-sum test gives p<0.05 for each frequency larger than 600Hz, while p>0.35 between type I and II when the frequency is below 200Hz.

Fig. 1.

(a) PGSE measurements of a doped water phantom (5mM CuSO₄) and three types of synchronized HL-60 cells with b values up to 10 ms/µm². Error bars represent standard deviations for six samples of each type and error bars of water represent the standard deviation of ten repeated measurements. (b) OGSE measurements of ADC vs. different frequencies for the doped water phantom and three types of synchronized HL-60 cells. Error bars represent standard deviations of six samples of each type. The sample temperature was at 18°C.

Extraction of Cell Micro-structural Parameters

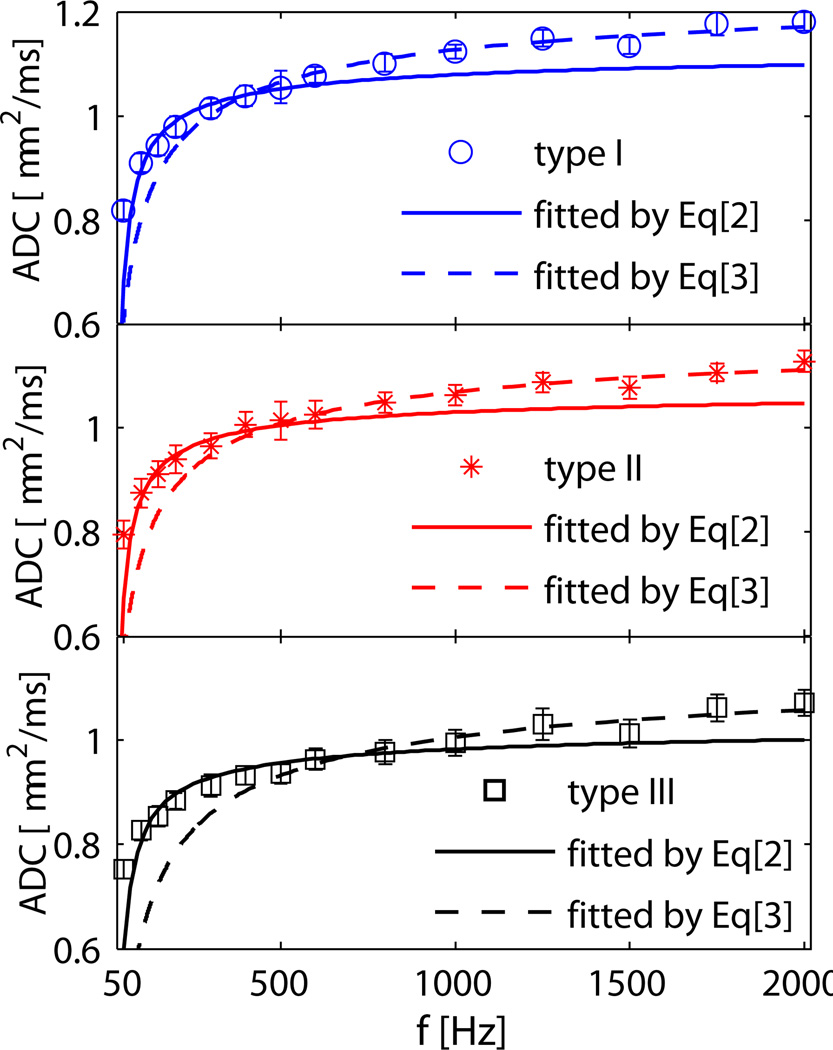
HL-60 is a promyelocytic leukemia cell line. The cells used in the current work grew in suspension, and their shapes were largely spherical, which was confirmed with light microscopy. Hence, it is appropriate to model HL-60 cell pellets as packed spheres. By fitting the OGSE data to analytical models, specific cell micro-structural parameters can be extracted, including cell size and intracellular diffusion coefficient D_in. Table1 shows the cell sizes from light microscopy and the results fitted using Eq.[2] and Eq.[3]. The mean OGSE ADCs over all six samples in each cell type and their corresponding fitted curves are shown in Fig.2. Eq.[2] fits the data of all samples well in the low frequency range (<500Hz) and gives the cell sizes of the three types of samples consistent with those obtained by microcopy (see Table1). However, Eq.[2] fails to explain the ADCs in the higher frequency range when the measured ADCs continue to increase with frequency, while Eq.[2] predicts ADCs should level out. Eq.[3] was then used to fit the ADCs in this high frequency range only, and gives values of cell S/V and D₀. The D₀ fitted by Eq.[3] are larger (~10%) than those obtained by Eq.[2]. The rank-sum test shows the fitted cell sizes between type I and II are indistinguishable (p>0.9), but the fitted cell size of type III are significantly different than those of type I and II (p<0.03). All the fitted diffusion coefficients and S/V’s are statistically different than each other (p<0.05).

Table 1.

Fitted results for three types of cells. All fitted parameters are statistically different from each other (p<0.05 by Wilcoxon rank-sum test), except the cell sizes of type I and II fitted by Eq. [2].

	microscopya	Fitted by Eq.[2]b		Fitted by Eq.[3]b
	diameter [µm]	diameter [µm]	Din [µm2/ms]	S/V [µm−1]	D0 [µm2/ms]
type I	10.22±2.44	11.14±0.64	1.14±0.02	1.23±0.09	1.29±0.02
type II	10.28±2.09	11.33±0.76	1.09±0.02	1.11±0.13	1.21±0.03
type III	9.20±1.92	10.21±0.47	1.03±0.03	1.36±0.15	1.16±0.04

^amean±SD of over 250 cells

^bmean±SD of all six samples in each cell type.

Fig. 2.

Experimental mean ADC data and corresponding fitted curves for three types of samples. Cells were assumed to be spheres by fitting to Eq.[2] (solid lines) to extract cell size and intracellular diffusion coefficient, and were fitted to Eq.[3] (dashed lines) to extract S/V and D₀.

DISCUSSION

In the current work, type II samples (with high portion of synchronized G2/M-phase cells) were obtained from type I samples (synchronized S-phase cells) by releasing cell arrest (growing for an additional six hours after removal and wash out of thymidine). The benefit of this method is that the average cell sizes of the two types of samples are very similar and, hence, very similar cell densities can be obtained by controlling centrifugation speed and time. When cell size and cell density are similar, ADC differences between the two samples are not apparent at long diffusion times. Differences between type I and II detected in OGSE measurements at high frequency do not arise from differences in cellularity, but instead are caused by changes within the cells. Type III samples were synchronized to M phase but with a different method, i.e. treating with 100ng/ml Nocodazole for 24 hours, which yields a much higher M phase fraction (87.3%) but a different cell size (~10% smaller) than those of type I and II. Hence, ADC differences between type I and III arise from differences at both cellular scales and sub-cellular scales. Some previous studies have suggested that using PGSE methods with high b values may suppress extra-cellular water signals and hence increase the sensitivity of conventional diffusion measurements to intracellular water (16). In the present work, type I and II cell samples were prepared with similar gross cellular properties, i.e. cell size and density, but with different sub-cellular characteristics, i.e. cell phase. No significant differences were observed by PGSE methods with b values up to 10 ms/µm². However, the PGSE method can differentiate type I and II samples from type III with either ADC or high b value signal attenuations and, moreover, the signal attenuation difference between type I/II and type III increases with b values. This implies that the high-b-value PGSE method with relatively long diffusion time has the ability to enlarge the detectable signal difference due to gross cellular properties, but it is likely insensitive to variations at sub-cellular scales.

The OGSE method used in the present study is able to detect changes in intracellular structure during the normal cell cycle by using relatively high frequencies (>500Hz) even though the samples have very similar gross cellular properties (e.g. type I vs. II). When both cellular and sub-cellular properties are different (type I and III), the OGSE method can detect sample differences over all frequencies, but with increased differences at higher frequencies. At low frequencies the OGSE data can be described by an analytical model (see Eq.[2]), which does not incorporate the influence of sub-cellular structure variations. The analytical model assumes a homogeneous intra-cellular diffusion coefficient, which is valid when the frequencies are low, i.e. diffusion time is long. In such a range, the characteristic diffusion length is comparable to the cellular size and much larger than the smaller dimensions of most intracellular structures. Hence, the intracellular diffusion properties are averaged and can be considered as homogeneous. The fitted cell sizes are in agreement with those from microscopy. However, this model does not predict that ADC will keep increasing at high frequencies, so there is clearly a need to incorporate more complex behavior within the cells. When frequencies are relatively high (f>500Hz) (see Fig.3), the diffusion time is sufficiently short (<~0.5ms) that the characteristic diffusion length is comparable to or smaller than major intra-cellular structures (length scales < ~1.3µm). In such circumstances, the detailed nature of the intracellular structures may influence the ADC, and the ADC keeps increasing with frequency. In this regime, when effective diffusion times are very short, S/V can be fitted using Eq.[3] and a different, slightly larger estimate of the diffusion coefficient is obtained. This larger value is closer to the free diffusion coefficient because some of the restriction effects that occur at sub-cellular scales are taken into account. However, the ADC of the cell samples continue to rise even at frequencies of a few kHz, and that the fitted D₀ by Eq. [3] are still much lower than the intrinsic water self-diffusion coefficient (~1.72µm²/ms) at the same temperature. This implies that there are restrictions or hindrances to free diffusion from even smaller intra-cellular structures that are averaged. The OGSE method provides a way to detect tissue structures at different length scales by “tuning” the frequency. The correction factor c used in Eq.[3] was obtained numerically from computer simulations and it might be different from the real values of cell samples, and hence the fitted S/V may be biased. However, this bias does not affect the relative S/V differences among different cell samples, and thus the fitted S/V can still be used as an indicator of intracellular structures in different cell cycle phases. With the numerically-generated correction factor used in the current work, the fitted values of S/V are consistent with previously published data. The S/Vs of type I and II samples are smaller than those obtained from packed erythrocytes, which has been reported as 1.34µm⁻¹ using Eq.[3] (5), but larger than 0.48±0.1µm⁻¹ obtained from HeLa cells (17). This is consistent with the difference in cell sizes. The HL-60 cells used in the current study have an average cell size 10.22µm for type I and 10.28µm for type II larger than red blood cells (6–8µm) and smaller than HeLa cells (21.0µm (17)). An exception has been found for the type III samples, which have an averaged cell size (9.20µm) closer to that of red blood cells. In such circumstances, S/V differences are mainly determined by intracellular structures, and hence type III samples have a slightly larger S/V (1.36µm⁻¹) than those of red blood cells even though the cell size is slightly larger.

The S/Vs of the type II and III samples are larger than I but D₀ of type I is larger than II and III. From this we infer that type II and III cells on average have more intracellular structure on the distance scale relevant to our measurements, which introduce more restrictions and hindrances to free diffusion in the intra-cellular space over time scales of order 1 millisecond. This would be consistent with the known changes within cells that arise during the G2/M phase compared to the S phase (23). In the latter, chromosomes are replicated, the amount of DNA is doubled at the end of the S phase, but the ploidy remains the same and both RNA transcription and protein synthesis overall are low. In the G2/M phase, on the other hand, there is considerable increase in protein synthesis mainly to manufacture of microtubules, and the major changes in organelles associated with cytokinesis prior to cell division.

In the current study, the OGSE measurements of packed cells ex vivo employed a micro-gradient coil using extremely high gradient strengths (up to 1052 G/cm) in order to probe ADCs at very high frequencies (up to 2 kHz). For in vivo studies, the highest OGSE frequency that can be used is usually limited by the strength and slew rate of practical gradient systems. Nevertheless, OGSE methods have been readily implemented in vivo on animal scanners to provide measurements with intermediate frequencies. For example, Does et al. applied OGSE methods on normal and ischemic rat brain in vivo with frequency up to 1 kHz with gradient strength up to 100 G/cm (10). Colvin et al. detected glioblastoma in rat brains (24) and assessed tumor early response to treatment (25) with frequency up to 240 Hz. However, although high frequencies (>1kHz) are readily achievable in clinical scanners, the maximum gradient strength (e.g. 8G/cm) limits the achievable b values and so OGSE measurements on human tissues are currently limited in practice.

CONCLUSIONS

The factors that influence the ADC of tissue water are of considerable interest but imperfectly understood. To assess the effects of specific structural changes on temporal diffusion spectra, a synchronized cell system was used in which sample cell sizes, cell densities and intra-cellular structure could be varied. The results show that the PGSE method is insensitive to sub-cellular changes due to cell cycle phases, but has the ability to detect changes caused by cell density/size differences. On the contrary, the OGSE method shows different sensitivities at different frequencies and detects changes in cell cycle when cell size and density are fixed. Specific structural parameters can be extracted from analytical models at corresponding frequency ranges. The results shown in the present work may be helpful for obtaining a better understanding of the dependence of ADC on diffusion time and cell physiological states, and shows the feasibility of the OGSE method to provide extra contrast other than cell density in diffusion-weighted MRI.