The Global Distribution of Infant Mortality: A subnational spatial view

Abstract

We describe the compilation of a spatially explicit dataset detailing infant mortality rates in over 10,000 national and subnational units worldwide, benchmarked to the year 2000. Although their resolution is highly variable, subnational data are available for countries representing over 90% of non-OECD population. Concentration of global infant deaths is higher than implied by national data alone. Assigning both national and subnational data to map grid cells so that they may be easily integrated with other geographic data, we generate infant mortality rates for environmental regions, including biomes and coastal zones, by continent. Rates for these regions also show striking refinements from the use of the higher resolution data. Possibilities and limitations for related work are discussed.

Introduction

The single greatest factor contributing to improved life expectancy over the past 100 years has been the reduction of infant mortality (Kitagawa 1977; Riley 2005; Bongaarts 2006). Most countries of the world now experience infant mortality rates (IMR) of less than 30 infants per 1000 live births (UNICEF 2004). Yet mortality declines have not been even. Most countries in Africa still experience infant and child mortality rates far above those found elsewhere. Using national level data, Black and colleagues (2003), find that half of all deaths of children under age 5 are concentrated in just six countries of the world (India, Nigeria, China, Pakistan, Democratic Republic of Congo, and Ethiopia) while very high rates of mortality are concentrated primarily in sub-Saharan Africa. While national data show a similar pattern for infant deaths, with half concentrated in the same six countries, spatially explicit subnational data would permit further quantification of spatial concentration and identify geographic “hotspots” or clusters of mortality, some of which would be expected to cut across national boundaries.

Furthermore, when mortality is represented spatially at moderate resolution, it opens up the possibility for a new type of analysis: systematic assessment of mortality with respect to locational factors. National-level and some micro-level analyses have suggested that mortality variation results in part from ecological conditions, in addition to the well-known socio-demographic and economic factors (Woods 2003; Jain 1985; Gemperli et al. 2004). However, national-level analyses are too coarse and obscure much ecological variation. Micro-level analyses, which are more amenable to inclusion of contextual variables (of an ecological nature or otherwise), lack global or even regional coverage. In order to systematically consider spatially-constructed ecological phenomena at an intermediate level of analysis, with units larger than individuals but smaller than whole countries, mortality must be rendered on the same scale.

Social scientists have recently begun to embrace subnational gridded demographic and economic data in an effort to consider biophysical and geographic factors such as climate, separately from state-level institutional ones (e.g., Hay et al. 2004, Nordhaus 2006, Balk et al. 2006). Gridded demographic data were previously limited to simple population counts. Gridded infant mortality rates, births and deaths are natural extensions. However, they use methods and underlying data that differ in some ways from population and GDP data, so it is imperative to identify the methods and data that underlie the new dataset.

Thus, the primary focus is paper is methodological. We do not therefore seek to interpret or theorise patterns of infant mortality, even although mapping infant mortality at new scales stimulates many hypotheses about the drivers of change. We introduce a global, spatially explicit, subnational dataset of infant mortality rates containing 10,370 spatially-referenced estimates for circa 2000. It is presented in two different spatial representations, as polygons and as grid cells, each useful for different types of analyses. We describe the data and methods used as well as the final products. In addition, we present some basic descriptive analyses, including an exploration of spatial patterns, in order to demonstrate potential applications for which subnational resolution is critical.

Data & methods

National infant mortality rates are reported for nearly every country in the world (UNICEF 2004; Figure 1).¹ For a sizable minority of countries, representing the vast majority of world population, subnational estimates are also available. Despite the fact that demographic surveys have collected data that would foster subnational disaggregation for over twenty years, little work has been done to compare measures subnationally across countries in a spatial framework (Balk et al. 2004; Root 1999; Curtis and Hossain 1998), and none that we are aware of with a global scope. As spatially explicit data and geographic information systems (GIS) software to process them become more widely available and sophisticated, it has become easier to place these estimates in a spatial context.

Figure 1.

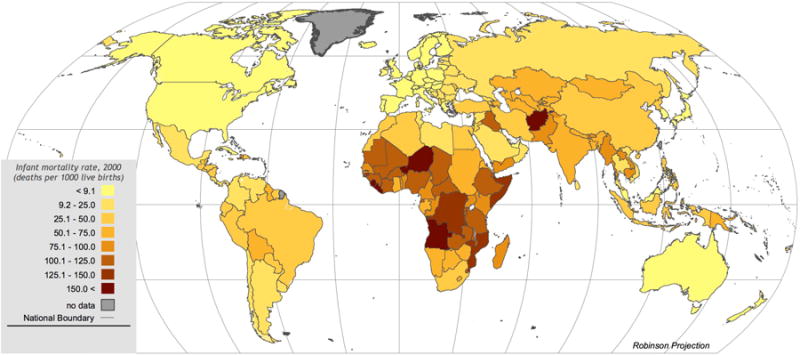
National IMR map

Compared to many other development indicators, the definitions and measurements associated with infant mortality (i.e., deaths and live births) are well standardized across countries.² Furthermore, methods to adjust national rates to account for reporting and definitional differences across countries are now well established (Hill and Yazbeck 1994, Hill et al. 1997).

Two disparate types of data were combined: mortality estimates for named geographic areas and boundaries associating spatial extents to these areas. First, subnational infant mortality estimates were collected for 77 countries, comprising 80% of world population and 90% of developing-country population.

Source information about the 77 subnational countries is shown in Table 1. Data are reported for a year within the period 1996-2003 for 69 countries. For the remaining eight countries, data from as early as 1990 were used. The most common subnational data sources were the Demographic and Health Surveys (DHS; 44 countries) and Multiple Indicator Cluster Surveys (MICS; 5 countries). Mortality is estimated in these surveys using a synthetic-cohort direct estimation procedure (Rutstein 2003) and the Brass Logit indirect method of estimation (United Nations, 1983), respectively.³

Table 1. Countries with subnational data.

Continent	Country	National 2000 IMR from UNICEF	Other National IMR	IMR Base Year	IMR Source (abbr.)	National Crude Birth Rate	Units with IMR Data		Missing any IMR Data	population (000′s; 2000)	area (square km)	population (000′s)/ IMR unit	area/IMR unit	Administrative Level		Method - general
Africa	Algeria	40	40	2000	MICS	22.8	4		No	30,291	2,302,498	7,573	575,624	0.5		Indirect estimation
Africa	Angola	154	150	2001	MICS	52.3	6		No	13,134	1,251,924	2,189	208,654	0.5		Indirect estimation
Africa	Benin	95	95	2001	DHS	41.5	6		No	6,272	115,828	1,045	19,305	0.5		Direct estimation
Africa	Botswana	74	48	1991	NHDR	30.6	9		No	1,541	559,502	171	62,167	1		Indirect estimation
Africa	Burkina Faso	107	109	1999	DHS	47.8	4		No	11,535	275,747	2,884	68,937	0.5		Direct estimation
Africa	Cameroon	95	80	1998	DHS	35.4	4		No	14,876	465,765	3,719	116,441	0.5		Direct estimation
Africa	Central African Republic	115	102	1994	DHS	37.7	6		No	3,717	622,868	620	103,811	0.5		Direct estimation
Africa	Comoros	61	84	1996	DHS	36.7	3		No	706	2,046	235	682	1		Direct estimation
Africa	Egypt	38	29.2	1998	NHDR	26.6	26		No	67,884	968,071	2,611	37,234	1		Vital statistics
Africa	Eritrea	53	57	2002	DHS	39.7	6		No	3,659	121,863	610	20,310	1		Direct estimation
Africa	Ethiopia	116	113	2000	DHS	42.5	11		No	62,908	1,123,714	5,719	102,156	1		Direct estimation
Africa	Gabon	60	61	2000	DHS	31.6	4		No	1,230	265,146	308	66,286	0.5		Direct estimation
Africa	Gambia	92	92	1993	NHDR	35.8	6		Yes	1,303	10,838	217	1,806	1		Indirect estimation
Africa	Ghana	62	61	1998	DHS	31.9	10		No	19,306	231,730	1,931	23,173	1		Direct estimation
Africa	Guinea	112	107	1999	DHS	42.9	5		No	8,154	245,860	1,631	49,172	0.75		Direct estimation
Africa	Kenya	77	77	2003	DHS	32.5	8		No	30,669	579,617	3,834	72,452	1		Direct estimation
Africa	Madagascar	86	99	1997	DHS	41.6	6		No	15,970	592,965	2,662	98,828	1		Direct estimation
Africa	Malawi	117	113	2000	DHS	44.6	3		No	11,308	94,958	3,769	31,653	1		Direct estimation
Africa	Mali	124	126	2001	DHS	49.9	6		No	11,351	1,248,137	1,892	208,023	0.75		Direct estimation
Africa	Mauritania	120	67	2000	DHS	41.8	5		No	2,665	1,036,905	533	207,381	0.5		Indirect estimation
Africa	Morocco	41	66	1995	DHS	23.2	7		No	29,878	669,159	4,268	95,594	0.5		Direct estimation
Africa	Mozambique	130	145.5	1997	DHS	41.2	11		No	18,292	777,123	1,663	70,648	1		Direct estimation
Africa	Namibia	56	38	2000	DHS	33.4	4		No	1,757	819,964	439	204,991	0.5		Direct estimation
Africa	Niger	159	136	1998	DHS	55.2	5		No	10,832	1,157,232	2,166	231,446	0.75		Direct estimation
Africa	Nigeria	102	71	1999	DHS	39.1	5		No	113,862	904,235	22,772	180,847	0.5		Direct estimation
Africa	Rwanda	118	117.4	2000	DHS	44	12		No	7,609	24,349	634	2,029	1		Direct estimation
Africa	Senegal	80	69	1997	DHS	37.1	4		No	9,421	196,151	2,355	49,038	0.5		Direct estimation
Africa	Somalia	133	132	1999	MICS	52.1	3		Yes	8,778	634,315	2,926	211,438	0.5		Indirect estimation
Africa	South Africa	50	42.2	1998	DHS	22.6	9		Yes	43,309	1,217,645	4,812	135,294	1		Direct estimation
Africa	Sudan	65	68	2000	MICS	33	16		Yes	31,095	2,492,385	1,943	155,774	0.75		Indirect estimation
Africa	Togo	80	80	1998	DHS	38.5	5		No	4,527	57,277	905	11,455	1		Direct estimation
Africa	Uganda	85	89	2000	DHS	50.7	4		Yes	23,300	206,968	5,825	51,742	0.5		Direct estimation
Africa	Tanzania	104	94.1	1996	DHS	39.3	6		No	35,119	891,021	5,853	148,504	0.5		Direct estimation
Africa	Zambia	102	107.7	1996	DHS	42.2	9		No	10,421	745,317	1,158	82,813	1		Direct estimation
Africa	Zimbabwe	73	60	1999	DHS	32.1	10		No	12,627	389,055	1,263	38,905	1		Direct estimation
Americas	Argentina	17	17.6	1999	National source	19	24		No	37,032	2,736,391	1,543	114,016	1		Vital statistics
Americas	Bolivia	59	61	2000	National source	29.3	9		No	8,329	1,069,350	925	118,817	1		Unknown
Americas	Brazil	35	49.5	1991	National source	19.7	4477		Yes	170,406	8,480,395	38	1,894	2		Indirect estimation
Americas	Canada	5	5.5	1997	National source	10.3	12	No		30,757	9,458,886	2,563	788,240	1	Vital statistics
Americas	Chile	11	10	1999	National source	18.2	28	Yes		15,211	721,229	543	25,758	1.5	Vital statistics
Americas	Colombia	20	24	2000	DHS	22.2	5	Yes		42,105	1,141,569	8,421	228,314	0.5	Direct estimation
Americas	Costa Rica	10	11.8	1996	National source	19.1	7	No		4,024	51,015	575	7,288	1	Vital statistics
Americas	Cuba	7	7	2000	National source	11.6	15	No		11,199	111,199	747	7,413	1	Unknown
Americas	Dominican Republic	35	37	1999	DHS	23.3	8	No		8,373	48,092	1,047	6,011	0.5	Direct estimation
Americas	Ecuador	27	30	1999	National source	23	16	Yes		12,646	246,700	790	15,419	1	Direct estimation
Americas	El Salvador	34	31	1999	NHDR	25.1	14	No		6,278	20,279	448	1,448	1	Unknown
Americas	Guatemala	39	49	1999	DHS	34.2	8	No		11,385	108,523	1,423	13,565	0.5	Direct estimation
Americas	Haiti	81	89	2000	DHS	30.3	9	No		8,142	26,876	905	2,986	1	Direct estimation
Americas	Mexico	25	24.9	2000	National source	22.4	2409	Yes		98,872	1,943,018	41	807	2	Indirect estimation
Americas	Nicaragua	34	35	2001	DHS	31.6	17	No		5,071	118,279	298	6,958	1	Direct estimation
Americas	Paraguay	26	36	1990	DHS	29.6	4	Yes		5,496	395,886	1,374	98,972	0.5	Direct estimation
Americas	Peru	32	33.6	2000	NHDR	23.3	25	No		25,662	1,289,475	1,026	51,579	1	Indirect estimation
Americas	United States	7	7.2	1998	National source	14.5	51	Yes		283,230	9,210,755	5,554	180,603	1	Vital statistics
Americas	Uruguay	15	17.8	1997	National source	16.8	19	No		3,337	173,985	176	9,157	1	Vital statistics
Americas	Venezuela	20	20	1997	National source	22.8	22	Yes		24,170	911,559	1,099	41,434	1	Vital statistics
Asia	Armenia	32	44	2000	DHS	9.7	11	No		3,787	28,277	344	2,571	1	Direct estimation
Asia	Bangladesh	54	79.7	1999	DHS	28.9	6	No		137,439	136,305	22,907	22,717	1	Direct estimation
Asia	Cambodia	95	92.7	2000	DHS	33.9	17	No		13,104	179,492	771	10,558	0.75	Direct estimation
Asia	China	32	26.37	2000	National source	14.5	2367	Yes		1,275,133	9,198,103	539	3,886	3	Indirect estimation
Asia	India	68	77	1991	NHDR	23.8	31	Yes		1,008,937	3,209,716	32,546	103,539	1	Unknown
Asia	Indonesia	35	47	1999	NHDR	20.7	26	No		212,092	1,898,776	8,157	73,030	1	Indirect estimation
Asia	Iran	36	31.7	1996	NHDR	20.3	26	No		70,330	1,590,351	2,705	61,167	1	Unknown
Asia	Jordan	28	29	1997	DHS	28	3	No		4,913	88,362	1,638	29,454	0.5	Direct estimation
Asia	Kazakhstan	60	61.9	1999	DHS	16.2	5	No		16,172	2,619,352	3,234	523,870	0.5	Direct estimation
Asia	Lebanon	28	26	2000	MICS	19.1	5	No		3,496	10,328	699	2,066	1	Indirect estimation
Asia	Mongolia	60	32.8	2000	National source	22.5	22	No		2,533	1,546,294	115	70,286	1	Unknown
Asia	Nepal	69	77	2001	DHS	32.9	5	No		23,043	139,087	4,609	27,817	1	Direct estimation
Asia	Pakistan	85	94	1991	DHS	35.9	4	Yes		141,256	785,320	35,314	196,330	1	Direct estimation
Asia	Philippines	30	36	1998	DHS	25.3	16	No		75,653	295,408	4,728	18,463	1	Direct estimation
Asia	Sri Lanka	17	13.3	2000	National source	16.4	25	No		18,924	65,830	757	2,633	2	Vital statistics
Asia	Thailand	25	7	1997	NHDR	17.3	76	No		62,806	513,618	826	6,758	1	Unknown
Asia	Turkey	38	48	1998	DHS	20.9	5	No		66,668	768,690	13,334	153,738	0.5	Direct estimation
Asia	Turkmenistan	75	72	2000	DHS	22.2	6	No		4,737	460,254	790	76,709	1	Direct estimation
Asia	Uzbekistan	51	20	1999	NHDR	21.7	13	No		24,881	412,914	1,914	31,763	1	Unknown
Asia	Viet Nam	23	33.1	1999	NHDR	20.2	53	No		78,137	328,535	1,474	6,199	1	Indirect estimation
Asia	Yemen	84	80	1997	NHDR	45	17	Yes		18,349	415,196	1,079	24,423	1	Unknown
Europe	Russian Federation	18	15.3	2000	National source	8.6	85	Yes		145,491	16,679,998	1,712	196,235	1	Vital statistics

For the -remainder of countries for which subnational data were available, data were reported in national Human Development Reports or by national statistical offices or ministries of health. Of these, ten report based on vital registration data, eight use indirect methods of various kinds, one uses direct estimation, and nine do not report the method used.

All of the survey-based data are subject to various sources of error and bias, many of which have been well documented (Hobcraft et al., 1984). Mothers who have died cannot be interviewed about whether their children have died. Women who had children in their 40s but reached their 50^th birthday before the time of the survey are also typically unsampled. Sample biases are also common in surveys. Indigenous groups, informal settlements, places in civil unrest, and refugees are often entirely unsampled, either because of political biases, missing sampling frames or prohibitive difficulties in carrying out a survey. Never married women are not sampled in certain Asian countries. In general, these errors are likely to bias rates downward misreporting of age at death. Sampling errors, typically larger for subnational regions than for whole countries, can cause survey results to deviate from true rates in either direction. Omissions of births and deaths, as well as misreporting of dates of birth and death, either random, in order to avoid answering further questions, or because particular populations (e.g., orphans) were not surveyed can result in biases upward or downward. Curtis (1995) provides a useful summary of these potential sources of error in the DHS surveys. Indirect estimation is subject to all of these except for dates of birth and death. In addition, it is subject to further reliance on the accuracy of mothers' ages, not just at the upper and lower margins, and to the relevance of the model used (i.e., North, South East or West; see Coale and Demeny, 1966) for a given population. Unfortunately, in most instances only sampling errors can be quantified.⁴ For DHS carried out before 1994, nearly all relative standard errors for national samples were between four and 10 percent (Curtis 1995).

The differences between these different calculation methods have generated a great deal of debate. Preston (1985) contends that direct methods are clearly better. Adetunji (1996) provides some further arguments as to why comparing estimates based on combinations of different methods may be problematic. However, Hill (1991) notes that in a selection of DHS, Brass-type indirect and direct methods provide broadly similar estimates, though indirect estimates may be somewhat noisier.

While vital statistics are ideal if the system has good coverage, if the system is weak, it can result in severe biases in either direction, depending on whether births or deaths suffer from greater underreporting. The United Nations Demographic Yearbooks first reporting the relevant years estimate that the ten countries for which we report subnational estimates based on vital statistics all have at least 90 percent coverage of live births and infant deaths, although these estimates are based largely on questionnaires answered by the relevant national statistical offices (United Nations 1997, 1998, 1999, 2000, 2001, 2002).⁵

Table 1 also indicates the number of reporting units for each country. Forty-five countries are specified at the first administrative level (i.e., equivalent to province), and 27 are specified somewhat more coarsely, though still with substantial subnational resolution. The remaining five countries have data at higher resolution than the first administrative level. Three countries—Brazil, China and Mexico—had estimates of infant mortality available at a very high-resolution (i.e. at the county level or better), based on various indirect methods.⁶ Eighty-nine percent of the units in the global collection represent a unit from one of these three countries. Outside these three countries, countries with any subnational data report for a mean of 13.5 (median 8) subnational units per country (Table 2).⁷

Table 2. Data resolution summary.

Data type	Data units	Countries	Average units per country	% world population	% non-OECD population
None (all small islands)	0	44	-	0.5%	0.1%
National	119	119	1	18.8%	10.0%
Subnational excluding
Brazil, China, Mexico	998	74	13	55.3%	60.4%
Brazil, China, Mexico	9253	3	3,084	25.4%	29.4%
Any subnational	10251	77	133	80.7%	89.8%
Any data	10370	196	53	99.5%	99.9%
Total	10370	240	43	100.0%	100.0%

We were unable to find a complete collection of subnational rates for 119 countries, so in these cases we used national values from UNICEF (2004). Most of these countries are either small or developed. The largest developing countries lacking subnational data are Democratic Republic of Congo, Myanmar, Iraq, North Korea, Malaysia, Afghanistan, and Saudi Arabia. We expect that the developed countries for which we lack subnational data have significantly less variation at the first or second administrative level. Furthermore, we expect that to the extent that they do have variation, it is unlikely to be explained by environmental factors. Thus we expect that if we were to find subnational data for these countries and use it to replace the national data, this would not substantially change the patterns we describe.

Second, because the year and source of the subnational estimates vary by country, they were adjusted to be consistent with the UNICEF (2004) national estimates for the year 2000. UNICEF has constructed a time series that adjusts nationally reported rates using multiple surveys to account for reporting, computational and definitional differences (Hill and Yazbeck 1994, Hill et al. 1997). This consistent means of temporal adjustment facilitates comparisons at a continental or global scope where data have been collected over a range of years, and several organizations within the UN system have come to use the UNICEF estimates (Haishan Fu, UNDP, personal communication).

The IMR value r_c,y,s,x for country c, year y from source s, at scale × (0 = national; 1 = subnational) were scaled to y=2000 national rates from UNICEF (denoted s = 0). The subnational values are denoted as vectors because the same adjustment is applied to all subnational values in the same country.

Given: $\overrightarrow{{\text{r}}_{\text{c},\text{y},\text{s},1}}$, r_c,2000,0,0 and r_c,y,s,0, we seek $\overrightarrow{{\text{r}}_{\text{c},2000,0,1}}$:

Source adjustment: $\overrightarrow{{\text{r}}_{\text{c},\text{y},0,1}}=\frac{\overrightarrow{{\text{r}}_{\text{c},\text{y},\text{s},1}}{\text{r}}_{\text{c},\text{y},0,0}}{{\text{r}}_{\text{c},\text{y},\text{s},0}}$

Temporal adjustment: $\overrightarrow{{\text{r}}_{\text{c},\text{2000},\text{0},1}}=\frac{\overrightarrow{{\text{r}}_{\text{c},\text{y},0,1}}{\text{r}}_{\text{c},\text{2000},0,0}}{{\text{r}}_{\text{c},\text{y},0,0}}$

Combining both adjustments, r_c,y,0,0 cancels, leaving:

$$\overrightarrow{{\text{r}}_{\text{c},2000,0,1}}=\frac{\overrightarrow{{\text{r}}_{\text{c},\text{y},\text{s},1}}{\text{r}}_{\text{c},\text{2000},0,0}}{{\text{r}}_{\text{c},\text{y},\text{s},0}}$$

In effect, subnational differentiation from the national (country-specific) source year is applied to the national base rate for 2000 reported by UNICEF. This has clear drawbacks, especially the assumption of a uniform rate of change within a country. However, we consider this loss in precision not significant enough to avoid attempting consistent subnational estimation. As subnational time series data become more widely available, further research should be undertaken to quantify the error introduced by adjustments of this nature.

Third, each estimate was assigned to a geographic boundary based on source material associated with the data or other maps of administrative regions. For most countries, appropriate spatial data are commonly available or constructible from public domain sources (e.g., ESRI 2002). Other countries required proprietary subnational boundary data.⁸ The average size (in population and area terms) of a unit with an associated IMR estimate is indicated in Table 1. The value depends both on the size of the country and the number of units (i.e., first-level administrative units are much larger in India than they are neighboring Bangladesh because India itself is much larger).

Fourth, although the administrative polygons are useful for some purposes, because they are irregular and of highly varying resolution, they were converted to a uniform grid. This produced one main analytic advantage. Like most other population parameters reported for administrative polygons, the infant mortality surface is subject to the modifiable areal unit problem (Openshaw and Taylor 1979). Discretizing a phenomenon that is continuous (or in this case, varying at a far higher resolution) is an arbitrary process. In the case of the infant mortality data, we are faced with a dataset with one value for Afghanistan, and over 4,000 for Brazil. Should one wish to analyze, for example, the relationship between the IMR and biophysical or environmental variables, such as the average elevation, using the reporting units, one would generate a single value for the entire country of Afghanistan, and one for a neighborhood of Rio de Janeiro. In other words, gridding allows for flexibility in accounting for variation in the right-hand side of a causal model predicting mortality even in areas where mortality data are locally uniform. However, it cannot increase information density, and as such, appropriate statistical models are required to account for this autoreplication.

Because infant mortality is a rate, scaling it to alternate geographies requires decomposition into numerators (live births) and denominators (deaths). Births (B) were estimated using national crude birth rates (CBR) from the UN Population Division and high-resolution population (P) estimates from CIESIN and CIAT (2005): B = CBR * P. The national CBR data add error to the subnational IMR distribution, but in general, if regional fertility varies less within a country than infant mortality at this scale, the estimates are still essentially accurate. To test this, we calculated the between-region coefficient of variation (CoV) of IMR and CBR for a collection of 101 DHS. For all but eight of them, the CoV of IMR is higher than the CoV of CBR. Deaths (D) are calculated analogously (D = IMR * B). Grids of births, deaths and rates were calculated at 0.25 degree and 2.5 minute resolution, corresponding to approximately 772 and 21 square kilometers, respectively, at the equator.

Results

The resulting dataset (CIESIN 2005a) is mapped in Figure 2. High-resolution patterns are most clearly evident in Mexico, China and Brazil, the countries with the largest number of units. Northeastern Brazil and Southwestern China stand out as high mortality areas within each country, but each of these areas contains some low mortality units as well. Other regions, despite lower resolution, show subnational patterns that cross borders. In sub-Saharan Africa, a western Sahel high mortality pattern emerges more clearly than within the national data. And high values in Andean regions of Peru and Bolivia face each other across a border. Figure 3 highlights the subnational distribution within each country. Variation increases with unit density, as one would expect. Still, Mexico has a standard deviation that is one third of Thailand's, despite having over thirty times as many units, so clearly a large number of units is only part of the reason for Brazil and China's wide distributions, Having an ability to detect which subnational regions have disproportionately high infant mortality rates is a valuable tool for policy and research. Increasing the subnational resolution is an aid towards this goal.⁹

Figure 2.

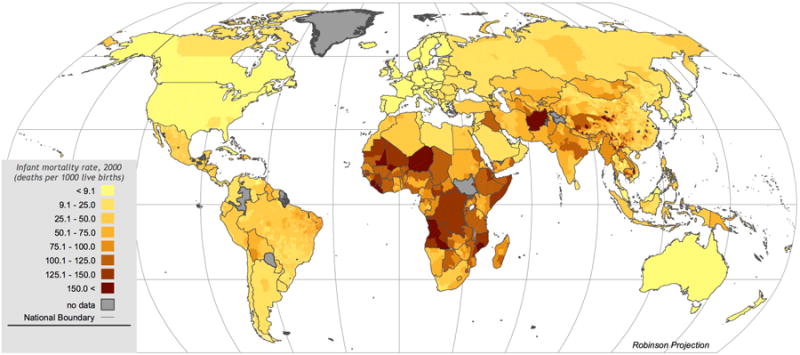
Subnational IMR map

Figure 3.

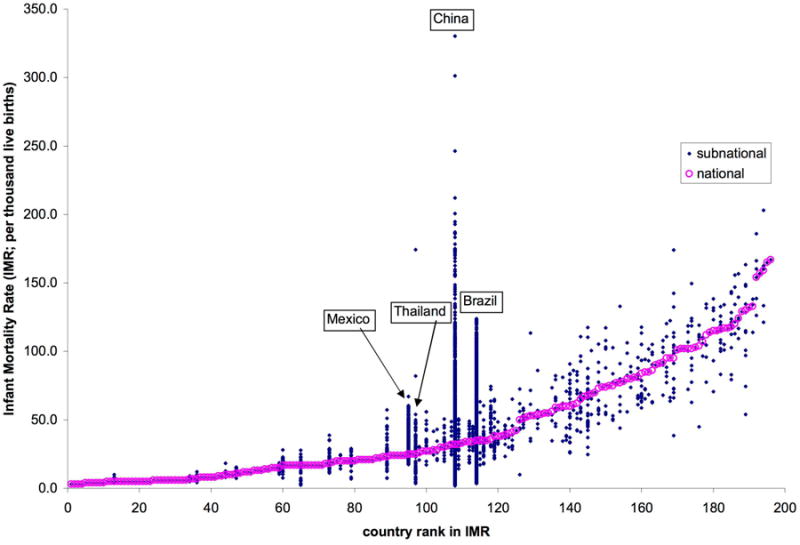
Scatter plot: subnational rates by national rate ranking

Researchers and policy makers also need to know where large numbers of infant deaths occur, not just where rates of mortality are high. As Figure 4 shows, these data can also be viewed in terms of absolute numbers of infant deaths. From this map, it is evident that a large fraction of the world's deaths occur in India, despite the fact that its rates are lower than those of several countries in Sahelian and Central Africa, and the fact that there is considerable variation in rates of mortality within India. This exercise serves as an important reminder that both absolute numbers and rates of infant deaths matter. However, in discussing spatial patterns we limit ourselves to discussing rates because they are more comparable across different sized units.

Figure 4.

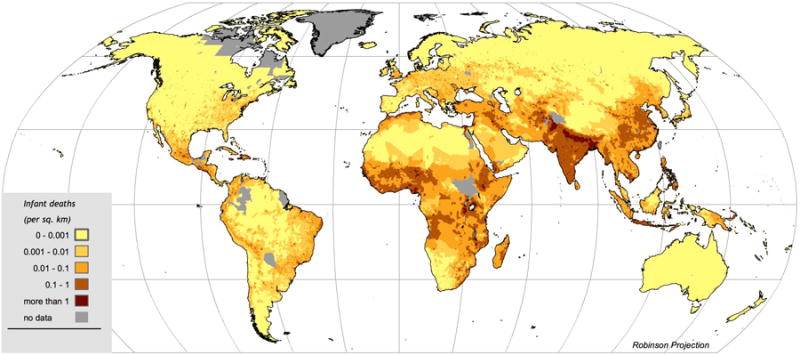
Deaths map

Spatial patterns

Our findings are consistent with those of Black et al. (2003) in that half of all infant deaths are concentrated in the same six countries as the most concentrated half of all child deaths,. However, the contribution of the present approach is that it allows us to further quantify the spatial concentration of infant mortality. Using a 0.25 degree unit of analysis, within these six countries, 55.9% of deaths are concentrated within 10.0% of land area that holds 34.4% of their combined population. This suggests a much greater concentration of mortality—both across space and population—than one would infer from national-level statistics alone. Expanding to the 20 countries with the most deaths, it takes 3.2% of world land area (holding 28.4% of world population) to reach half their deaths - this gives 1.72 billion persons in 4.15 million square kilometers, 50% of these 20 countries' population in 11% of their area. Globally, half of all deaths are concentrated in 2.5% of global populated land area holding 29.3% of global population. In contrast, the most concentrated half of world population lives on 2.9% of populated land area, but accounts for 38.2% of infant deaths. It is well known that people are highly concentrated spatially in areas that are desirable for various reasons. What is interesting here is that deaths are consistently more concentrated than people, no matter whether we consider all countries or the six or 20 with the most deaths. Globally, this can best be seen by the fact that it takes 2.5% of global land area to find half of all infant deaths, 14% less than the 2.9% required to find half of global population.

Spatial data also allow us to formally consider the degree to which similar mortality rates cluster by calculating measures of spatial autocorrelation. We do so using the administrative polygon data to avoid errors due to autoreplication associated with the grid. Of course, this clustering is also present in the grid Downstream analysts of either dataset are advised to account for spatial dependence to produce corrected standard errors and unbiased regression coefficients (see for example, Voss et al, 2006). We calculated Global Moran's I (Moran 1950) statistics and Local Indicators of Spatial Autocorrelation (LISA) maps (Anselin 1995).¹⁰ The Moran's I values in Table 3 indicate the strength of spatial autocorrelation for selected regions. In all continents, there is a high degree of spatial autocorrelation—that is, greater than 0.50. In the map in Figure 5, units are placed in one of four categories if their LISA values are significant at 5% after 9999 iterations in Geoda software (Anselin et al. 2006). LISA maps identify clusters of mortality regimes. High-high clusters indicate places of high IMR surrounded by neighbors with high IMR. Low-low clusters are defined analogously. High-low and low-high clusters are (respectively) high and low spatial outliers, places with neighbors of an opposing mortality regime. The remaining units are neither high nor low IMR clusters (but could either be mid-range IMR clusters or moderately opposing IMR regimes).

Table 3. Moran's I for selected regions.

region	I
Global	0.7533
Africa	0.6837
Asia	0.5976
Eurasia	0.6013
South America	0.8781
North America	0.6510
Mexico	0.5402

Figure 5.

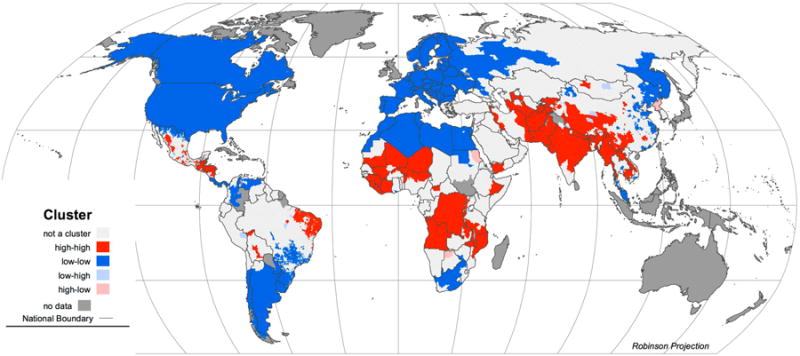
Lisa plot: Global

When the whole world is considered together (Figure 5), virtually all of Africa is a high mortality cluster, along with a swath of Asia extending in a band of varying width from northern Uzbekistan to central Vietnam. Only parts of northeastern Brazil and one province of Bolivia stand out as significant high-high clusters in the Americas. North America, Europe, the southern cone of South America, and much of coastal China constitute the majority of the largest low-low clusters, not surprisingly. China also has the highest concentration of low-high and high-low clusters. Even among the countries identified as the top six contributors to global infant mortality by the study of Black and colleagues--India, Nigeria, China, Pakistan, Congo (DRC) and Ethiopia--mortality is clustered differentially. In China, for example, all four kinds of clusters coexist, though low-low and high-high dominate in the northeast and southwest, respectively.

Only when the rest of the world is excluded are more significant subnational patterns seen in Africa, with low mortality clusters in the north and south extending as far inward as Sudan and Zimbabwe, respectively, as shown on the continental LISA map in Figure 6. Throughout Africa, subnational patterns emerge, and we would expect more to be revealed were subnational data available everywhere: some countries entirely included in the high mortality clusters are represented by national-level data only (e.g., Congo, Cote d'Ivoire, Liberia).¹¹ But even in Nigeria, one of the countries on Black's top-six list, rates of mortality in the somewhat less populous north are higher and more like those in Nigeria's Sahelian neighbors, than the rates in the coastal and more densely populous southern region of the country.

Figure 6.

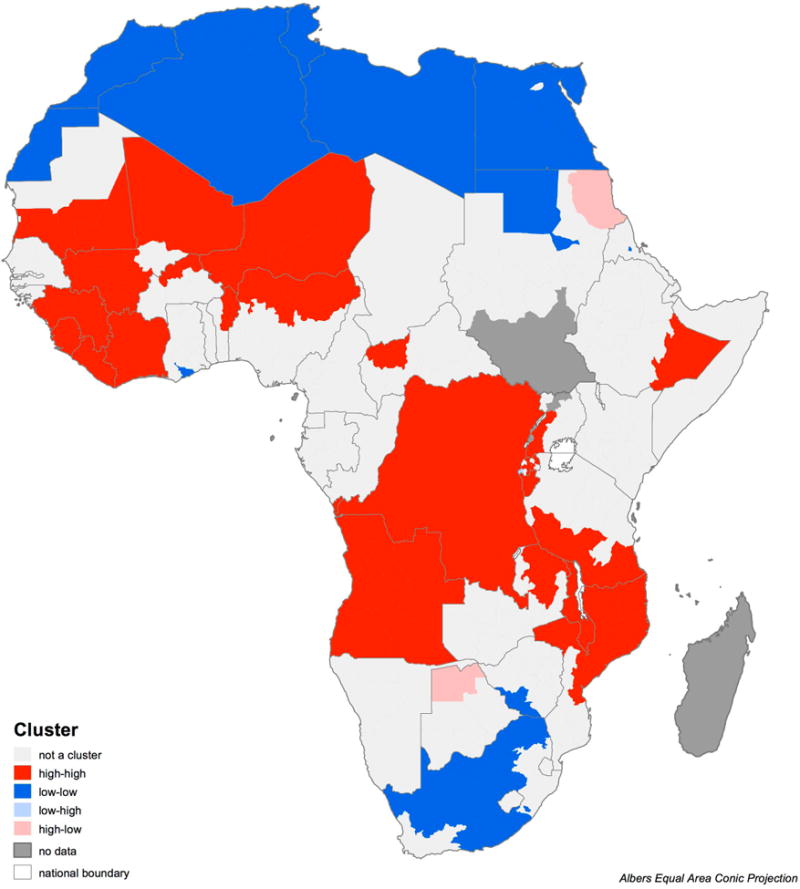
Lisa plot: Africa

The LISA maps also demonstrate that the value of disaggregation can increase beyond the first administrative level. Using the example of Mexico (Figure 7) which has data available for both states (first level) and municipios (second level), it is evident that effective policy targeting would be enhanced by further disaggregation. The first-level data mask clusters of high IMR most strikingly in the southwestern portion of Chihuahua state. The state-level data also mask the analogous low-mortality regimes found along the border with the United States and around Mexico City. State-level data alone could conceivably direct resources away from localities that may have greater needs.

Figure 7.

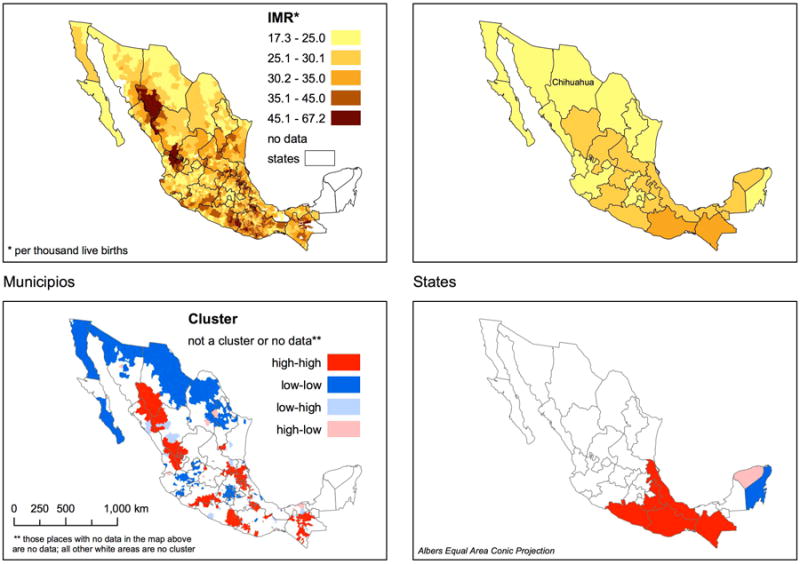
Lisa plots: Mexico

Linking Population to Environment

Why do these spatial patterns matter? Not only does assessment of patterns assist in targeting policy interventions, but spatial delineation of demographic phenomena is a precondition for systematic analyses of spatial co-variation. The challenges associated with such analyses are formidable. In addition to the usual problems associated with linking data from disparate sources and measures, there are computational issues associated with the required matrix multiplication of spatial statistics for large data sets, and the fact that we only have aggregate data for a fundamentally individual phenomenon. In achieving global scope, with increasingly fine subnational units of analysis, we are thus unable to account for individual or family level factors. In the framework of Mosley and Chen (1984), we are limited to community level ecological or economic factors.

While a rich multivariate model exploring the spatial correlates of infant mortality is beyond the scope of the present work, some simple observations about the variation of infant mortality across environmental zones are in order. We view these analyses as illustrative first steps in building a fuller model. Here we consider IMR disaggregated by biome—that is, major habitat type or ecoregion (Olson et al. 2001, Olson and Dinerstein 1998)—and distance to sea-coast. Each can be viewed best as a simple proxy for different aspects of livelihoods, useful because it is related to some measure of interest and because its subnational variation is well measured.

Distance to sea-coast has been previously identified as having strong association with population distribution (Small and Cohen, 2004), GDP per capita (Mellinger et al. 2000, Nordhaus 2006), and disease burden (Sachs and Gallup 2001). Coastal proximity is also used in studies as a proxy for natural access to resources including fisheries, transportation and world markets, and other ecosystem services that have been associated with improving well-being (Alder et al, 2006). These factors, through improved access to markets and services, in turn influence child mortality outcomes (Hill and Pebley 1989, Reher and Sanz-Gimeno 2000). In theory, any of these factors could be measured directly, but no good global data are presently available for any of them. We too therefore consider distance-to-coast as one measure of access.

Biomes are used as a proxy for differences in ecological resources. They represent climate- and vegetation-based resources of the world's ecosystems (Olson and Dinerstein, 1998). Biome maps were constructed for use by conservation biologists (Olson et al., 2001) but have been used more broadly for example in assessing human well-being in different ecosystems (Levy et al., 2005). They are preferred to the simpler combinations of climatic conditions (precipitation and temperature) alone used by Mellinger et al. (2000) and others in studies of well-being because they allow for more complex variation in biological resources that interact with climatic variables (i.e., distinctions among vegetative systems in equally hot and rainy conditions.)

We calculated IMR values for each biome, grouped by continent, using both the present gridded dataset (shown in Table 4) and one based on national IMR values (not shown), both using a 0.25-degree unit of analysis. The two largest biomes in Africa, “tropical and subtropical moist broadleaf forest” and “tropical and subtropical grassland, savanna, and shrubland”, home to over 75% of births in the continent, have remarkably similar rates above the continental average, with several of the remaining biomes much lower. Deserts show strikingly lower rates than in other biomes, but they account for a small share (less than 4%) of all births on the continent and predominate in relatively well-off and oil-rich northern Africa. In Asia, however, deserts—accounting for more than 1/6 of the births—have a higher rate than any other biome. Consistent with global analyses (Levy et al. 2005), deserts similarly experience much higher than average mortality in South America and Europe. A priori expectations that mortality would be higher in resource-poor and water-scarce deserts are largely borne out here. Yet the presence of oil in some desert regions further indicates the necessity to evaluate and account for omitted variables; should a spatial database of mineral resources be available, it could be used in connection with biomes. From national level-statistics, it is not immediately obvious that populations in desert regions experience higher IMR.

Table 4. Infant mortality rates by biome by continent.

	Africa		Asia		South America		Europe		North America		Oceania		Total
Biome	IMR	% of births in continent	IMR	% of births in continent	IMR	% of births in continent	IMR	% of births in continent	IMR	% of births in continent	IMR	% of births in continent	IMR	% of births in continent
Tropical and subtropical moist broadleaf forest	105	24.4%	54	42.2%	28	49.6%			35	11.5%	59	39.7%	60	34.1%
Tropical and subtropical dry broadleaf forest	86	0.3%	67	11.2%	33	5.9%			26	12.5%	18	1.4%	61	7.8%
Tropical and subtropical coniferous forest			71	0.5%					35	12.7%			45	1.1%
Temperate broadleaf and mixed forest			24	20.2%	11	1.3%	9	69.6%	7	27.0%	6	44.4%	19	17.7%
Temperate conifer forest	37	0.2%	56	0.9%			10	3.5%	7	7.1%			30	1.2%
Boreal forest/Taiga			39	0.0%			14	4.7%	5	0.3%			13	0.3%
Tropical and subtropical grassland, savanna, and shrubland	106	50.8%	70	0.5%	22	12.2%			7	1.4%	12	2.2%	100	12.9%
Temperate grassland, savanna, and shrubland			43	2.5%	16	6.5%	19	7.7%	7	9.6%	6	2.9%	28	2.9%
Flooded grassland and savanna	51	4.9%	34	0.3%	19	1.0%	20	0.2%	8	0.6%			46	1.4%
Montane grassland and shrubland	102	8.7%	66	1.1%	40	3.7%	27	0.0%			47	0.4%	90	2.9%
Tundra							12	0.3%	6	0.0%			11	0.0%
Mediterranean forest, woodland, and scrub	35	5.8%	28	1.5%	11	2.1%	6	13.8%	7	4.9%	6	8.3%	23	3.5%
Deserts and xeric shrubland	61	3.7%	76	17.5%	37	15.5%	21	0.1%	19	11.8%	6	0.6%	69	12.8%
Mangrove	112	1.2%	53	1.7%	37	2.2%			25	0.5%	69	0.1%	62	1.4%
Total	97	100.0%	53	100.0%	28	100.0%	10	100.0%	18	100.0%	27	100.0%	57	100.0%

Some of the smaller biomes—especially those found on most or all continents—exhibit clear and consistent patterns. “Montane grassland and shrubland” and mangroves have much higher than average mortality on nearly all continents where they are present. Such biomes, in part because they are small, are likely lost in a national-level non-spatial view of mortality, but with this view it becomes apparent that are distinguishable. Both types of lands could be considered relatively marginal from human livelihood perspective, thus the potential for higher rates of mortality. Similarly, “flooded grasslands and savannah” have lower IMR than average in all continents (except in Europe), perhaps because these regions are hospitable to agriculture and raising livestock. Of course, establishing truly causal mechanisms between biomes and mortality would require further analysis.

When this analysis is done with national-level IMR data, there are striking differences, especially in Asia, where the IMR for “temperate broadleaf and mixed forest” increases by more than 25%. In the same reanalysis, IMR in South American deserts decreases by over 20%, because of muted correlation with high rates in northeastern Brazil. While the presence of different biomes in a country will have implications for its economic diversification, one's local biome is more likely to have a direct impact in terms of agricultural livelihoods.

Coastal proximity also shows several clear patterns. Figure 8 shows IMR by continent and by distance between grid-cell centroid and the nearest sea-coast in deciles.¹² In Africa and Asia, IMR is positively correlated with distance to coast; though the farthest decile has somewhat lower IMR than the next two in Africa and five in Asia. In both of these continents, the tenth decile has far fewer cells, and includes portions of some relatively advantaged (in economic terms) locations, such as oil-rich Northern African nations. It is not news that remote locations experience higher mortality in poor, but this is strong evidence reconfirming that finding. As with biomes, further study on causality is warranted.

Figure 8.

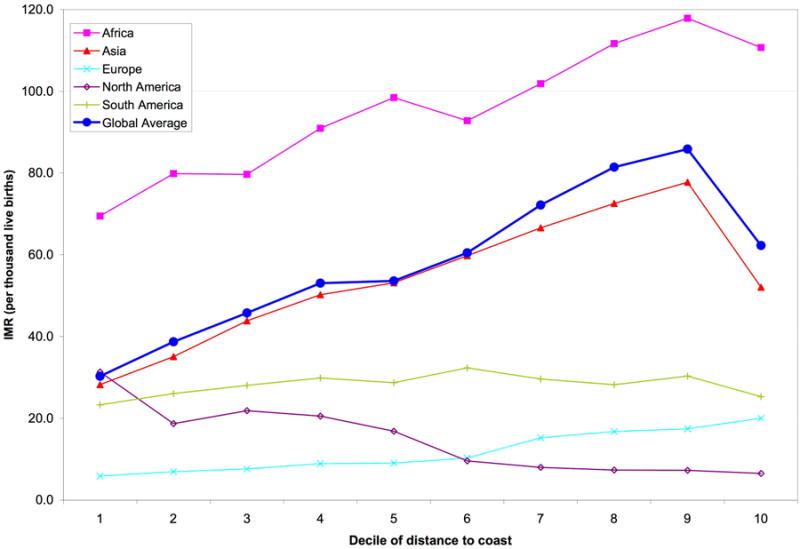
IMR by continent by decile of distance to coast

In South America and Europe, the relationship is for the most part flat or weak. In North America, it is opposite from expected. This result for North America is likely explained by its compositional nature: poor North American countries are much smaller and more disproportionately coastal than the large North American countries, Canada and the United States, whose subnational distributions are also significantly narrower than their neighbors'. In South America, the top two to three deciles are almost entirely in Brazil, a relatively wealthy country and the one with by far the highest resolution data on the continent. The fact that any positive effects of coastal proximity are less or not at all apparent in North America and Europe is consistent with our prediction that environmental factors would have little explanatory power in developed countries. The South American result is more surprising, but may serve as a reminder that in the analysis of any spatial data, resolution (or as in this case, the underlying resolution of the input data) matters. The transformation to a uniform grid does not alter that, and users must be mindful of these limitations. But as we seek finer inputs and transform them so that they may used easily in combination with other spatial data, it becomes possible to discern patterns associated with underlying geographic or locational features from those of data collection and resolution

Conclusion

This analysis has shown that subnational patterns of infant mortality are distinguishable from national-level and coarser subnational patterns. Spatial clustering in mortality rates is more prominent, though it varies a great deal by region. Lastly, there are strong patterns in biophysical or geographic correlates of mortality, some of which are partially obscured by national data.

There is ample room for future work in the analysis of spatial patterns, correlates and determinants of mortality and related socio-demographic characteristics, especially from regional and global perspectives. Some analytical work already underway will consider multivariate relationships between IMR and potential biophysical determinants, including elevation, climate and soils. Yet the possibilities for integration with other spatial phenomena—including those which are not environmental in nature (such as health districts, clinic locations, or road networks)—are vast. The IMR data used in this analysis are publicly available.¹³

Another area of future work is further data development. Clearly subnational infant mortality data with greater consistency (i.e., reconciling across methods of IMR calculation and across years of observation) and of higher resolution across all countries would be ideal. Higher-order subnational units of the kind we have here for Mexico, Brazil and China would be ideal where population sizes are large enough to generate stable rates.

Even using the coarse survey regions described here, mapping other indicators may provide significant insights with relatively little effort. The methods required to develop this dataset are largely transferable to other similarly well-defined indicators such as those describing fertility or anthropometric status. While reporting regions for IMR are occasionally coarser than those for other rates, they are usually the same in the major international household surveys, and so the same data aggregation techniques and GIS boundary data can be used to map them. Under-nutrition, believed to be the underlying cause of a substantial proportion of child deaths (Black et al. 2003), has already been georeferenced—as estimates of underweight (CIESIN 2005b) and stunted (FAO 2004) children—though means for scaling across survey years have not yet been developed so that these data represent a period of observation rather a single target year. Work on other indicators such as immunization rates and access to safe water has not progressed as far, in part because of differences in definition across surveys, but an increasing number are available online via DHS' StatMapper Service (http://statmapper.mapsherpa.com/). They are critical for establishing equity especially within the framework of the United Nations Millennium Development Goals and other development objectives.

With investments in the geospatial data to accompany historic surveys, changes occurring at a subnational scale—both in terms of the survey regions and associated biophysical or spatial characteristics (e.g., drought, infrastructure)—can be modeled over time, to reconsider classical demographic issues in a new light and investigate new ones.